Rheological changes in melts and magmas induced by crystallization and strain rate

Francesco Vetere; Gianluca Iezzi; Diego Perugini; Francois Holtz

doi:10.5802/crgeos.125

Avertissement : cette traduction est mise à la disposition du public dans le but d'élargir la diffusion scientifique de l'article original, mais n'a été vérifiée ni par les auteurs (à moins que leurs noms figurent parmi ceux des auteurs de la traduction) ni par l'équipe éditoriale de la revue. Cette version n'engage pas la responsabilité scientifique des éditeurs. La version originale reste la seule version scientifique de référence.

Changements rhéologiques dans les liquides et les magmas induits par la cristallisation et le taux de déformation
Titre original : Rheological changes in melts and magmas induced by crystallization and strain rate

Francesco Vetere ^1,^2,³ ; Gianluca Iezzi ^2,⁴ ; Diego Perugini ⁵ ; Francois Holtz ³

¹ Dipartimento di Scienze Fisiche, della Terra e dell’Ambiente (DSTA) Università di Siena 53100, Siena, Italy
² Dipartimento di Ingegneria & Geologia (InGeO), Università G. D’Annunzio di Chieti-Pescara, Via dei Vestini 31, 66100, Chieti, Italy
³ Institut of Mineralogy, Leibniz Universität Hannover, Callinstrasse 3, 30167 Hannover, Germany
⁴ Istituto Nazionale di Geofisica e Vulcanologia, INGV, Via di Vigna Murata 605, 00143, Roma, Italy
⁵ Department of Physics and Geology, University of Perugia, Piazza Università 1, 06100 Perugia, Italy

Article du numéro thématique : Le verre, un matériau omniprésent

Traduit par :

Romain Dziegielinski ^a

^a

Traduction du résumé

Cette étude met en évidence les variations rhéologiques et les proportions de phases induites par les événements de refroidissement de la température superliquide (fonte) aux températures subliquidus. Elle fournit une vue d'ensemble de la réponse rhéologique des systèmes magmatiques soumis à un refroidissement dynamique et à une déformation par cisaillement. Les deux paramètres principaux qui sont importants pour modéliser les propriétés rhéologiques de ces systèmes cristallisants et qui sont simultanément peu étudiés jusqu'à présent sont la cristallisation et les vitesses de déformation. La réponse à des taux de déformation relativement élevés se traduit par un comportement de rhéofluidification dans les systèmes partiellement cristallisés soumis à un taux de cisaillement variable et doit être prise en compte dans les processus magmatiques. En raison de la lenteur de la cristallisation des matières fondues riches en SiO, les données sont principalement disponibles pour les systèmes mafiques, ce qui ne permet pas une réévaluation générale. Une tentative de modélisation des données bibliographiques disponibles pour les systèmes moins évolués dans des scénarios dynamiques et une comparaison avec l'approche de l'algorithme MELTS (conditions d'équilibre thermodynamique) sont fournies. Étant donné qu'il est difficile de comparer les données expérimentales obtenues à l'aide de différentes méthodologies, nous nous concentrons principalement sur les données obtenues à l'aide de la technique du cylindre concentrique. Cela souligne le fait qu'un protocole expérimental général est nécessaire pour comparer et modéliser les données de viscosité afin de prédire l'évolution rhéologique dynamique des roches volcaniques.

Compléments :
Des compléments sont fournis pour cet article dans le fichier séparé :

crgeos-125-suppl.pdf

Métadonnées de la traduction

Traduction mise en ligne le : 2023-12-11

DOI : 10.5802/crgeos.125-fr

Mot clés : Viscosité, Nucléation et croissance des cristaux, Rhéologie du magma, Taux de refroidissement, Modélisation

Licence :

CC-BY 4.0

Droits d'auteur : Les auteurs conservent leurs droits

@article{CRGEOS_2022__354_S1_227_0,
     author = {Francesco Vetere and Gianluca Iezzi and Diego Perugini and Francois Holtz},
     title = {Rheological changes in melts and magmas induced by crystallization and strain rate},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {227--248},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {354},
     number = {S1},
     year = {2022},
     doi = {10.5802/crgeos.125},
     language = {en},
}

TY  - JOUR
AU  - Francesco Vetere
AU  - Gianluca Iezzi
AU  - Diego Perugini
AU  - Francois Holtz
TI  - Rheological changes in melts and magmas induced by crystallization and strain rate
JO  - Comptes Rendus. Géoscience
PY  - 2022
SP  - 227
EP  - 248
VL  - 354
IS  - S1
PB  - Académie des sciences, Paris
DO  - 10.5802/crgeos.125
LA  - en
ID  - CRGEOS_2022__354_S1_227_0
ER  -

%0 Journal Article
%A Francesco Vetere
%A Gianluca Iezzi
%A Diego Perugini
%A Francois Holtz
%T Rheological changes in melts and magmas induced by crystallization and strain rate
%J Comptes Rendus. Géoscience
%D 2022
%P 227-248
%V 354
%N S1
%I Académie des sciences, Paris
%R 10.5802/crgeos.125
%G en
%F CRGEOS_2022__354_S1_227_0

Romain Dziegielinski.  Changements rhéologiques dans les liquides et les magmas induits par la cristallisation et le taux de déformation (2023) doi : 10.5802/crgeos.125-fr (Francesco Vetere; Gianluca Iezzi; Diego Perugini; Francois Holtz. Rheological changes in melts and magmas induced by crystallization and strain rate. Comptes Rendus. Géoscience, Volume 354 (2022) no. S1, pp. 227-248. doi : 10.5802/crgeos.125)

Traduction du texte intégral (Proposez une traduction dans une autre langue)

1. Introduction

Le comportement rhéologique des liquides silicatés et des magmas est d'une grande importance pour comprendre comment ils se forment, se déplacent et se déposent à l'intérieur et à la surface de la Terre. Un rôle particulier dans l'évolution magmatique est exercé par le(s) degré(s) de surfusion des liquides/magmas ; il est défini comme la différence entre la température du système et la température à laquelle une phase sature dans le liquide donné [Kirkpatrick 1981; Giuliani et al. 2021]. D'un point de vue thermodynamique, l'apparition de phases solides à partir d'un magma est déterminée par le degré de surfusion. Cependant, la nucléation et la croissance des cristaux d'une phase minérale sont également régies par des processus cinétiques [Lofgren 1980 ; Dowty 1980 ; Hammer 2008 ; Iezzi et al. 2008, 2009 ; Vetere et al. 2013, 2015 ; Giuliani et al. 2020a, b]. La variation globale du taux de nucléation s'étend sur plusieurs ordres de grandeur, tandis que la variation des vitesses de croissance est plus limitée [Swanson 1977 ; Kirkpatrick 1981 ; Lasaga 1997 ; Cashman 1988 ; Hammer et Rutherford 2002 ; Zhang 2008 ; Iezzi et al. 2009 ; Mollo et Hammer 2017 ; Giuliani et al. 2020a]. Pour une composition chimique du magma similaire, un faible taux de nucléation produit peu de cristaux qui deviendront grands, tandis qu'un taux de nucléation élevé se traduira par un grand nombre de minuscules cristaux [Hammer 2008 ; Iezzi et al. 2009 ; Higgins 2006 ; Mollo et Hammer 2017]. La nucléation est favorisée dans les liquides silicatés à forte diffusion chimique, c'est-à-dire pauvres en SiO₂ et riches en H₂O, tandis que les liquides pauvres en SiO₂ et en H₂O sont moins favorables à la nucléation et ont tendance à se vitrifier [Iezzi et al. 2009 ; Vetere et al. 2015].

Les processus de nucléation et de cristallisation ont des implications profondes sur la rhéologie des magmas et des laves, qui dépend de la quantité volumétrique de phases solides ainsi que de leur taille et de leur forme [Gonnermann et Manga 2007]. Par conséquent, une connaissance claire des processus de nucléation et de cristallisation entraînés par la solidification, soit par refroidissement, soit par dépressurisation induite par le dégazage, est la clé pour comprendre la rhéologie du magma et son évolution avant qu'il ne se transforme en une roche solide.

Le style éruptif des volcans est fortement affecté par les propriétés viscoélastiques du magma [Dingwell 1996 ; Gonnermann et Manga 2007 ; Cassidy et al. 2018, et référence incluse] et, comme le montrent Petrelli et al. [2018], par leurs échelles de temps associées. En effet, les conditions P-T-fO₂ pour une composition magmatique de départ (X) déterminent son comportement de solidification et son évolution rhéologique [Lanzafame et al. 2013, 2017].

La cristallisation dans des conditions cinétiques imposées 𝛥T∕𝛥t et/ou 𝛥P∕𝛥t a été étudiée expérimentalement et principalement pour des compositions mafiques jusqu'à présent [Arzilli et al. 2019 ; Polacci et al. 2018 ; Hammer 2008 ; Conte et al. 2006 ; Fiege et al. 2015, et référence incluse], tandis que les fluides magmatiques hautement évolués sont plus difficiles à étudier expérimentalement (chronophages), en particulier dans des conditions sèches [Vetere et al. 2013, 2015]. De nos jours, il est reconnu que des conditions de déséquilibre se produisent souvent dans les processus naturels [Kolzenburg et al. 2018 ; Vetere et al. 2019, 2021, et référence incluse]. De plus, des ambiguïtés persistent dans notre compréhension de l'interaction entre la nucléation et la croissance des cristaux sur la variation rhéologique du magma (viscosité et masse volumiques apparentes) à mesure qu'il évolue de la température de liquidus à la température de transition vitreuse, T_g. La vitesse de refroidissement et la vitesse de dégazage induites par la dépressurisation des blocs magmatiques influencent les caractéristiques texturales, pétrologiques et géochimiques, ainsi que le comportement volcanique, allant de l'effusion de lave d'intensité modérée jusqu'à l'extrême violence de l'éruption explosive [Armienti 2008 ; Hammer 2008 ; Applegarth et al. 2013 ; Shea et Hammer 2013 ; Fiege et al. 2015 ; Mollo et Hammer 2017 ; Arzilli et al. 2019, et références incluses].

En raison des changements dans la chimie des liquides résiduels et la croissance de la phase solide (lorsque le liquide se solidifie en dessous de la température de liquidus, T_L), on s'attend à ce que les propriétés telles que la viscosité et la masse volumique apparentes varient, avec un impact significatif sur la capacité du magma à se déplacer [Giuliani et al. 2021]. Pour avoir une vue d'ensemble de ce scénario naturel et en raison du manque de données directes de terrain [Chevrel et al. 2019, 2018, 2015], l'approche expérimentale est d'une importance capitale pour mieux comprendre comment le magma se comporte lorsqu'il se déplace à l'intérieur ainsi qu'à la surface de la Terre.

Dans cet article, après une discussion générale sur la nucléation et la croissance des minéraux dans les liquides silicatés et les magmas et sur les lois générales et les modèles les plus utilisés régissant la rhéologie du magma, nous nous concentrerons à la fois sur les données expérimentales récentes sur les systèmes naturels/synthétiques et sur l'approche numérique dans le but d'examiner les différences entre les conditions d'équilibre et de déséquilibre sur la solidification des compositions mafiques et leur impact sur le comportement rhéologique. Plus précisément, nous allons contraindre et modéliser les changements rhéologiques induits par le refroidissement et par les contraintes de cisaillement. Les résultats indiquent que les interactions complexes entre les processus de cristallisation et le comportement rhéologique sont la clé pour comprendre le comportement des magmas dans les systèmes naturels. Nous mettrons également l'accent sur les futures approches expérimentales possibles afin de jeter un nouvel éclairage sur ces processus naturels importants qui pourraient être applicables à la solidification induite par la dépressurisation des magmas riches en matières volatiles.

2. État de l'art

Les processus et scénarios pétrologiques sont interprétés et reconstruits principalement en étudiant les propriétés cristallochimiques des phases [Giuliani et al. 2021, 2022]. Cette approche suppose généralement un équilibre thermodynamique entre les liquide magmatiques et leurs phases minérales/volatiles. À partir des lois thermodynamiques, des variables intensives des systèmes magmatiques peuvent être obtenues par le bais de la chimie cristalline des minéraux et des liquides coexistants, de manière à suivre l'évolution des magmas [par exemple, Putirka 2008, et références incluses]. Cependant, nous avons maintenant des preuves manifestes de l'existence de caractéristiques de déséquilibre dans les roches intrusives et surtout volcaniques [par exemple, De Paolo et Getty 1996 ; Roselle et al. 1997 ; Müller et al. 2004 ; Nabelek 2007 ; Baker 2008 ; Mollo et Hammer 2017 ; Giuliani et al. 2021]. La communauté scientifique est donc consciente que les changements de composition des minéraux dans les roches volcaniques ne sont pas nécessairement liés aux conditions d'équilibre, mais plutôt fréquemment à un état de déséquilibre [par exemple, Baker et Grove 1985 ; Hammer 2006, 2008 ; Iezzi et al. 2008, 2011 ; Del Gaudio et al. 2010 ; Mollo et al. 2010, 2011a, b]. Pour une composition chimique globale d'une même coulée magmatique, l'augmentation du degré de sous-refroidissement et du taux de déformation (c'est-à-dire les mécanismes d'étirement et de plissement) induit et facilite progressivement les processus de nucléation et de cristallisation [Swanson et Ottino 1990 ; Perugini et al. 2008 ; Rossi et al. 2019 ; Tripoli et al. 2019] ; à leur tour, ils affectent fortement le comportement rhéologique des magmas qui finissent par remonter des profondeurs et se déposer à la surface de la Terre. Les déformations se produisant dans les magmas dynamiques favorisent la nucléation et la croissance des cristaux ; le mouvement d'un magma alimente de manière continue en ingrédients nouveaux les cristaux à peine formés [Vetere et al. 2020 ; Vetere et Holtz 2020] par rapport à un état statique. Aussi, afin de mieux comprendre la rhéologie des systèmes complexes, un autre aspect important est lié au retard dans la nucléation et la croissance des cristaux qui devient progressivement plus élevé à faible degré de surfusion, c'est-à-dire proche de la température de liquidus [Rusiecka et al. 2020 ; Giuliani et al. 2020b].

La rhéologie est définie comme la science qui étudie la déformation des matériaux dans des conditions bien définies. Comme le défini Mezner [2014], le terme rhéologie (c'est-à-dire la science de l'écoulement) dérivé du mot grec « rhein » qui est équivalent au mot «couler». Appliquée à la volcanologie, la rhéologie des magmas étudie essentiellement l'écoulement des liquides ou des magmas soumis à des contraintes différentes, dans les chambres magmatiques, le long du trajet vers la surface ou lors de l'écoulement à la surface de la Terre ou d'une autre planète (Mercure ou Mars, par exemple). En partant de la définition du magma, cela implique également que le comportement rhéologique dépend principalement des phases présentes dans un système (fluides ± cristaux ± éléments volatils exsolvés et dissous), qui dépendent d'une variété de paramètres tels que la pression, la température et la fO₂ pour un système chimique bien défini. En outre, il est désormais clair qu'un tel comportement peut changer si les phases sont soumises à une certaine contrainte [par exemple, une dépendance au taux de cisaillement ; Vetere et Holtz 2020 et référence incluse]. Dans la description classique des données rhéologiques, afin de paramétrer toute suspension, il est nécessaire de définir clairement la relation entre la contrainte de cisaillement imposée (en Pa) et le taux de déformation par cisaillement ( $\dot{𝛾}$ en s⁻¹ ; c'est-à-dire le taux de déformation). Cette relation peut être utilisée pour caractériser le comportement de l'écoulement et la courbe d'écoulement associée. Le régime d'écoulement est généralement défini comme newtonien lorsqu'il existe une proportionnalité simple entre la contrainte et la déformation :

𝜎 = 𝜂 \cdot \dot{𝛾},

(1)

où 𝜂 (en Pa⋅s) représente la viscosité newtonienne (Figure 1).

Figure 1.
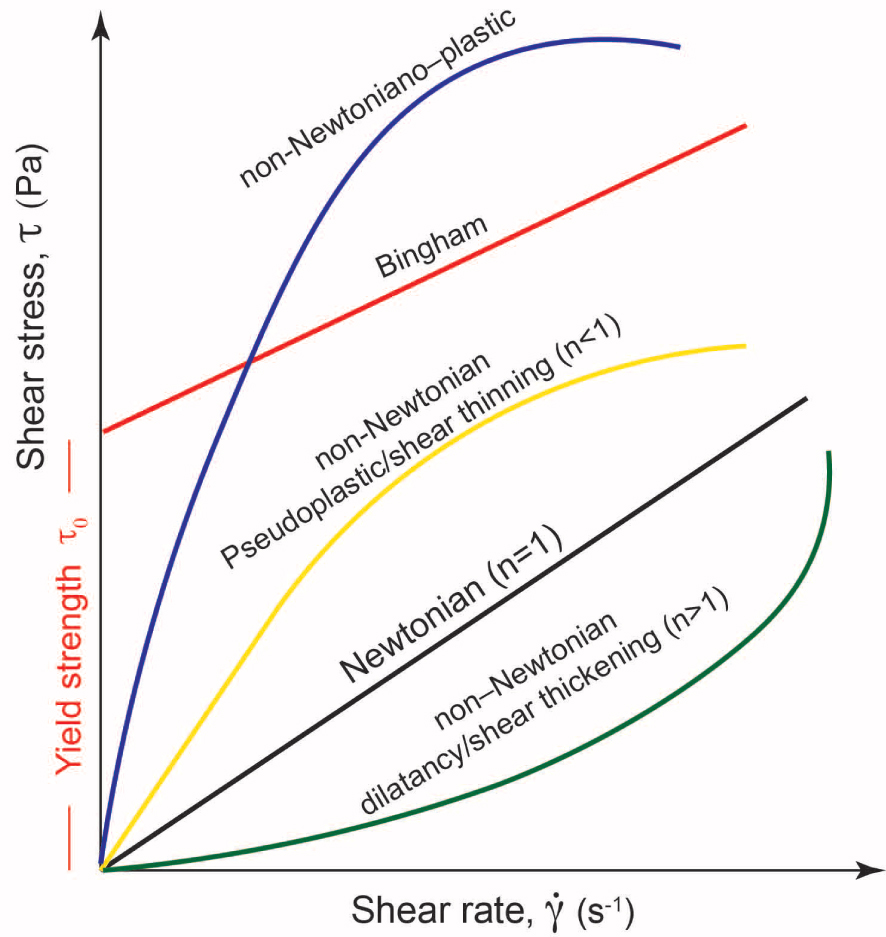
Comportement newtonien et non-newtonien [Lenk 1967]. 𝜏_y est la limite d'élasticité qui doit être dépassée afin d'initier l'écoulement ; n est l'indice d'écoulement décrivant le degré de comportement non-newtonien. Pour les matériaux newtoniens, 𝜏_y = 0, n = 1, et la consistance de l'écoulement K = ; les matériaux rhéoépaississants et rhéofluidifiants sont définis par n > 1 et n < 1, respectivement.

Cependant, dans les systèmes multiphasiques et complexes, tels que le magma, on observe une déviation du comportement newtonien et la contrainte de cisaillement n'est pas simplement proportionnelle au taux de déformation. Les cas suivants sont courants : (1) une contrainte minimale est requise avant que l'écoulement visqueux ne commence (également appelé régime de Bingham) ou (2) les deux comportements ci-dessus sont combinés, ce qui est exprimé par le modèle de Herschel–Bulkley [Herschel et Bulkley 1926] :

𝜎 = 𝜏_{y} + K {\dot{𝛾}}^{n},

(2)

où 𝜏_y est la limite d'élasticité, K est la consistance de l'écoulement et n l'indice d'écoulement (les détails sont présentés dans la figure 1) [Herschel et Bulkley 1926 ; Wildemuth et Williams 1984 ; Mueller et al. 2010 ; Mader et al. 2013 ; Moitra et Gonnermann 2015].

L'apparition d'une rhéologie non-newtonienne dans les liquides silicatés a été étudié par Webb et Dingwell [1990a, b] en utilisant des techniques d'élongation des fibres. Les compositions de liquides choisies sont une rhyolite à haute teneur en silice, une andésite, un basalte tholéiitique et une néphélinite. La viscosité a été déterminée comme le rapport entre la contrainte de traction appliquée et le taux de déformation observé. Comme l'ont rapporté les auteurs, « avant les expériences, chaque fibre a d'abord été recuite à une température pendant une période de 10⁴ s. Ce temps d'équilibrage est supérieur à la fois aux temps de cisaillement et de relaxation volumique d'un liquide, avec 𝜂v = 𝜂 s = 10¹² Pa⋅s et G_∞ (module de cisaillement) ≈ K_∞ (module d'élasticité isostatique) 10 GPa (t_V = t_S = 100 s). » Cependant, les mesures ne comportaient pas de contrôle in situ de la température de l'échantillon et ne tenaient pas compte des effets de l'échauffement visqueux. La figure 2 illustre la réduction de viscosité apparente due à l'effet de l'échauffement visqueux. Comme le rapporte Cordonnier et al. [2012], « les fluides dont la viscosité dépend de la température sont affectés par un échauffement visqueux une fois que cette source de chaleur surmonte la perte de chaleur (c'est-à-dire le transfert de chaleur par conduction, convection et/ou rayonnement) ». Cet effet, malgré l'augmentation des taux de cisaillement, éloigne les magmas de la transition vitreuse [Gonnermann et Manga 2007]. Yue et Bruckner [1996] ont réanalysé les observations sur l'allongement des fibres et ont formulé une correction pour la dépendance de la viscosité au taux de déformation qui inclut explicitement les effets de l'échauffement visqueux. La question de savoir si l'échauffement visqueux peut avoir eu un effet mesurable sur les déterminations antérieures de l'apparition de la viscosité non newtonienne n'est pas définitivement tranchée.

Figure 2.
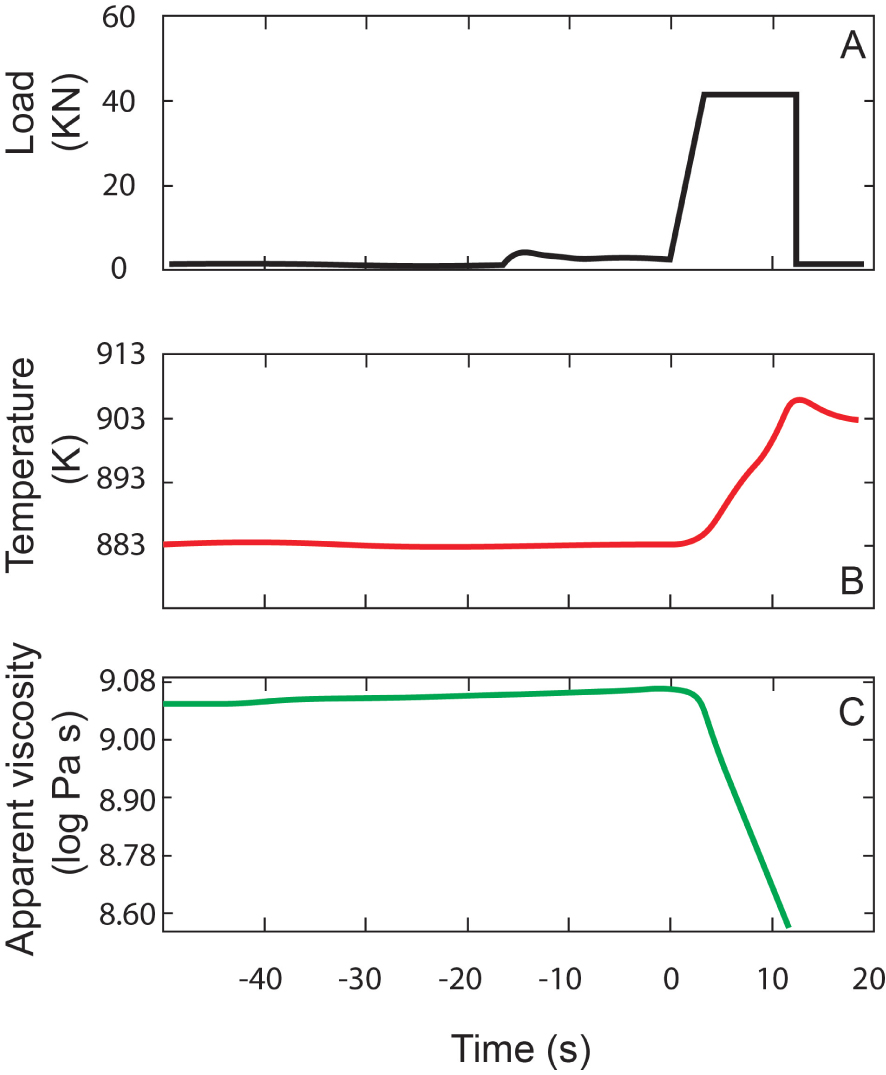
Résultats des mesures de viscosité à l'aide d'un viscosimètre à plaques parallèles sur verre de départ certifié NIST comme indiqué dans Cordonnier et al. [2012]. (A) Charge appliquée à l'échantillon ; (B) en raison de la charge appliquée (lorsqu'elle est suffisamment élevée), la température dans l'échantillon augmente ; (C) à mesure que la température augmente (B) la viscosité diminue. Cette chute de viscosité s'explique par l'augmentation de la température et peut également être prédite par l'équation de Vogel-Tamann-Fulcher [Hess et al. 2007].

Comme les suspensions magmatiques dépendent du taux de déformation et sont donc sensibles à la contrainte de cisaillement appliquée, il est courant de définir la viscosité relative 𝜂_r comme suit :

𝜂_{r} = \frac{𝜂_{app}}{𝜂_{l}},

(3)

où 𝜂_app définit le rapport entre une contrainte donnée à un taux de déformation donné, ce qui signifie que les résultats obtenus ne sont valables que pour des conditions de déformation spécifiques et, par conséquent, varient en fonction du taux de déformation, et 𝜂_l représente la viscosité du liquide. Une attention particulière doit être accordée au fait que la suspension polyphasique se déforme lorsqu'elle est soumise à une contrainte ; pour les magmas, la déformation la plus courante concerne le cisaillement, tandis que d'autres types de déformation comme les comportements oscillatoires, de traction ou de compression sont limités ou même absents [des détails sont donnés dans Dingwell 1995 ; Dingwell et Webb 1989 ; Webb et Dingwell 1990a, b]. Il semble logique que la viscosité d'une suspension est différente de la viscosité du composant liquide. De plus, les phases solides dans les suspensions peuvent varier en termes de volume, de taille et de forme, ce qui peut considérablement affecter la rhéologie du système [Kerr et Lister 1991 ; Mueller et al. 2010 ; Pistone et al. 2016 ; Arzilli et al. 2019 ; Kolzenburg et al. 2020, et référence incluse]. Par exemple, des particules allongées ou aplaties pourraient être présentes dans le magma et opposer une résistance, différente de la contrainte de cisaillement appliquée et, par conséquent, à la capacité de l'écoulement (par exemple, si les axes principaux des particules sont alignés sur la direction d'écoulement, leur influence sur la vitesse d'écoulement est mineure contrairement aux cas où les axes principaux des particules sont orthogonaux à l'écoulement).

Vona et al. [2011] ont fourni une méthodologie pour suivre l'évolution de la viscosité apparente au fur et à mesure des processus de cristallisation. La figure 3a présente une courbe en forme de S où les processus de relaxation, d'incubation, de nucléation et de cristallisation avec un plateau final (indiquant la fin du processus de cristallisation) sont mis en évidence. Cette représentation est confirmée par des données expérimentales pour différentes compositions (comme celles présentées dans le paragraphe suivant). La pente de la courbe est liée à la réponse du liquide lorsque la température est inférieure au liquidus. En d'autres termes, la courbe indique le temps nécessaire à un liquide pour se détendre et commence éventuellement à nucléer une phase solide. Comme on pouvait s'y attendre, les systèmes très fluides réagissent beaucoup plus rapidement que les systèmes plus visqueux, ce qui est clairement mis en évidence dans les figures 3b–d où trois liquides différents avec des compositions variant de l'andésite (composition intermédiaire typique entre le basalte et la rhyolite) au basalte et à la pyroxénite (une roche ignée ultramafique constituée essentiellement de minéraux du groupe des pyroxènes) sont comparés. De toute évidence, si l'on considère les courbes rouges de la figure 3 (par exemple, des expériences effectuées à un taux de cisaillement = 0.1 s⁻¹), la composition de pyroxénite la plus dépolymérisée (figure 3d) réagit plus rapidement (environ 1800 s) que le basalte (env. 2 × 10⁴ s ; figure 3c) et le basalte réagit plus rapidement que la composition andésitique (env. 3 × 10⁴ s ; figure 3b).

Figure 3.
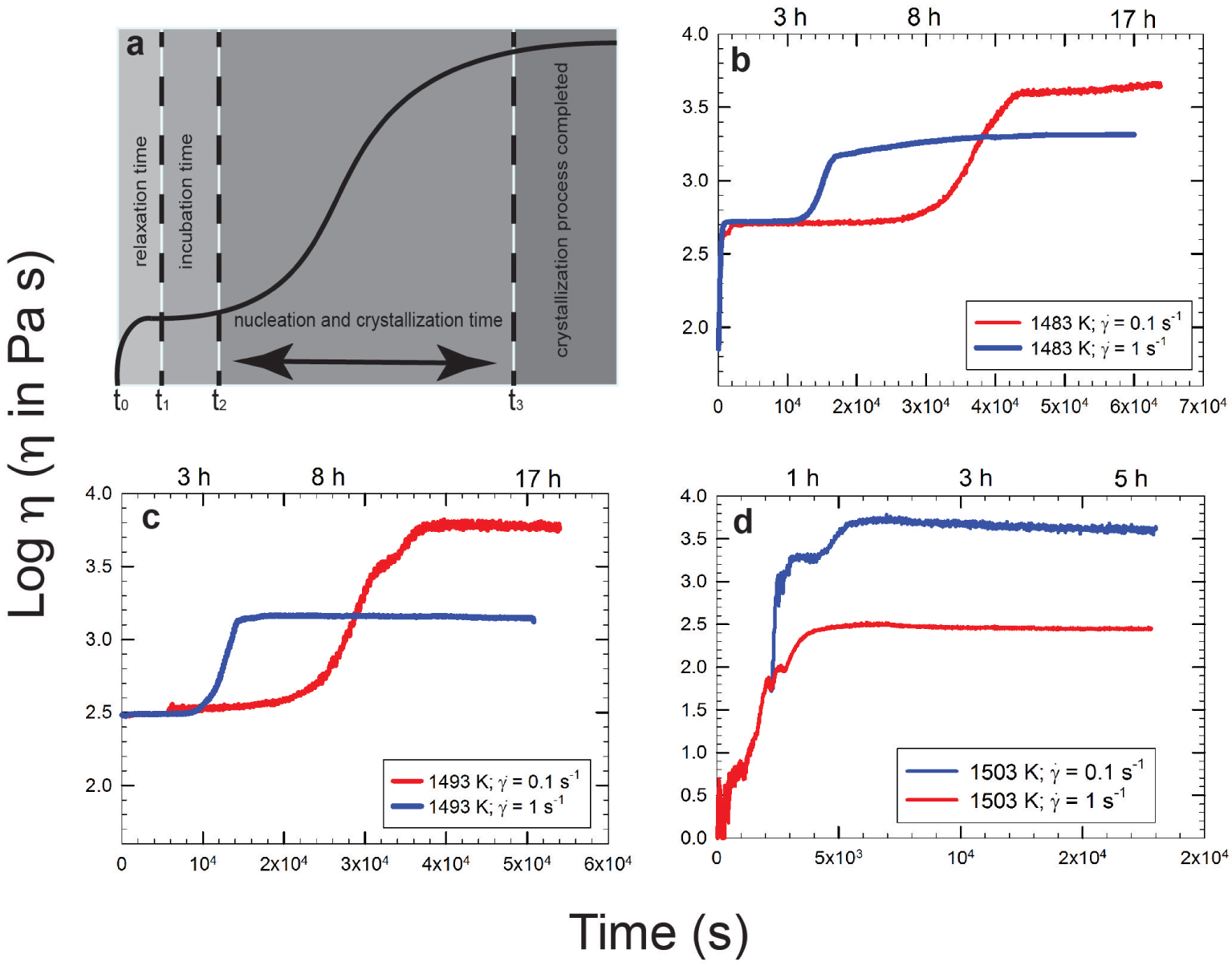
Remarque : Variation apparente de la viscosité en fonction du temps ; (a) redessiné à partir de Vona et al. [2011] tandis que (b–d) sont redessinés à partir de Vetere et Holtz [2020] et se réfèrent à (b) l'andésite des éruptions Calbuco 2015, (c) le basalte de l'Etna de l'éruption de 122 av. J.-C., et (d) la pyroxénite de la coulée de Theo qui est analogue des échantillons de coulée de lave martienne. Les courbes bleue et rouge se réfèrent à des expériences effectuées à un taux de cisaillement de 1 et 0.1 s⁻¹, respectivement. On remarque le comportement de rhéofluidification (la viscosité apparente diminue à mesure que le taux de cisaillement augmente) avec les processus de nucléation et de cristallisation liés aux taux de déformation appliquée (voir le texte pour plus de détails).

La dernière réflexion sur les systèmes partiellement cristallisés concerne l'approche par ce qu'on appelle le coefficient de tassement maximal (𝛷_m) où la viscosité d'une suspension (donc, la capacité d'un système liquide comportant des cristaux à s'écouler) tend vers l'infini et où il peut se produire une transition d'un comportement visqueux à un comportement élastique. _𝛷 dépend de la taille, de la forme et de la distribution des particules et sa valeur au cours d'un écoulement peut changer en raison de l'orientation possible des cristaux relative à la direction de l'écoulement [voir le concept de rhéologie de pourcentage critique de fusion (rheological critical melt percentage), RCMP tel que discuté dans Arzi 1978 et examiné par Rosenberg et Handy 2005].

3. Compositions étudiées

Les compositions globales réexaminées et utilisées dans cette article sont rapportées dans la figure 4 (annexe supplémentaire 1), sur laquelle on effectue un contrôle cinétique des événements de cristallisation, des tests rhéologiques et/ou une modélisation numérique.

Figure 4.
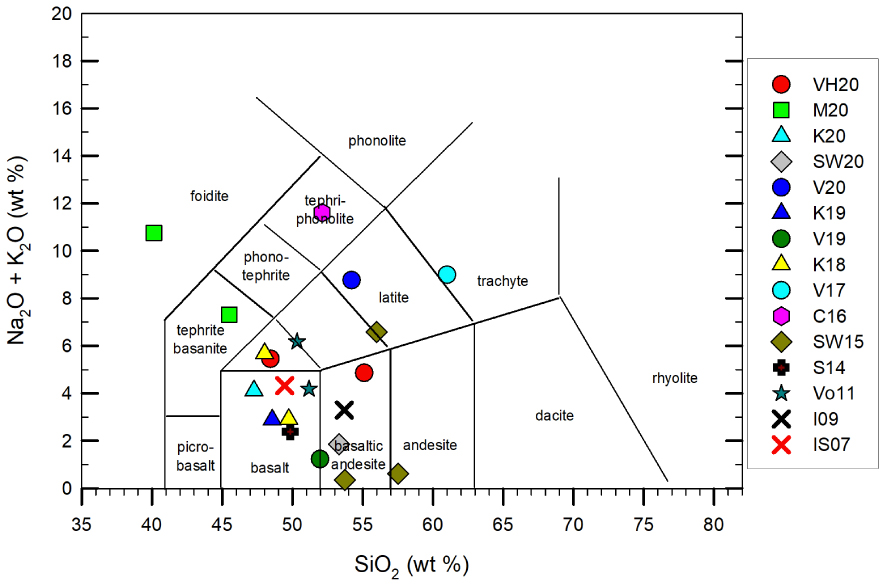
Remarque : Diagramme total des alcalins en fonction de la silice pour les compositions de départ étudiées. VH20 fait référence à Vetere et Holtz [2020] ; V20, 19 et 17 font référence à Vetere et al. [2020, 2019, 2017, respectivement] ; M20 fait référence à Morrison et al. [2020] ; K20, 19 et 18 comme dans Kolzenburg et al. [2020, 2019, 2018, respectivement] ; SW20 et 15 se réfèrent à Sehlke et Whittington [2020, 2015] ; C16 se réfère à Campagnola et al. [2016] ; S14 renvoie à Sehlke et al. [2014] ; Vo11 fait référence à Vona et al. [2011] ; I09 à Ishibashi [2009] et IS07 à Ishibashi et Sato [2007].

Un premier ensemble de données de composition comprend des données expérimentales rhéologiques dans lesquelles la contrainte de cisaillement varie dans des conditions isothermes, idéalement à un degré fixe de surfusion [Morrison et al. 2020 ; Sehlke et Whittington 2020, 2015 ; Vetere et Holtz 2020 ; Vetere et al. 2020, 2017 ; Campagnola et al. 2016 ; Sehlke et al. 2014 ; Vona et al. 2011 ; Ishibashi 2009 ; Ishibashi et Sato 2007]. Cependant, il est important de préciser que les suspensions magmatiques sont des systèmes chimiques complexes, où les phases de cristallisation ont des compositions différentes de celles des liquides d'origine [Iezzi et al. 2020]. Ainsi, même dans des conditions isothermes, le temps de cristallisation détermine un changement dans la composition des phases cristalline et liquide. Le deuxième ensemble de données, bien que très limité, comprend des données rhéologiques dérivées d'événements de cisaillement et de refroidissement agissant sur des liquides silicatés, et représente les scénarios les plus proches des scénarios naturels [Vetere et al. 2019 ; Kolzenburg et al. 2020, 2019, 2018].

Ces deux ensembles de données expérimentales ont été obtenus avec la même méthodologie (c'est-à-dire, avec des cylindres concentriques) et reflètent une gamme de viscosité de 10¹–10⁶ Pa⋅s, donc, des liquides silicatés partiellement cristallisés, où le régime dynamique du magma est dicté par la cristallinité (𝛷). Habituellement, ce régime varie de dilué (où 𝛷 varie entre 0.05 et 0.25 et où les particules ont une interaction faible à modérée, principalement en fonction du rapport d'aspect des particules) au régime semi-dilué (∼ 0.25 〈𝛷〉 ∼ 0.6) où les particules interagissent fortement entre elles avec une orientation possible avec la direction de l'écoulement [Figure 5 ; Hoover et al. 2001 ; Saar et al. 2001 ; Vetere et Holtz 2020]. Les deux régimes définissent des systèmes non-newtoniens avec un comportement de rhéofluidification (faible ou fort, selon 𝛷) avec une évolution possible de la limite apparente d'élasticité (Figure 1). Ces données révèlent l'importance de la dynamique appliquée aux liquides silicatés lors du refroidissement, comme nous le verrons plus loin.

Figure 5.
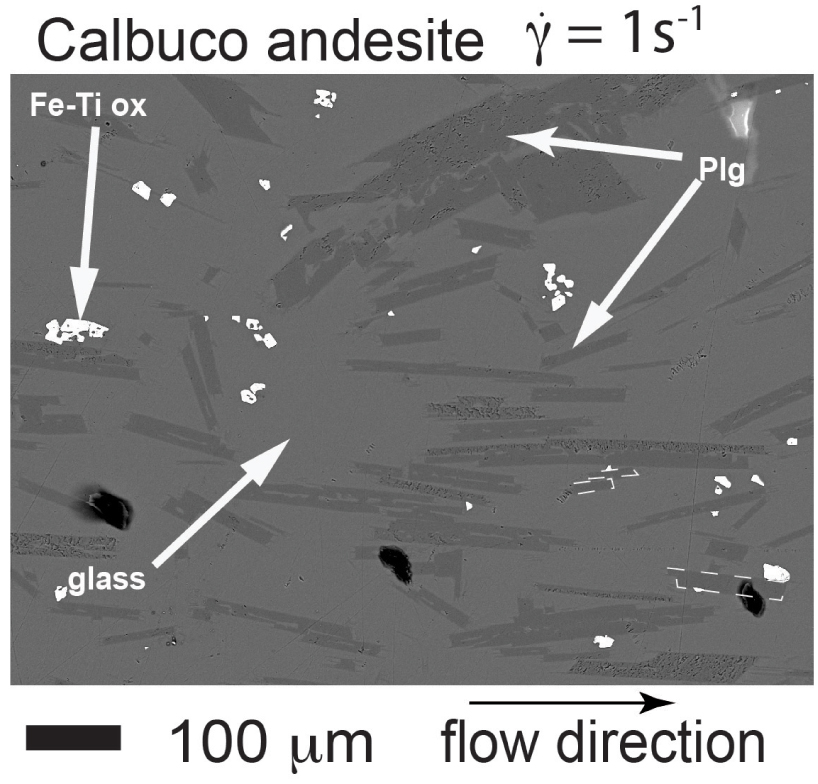
Résultats expérimentaux obtenu à partir d'un cylindre concentrique d'andésite de Calbuco au taux de cisaillement de 1 s⁻¹ et à la température de 1483 K comme dans Vetere et Holtz [2020]. Les phases sont les oxydes de Fe–Ti, le plagioclase (plg) et le verre. On remarque l'orientation du plagioclase (plg) dans la direction d'écoulement.

4. Simulation numérique

Le code AlphaMELTS a été utilisé pour suivre l'évolution de la phase pour les compositions présentées dans la figure 4 lorsque la température diminue, passant des conditions du liquidus au subliquidus. Le logiciel alphaMELTS (V. 1.9) fournit une interface textuelle simple aux versions de sous-programme des algorithmes MELTS, pMELTS et pHMELTS [Asimow et Ghiorso 1998 ; Smith et Asimow 2005 ; Ghiorso et al. 2002 ; Ghiorso et Sack 1995]. Adapté aux systèmes multi-composants, il permet de calculer des assemblages à l'équilibre au cours d'une évolution thermodynamique défini par l'utilisateur (pour plus de détails sur le logiciel, voir l'adresse suivante : http://melts.ofm-research.org/ et https://magmasource.caltech.edu/forum/).

L'évolution des compositions des liquides résiduels est indiquée à la figure 6a et l'évolution de la proportion de liquide en fonction de la température est indiquée à la figure 6b (en % vol). Dans les deux cas, une comparaison directe avec les données de la littérature est fournie. La température de liquidus calculée est également disponible dans l'annexe supplémentaire 1 pour toutes les compositions étudiées. En général, on obtient des valeurs de plus en plus faibles au fur et à mesure que la chimie des systèmes évolue vers des systèmes plus siliciques (teneur plus élevée en SiO₂), comme prévu, vers des conditions d'équilibre pour les liquides modélisés. L'évolution de SiO₂ prédite à la figure 6a pour les échantillons I09, Vo11Stromboli et Vo11Etna, comme pour les échantillons M20NYI et SW15NVP-Na, présente des valeurs plus élevées que les données expérimentales, tandis que le contraire est observé pour l'échantillon S14, M20NYA et, dans les deux cas, les différences deviennent importantes à des températures plus basses. En général, les prédictions des évolutions de l'Al₂O₃ sont plus précises que celles des oxydes de CaO et de MgO, tandis que le FeO^tot est surestimé pour les échantillons M20NYA, C16 et sous-estimé pour les échantillons Vo11Stromboli, SW15NVP et M20NYI, respectivement. La différence entre les données expérimentales et les données prédites par alphaMELTS est particulièrement importante pour les compositions M20NYI et M20NYA. Comme indiqué dans Morrison et al. [2020], cela est lié aux différences de fugacité d'oxygène (les données expérimentales sont obtenues dans des conditions plus réduites). Ainsi, nous nous concentrerons uniquement sur les données rhéologiques pour ces compositions. Les différences observées peuvent être attribuées à deux aspects : (i) la précision héritée des calculs thermodynamiques et (ii) l'apparition de conditions de déséquilibre dans les produits analysés (Figure 6a).

Figure 6a.
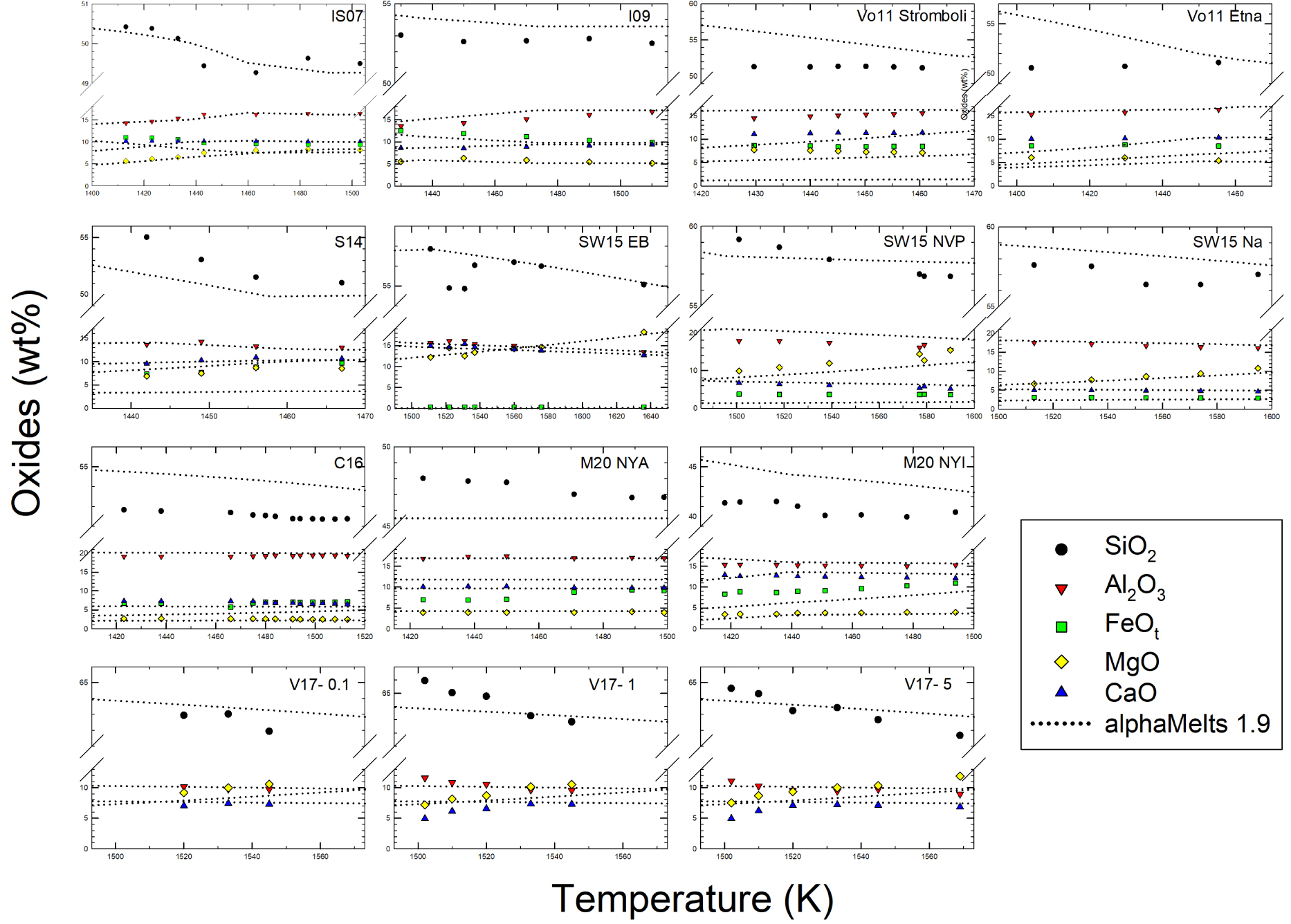
Évolution des liquides SiO₂, Al₂O₃, FeOt, MgO et CaO en fonction de la température lorsque les systèmes se refroidissent à partir de la température du liquidus. Les symboles se réfèrent aux données expérimentales tandis que les lignes pointillées se réfèrent à la prédiction obtenue en utilisant alphaMELTS 1.9. Le titre de chaque diagramme fait référence aux compositions chimiques telles qu'indiquées à la figure 4.

Figure 6b.
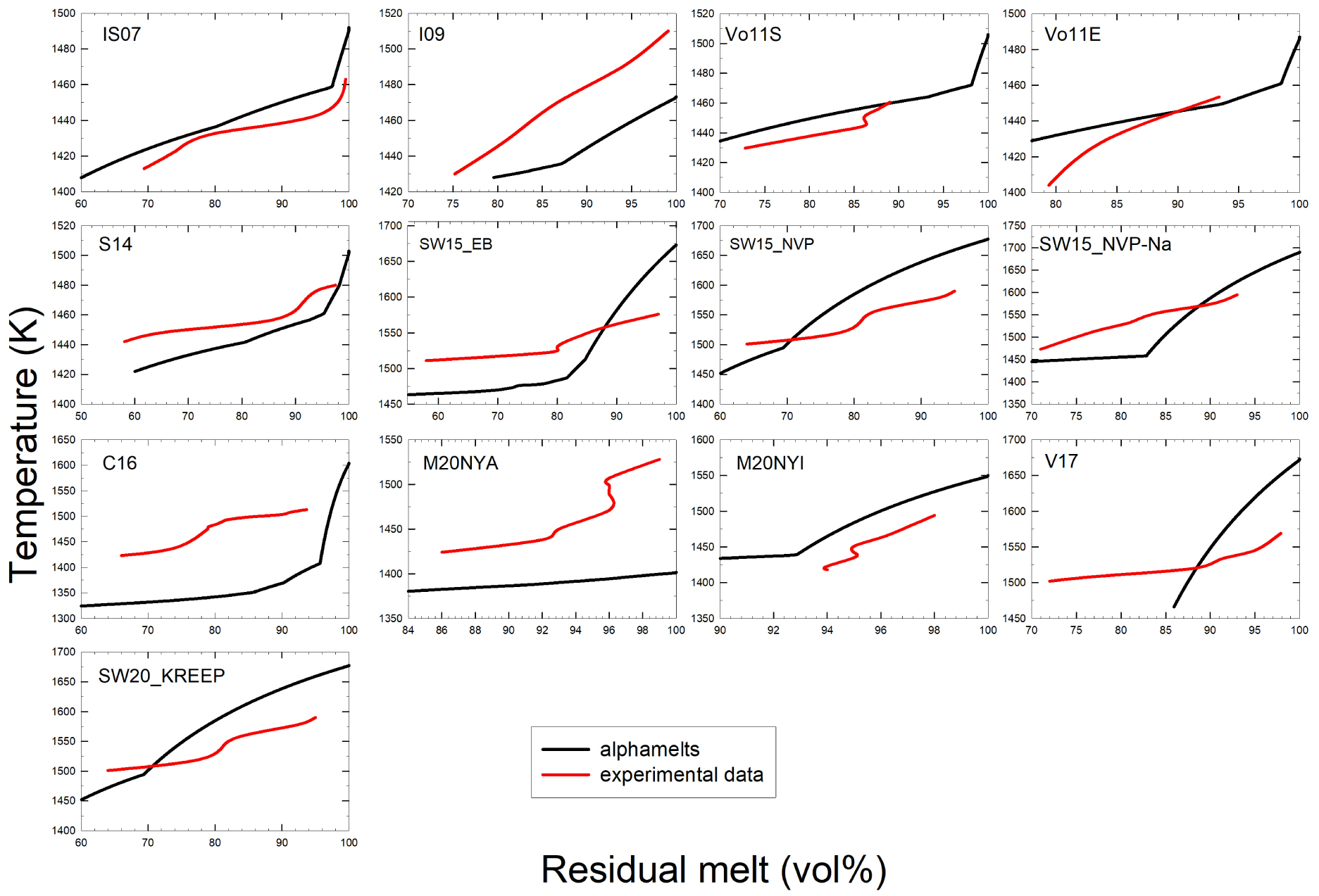
Comparaison du volume de liquide résiduel (% vol) obtenu à partir de données de la modélisation et des données expérimentales. Le titre de chaque diagramme correspond aux numéros d'échantillon fournis dans les figures 4 et 6a. Les courbes rouges se réfèrent aux données expérimentales tandis que les courbes noires sont celles dérivées des résultats alphaMELTS 1.9. Les courbes rouges ajustées aux données expérimentales présentent parfois des formes en S parce que les courbes ont été tracées pour s'adapter exactement aux fractions de liquide déterminées. Cependant, un tel comportement n'est pas réaliste et reflète la grande incertitude dans la détermination du rapport liquide/cristaux. Les données se réfèrent à la pression ambiante.

Figure 6c.
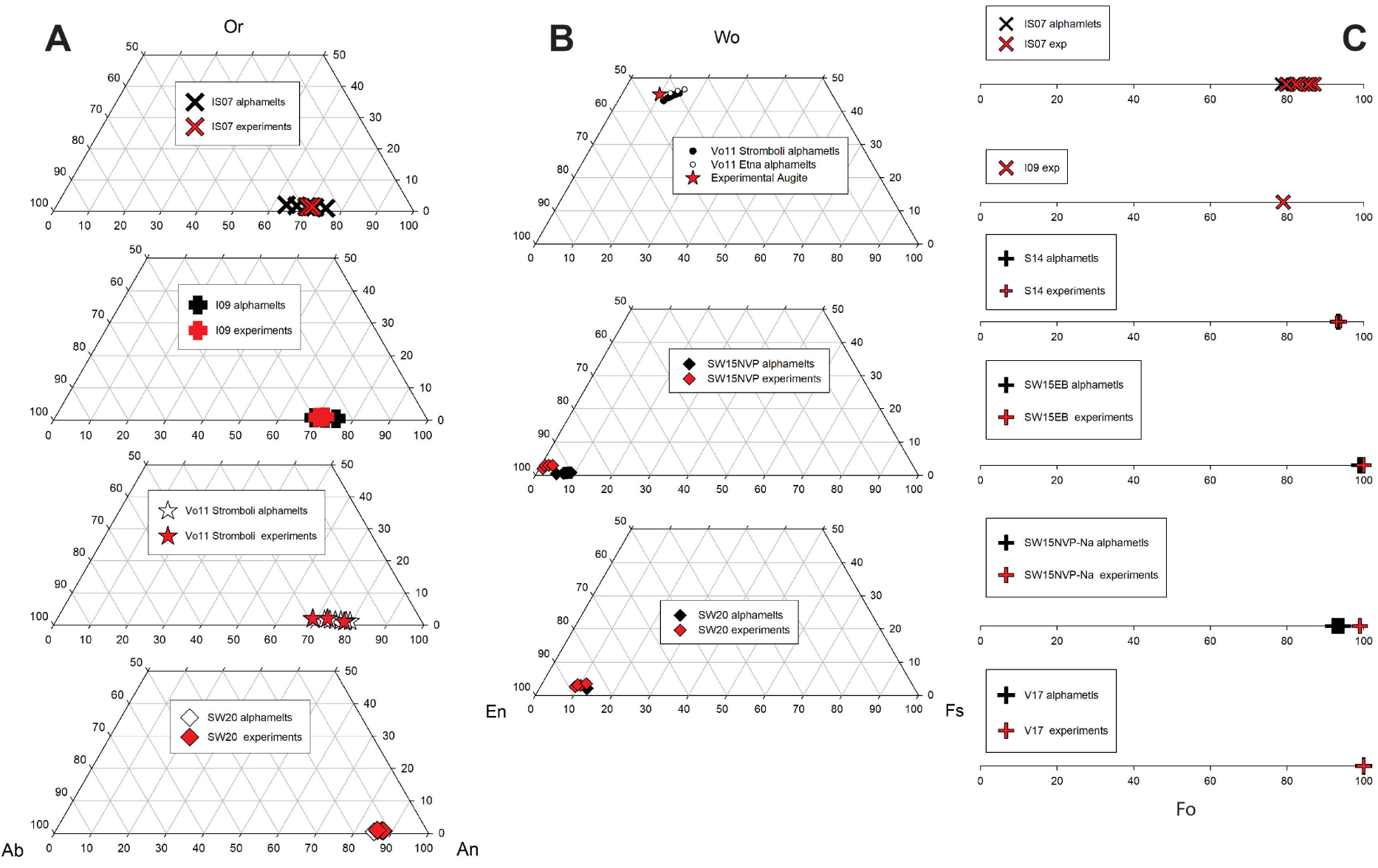
(A) Plagioclase, (B) pyroxène et (C) compositions d'olivine pour certains des systèmes magmatiques étudiés. On remarquera que la gamme de composition des données expérimentales et de la modélisation est similaire.

Figure 6d.
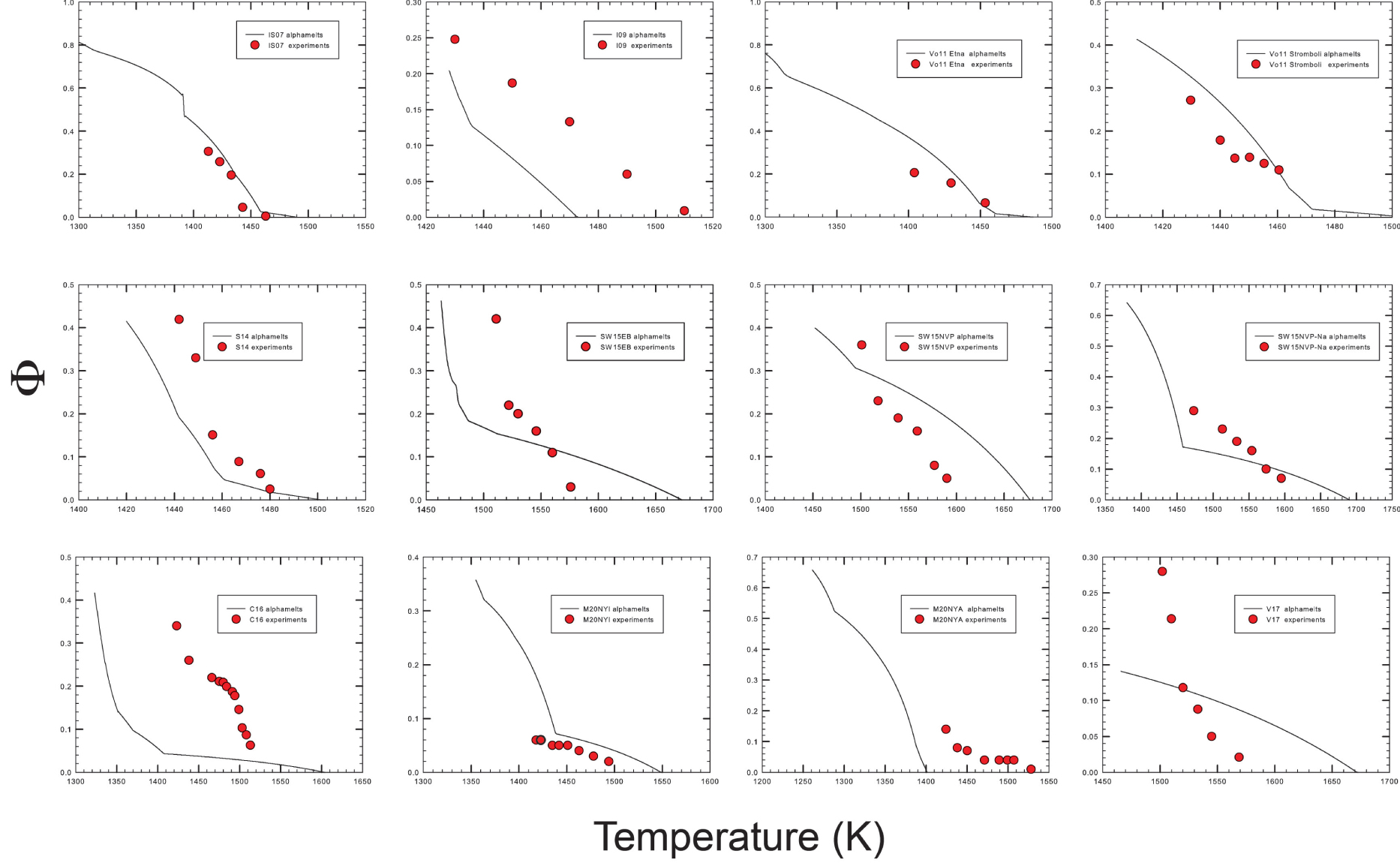
Cristallinité en fonction de la température pour les compositions indiquées dans la figure 4.

Les calculs expérimentaux et thermodynamiques montrent que la fraction liquide diminue avec la température, comme prévu. En général, l'effet très faible de la température sur la cristallinité prédit par les alphaMELTS 1.9 dans le domaine des hautes températures n'est pas reproduit par les données expérimentales (en particulier pour les compositions M20NYA, V17, C16, SW15NVP-Na, SW15_EB, S14 et I09). Dans la plupart des cas, le volume de liquide résiduel est beaucoup plus faible que les volumes prévus et les températures de liquidus extrapolées à partir des données expérimentales sont inférieures aux températures de liquidus prévues. Par conséquent, l'effet de la température sur la cristallinité des produits expérimentaux est plus prononcé que prévu (voir également la figure 6d avec la cristallinité des expériences individuelles).

La composition des phases solides a été compilée à partir des données de la littérature et est présentée dans la figure 6c(A–C). Les compositions de plagioclase (plg), de pyroxène (px) et d'olivine (ol) qui ont cristallisé dans les expériences sont comparées aux compositions prédites avec alphaMELTS 1.9. Les compositions prédites et expérimentales présentent en général une bonne concordance. Ceci indique qu'alphaMELTS 1.9 réussit à prédire les compositions minérales à l'équilibre, mais que la prédiction des proportions des phases est plus problématique, ce qui peut être dû à l'étalonnage du modèle à partir d'expériences statiques. L'application d'une contrainte de cisaillement aux expériences de cristallisation devrait favoriser la cristallisation et réduire le délai précédant la nucléation [Rusiecka et al. 2020 ; Vetere et al. 2021]. Ainsi, les mécanismes possibles pour expliquer cette différence de cristallinité pourraient être liés à l'agitation continue des liquides à taux de cisaillement élevé dans des expériences dynamiques qui rapprochent les « ingrédients alimentant la croissance » nécessaires (éléments nécessaires à la construction d'une structure cristalline) des surfaces des cristaux individuels et qui facilite la croissance cristalline (voir ci-dessous).

5. Modélisation des données expérimentales en faisant varier le taux de cisaillement et la teneur en cristaux

En raison des difficultés inhérentes à la réalisation d'expériences, les données expérimentales disponibles sur les processus de cristallisation dans des conditions dynamiques sont encore relativement rares, comme indiqué ci-dessus. De plus, la rareté des données expérimentales sur les systèmes plus évolués résulte des limites de la technique expérimentale (Figures 6a–6d). En particulier, la gamme de viscosité qui peut être étudiée avec l'appareil le plus courant pour atteindre des valeurs de contrainte et de viscosité élevées (par exemple, 𝜂>10⁶ Pa⋅s) ne couvre pas celle des liquides silicatés à température modérée et même avec de faibles quantités de cristaux. Nous avons recueilli 415 données expérimentales de viscosité dans la littérature (voir les annexes supplémentaires 1 et 2) sur différentes compositions mafiques à intermédiaires à différentes températures, taux de cisaillement, volume de cristaux et rapport d'aspect 2D. Toutes les données ont été obtenues avec la même méthodologie en utilisant un appareil à cylindres concentriques et la majorité montrent une diminution de la viscosité apparente (dans des conditions isothermes) à mesure que le taux de déformation augmente, ce qui indique l'effet bien connu de rhéofluidification comme mentionné ci-dessus.

Outre les données de viscosité, un résultat général pour la plupart des systèmes étudiés est que l'augmentation du taux de déformation favorise une croissance rapide des cristaux. Les expériences de cristallisation dynamique montrent qu'il suffit d'environ 6000 s pour produire environ 22 % de surface de cristaux ayant des longueurs de cristaux de plagioclase d'environ 300 mm, reflétant une valeur des vitesses de croissance de 5 × 10⁻⁶ cm/s [Vetere et Holtz 2020], beaucoup plus rapide que celles rapportées dans la littérature [c'est-à-dire 10⁻⁸–10⁻⁹ cm/s ; Pupier et al. 2008].

Compte tenu du fait que l'eau et d'autres substances volatiles influent sur la rhéologie des liquides silicatés [Fiege et al. 2015, et référence incluse], la vitesse de croissance des cristaux pourrait également dépendre des taux de déformation dans les magmas hydratés dynamiques. La littérature fournit différents modèles généraux capables de reproduire des comportements de viscosité apparente ou relative en fonction de la teneur en cristaux, du taux de cisaillement et du rapport d'aspect des phases solides. La plupart d'entre eux utilisent la viscosité à l'état liquide afin d'obtenir la viscosité relative des suspensions (liquide + cristaux ; voir (3)), en adoptant des modèles de viscosité généraux tels que ceux proposés par Hui et Zhang [2007] ou Giordano et al. [2008]. Une liste des modèles les plus utilisés est fournie dans le tableau 1.

La figure 7 donne un aperçu des données de viscosité relative et certains des modèles fournis dans le tableau 1 sont représentés à des fins de comparaison. Toutes les données expérimentales traitées à des taux de déformation différents montrent un comportement de rhéofluidification (symboles identiques avec la même teneur en cristaux mais différents 𝜂_r la figure 7) et les différences de viscosité relative augmentent en fonction de l'accroissement de l'écart entre un taux de cisaillement faible et un taux de cisaillement élevé. Par exemple, Sehlke et Whittington [2015] montrent que la viscosité NVP-Na varie de 7500 à 1500 Pa⋅s car le taux de cisaillement varie de 0,01 à 5 s^-1 à 1473 K avec une teneur en cristaux de 29 % vol. Vetere et al. [2017] montrent une diminution d'𝜂_app d'environ 10200 à 1100 Pa⋅s à 1502 K et environ 28 % vol de cristal, car le taux de cisaillement varie de 0,1 à 5 s⁻¹ dans les compositions des liquides silicatés synthétiques analogues au mercure (pour plus de détails, se référer à l'annexe supplémentaire 2).

Figure 7.
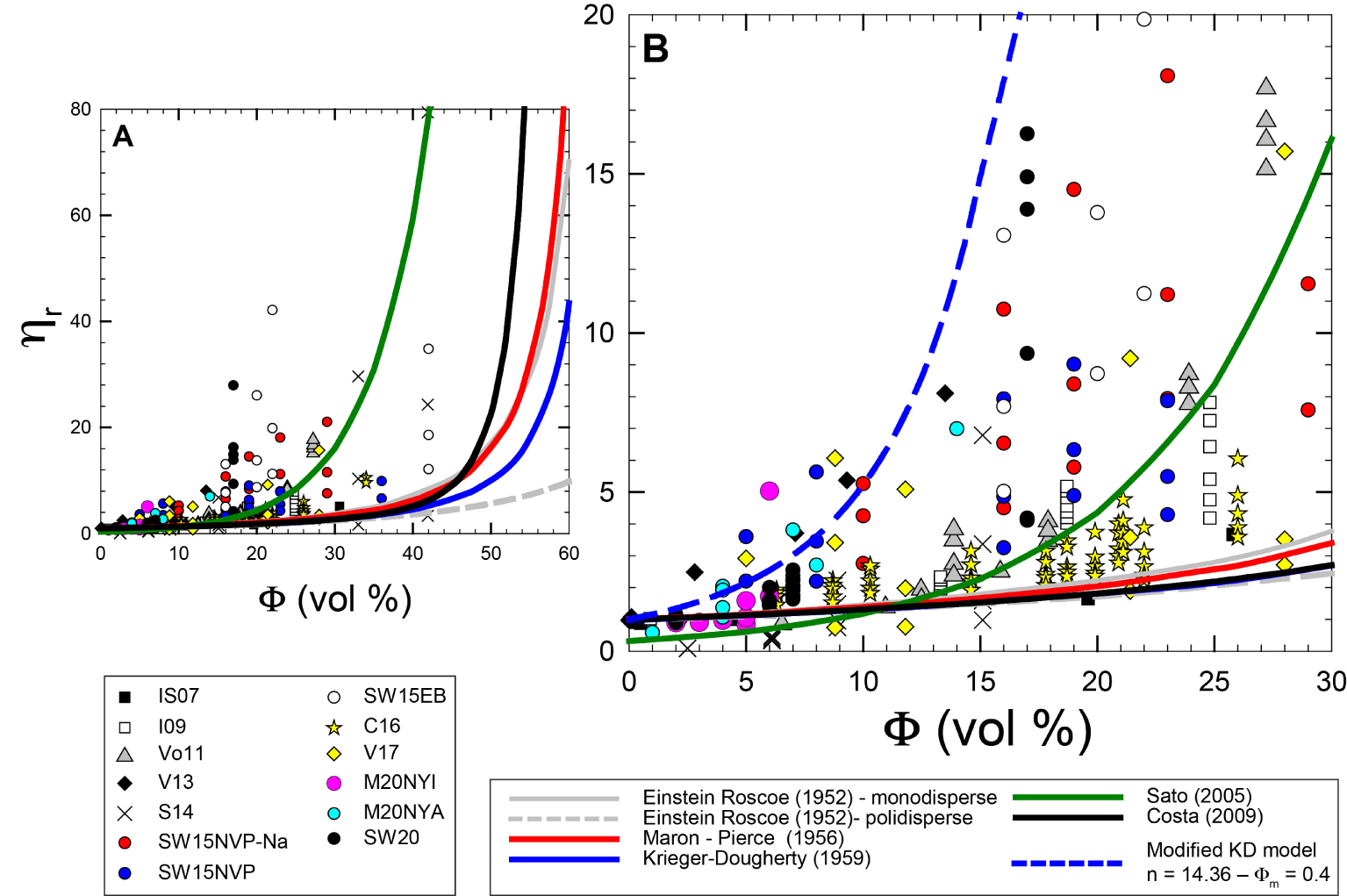
Évolution de la viscosité relative en fonction de la teneur en cristaux en % vol. (A, B) reproduisent des jeux de données identiques avec des échelles différentes afin de mieux apprécier la différence de viscosité relative induite par des taux de cisaillement différents. On notera également que dans (B) une équation KD modifiée [Krieger et Dougherty 1959] capable de reproduire la viscosité relative pour les systèmes de départ précoces tels que ceux déformés à un taux de cisaillement relativement faible.

Aucun des modèles présentés ici ne permet de prédire l'ensemble des données expérimentales. Du fait des différents paramètres utilisés pour la modélisation. Par exemple, le fait que 𝛷_m puisse varier au cours de la déformation en raison de l'alignement possible des particules modifiera évidemment le comportement rhéologique. Et cela, jusqu'à présent, n'est pas prévisible. En outre, l'utilisation de l'analyse d'images pour déterminer les proportions de la phase solide peut conduire à certaines incertitudes et il est nécessaire de disposer d'un ensemble de données statistiquement représentatif d'images BSE sélectionnées le long de différentes orientations de l'échantillon étudié. Ainsi, lorsque l'on utilise peu d'images BSE, AS (AS = axe long/court des cristaux), et les proportions volumiques moyennes pourraient être influencées par l'orientation de la section 2D dans un échantillon avec un réseau cristallin 3D important [Lanzafame et al. 2017]. Idéalement, des données analytiques basées sur des approches tomographiques [Polacci et al. 2018 ; Arzilli et al. 2019] apporterait la solution à ce problème mais, jusqu'à présent, en particulier lors de l'utilisation d'appareils à cylindres concentriques, c'est une tâche très difficile et les techniques doivent être améliorées. La figure 7 montre également qu'il est possible de modifier certains des paramètres utilisés dans une équation afin d'obtenir une meilleure adéquation avec les données expérimentales. C'est le cas, par exemple, du modèle proposé par Krieger et Dougherty [1959] qui pourrait mieux reproduire les données expérimentales en faisant varier les paramètres B et 𝛷_m comme cela est fait dans la figure 7B et le tableau 1. Cependant, un modèle rhéologique plus exhaustif doit englober les transitions rhéologiques d'une faible viscosité, où le régime d'écoulement est principalement celui des liquides en suspension, à un régime de viscosité élevée, où des paramètres tels que la forme, l'orientation et le volume des particules dominent.

	Modèle	Références à la littérature
1	𝜂_r = (1 + B𝜙)	Einstein [1906] ; Système dilué (𝛷< 0,25) B = 2.5
2	𝜂_r = 1 + B𝛷 + B₁𝛷²	Guth et Gold [1938] ; Système dilué (5 < 0.25) et particules sphériques B = 2.5, B₁ = 14.
3	$𝜂_{r} = {(1 + \frac{1.25 𝛷}{1 - \frac{𝛷}{𝛷_{m}}})}^{- 2}$	Eilers [1941, 1943]
4	$𝜂_{r} = e^{\frac{B 𝛷}{1 - 𝛼 𝛷}}$	Vand [1948]
5	𝜂_r = 1 −𝛼𝛷^−B	Roscoe [1952] ; 𝛼 = 0.135, B = 2.5
6	$𝜂_{r} = {(1 - \frac{𝛷}{𝛷_{m}})}^{- 2}$	Maron et Pierce [1956]
7	$𝜂_{r} = {(1 - \frac{𝜙}{𝜙_{m}})}^{- B 𝜙_{m}}$	Krieger et Dougherty [1959]
8	$𝜂_{r} = {(1 - \frac{𝜙}{𝜙_{m}})}^{- B 𝜙_{m}}$	Krieger et Dougherty [1959] ; B = 2.5 pour les particules sphériques ; pour les particules allongées, B pourrait être modifié
9	$𝜂_{r} = exp \{[{(2.5 + \frac{𝜙}{𝜙_{m} - 𝜙})}^{𝛼}] \cdot \frac{𝜙}{𝜙_{m}}\}$	Gay et al. [1969] ; 𝛼 = 0.48
10	$𝜂_{r} = {(1 - 𝛼 \frac{\frac{𝜙}{𝜙_{m}}}{1 - \frac{𝜙}{𝜙_{m}}})}^{2}$	Chong et al. [1971] ; 𝛼 = 0.75
11	$𝜂_{r} = \frac{1}{{(1 - \frac{𝛷}{𝛷_{m}})}^{𝛷_{m}}}$	Wildemuth et Williams [1984]
12	$𝜂_{r} = 1 + \frac{3 π}{8} \frac{𝛽}{𝛽 + 1} [\frac{3 + 4.5 𝛽 + 𝛽^{2}}{𝛽 + 1} - 3 (1 - \frac{1}{𝛽}) ln (𝛽 + 1)]$	Shapiro et Probstein [1992] ; $𝛽 = \frac{{(\frac{𝜙}{𝜙_{m}})}^{\frac{1}{3}}}{1 - {(\frac{𝜙}{𝜙_{m}})}^{\frac{1}{3}}}$
13	$𝜂_{r} = \frac{1 + 𝜑^{𝛿}}{{\{1 - 𝛼 \cdot erf [(\frac{\sqrt{π}}{2 𝛼} \cdot 𝜑) (1 + 𝜑^{\dot{𝛾}})]\}}^{B 𝛷_{m}}}$	Costa [2005] ; $𝜑 = \frac{𝜙}{𝜙_{m}}$
14	$𝜙_{m} = 0.066499 tanh (0.913424) log (\dot{𝛾}) + 3.850623 + 0.591806$ $𝛿 = - 6.301095 tanh [(0.818496) log (\dot{𝛾}) (0.818496) log (\dot{𝛾}) + 2.86] + 7.462405$ $𝛼 = - 0.000378 tanh [(1.148101) log (\dot{𝛾}) + 3.92] + 0.999572$ $𝛾 = 3.987815 tanh [(0.8908) log (\dot{𝛾}) + 3.24] + 5.099645$	Caricchi et al. [2007] dans Costa [2005] avec un taux de déformation variable
15	$𝜂_{r} = {(\frac{1 - 𝜑^{𝛿}}{{[1 - F (𝜑 𝜀 𝛾)]}^{B 𝛷_{m}}})}^{- B 𝛷_{m}}$ où : $F = (1 - 𝜉) \cdot erf [\frac{\sqrt{π}}{2 (1 - 𝜉)} 𝜑 (1 + 𝜑^{𝛿})]$ et $𝜂_{*} = 𝜂 (𝛷_{m}) = 2 {[1 - (1 - 𝜉) erf (\frac{\sqrt{π}}{(1 - 𝜉)})]}^{- B 𝛷_{m}}$	Costa et al. [2009] ; $𝜑 = \frac{𝜙}{𝜙_{m}}$
16	$log (𝜂_{r}) = (- 0.06 exp (6 𝛷)) log (\frac{𝜏}{𝜏_{crit}})$	Cordonnier et al. [2009] ; 𝜎 est la contrainte différentielle, 𝜎_crit est la contrainte limite (10⁹ Pa), et (0.06 exp(6*𝜙)) est la relation de dépendance de la contrainte cristalline avec 𝜙 la fraction cristalline.
17	$𝜂_{r} = {(1 - \frac{𝛷}{𝛷_{m}})}^{- 𝛼 𝛷_{m} [1 + 𝛽 ln (1 - \frac{𝛷}{𝛷_{m}}) ln \dot{𝛾}]}$	Ishibashi [2009]
18	$𝜂_{r} = {(1 - \frac{𝛷}{𝛷_{m}})}^{- 2 [1 - 𝛼 log (\dot{𝛾})]}$	Vona et al. [2011]
19	$𝜂_{r} = {(1 - \frac{𝛷}{𝛷_{m}})}^{- 𝛼}$	Moitra et Gonnermann [2015] ; 𝛼 = 1.92
20	$𝜂_{r} = {(1 - \frac{𝛷_{m} - 𝛷}{𝛷_{m} (1 - 𝛷)})}^{- \frac{2.5 𝛷_{m}}{1 - 𝛷_{m}}}$	Faroughi et Huber [2015]
21	$𝜂_{r} = 𝜂_{r (max)}^{\frac{1 - exp (- k 𝛷^{n})}{1 - exp (- k)}}$	Liu et al. [2017] ; 𝜂_r(max) est la valeur pour 𝛷 = 1. k et n sont des paramètres ajustables

Pour plus de détails, se référer à la documentation fournie.

Nous avons effectué divers tests sur l'ensemble de données fourni dans l'annexe supplémentaire 2 pour définir un éventuel modèle complet de viscosité apparente/relative. La meilleure solution a été donnée par une approche polynomiale, bien qu'elle ne fournisse pas d'excellents résultats. Nous proposons une approche empirique pour déduire la viscosité apparente de (1) le taux de cisaillement et le volume des phases solides ou (2) l'AS et le volume des cristaux dans les suspensions des liquides silicatés. Les résultats sont basés sur les 415 données expérimentales présentées dans l'annexe supplémentaire 2, interpolées par une approche polynomiale simple capable de construire une surface 3D pour laquelle sont pris en compte, dans un cas, la viscosité logarithmique, le taux de cisaillement et le volume de cristaux, et la viscosité logarithmique, l'AS et le volume de cristaux dans l'autre cas. (Figure 8). La viscosité apparente peut être estimée à l'aide des expressions suivantes :

log 𝜂_{app} = a + b \cdot ln \dot{𝛾} + c \cdot 𝛷 + d \cdot {(ln \dot{𝛾})}^{2} + e \cdot 𝛷^{2} + f \cdot 𝛷 \cdot ln \dot{𝛾}

(4)

et

log 𝜂_{app} = a + \frac{b}{ln AS} + \frac{c}{{AS}^{1.5}} 𝛷 + d \cdot exp (- AS) + e \cdot 𝛷 \cdot ln 𝛷,

(5)

où 𝜂_app est la viscosité apparente, le taux de cisaillement, la teneur en cristaux (% vol) et le rapport d'aspect du cristal AS. Les paramètres fixes pour (4) sont a = 1.917, b = −0.034, c = 9.258, d = −0.032, e = −14.958, et f = −0.737. Les paramètres de (5) sont a = 1.419, b = 0.313, c = −5.952, d = 10.499, et e = −6.481. Ces paramètres ont été obtenus par régressions non linéaires produisant une racine de l'erreur quadratique moyenne (REQM) de 0.316 et 0.319 et une erreur absolue moyenne (EAM de 0.257 et 0.255 pour (4) et (5), respectivement. La comparaison de 𝜂_app prédite par (4) et (5) avec les données expérimentales est présentée à la figure 9A et B, respectivement.

Figure 8.
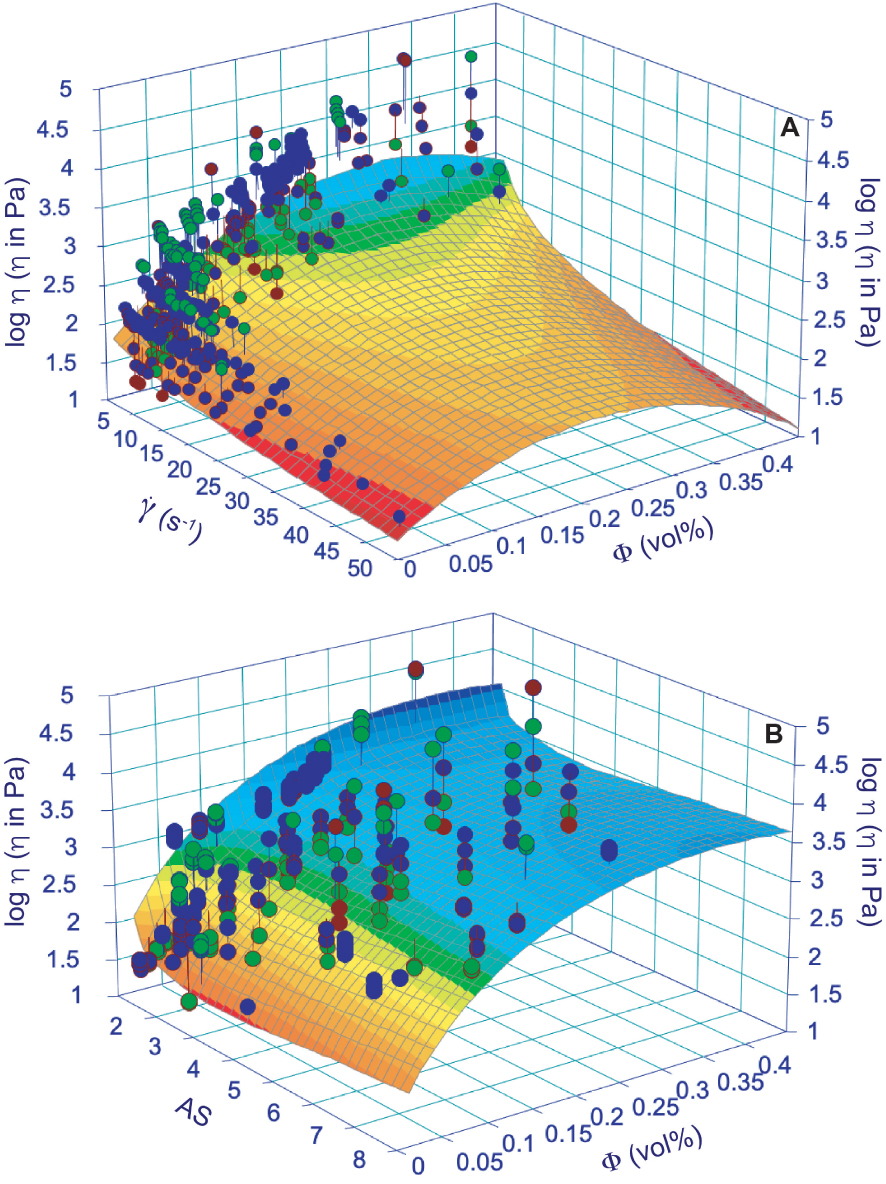
Modélisation de surface de la viscosité apparente en fonction du taux de cisaillement (en s⁻¹) et de la teneur en cristaux (𝛷 ; A) et du rapport d'aspect (AS) et de la teneur en cristaux (𝛷 ; B). Le modèle est basé sur 415 données expérimentales fournies dans l'annexe supplémentaire 2 dérivées de la composition chimique comme dans la figure 4 et l'annexe supplémentaire 1. Les approches polynomiales (donnant les meilleurs résultats en termes de R²) sont fournies dans le tableau 1 avec les meilleurs paramètres d'ajustement et R².

Figure 9.
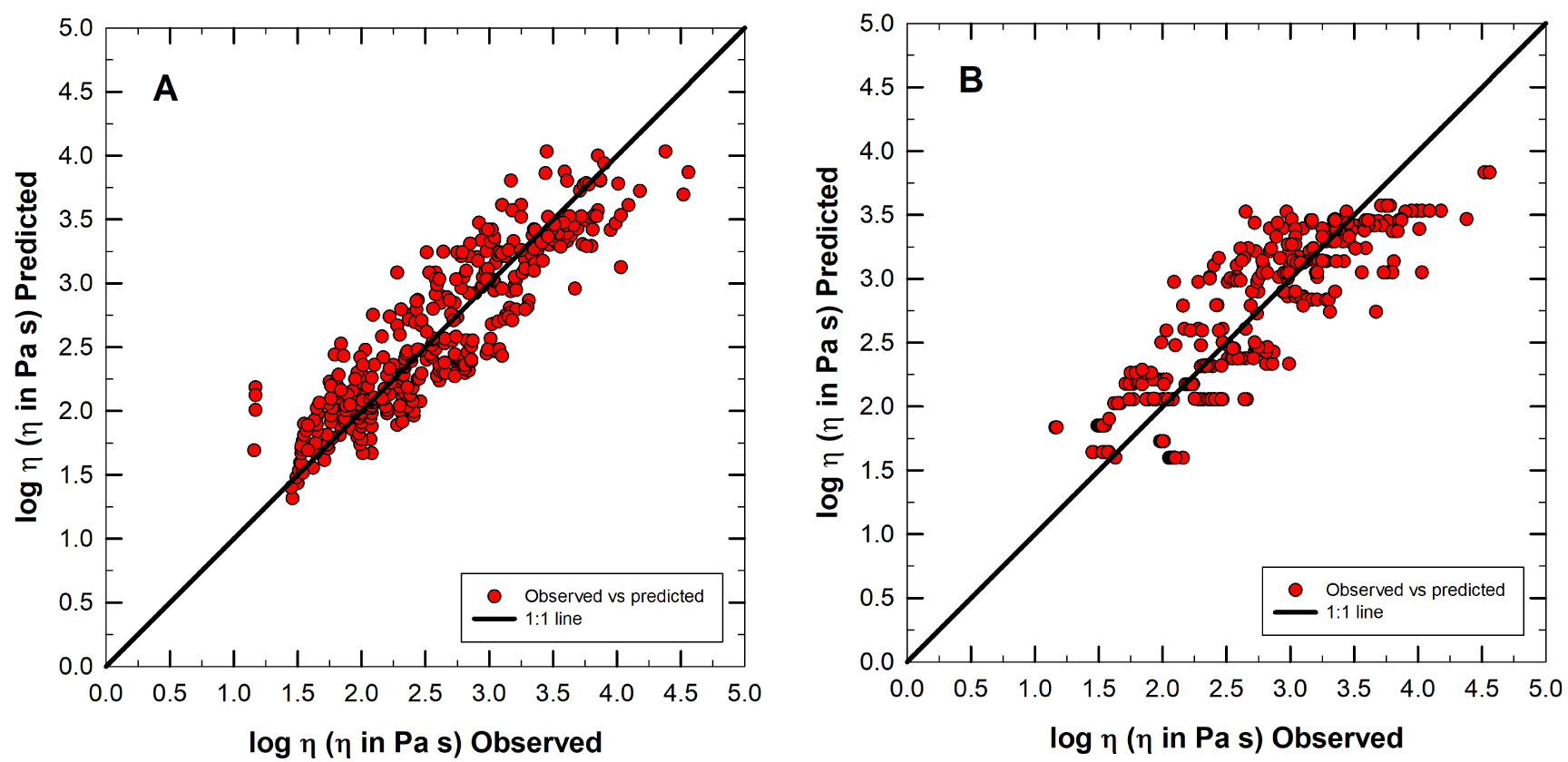
log𝜂 observé en fonction de celui prédit par (4) et (5). (A) fait référence à (4) avec R² = 0.80 tandis que (B) fait référence à (5) avec R² = 0.75.

6. L'effet du taux de cisaillement, de la teneur en cristaux et des vitesses de refroidissement

L'effet concomitant du taux de cisaillement et de la vitesse de refroidissement sur la cristallinité et la rhéologie peut être extrait des données expérimentales à une pression atmosphérique, principalement obtenues pour la composition mafique. Cependant, la rhéologie des systèmes cristallisant à la suite de la décompression induite par le dégazage en fonction du taux de décompression et du taux de cisaillement n'a jamais été étudiée expérimentalement. De telles expériences simuleraient l'approche la plus proche des conditions géologiques pertinentes, en particulier l'ascension des magmas dans les cheminées et les dykes.

Vetere et al. [2020, 2019] et Kolzenburg et al. [2020, 2019, 2018, 2017] ont effectué des expériences à une pression atmosphérique. En raison de l'augmentation progressive de la cristallinité en fonction du temps pendant le refroidissement (contrairement aux expériences classiques de viscosité isotherme présentées aux paragraphes 4 et 5), la viscosité apparente n'atteindra jamais une valeur stable en raison des conditions de non-équilibre des liquides présentant des suspensions cristalline. Comme le montrent Kolzenburg et al. [2018], la croissance des cristaux est progressivement limitée et potentiellement entravée dans les systèmes statiques (par exemple, sans cisaillement) parce que le liquide (intra-cristallin résiduel) environnant est appauvrie en éléments compatibles (déjà incorporés par les premiers événements de croissance) nécessaires à la poursuite de la croissance des cristaux. En outre, le refroidissement et les premières phases de cristallisation enrichissent les liquides résiduels et intra-cristallins en composants à diffusion lente (SiO₂ et Al₂O₃), tandis que la chute de température détermine un ralentissement progressif des éléments chimiques. La croissance dendritique est la conséquence de telles situations, lorsque le mouvement des espèces chimiques est limité dans un liquide silicaté en cours de solidification ; si la diffusion est très lente par rapport à l'état cinétique, cela empêche la nucléation et déclenche la formation du verre [Kirkpatrick 1981 ; Lofgren 1980 ; Shea et Hammer 2013 ; Vetere et al. 2013, 2015]. Le cisaillement ou toute autre déformation agissant sur les magmas et les liquides silicatés améliorent la diffusion des éléments par transfert de masse.

Comme indiqué dans Kolzenburg et al. [2017], les systèmes refroidis dans la même plage thermique cristallisent plus rapidement (à faible 𝛥T et haut T) et plus abondamment avec des taux de cisaillement progressivement croissants. Cette observation a également été remarquée pour des expériences isothermes dans des conditions de subliquidus par Kouchi et al. [1986], Vona et Romano [2013], Chevrel et al. [2015], et Vetere et al. [2017] et il est maintenant largement admis que l'augmentation du taux de cisaillement augmente la vitesse de croissance des cristaux. En outre, Vetere et al. [2019, 2020] ont montré que le taux de cisaillement pendant le refroidissement influence la vitesse de croissance des phases solides. En particulier, la vitesse de croissance de l'olivine, dans la pyroxénite liquide à une vitesse de refroidissement de 10 K/h est d'environ. 5.3 × 10⁻⁶ cm/s. Le cristal de clinopyroxène dans les liquides shoshonitiques présente des vitesses de croissance entre 1.2 et 2.1 × 10⁻⁶ cm/s lorsque les vitesses de refroidissement varient de 10 à 100 K/h, respectivement, à un taux de déformation de 1 s⁻¹.

Comme le montre une simulation de conditions magmatiques [Petrelli et al. 2016], les mécanismes invoqués comme responsables de ces vitesses de croissance rapide des cristaux pourraient être une alimentation continue en « ingrédient frais » des surfaces des cristaux individuels. L'agitation rapide améliore également la formation de nouveaux noyaux cristallins, comme suggéré par Emerson [1926], Cashman et al. [1999], et Vona et Romano [2013]. Enfin, la fugacité de l'oxygène joue également un rôle important sur les processus de cristallisation et les changements rhéologiques associés [Kolzenburg et al. 2020]. Par exemple, l'augmentation de la fO₂ dans les magmas atteignant la surface de la Terre peut conduire à un décalage progressif des températures de cristallisation à l'équilibre.

Un exemple de l'évolution de la viscosité apparente avec une température décroissante et une cristallisation concomitante est donné à la figure 10 pour trois magmas mafiques différents : la pyroxénite, le basalte et la shoshonite. Les conditions expérimentales de la figure 10 sont identiques pour la pyroxénite et la shoshonite (vitesse de refroidissement de 10 K/h et taux de cisaillement de 1 s⁻¹), tandis que pour le basalte, la vitesse de refroidissement appliquée est légèrement supérieure (30 K/h) et le taux de cisaillement légèrement inférieur (0,77 s⁻¹). Ces différences sont minimes, mais en termes de réactivité au refroidissement, la pyroxénite est la plus rapide. Les points d'inflexion dans l'évolution de la viscosité avec la diminution de la température sont liés au début de la cristallisation des phases minérales. Les compositions de la pyroxénite, du basalte et de la shoshonite (composition indiquée dans la figure 4 et dans l'annexe supplémentaire 1) ont une température de liquidus, calculée en utilisant des alphaMELTS de 1543, 1444 et 1452 K, respectivement. Il est évident que la cristallisation se produit très rapidement après avoir atteint la température de liquidus pour la pyroxénite. L'intervalle de température (et de temps) entre le liquidus et la température de cristallisation est plus grand pour le basalte, et encore plus grand pour la shoshonite. En termes structuraux, la variabilité chimique des liquides silicatés pourrait être décrite par le nombre d'oxygènes non-pontants (ONP) par cation à coordination tétraédrique (T) [Mysen et Richet 2005] :

\frac{ONP}{T} = \frac{1}{T} \cdot \sum_{i = 1}^{i} n \cdot M_{i}^{n +},

(6)

où T est l'abondance atomique totale des cations à coordination tétraédrique,

M_{i}^{n +}

est la proportion de cations modificateurs de réseau, "i"», de charge électrique n+ après soustraction de la portion nécessaire à l'équilibrage de charge des cations trivalents sur les sites tétravalents [Mysen et Richet 2005]. Les valeurs ONP/T résultantes sont de 1.14, 0.66 et 0.36 pour la pyroxénite, le basalte et la shoshonite liquides, respectivement. Cela montre que des valeurs élevées de ONP/T sont liées à une mobilité cationique plus élevée favorisant un réarrangement rapide des noyaux afin d'atteindre « l'unité structurelle minimale » pour une croissance cristalline ultérieure [Mysen et Richet 2005]. Les courbes de la figure 10 reflètent l'effet de la structure liquide sur le retard de nucléation et de croissance des cristaux pendant le refroidissement, comme indiqué également dans Vetere et al. [2015] et Iezzi et al. [2017]. Néanmoins, davantage données sont nécessaires pour éventuellement définir une meilleure relation entre la vitesse de refroidissement, la contrainte de cisaillement appliquée, la croissance cristalline et le rapport ONP/T afin de modéliser l'évolution de la viscosité des magmas en cours de cristallisation.

Enfin, il est récemment devenu évident que la formation de nanolites d'oxyde de fer peut affecter la composition du liquide résiduel et induire des changements dans les processus de nucléation et de croissance des cristaux et donc sur la réponse rhéologique du magma [Vetere et al. 2015 ; Di Genova et al. 2020, et référence incluse]. Bien que ces phases soient trop petites pour être quantifiées analytiquement avec la plupart des techniques classiques appliquées pour caractériser l'ensemble des données présentées, l'apparition potentielle de ces phases pourrait influencer les données dans certaines charges expérimentales.

Figure 10.
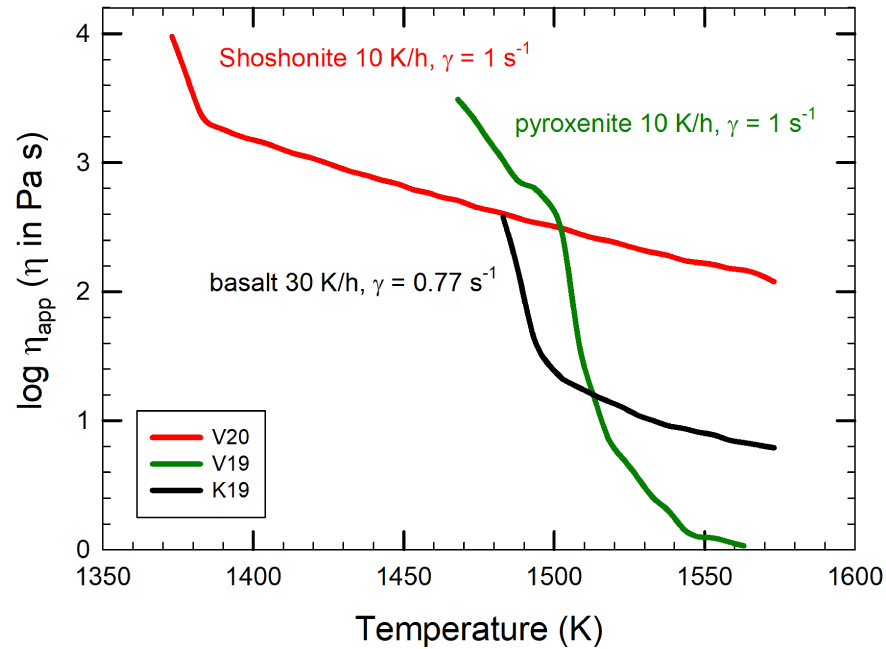
Viscosité apparente (Pa⋅s) en fonction de l'évolution de la température (K) pour les compositions de basalte, de pyroxénite et de shoshonite liquides comme dans la figure 4 et l'annexe supplémentaire 1. On remarque la diminution de la viscosité à mesure que les liquides refroidissent et cristallisent.

7. Conclusion et enjeux futurs

Cette étude montre que les liquides silicatés soumis à différents taux de déformation montrent un comportement de rhéofluidification à la fois sur les liquides pures ainsi que sur les systèmes partiellement cristallisés, où la teneur en cristaux ne dépasse pas environ 40 % vol. Il est évident qu'il existe encore un besoin d'expériences visant à accroître l'ensemble des données disponibles simulant l'évolution de la viscosité dans les systèmes dynamiques en cours de cristallisation. Les études futures devront également aborder l'effet de la pression, du dégazage et de la cristallisation associée pour étendre les modèles de rhéologie au déséquilibre aux conditions magmatiques crustales. Une stratégie commune et rationnelle est nécessaire pour étudier la rhéologie du magma en utilisant un protocole expérimental commun et systématique, ce qui est particulièrement pertinent pour l'approche par l'utilisation d'un dispositif à cylindres concentriques. D'un point de vue général, la déformation appliquée aux liquides silicatés augmente les taux de nucléation et les vitesses de croissance des phases cristallines par rapport aux conditions statiques. Ce point doit être pris en compte dans la modélisation des comportements magmatiques et volcaniques, car le comportement rhéologique pourrait radicalement s'écarter de celui prédit sur la base d'approches expérimentales statiques et de la modélisation à l'équilibre.

Conflits d’intérêts

Les auteurs n'ont aucun conflit d'intérêts à déclarer.

Remerciements

Cette étude a été financée par le projet « Fondi Ateneo de l'Université G. D’Annunzio », le projet PRIN (2009PZ47NA_003) « Experimental determination of the glass-forming ability (GFA), nucleation and crystallization of natural silicate melts » et le projet PRIN (2017J277S9_003) « Time scales of solidification in magmas: Application to Volcanic Eruptions, Silicate Melts, Glasses, Glass-Ceramics » attribué à GI. Nous remercions la fondation Alexander von Humbold d'avoir accordé une bourse de recherche à FV.

Bibliographie

[Applegarth et al., 2013] L. J. Applegarth; H. Tuffen; M. R. James; H. Pinkerton Degassing-driven crystallisation in basalts, Earth Sci. Rev., Volume 116 (2013), pp. 1-16 | DOI

[Armienti, 2008] P. Armienti Decryption of igneous rock textures: crystal size distribution tools, Rev. Mineral., Volume 69 (2008), pp. 623-649 | DOI

[Arzi, 1978] A. Arzi Critical phenomena in the rheology of partially melted rocks, Tectonophysics, Volume 44 (1978), pp. 173-184 | DOI

[Arzilli et al., 2019] F. Arzilli; G. La Spina; M. R. Burton; M. Polacci; N. Le Gall; M. E. Hartley et al. Magma fragmentation in highly explosive basaltic eruptions induced by rapid crystallization, Nat. Geosci., Volume 12 (2019), pp. 1023-1028 | DOI

[Asimow and Ghiorso, 1998] P. D. Asimow; M. S. Ghiorso Algorithmic modifications extending MELTS to calculate subsolidus phase relations, Am. Mineral., Volume 83 (1998), pp. 1127-1132 | DOI

[Baker and Grove, 1985] M. B. Baker; T. L. Grove Kinetics controls on pyroxene nucleation and metastable liquid line of descent in a basaltic andesite, Am. Mineral., Volume 70 (1985), pp. 279-287

[Baker, 2008] D. R. Baker The fidelity of melt inclusions as records of melt composition, Contrib. Miner. Petrol., Volume 156 (2008), pp. 377-395 | DOI

[Campagnola et al., 2016] S. Campagnola; C. Romano; A. Vona; C. G. Giordano Crystallization kinetics and rheology of leucite-bearing tephriphonolite magmas from the Colli Albani volcano (Italy), Chem. Geol., Volume 424 (2016), pp. 12-29 | DOI

[Caricchi et al., 2007] L. Caricchi; L. Burlini; P. Ulmer; T. Gerya; M. Vassalli; P. Papale Non-Newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics, Earth Planet Sci. Lett., Volume 264 (2007), pp. 402-419 | DOI

[Cashman et al., 1999] K. Cashman; C. Thornber; J. Kauahikaua Cooling and crystallization of lava in open channels, and the transition of Pahoehoe Lava to “A”(a)over-bar, Bull. Volcanol., Volume 61 (1999), pp. 306-323 | DOI

[Cashman, 1988] K. Cashman Crystallization of Mount-St-Helens 1980–1986 dacite—a quantitative textural approach, Bull. Volcanol., Volume 50 (1988), pp. 194-209 | DOI

[Cassidy et al., 2018] M. Cassidy; M. Manga; K. Cashman; O. Bachmann Controls on explosive-effusive volcanic eruption styles, Nat. Commun., Volume 9 (2018), 2839 | DOI

[Chevrel et al., 2015] M. O. Chevrel; C. Cimarelli; L. deBiasi; J. B. Hanson; Y. Lavallée; F. Arzilli; D. B. Dingwell Viscosity measurements of crystallizing andesite from Tungurahua volcano (Ecuador), Geochem. Geophys. Geosyst., Volume 16 (2015), pp. 870-889 | DOI

[Chevrel et al., 2018] M. O. Chevrel; A. J. Harris; M. R. James; L. Calabrò; L. Gurioli; H. Pinkerton The viscosity of pāhoehoe lava: in situ syn-eruptive measurements from Kilauea, Hawaii 2, Earth Planet. Sci. Lett., Volume 493 (2018), pp. 161-171 | DOI

[Chevrel et al., 2019] M. O. Chevrel; H. Pinkerton; A. J. L. Harris Measuring the viscosity of lava in the field: A review, Earth-Sci. Rev., Volume 196 (2019), 102852 | DOI

[Chong et al., 1971] J. Chong; E. Christiansen; A. Baer Rheology of concentrated suspensions, J. Appl. Polym. Sci., Volume 15 (1971), pp. 2007-2021 | DOI

[Conte et al., 2006] A. M. Conte; C. Perinelli; R. Trigila Cooling kinetics experiments on different Stromboli lavas: Effects on crystal morphologies and phases composition, J. Volcanol. Geotherm. Res., Volume 155 (2006) no. 3–4, pp. 179-200 | DOI

[Cordonnier et al., 2009] B. Cordonnier; K. U. Hess; Y. Lavallee; D. B. Dingwell Rheological properties of dome lavas: case study of Unzen volcano, Earth Planet Sci. Lett., Volume 279 (2009), pp. 263-272 | DOI

[Cordonnier et al., 2012] B. Cordonnier; S. M. Schmalholz; K. U. Hess; D. B. Dingwell Viscous heating in silicate melts: An experimental and numerical comparison, J. Geophys. Res., Volume 117 (2012), B02203 | DOI

[Costa et al., 2009] A. Costa; L. Caricchi; N. Bagdassarov A model for the rheology of particle-bearing suspensions and partially molten rocks, Geochem. Geophys. Geosyst., Volume 10 (2009) no. 3, Q03010 | DOI

[Costa, 2005] A. Costa Viscosity of high crystal content melts: dependence on solid fraction, Geophys. Res. Lett., Volume 32 (2005), L22308 | DOI

[Del Gaudio et al., 2010] P. Del Gaudio; S. Mollo; G. Ventura; G. Iezzi; J. Taddeucci; A. Cavallo Cooling rate-induced differentiation in anhydrous and hydrous basalts at 500 MPa: implications for the storage and transport of magmas in dikes, Chem. Geol., Volume 270 (2010), pp. 164-178 | DOI

[De Paolo and Getty, 1996] D. J. De Paolo; S. R. Getty Models of isotopic exchange in reactive fluid-rock systems: implications for geochronology in metamorphic rock, Geochim. Cosmochim. Acta, Volume 60 (1996), pp. 3933-3947 | DOI

[Dingwell and Webb, 1989] D. B. Dingwell; S. L. Webb Structural relaxation in silicate melts and non-Newtonian melts rheology in geologic processes, Phys. Chem. Miner., Volume 16 (1989), pp. 508-516 | DOI

[Dingwell, 1995] D. B. Dingwell Viscosity and anelasticity of melts, Mineral Physics and Crystallography (A Handbook of Physical Constants AGU Reference Shelf), Volume 2, American Geophysical Union, Washington, 1995, pp. 209-217 | DOI

[Dingwell, 1996] D. B. Dingwell Volcanic dilemma: flow or blow?, Science, Volume 273 (1996), pp. 1054-1055 | DOI

[Di Genova et al., 2020] D. Di Genova et al. In situ observation of nanolite growth in volcanic melt: A driving force for explosive eruptions, Sci. Adv., Volume 6 (2020), eabb0413 | DOI

[Dowty, 1980] E. Dowty Crystal growth and nucleation theory and the numerical simulation of igneous crystallization, The Physics of Magmatic Processes (R. B. Hargraves, ed.), Princeton University Press, Princeton, NJ, USA, 1980, pp. 419-485 | DOI

[Eilers, 1941] V. H. Eilers Die viskosität von emulsionen hochviskoser stoffe als funktion der konzentration, Kolloid-Zeitschrift, Volume 97 (1941), pp. 313-321 | DOI

[Eilers, 1943] H. Eilers Die viskositäts-konzentrationsabhängigkeit kolloider systeme in organischen lösungsmitteln, Kolloid-Zeitschrift, Volume 102 (1943), pp. 154-169 | DOI

[Einstein, 1906] A. Einstein Eine neue Bestimmung der Molekul dimensionen, Ann. Phys., Volume 19 (1906), pp. 289-306 | DOI | Zbl

[Emerson, 1926] O. H. Emerson The formation of aa and pahoehoe, Am. J. Sci., Volume 68 (1926), pp. 109-114 | DOI

[Faroughi and Huber, 2015] S. A. Faroughi; C. Huber A generalized equation for rheology of emulsions and suspensions of deformable particles subjected to simple shear at low Reynolds number, Rheol. Acta, Volume 54 (2015), pp. 85-108 | DOI

[Fiege et al., 2015] A. Fiege; F. Vetere; G. Iezzi; A. Simon; F. Holtz The roles of decompression rate and volatiles (H $_{2}$ O + Cl $\pm$ CO $_{2}$ $\pm$ S) on crystallization in (trachy-) basaltic magma, Chem. Geol., Volume 411 (2015), pp. 310-322 | DOI

[Gay et al., 1969] E. Gay; P. Nelson; W. Armstrong Flow properties of suspensions with high solids concentration, AIChE J., Volume 15 (1969), pp. 815-822 | DOI

[Ghiorso and Sack, 1995] M. S. Ghiorso; R. O. Sack Chemical mass transfer in magmatic processes: IV. A revised and internally consistent thermodynamic model for the interpretation and extrapolation of liquid–solid equilibria in magmatic systems at elevated temperatures and pressures, Contrib. Mineral. Petrol., Volume 119 (1995), pp. 197-212 | DOI

[Ghiorso et al., 2002] M. S. Ghiorso; M. M. Hirschmann; P. W. Reiners; V. C. Kress III The pMELTS: A revision of MELTS for improved calculation of phase relations and major element partitioning related to partial melting of the mantle to 3 GPa, Geochem. Geophys. Geosyst., Volume 3 (2002) no. 5, pp. 1-36 | DOI

[Giordano et al., 2008] D. Giordano; J. K. Russell; D. B. Dingwell Viscosity of magmatic liquids: a model, Earth Planet. Sci. Lett., Volume 271 (2008), pp. 123-134 | DOI

[Giuliani et al., 2020a] L. Giuliani; G. Iezzi; H. Tyler; M. Davis; A. Elbrecht; F. Vetere; M. Nazzari; S. Mollo The onset and solidification path of a MORB by in-situ (DSC) and ex-situ investigations, Front. Earth Sci., Volume 8 (2020), 337 | DOI

[Giuliani et al., 2020b] L. Giuliani; G. Iezzi; F. Vetere; H. Behrens; S. Mollo; F. Cauti; G. Ventura; P. Scarlato Evolution of textures, crystal size distributions and growth rates of plagioclase, clinopyroxene and spinel solidified at variable cooling rates from a mid-ocean ridge basaltic liquid, Earth Sci. Rev., Volume 204 (2020), 103165 | DOI

[Giuliani et al., 2021] L. Giuliani; G. Iezzi; S. Mollo Dynamics of volcanic systems: physical and chemical models applied to equilibrium versus disequilibrium solidification of magmas, Dynamic Magma Evolution (F. Vetere, ed.) (American Geophysical Union, Geophysical Monograph), Volume 254, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2021, pp. 101-132 | DOI

[Giuliani et al., 2022] L. Giuliani; F. Vetere; G. Iezzi; M. Nazzari; S. Mollo; H. Behrens; P. Scarlato; G. Ventura Crystal-chemical variations of spinel, clinopyroxene, and plagioclase in MORB basaltic melt induced by continuous cooling, Chem. Geol., Volume 594 (2022), 120765 | DOI

[Gonnermann and Manga, 2007] H. M. Gonnermann; M. Manga The fluid mechanics inside a volcano, Annu. Rev. Fluid Mech., Volume 39 (2007), pp. 321-356 | DOI | MR | Zbl

[Guth and Gold, 1938] E. Guth; O. Gold Viscosity and electroviscous effect of the AgI sol. II. Influence of the concentration of AgI and of electrolyte on the viscosity, Phys. Rev., Volume 53 (1938), p. 322

[Hammer and Rutherford, 2002] J. E. Hammer; M. J. Rutherford An experimental study of the kinetics of decompression-induced crystallization in silicic melt, J. Geophys. Res., Volume 107 (2002) no. B1, 2021 | DOI

[Hammer, 2006] J. E. Hammer Influence of fO $_{2}$ and cooling rate on the kinetics and energetics of Fe-rich basalt crystallization, Earth Planet. Sci. Lett., Volume 248 (2006), pp. 618-637 | DOI

[Hammer, 2008] J. E. Hammer Experimental studies of the kinetics and energetics of magma crystallization, Rev. Mineral. Geochem., Volume 69 (2008) no. 1, pp. 9-59 | DOI

[Herschel and Bulkley, 1926] W. Herschel; R. Bulkley Konsistenzmessungen von Gummi-Benzollösungen, Kolloid-Z., Volume 39 (1926), pp. 291-300 (Measurement of consistency as applied to rubber-benzene solutions, Proc. ASTM 82, 1925) | DOI

[Hess et al., 2007] K. U. Hess; B. Cordonnier; Y. Lavallee; D. B. Dingwell High-load, high-temperature deformation apparatus for synthetic and natural silicate melts, Rev. Sci. Instrum., Volume 78 (2007) no. 7, 075102 | DOI

[Higgins, 2006] M. D. Higgins Quantitative Textural Measurements in Igneous and Metamorphic Petrology, Cambridge University Press, Cambridge, 2006 | DOI

[Hoover et al., 2001] S. R. Hoover; K. V. Cashman; M. Manga The yield strength of subliquidus basalts—experimental results, J. Volcanol. Geotherm. Res., Volume 107 (2001), pp. 1-18 | DOI

[Hui and Zhang, 2007] H. Hui; Y. Zhang Toward a general viscosity equation for natural anhydrous and hydrous silicate melts., Geochim. Cosmochim. Acta, Volume 71 (2007) no. 2, pp. 403-416 | DOI

[Iezzi et al., 2008] G. Iezzi; S. Mollo; G. Ventura; A. Cavallo; C. Romano Experimental solidification of anhydrous latitic and trachytic melts at different cooling rates: The role of nucleation kinetics, Chem. Geol., Volume 253 (2008), pp. 91-101 | DOI

[Iezzi et al., 2009] G. Iezzi; S. Mollo; G. Ventura Solidification behaviour of natural silicate melts and volcanological implications, Volcanoes: Formation, Eruptions and Modelling (N. Lewis; A. Moretti, eds.), Nova Publishers, New York, 2009, pp. 127-151

[Iezzi et al., 2011] G. Iezzi; S. Mollo; G. Torresi; G. Ventura; A. Cavallo; P. Scarlato Experimental solidification of an andesitic melt by cooling, Chem. Geol., Volume 283 (2011), pp. 261-273 | DOI

[Iezzi et al., 2017] G. Iezzi; A. L. Elbrecht; M. Davis; F. Vetere; V. Misiti; S. Mollo; A. Cavallo Glass Stability (GS) of chemically complex (natural) sub-alkaline glasses, J. Non Cryst. Solids, Volume 477 (2017), pp. 21-30 | DOI

[Iezzi et al., 2020] G. Iezzi; J. E. Hammer; A. Whittington; D. R. Neuville Editorial: research topic crystal nucleation and growth in magmatic suspensions, Front. Earth Sci., Volume 8 (2020), 607972 | DOI

[Ishibashi and Sato, 2007] H. Ishibashi; H. Sato Viscosity measurements of subliquidus magmas: Alkali olivine basalt from the Higashi-Matsuura district, Southwest Japan, J. Volcanol. Geotherm. Res., Volume 160 (2007) no. 2007, pp. 223-238 | DOI

[Ishibashi, 2009] H. Ishibashi Non-Newtonian behavior of plagioclase-bearing basaltic magma: Subliquidus viscosity measurement of the 1707 basalt of Fuji volcano, Jpn J. Volcanol. Geotherm. Res., Volume 181 (2009) no. 1–2, pp. 78-88 | DOI

[Kerr and Lister, 1991] R. C. Kerr; J. R. Lister The effects of shape on crystal settling and on the rheology of magmas, J. Geol., Volume 99 (1991), pp. 457-467 | DOI

[Kirkpatrick, 1981] R. J. Kirkpatrick Kinetics in crystallization of igneous rocks, Rev. Mineral. Geochem., Volume 8 (1981), pp. 321-397

[Kolzenburg et al., 2017] S. Kolzenburg; D. Giordano; T. Thordarson; A. Höskuldsson; D. B. Dingwell The rheological evolution of the 2014/2015 eruption at Holuhraun, central Iceland, Bull. Volcanol., Volume 79 (2017) no. 6, 45 | DOI

[Kolzenburg et al., 2018] S. Kolzenburg; D. Giordano; K. U. Hess; D. B. Dingwell Shear rate-dependent disequilibrium rheology and dynamics of basalt solidification, Geophys. Res. Lett., Volume 45 (2018), pp. 6466-6475 | DOI

[Kolzenburg et al., 2019] S. Kolzenburg; D. Giordano; A. Di Muro; D. B. Dingwell Equilibrium viscosity and disequilibrium rheology of high magnesium basalt from Piton de la Fournaise volcano, La Reunion, Indian Ocean, France, Ann. Geophys., Volume 62 (2019) no. 2, VO218 | DOI

[Kolzenburg et al., 2020] S. Kolzenburg; K. U. Hess; K. Berlo; D. B. Dingwell Disequilibrium rheology and crystallization kinetics of basalts and implications for the phlegrean volcanic district, Front. Earth Sci., Volume 8 (2020), 187 | DOI

[Kouchi et al., 1986] A. Kouchi; A. Tsuchiyama; I. Sunagawa Effect of stirring on crystallization kinetics of basalt: Texture and element partitioning, Contrib, Mineral. Petrol., Volume 9 (1986), pp. 429-438 | DOI

[Krieger and Dougherty, 1959] I. M. Krieger; T. J. Dougherty A mechanism for non-Newtonian flow in suspensions of rigid spheres, Trans. Soc. Rheol., Volume 3 (1959), pp. 137-152 | DOI

[Lanzafame et al., 2013] G. Lanzafame; S. Mollo; G. Iezzi; C. Ferlito; G. Ventura Unravelling the solidification path of a pahoehoe “cicirara” lava from Mount Etna volcano, Bull. Volcanol., Volume 75 (2013) no. 4, pp. 1-16 | DOI

[Lanzafame et al., 2017] G. Lanzafame; G. Iezzi; L. Mancini; F. Lezzi; S. Mollo; C. Ferlito Solidification and Turbulence (Non-laminar) during magma ascent: Insights from 2D and 3D analyses of bubbles and minerals in an Etnean dyke, J. Petrol., Volume 58 (2017) no. 8, pp. 1511-1534 | DOI

[Lasaga, 1997] A. C. Lasaga Kinetic Theory in the Earth Sciences, Princeton University Press, Princeton, NJ, USA, 1997

[Lenk, 1967] R. Lenk A generalized flow theory, J. Appl. Polym. Sci., Volume 11 (1967), pp. 1033-1042 | DOI

[Liu et al., 2017] Z. Liu; L. Pandelaers; B. Blanpain; M. Guo Viscosity of heterogeneous silicate melts: assessment of the measured data and modeling, ISIJ Int., Volume 57 (2017), pp. 1895-1901 | DOI

[Lofgren, 1980] G. Lofgren Experimental studies on the dynamic crystallisation of silicate melts, The Physics of Magmatic Processes (R. B. Hargraves, ed.), Princeton University Press, Princeton, NJ, USA, 1980, pp. 487-551 | DOI

[Mader et al., 2013] H. M. Mader; E. W. Llewellin; S. P. Mueller The rheology of two-phase magmas: A review and analysis, J. Vol. Geotherm. Res., Volume 257 (2013), pp. 135-158 | DOI

[Maron and Pierce, 1956] S. H. Maron; P. E. Pierce Application of Ree–Eyring generalized flow theory to suspensions of spherical particles, J. Colloid Sci., Volume 11 (1956), pp. 80-95 | DOI

[Mezner, 2014] T. G. Mezner The Rheology Handbook, Vincentz Network, Hanover, 2014

[Moitra and Gonnermann, 2015] P. Moitra; H. M. Gonnermann Effects of crystal shape- and size-modality on magma rheology, Geochem. Geophys. Geosyst. (2015) | DOI

[Mollo and Hammer, 2017] S. Mollo; J. E. Hammer Dynamic crystallization in magmas, Mineral Reaction Kinetics: Microstructures, Textures, Chemical and Isotopic Signatures (W. Heinrich; R. Abart, eds.) (EMU Notes in Mineralogy), Volume 16, European Mineralogical Union and the Mineralogical Society of Great Britain & Ireland, Twickenham, 2017, pp. 1-46

[Mollo et al., 2010] S. Mollo; P. Del Gaudio; G. Ventura; G. Iezzi; P. Scarlato Dependence of clinopyroxene composition on cooling rate in basaltic magmas: Implications for thermobarometry, Lithos, Volume 118 (2010), pp. 302-312 | DOI

[Mollo et al., 2011a] S. Mollo; G. Lanzafame; M. Masotta; G. Iezzi; C. Ferlito; P. Scarlato Cooling history of a dike as revealed by mineral chemistry: A case study from Mt, Etna Volcano. Chem. Geol., Volume 283 (2011), pp. 261-273

[Mollo et al., 2011b] S. Mollo; K. Putirka; G. Iezzi; P. Del Gaudio; P. Scarlato Plagioclase-melt (dis)equilibrium due to cooling dynamics: implications for thermometry, barometry and hygrometry, Lithos, Volume 125 (2011), pp. 221-235 | DOI

[Morrison et al., 2020] A. Morrison; A. Whittington; B. Smets; M. Kervyn; A. Sehlke The rheology of crystallizing basaltic lavas from Nyiragongo and Nyamuragira volcanoes, D.R.C. Volcanica, Volume 3 (2020) no. 1, pp. 1-28 | DOI

[Mueller et al., 2010] S. Mueller; E. W. Llewellin; H. M. Mader The rheology of suspensions of solid particles, Proc. R. Soc. A: Math. Phys. Eng. Sci., Volume 466 (2010), pp. 1201-1228 | DOI

[Mysen and Richet, 2005] B. Mysen; P. Richet Silicate Glasses and Melts, Developments in Geochemistry, 10, Elsevier Science, Amsterdam, 2005, pp. 291-327

[Müller et al., 2004] T. Müller; L. P. Baumgartner; C. T. Foster; T. W. Vennemann Metastable prograde mineral reactions in contact aureoles, Geology, Volume 32 (2004), pp. 821-824 | DOI

[Nabelek, 2007] P. I. Nabelek Fluid evolution and kinetics of metamorphic reactions in calc-silicate contact aureoles from H $_{2}$ O to CO $_{2}$ and back, Geology, Volume 35 (2007), pp. 927-930 | DOI

[Perugini et al., 2008] D. Perugini; M. Petrelli; G. Poli A virtual voyage through 3D structures generated by chaotic mixing of magmas and numerical simulations: a new approach for understanding spatial and temporal complexity of magma dynamics, Vis. Geosci., Volume 13 (2008), pp. 1-24 | DOI

[Petrelli et al., 2016] M. Petrelli; K. El Omari; Y. Le Guer; D. Perugini Effects of chaotic advection on the timescales of cooling and crystallization of magma bodies at mid crustal levels, Geochem. Geophys. Geosyst., Volume 17 (2016) no. 2, pp. 425-441 | DOI

[Petrelli et al., 2018] M. Petrelli; K. El Omari; L. Spina; Y. Le Guer; G. La Spina; D. Perugini Timescales of water accumulation in magmas and implications for short warning times of explosive eruptions, Nat. Commun., Volume 9 (2018) no. 1, 770 | DOI

[Pistone et al., 2016] M. Pistone; B. Cordonnier; P. Ulmer; L. Caricchi Rheological flow laws for multiphase magmas: An empirical approach, J. Volcanol. Geotherm. Res., Volume 321 (2016), pp. 158-170 | DOI

[Polacci et al., 2018] M. Polacci; F. Arzilli; G. La Spina et al. Crystallisation in basaltic magmas revealed via in situ 4D synchrotron X-ray microtomography, Sci. Rep., Volume 8 (2018), 8377 | DOI

[Pupier et al., 2008] E. Pupier; S. Duchene; M. J. Toplis Experimental quantification of plagioclase crystal size distribution during cooling of a basaltic liquid, Contrib. Mineral. Petrol., Volume 155 (2008) no. 5, pp. 555-570 | DOI

[Putirka, 2008] K. D. Putirka Thermometers and barometers for volcanic systems, Reviews in Mineralogy and Geochemistry, Volume 69, Mineralogical Society of America, Virginia, USA, 2008, pp. 61-120 | DOI

[Roscoe, 1952] R. Roscoe The viscosity of suspensions of rigid spheres, J. Appl. Phys., Volume 2 (1952), pp. 267-269

[Roselle et al., 1997] G. T. Roselle; L. P. Baumgartner; J. A. Chapman Nucleation-dominated crystallization of forsterite in the Ubehebe peak contact aureole, California, Geology, Volume 25 (1997), pp. 823-826 | DOI

[Rosenberg and Handy, 2005] C. L. Rosenberg; M. R. Handy Experimental deformation of partially melted granite revisited: Implication for the continental crust, J. Metamorph. Geol., Volume 23 (2005), pp. 19-28 | DOI

[Rossi et al., 2019] S. Rossi; M. M Petrelli; D. Morgavi; F. Vetere; R. Almeev; R. Astbury; D. Perugini The role of magma mixing on pre-eruptive dynamics at the Aeolian Islands (Southern Tyrrhenian Sea, Italy), Lithos, Volume 324–325 (2019), pp. 165-179 | DOI

[Rusiecka et al., 2020] M. K. Rusiecka; M. Bilodeau; D. R. Baker Quantification of nucleation delay in magmatic systems: experimental and theoretical approach, Contrib. Mineral. Petrol., Volume 175 (2020) no. 5, 47 | DOI

[Saar et al., 2001] M. O. Saar; M. Manga; K. V. Cashman; S. Fremouw Numerical models of the onset of yield strength in crystal–melt suspensions, Earth Planet. Sci. Lett., Volume 187 (2001), pp. 367-379 | DOI

[Sehlke and Whittington, 2015] A. Sehlke; A. G. Whittington Rheology of lava flows on Mercury: An analog experimental study, J. Geophys. Res.: Planets, Volume 120 (2015), pp. 1924-1955 | DOI

[Sehlke and Whittington, 2020] A. Sehlke; A. G. Whittington Rheology of a KREEP analog magma: xperimental results applied to dike ascent through the lunar crust, Planet. Space Sci., Volume 187 (2020) no. 2020, 104941

[Sehlke et al., 2014] A. Sehlke; A. G. Whittington; B. Robert; A. Harris; L. Gurioli; E. Médard; A. Sehlke Pahoehoe to àà transition of Hawaiian lavas: an experimental study, Bull. Volcanol., Volume 76 (2014) no. 11, 876 | DOI

[Shapiro and Probstein, 1992] A. P. Shapiro; R. F. Probstein Random packings of spheres and fluidity limits of monodisperse and bidisperse suspensions, Phys. Rev. Lett., Volume 68 (1992), p. 1422 | DOI

[Shea and Hammer, 2013] T. Shea; J. E. Hammer Kinetics of cooling- and decompression-induced crystallization in hydrous mafic-intermediate magmas, J. Vocanol. Geotherm. Res., Volume 260 (2013), pp. 127-145 | DOI

[Smith and Asimow, 2005] P. M. Smith; P. D. Asimow Adiabat_1ph: A new public front-end to the MELTS, pMELTS, and pHMELTS models, Geochem. Geophys. Geosyst., Volume 6 (2005), Q02004 | DOI

[Swanson and Ottino, 1990] P. D. Swanson; J. M. Ottino A comparative computational and experimental study of chaotic mixing of viscous fluids, J. Fluid Mech., Volume 213 (1990), pp. 227-249 | DOI | MR

[Swanson, 1977] S. E. Swanson Relation of crystal-growth rate to the granitic textures, Am. Mineral., Volume 62 (1977), pp. 966-978

[Tripoli et al., 2019] B. Tripoli; M. Manga; J. Mayeux; H. Barnard The effects of deformation on the early kinetics of basaltic magmas, Front. Earth Sci., Volume 7 (2019), 250 | DOI

[Vand, 1948] V. Vand Viscosity of solutions and suspensions. I. Theory, J. Phys. Chem., Volume 52 (1948), pp. 277-299 | DOI

[Vetere and Holtz, 2020] F. Vetere; F. Holtz Rheological behavior of partly crystallized silicate melts under variable shear rate, Dynamic Magma Evolution (F. Vetere, ed.) (Geophysical Monograph Series), Wiley, Hoboken, NJ, USA, 2020 | DOI

[Vetere et al., 2013] F. Vetere; H. Sato; H. Ishibashi; R. De Rosa; P. Donato Viscosity changes during crystallization in shoshonitic magma: new insight on the lava flow emplacement, J. Mineral. Petrol. Sci., Volume 108 (2013) no. 3, pp. 144-160 | DOI

[Vetere et al., 2015] F. Vetere; G. Iezzi; H. Beherens; F. Holtz; G. Ventura; V. Misiti; A. Cavallo; S. Mollo; M. Dietrich Glass forming ability and crystallization behaviour of sub-alkaline silicate melts, Earth-Sci. Rev., Volume 150 (2015), pp. 25-44 | DOI

[Vetere et al., 2017] F. Vetere; S. Rossi; O. Namur; D. Perugini; D. Morgavi; V. Misiti; P. Mancinelli; M. Petrelli; C. Pauselli Experimental constraints on the rheology, eruption and emplacement dynamics of lavas from Mercury Northern Volcanic Plains, J. Geophys. Res.: Planets, Volume 122 (2017), pp. 1-17

[Vetere et al., 2019] F. Vetere; M. Murri; M. Alvaro; M. C. Domeneghetti; S. Rossi; A. Pisello; F. Holtz; D. Perugini Viscosity of Pyroxenite Melt and its Evolution during Cooling: an experimental approach, JGR-Planets, Volume 124 (2019), pp. 1451-1469

[Vetere et al., 2020] F. Vetere; A. Mazzeo; D. Perugini; F. Holtz Viscosity behaviour of silicate melts during cooling under variable shear rates, J. Non-Cryst. Solids, Volume 533 (2020), 119902 | DOI

[Vetere et al., 2021] F. Vetere; M. Petrelli; D. Perugini; S. Haselbach; D. Morgavi; A. Pisello; G. Iezzi; F. Holtz Rheological evolution of eruptible Basaltic-Andesite Magmas under dynamic conditions: The importance of plagioclase growth rates, J. Volcanol. Geotherm. Res., Volume 420 (2021), 107411 | DOI

[Vona and Romano, 2013] A. Vona; C. Romano The effects of undercooling and deformation rates on the crystallization kinetics of Stromboli and Etna basalts, Contrib. Mineral. Petrol., Volume 166 (2013) no. 2, pp. 491-509 | DOI

[Vona et al., 2011] A. Vona; C. Romano; D. B. Dingwell; D. Giordano The rheology of crystal-bearing basaltic magmas from Stromboli and Etna, Geochim. Cosmochim. Acta, Volume 75 (2011) no. 11, pp. 3214-3236 | DOI

[Webb and Dingwell, 1990a] S. L. Webb; D. B. Dingwell Non-newtonian rheology of igneous melts at high stresses and strain rates: experimental results for rhyolite, andesite, basalt, and nephelinite, J. Geophys. Res., Volume 95 (1990), pp. 15695-15701 | DOI

[Webb and Dingwell, 1990b] S. L. Webb; D. B. Dingwell The onset of non-Newtonian rheology of silicate melts, Phys. Chem. Minerals, Volume 17 (1990), pp. 125-132

[Wildemuth and Williams, 1984] C. Wildemuth; M. Williams Viscosity of suspensions modeled with a shear-dependent maximum packing fraction, Rheol. Acta, Volume 23 (1984), pp. 627-635 | DOI

[Yue and Bruckner, 1996] Y. Z. Yue; R. Bruckner On the different descriptions of the non-Newtonian viscosity (shear-thinning effect) of glass melts with respect to heat dissipation, Gerlands Beitr. Geophys., Volume 69 (1996) no. 6, pp. 179-185

[Zhang, 2008] Y. Zhang Geochemical Kinetics, Princeton University Press, Princeton, NJ, USA, 2008

Commentaires - Politique