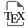Comptes Rendus
Analyse et géométrie complexes
A note on the weighted log canonical threshold
Nguyen Van Phu1
1 Faculty of Natural Sciences, Electric Power University, Hanoi, Vietnam
Comptes Rendus. Mathématique, Volume 361 (2023), pp. 969-971.

In this paper, we introduce and study a set relative to singularities of plurisubharmonic functions. We prove that this set is countable under the condition h>0 on 𝔹∖{0}.

Reçu le :
Révisé le :
Accepté le :
Publié le :
DOI : 10.5802/crmath.456
Classification : 32U05, 32U15, 32U40, 32W20
Nguyen Van Phu 1

1 Faculty of Natural Sciences, Electric Power University, Hanoi, Vietnam
Licence : CC-BY 4.0
Droits d'auteur : Les auteurs conservent leurs droits 
@article{CRMATH_2023__361_G6_969_0,
     author = {Nguyen Van Phu},
     title = {A note on the weighted log canonical threshold},
     journal = {Comptes Rendus. Math\'ematique},
     pages = {969--971},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {361},
     year = {2023},
     doi = {10.5802/crmath.456},
     language = {en},
}
TY  - JOUR
AU  - Nguyen Van Phu
TI  - A note on the weighted log canonical threshold
JO  - Comptes Rendus. Mathématique
PY  - 2023
SP  - 969
EP  - 971
VL  - 361
PB  - Académie des sciences, Paris
DO  - 10.5802/crmath.456
LA  - en
ID  - CRMATH_2023__361_G6_969_0
ER  - 
%0 Journal Article
%A Nguyen Van Phu
%T A note on the weighted log canonical threshold
%J Comptes Rendus. Mathématique
%D 2023
%P 969-971
%V 361
%I Académie des sciences, Paris
%R 10.5802/crmath.456
%G en
%F CRMATH_2023__361_G6_969_0
Nguyen Van Phu. A note on the weighted log canonical threshold. Comptes Rendus. Mathématique, Volume 361 (2023), pp. 969-971. doi : 10.5802/crmath.456. https://comptes-rendus.academie-sciences.fr/mathematique/articles/10.5802/crmath.456/

[1] Jean-Pierre Demailly Monge-Ampère operators, Lelong Numbers and Intersection theory, Complex analysis and geometry (The University Series in Mathematics), Plenum Press, 1993, pp. 115-193 | DOI | Zbl

[2] Jean-Pierre Demailly; Phạm Hoàng Hiệp A sharp lower bound for the log canonical threshold, Acta Math., Volume 212 (2014) no. 1, pp. 1-9 | DOI | MR | Zbl

[3] Jean-Pierre Demailly; János Kollár Semi-continuity of complex singularity exponents and Kähler–Einstein metrics on Fano orbifolds, Ann. Sci. Éc. Norm. Supér., Volume 34 (2001) no. 4, pp. 525-556 | DOI | Numdam | Zbl

[4] Tommaso de Fernex; Lawrence Ein; Mircea Mustaţă Bounds for log canonical thresholds with applications to birational rigidity, Math. Res. Lett., Volume 10 (2003) no. 2-3, pp. 219-236 | MR | Zbl

[5] Tommaso de Fernex; Lawrence Ein; Mircea Mustaţă Shokurov’s ACC Conjecture for log canonical thresholds on smooth varieties, Duke Math. J., Volume 152 (2010) no. 1, pp. 93-114 | MR | Zbl

[6] Le Mau Hai; Phạm Hoàng Hiệp; Trinh Tung Estimates of level sets of holomorphic functions and applications to the weighted log canonical thresholds, J. Geom. Anal. (2021), pp. 3783-3819 | MR | Zbl

[7] Phạm Hoàng Hiệp A comparison principle for log canonical threshold, C. R. Acad. Sci. Paris, Volume 351 (2013) no. 11-12, pp. 441-443 | DOI | MR | Zbl

[8] Phạm Hoàng Hiệp The weighted log canonical threshold, C. R. Acad. Sci. Paris, Volume 352 (2014) no. 4, pp. 283-288 | DOI | Numdam | MR | Zbl

[9] Phạm Hoàng Hiệp Continuity properties of certain weighted log canonical thresholds, C. R. Acad. Sci. Paris, Volume 355 (2017) no. 1, pp. 34-39 | DOI | Numdam | MR | Zbl

[10] Phạm Hoàng Hiệp Log canonical thresholds and Monge–Ampère masses, Math. Ann., Volume 370 (2018) no. 1-2, pp. 556-566 | Zbl

Cité par Sources :

Commentaires - Politique