1 Introduction
In recent years, dramatic advances made in genetic and molecular biology have led to detailed descriptions of a number of events in early embryological development. This unprecedented flood of experimental data may allow us to understand how genes and proteins work collectively in cells to develop an individual. This is one of the great challenges for modern science, but in the absence of specific mechanistic details, it is an impossible task. To understand the mechanisms underlying developmental events it is necessary to bridge the gap between experimental observations at the biochemical and genetic levels and those at the cellular level. In other areas of biology, such as neurophysiology, mathematical modelling has led to fundamental insights and discoveries through a process of synthesis and integration of experimental observations. In such cases, mathematical modelling techniques are used as a research tool, comparable with any powerful laboratory technique, for hypotheses testing and for making experimentally verifiable predictions.
Somitogenesis is a fascinating developmental process for studying such issues, because it has a long history of experimentation at the cellular level and, recently, a number of key molecular components have been identified. In addition, somitogenesis serves as a model process for studying pattern formation and a number of different aspects of embryogenesis, such as the role of biological clocks during development, gene expression and cell differentiation, cell-cell signalling and signalling cascades, cell migration and adhesion 〚1〛.
In vertebrates and cephalochordates, the body axis is divided along the cranio-caudal axis into similar repetitive structures known as somites. These structures are formed during the regression of the primitive streak, when the neural tube folds to gather at the centre of the embryo and the segmental plates, often referred to as the paraxial mesoderm or presomitic mesoderm (PSM), are periodically segmented to produce somites as spheres of cells formed on each side of the anterior-posterior (AP) axis in a cranio-caudal sequence (see Fig. 1). A somite is formed by the condensation of groups of mesenchymal cells, which become polarised and form a three-dimensional epithelium. Somites are divided by a fissure into anterior and posterior halves that differ in their gene expression and differentiation. Later in development, somites govern the segmental organisation of peripheral spinal nerves, vertebrae, axial muscles, and the metameric distribution of early blood vessels 〚2, 3〛.
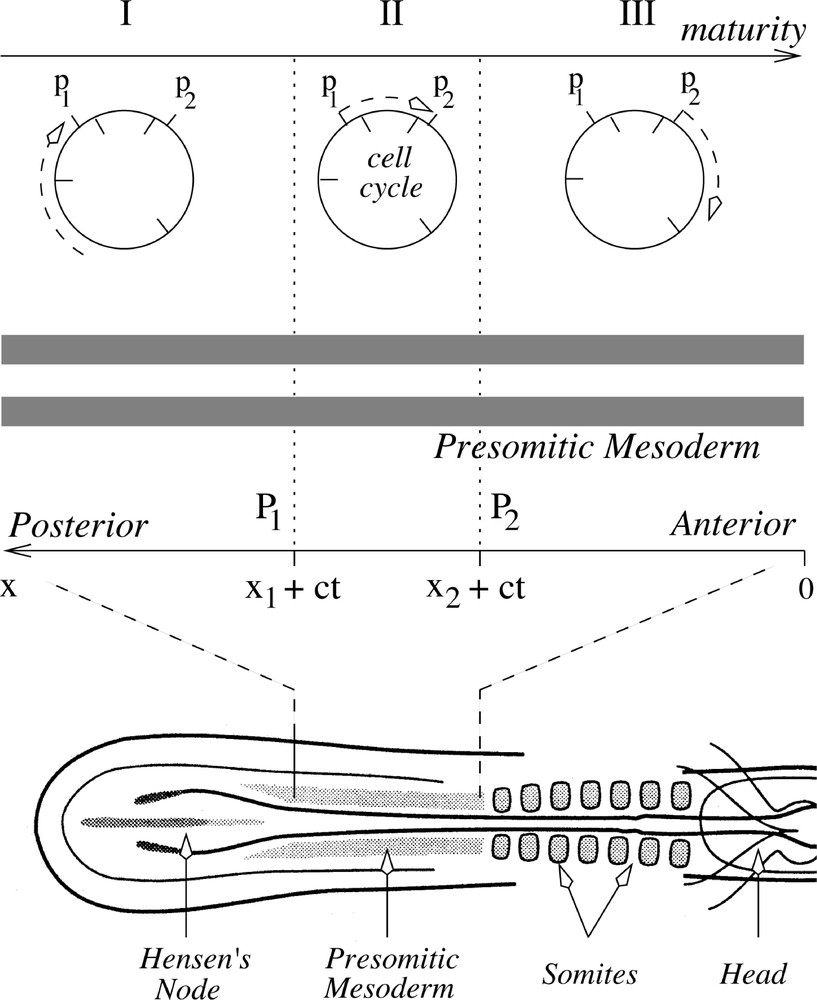
Diagrammatic representation of the cell cycle model illustrating the two time points P1 and P2 and the three key stages proposed by the cell cycle model. Cells at the posterior-most margin of the PSM (I) are at a younger developmental age than those undergoing somitogenesis. As these cells mature, they become capable (II) of responding to the signalling molecule which is secreted by cells at P2. As they mature to the next stage (III) they begin to form somites. At stage (III) they are no longer able to respond to or emit a signal. (Redrawn with modifications from 〚4〛).
Cells condense into somites by undergoing changes in their adhesive and migratory properties until they have arrived at their destination, and later differentiate according to the developmental program 〚5, 6〛. The condensation of mesenchymal cells and the formation of somites is most likely triggered by the interaction of cell adhesion molecules (CAMs), such as N-cadherins, on the surface membrane of somitic cells. At least one type of Ca2+-independent CAM, known as NCAM, and two Ca2+-dependent CAMs, namely cadherin 11 and N-cadherin, are expressed in cells of the PSM during somitogenesis. Expression of NCAM, N-cadherin and cadherin 11 are high in the anterior part of the PSM, coinciding with the condensation of mesenchymal cells and the formation of somites. NCAM and N-cadherin are expressed in the entire somite, whereas cadherin 11 is restricted to the posterior half of the somite 〚7–9〛. The importance of N-cadherin in somite formation is further supported by phenotypes of mouse embryo mutant for N-cadherin 〚10〛 and also by antibody-blocking experiments 〚11〛. Somites in N-cadherin mice mutants are smaller and irregular. Mutations in NCAM and cadherin 11 show no structural anomaly on somite formation 〚12, 13〛. This requires spatial and temporal control of the expression of CAMs and other components like integrins. The regulation of these components is unknown: it might be an intrinsic activity of the PSM or require an inductive signal (presently unknown).
Genetic or environmental factors can disturb somitogenesis, and there are many clinical conditions which occur as a result. The total number of somites is regulated in an embryo. The variation in somite number among vertebrates is very small. Somite numbers are usually around 50–70, except in the case of snakes which can have several hundred 〚14〛. The variability of somite number within a species is less than 5% 〚15〛. However, the number of somites can be altered by environmental disturbances 〚5〛. For example, heat shock applied to chick embryos can induce the formation of an extra somite 〚16〛 and in cold-blooded vertebrates the duration of somite formation is temperature-dependent 〚17〛.
There is very strong evidence that somite and somitic boundary formation is controlled by one or two segmentation clocks. The first experimental evidence to support the segmentation clock was obtained after heat shock was applied to embryos. When a single heat shock is applied to chick embryos 〚18〛 several somitic anomalies, which may be uni- or bilateral, appear separated by relatively constant distances of six to seven normal somites. The repeated anomalies suggest that heat shock affects an oscillatory process within the somite precursor cells 〚18–20〛. In addition, there appears to be some degree of cell-cycle synchrony between the cells in the PSM which are destined to segment together to form a somite 〚21〛. Similar periodic anomalies in somite formation can also be caused by drugs inhibiting cell-cycle progression 〚19〛. These experimental observations link the segmentation clock with the cell-cycle.
Recently, the study of the expression of c-hairy-1 and lunatic fringe (l-fng) in the PSM of chick embryos has provided molecular evidence for the existence of a clock 〚22, 23〛. During segmentation, the cells of the PSM go through at least 12 cycles of c-hairy-1 and l-fng expression before becoming part of a somite, while more cells are continuously incorporated into the posterior end of the PSM. During the time taken for one somite to form, the expression of c-hairy-1 and l-fng appears to sweep along the PSM in the posterior-anterior direction, narrowing as it moves along. This wavefront-like expression finally stops and is maintained only within the caudal half of each forming somite 〚22, 23〛 activating several genes of the Notch/Delta pathway 〚24〛. However, it is not yet known whether the major role of c-hairy-1 an l-fng is in the allocation of cells to individual somites or rather in the subdivision of somites into rostral and caudal compartments 〚4〛.
Although the principle differentiation pattern of all somites is very similar, subsequent differentiation causes groups of somites to form unique anatomical structures, depending on their position along the AP axis. There is now a large body of experimental work showing that positional specification of the PSM requires members of the Hox gene family 〚25–27〛. Interestingly, the five to seven somite interval corresponding to the duration of the cell-cycle in the chick embryo correlates with the length of somite derivatives sharing the same regional identity at the vertebral level 〚19〛.
Despite considerable experimental work, many questions still remain. We can divide these into three categories.
- 1. (i)Segmentation. What regulates the segmentation of the PSM? What drives the segmentation clock? Is there a relation between the cell-cycle and the c-hairy-1 and l-fng oscillations? What regulates the refinement of these oscillations in the PSM? What is the interplay between l-fng and the Notch-Delta pathway? What determines differentiation into anterior and posterior halves within a somite? How can the heat shock experiments be explained?
- 2. (ii)Shape of segments. What are the mechanical forces involved in the formation of a somite? How do cell aggregation, migration, alignment and cell-shape changes contribute to somite formation? What regulates the number and size of somites?
- 3. (iii)Positional information. What determines the regional specification of somites? What is the role of cell division in this process? What is the precise role of the Hox gene family in this process and how is it controlled?
During the past three decades, several mathematical models 〚29–34〛 have been proposed to address some of these questions. These models, in the main, consist of coupled systems of non-linear partial differential equations proposed to describe the spatio-temporal dynamics of cells in the PSM. Recently, we have reviewed a large number of theoretical models for somitogenesis and have found that although some of these successfully account for certain aspects of somitogenesis, they fail to explain, or even contradict, other observations 〚1, 33〛. In a previous paper, we have claimed that in the light of recent molecular evidence the cell cycle model of Stern and co-workers 〚19, 20〛 is still a realistic model for segmentation that incorporates several known aspects of somitogenesis better than most models. Furthermore, we developed a mathematical formulation which enables us to test the cell cycle as the segmentation clock, the effects of heat shock in somite formation and make experimentally verifiable predictions 〚4〛. However, the previous study did not incorporate other aspects such as boundary formation, the affect of cell movement and adhesion, and positional information effects in somite differentiation. In the present article we review some of the key experimental results and theoretical models of somitogenesis. In addition, we extend our mathematical formulation of the cell cycle model for somitogenesis by adding a third equation to account for the cell density. In Section 2, after introducing the mathematical assumptions and formulation under which the model must operate, we present a qualitative description of the behaviour of the model solving numerically the governing equations. In Section 3, some conclusions of the model are discussed with special emphasis on the nature of the segmentation clock, followed by the presentation of a model for the regionalisation of somites. Finally, we suggest future work to be done in somitogenesis experimentally and theoretically.
2 The cell cycle model
The cell cycle model of Stern and collaborators 〚19, 20〛 links the cell cycle with somite segmentation. This hypothesis is supported by the following observations: (1) the existence of discrete regions of cell synchrony in the PSM, (2) a cell cycle duration of 9 hours, which corresponds to the development of six to seven somites in the chick embryo, and (3) periodic anomalies caused by heat shock experiments are mimicked by drugs inhibiting the progression of the cell cycle.
The formation of a somite is explained by assuming that there are two successive time points, P1 and P2, a time interval of 1/7 of the cell cycle time apart. Somite cells recognise the P1–P2 time window. According to the model, cells destined to form somites leave Hensen's node strictly in the order in which they were derived from founder cells in the node, and they remain in that order. Hence there is some degree of cell cycle synchrony of somite cells at the same level, and these cells will be arranged along the embryonic axis in the same order as they are positioned in their cell cycles; older cells further anterior than younger ones 〚35〛. We assume that a fraction of the cohort of cells destined to segment together reach P2 before others and produce a signal to which cells situated between P1 and P2 would respond by later increasing their adhesion to each other shortly before segmentation, regardless of their position within the PSM. The signal produces a somitic factor, which according to our hypothesis is the precursor of a CAM. It has been demonstrated that CAMs can direct cell differentiation, regulate gene expression and tissue formation 〚36, 37〛. Thus, the resulting group of cells would actually undergo segmentation one cell cycle after the P1–P2 time window. As they move out of the P1–P2 window, cells become refractory to the signal and/or unable to signal (see Fig. 1).
The model proposes that heat shock temporarily blocks the cell cycle, so altering the number of cells that segment together. Such an alteration would occur once in each cell cycle in the segmental plate posterior to the P1–P2 time window, accounting for the repetitive anomalies resulting from heat shock.
We have recently formulated these ideas mathematically 〚see for details Appendix A〛 as a coupled system of nonlinear partial differential equations and have shown that the resultant mathematical model can account for the periodic abnormalities observed after a single heat shock, as well as the cell autonomous character of somite formation in the PSM explants and the transplantation experiments reversing the AP axis 〚4〛. The model postulates the existence of two chemicals: a somitic factor and a signalling factor, with concentrations denoted, respectively, by u and v. In words, the signalling part of the model 〚equations (A.1) and (A.2)〛 takes the form:
It is assumed that the production of u is of an autocatalytic nature enhanced by v but saturating for large u. The signal v is emitted at P2 and is assumed to diffuse rapidly. Its production rate is assumed to be inhibited by the somitic factor u, so that cells which have already been specified as somitic (and hence have a high u concentration) cannot signal. We assume that both u and v degrade linearly. The particular form of kinetics are chosen to exhibit a switch-like behaviour – the emission of v activates the production of u, which then quickly reaches its saturating level (specifying a block of tissue as 'somitic'). In turn, this concentration of u inhibits further production of v so that only a spatially confined block of tissue is specified as somitic.
The above model, for somite determination, operates one cell cycle before a somite actually forms. If we wish to model the cell movements during somitogenesis, we have to add to this model, an equation for the response of cell density to the signalling 〚equation (A.3) in Appendix A〛. The cells are assumed to diffuse randomly and to respond haptotactically to gradients in v. Furthermore, we assume that movement depends on the concentration level of v. In words, we assume that a block of cells, specified as somitic, clump together in response to adhesive gradients (determined by v) in regions of sufficiently high v concentration 〚equations (A.4) and (A.5) in Appendix A〛.
In our numerical simulations, the equations are solved on a closed bounded interval of , which we denote by ; typically . This domain is large enough to ensure that conditions at the boundary do not affect the patterning process. As an approximation to these infinite domain boundary conditions we impose zero flux boundary conditions at x=-10 and x=10 (diffusion of v out of the domain is not considered).
2.1 The signalling behaviour of the model
In equations (A.1)–(A.2) of the Appendix A, we have presented a mathematical formulation of the cell cycle model proposed by Stern and collaborators 〚19, 20〛. In this mathematical model, at time t=0, the somitic factor concentration is approximately equal to zero for all cells posterior to and the somitic factor reaches its maximum concentration for cells anterior to while the concentration of signalling molecule is around its minimum value throughout the domain. As time increases, somites will form and the pattern of somitic factor and signal concentration moves caudally at the same rate as somites are formed. As the somitic factor concentration u rises it inhibits the signal v production, and the pulse-like distribution of the signal v quickly falls returning to its minimun value. These low values of the somitic factor u activate the signal v production leading to a second pulse in the signal v. From this description, it is clear that there is a small delay between signalling and specification. Hence, cells gain the potential to form a somite a short time after the signal is emitted. Although cells passing point P2 at time t=0 start producing the signal v almost immediately, the pulse-like signal does not rise and fall in an instant. It is not until later that the signal v is sufficiently high to activate u.
A typical numerical solution to (A.1)–(A.2) is shown in Fig. 2. The results show successive pulses of v, occurring about 200 time units apart. A pulse in the signal v is emitted at x≈0 leading to a jump in the somitic factor u between points x≈0 and x≈1. This jump in the somitic factor u corresponds to a collection of cells that will later form a somite. The first pulse at x≈0 is followed by a second at x≈1 and a third at x≈2, causing a series of jumps in the somitic factor u along the x-axis.
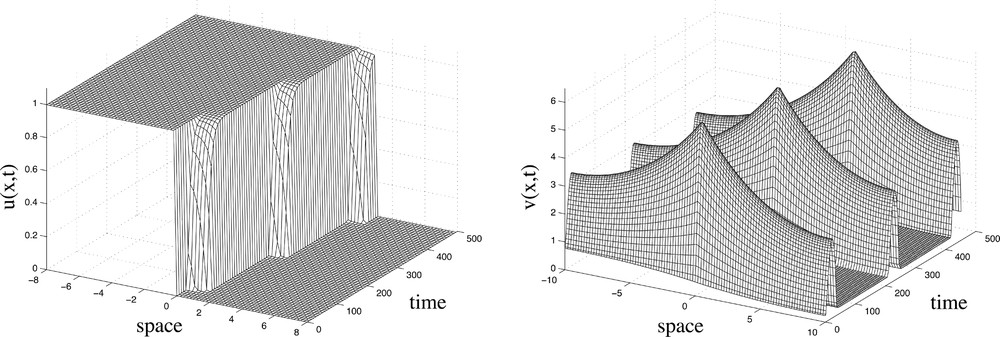
Numerical solution for the model equations (A.1) – (A.2) showing the spatio-temporal dynamics of the somitic factor and the signalling molecule Each peak of the signal v results in an abrupt increase in the somitic factor u which, in turn, triggers somite specification. Three “somites” are shown. Parameter values are μ=10-4, c=5×10-2, κ=10, ϵ=10-3, D=50, γ=0.01.
The process begins with the formation of the first peak in the signal v (see Fig. 2) at the position of P2, quickly followed by a surge of the signal v throughout the spatial domain. The concentration of the signal v then decreases rapidly to a constant level. In response to this pulse-like signal, a fairly rapid increase in the somitic factor u occurs between P1 and P2. Thus we have a wavefront of the somitic factor u moving down the axis in jumps, as successive groups of cells are triggered to become somitic. Note that the level of the somitic factor u rises at approximately the same time in all cells between P1 and P2 when a signal is emitted. According to the cell cycle model, this results in the coordinated segmentation of a somite.
The effects of heat shock in somite formation are also considered in our mathematical formulation. Single heat shock experiments of Primmett and collaborators 〚18〛 in chick embryos resulted in multiple but discrete segmental anomalies. Up to 4 segmental anomalies could be observed in an embryo, including one small somite, one large somite or two fused somites. The experimental evidence 〚18〛 suggests that the pattern of anomalies depends on the relation between two parameters: (i) the number of somites formed per cell cycle, which is approximately 6 to 7 somites, and (ii) the length of the block caused by heat shock relative to the time between P1 and P2.
Within the framework of the cell cycle model heat shock treatment of an embryo has the effect of increasing the time between the points P1 and P2, since it blocks the cell cycle. In the mathematical formulation this leads to a delay in the production of the somitic factor u and the signal v 〚details are discussed in Appendix B〛.
In Fig. 3, we present the results of a heat shock on the pulse of signalling molecule u. In this figure, a schematic representation of the first ten somites shows a sequence of one normal, two abnormal, four normal, two abnormal and one normal somite. This shows that the model can exhibit periodic anomalies due to heat shock.
Schematic representation of the spatio-temporal pattern in the somitic factor u obtained by solving (A.1)–(A.2) subject to the condition (B.2) with parameter values μ=10-4, c=5×10-2, κ=10, ϵ=10-3, D=25, γ=0.01. The effect of the heat shock over one cell cycle was simulated by choosing i=0, δ=2, ψ=6.333 and η=0.6. The delay results in a sequence of one normal, two abnormal, four normal, two abnormal and one normal somite. Each somite of the diagram corresponds to one pulse in u as shown in Fig. 2.
The mathematical formulation of the cell cycle model enables us to predict correctly the anomalies caused by exposing the embryo to a single heat shock. We can also use the model to make experimentally testable predictions on the outcome of heat shock treatments occurring at different times and on the effects of multiple heat shock treatments. For example, we predict that applying two heat shocks during one cell cycle would produce a sequence of abnormal somites separated by one normal somite. This is presently being tested experimentally.
2.2 The inclusion of cell density
We incorporate the effect of cell adhesion and movement by including equation (A.3) and assume that somitogenesis follows the mechano-chemical theory of biological pattern formation 〚38–41〛. Note that somite formation occurs one cell cycle after cells have been specified as somitic, decoupling the signalling from the compaction process.
As mentioned in the Introduction (Section 1), the condensation of mesenchymal cells and the formation of somites is most likely triggered by the interaction of CAMs, such as N-cadherins, on the surface membrane of somitic cells. This requires spatial and temporal control of expression of CAMs and other components like integrins. Our key biological assumption is that changes in the concentration of the signalling molecule v are related to the density of adhesive sites to which cells in the PSM can attach. Therefore, our model incorporating cell density can be viewed as a chemical pre-pattern model.
In our mathematical formulation, we assume that somitic cells 〚density 〛 satisfy a cell conservation equation in which two main factors, haptotaxis Jh and diffusion Jd, contribute to the cellular flux in the PSM. We have assumed in our model that cells firstly aggregate after experiencing a level of signalling molecule (v) above a certain threshold. Secondly, cell movement is limited to certain regions in the spatio-temporal domain 〚details are presented in Appendix C〛.
Fig. 4 depicts a series of periodic cell aggregations of equal height. These clusters of somitic cells of equal size are formed at regular time intervals. Note that changes in cell density are highly localised, leading to deep troughs in cell density. Cell aggregation occurs in much of the spatio-temporal domain where v is high (see previous simulation in Fig. 2). The compaction process begins at the anterior end of the embryo and moves towards the posterior as a wave. This wave is static in the trunk of the embryo, with cells moving up the PSM as development proceeds.
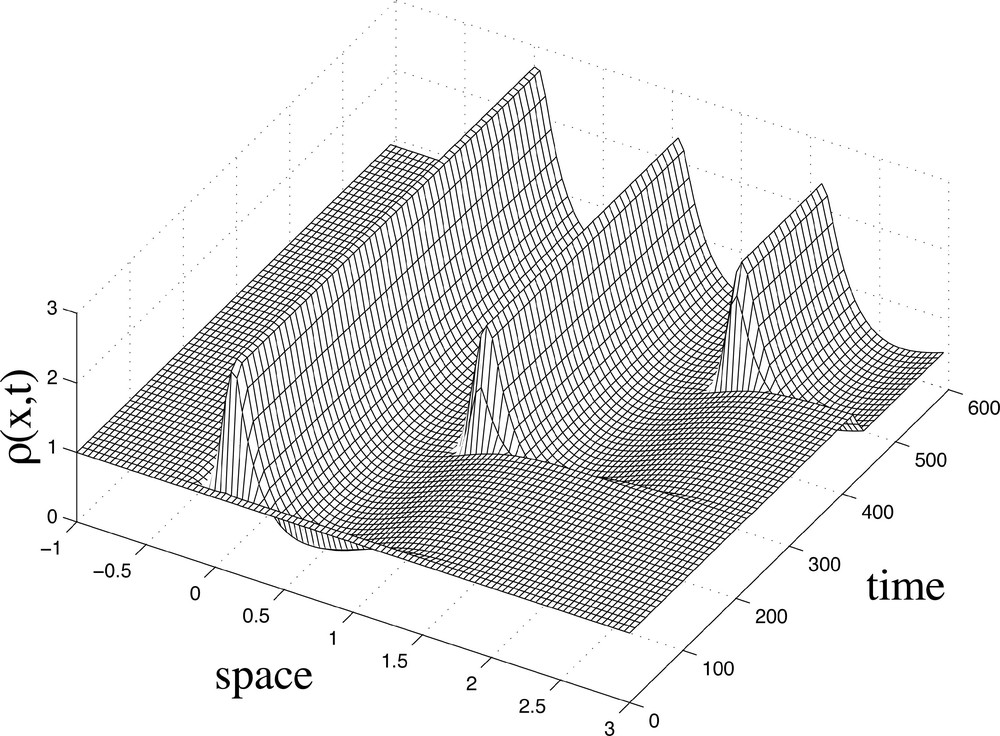
Numerical solution for the model equation (A.3) showing the spatio-temporal dynamics of Each peak of ρ corresponds to a cluster of somitic cells formed by the aggregation of cells where v is high. Parameter values are μ=10-4, c=5×10-2, κ=10, ϵ=10-3, D=50, γ=0.01, k1=0.1, k2=0.02, ξ=6.
3 Discussion
In this paper we have presented and extended a mathematical formulation of the cell cycle model for somitogenesis by adding a third equation to account for cell density. Our mathematical model is based on two key assumptions: (i) the signalling process is decoupled from the compaction process, and (ii) somites are formed as clusters of cells by changes in the concentration of a signalling molecule.
The first assumption is supported by the experimental evidence of Stern and collaborators 〚19, 20〛 linking the cell cycle with somite segmentation. Cell aggregation and compaction during somitogenesis is thought to be due to the interaction of CAMs in the PSM. The mechanisms that regulate the spatio-temporal activation and inhibition of CAMs are unknown. We postulate that the formation of clusters of somitic cells is driven by an adhesive gradient related to the signalling molecule.
In the full mathematical formulation (A.1)–(A.3) of our model, the somitic potential factor u is produced in response to the signalling molecule v. Cells at positions on the axis where u≈1 are termed somitic, while those where u≈0 are non-somitic. The signalling molecule v acts as a chemical morphogen providing a spatio-temporal pre-pattern of somitic and non-somitic cells, while u is providing the positional information for the cells in the PSM, which move depending on the concentration of u 〚42〛. This sub-model may be thought of as providing a chemical (or molecular) pre-pattern to which cells respond via movement 〚equation (A.3)〛. To our knowledge, this is the first model to combine two of the major theories for spatial patterning.
Our results indicate that the cell cycle mechanism can indeed give rise to the periodic pattern of somites observed in normal embryos and also to the abnormal patterns observed after heat shock. It is worth noting that one possible scenario is that two separate clocks linked to the cell cycle regulate somitogenesis. Supporting this suggestion is the finding that another member of the hairy-enhancer of split family, her-1, has been characterised in zebrafish as having an expression pattern in every other somite 〚43〛, unlike any gene thus far described in other vertebrates 〚4〛.
If one clock exists, then a direct link between the cell cycle and the c-hairy-1/l-fng cycling is not obvious. To date, there is no molecular mechanism relating the cell cycle and the c-hairy-1 and the l-fng oscillations. Nevertheless, there is evidence 〚44, 45〛 suggesting that the cell cycle and the c-hairy-1 oscillations are regulated by post-translational modifications such as phosphorylation, and therefore could be part of the same clock. Recently, Kaern and collaborators 〚34〛 have proposed, in agreement with Meinhardt 〚31〛, that segmentation is controlled by one segmentation clock (which has c-hairy-1 and l-fng as components or products) and by the AP subdivision of somites.
In our model, we formulated mathematically a mechanism which regulates segmentation independently of the c-hairy-1/l-fng oscillations. This model also assumes that segmentation occurs independently from AP subdivision. One important point to make is that several mouse mutants reveal that although AP subdivision plays a role in determining somite boundaries, this is not inextricably linked to the initial subdivision of the PSM into discrete units. For example, in most of the Notch pathway mutants, some sort of somites start forming despite the failure of the normal AP subdivision mechanism, but by the time that they should split into AP halves they fall apart and regular segmentation disappears 〚46〛. This suggests that the hairy or lunatic oscillations (these genes are part of the Notch signalling system) are more likely to be part of the mechanisms for the AP subdivision of somites and affect boundary formation indirectly (or later).
In a previous paper, we have addressed the AP subdivision mechanism by developing our own model, which we call the clock-and-induction model 〚33〛. This theoretical description introduces a counting mechanism for cells in the PSM produced by a stationary phase gradient of l-fng. Cell maturation is the result of motion along this gradient. We suggest that l-fng mRNA is expressed periodically and its stable product – a protein – accumulates in a cellular membrane. The formation of a new intersomite boundary could be triggered by the Notch-Delta pathway when a certain threshold is reached; the timing of this response will correspond to a certain number of completed cycles of l-fng expression. Interestingly, several independent experimental groups have recently shown that l-fng mRNA is translated into a stable protein that accumulates in the endoplasmic reticulum and which forms a complex with the Notch protein 〚47–50〛. Then, once a somite is formed the formation of the AP pattern would be triggered by a signalling pathway. In the clock and induction model, we proposed that an induction mechanism by the Notch and Delta signalling pathway would be responsible for the AP pattern. However, in the light of recent experimental evidence 〚51〛, the fibroblast growth factor (FGF) signalling pathway could play an important role in this process. Members of the FGF family are important signalling molecules in several inductive and patterning processes during early embryogenesis. During the formation of the vertebrate nervous system 〚52–54〛 and somitogenesis 〚55〛, FGF8 acts as a signal to determine the AP patterning.
4 Future work: regionalisation of somites
Vertebrae in different regions of the vertebral column are morphologically different, suggesting that somites have defined positional information identities. After somites have been formed a subsequent differentiation process gives rise to unique anatomical structures depending on position along the AP axis. Experiments in chick embryos demonstrate that the positional specification of somites occurs early during somitogenesis 〚56–62〛. When cervical somites are replaced with somites from the trunk region, rib-like structures develop in the cervical vertebral column of the embryo. When thoracic somites are replaced by cervical somites, embryos do not develop ribs 〚56〛.
To our knowledge, the only model that addresses the regional differences of somites is Meinhardt's reaction diffusion type model 〚31, 63〛 for segmentation. This model proposes that the specification of anterior (a) and posterior (p) half-somites occurs by wave-like processes initiated at the posterior end of the PSM, moving anteriorly until it comes to rest at a given distance from the last formed half-somite. The two states, a and p, locally exclude each other, but stimulate each other over a long range. Cells switch from one state to the other until finally reaching a stable state. This can lead to a pattern of stable ... apapap ... stripes forming from anterior to posterior. If the transition from, say p to a, allows a change of segmental specification then each ap pair (or segment) will have a more posterior specification than its predecessor. Thus a segmental pattern can be generated in which segments have different regional characteristics. To set up this pattern, Meinhardt proposed an extracellular diffusive morphogen gradient in which threshold concentrations of the morphogen are required for successive p to a transitions.
However, Meinhardt's model cannot easily explain the results of the experiments demonstrating the positional specification of somites. If an extracellular morphogen gradient set up the somitic pattern, the model would predict that somites would differentiate according to their new position, but in reality specification occurs according to their original location. One would have to assume that rostral-caudal determination occurs very early and is fixed before isolation or rotation of the PSM. This possible explanation requires more detailed investigation.
The cell cycle model proposed originally by Stern and collaborators 〚19, 20〛 does not account for the regionalisation of individual somites leading to specific vertebrae. However, it is very important to notice (as mentioned in Section 1) that vertebrae, at least in the chick embryo, are regionalised in multiples of 6 to 7 somites, which correspond to the number of somites formed per cell cycle. This correlation implicates the cell cycle in the temporal regulation of regional identity specification but with specific reference to the role of Hox genes.
We proposed a mechanism of control which invokes, as in the clock-and-induction model 〚33〛, a cytoplasmatic gradient in the concentration of a factor regulating regional identity specification. Cell division would distribute the cytoplasmic determinant changing its concentration between the mother and daughter cells and thereby confer different fates on the mother and daughter cells activating the family of the Hox genes.
There is now a large body of experimental work showing that positional specification of the PSM requires members of the Hox gene family 〚25〛. Hox gene activation during development correlates with gene position in the Hox complex, a property referred to as collinearity. The spatial and temporal collinearity in the expression of these genes results in unique combinations of Hox genes in defined groups of somites and their derivatives along the AP axis 〚64, 65〛. This led to the suggestion that a Hox code specifies the identity of somites 〚26, 27〛. The role of Hox genes in positional specification has been analysed by interfering with or altering the expression of single Hox genes or by simultaneously perturbing the expression with retinoic acid, which is implicated in the specification of the axes during development 〚66〛. It has also been proposed that the FGF signalling pathway is involved in the caudalisation of somites by coordinating either the segmentation process or the mechanism involved in somite boundary formation and the spatio-temporal Hox gene activation 〚51, 55, 67〛.
The mechanism we proposed for the activation of the Hox genes is the same as that proposed during limb development 〚68〛. The cytoplasmatic determinants are molecules which bind with high affinity to the Hox complex blocking access to the transcription machinery. The transcriptional antagonist would become diluted by successive cell divisions allowing access to the genes of the Hox complex. As dilution progresses many more genes of the Hox complex are expressed allowing somitic regionalisation.
A similar sort of behaviour of cell cycle kinetics has been modelled for cell growth and maturation during carcinogenesis (see, for example, 〚69〛). In the literature, there has been a predominant trend to model this process by (i) a branching process approach and (ii) a partial differential equations approach 〚70〛. A typical partial differential equation formulation is the Lotka-von Foster equation, where chronological time, cell age, population density and growth rate terms are described in a transport equation with additional boundary conditions 〚71〛.
This idea can be also applied to lineage intrinsic specification, in which an asymmetric cell division distributes some sort of cytoplasmic determinant unequally between daughter cells and thereby confers different fates on distinct daughter cells and their descendants. In certain organisms, such as the nematode Caenorhabditis elegans and other protostomes, the invariant patterns of asymmetric cell division and differentiation arise from mechanisms operating through lineage cell ancestry and cell-cell adhesion interactions.
Experimental research is presently being carried out to study the key components of the molecular clock and how the molecular oscillations are modulated by the cellular aspects of somitogenesis. A challenging future problem for mathematical modelling will involve linking the pattern formation mechanisms at the cellular level with the molecular control of cell properties in other developmental processes. So far, somitogenesis has proven to be an excellent potential example for a detailed study of the marriage between cellular and molecular biology.
Acknowledgements
This research (SS) has been funded by the José Gregorio Hernández Award (Academia Nacional de Medicina, Venezuela; Pembroke College, Oxford), ORS Award (Committee of Vice-Chancellors and Principals of the Universities the United Kingdom), Programa de Cofinanciamiento Institucional IVIC-CONICIT (CONICIT, Caracas) and Lord Miles Senior Scholarship in Science (Pembroke College). PKM would like to acknowledge the School of Mathematical Sciences, Queensland University of Technology for their hospitality and support via a QUT Visiting Fellowship. DMI was funded by a Marie Curie Fellowship as part of the Training and Mobility of Researchers (TMR) programme administered by the European Commission. DJG would like to thank the Medical Research Council for a Career Development Fellowship.
Appendices
A Model equations
The model equations are developed in two spatial dimensions but many of the key properties of the model can be understood by considering the one-dimensional version. In this case, the model equations in non-dimensional form are:
| A.1 |
| A.2 |
| A.3 |
| A.4 |
| A.5 |
The embryonic axis is taken fixed with respect to the cells, and the node and segmental plates assumed to move down it at a constant rate c. We consider
We have derived 〚4〛 constraints on the model parameter values to ensure that the cells of a potential somite adhere together resulting in the segmentation of a discrete somite. Setting κ⪢1, γ⪡1, μ⪡1, ϵ⪡1 and D⪢1, we ensure that the constraints on the model parameter values are satisfied. The speed of the pattern is taken, for illustrative purposes, to be c = 5 × 10–3 in non-dimensional terms.
B The effects of heat shock in somitogenesis
The experimental evidence 〚18〛 suggests that the pattern of anomalies depends on the relation between two parameters: (i) the number of somites formed per cell cycle which is approximately 6 to 7 somites, and (ii) the length of the block caused by heat shock relative to the time between P1 and we estimate η≈0.6 (equal to the time duration of heat shock divided by the time to form a somite).
The heat shock treatment of an embryo has the effect of increasing the time between the points P1 and P2 in the cell cycle model for somite formation as it blocks M phase of the cycle. This leads to a delay in the production of u and v. The heaviside terms can be carefully modified to mimic the required delay. Note that in (A.1) – (A.2), for a given point x, the production of u and v begins at and t=x/c, respectively. To simulate the effect of heat shock, we partition the x-axis into intervals for where
| B.2 |
The effect of condition (B.2) on the signalling process produces a discontinuity in the heaviside function χu at the point x=αi when and at the point when When the discontinuity in the heaviside function remains fixed at x=αi until Therefore, points in the interval are unable to respond to changes in the concentration of v until time If at there is a pulse in v, then for only cells allocated in points where x≤αi will respond to the signal. The cells which lie in the interval are unable to respond until at which time the concentration of v may be too low to activate production of u. Condition (B.2) also produces a discontinuity in the heaviside function χv at the point x=αi when t=αi/c and at the point when When t≥αi/c, the discontinuity in the heaviside function remains fixed at x=αi until time Hence, there is no pulse in v until although u may be low for x≥αi. The pulse in v emitted at is much larger than normal as all points in the interval can begin production of v.
C Cell density equation
We assume that somitic cells 〚density 〛 satisfy a cell conservation equation in which two main factors, haptotaxis Jh and diffusion Jd, contribute to the cellular flux in the PSM
These two processes are highly nonlinear because τ and Dρ need to be chosen as functions of v for biological realism. The details leading to these results will be reported elsewhere. We have chosen τ and Dρ 〚see, (A.4) – (A.5)〛 based on two assumptions. Firstly, cells aggregate after experiencing a level of signalling molecule above a certain threshold. Secondly, cell movement is limited to regions in the spatio-temporal domain where x>ct. Our numerical simulations yield results consistent with those observed in vivo.