1 Introduction
Plusieurs études ont mis en évidence le fait que de nombreux phénomènes critiques biologiques, naturels, sociologiques et économiques obéissaient à une loi log-périodique : tremblements de terre 〚1〛, krachs boursiers 〚2〛, sauts évolutifs au cours de l’évolution des espèces 〚3, 4〛, crises économiques 〚5〛, phénomènes de turbulence 〚6〛... Émerge ainsi l’idée que ce type de comportement des crises temporelles pourrait se révéler très général, aussi bien dans le monde inorganique qu’organique. Ces phénomènes trouvent une description et une explication dans le cadre plus large de l’étude des lois invariantes d’échelle et de la relativité d’échelle 〚7–9〛. Plusieurs éléments caractérisent ces différents phénomènes évolutifs : structures fractales, existence de ruptures, organisation hiérarchique, existence d’accélérations ou de décélérations et possibilité de prédictibilité, mais à caractère indéterministe (probabiliste), de la survenue de crises temporelles futures.
Dans le cas précis de l’évolution des espèces, la démarche a été de constater la présence de sauts évolutifs majeurs qui sont à l’origine de bifurcations. Le schéma évolutif global est alors assimilé à un arbre de la biodiversité, « l’arbre de la vie », dont les nœuds sont identifiés aux sauts évolutifs et les longueurs des branches aux intervalles de temps entre ces événements majeurs 〚3〛. Afin d’obtenir les données les plus significatives possibles, les analyses ont exclusivement porté sur des cladogrammes établis par les divers spécialistes des groupes considérés 〚10〛. Ces phénomènes sont décrits par une loi de type : Tn = Tc + (T0 – Tc) g–n, où Tc est l’époque critique de convergence (ou de divergence dans le cas d’une décélération), T0 un événement quelconque de la lignée, n le rang de survenue d’un événement donné et g le rapport d’échelle entre intervalles de temps successifs (supposé constant en première approximation, ce qui relève de l’invariance d’échelle discrète). Écrite sous une autre forme, cette loi devient : log(Tn – Tc) = log(T0 – Tc) – n log g, ce qui signifie une organisation périodique des événements du point de vue de cette variable logarithmique.
Une telle accélération « log-périodique », statistiquement significative, a ainsi été retrouvée, à différentes échelles, pour l’évolution globale de la vie, depuis la première cellule, pour les équidés d’Amérique du Nord, les rongeurs (diversification actuelle), pour les dinosaures sauropodes et théropodes et pour les primates, vers des époques critiques Tc différentes dépendant de la lignée. Une loi de décélération a été observée, en revanche, pour les échinodermes et le début de diversification des rongeurs.
Dès lors, eu égard aux relations souvent dressées entre la phylogénie et l’embryologie 〚11, 12〛, il semblait intéressant de vérifier si une telle loi pouvait s’appliquer à une autre échelle de l’évolution du vivant, à savoir le développement de l’embryon. La méthodologie proposée dans les études antérieures est mise à l’épreuve ici pour le cas des grandes étapes connues de l’embryologie humaine. Par extension, il a été recherché si un prolongement pouvait être opéré après la naissance, en reprenant les grandes étapes du développement de l’enfant et de l’adolescent, même s’il est plus délicat de fixer des âges précis correspondant à des sauts significatifs en raison des grandes variabilités inter-individuelles.
2 Matériel et méthodes
2.1 Définition des étapes prises en compte
La principale difficulté de l’exercice est de situer les dates repères qui constituent autant de marches ou de nœuds dans la poursuite du développement. Ces grands événements doivent correspondre à l’apparition d’une innovation majeure, d’une différenciation nouvelle, d’un saut qualitatif important. Les étapes qui sont mentionnées ci-après correspondent à un consensus général parmi les embryologistes 〚13–15〛. Celles signalées après la phase embryonnaire correspondent plus particulièrement aux étapes du développement du système nerveux 〚15, 16〛 et celles après la naissance au développement psychomoteur de l’enfant 〚17, 18〛.
L’embryologie exprime de la façon suivante les grandes étapes du développement après le temps 0 de la fécondation.
- • Le stade « deux cellules » (deux blastomères) est atteint 30 h après la fécondation.
- • Les divisions cellulaires successives aboutissent ensuite à la formation d’un amas cellulaire, la morula (16 blastomères) au troisième jour. Les cellules expriment jusqu’à ce stade d’une façon équivalente tout le potentiel génétique de l’individu (totipotence).
- • Au quatrième jour, il se forme une cavité : l’œuf est appelé blastocyte ; les cellules se différencient en une couche externe, le trophoblaste (qui deviendra le placenta et ses annexes) et une masse cellulaire interne, l’embryoblaste, à partir de laquelle l’embryon se développera.
- • Au sixième jour, se produit la nidation ; le blastocyte adhère à l’épithélium de l’endomètre. Le trophoblaste prolifère et se différencie pour préparer l’implantation de l’œuf dans l’endomètre, qui se produit au dixième jour. Ces étapes ne sont pas à proprement parler des étapes de développement de l’embryon lui-même.
- • Au cours de la deuxième semaine se produit la différenciation entre l’entoblaste et l’ectoblaste. À noter qu’au dixième jour, les cellules sont encore plus ou moins pluripotentes (elles ne sont plus totipotentes, mais peuvent se différencier en un grand nombre de tissus). Au 14e jour se constituent les membranes oro-pharyngée, d’une part, et cloacale, d’autre part.
- • La gastrulation est l’étape majeure au cours de laquelle le disque embryonnaire didermique devient un embryon tridermique. La gastrula débute à la troisième semaine. Trois structures importantes se constituent : la ligne primitive (15e jour), la chorde dorsale (16e jour) et le tube neural (neurulation) en fin de troisième semaine ; l’ébauche cardiaque commence à battre à la même date.
- • Entre la quatrième et la huitième semaine, l’événement majeur est la délimitation de l’embryon. On passe à un embryon sensiblement cylindrique et trois plicatures le délimitent dans un plan transversal (plicature transversale) et dans un plan longitudinal (plicatures craniale et caudale). Dans le même temps, les arcs branchiaux se développent. Au 28e jour, quatre paires d’arcs branchiaux sont présentes, tandis qu’apparaissent les ébauches des membres. Pendant la cinquième semaine, l’extrémité céphalique croît. Au cours de la sixième semaine, la segmentation des membres se poursuit. Les différents éléments présents deviennent de plus en plus apparents, la face se forme entre la cinquième et la huitième semaine. On arrive, à la fin de la huitième semaine, à un embryon qui a acquis son aspect humain. On considère qu’entre la cinquième et la neuvième semaine, les cellules ont une multipotence élargie (possibilité de se différencier en plusieurs tissus différents).
- • On considère que c’est à la fin du deuxième mois que se termine la période embryonnaire, à l’issue de laquelle l’ensemble des organes est en place : alors commence la période fœtale.
- • Le développement du système nerveux central débute dès la troisième semaine par la neurulation, comme indiqué ci-dessus, pour terminer la mise en place de toutes les structures vers la douzième semaine. La plaque corticale est identifiable à partir de la neuvième semaine. La multiplication neuronale est intense à cette période, pour s’épuiser vers la seizième semaine. Les premières synapses se réalisent dès le 60e jour et cette synaptogenèse se poursuit après la naissance. La myélinisation enfin débute plus tardivement, pour s’achever au moment de la puberté. Le cerveau arrêtera de croître à l’âge de cinq ans.
- • La maturation des organes sexuels survient entre la troisième et la 12e semaine.
- • La maturation des cellules hématopoïétiques et des lymphocytes connaît aussi une étape importante à 12 semaines : les cellules hématopoïétiques de première génération disparaissent pour laisser place aux cellules issues de l’hématopoïèse hépatique ; la différenciation des lymphocytes T et la possibilité de synthétiser des immunoglobulines commencent aussi à cette date.
- • La formation des poumons débute vers le 24e–26e jour ; ils atteignent une structure histologique quasi définitive vers la 24e–26e semaine. C’est cette date qui constitue le seuil de viabilité minimale d’un fœtus né avant terme.
- • La naissance intervient en principe 266 j (38 semaines) après la fécondation.
Après la naissance, les grandes étapes du développement psychomoteur de l’enfant sont les suivantes 〚17, 18〛 :
- • prise de contact/identification de sa propre personne, préhension : 6–8 mois ;
- • phase de déplacement, phase d’imitation : 9 mois ;
- • marche : 12–18 mois ;
- • acquisition du langage, abstraction : entre 1 an et 2 ans et demi ;
- • sociabilisation et dents de lait toutes sorties : 3–4 ans ;
- • phase d’identification et apparition des dents définitives : 5–7 ans ;
- • phase d’opposition, pré-adolescence et maturité sexuelle : 10 ans ;
- • puberté, découverte de la sexualité : 11–13 ans ;
- • acquisition de l’autonomie par rapport aux parents, majorité : 18–25 ans.
Il est clair que, dans ces dernières étapes, les variations inter-individuelles sont importantes et que les barres d’erreur augmentent au fur et à mesure de l’avancement dans l’existence : il est délicat de choisir tel ou tel événement. En même temps, des phases proches dans le temps peuvent être regroupées. Il peut être considéré par exemple que la phase de contact de 6–8 mois et la phase de déplacement à 9 mois ne constituent qu’une seule phase, mais le choix peut être discuté. De même, l’ensemble du processus d’acquisition de la marche, d’une part, du langage d’autre part, se déroule sur plusieurs mois, avec des périodes de recoupement. C’est vers 2 ans–2 ans et demi qu’une étape importante est franchie. Enfin, seule une étape à 12 ans sera prise en compte et non une à 10 et une à 12. Les analyses statistiques précédemment réalisées 〚4, 10〛 montrent que ces variations ne modifient en rien la loi d’évolution.
Ces données sont résumées dans le Tableau 1, qui donne la liste des événements retenus ainsi qu’un intervalle de confiance de leurs dates correspondantes.
Liste des événements retenus, suivis des dates minimales et maximales pour chacun d’entre eux.
| Rang | Événements | Équivalent jours |
| 0 | fécondation | 0 |
| 1 | deux cellules | 1,25 |
| 2 | morula | 3 |
| 3 | blastocyte | 4–5 |
| 4 | deux couches | 6–8 |
| 5 | pluripotence | 10–12 |
| 6 | gastrulation | 16–21 |
| 7 | ébauche des membres | 28–35 |
| 8 | fin de la phase embryonnaire | 49–63 |
| 9 | 11–13 semaines | 77–91 |
| 10 | 24–26 semaines | 168–182 |
| 11 | naissance | 259–273 |
| 12 | 6–9 mois | 449–540 |
| 13 | 18–30 mois | 815–1180 |
| 14 | 3–4 ans | 1361–1726 |
| 15 | 5–7 ans | 2091–2821 |
| 16 | 11–13 ans | 4281–5011 |
| 17 | 18–22 ans | 6836–8296 |
2.2 Analyse statistique
Les dates observées Tn de la chronologie embryonnaire seront ajustées à la loi à deux paramètres g et Tc : Tn = Tc + (T0 – Tc) g–n. Nous déterminerons simultanément les valeurs de g et Tc à partir des séquences de données observées par ajustement numérique (méthode des moindres carrés). On utilisera comme estimateur statistique la variable t de Student associée au coefficient de corrélation dans le diagramme 〚rang n de l’événement, log(Tc – Tn)〛 (cf. Fig. 1). Pour chaque valeur de Tc, on calcule les valeurs de g et de t. Les valeurs optimisées de g et Tc correspondent alors au pic de la courbe t = f(Tc) (cf. Fig. 2). Cependant, les rangs des événements étant a priori classés dans l’ordre chronologique, le niveau de signification statistique associé à une valeur donnée de t n’est pas celui d’une étude de corrélation ordinaire. Des simulations Monte-Carlo ont donc été effectuées pour calibrer cet estimateur en appliquant la même analyse à des dates choisies au hasard et triées par ordre chronologique. Les niveaux de probabilité donnés dans la suite sont déduits de cette méthode. On trouve, en particulier, que les seuils de probabilité de 1/100 et 1/1000 (3 σ pour une gaussienne) correspondent, selon le nombre de dates, aux valeurs du pic de la variable t de Student reportées dans le Tableau 2.
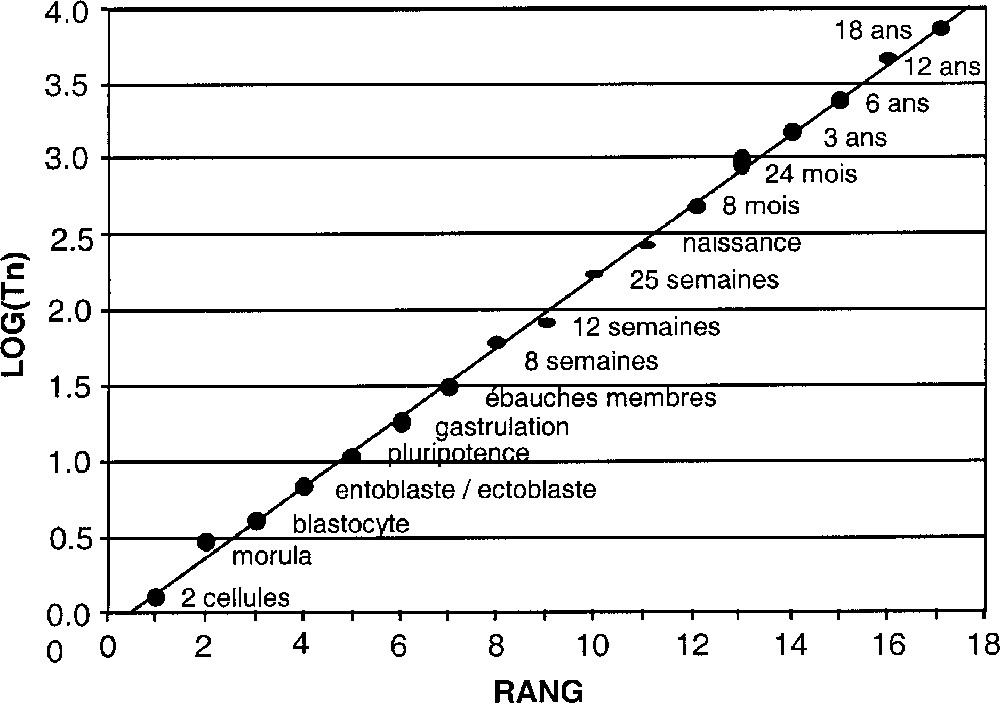
Logarithme décimal log Tn des dates des étapes du développement humain, comptées à partir de la conception, en fonction de leur rang n. La hauteur des points donne l’intervalle de confiance sur les dates (cf. Tableau 1 ; on a supposé une barre d’erreur de ±12% sur les trois premières dates).
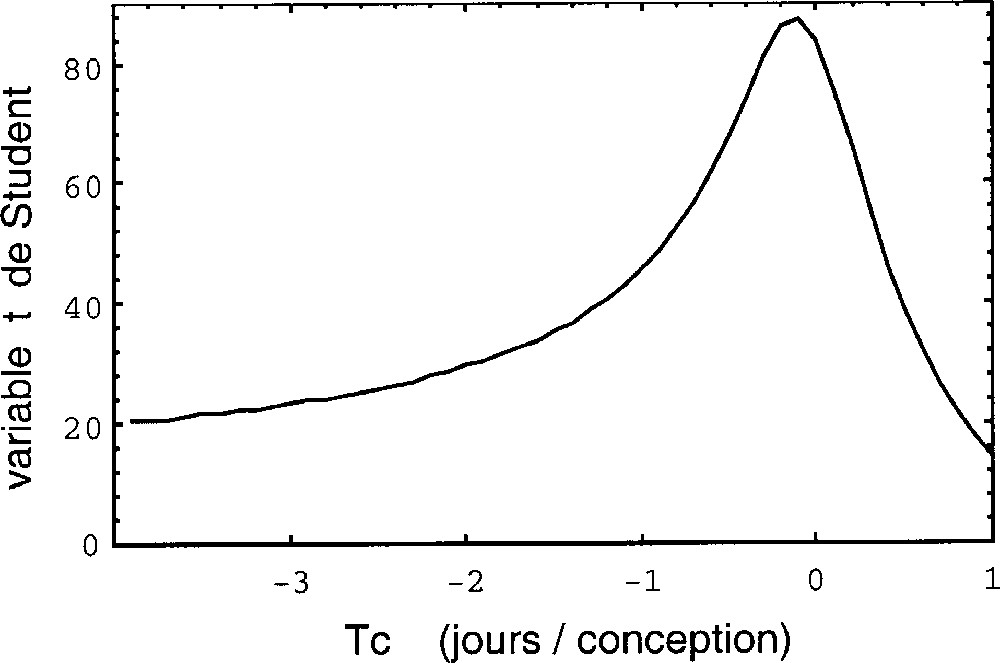
Variation de la variable de Student associée à la corrélation (n, log Tn), en fonction de la variation de l’époque critique Tc pour les données du développement humain depuis la conception (origine exclue) jusqu’à l’âge adulte (voir Fig. 1). On trouve un meilleur ajustement pour une époque critique Tc = –0,1 ± 0,7 j, en très bon accord avec la date de conception (T0 = 0). La probabilité d’obtenir un tel pic 〚t(Tc) = 87,3〛 par hasard est inférieure à 10–4.
Valeurs des pics de la variable t de Student correspondant aux seuils de probabilité de 1/100 (2,3 σ) et 1/1000 (3 σ) selon le nombre de données de l’échantillon.
| n | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 |
| t (1‰) | 100 | 50 | 46 | 42 | 37 | 38 | 44 | 50 | 52 |
| t (1%) | 34 | 28 | 27 | 27 | 26 | 30 | 32 | 37 | 40 |
3 Résultats
Plusieurs simulations ont été réalisées avec tout ou partie des dates pour estimer la convergence de ces étapes avec le modèle log-périodique et évaluer la probabilité de trouver une telle combinaison.
3.1 Données sans l’origine jusqu’à la naissance
On trouve dans ce cas une valeur optimisée de Tc de –0,3 (+0,8, –1,5) j (erreur donnée par la largeur à mi-hauteur), avec t(Tc) = 41,5. La probabilité d’obtenir un tel ajustement par hasard est P < 10–3 (N = 11 points). Le paramètre g est égal à 1,67 ± 0,02, une valeur comparable à ce qui était trouvé lors de l’analyse de l’arbre évolutif des espèces. On confirme ainsi une décélération significative à partir de la date de conception, aux barres d’erreur près. La date de conception Tc est rétroprédite à partir des événements ultérieurs, à 7 h près.
3.2 Données depuis la conception (origine exclue) jusqu’à l’âge adulte (18 ans)
La Fig. 2 fournit une valeur de Tc de –0,1 (+0,5, –1,0) j, avec t(Tc) = 87,5. La probabilité d’obtenir un tel ajustement par hasard est de P < 10–4 (N = 17 points). Ce résultat est statistiquement hautement significatif. Le paramètre g est égal à 1,71 ± 0,01, soit encore une valeur similaire à ce qui était retrouvé dans l’analyse de la phylogénie. Les dates du développement entre la naissance et la fin de croissance améliorent encore la précision et la signification statistique. La date de conception Tc est obtenue à 2 h près.
3.3 Données du développement postérieures à la naissance
Dans ce cas on trouve un Tc égal à –130 ± 150 j, avec t(Tc) = 35,4. La probabilité d’obtenir un tel ajustement par hasard est de P < 2×10–3 (N = 7 points). On trouve Tc = –70 j si on enlève la date de naissance (avec une plus grande erreur). La valeur de g = 1,62 reste proche des valeurs précédentes.
4 Discussion
Le résultat principal de ce travail indique l’existence d’une analogie entre phylogénie et développement embryologique sur le plan de l’évolution, mais à des échelles différentes, l’ontogenèse étant liée à la phylogenèse 〚12〛. Le modèle log-périodique décrit en effet, avec un haut niveau de signification statistique, aussi bien la chronologie évolutive d’un grand nombre de lignées de l’arbre de vie que les étapes de l’embryologie humaine. La valeur du paramètre g est en outre très proche, soulignant encore l’analogie entre les deux phénomènes.
La capacité descriptive du modèle log-périodique est moins marquée après la naissance, mais cette relative lacune peut parfaitement être expliquée par l’importance des variations inter-individuelles. Les étapes marquantes de l’enfance et de l’adolescence sont affectées de barres d’erreur plus importantes. Dans la simulation réalisée, les points qui suivent la naissance décélèrent depuis une date située plus d’un an avant la naissance, la date de conception étant incluse dans les barres d’erreur. L’information sur le temps de gestation semble donc rester présente, bien que d’une manière grossière, dans la chronologie des étapes du développement de l’enfant (on peut citer à cet égard les travaux de Sornette 〚19, 20〛 concernant la prédictibilité de la naissance). Ce phénomène pourrait s’éprouver en appliquant la même analyse au développement d’autres espèces.
Il reste possible, dans ces conditions, sur la base des données utilisées, de prolonger théoriquement la série. On trouve alors les étapes suivantes en utilisant une valeur de g de 1,71 : une étape entre 30 et 35 ans, une autre vers 52–57 ans et une troisième peu avant 100 ans.
Les deux dernières étapes rendent compte aisément de l’observation usuelle de changements de capacités physiques et intellectuelles, même si, là encore, les variations individuelles sont énormes. La valeur autour de 33 ans correspond à l’apogée de la vie physiologique humaine avant qu’elle ne commence à se dégrader.
5 Conclusion
La loi log-périodique qui décrit les phénomènes critiques biologiques, inorganiques ou économiques s’applique également aux diverses étapes du développement embryologique humain. Nous nous sommes cantonnés ici à une analyse purement descriptive, mais on peut rappeler que ce type de loi peut se déduire dans le cadre du groupe de renormalisation 〚1, 6, 7〛 et de la relativité d’échelle 〚8, 9〛. Elle ne nous donne pas d’informations sur les mécanismes d’évolution eux-mêmes (car elle se situe au seul niveau de la chronologie), mais plutôt sur une forme de contrainte qui s’applique à eux comme à d’autres phénomènes critiques. L’une des interprétations est liée à l’observation du fait qu’il s’agit de phénomènes à mémoire, chaque niveau d’organisation prenant appui sur les précédents, sans saut en arrière possible. À cet égard, les analogies d’évolution entre phylogénie et embryologie, qui en fin de compte obéissent aux mêmes contraintes (différenciation des couches cellulaires, puis des tissus, puis des organes…) illustrent la mise en œuvre d’un tel phénomène à mémoire à toutes les échelles d’organisation du vivant.
Remerciements
Ce travail constitue une contribution au thème Signal morphologique de l’Évolution de l’UMR CNRS 5561 « Biogéosciences–Dijon ». Nous remercions Didier Marchand pour sa revue critique, ainsi que Didier Sornette pour ses utiles remarques.
Abridged version
Several studies have shown that many biological, natural, sociological and economic critical phenomena obey a log-periodic law: earthquakes 〚1〛, stock market crashes 〚2〛, evolutionary leaps 〚3, 4〛, economic crisis 〚5〛 and turbulence phenomena 〚6〛. Thus emerges the idea that this behaviour typical of temporal crisis could be extremely widespread, as much in the organic world as in the inorganic one. These phenomena can be described and explained within the vaster framework of the study of scale invariance laws and scale relativity 〚7–9〛. Several elements characterise these different evolutionary phenomena: fractal structures, hierarchy levels, the existence of ruptures, accelerations and decelerations, the possibility of predictability (in a statistical way, with indeterministic characters) of future temporal crises.
In the case of species evolution, we observed the occurrence of major evolutionary leaps leading to bifurcations. The global pattern is assimilated to the tree of life, whose bifurcations are identified to evolutionary leaps and branch lengths to the time intervals between these major events 〚3〛. These phenomena are described by a law of the type: Tn = Tc + (T0 – Tc) g–n, where Tc is the critical convergence time (or critical divergence time in the case of deceleration), T0 is any event in the lineage, n the rank of occurrence of a given event and g the scale ratio between successive time intervals. Such a chronology is periodic in terms of logarithmic variables, i.e. log(Tn – Tc) = log(T0 – Tc) – n log g. In order to obtain the most significant data possible, analyses are exclusively based on cladograms established by specialists in the specific field studied 〚10〛.
A statistically significant log-periodic acceleration was found at different scales for global life evolution, for primates, for sauropod dinosaurs, for rodents and North American equidae. A deceleration law was conversely found for echinoderms and for the first steps of rodent evolution.
Considering the relationships between phylogeny and ontogeny 〚11, 12〛, it appeared interesting to verify whether such a law could be applied to living evolution on another scale, that of ontogeny. The proposed methodology used in previous studies is here applied to the major stages of human embryology.
We have tried to extend this analysis to the major stages in post-birth development from childhood to adolescence, even though it is more difficult to define a precise age for a significant leap, because of great inter-individual variability.
The 266-day (38 weeks) pre-birth periods retained correspond to a general consensus amongst embryologists 〚13–15〛. After birth, we considered the main stages of child psychomotricity development 〚17, 18〛.
We show that the log-periodic law describing critical biological, inorganic and economic phenomena may also be applied to the various stages of human embryological development. Our analysis is purely descriptive, but it is important to remember that this type of law can be deduced from the renormalization group laws 〚1,6,7〛 and from scale relativity 〚8, 9〛. It gives no information on evolution mechanisms but on a constraint that applies here as in other critical phenomena.
One possible interpretation is that it concerns memory phenomena, with each level of organisation building on previous levels, with no possibility of backward leaps. The evolutionary analogies between phylogeny and ontogeny that obey the same constraints (cell differentiation, tissue and organ building) illustrate the expression of such a memory phenomenon at each scale of organisation of the living world.


