1 Biological and physical introduction
Pattern formation of branching organs (lungs, kidney, mammary glands, etc.) is not well understood. Needless to say, it is crucial to better understand this process in order to make progress in such fields as intensive care to premature newborns, treatment of pulmonary pathologies, effects of hypertension on the morphology of kidneys etc.
It has been proposed recently that the branching morphogenesis (BM) of organs consists of a viscous fingering of the epithelium as it penetrates into the mesenchyme 〚1, 2〛. In physical problems, viscous fingering occurs when an interface I is pushed into a fluid medium M, by action of mechanical pressure 〚3〛. The word ‘fingering’ was coined metaphorically because the result is somewhat reminiscent of the shape of fingers. When the less viscous fluid is pushed towards the more viscous fluid, the interface I tends to develop finger-like branches, one or just a few branches in a finite medium, and an arbitrary number of such branches in a wider domain. The so-called Mullins–Sekerka 〚3, 4〛 instability favours growth of tubes and branches by action of the point effect in the pressure field, and it sets their typical diameter to a capillary length imposed by surface tension at the interface.
In the absence of surface tension anisotropy, this instability leads to growth of disordered patterns, which belong to a universal family of dichotomous tip-splitting patterns 〚3–5〛. This family is generally called the DLA family, from Diffusion Limited Aggregation, a model that also generates this type of patterns 〚4〛. However, in the presence of an anisotropic surface tension, the pattern is more regular, and it exhibits side-branches, instead of dichotomies, which bud out at specific angles. These patterns are known as dendrites. This is examplified by the shape of snowflakes 〚6〛, which is selected (in a strict physical meaning) by the crystalline anisotropy of the underlying atomic lattice. The regular branches of dendritic crystals are aligned with crystallographic directions.
When this model is adapted to biological growth 〚2〛, the interface I is the epithelium/basement membrane/fibroblasts interface, the medium M is the mesenchyme, and the pressure is the intra-luminal pressure. The surface tension is that of the epithelium/basement membrane/fibroblasts interface. The model gives a straightforward mechanical explanation for the very existence of branched tubes in such organs. It accounts naturally for the pattern of growth of branching organs in several instances, where the organs are indeed disordered, especially in distal regions, or when the epithelium is cultured in matrigel. However, viscous fingering falls short of describing regular patterns of branching morphology in biology because the current alternative to disordered structures 〚3–5〛 is snowflake like dendritic growth in the presence of a crystalline anisotropy.
Several facts show that BM is quite often not dominated by statistical noise: the branching points are stereotypic (branching points look similar), they are deterministic (branching occurs at specific places), and branching has memory effects (the next branching event is often in a plane at right angles to the previous one). The typical shape of bifurcation points consists of three co-planar straight tubes connected with precise angles. This is especially true of proximal parts of organs.
Although this can be recognised as a specific kind of order, this order of branching organs certainly does not look like a crystalline order. Organ ducts or airways do not look like crystal dendrites, and branches of organs are not oriented in crystallographic directions. It is obviously not a crystalline anisotropy of a 3D lattice of cells that stabilises the ducts, drives the branching and selects the overall regular pattern of organs.
In this article, we show that the typical orientational order (nematoid) of fibroblasts, which is also observed in fingerprints, has an anisotropic surface tension with morphogenic consequences. This anisotropy induces the correct shape selection of actual fingers and the pattern of iteration of BM.
2 The nematic order of fibroblasts
The epithelium is an ordered layer of cells 〚8〛. The mesenchyme is composed principally of fibroblasts. Epithelium and the mesenchyme connect via a basement membrane. There is little information about the epithelium structure although it is almost always represented in cross section as a regular arrangement. Information on fibroblast organisation is more abundant: in vitro, fibroblasts tend to orient themselves along their longitudinal direction and generate streams of cells which adopt the 2D order known as nematic order in physics of liquid-crystals. Also, collagen fibres are laid down by fibroblasts. The nematic order is characterised by a local alignment of the features (collagen fibres, and fibroblasts, in this case), which tend to form a global order. If the order were globally perfect, all the entities (fibres and cells) would be aligned parallel to one direction. But there always remain topological defects in this order, the most frequent of them being known as 1/2 defects or ‘hair parting’ (Fig. 1A) and –1/2 defects or ‘zebra shoulder’ (Fig. 1B) 〚8〛. The existence of such an order in vivo is evidenced by the structure of actual fingerprints, and it is claimed to exist in all organs mesenchyme (see especially 〚9〛, Chap. 18, Fig. 3). The nematic arrangement, as represented generally in 2D, cannot be reconstructed in 3D without defects of the order. We now address the question of the equilibrium shape of a surface with such an orientational order.
A. Typical nematic order of fibroblasts with a 1/2 defect (‘hair parting'), in vitro. B. Typical nematic order of fibro 〚8〛.© Elsdale T.R. and Wasoff F.L.
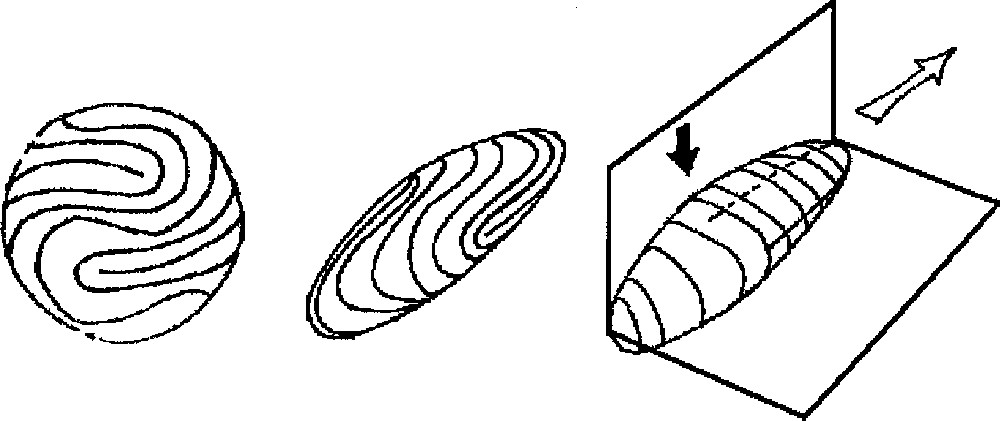
A. (Left) Symmetrisation of the finger. From the pattern of fingerprints, we construct a ‘spherical fingerprint' by symmetrising the pattern across the dorso-ventral plane and the proximo-distal one. We get a typical arrangement as shown here. The choice of the defect inside the U-turn may be slightly different; it does not matter. For the sake of clarity, we have put four simple 1/2 defects. They appear as dead-ends, around which streams of lines make a U-turn. B and C. Construction of the ‘fingerprint crystal' as estimated from the surface tension (tensor) distribution. Middle, the shape and its distribution of streamlines. Right, a drawing showing the planes of symmetry. Directions of weaker surface tension correspond to smaller radius of curvature. The pattern that is obtained is extremely reminiscent of an actual fingertip. Also, this predicts the small radius of curvature between the dorsal and ventral sides, the larger radius from the left and right sides of a finger, and the little bulge in the defect region in the centre of the ventral side of the fingertip pulp (black arrow). The white arrow points to the direction of fast growth (see text), the black points to the regions of secondary growth. These directions are found in perpendicular planes, and the shape exhibits a symmetry breaking along these planes, with respect to the sphere. For the sake of clarity, we have drawn a rather sharp resulting shape; of course, the sharpness will depend on the actual values of the surface tensions. One should note that, in crystal growth, an anisotropy of the order of 1% is enough to select the growth direction.
3 The equilibrium shape of a fingerprint crystal
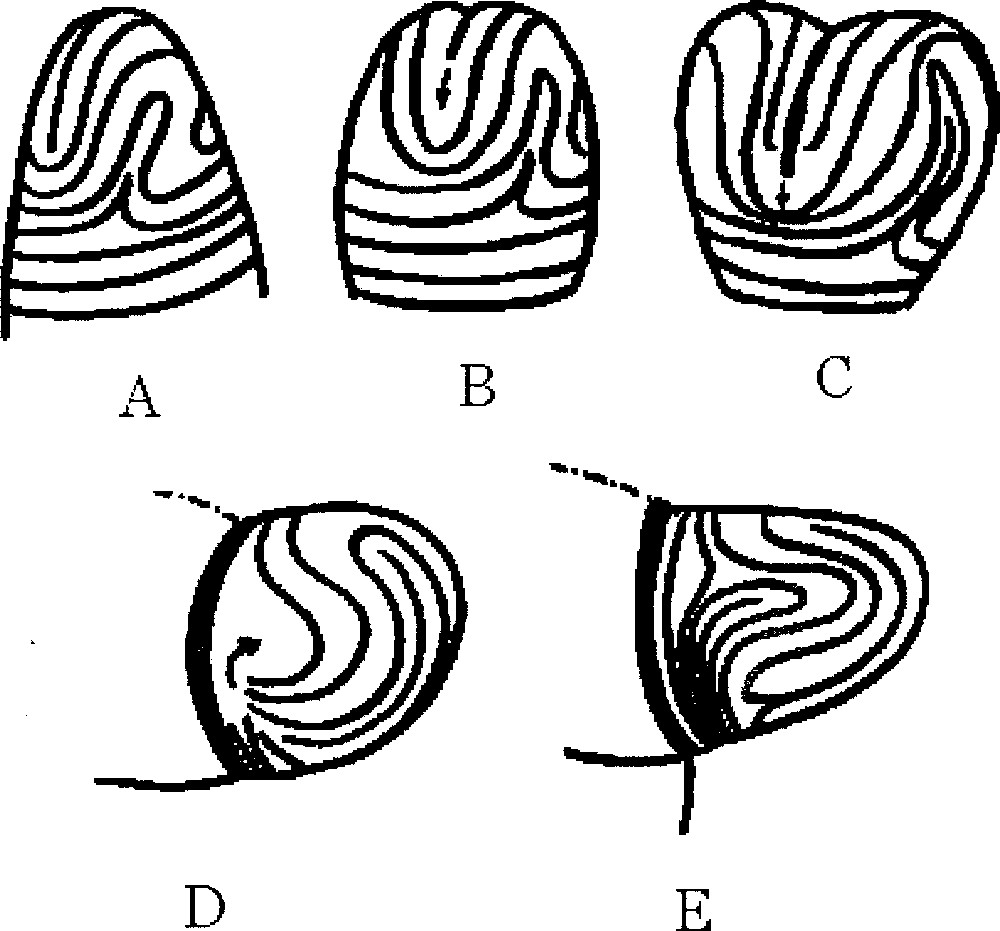
Let us bear in mind that fingerprints always exhibit an arrangement of defects like the one represented in Fig. 2A mathematical theorem, also valid for end of tubes or for hair on the head, states that one cannot cover a spherical or hemispherical structure with aligned ‘particles’; hence the existence of defects of the alignment on the epidermal ridges. Far from the tip of the finger, towards the second phalanx, the lines run in a circular azimuthal arrangement. Towards the apex of the finger, the pattern changes to a stream of lines that runs from the left side to the right side of the finger, generally forming an arch parallel to the nail’s edge. This general structure is observed in more than 95% of the fingers. 60% of human fingers exhibit a loop pattern in the centre of the finger, 30% exhibit a whorl, and 5% exhibit an arch 〚10〛. The remaining 5% patterns have more complex loops. A few people do not have epidermal ridges (very rare inheritable trait). Identical twins do not have the same patterns. For the sake of simplicity, we symmetrise completely the streamlines observed at the fingertip, and get the sphere shown in Fig. 3A, with the corresponding streamline pattern. The possible cell orientations are as shown in Fig. 4.
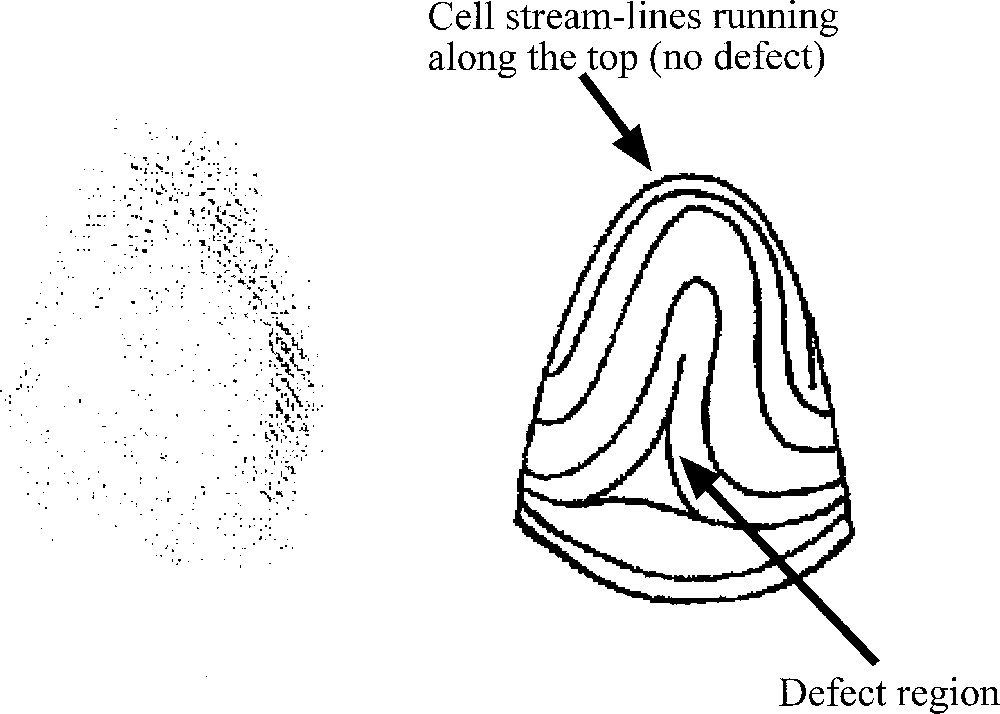
Typical fingerprint. The turn of the streamlines in the middle of the ventral side of the finger around one or two defects is universal, although the exact pattern may be slightly different from one person to another. There exist three main types of fingerprints ‘core' in the classification of forensic science; two thirds of the people have the kind of fold shown here. The remarkable feature of this pattern is that the ridge stream always runs parallel to the plane of the hand at the finger apex, and the curvature of the finger is maximal in the region that runs from the dorsal to the ventral side of the finger, i.e., perpendicular to the streamlines. There may exist also spiral patterns (30% of fingers), and arches or tents (5%). They share the same general shape, except for the centre of the defect. We shall make use of drawings like the one to the right, which represents a 3D sketch of a fingerprint. The reader is encouraged to look at his own hand to see what kind of fingerprints he (or she) has. Fingerprints become visible around week 9 of pregnancy.
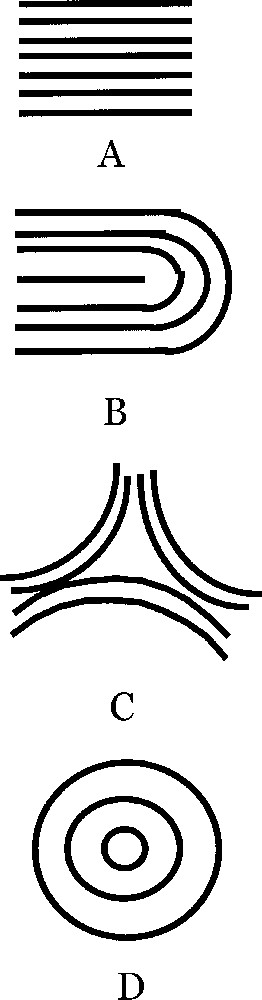
If we magnify typical regions of the surface of fingerprints we may find regions as in this figure. A. Parallel lines. B. U-turn with a 1/2 defect. Absent from our ‘spherical fingerprint' are the triangular defect C and the target pattern D. A has a clear 2-directional anisotropy, which generates an anisotropic surface tension, namely, the surface tension is higher in the parallel direction (persistence length of fibroblasts), while it is weaker in the perpendicular direction, as is classically well known for associated elongated structures. C has a 3-fold anisotropy, and D has no anisotropy, but instead has a radial and an azimuthal surface tension. B has an anisotropy up to the region of the defect itself, where there is a locally isotropic region.
Now, the tension of such a fibered sphere is not a constant, nor a scalar. The local tension or stiffness depends on the local topology, and at a given point, on the direction (tensorial behaviour). Since fibroblasts are elongated, the flexibility of the 2D surface on which there is a nematic arrangement of fibroblasts is higher in the transversal than in the longitudinal direction, just as for fibre-like materials. This generates a local distribution of surface tension lowest in the perpendicular and higher in the longitudinal direction of the fibroblasts stream. Around a defect like in Fig. 4B, the surface tension has a radial and normal component at the end of the defect. Around a defect like in Fig. 4D, there is a centre with a surface tension intermediate between the perpendicular and longitudinal one of in Fig. 4A. Now, if we consider the sphere represented in Fig. 3A, and draw by hand the equilibrium shape that would be generated by such a distribution of surface tension, we get the image in Fig. 3B, because, to resist internal pressure force, such a fibrous surface must be more bent in regions where the density of parallel lines is higher (the resistance to bending of the surface is higher when the lines are more curved). A complete numerical solution is shown in Fig. 5 for the somewhat simpler problem of an elastic membrane deformed in the Z-direction. The intuitive extrapolation in Fig. 3B gives exactly the features of the actual fingers of our hands, especially, it predicts a bulge pointing outwards in the region of the 1/2 defect. This simple model then predicts the existence of a spontaneous equilibrium shape of the ‘fingerprint crystal’, with a specific, almost deterministic, orientation of cell lines, giving a specific pattern of local surface tension, and the corresponding features of the finger shape in 3D. It predicts the correct position and orientation of defects in the core of fingerprints. This position is not random, although it does not require a genetic coding. This position of defects, with the corresponding orientation of fingerprint is observed in 95% of human fingers, and also at tails of monkeys. A very important prediction (confirmed by the facts) is that the defects of the nematic order in fingers are always in the approximate centre of the finger where there is a bulge, all the more pronounced as the loop or whorl is longer. Another crucial prediction, also confirmed by the facts, is that the 2D stream of lines near the defect induces a plane in 3D perpendicular to the stream of lines at the tips, so the existence of a symmetry-breaking, forming two planes pointing out at right angles is already ‘coded’ in the shape of the lines (Fig. 3B and C).
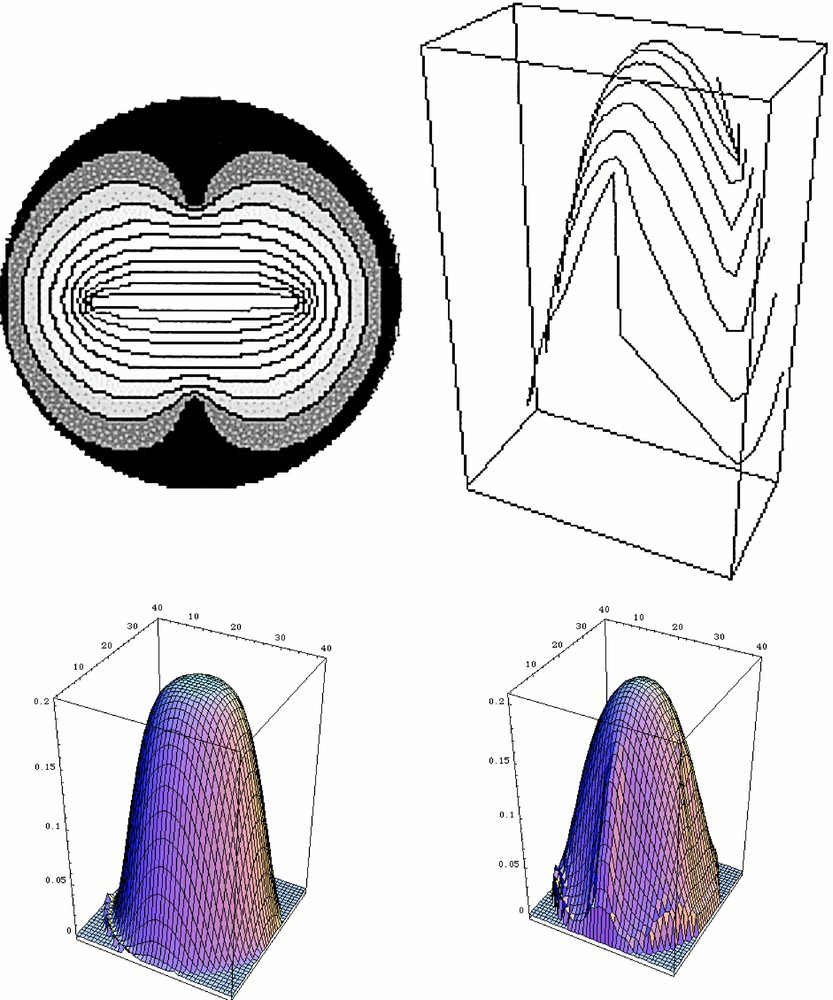
Solution of the problem for a circular skin stretched across a circle, and under a vertical load. This computation is done in three steps. First, a plausible fingerprint pattern is generated. In order to do so, we simply solve for the Laplacian operator between four ‘defects'. The outer circle and the two outer defects are set at potential zero, and the segment joining the two defects in the centre is set at potential one. This generates a set of lines that we use as ‘fingerprints' (Top left). Next, the orientation of the tangent and transverse directions are calculated everywhere. Next, the deformation under uniform load of the membrane stretched across the circle is calculated, taking into account, at each point, the local tensorial anisotropy (longitudinal vs transversal). Let us call Φ(x,y) the deformation: Φ(x,y) is calculated by solving the equation grad 〚Rlocal〛–1 〚A〛 〚Rlocal〛 grad Φ(x,y) = load. In this operator, 〚Rlocal〛 is the local rotation matrix that is used to project the gradient on the local rotated frame composed of the tangent and transverse vectors. 〚A〛 is the diagonal anisotropy tensor 〚A1, 0, 0, A2〛. For the calculation shown here, A1 = 1, and A2 = 0.25. This equation corresponds to a simple elastic membrane problem with uniform load. We acknowledge that the true biological material may have a more complex constitutive equation. Especially, we expect the elasticity parameters to be different in the embryo and in the adult. The bottom left image shows the starting condition (isotropic), and the bottom right the deformed shape. This provokes a global symmetry breaking of the pattern, with two planes at right angles. The top right image shows how the fingerprint dresses the deformed tip. These calculations were done with Mathematica®.
4 Fingering of a fingerprint crystal
Since this reasoning predicts the existence of a spontaneous equilibrium shape of the ‘fingerprint crystal’, let us explore the out-of-equilibrium shape, and especially, the branching mechanism. Although many genes, such as Sty, Shh, HGF, GDNF, BMP4, etc. 〚11〛, whose expression correlate with branching, affect the morphogenesis upon the gene disruption, such information does not lead to the description of a tube of a specific shape, nor of the highly stereotypic and iterative branching in proximal regions. Especially, it hardy explains how changes in branching planes occur (organs are 3D trees). Rather, it may be that genetics provides an understanding of the temporal events underlying the growth of the ducts, and of the magnitude of the material parameters such as surface tension, but also that the physics of moving boundaries provides the framework of the growth process.
If we consider the anisotropy of surface tension generated by the fingerprint, the selected growth direction is the one aligned with the sharp direction of the tip where there is a parallel stream of fibroblasts (white arrow in Fig. 3C). At right angles to this direction in the region of the defect, one finds the second most rapid direction where the streamlines make a turn perpendicular to the tip of the finger. We deduce from this physical principle that fingering of a fingerprint will form a stable growing dome with the direction of growth automatically adjusted to the pattern of streamlines seen on the fingerprints. A region of secondary branching (budding) exists, somewhat down the tip. Why is such a fingerprint pattern selected by the growth in the first place? The answer is rather simple: the only simpler alternative would be a target pattern (Fig. 4D). However, a single target pattern with the central defect growing forward is not the most rapid configuration of growth. Moreover, a target pattern occupying the entire fingertip requires an almost perfect arrangement of streamlines that will not be observed in practice (and it is actually not observed on normal human fingers), because any cleft formation will destroy the target arrangement.
How, then, will such a growing tube actually branch? There exists evidence that collagen bundles form at tips 〚12〛, and therefore strengthen the initial clefts. But when and where are these bundles created? (Fig. 6). Existing work on the reaction of fibroblasts to mechanical stress implies that the laying down of collagen fibres is a consequence of mechanical stress imparted on them 〚13 ,14〛. These works imply that, as the ducts approach an obstacle, such as the capsule or another duct, they should undergo a T-shaped dichotomisation. Experiments show that this T-shaped splitting is rapidly remoulded into the stereotypic branching, which is not actually T-shaped, but more Y-shaped 〚15〛 (Fig. 7). If we take into account the nematic order of fibroblasts, the collagen will be deposited parallel to the existing template of fibroblasts, when the duct approaches close enough to the capsule or another duct so as to generate a high mechanical stress. This will arrest the fastest and stable direction as defined above, and new tips will emerge from the sides, at right angles, since these are, according to the construction in Fig. 3, the second fastest growing directions. In existing work, it is assumed that the collagen bundle forms on the ‘ridges of the mesenchyme’ 〚12〛.
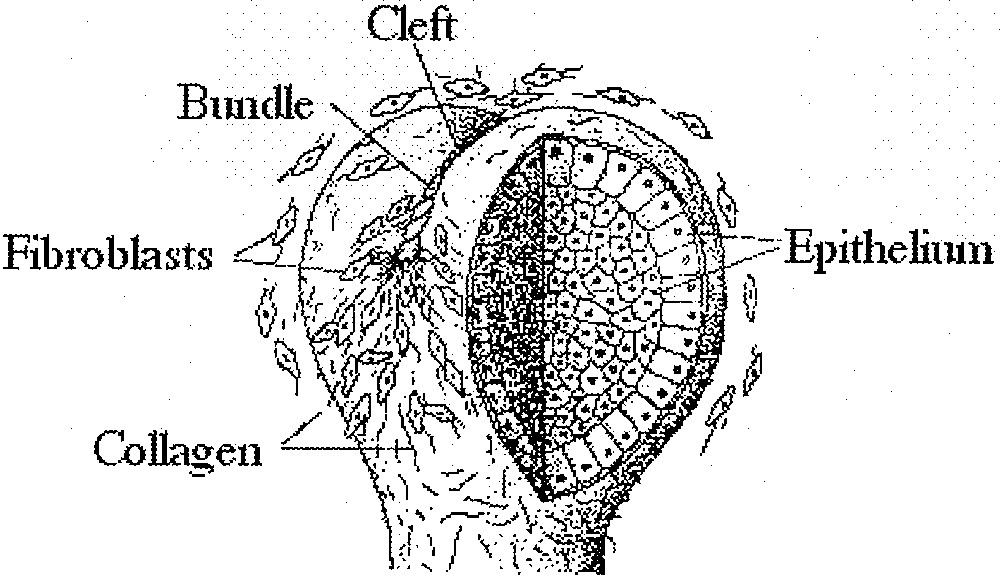
Mechanism of collagen bundles formation (adapted from 〚12〛). According to existing work, collagen fibres polymerise under the action of fibroblasts at the apex of the duct. Nothing is known about the choice of the orientation of the bundle, and why it should be at right angles (in many instances) to the previous dichotomisation. It is stated that the polymerisation occurs along the ‘mesenchyme ridges'. This pictorial representation already shows streams of fibroblasts cells, which is a sign of the existence of a nematic order (as observed in vitro).
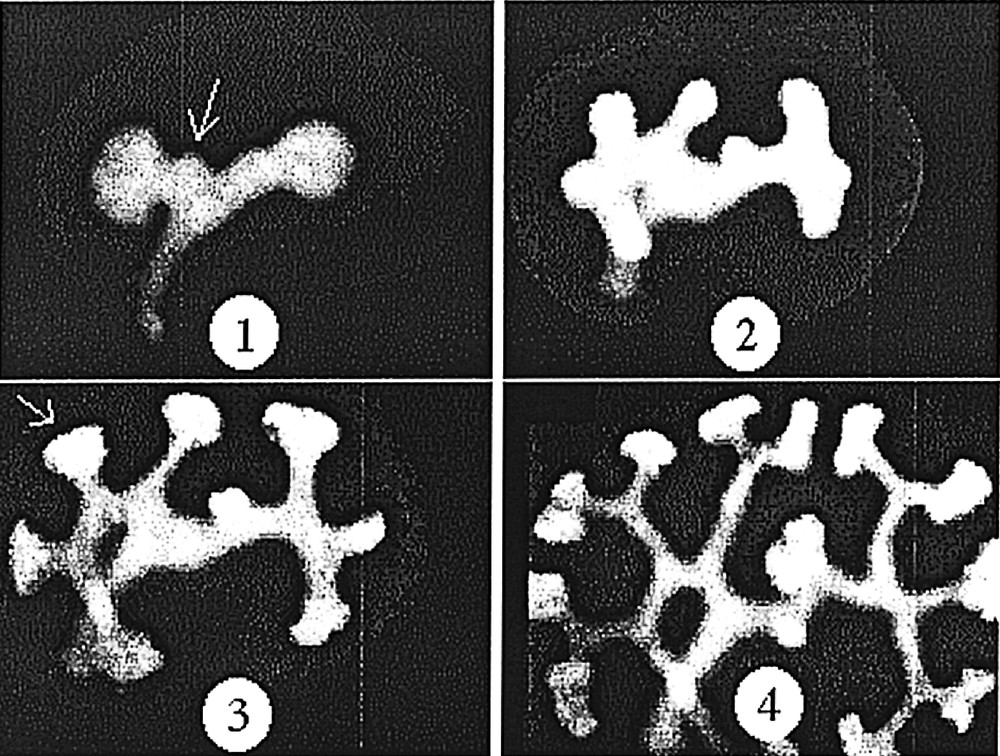
Development of the kidney, as observed in vitro, in a GFP mouse embryo. One can notice that the angles of the dichotomies and of the buddings are stereotypic (sharp with a strong tendency to be at 120°). However, the stereotypy is not immediate, it is achieved after some time. The stereotypy is easily accounted for by a ‘zebra shoulder' defect connecting three domains of different orientation, as classical in the nematic phase. Both buddings and tip-splittings exhibit eventually the same angles. The budding pointed by the arrow in 1 is remoulded in to a stereotypic angle. The T-shaped dichotomy pointed by the arrow in 3, is remoulded into a stereotypic angle. Materials and methods about this experiment are found in 〚15〛.
Hence, dichotomous tip-splitting starting at right angles will naturally occur when the ducts will be under stress at their tips. If there is little stress, then the model predicts that a stable duct grows and ‘emits’ lateral buds down the tip, in the region of the defect.
Why should the tip-splitting mechanism lay down a pattern such that the next dichotomy should or can be in a plane perpendicular to the current one, leading to a 3D tree? This comes from the symmetry breaking, described in Fig. 3B and C. Let us look at what happens when the collagen fibres are laid down on the ‘fingerprint’ pattern to arrest its growth. The formation of the collagen cleft along the tip amounts to a cut across a vertical plane passing through the apex (Fig. 8A). This generates two halves that will behave as independent growing ducts. These two halves keep a ‘memory’ of the dichotomy such that the next dichotomy is at right angles, in the following way. If we looked at the lines formed when a massive cut was made across the symmetry plane of the fingerprint pattern, we would see two types of lines, e.g. on the finger, follow the nail’s plane down to the region just before the first joint of any finger. We would find lines that run in circle azimuthally and lines that are azimuthal on the finger’s side, and then turn towards the defect region. When the collagen cut runs across the streamlines as in Fig. 8B–D, it leaves both types of lines with ‘dead ends’. These dead ends have to reorganise, as in a liquid crystal, possibly leaving non-resolvable topological defects. The persistence length of the fibroblasts plus their bonds induces a line tension of each stream of cells, which makes it statistically unlikely that each line will reconnect to its neighbouring one. The stream of lines that used to run azimuthally along the tube (now cut in two) has to reconnect with the other cut lines. They will not reconnect with the lines on the other side of the initial (now cut) duct, but instead directly to the lines that run down from the defect (the U-turn in the centre of the finger ventral side). This will happen on both sides, and create the germ of two U-turn on each side of the collagen cleft defects (so, two for each new duct, a total of four). We arrive at the situation in Fig 8E, where only one new duct is shown, which continues its growth. As the central, fast growing line goes up, the anisotropy extends the stream of lines and makes it very concave, while the U-turn moves inside the concavity, and the topology is back to the same topology as prior to the dichotomy, except that the pattern is rotated by 90° in one of the siblings ducts, and at –90° in the other one. In order to better understand this process, we supply the symbolic representation in Fig. 9, in which we symbolise a defect region with squares, and the stream-lines having a topology like in Fig. 4A with dark lines. Although the detail of the reorganization process may be debatable, the crucial point is that the cap of a fibered tube contains three specific orthogonal directions: the growth direction, the direction of the stream of lines at the apex, and the axis of the defects. When a tip is arrested by laying down collagen along the stream-lines at the apex, the direction of the defects becomes the new growth direction, the initial growth direction gives the direction of stream-lines at the new apex, and new defects are generated, which complete the 3-axe pattern. The branching ducts that emerge have a plane of symmetry that is at right angles of the previous one. This would be true, even if the pattern of collagen alignment were only restricted to a narrow region around the cleft.
Mechanism of cleft formation on a fingering fingerprint. A. The growing tip, before the dichotomy. B. If, as shown in 〚12〛, a bundle starts forming at the top, it will align itself along existing lines of the mesenchyme (which are called in 〚12〛 mesenchyme ridges) and arrest the tip along the flow of stream-lines that runs parallel to the narrower directions (sharp line with black arrow). C. As the bundle moves down, it intersects lines that run down from the defect and lines that run azimuthally around the duct. The crucial moment is between C and D. The cut by the bundle generates what will be the horizontal (azimuthal) direction for the next generation. The new azimuthal direction leaves all the cut stream-lines in a disordered state that has to rearrange to form ordered streams of cells. Two types of streamlines are cut: the ones that run down from the defects (front and backside) and the ones that used to be azimuthal in the previous ‘fingerprint'. This situation is remarkable in that it contains the germ for four new U-turn defects, located on either side (left and right) of the initial U-turn defect, which will become the two new defects of each one of the new ducts emerging after the bundle has formed. Because of the line tension of the streamline, the reconnection will form such new U-turn defects. As the pattern grows, the selection rules favour the former U-turn, which grows up to form the apex of the newly growing bud, and this brings the two-U-turn defects on either sides of this new tip. The pattern is almost identical to the pattern on the tube before the dichotomy, except that it is rotated at 90°. On the other sibling, the same process occurs, leading to a new branch at –90°.
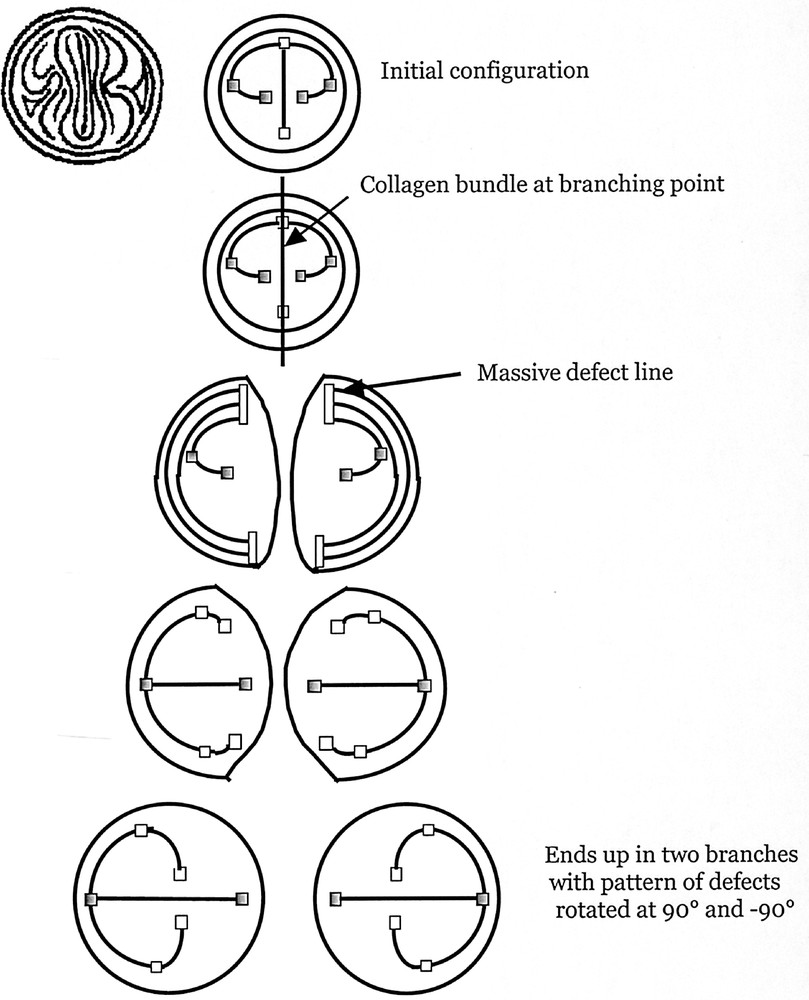
The formal representation of the dichotomization, with defects represented as squares, and a few growing streamlines as black bars. To help the reader, we represent one growing pattern of ‘fingerprints' (symmetrised across the nail), in the first row, extreme left, facing the reader; next to it (first row) the symbolic representation. We have coloured in grey two of the defects, so that the reader can follow them in the next rows. This symbolic representation illustrates more simply the scheme of the iterative process. In the top left, the outer circle is the cylinder of the tube (or duct). Inside this circle we see the stream of cells (vertical) running at the apex. On the sides, there are 1/2 defects that slightly curve towards the apex. At the cleft point (second row), a bundle goes across the apex, and runs down towards the cylinder. This splits the tip in two (third row). Two massive defect regions are created where the bundle cuts the lines running azimuthally around the cylinder. These regions are the germs of the new 1/2 defects (fourth row). The orientation of the bundle already prepares the new defects to evolve towards the centre of the newly formed ‘finger'. Eventually, the 1/2 defect of the previous duct grows along the apex of the new duct, and new 1/2 defects appear on its sides (as in Fig. 2). The pattern of the new ‘fingerprint' is at right angles of the previous one.
To predict even more accurately the stereotypical branching behaviour, we now observe that three tubes covered with fibroblasts arranged in an azimuthal direction generate automatically a defect structure known as a ‘zebra-shoulder’, also easily found on the palm of the hand, at the basis of fingers (Fig. 10). This zebra-shoulder pattern corresponds to a –1/2 defect that allows the three domains of aligned fibroblasts to connect. Therefore, the angle of the dichotomy has eventually a specific value, given by the tension forces generated by the zebra-shoulder defect (actually two such defects). During the branching event, even if the pattern is not strictly arranged, the fibroblasts will stabilise the intersection of the tubes in this pattern after some time (Fig. 7). The delay corresponds to the time for the fibroblasts arrangement to crystallise. By iterating this process we are able to predict the tip-splitting branching pattern of dichotomous organs (Fig. 10).
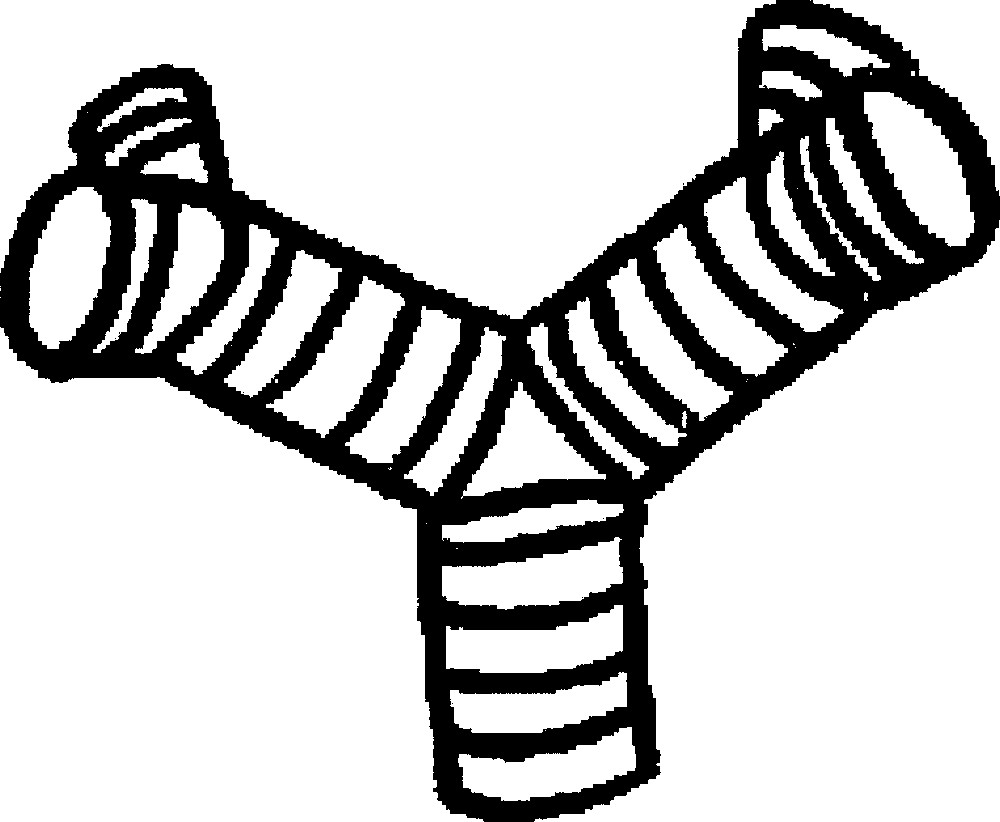
Stereotypy of the angle between branches, and pattern after two dichotomies. The cleft formation acting upon a fingertip structure generates the defect structure visible here. This is known in physics as a ‘zebra shoulder' pattern. This makes it possible to connect branching ducts, in which the construction elements (the cells) run azimuthally, by 2 simple – 1/2 topological defects. This defect generates its own tension forces that stabilize the point of branching at a specific angle, and with co-planar branches, but the plane rotates with the generation order.
5 Discussion and conclusion
Viscous fingering provides, from first principles, a branching mechanism that is able to create a primitive organ 〚2〛, and an explanation of why tubes should at all exist and have a tendency to branch. The only duties of cells are to maintain their cohesiveness as a 2D sheet, to create an osmotic pressure across the sheet (higher pressure in the lumen), and to proliferate in response to mechanical forces.
However, a branching process using classical viscous fingering is not very efficient in that, although it provides a mechanism for construction of an organ with a large surface area, it tends to leave large unused voids, and to create a disordered shape. Real branched organs are space filling, no useless voids are left and the pattern is generally more organised. This is explained by the framework presented here: under some genetic mutation, if the cells and molecules composing the sheet adopt an elongated shape, they shift the universality class of the growing pattern. This shift occurs from the disordered structure to the budding/dichotomous structure, with 120° and perpendicular planes of branching, as explained here. This tends to orient the new ducts towards unexplored regions, and generates an iterative process close to deterministic, which fills the volume regularly.
Since the collagen is laid down by fibroblasts on the outside of the epithelium, the patterning process is driven by the outer side of the basement membrane towards the mesenchyme, as is well known empirically 〚11, 14–16〛. The details, such as angles and diameters of ducts, will depend on the exact shape of fibroblasts, their density and bond strength and the local tension. The model predicts that without mesenchyme at all, the shape reverts to the random pattern, which is indeed the case 〚17〛.
It seems that not all organs are as stereotypic, and also that stereotypy decreases in the distal regions, as the pattern grows 〚9, 17–19〛. As is well known in this sort of viscous-fingering process, the actual shape is the result of the interplay between the mechanical field of growth, and the surface tension. One has to actually ‘run the movie’ to see how the branching will unfold. A general trend is that dichotomous growth will be the rule in the distal, more stressed parts, and less favourable in the proximal regions, a fact which is observed, especially for the lung 〚19〛. This explains the epigenetic role of the context in matters of BM.
The genetics may act as a timetable rather than a blueprint. Of course, gene expression fixes the values of the physical parameters of the growth, and it provides growth factors and metabolites to the cells. We may compare this situation to the skin of the abdomen of a pregnant woman: the skin area increases during pregnancy under the action of the internal pressure, but the shape of the abdomen is fixed by the internal pressure, not by a fine tuning of gene expression. However, such a fine-tuning is necessary to preserve and maintain the microstructure of the tissue.
In conclusion, we have shown that the nematic or fibrous order of living tissue has important morphogenic consequences. Viscous fingering provides the general mechanism of BM, and the surface tension imposes such details as stable ducts, lateral budding near the tips, dichotomy with memory, stereotypy of the angles, optimal 3D filling. The nematic organization of cells is well known to exist in vitro. There exist clues that this arrangement exists in vivo 〚9〛. The fact that it is possible and commonplace is well demonstrated by the epidermal ridges of friction skin. Reconnection of tubes at dichotomies implies topological defects such as zebra-shoulders. Zebra-shoulder patterns are obviously present on hands; they are also found at bifurcations of vessels, and at connections of cartilage rings of the trachea and bronchiae. It should be insisted that the physics of the problem is fully 3D, and that it cannot be treated by 2D approximations.
Universality classes and ‘selection’ of shapes in physics supply selection mechanisms for biological structures, and pathways for genetic convergences. The physics described here has to be taken into account in other instances as well. It may explain the stereotypy of branching of certain amoeba colonies, fungi and even cancerous tumours, in cultures, which show a well-established branching angle, especially in the presence of collagen (Fig. 1L in 〚20〛). The alignment of fibres in plant tissue may play a similar role in the stability of meristem tips and in the branching stereotypy of plants.
Finally, the model may help in predicting the outcome of experiments. For example, it explains naturally why a forced higher-pressure gradient induces automatically (in utero) a more ramified pattern, as known experimentally 〚21〛. Also, since the stiffness of the tissue is an important issue, enzymes which degrade the basement membrane, or interfere with collagen, play a role in shifting the growth from dichotomous to budding 〚19〛. This is how they provide morphogenic information.
Acknowledgements
The authors are grateful to Frank Constantini for his interest in this work, and his support.
Version abrégée
1 Introduction
La formation des organes arborisés (rein, poumon, glandes mammaires, etc.) est mal comprise. Or, il est crucial de bien comprendre ce phénomène, si l’on souhaite progresser dans de nombreux domaines de la médecine, comme le soin aux grands prématurés, la régénération des organes ou l’effet de l’hypertension sur les reins etc. Dans un livre 〚1〛 et dans une note précédente 〚2〛, l’un de nous a exposé les arguments permettant d’avancer que la formation des structures arborisées dans le vivant est un mécanisme de digitation visqueuse de l’épithélium à travers le mésenchyme.
Rappelons en quoi consiste ce mécanisme. L’interface I entre un fluide A peu visqueux et un fluide B plus visqueux développe des ramifications lorsque le fluide le moins visqueux est poussé vers le fluide le plus visqueux. L’instabilité qui engendre les branches est l’instabilité de Mullins–Sekerka 〚3〛. On peut la décrire simplement de la façon suivante. Si l’on pousse A vers B, plus visqueux, l’interface I se déforme et prend une allure de pointe, de doigt, puis d’arbre, car, dès que la moindre bosse apparaît, elle voit devant elle un gradient de pression plus fort ; comme la vitesse de croissance est proportionnelle à ce gradient, cette bosse s’accroît encore davantage. Ces instabilités s’accumulent pour former une arborisation. Cette arborisation est désordonnée si la tension de surface est isotrope, mais elle peut être régulière si la tension de surface est anisotrope. C’est ainsi que la tension superficielle de l’interface est responsable de la sélection de formes régulières, par exemple le flocon de neige, au détriment des formes désorganisées 〚3, 6〛. Une anisotropie de 1% suffit à provoquer cette sélection〚6〛.
L’application à la morphogenèse consiste à identifier l’interface I comme étant l’interface épithélium/mésenchyme, le fluide A comme étant le liquide occupant la lumière intérieure à l’organe, et le fluide B comme étant le tissu dans lequel pénètre l’épithélium. La preuve expérimentale la plus forte est que la croissance des organes requiert un excès de pression du côté de la lumière 〚21〛. Ceci permet d’expliquer naturellement la forme de ces organes dans les circonstances où ils sont désordonnés.
Mais il arrive que ces organes soient très réguliers, sans que leur ordre n’évoque un ordre sous-jacent cristallin. L’occupation de l’espace par les branches proximales est souvent très optimisée, les angles et les positions des branchements sont bien définis 〚7, 8, 19〛 et une dichotomie de deux branches à 120° est souvent suivie par une dichotomie de deux branches branchant également à 120° 〚19, 22〛, mais dans un plan perpendiculaire au plan de la dichotomie précédente (sorte de « mémoire »). Les cancers eux-mêmes peuvent produire également des branches régulières, présentant des branchements typiques à 120° ; ce dernier cas, justement, s’observe en présence de collagène 〚20〛. Finalement, il semble bien que le mécanisme de base de ce type de croissance soit une digitation désordonnée, à laquelle s’ajoutent des facteurs susceptibles d’auto-organiser la croissance en une arborisation très régulière, présentant des angles de branchement caractéristiques (120°) et des effets de mémoire (plans à angles droits) sans rapport avec la physique des dendrites cristallines.
S’agissant d’explications en termes de signaux biochimiques, il faut remarquer que le nombre de gènes identifiés dans ce type de croissance est restreint et que toute théorie devra faire appel à assez peu de matériel génétique 〚11〛. À l’appui de cette remarque, notons que le changement d’un motif de branchement vers un autre est parfois associé à l’expression d’un type unique de collagène 〚19〛 ; or, un chaînon manque, qui permettrait d’attribuer à une telle concentration en collagène pareil pouvoir morphogénétique.
Nous montrons dans cette note que la digitation visqueuse peut régulariser une interface biologique n’ayant pas d’ordre cristallin, à condition de prendre en compte une forme particulière de tension de surface : la tension de surface d’une surface fibrée.
2 La tension de surface d’une empreinte digitale
Nous montrons maintenant comment le caractère fibré induit une anisotropie de tension des « tissus » biologiques, en commençant par les doigts, puis nous extrapolerons la construction aux organes arborisés.
Les cellules de la peau, et plus généralement des tissus vivants, présentent un ordre orientationnel, que l’on retrouve dans la structure macroscopique des empreintes digitales. Sur le plan de la structure microscopique, les fibroblastes sont des cellules allongées qui, en outre, fabriquent des molécules de collagène, elles-mêmes très allongées. C’est un fait courant que l’ensemble cellules + collagène adopte in vitro un ordre nématique, c’est-à-dire un ordre orientationnel où toutes les « particules » tendent à s’aligner les unes avec les autres (voir Fig. 1). Cet ordre n’est jamais parfait, et, aussi bien en physique qu’en biologie demeurent des défauts résiduels appelés 1/2 (« épi ») et –1/2 (« épaule de zèbre ») 〚8〛. Ces défauts sont bien observés in vitro 〚8〛. Ces types de défauts sont incontournables lorsqu’il s’agit de couvrir un tube fermé, une sphère ou une demi-sphère avec des « particules » allongées alignées, car un théorème mathématique stipule qu’on ne peut couvrir une telle forme avec un champ de vecteur différentiable en tout point. Ces défauts sont présents partout sur la main, où l’on identifiera sans difficulté les géométries correspondantes.
Si l’on regarde précisément les doigts, on comprend que la forme de la pulpe des doigts est liée à la distribution de tension imposée par le nappé en empreintes digitales, et, plus précisément, par la tension du derme sous-jacent, comme nous allons le montrer. Considérons une empreinte ordinaire, comme celle représentée sur la Fig. 3. Cette empreinte est typique. Contrairement à une idée répandue, les empreintes digitales des humains sont très semblables. Seul le détail fin permet de distinguer un humain d’un autre. Dans les grandes lignes, toutes les empreintes tombent dans trois catégories 〚10〛 :
- • 60% des doigts humains ont une empreinte présentant une boucle ;
- • 30% des doigts humains ont une empreinte présentant une spirale ;
- • 5% des doigts humains ont une empreinte sans spirale ni boucle, qualifiée d’« arche » ou de « tente », en science légale (Fig. 5).
Partant de la forme d’une empreinte digitale, nous proposons, afin de simplifier le problème, de symétriser complètement le doigt, à travers le plan de l’ongle, et à travers la ligne de base de l’ongle, de façon à former une empreinte digitale sphérique. Aux nuances près exposées ci-dessus, on obtient une distribution d’empreintes digitales évoquant une balle de tennis (Fig. 3). Nous avons également simplifié la structure du défaut central à la pulpe du doigt, qui pourrait être différent.
L’équilibre d’une membrane fibrée (nématique) sera associée, en chaque point, à des flexions différentes dans le sens longitudinal et dans le sens transversal. En tenant compte de ce tenseur local de tension de surface, on peut tracer qualitativement la forme du cristal d’empreinte digitale (Fig. 3). L’anisotropie locale des propriétés physiques du tissu brise la symétrie de la sphère. La construction de ce « cristal digital » présente la forme d’un doigt : un peu pointu dans une direction, plus aplati dans l’autre, et le raccord autour du défaut crée une petite bosse à l’endroit où les lignes commencent à repartir dans le sens opposé. Cette bosse est d’autant plus marquée que la ligne de défaut terminant en impasse est plus longue. C’est bien la forme d’un doigt. Un calcul explicite est présenté sur la Fig. 5, pour le cas un peu plus simple d’une membrane présentant une figure d’empreinte digitale, que l’on met en charge uniformément.
Le calcul prédit donc que la répartition des empreintes digitales sur le doigt n’est pas le fruit du hasard. Il s’agit simplement de la façon naturelle dont sont co-construits la forme du doigt et l’empreinte correspondante. On n’oubliera pas que, si l’apoptose agrandit l’espace entre les doigts, cette mort cellulaire ne se produit qu’au début de la formation des doigts. Pendant la presque totalité de la gestation, les doigts croissent effectivement.
Bien que les défauts ne soient pas codés génétiquement, la physique prédit qualitativement le rapport d’aspect du doigt, l’orientation des lignes sur le doigt, la position des défauts et la présence d’une petite bosse au centre du doigt, avec une construction quasiment déterministe. Aucune étude de marquage génétique n’est capable de telles prédictions.
Insistons sur le fait que la structure globale des empreintes réelles est systématiquement la même : une nappe de lignes passe au sommet du doigt, et les défauts sont laissés au centre de la pulpe. Si l’on symétrise par la pensée le doigt à travers le plan de l’ongle, on constate qu’un tube fermé à son extrémité, coiffé d’empreintes digitales, présente les défauts à angle droit de la direction du tube, légèrement en arrière de la pointe. En outre, l’axe de ces défauts forme avec l’axe du doigt un plan de symétrie qui est perpendiculaire au plan de l’ongle. On reconnaît donc dans la distribution naturelle de filaments couchés sur un tube fermé, la présence de deux plans orthogonaux, inscrits dans la distribution de ces filaments. C’est l’anisotropie des propriétés physiques du tissu qui brise la symétrie et révèle dans la forme le nappé des filaments.
3 La stéréotypie des organes branchés
La description du calcul de la forme du doigt, à partir de l’empreinte donnée ci-dessus est une construction d’équilibre. À partir de là, on peut chercher à comprendre la formation des tubes et des organes arborisés, comme l’équivalent hors équilibre. La croissance hors équilibre d’une empreinte digitale conduira naturellement à la sélection d’un doigt stable, cette fois non plus au sens de la physique de la digitation visqueuse, mais au sens des vrais doigts de la main. Ainsi, on doit dire que « la digitation d’une empreinte digitale forme un doigt », ce qui est relativement surprenant du point de vue épistémologique.
Ce que nous avons dit de l’ordre nématique in vitro vaut pour les organes arborisés également. Les biologistes reconnaissent l’existence d’un ordre nématique des fibroblastes, in vivo, dans tous les organes dont nous parlons, au moins implicitement (Chap. 18 de 〚9〛). Dans le cas particulier du poumon, une représentation ordinaire, comme celle de Nakanishi, montre les fibroblastes s’alignant le long de lignes de courant, ainsi que le feraient des molécules d’un cristal liquide nématique, sans que cet alignement ne fasse l’objet d’aucun commentaire 〚12〛 (Fig. 7). En outre, les coupes systématiquement montrées par les biologistes à deux dimensions, comme celles de la référence 〚9〛, ne sont pas reconstructibles en 3D, si l’on ne suppose pas l’existence de défauts de l’ordre. Pour finir, il est bien connu que les organes forment des lignes et anneaux de cartilages autour des tubes. Ces cartilages forment parfois des cercles complets dans la direction azimuthale des bronches, des raccords en épaule de zèbre aux jonctions, mais le plus souvent des arrondis en épis semblables à ceux trouvés sur les empreintes digitales.
Peut-on alors en déduire le caractère ordonné de l’arborescence ?
Il faut d’abord poser la question du branchement latéral. En physique de la croissance cristalline, la pointe elle-même d’une dendrite est stable et les branchements ont lieu suivant les directions secondaires déterminées par l’anisotropie de la tension de surface. Un point important est que cette cause, qui a un grand effet, est fort petite. Une anisotropie de l’ordre de 1% suffit à déterminer les directions de croissance. Si l’on transpose ce raisonnement à la croissance et au branchement de tubes coiffés d’une empreinte digitale, on constate que les directions privilégiées de branchement vont être situées vers le centre du défaut, à angle droit de la direction stable de croissance. On s’attend donc à la croissance d’un tube émettant, par bourgeonnement (budding), des branches légèrement en arrière, à angle droit de la direction de croissance principale. Ce type de branchement est nettement observé dans la morphogenèse du poumon 〚11, 19〛.
Voyons maintenant comment expliquer les dichotomies.
Dans de nombreux cas, comme par exemple dans le cas des reins, ou dans les parties distales du poumon 〚15, 18–21〛, la digitation se fait par dichotomie plutôt que par bourgeonnement latéral. L’explication en termes de digitation d’une empreinte digitale est assez naturelle. On observe que la dichotomie a lieu lorsque les tuyaux arrivent près du sac entourant l’organe (la capsule), et pour ainsi dire percutent les limites de l’organe. Dans le cas d’une croissance dendritique ou de la digitation visqueuse, il peut parfaitement arriver qu’une dendrite ou un doigt visqueux atteigne les limites géométriques de sa zone de croissance (parois par exemple) et qu’une direction secondaire de croissance prenne le relais. On comprend aisément, dans le cas d’un organe, qu’un tuyau stabilisé par l’anisotropie de la tension des lignes d’empreinte ait néanmoins à bifurquer lorsqu’il rentre en collision avec les limites physiques imposées par la capsule dans lequel il se forme, ou bien en collision avec un autre tube (Fig. 8). Il faut alors procéder à une dichotomie de la forme de l’empreinte.
Pour dichotomiser qualitativement la forme d’une empreinte, nous proposons la construction de la Fig. 9. L’idée est la suivante. Des travaux récents ont montré qu’au moment de percuter les limites du mésenchyme, du collagène est produit qui arrête le tuyau, en créant une sorte de « cordelette » 〚12〛. Cette cordelette de collagène est alignée avec les « rides du mésenchyme » (mesenchyme ridges, à rapprocher de epidermal ridges). Dans les articles cités, nul ne sait quelle est l’origine de ces rides du mésenchyme, sinon des lignes de fibroblastes. Dans notre modèle, ces rides sont naturellement les lignes de fibroblastes constituant l’équivalent d’une empreinte digitale. On est tenté alors d’effectuer une dichotomie de l’empreinte digitale à travers une ligne qui court le long du sommet de l’empreinte, parallèlement à la nappe de lignes d’empreinte, étant admis que si une cordelette plus rigide arrête le tuyau, cette cordelette est nécessairement alignée avec le motif de l’empreinte. Cette construction est possible, et elle engendre deux doigts séparés. Au cours de cette dichotomie, il faut réorganiser les lignes qui sont coupées ; or, la tension de ligne des fibroblastes va favoriser à coup sûr un raccordement des lignes voisines entre elles, ce qui engendre deux doigts indépendants présentant des défauts situés à angle droit d’une dichotomie sur l’autre.
On peut discuter le détail de cette réorganisation, le point crucial étant que l’orientation naturelle des lignes sur une extrémité de tube fermé présente trois axes à angles droits : l’axe du tube, l’axe des lignes passant au sommet, et l’axe joignant les défauts. Si l’on arrête la croissance dans l’axe du tube en immobilisant les lignes passant au sommet, l’axe joignant les défauts devient l’axe de croissance, l’axe de croissance devient l’axe des lignes passant au sommet et de nouveaux défauts apparaissent, qui complètent le trièdre. Ainsi, la croissance se poursuit mais les lignes au sommet des nouveaux tubes sont dans un plan (axe du nouveau tube, axe des lignes au sommet) perpendiculaire au précédent. Cette explication n’est pas simple, mais elle a le mérite d’expliquer un phénomène extraordinaire : l’existence de divisions dans un même plan et la succession des plans de dichotomies à angles droits.
L’organe aura donc une tendance plus marquée au bourgeonnement latéral (poumon) ou à la dichotomie (rein), suivant que le milieu (la capsule + son mésenchyme) dans lequel croissent les branches impose une contrainte plus ou moins grande. Si le tube croît lentement, les branches latérales se forment par bourgeonnement, et rien n’empêche le tube initial de poursuivre sa croissance (cas du poumon). Si les branches avancent plus vite, les tuyaux percutent la capsule et se divisent sous l’effet de la contrainte, pour poursuivre leur croissance de part et d’autre, en explorant des parties latérales du mésenchyme. En fin de croissance, quand l’expansion de la capsule contre les autres organes est plus difficile, la dichotomie est la règle, et le bourgeonnement impossible en pratique, ce qui est effectivement observé 〚18, 19〛. Néanmoins, le type exact de branchement dépend du contexte, et, au coup par coup, tout organe peut produire des branchements par dichotomie ou bien par bourgeonnement.
La prédiction de la forme des organes ne s’arrête pas là. En effet, la dichotomie divise naturellement le doigt incident et les deux doigts émergents en trois domaines de fibroblastes d’orientations différentes, qui se raccordent au point de bifurcation suivant un motif nématique de défaut de type –1/2 (il y a, en fait, deux défauts « épaule de zèbre », l’un en avant et l’autre en arrière). Au point de bifurcation, les forces de tension impliquent une symétrie ternaire du branchement, et donc un caractère stéréotypé de la division, comme couramment observé dans les organes stéréotypés (reins, poumon, glande mammaire, notamment). Le modèle prédit donc qualitativement la structure observée du branchement des organes (Fig. 10).
4 Discussion
Les études génétiques mettent en évidence la présence de gènes qui sont, soit des facteurs de croissance, soit des enzymes qui permettent ou inhibent la synthèse de collagène 〚21〛. Aucune de ces études ne permet, dans le domaine strictement biologique, d’identifier clairement l’élément structurant qui permet aux organes d’aboutir à la forme qu’ils ont. Le modèle présenté inclut l’aspect physique de la poussée d’une interface à travers un milieu, et il inclut en outre la structure particulière de la tension de surface. C’est-à-dire qu’il contient la physique qui manque à l’expression des signaux biochimiques. Le modèle explique l’existence d’un mode de branchement par bourgeonnement latéral (dit side-branching en physique, budding, en biologie) et l’existence d’un mode de branchement par dichotomie (tip-splitting, en physique).
Le modèle pointe clairement vers les paramètres sur lesquels l’évolution peut jouer pour créer ou modifier les organes. En physique, les formes tombent en principe dans des classes d’universalités déterminées : on parle de la classe DLA, ou bien de la classe dendritique 〚4〛, suivant qu’il y a ou non une anisotropie cristalline. Une classe nouvelle apparaît si les éléments dont la structure est composée ont une tendance à s’aligner. Il s’agit d’une classe de formes ordonnées, mais non dendritiques ; appelons-la classe « dendrites nématiques ». La forme à 3D de ces dendrites est en quelque sorte induite par le dessin 2D des fibres. On comprend pourquoi cette classe a été sélectionnée : le remplissage de l’espace est très homogène. La dichotomie à plans à angles droits et à 120° dans le plan assure un remplissage efficace du volume, donc un rendement (lait, air, urine, sperme, etc.) plus élevé. Avec des angles de plans successifs à 90° et avec des fourches à 120° dans le plan, on explore tout l’espace en quatre itérations. Dans des temps anciens, un organe irrégulier a pu transitoirement exister, avant que la sélection ne favorise les organes du type dendrites nématiques. Mais la trace de l’existence de ces organes se retrouve dans les parties distales, moins organisées, dans certaines glandes très peu stéréotypes (glandes sébacées, prostate, thyroïde) et dans les expériences in vitro, où l’on forme facilement des formes non stéréotypées. Le caractère universel de ce type de croissance favorise naturellement les convergences évolutives.
Pour conclure, nous souhaitons énoncer que le fait que la digitation d’une empreinte digitale joue un rôle dans la forme des doigts et le fait que la sélection au sens physique joue un rôle dans la sélection au sens biologique nous frappent bien davantage que comme une simple coïncidence. En outre, le fait que l’empreinte digitale soit liée à l’« identité », est plus qu’une métaphore.