1 Introduction
Several pattern-forming processes indicate that they are under control of highly dynamic mechanisms. For instance, chemotactically sensitive cells or axonal growth cones stretch out protrusions in a seemingly irregular way, but preferentially toward the direction to which the cell should move. The subsequent adhesion of the protrusions to the substrate and their retraction leads to a movement of the cell toward the target region. Minute external asymmetries are sufficient to achieve a preferential localization of these protrusions on the cell surface [1,2]. This requires patch-like signals in the membrane that locally reorganizes the cytoskeleton and the insertion of membrane material. What generates this flashing up of signals? How are these signals localized by external guiding cues?
In other systems, the dynamic aspect of pattern formation is less obvious. Leaves, for instance, are sequentially initiated closely behind the tip of a growing shoot. Cells leaving this zone of high cell proliferation become competent to form leaves. On many plants the leaves appear in a helical arrangement. The displacement from one leaf to the next is close to the golden angle of 137.5°. How are such signals generated that jump around in the leaf-forming zone?
Pattern formation is accomplished by the interaction of molecules. Models that account for pattern formation should reveal the required types of molecular interactions. Therefore, a theory has to describe the concentrations of the molecules as function of position and time. The concentration changes per time unit depend on the actual production and decay rates of the molecules and on the exchange with neighbouring regions by diffusion, active transport or convection. Other substances involved in this process regulate these rates. Having equations that describe the concentration changes per time unit allows computing the concentrations at a somewhat later time. By a repetition of such calculations, the total time course of the concentration profiles can be obtained, allowing a comparison with the observed patterns. Since these equations are expected to have non-linear terms, they can be solved, as the rule, only by numerical methods.
The analysis of pigment patterns on tropical seashells [3,4] has provided an inroad into processes that generate permanently changing spatial patterns. Fig. 1A provides an example. A mollusc can enlarge its shell only by addition of new material at the growing edge. As a rule, only during this marginal growth new pattern elements are added. Therefore, the two-dimensional shell pattern is a time record of the one-dimensional pattering process at the growing edge. Once new material is added at the margin, the pattern remains fixed, since the shell consists of non-living, calcified material. The pattern on the shell shown in Fig. 1A displays oblique rows of dots. Such a pattern indicates that local signals for pigment depositions are only generated for a certain period, and that these signals disappear and reappear somewhat later at a displaced position. It is easy to see that the helical arrangement of seedlings on a fire cone (Fig. 1B) requires an analogous mechanism. For the understanding of this dynamic patterning, the generation of stable patterns has to be described first, since this provides the prerequisites to understand how these signals can disappear and reappear at a different position.

Signals that flash up at displaced positions. (A, B) Both, the pigmentation pattern on a seashell and the seedlings of a fir cone are time records of a one-dimensional patterning process, either along the growing margin of the shell or in a narrow zone behind the apical meristem at the tip of the shoot. (C) Model: such patterns can be generated by one activator (black) whose autocatalysis is compensated by two inhibitors, one that has a long-range but a short-time constant (red) and one that remains more localized but has a long time constant (green). Activation remains spatially confined due to the action of the long-ranging antagonist. The slowly accumulating but long-lasting inhibitor causes a subsequent deactivation. A new activation can occur only at a position where both inhibitions are low. In the course of time oblique rows appear (for further computational details and software, see [4]).
2 Primary pattern formation by local autocatalysis and long-range inhibition
Pattern formation from initially more or less homogeneous situations is not restricted to living systems. The formation of sand dunes, patterns of erosion, lightning, stars and galaxies are examples for pattern formation in non-animated systems. The possibility of generating patterns by the interaction of two substances with different diffusion rates was discovered by Turing [5]. However, a different spread of two interacting substances does not guarantee pattern-forming capabilities. In fact, only a very restricted class of interactions allows pattern formation. We have proposed that pattern formation is based at local self-enhancement and long-range inhibition [6–8]: small local elevations above the average grow further on the expense of the surroundings. It is easy to see that the examples of inorganic pattern formation mentioned above are based on the same principle.
For biological pattern formation, a possible molecular realization can consist of a substance that has an autocatalytic feedback on its own synthesis; we have called this substance the activator a(x). The production rate of the activator is slowed down by a long-ranging molecule, the inhibitor b(x), which is produced under the control of the activator. The following set of partial differential equations describe a possible interaction:
| (1a) |
| (1b) |
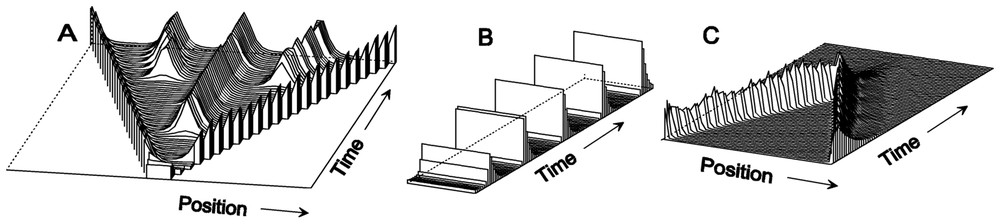
Stable patterns, oscillations and travelling waves: elementary patterns generated by self-enhancement coupled with an antagonistic reaction (equations (1)). (A) Stable patterns result if the inhibitor has a long-range and a shorter half-life than the activator. In growing field, first a monotonic gradient is formed. Insertion of further maxima in the enlarging interstices leads to periodic patterns (Da=0.01, ra=0.02, ba=0.15, Db=0.4, rb=0.03, bb=0). (B) Oscillations occur if the half-life of the inhibitor is longer than that of the activator (Da=0.015, ra=0.06, ba=0.1, Db=0.4, rb=0.03, bb=0). (C) Travelling waves are possible if under these conditions the activator, but not the inhibitor, diffuses (Da=0.005, ra=0.06, ba=0, Db=0, rb=0.03, bb=0.004). Such waves annihilate each other upon collision. For initiation, they need either a local trigger (as shown) or a pacemaker region.
In contrast, oscillations will occur if the inhibitor has a longer half-life than the activator (Fig. 2B). A non-diffusible inhibitor can lead under this condition to travelling waves (Fig. 2C). Such behaviour is well known from waves in an epidemic. The epidemic can spread since the autocatalytic agent, the virus, can be transmitted from one individual to the next one, while the antagonistic reaction – the action of the immune system – remains confined to the individuum. Oscillations and travelling waves play a crucial role in many biological systems, for instance in the signalling of neurons or in formation of pigment patterns on seashells (see Fig. 3). The theory of oscillating systems in biology is well developed [4,11–16].
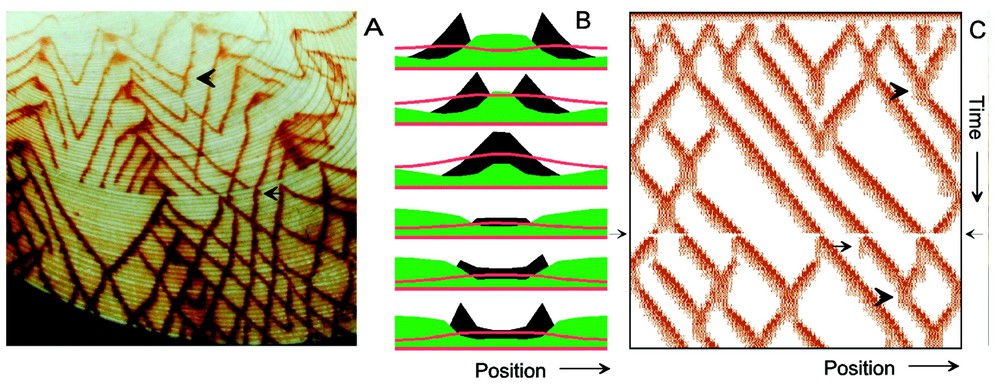
Travelling waves that penetrate each other. (A) The shell of Tapes literatus. Oblique lines result from a wave-like movement of the signals in the mantle gland that cause pigment deposition. The crossings of the lines result from mutual penetration of waves. (B) Simulation of wave formation and penetration. The local depletion of a substrate (b in equations (3); green) leads to a local destabilisation. The diffusion of the activator (black) causes a trigger of neighbouring cells where the substrate concentration is still high. If two waves collide, the activator concentration first drops but recovers due to the concomitant drop of the long-ranging inhibitor (red). The site of collision becomes the new starting point of two divergent waves. (C) Simulation in a larger field [3,4]. Wave formation does not require a pace maker or a local initiation. Penetration and Y-shaped merging (arrowheads) are correctly described. After a global perturbation, many waves terminate simultaneously. In some cases, waves reappear, preferentially with bifurcations. Some of the initiated branches do not survive (arrow), a fact that strongly supports the postulated long-range inhibition. Equations (3) with Da=0.01, ra=0.08, ba=0.0001, sa=1, Db=0, rb=0.004, bb=0.1, cc=1, Dc=0.4, rc=0.1, sc=11. The global perturbation is introduced by a general reduction of the activator concentration to 20% of the actual value at the time indicated by arrows on the time axis.
The two activator-independent production terms ba and bb can have important functions. ba is required to initiate autocatalysis when necessary, e.g., during regeneration, insertion of new maxima (Fig. 2A) or during oscillations (Fig. 2B). In contrast, a non-zero bb can suppress the spontaneous onset of activation. In this case, the system remains asleep until an inducing trigger occurs that elevates the activation above a threshold. In the case of travelling waves, this trigger is obtained from neighbouring cells (Fig. 2C).
The activator–inhibitor reaction is, of course, only an example. In most inorganic systems with pattern forming capabilities, the antagonistic effect results from a depletion of a prerequisite that is required for the self-enhancing process. Equations (2) describe a possible interaction between an activator a(x) and a substrate b(x) that is consumed during the autocatalysis [6]:
| (2a) |
| (2b) |
3 Self-destabilization of a once established pattern: jumping signals and penetrating waves
Patterns generated in this way obtain a stable steady state supposed that the antagonist has a shorter time constant than the self-enhancing component(s). As mentioned above, there are, however, situations indicating that the corresponding signals are only present for a short period. This will occur if a second antagonistic reaction, with a longer time constant, is at work, causing a breakdown of the maximum shortly after it has been generated [3,4]. While the primary antagonist has to spread rapidly, the second antagonist has to remain more local to accomplish the destabilisation. Two possible molecular interactions are given below. The mechanism described in equations (3) is an activator–substrate interaction (equations (2)) enriched by an additional inhibitor c(x).
| (3a) |
| (3b) |
| (3c) |
The inhibitor c(x), produced under activator control, slows down the autocatalysis, and, therewith, also the removal rate of the substrate b(x); cc accomplishes a Michaelis–Menten-type limitation of the reaction rate at low concentrations of the long-lasting inhibitor c; sc describes its efficiency; sa leads to an upper bound of the autocatalysis at high a concentrations. Either b or c can accomplish the long-ranging or long-lasting function respectively.
To give another example, an activator may not only catalyse a single inhibitor species but two. Again, one inhibitor has to have a long time constant and has to spread only slowly. Both inhibitors act in an additive way.
| (4a) |
| (4b) |
| (4c) |
Depending on the parameters, the local de-stabilization by the second long-lasting antagonistic reaction can lead to two different patterns. Either the activation is permanently shifted into a neighbouring region, causing travelling waves. Alternatively, the activation disappears and reappears at a displaced position. Both types of behaviours have parallels in very different biological systems that should be discussed in the following sections. Transitions between both modes do occur within one system, indicating that both modes have indeed a common molecular basis (see Fig. 4).
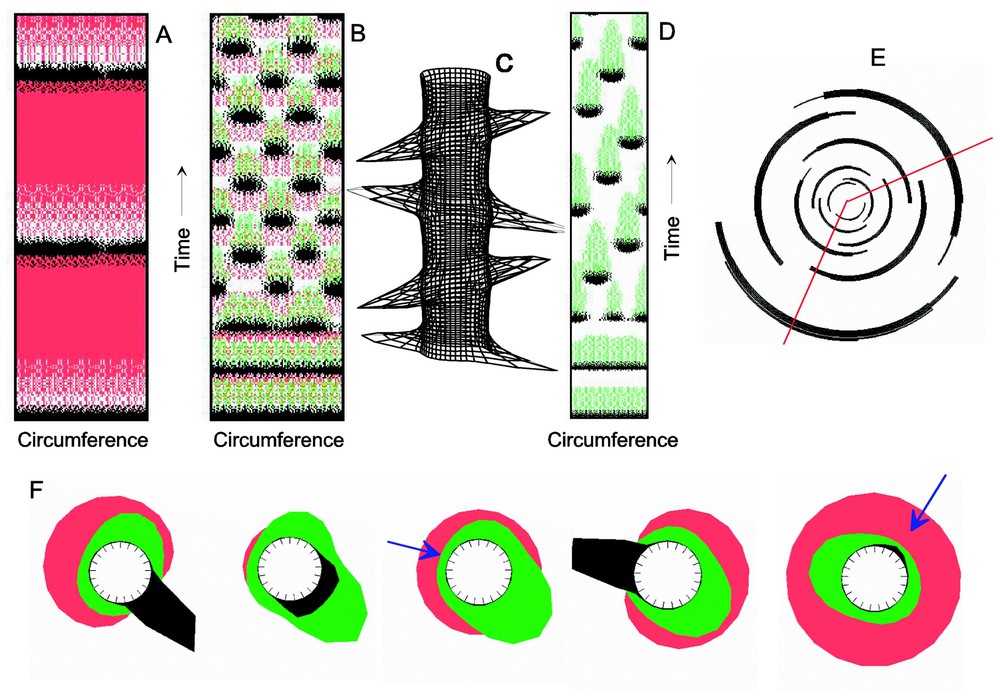
A model for phyllotaxis. All simulations made in a ring of cells; the rectangles correspond to cut-open cylinders showing the concentrations in the ring as a function of time. (A) A reaction in an oscillating regime based on autocatalysis and a single antagonistic reaction is unable to generate also a pattern in space, although the corresponding conditions are satisfied. Activator (black)-depleted substrate (red) mechanism, equations (2) with Da=0.002, ra=0.003, ba=0.01, Db=0.2, rb=0, bb=0.0005). (B, C) With an additional inhibitor (green), the initially homogeneous oscillation desynchronises. Signals are formed in pairs at 180° position and each subsequent pair appears at maximum distance from the previous signals, i.e., in 90° positions (C). Equations (3) are used with parameters as above and Dc=0.0005, rc=0.0002, sa=0.1. (D–F) If the half-life of the inhibitor is longer (rc=0.0001), the inhibitor remnant from even earlier primordia plays a role. Signals appear in a helical arrangement. (E) Same simulation in a plot as it is frequently used in botanical textbooks: youngest signals are plotted close to the centre, the older further to the margin. The displacement by the golden angle (red lines) is clearly visible. (F) Snapshots of the distributions in the leaf-forming zone. The next primordia form at the position where the long lasting inhibitor is lowest (arrows) and if sufficient substrate has accumulated. The depletion of the substrate (red, possibly auxin) keeps the signal for the next primordia localized.
4 Formation travelling waves without a pacemaker
If the autocatalytic component spreads somewhat faster than the long-lasting antagonistic reaction or if the maximum is somewhat flattened due to saturation, cells at the flank of the maximum can achieve a higher activator production than in the centre. Under this condition, the maximum starts to move (Fig. 3). At the new position, the maximum will also be ‘poised’ and thus forced to move further. Since the second antagonistic reaction is long lasting, the movement will continue into the same direction, i.e., away from the preceding activation. This leads to travelling waves.
Modelling of travelling waves is in an advanced state, especially due to the study of the Belusov–Zhabotinsky reaction [15,19,20] and wave formation in the slime mould Dictyostelium discoideum [21,22]. However, there are substantial differences between these classical travelling waves and those to be described. As mentioned, the classical waves in excitable media depend on a mechanism that is similar to the spread of an epidemic: a self-enhancing reaction leads to an avalanche-like increase, while a long-lasting antagonistic reaction brings the system back to the initial situation. These waves need two components only. With appropriate parameters, the interaction given in equations (1) and (2) can produce such waves. If two such waves collide, they annihilate each other, since a wave cannot enter a region that is refractory due to the remnants of the antagonistic component of the counter wave (Fig. 2C). This mutual annihilation is a typical behaviour of the Belusov–Zhabotinsky waves. The formation of such waves depends on pacemaker regions, i.e., on regions in which the oscillation occurs somewhat faster. Here, the next activation occurs always a bit earlier, giving rise to the new waves. Without such pacemaker region, all elements may oscillate in phase. The small spread of the self-enhancing component leads to a synchronization. There is no tendency for a de-synchronization.
The pattern on the shell shown in Fig. 3A document a different behaviour. Since the shells preserve a space-time record, the oblique lines are a protocol of travelling waves. Obviously, they do not need a pacemaker since there is no particular area from which the waves start. Their crossings result from mutual penetrations. These features are reproduced in the simulation using the interaction given by equations (3) (Fig. 3B and C). A pacemaker region is not required, since due to the long-ranging antagonist, the interaction has the capability to generate local maxima from which waves can start. Turing [5] already described in his well-known paper that the spontaneous generation of travelling waves in a homogeneous field requires the interaction of three substances, a discovery that is almost forgotten. Whether the three component interactions of Turing are mathematically equivalent to the activator–two-antagonist concept discussed here remains to be shown.
The reason why wave penetration can occur in systems employing two antagonists is easily understood (Fig. 3B). In a reaction according to equations (3) in the appropriate parameter range, the activator a together with the (non-diffusible) substrate b can form a steady-state activation. Due to diffusion, the activation can spread and infect neighbouring cells. Each newly activation occurs with some overshoot. The concomitantly produced surplus of the diffusible inhibitor c contributes to extinguish the activation of the preceding cells, which is more susceptible due to the reduced substrate concentration. Therefore, apparently normal travelling waves result. However, if two waves collide, the situation is different. At the point of collision, the spread of both waves comes temporarily to rest. Therefore, no subsequently activated cells are available to extinguish the activation of the cells at the point of collision. Since the diffusing inhibitor decays rapidly, the activation is maintained until the refractory period of the neighbouring cells is over. Cells next to the point of collision become activated again and extinguish via the diffusible inhibitor the activation of the cells at the point of collision. With this step, the penetration is completed. This penetration is therefore connected with a transient change in the wave velocity, a feature known from soliton waves in physics.
The shell shown in Fig. 3A displays an interesting perturbation. Presumably triggered by an external event, several waves terminate at a sudden moment. After a lag period, new waves emerge, that are in register with the terminated waves. This can be simulated under the assumption that the external event led to a dramatic reduction of the activator concentration. In terms of the model, after decay of the long-lasting antagonist, the remnant activation may be high enough to trigger a new wave. Initially these waves can spread to both sides, leading to a bifurcation shortly after the general breakdown. This feature is in full agreement with the natural pattern.
5 Signals flashing up at displaced positions
The wave formation described in the preceding section depends on the shift of the activation into a neighbouring region. As suggested by the examples given in Fig. 1A, in other systems the activation is not continuously shifted, but disappears and reappears at a displaced position.
If the long-lasting antagonistic reaction has a range somewhat larger than that of the self-enhancing component, such a shift is not possible, since the immediate neighbourhood is also poisoned. Under this condition, the maxima tend to collapse sometimes after their generation. Such behaviour is especially likely if the primary pattern forming reaction is also in an oscillating regime. In the case both antagonistic reactions are realized by inhibitors, both inhibitors have to decay until a new activation can be triggered from an activator-independent baseline production (ba in equations (4)). The new activation has to appear at a displaced position, since the previous places are still forbidden due to remnants of the long-lasting inhibitor. This is clearly visible in the simulation in Fig. 1C. The new activation can only occur in regions where the concentration of both the far-spreading (red) and the long-lasting inhibitor (green) becomes sufficiently low. In the time record as given in sea shells, this leads to sequential appearance of spots that have a defined displacement from preceding spots. In the course of times oblique rows of dots emerge.
The question may arise why a simple reaction, for instance, that described by equations (2), is insufficient for activations that flash up at changing positions. The condition for pattern formation (Db⪢Da) and the condition for oscillation (bb<ra) can be satisfied simultaneously. However, in such a simple system, all cells would reach the threshold for triggering the next activation simultaneously, since the substrate distributes evenly due to its high diffusion rate. Only after this trigger, spatial pattern formation can proceed in which neighbouring cells compete with each other. Therefore, before the uniform activation can resolve into well-separated maxima, the activation will break down due to the depletion of the substrate (Fig. 4A). Thus, the generation of well-separated activations at positions with a predictable displacement requires the combined action of two antagonists that differ in their range and time constant.
6 Phyllotaxis: initiation of leaves along spirals
The regular initiation of new leaf primordia behind the tip of a growing shoot [23], the so-called phyllotaxis, seems to have nothing in common with any pattern on seashells. This impression is, however, misleading. On growing shoots as in shells, the new pattern elements are initiated in a narrow zone. The tip of the shoot, the meristem, contains undifferentiated cells that divide rapidly. Only cells just leaving this zone are able to form new leaves. Thus, the leaf-forming zone has the geometry of a narrow ring (for recent review, see [24]). Common are leaf arrangements at which each new leaf appears at alternating opposing positions (distichous patterns). Also common is a pair-wise arrangement in which each subsequent pair is rotated by 90° (decussate arrangement). These patterns can be simulated with the basic model of equations (1) [25]. According to classical models, the initiation of a new leaf is inhibited by existing leaves [26]. Therefore, a new leaf can be initiated only at a certain distance from the last formed leaf. This long-range inhibition could be a part of the general pattern-forming mechanism we propose. Together with the self-enhancement, our model explains why a leaf can be formed although it is in the centre of this leaf-inhibiting zone [27].
Many flowering plants display, however, a helical patterns, indicating that that the new leaves are formed at regularly displaced positions, a situation similar to the displaced dots on the sea shells discussed above (Fig. 1A). The displacement between subsequent leaves is close to 137.5°, the golden angle. This helical arrangement requires that the positioning of a new leaf is not only influenced by the last but also by the earlier leaves. This is easily understandable. Imagine that a first leaf exists. The second can appear at 180°. If the third leaf to be formed is exposed to some inhibitory influence from the first, it cannot be formed at the same circumferential position as the first and will become displaced. By modelling it has turned out that this requires again two antagonists with different properties. Assuming only one rapidly diffusing inhibitor, the asymmetry of the inhibition originating from the penultimate leaf would be very low and no reliable positioning influence would be possible. The situation is different, however, if two antagonists are involved. The long-lasting but slowly spreading antagonist would signal that this angular position next to the meristem has been used recently (Fig. 4D and E; [8]). According to this model, the helical arrangement does not result from an inhibitory influence of the earlier leaves directly, but from the remnants of the long-lasting antagonist in the leaf-forming zone that a preceding leaf has left behind at this position. This view is supported by the recent finding that new leaf primordia become rapidly disconnected from the leaf-forming zone by closing the cellular junctions between the cells [28,29], a feature that would make a direct inhibitory influence of preceding leaves unlikely.
Recent observations have shown that the plant hormone auxin is required as prerequisites in leave initiation [30,31]. Suppression of auxin transport suppresses leaf initiation, a situation that can be rescued by a local supply of auxin. This suggests that one of the expected antagonistic reaction results from a depletion of auxin in a wider surrounding. For this reason, equations (3) have been used to simulate the phyllotactic pattern given in Fig. 4. The spread of auxin is assumed there to be accomplished by diffusion. A more realistic model has to include its active transport. From the model it is expected that the auxin concentration declines at a new leaf initiation site, in contrast to the expectation discussed in the literature [32]. If auxin is present but its spread is blocked, it is expected that the leaf initiation signals remain present but do not form a pattern. This is in agreement with the observation that blocking of auxin transport leads to a ring-shaped expression pattern of markers for organ identity [31], i.e., the normal phyllotactic pattern is lost.
In whorl-like patterns, the primordia are closely together around the circumference but their separation along apical-basal axis is large (for an example see, e.g., [33]). Such patterns support the proposed separation into a component responsible for the patterning around the circumference (long ranging antagonist) and a component for a patterning in time, i.e., for apical-basal patterning (long lasting antagonist). At a particular time, many primordia appear closely spaced in a ring-like arrangement. Only after substantial further outgrowth, the next ring appears.
So far for leaf initiation at changing positions around the meristem, but what generates the signal for the meristem itself? Molecular components found in meristem formation (for reviews, see [24,34]) are compatible with the mechanism for stable pattern formation outlined in the introduction. WUS, a homeobox protein, is regarded as the primary meristem organizer. STM is necessary to maintain WUS activation [35] and vice versa, suggesting that WUS/STM is part of the expected activating system. WUS controls the CLV3 gene, a ligand involved in WUS inhibition [36], suggesting that CLV3 together with CLV1 and CLV2 is part of the inhibitory system. As expected, CLV3 is produced only in the activated region, although its action is of longer range. Moreover, the CLV genes not only inhibit WUS, but also promote organ formation. Thus, meristem/leaf patterning seems to have much in common with patterning in hydra where a primary system controls hypostome formation, which, in turn, generates the precondition for a secondary system that initiates the surrounding tentacles [37].
7 Chemotactic orientation of cell polarity
Many cells are able to perform an oriented movement towards a target area that secrete signalling molecules. With a growth cone on an outgrowing axon, nerve cells posses a ‘search organ’ for path finding (Fig. 5) [38]. The cells are able to detect concentration differences of the signalling molecules as low as 1–2% on their cell surface and orient their internal polarity appropriately [1,2]. This requires a very sensitive detection system. For the oriented movement, cell stretch out protrusions preferentially in the direction to be moved. Many molecules involved in this process are known (see [39,40]).
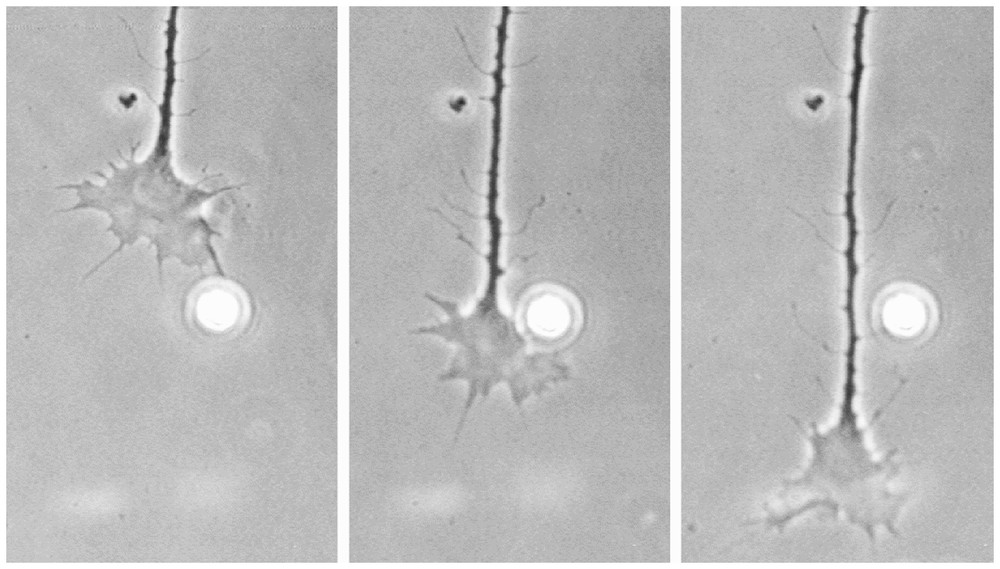
Snapshots of a nerve that grows in vitro. Protrusions are stretched out and are retracted again in a seemingly random way, indicting that there is a highly dynamic internal pattern-forming system that works even in the absence of orienting signals. To allow an oriented outgrowth minute concentration differences of guiding molecules must be able to bias the position at which these protrusions appear. A corresponding model is shown in Fig. 6 (photograph kindly supplied by J. Löschinger).
An important hint for the nature of the underlying mechanism is the fact that this stretching out and retraction occurs also in the absence of external signals. This indicates a patterning system that is permanently active within a cell. In the absence of external signals, the protrusions are stretched out at more or less random orientations (Fig. 5, see also Fig. 7), while in the presence of a signal this dynamic patterning obtains a bias towards the target region. In the following, the ingredients of a mechanism are described, that are able to accomplish this task.
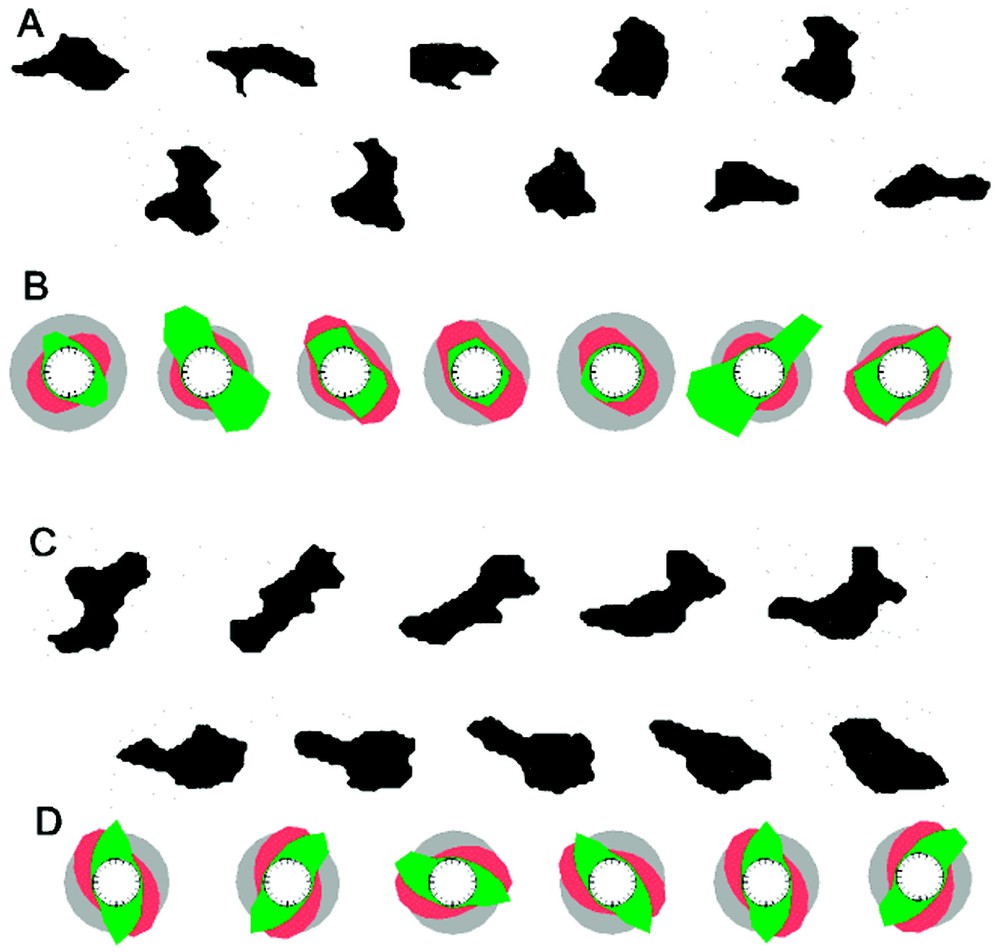
Formation of protrusions at non-random positions in the absence of orienting signals: observations by Killich et al. [45,46] with isolated cells of Dictyostelium. (A) Protrusions appear frequently pair-wise at opposite positions. After retraction, new pairs emerge displaced by 90°. (B) In the model, the protrusions are regulated back by a long lasting antagonistic signal (red). Their remnants are sufficient to enforce the new signals to appear at previously unoccupied places, i.e., at 90°. (C) Another observed mode is a wave-like rotation of the protrusions around the cell. (D) Model: With a small increase of the substrate production (bb in equation (3b)), the activation does not collapse, but escapes into an adjacent region. A rotation of the signal around the cell surface results (calculated with equations (3) and da=0.0015; ra=0.02; si=0.02±2.5% random fluctuations; ba=0.003; sa=3, db=0.4; rb=0; bb=0.0035 (B) or 0.0045 (D); cc=0; dc=0.002; rc=0.004; sc=1).
8 Maintenance of the directional sensitivity: destabilization of the hot spots opens the opportunity to create new signals
If a pattern-forming system is still in the instable homogeneous steady state, the system is very sensitive to external perturbations. Minute asymmetries are decisive at which position the maximum will emerge. In the absence of such an asymmetry, random fluctuations can be decisive. The situation may be compared with a pencil balancing on its tip. It will fall down and minute differences decide in which direction it will fall. However, a chemotactic cell has not only to decide once in which direction to go but has to adapt permanently to an optimum orientation. The pencil-analogy illustrates the problem. After it has dropped down, i.e. after transition from the instable to a stable equilibrium, a much higher external influence would be necessary to reorient the pencil. This illustrates that the problem is not so much to achieve the sensitivity but to maintain the sensitivity of a cell even after the internal amplification already led to a strong internal pattern.
The following model has turned out to accomplish a permanent sensitivity [41]. The autocatalysis required for the internal amplification saturates at high activator concentrations. This leads to an enlargement of the activated region at a lower absolute level (Fig. 6A and B). The inhibition spreads rapidly over the whole cell, leading to an overall competition. Only a certain fraction of the cell cortex can become activated. If the activation does not spread on the cell surface, the activated regions need not to be coherent. In the absence of an orienting signal, their positions are determined by fluctuations and appear at random. With an external signal the internal signals appear where the combined influence of the external signal and the random fluctuations are highest (Fig. 6C). A stronger external signal will lead to a more focussed appearance of the internal maxima.
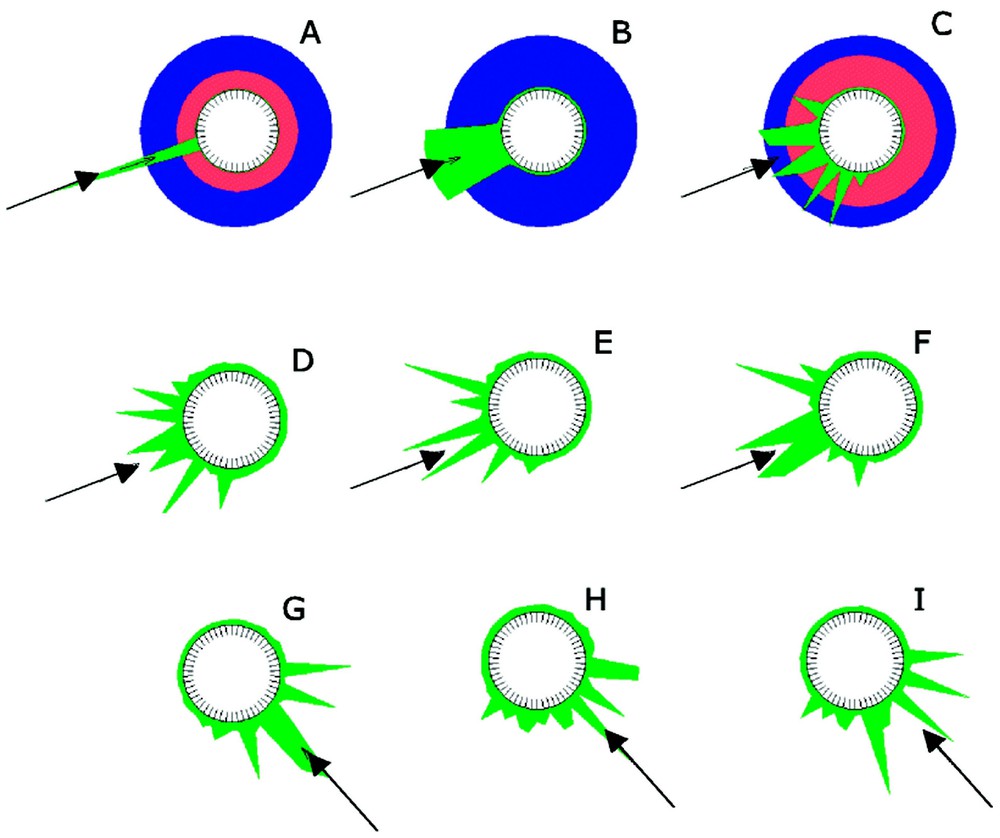
Model for the chemotactic orientation of cell polarity [41]. The external signal (blue) is on one side (arrow) 2% stronger that on the opposite side. It has a positive influence on a cell internal pattern-forming system (activator: green, inhibitor: red). (A) Without saturation, the signal is very sharp. (B) With saturation in the self-enhancing process, a broader activated zone is formed. (C) If it is realistically assumed that some statistical variations in the ability to perform the self-activation exist at the cell cortex, somewhat irregular spots emerge. They appear preferentially on the site oriented towards the signal source. (D–F) If these hot spots have only a limited half-life, new one emerges after the older disappear. (G–I) After a change in the orientation of the external signal (arrow), the locations of the temporary signals adapt rapidly to the new direction. Simulation with equations (5), ra=0.02, ba=0.1; sa=0.005; rb=0.03; bc=0.005 and rc=0.013; Michaelis–Menten type constant cc=0.2.
A permanent sensitivity can be obtained if these internal signals have only a limited half-life. This is the case if a second local antagonistic reaction causes a breakdown of the individual internal signals after a certain time. The deactivation of one region leads to a lowering of the long-ranging antagonistic reaction and enforces therewith the formation of a new activation at another position on the cell surface. Which region will win this race depends on the external signal and the cell internal state of the pattern-forming mechanism. Fig. 6D–I shows snapshot of corresponding distributions. On time average, the maxima point in the direction where the signalling molecule is coming from. In the simulation, it is assumed tat the external signal has a positive influence on the internal patterning system. After a change in the direction of the external signal, the cell internal pattern follows rapidly. Thus, with two antagonistic reactions, the maintenance of a permanent sensitivity in a chemotactic cell requires a mechanism analogous to that discussed above for shell patterns and phyllotaxis. For the simulation Fig. 6D–I, the following equation has been used:
| (5a) |
| (5b) |
| (5c) |
This model offers a simple mechanism for an important process that plays a role the in the patterning of the nervous system [38], in the movement of cells during development and during inflammation [42]. Calcium plays presumably a pivotal role in the formation of cell polarity [43], a fact that can be integrated into the model in a straightforward manner [41]. Not yet included into the model is the fact that the same molecules can work as attractants or repellents, depending on other molecules to which the growth cone is exposed [44].
9 Coordinated cell shape changes in the absence of external signals
Observations of isolated cells of the slime mould Dictyostelium discoideum have shown that even in the absence of external signals, the formation of protrusions occurs in a non-random way [45,46]. Two modes are especially frequent (Fig. 7A and C). In the first mode, protrusions stretch out at two opposing sides. After their retraction, a new pair results, with a 90° orientation in respect to the preceding one. The second mode leads to protrusions that move around the cells in a wave-like manner. In terms of the model, these observations show that in the absence of external signals the cells are so sensitive that remnants of the long-lasting antagonist are sufficient for orientation. As shown in Fig. 7B and D, the model describes both modes. According to the model, the oscillation in counter phase corresponds to the leaf initiation in 90° pairs (Fig. 4B and C), underlining the proposed inherent similarity of phyllotaxis and chemotactic orientation.
10 Conclusion
Highly dynamic pattern-forming processes can be described by one autoregulatory reaction that is balanced by two antagonistic reactions. Such systems allow a simultaneous patterning in space and in time and may never reach a stable steady state. Patterning in diverse biological situation is proposed to depend on such processes. The position of the newly formed high concentrations can either depend on minute external signal (as in chemotaxis) or on the remnants of the antagonistic effects (as in leaf formation and shell patterning). The examples given are certainly not exhaustive. The centre finding in E. coli for the localization of the division plane is based on a wave that oscillates around the centre, keeping in this way the centre free of any division inhibitor [47]. The known molecules suggest that this wave formation is based on a similar mechanism [48].
The destabilization of a once-generated pattern has an antipode in a mechanism in which a pattern leads on the long term to a stabilization of the pattern, not to a destabilization, as discussed above. The competence of cells to perform the pattern forming reaction is then preferentially maintained in regions near to an activated (organizing) region. In this way, the formation of multiple maxima during growth as shown in Fig. 2A can be avoided. This is an important prerequisite to generate extended embryonic axes in a reliable way [7,10]. Thus, a positive or a negative feedback of a pattern on its own adds new features that play important roles in development.



