On the mechanochemical theory of biological pattern formation with application to vasculogenesis

James D. Murray

doi:10.1016/S1631-0691(03)00065-9

Biological modelling / Biomodélisation

On the mechanochemical theory of biological pattern formation with application to vasculogenesis
[Théorie mécanique de formation des motifs biologiques et application à la genèse des vaisseaux]

Présenté par : Jacques Ricard

James D. Murray ¹

¹ Department of Applied Mathematics, University of Washington, Box 352420, Seattle, WA 98105-2420, USA

Comptes Rendus. Biologies, Volume 326 (2003) no. 2, pp. 239-252.

Résumés

Anglais
Français

We first describe the Murray–Oster mechanical theory of pattern formation, the biological basis of which is experimentally well documented. The model quantifies the interaction of cells and the extracellular matrix via the cell-generated forces. The model framework is described in quantitative detail. Vascular endothelial cells, when cultured on gelled basement membrane matrix, rapidly aggregate into clusters while deforming the matrix into a network of cord-like structures tessellating the planar culture. We apply the mechanical theory of pattern formation to this culture system and show that neither strain-biased anisotropic cell traction nor cell migration are necessary for pattern formation: isotropic, strain-stimulated cell traction is sufficient to form the observed patterns. Predictions from the model were confirmed experimentally.

Nous décrivons la théorie mécanique de formation des motifs (théorie de Murray–Oster), qui repose sur une base biologique bien documentée expérimentalement. Le modèle quantifie l'interaction des cellules avec la matrice extracellulaire par l'intermédiaire de forces générées par la cellule. Le cadre du modèle est décrit quantitativement en détail. Les cellules vasculaires endothéliales, lorsqu'elles sont cultivées sur une matrice membranaire couverte d'un gel, s'agrègent rapidement en amas, et en déformant la matrice en un réseau de structures allongées. Nous appliquons la théorie mécanique de formation des motifs à ce système en culture et montrons que, ni une traction cellulaire anisotrope déviée par sustension, ni une migration cellulaire ne sont nécessaires à la formation des motifs : une traction isotrope stimulée par la tension suffit à former les motifs observés. Les prédictions du modèle ont été vérifiées expérimentalement.

Métadonnées

Reçu le : 2002-12-10
Accepté le : 2002-12-13
Publié le : 2003-02-01

PMID

DOI : 10.1016/S1631-0691(03)00065-9

Keywords: pattern formation, mechanical theory, cell culture
Mot clés : formation des motifs, théorie mécanique, culture des cellules

Affiliations des auteurs :

James D. Murray ¹

¹ Department of Applied Mathematics, University of Washington, Box 352420, Seattle, WA 98105-2420, USA

@article{CRBIOL_2003__326_2_239_0,
     author = {James D. Murray},
     title = {On the mechanochemical theory of biological pattern formation with application to vasculogenesis},
     journal = {Comptes Rendus. Biologies},
     pages = {239--252},
     publisher = {Elsevier},
     volume = {326},
     number = {2},
     year = {2003},
     doi = {10.1016/S1631-0691(03)00065-9},
     language = {en},
}

TY  - JOUR
AU  - James D. Murray
TI  - On the mechanochemical theory of biological pattern formation with application to vasculogenesis
JO  - Comptes Rendus. Biologies
PY  - 2003
SP  - 239
EP  - 252
VL  - 326
IS  - 2
PB  - Elsevier
DO  - 10.1016/S1631-0691(03)00065-9
LA  - en
ID  - CRBIOL_2003__326_2_239_0
ER  -

%0 Journal Article
%A James D. Murray
%T On the mechanochemical theory of biological pattern formation with application to vasculogenesis
%J Comptes Rendus. Biologies
%D 2003
%P 239-252
%V 326
%N 2
%I Elsevier
%R 10.1016/S1631-0691(03)00065-9
%G en
%F CRBIOL_2003__326_2_239_0

James D. Murray. On the mechanochemical theory of biological pattern formation with application to vasculogenesis. Comptes Rendus. Biologies, Volume 326 (2003) no. 2, pp. 239-252. doi : 10.1016/S1631-0691(03)00065-9. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/S1631-0691(03)00065-9/

Version originale du texte intégral

1 Introduction and biological background

Among the most crucial issues in development are the evolution of spatial patterns and the mechanisms which create them. Much progress has been made in furthering our understanding of the basic principles that patterning mechanisms must possess to be able to generate specific spatial patterns. Even so, we still do not know, with any certainty, definitive details of a single pattern formation mechanism which is involved in development. Morphogenetic model mechanisms can suggest possible scenarios as to how pattern is laid down, and sometimes when (as for example, in the experimentally confirmed case of stripe patterning on the alligator Alligator mississippiensis [1]) and how the embryonic form might be created. It is now widely accepted that dramatic progress can come about through a genuine interdisciplinary approach involving experimentalists and theoreticians. The books by Murray [2,3] discuss in detail many such successful case studies.

Embryogenesis proceeds through a series of sequential processes which generate specific patterns at each stage. The network pattern observed in vasculogenesis and angiogenesis, for example, are typical examples: how they are formed is an important and question particularly in view of the work of Folkman and his colleagues (see, for example, [4,5]) on the crucial role angiogenis plays in the growth of solid tumours.

Broadly speaking, there are two prevailing views of pattern generation that have influenced the thinking of embryologists. One is the long standing and well known Turing chemical pre-pattern approach [6] and the Murray–Oster continuum mechanochemical approach (see, for example, [7–10]). The former requires cells to respond to a concentration level such as a positional information approach [11] applications of which are given in [12]. Important related mechanisms involve cells and chemotaxis, the aggregation effect whereby cells move up concentration gradients of chemoattractants. Practical examples of both experiment and theory involving bacteria are described in [13–15]. General descriptions, a full discussion of pattern formation mechanisms and real biological examples are given in [2,3]. A good view of the current state of pattern formation modelling in several different areas is given in [16,17].

2 Mechanochemical mechanisms for generating pattern and form

The mechanochemical modelling framework is based on the observation [18] that “relatively simple cellular forces can give rise to complex changes in form”. This concept was clearly demonstrated by experiments in which fibroblast cells are placed on an elastic substratum. The cells spread and migrate, concurrently generating strong traction forces which deform the substratum creating tension patterns on the elastic sheet [19]. The latter experiments and the (even now) illusive nature of morphogens were the impetus for the initial development of the mechanochemical modelling approach [7–9]. The quantification of these types of cellular forces has been studied, for example, by Traqui and his colleagues [20] and Moore [21].

Mesenchymal cells, on which we focus here, are spread within a three-dimensional fibrous extracellular matrix (ECM) and migrate within the matrix: they can secrete (and degrade) matrix as well as exert traction forces on the ECM environment. That is, these cells are capable of significantly altering their environment. So, within this simple framework, the cells can create spatial heterogeneity and generate form simultaneously if the parameters are in appropriate experimentally reasonable ranges. Perhaps most crucial, however, is that with such a model mechanistic framework the variables involved and the consequences of their interaction can be observed and measured experimentally.

The power of mathematical modelling lies in its ability to make predictions and suggest experiments. Mechanochemical theory is particularly well-suited to connecting theory with experiment since the model structure is firmly based on empirically measurable quantities (e.g., cell density, matrix density, cell traction forces and known chemicals) and the consequence of varying such quantities can be clearly observed.

Here we give a brief introduction to the mechanochemical theory of morphogenesis and, by way of example, describe a recent successful application to vascular network formation where the theory and experiment are sufficiently close to be able to suggest some of the essential elements in the biological mechanism which create these specific biological patterns and final structure.

The basic mechanical model hinges on two key experimentally determined properties of mesenchymal cells in vitro: (i) cells migrate within a tissue substratum made up of fibrous ECM and other cells; (ii) cells can generate large traction forces. The models try to mimic the mechanical interaction between the motile cells and the viscoelastic substratum (ECM) within which they move.

Mesenchymal cells move by exerting forces on their surrounding, consisting of the viscoelastic fibrous ECM and the surface of other cells. They use their cellular protrusions, the filopodia or lamellapodia, which stretch out from the cell in all directions, to grip whatever is available and pull. As the cells move through the ECM they deform it by virtue of their traction forces. These deformations in the ECM induce anisotropy effects which in turn affect the cell motion. Analysis of models incorporating these various effects show that coordination of such effects result in spatially organized cell aggregations. The general modelling scenario underlying the models is shown schematically in Fig. 1.

Fig. 1
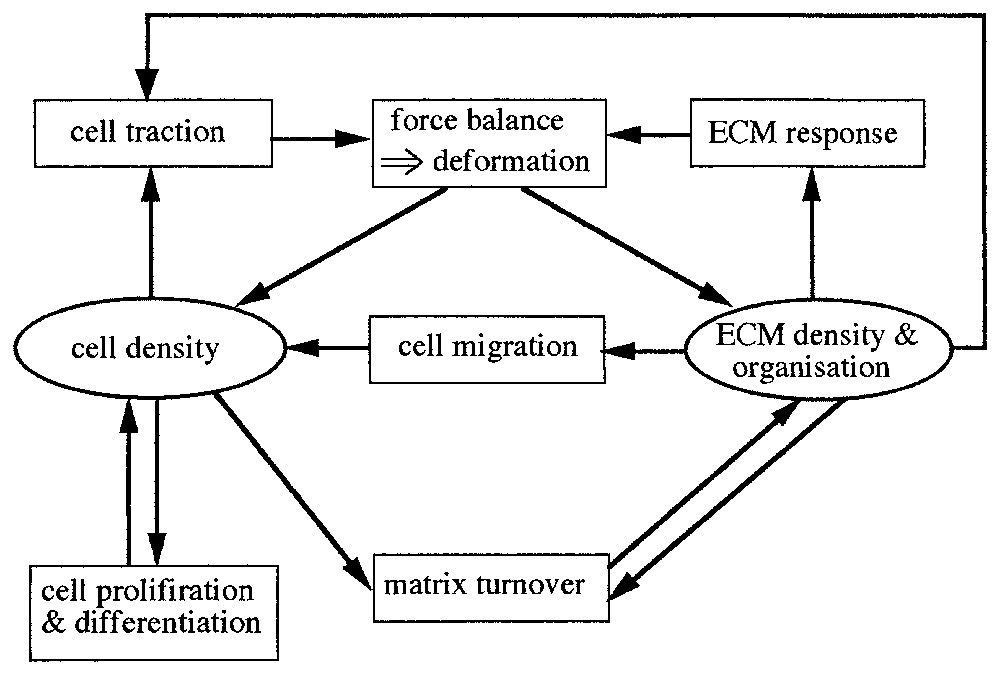
Key variables and processes in dermal/fibroblast cell-tissue patterning. This structure underlies the mathematical model: each variable (cell density, ECM density, forces) requires an evolution equation which incorporates terms corresponding to the various processes. The force balance box determines the matrix deformation. ECM refers to extracellular matrix.

The model is a continuum one, consisting of three equations governing (i) the cell population density, (ii) the mechanical balance of the forces between the cells and the ECM and (iii) the conservation law for the ECM. Here we give only the equations in words to indicate the principles: brief mathematical details are given in the appendix with full discussions in [2,3].

2.1 Cell density conservation

Many factors, with varying levels of importance, affect the movement of embryonic cells within a tissue substratum which is made up of fibrous ECM. For example, some of the more obvious are:

– chemotaxis, the process by which cell motion is directed by a chemical gradient,
– contact guidance, when the substratum defines a preferred direction of cell motion,
– contact inhibition, inhibiting motion and reducing individual cell traction forces as a consequence of high cell densities,
– convection, which transports cells and ECM due to local deformation in the matrix.

The forces exerted on the ECM by other cells induce passive movement of cells on the ECM. Diffusion is the usual random dispersal of cells with general motion down a cell density gradient: it can include biased or tissue-guided diffusion. Haptotaxis is the process by which ECM gradients affect cell movement. Cell tractions generate gradients of matrix density, which are in turn associated with the density of adhesive cites for cell lamellapodia to bind to. Since cells can get a stronger grip on denser matrix (up to a certain density) cells tend to move up an adhesive/matrix gradient. Galvanotaxis is movement due to the field generated by electric potentials, which are known to exist in embryos. These effects are all well documented experimentally. The model field equations encapsulate the key features which affect cell movement within its extracellular environment. For illustration we shall not include all of the effects just mentioned but it will be clear how they can be incorporated: see [2,3] for a full discussion and the mathematical representation and quantification of the terms.

Within a fixed control volume, cell density is conserved according to equation (1):

rate of change of cellular density = convection + diffusion + haptotaxis + mitosis - cell death

(1)

where cell death refers to programmed cell death. Diffusion is dispersive, while haptotaxis is aggregative. The competition between aggregation and dispersion is primarily what determines whether or not patterning will occur.

Contact guidance is involved in the formation of cell-matrix networks discussed below. Such guidance can be modelled in different ways. One possibility is to make the diffusion directed diffusion. In this case, the diffusion coefficient is a function of the elastic strain of the ECM (see, for example, [3]). This dependence implies that the strain of the matrix can grossly affect the direction of cell movement as we shall see in the section on network formation.

The matrix mechanical behaviour is dominated by the fibrous collagen component of the ECM. Local disturbances in the matrix density can induce convection of the matrix. Also, as (mesenchymal) cells move through the matrix environment, they can secrete and/or degrade the ECM: this occurs, for example, in wound healing.

2.2 Conservation of matrix density

The conservation equation for the ECM density is then given by equation (2):

rate of change of matrix density = convection + secretion - degradation

(2)

In many applications, the secretion term is often negligible on the time scale of the pattern formation, as is the case in the experiments associated with the matrix network related to vasculogenesis discussed below.

2.3 Mechanical interaction of cell and matrix

Since inertial terms are small in development, the governing equation for the mechanical interactions between the cells and matrix is simply that the sum of the various forces are in equilibrium within the tissue. We thus have (equation (3)):

forces on the body = cell traction forces + viscoelastic restoringforces of the matrix = 0

(3)

2.4 Viscoelastic matrix material

The stress–strain relation in such a complex tissue matrix is almost certainly nonlinear and plastic. There is still no experimental evidence which would allow us to postulate the actual form of the relation. Many patterns result from relatively small deformations and cell density differences (one example occurs in the formation of papillae, the dermal condensations of cells which presage feather and scale formation). We make the assumption that for small strains, cell-matrix material forces can be modelled by a linear viscoelastic response [22]. The matrix stress then consists of a viscous and an elastic component:

{stress}_{matrix} = {stress}_{viscous} + {stress}_{elastic}

with the viscous component of the stress proportional to the rate of change of the strain in the matrix.

2.5 External body forces

There are often external forces acting on the tissue body we are attempting to model. These forces may be due to attachment of the matrix to a substrate or in the case of network formation we discuss below, to the base of the experimental vessel. The body forces holding the tissue in various places can reasonably be modelled as proportional to the density of matrix and the displacement of the matrix. Alternatively in the matrix network situation discussed later it is more appropriate to relate the attachment force to the viscous drag: we come back to this below.

Although at the time of the formulation of this modelling approach [7–9] the mechanical properties of ECM and cell-matrix interactions had not been quantified, recent experimental advances have focused on these mechanical aspects of tissue interactions. As a result, many of the parameters described in the model formulation can be estimated. As well as the work mentioned above [20,21] the viscoelastic properties of mesodermal cells during early development have been quantified [22]. In the cell-matrix experiments described below parameter estimations have also been obtained.

In many developmental situations (wound healing is one) chemicals can play a significant role in the pattern formation process and therefore should be included in the model. Although chemical dynamics can be incorporated in principle relatively simply, but only if we have some idea of how they interact with the cells and matrix. At this stage, these interactions are generally still uncertain.

The mathematical investigation of these model equations involves linear analysis about the steady states to obtain what is called the dispersion relation which predicts the pattern formation potential. The analysis (see, for example, [2 or 3] for a full discussion) results in a remarkably wide variety of dispersion relations which indicate a rich spectrum of nonlinear spatial patterns. The nonlinear spatial patterns almost always have to be obtained by numerical simulation of the equations. As expected the type of patterns possible depend on which effects are included in the model mechanism. Another aspect of these mechanical models is their robustness to parameter variation. It is essential to know, at least approximately, the parameter domain for specific patterns because this is one of the optimal ways to assess model robustness. In the remainder of this article we discuss an application of mechanochemical theory to vascular network formation.

3 In vitro vascular network formation

Mechanical and fluid mechanical forces play essential roles in the overall development of vasculature. As early as 1893 [23] the importance of (fluid) mechanical factors in the growth of blood vessels during development was pointed out. In a review [24] of this and other works on mechanical forces on angiogenesis these early observations of how vascular sprouting in the growing embryo might occur as a result of a combination of velocity of blood and pressure are described. Another review on some of the roles of mechanical forces in vascular development and remodeling is given in [25].

The development of in vitro angiogenesis systems is a controlled means of studying vessel formation. Such systems have shown the important mechanical role that the ECM plays in angiogenesis. It provides, among other things, a scaffold necessary for cell migration and morphogenesis (for example, [26,27]). As we described, cells can not only produce or degrade their ECM but also alter its structure by applying mechanical forces. Through matrix production and degradation, cells can influence the mechanical properties of their ECM and, through their mechanical forces, they can reorganise its fibrous components into matrix lines that the cells use as migratory pathways and movement cues. Such a mechanical scenario in which cell-ECM interactions can be orchestrated to form complex spatial patterns in development make it a very good candidate for the application of the Murray–Oster mechanical theory. The ability of the cell-matrix interaction to effect an alignment of the matrix thus influencing cell movement is quite common in development: some discussion of these is given in [26–29] but the key reference is the 1998 book [30] on vascular morphogenesis.

Of particular relevance to this section is in vitro work on vascular network formation [26,27]. This work helps to elucidate the mechanism of vascular network formation in vitro [26]. It is shown that networks are not specific to endothelial cells since a variety of traction exerting cells, not necessarily endothelial cells, can form networks when cultured on gelled basement membrane (Matrigel). Moreover, cells cultured on different substrates (Matrigel, type I collagen gels), also form networks provided the matrix is malleable enough. These studies suggest that the mechanism lacks cellular/matrical specificity and that a physical/mechanical mechanism could possibly explain the generality of the network forming process.

Here we describe a basic mathematical mechanical model mechanism with the aim of showing that a purely mechanical mechanism could be responsible for the observed patterns and how they are actually formed in development. Such a mechanical model does not specify the type of cells and matrix involved but rather only considers the possible mechanical interactions between the various components. We test the model against the patterns observed by particular experiments and we further use the model to quantitatively describe the interaction between the various mechanical properties and the network and their pattern forming abilities.

Experiments [26,27] show that bovine aortic endothelial cells (BAEC), cells of the murine Leydig cell line TM3, adult human dermal fibroblasts and human smooth muscle cells when cultured on Matrigel are observed to form networks. The process for all cell lines is similar: cells adhere onto the matrix and start pulling on it. The pulling results in movement of the matrix and the cells that have adhered to it, eventually forming cell aggregates with significant amounts of matrix accumulated underneath the aggregates. As a result cellular traction tension lines appear around the clusters. In time, the matrix components appear to form fibrous lines between neighboring clusters and along the tension lines. Once the lines form, the cells become actively motile and migrate onto the matrix pathways, thus forming cellular cords. Eventually the culture plane is tessellated with polygons with sides defined by the cellular cords [26]: see also Fig. 2a.

Fig. 2
(a) Experimental angiogenesis. Bovine aortic endothelial cells, cultured 48 h in a subconfluent monolayer on top of a layer of Matrigel, organized into a planar network of cords. Each cord (example, arrow) is comprised of many cells. Image is viewed by darkfield illumination. Bar at lower left=200 μm. Image used was kindly provided by Dr. C. Little. (b)–(d) Numerical results of the model equations. The figure shows the cell density distribution across the dish. White areas denote areas of large cell densities (up to 6 times the initial seeding densities) and dark areas denote regions of low cell densities. Initially the cells are approximately uniformly distributed throughout the dish, with some small random variations in the density. With time some cells cluster and other areas become less populated. Small-sized polygons appear, some of which grow in size while others close in, in a sphincter-like manner. Figures represent pattern at 7 h (b), 20 h (c), and 24 h (d). The size of one square corresponds to 800 μm. The distribution of matrix is similar to that of the cell densities. (The parameter values – with the parameters defined in the Appendix A – used in the simulations were: τ=0.06 dyn/cell, $E = 20 dyn {cm}^{- 2}$ , μ₁=1.5×10⁷ Pe, μ₂=0.9×10⁷ Pe, $D = 0.46 \times 10^{- 11} {cm}^{2} s^{- 1}$ , ν=0.2, $s = 10^{10} dyn s {cm}^{- 3}$ , $n_{0} = 10^{5} cells {cm}^{- 2}$ , λ=4×10⁻¹³.)

Collagen (an ingredient of tissue matrix) content influences the formation of networks, presumably by altering matrix stiffness and thereby the effect of the cell-exerted traction onto the matrix. Thickness of the matrix layer also influences the size of the networks formed: thin layers of matrix resulted in small or no network formation. On a ramp of increasing matrix thickness, larger cellular networks form on the thicker areas of matrix: refer also to Fig. 3c.

Fig. 3
Numerical simulations, (a)–(c), of cellular networks formed on a gradient in matrix density. On the top we had initially a matrix that was a tenth of the thickness of the matrix on the lower side of the square. Smaller networks form in the presence of a thinner matrix (top side). (a) is the initial distribution and (b) and (c) are the distributions as time increases. Parameter values are the same as in Fig. 2.

These results suggest that mechanical interactions are of primary importance for the development of pattern. Mathematical descriptions of the interactions, which we describe below, confirm the crucial role that mechanical forces play in the network pattern formation and provide a tool for assessing which mechanical properties of the ECM control the patterning process as well as how the parameters may modulate pattern size. It also provides various experimental scenarios to highlight the effect of experimentally variable parameters, such as gel thickness, density of cells and so on.

Since in the experiments [26,27] there is neither matrix production nor degradation we require only two equations, namely cell density conservation and a force balance equation. The effect of the matrix density is incorporated in the matrix thickness on the dish. As the cells pull the matrix, it moves across the dish. Experiments indicate that some matrix fibrils remain attached to the dish, while the rest are dragged across the lower parts of the matrix. The net effect on the surface of the matrix of the attachment of the fibrils on the dish, is a resistance, which in a planar situation we treat as a resistive viscous drag.

Because the thickness of the experimental gel on which the cells are embedded is very thin, and in particular, relative to the cell-matrix spatial domain, a two-dimensional model is sufficient at this stage.

3.1 Mathematical model

The two-dimensional mathematical model quantifies the basic experimental mechanical scenario described above. We do not include cell proliferation: on the Matrigel cultures the first cell aggregates and lines of tension appear after 4 h and the networks are complete within about 24 h. The time between two subsequent cell mitoses is about 17 hours for endothelial cells so we assume that no significant changes in the cell populations occur which could influence the pattern forming process.

Local changes in the cell density are a combination of mainly two movements, the convective flux and an anisotropic strain-dependent random motion tensor. We thus consider that cell movement can be approximated by a random walk that is biased along areas of matrix alignment. The resulting conservation equation for the cell density in words from equation (1) is then (equation (4)):

rate of change of cell density = convection + strain - dependent diffusion

(4)

Here the diffusion coefficient is dependent on the matrix strain whose particular form depends on the specific assumption about how cells perform their random movements. Its specific form for small strain was derived [31] under the assumption that the movement bias increases in expansion along one direction and/or compression in the perpendicular direction.

In the initial analysis [28], we did not consider strain-dependent active movement so that we could test whether network formation is possible under just cell-exerted traction.

3.1.1 Forces within the extracellular matrix

The width of the matrix sample in the dish is much larger than the thickness of the matrix so we approximate the matrix as a two-dimensional material. Moreover, we assume that the traction exerted by the cells remains confined in the plane parallel to the dish (or, approximately, the matrix) surface. In other words, we consider the material to be under a plane-stress assumption. The movement of the matrix is resisted by attachment of the matrix to the dish. In vivo planar angiogenesis is, by comparison, influenced by the potential attachment and continuation of the fibrous and cellular components of the adjacent tissue and is more accurately described by the three-dimensional model equivalent.

The key forces are of course those generated by the cells. The others are generated as a direct consequence. So, forces that are present in the tissue are: (i) the cell-exerted traction; (ii) the resistance due to the matrix-dish contact; (iii) the viscoelastic forces of the matrix material, which are resisting the deformation. Again since the time required for generation of the pattern is relatively long and the size of the pattern is small in absolute terms, inertia effects are negligible and the forces at any given point are again considered to be in equilibrium.

In response to a force, the matrix is displaced slowly due to its viscous properties. If strains developed in collagen gels are small (less than 10%) then the gels have been found to respond linearly to applied stresses [32,33]. We therefore again describe the matrix response as that of a linear viscoelastic body.

The equation reflecting the balance of these forces (F) is then (cf. equation (3))

F_{cells} (cell - exerted traction) + F_{anchoring} (attachment on dish) + F_{matrix} (viscoelastic restoring forces) = 0

(5)

Again as above we consider the cell traction forces and the matrix response as arising from the corresponding stresses within the matrix medium. So, F_cells, the forces in the matrix due to the cells and F_matrix the viscoelastic force in the matrix material. F_anchoring is an external (body) force resisting the matrix displacement. The cell traction F_cells depends on the local cell density initially increasing with the cell density eventually decreasing with large enough cell densities.

The viscoelastic stresses we consider to be made up of elastic and viscous parts as in the last section. The difference here is associated with the drag of the matrix across the dish. As the cells pull the matrix, it moves across the dish. Experiments indicate that some matrix fibrils remain attached to the dish, while the rest are dragged across the lower parts of the matrix. The net effect on the matrix surface due to the fibril attachments to the dish, is a resistant force. In this two-dimensional model we treat such resistance as a viscous drag.

Since the vertical stress is zero we can derive a relation between the strain components in the three directions [3,28].

The detailed quantification of the two equations for cell conservation and balance of forces together constitute the model mechanism. The equations were solved with the appropriate boundary conditions and initial conditions in cell density and matrix distribution in keeping with the experimental set-up [26,27] (see the Appendix A and [3] for a full discussion). Where these parameters specifically appear in the model is shown in the Appendix A.

3.2 Estimation of the parameters

Since there is a close relation between this application of the mechanical theory and in vitro experiments we were able to derive estimates for various parameters describing cell behavior and matrix properties. This is one of the most important aspects of the application of the theory. These parameters are defined in the Appendix A where it is shown where they appear in the model equations.

The stiffness of the matrix is represented by the elastic modulus of the material (E, $dyn {cm}^{- 2}$ ) and is determined primarily by the type, amount and organization of its fibrous components. For example, the anterior porcine vitreous body and the posterior bovine vitreous body were found to have similar collagen contents and gave elastic moduli of $26.93 dyn {cm}^{- 2}$ and $8.01 dyn {cm}^{- 2}$ , respectively [31,34]. Since the collagen gels used in the vascular network-forming experiments have collagen content comparable to that of the vitreous bodies mentioned, we assume that these gels' elastic moduli are within a similar range.

The shear viscosity of $2.1 mg {ml}^{- 1}$ collagen I gel has been measured using creep tests to be 7.4×10⁶ Pe [33] while that of the posterior bovine vitreous body was estimated to be 2.5×10² Pe [32].

Traction per cell (τ dyn/cell) we consider to be comparable to that of human umbilical vein endothelial cells which is approximately $6.1 \times 10^{4} dyn {cm}^{- 2}$ [34]. From these results we estimate the traction force per cell to be in the region of τ≈0.15– 0.27 dyn/cell.

The Poisson ratio (ν, $cm {cm}^{- 1}$ ) can be theoretically measured by extending a material by a certain amount and measured by its compression on the perpendicular direction. The ratio of relative extension to compression on the perpendicular direction gives the magnitude of the parameter. In practice, such measurements for soft materials such as collagen gels can be very difficult, not least because the value of ν changes in time. The Poisson ratio for the fibre network of such gels is estimated at ν≈0.2 [35].

Cell motility for endothelial cells has been calculated using migration assays. The values reported for endothelial (Human Microvessel Endothelial Cells) on gelatin were $9.5 \pm 1.2 \times 10^{- 9} {cm}^{2} s^{- 1}$ in the presence of endothelial cell growth factor and $2.6 \pm 0.6 \times 10^{- 9} {cm}^{2} s^{- 1}$ in its absence and $19.3 \pm 4.22 \times 10^{- 9} {cm}^{2} s^{- 1}$ on fibronectin [36].

In our investigation, we were concerned with the initial stages of network pattern emergence where the strains are still small and we can assume that the parameters stay approximately constant.

4 Results

The model mechanism system of equations was analyzed analytically and numerically [3,28,29]. In Fig. 2 we show a selection of the results of the analysis. Analysis showed that small variations in cell density could trigger matrix displacements if the following relation between the model (and real biological) parameters obtains:

\frac{τ}{E} > \frac{1}{1 - ν^{2}} \frac{1}{c_{0}}

(6)

where τ is the cell traction per cell, E and ν are respectively the elastic Young's modulus and Poisson ration of the matrix, c₀=4×10⁴–

2 \times 10^{5} cells {cm}^{- 2}

[26] is the initial cell seeding density.

The relation (6) suggests a basic, and intuitively reasonable, rule that could make patterns possible: patterns are more likely to form if the cell traction τ is sufficiently large, or if the matrix stiffness E is sufficiently low or if the initial seeding density is relatively large. The results are in general agreement with experimental findings. For example, when cell traction was inhibited or matrix stiffness greatly increased, no patterns formed [26]. Also, increases in the cell plating densities facilitates the formation of pattern. We can see why, since if few cells are seeded, they have difficulty in deforming the matrix and starting the patterning process.

This inequality predicts when pattern could form, but does not predict the type of pattern formed. The pattern described by the equations can be determined by solving the governing equations numerically. Numerical simulations [28] show that network formation is possible through a purely mechanical process as in Fig. 2 (see also Fig. 3).

The numerical simulations clearly showed network formation and subsequent remodelling: some polygons grew larger and others closed in, in a sphincter-like manner. There was a direct correspondence between areas of large cell density and areas of high matrix density, just as we would expect (see the experimental image in Fig. 2a).

The choice of parameters influenced the formation of pattern and rate at which the network pattern formed. If traction was too low, the plating density too low, or the stiffness too high, no patterns formed. If, on the other hand, stiffness was too low or traction too high, cells and the matrix formed clusters but no matrix cords were observed.

Viscosity of the matrix, as to be expected intuitively, influenced the time it took for the pattern to appear, provided traction and stiffness were within the appropriate range, but did not determine whether pattern would form or not.

The matrix density played a significant role in the size of the network formed. Since the matrix density in these experiments is directly related to the thickness of the membrane we simulated a situation in which there was a gradient in matrix density. We predicted that a network with a gradient in network size would be formed. Fig. 3 shows the results [28] of such a numerical simulation of the model equations. Subsequent experiments confirmed this prediction.

We then investigated how essential the directed diffusion was by solving the equations without any diffusion. One of the initially surprising and important findings was that random motility of cells was not necessary for the formation of pattern. Networks would still form, provided the seeding density was sufficiently large.

4.1 Results from the mechanical theory

Mathematical analysis and simulation of the model mechanism give insight as to which elements are crucial to the development of pattern, help assess the relative importance of such elements, and predict how changes in these factors affect pattern growth and shape. In this way, the model is useful in assessing the biological conditions under which a pattern may or may not form.

We have presented a simple, purely mechanical model for network pattern formation in vitro, in which cellular traction forces play a crucial role in forming the planar pattern of cellular aggregates, cords and matrix deformations observed in vitro. In spite of the simplifying assumptions in the model the results show that in the absence of traction, as in the in vitro system, no pattern forms, supporting our hypothesis that the pattern forms as a result of cellular traction forces. The evolution of the pattern from the model proceeds in the same manner as the in vitro pattern, with irregular polygons both increasing in size and decreasing in number, with the smallest polygons pinching off and vanishing.

As in the in vitro system, pattern forms in our system only when the ratio of traction forces and seeding cell density to gel stiffness is above a certain threshold. Our model results confirm that on thicker gel larger polygons will form. It also indicates that isotropic cellular traction is sufficient for pattern formation. We further found that if cellular traction is sufficiently high or the plating densities large, then traction forces alone can lead to formation of networks. Biased cellular migration may be a component of pattern formation in vivo and in vitro, but we have shown it is not a necessary feature.

We also found that matrix thickness is an important factor influencing the pattern. Cells spread on a matrix whose thickness increased from one end of the dish to the other, formed polygon networks whose size increased with increasing thickness of the gel. The numerical simulation results are in agreement with the experimental results [26].

5 Discussion and some general concluding remarks

The mechanochemical theory of pattern formation has been proven to be important in the study of a spectrum of biological processes such as wound healing, angiogenesis, and limb development, to name just a few. One of the significant features of the applicability of this theoretical framework to a wide variety of problems is that the definable parameters are in principle all measurable experimentally. Although a great deal of experimental work has been devoted to the molecular biology of development, few studies have focused on mechanical aspects: they are technically difficult.

Although certain morphogenetic events can be described by chemical and/or mechanical mechanisms, the vast majority of pattern formation events are the result of the interaction of chemical and mechanical processes. For this reason, mechanochemical theory is a broadly applicable, powerful tool in defining mechanisms for numerous developmental events.

Why use mathematics to study something as intrinsically complicated and ill-understood as development, angiogenesis, wound healing and so on? We suggest that mathematics, rather mathematical modelling, must be used if we ever hope to genuinely and realistically convert an understanding of the underlying mechanisms into a predictive science. Mathematics is required to bridge the gap between the level on which most of our knowledge is accumulating (cellular and below) and the macroscopic level of the patterns we see. In wound healing, scar formation itself is a major concern of the surgeon and the patient. A mathematical approach lets us explore the logic of pattern formation. Even if the mechanisms were well understood – and they certainly are not at this stage – mathematics would be required to explore the consequences of manipulating the various parameters associated with any particular scenario. In the case of wound healing, and it will be increasingly so in angiogenesis with the related cancer component, the number of options that are fast becoming available to wound and cancer managers will become overwhelming unless we can find a way to simulate particular treatment protocols before applying them in practice. The latter has been already of use in understanding the efficacy of various treatment scenarios with brain tumours (glioblastomas) (see [3] for a full discussion and new two-step treatment regimes for skin cancer [37].

There is no doubt that we are a long way from being able to reliably simulate actual developmental scenarios. Not only is the active cellular control of the key processes poorly understood, in the case of wounds, for example, they are difficult to reproduce, with similar wounds on different parts of the same body healing at different rates and with different results. Despite these limitations, we argue that exploring the logic of biological processes is worthwhile even in our present state of knowledge. It allows one to take a hypothetical mechanism and examine its consequences in the form of a mathematical model, making predictions and suggesting experiments that would verify or invalidate the model; even the latter casts light on the biology. Indeed, the very process of constructing a mathematical model can be useful in its own right. Not only must one commit to a particular mechanism, but one is also forced to consider what is truly essential to the process, the key players (variables) and the key processes by which they evolve. We are thus involved in constructing frameworks on which we can hang our understanding. The equations, the mathematical analysis and the numerical simulations that follow serve to reveal quantitatively as well as qualitatively the consequences of that logical structure.

Theoretical studies have served to highlight where our knowledge is deficient and to suggest directions in which fruitful experimentation might lead us. A crucial aspect of this research is the interdisciplinary content. A critical test of all of these theoretical constructs is in their impact on the experimental community. We believe that genuine collaboration between experimentalists and applied mathematicians will lead us more rapidly towards a fuller understanding, if not a complete one, of the biological processes involved in pattern formation and a vast array of medical problems.

Appendix A

Here we briefly give the mathematical description of the mechanical theory as it applies to vascular network theory.

The two-dimensional mathematical model quantifies the basic experimental mechanical scenario described above. We do not include cell proliferation: on the Matrigel cultures the first cell aggregates and lines of tension appear after 4 h and the networks are complete within about 24 h. The time between two subsequent cell mitoses however is about 17 h for endothelial cells so we assume that no significant changes in the cell populations occur which could influence the pattern forming process.

Local changes in the cell density are then a combination of mainly two movements, the convective flux and an anisotropic strain-dependent random motion tensor. We thus consider that cell movement can be approximated by a random walk that is biased along areas of matrix alignment. The conservation equation for the cell density, denoted by c ( $cells {mm}^{- 2}$ ), is

\frac{\partial c}{\partial t} = - \nabla \cdot (c \frac{\partial u}{\partial t}) + \nabla \cdot \nabla \cdot (D (ϵ) c)

where the strain tensor

ϵ = \frac{1}{2} (\nabla u + \nabla u^{T})

and

u

is the displacement vector of the ECM. Here D(ε) is the random motion tensor, dependent on the matrix strain ε, whose particular form depends on the specific assumption about how cells perform their random movements. Its specific form for small strain was derived [31] under the assumption that the movement bias increases in expansion along one direction and/or compression in the perpendicular direction and is given by:

D (ϵ) = D_{0} (\begin{matrix} 1 + \frac{ϵ_{xx} - ϵ_{yy}}{2} & \frac{ϵ_{xy} + ϵ_{yx}}{2} \\ \frac{ϵ_{xy} + ϵ_{yx}}{2} & 1 - \frac{ϵ_{xx} - ϵ_{yy}}{2} \end{matrix})

Here ε_xx, ε_yy, ε_xy, ε_yx represent the two-dimensional components of the strain tensor, ε, and D₀ is the motility coefficient when no strain is present.

The key forces are those generated by the cells. The others are generated as a direct consequence. So, forces that are present in the tissue are: (i) the cell-exerted traction; (ii) the resistance due to the matrix-dish contact; (iii) the viscoelastic forces of the matrix material which are resisting the deformation. Since inertia effects are negligible the forces at any given point are considered to be in equilibrium.

In response to a force, the matrix is displaced slowly due to its viscous properties. We describe the matrix response as that of a linear viscoelastic body. The equation reflecting the balance of these forces is then

F_{cells} (cell - exerted traction) + F_{anchoring} (attachment on dish) + F_{matrix} (viscoelastic restoring forces) = 0

We consider the cell traction forces and the matrix response as arising from the corresponding stresses within the matrix medium. So, F_cells=∇·σ_cells, with σ_cells the stress tensor in the matrix due to the cells and F_matrix=∇·σ_matrix with σ_matrix the viscoelastic stress tensor in the matrix material. F_anchoring is an external (body) force resisting the matrix displacement.

The cell traction F_cells depends on the local cell density as described earlier and it decreases with large enough cell densities. We take the cell-exerted stress on the matrix due to the cells as

σ_{cells} = \frac{τ c}{1 + λ c^{2}} I

where

I

is the unit tensor. The parameter τ (dyn/cell) represents the stress that one cell exerts on the matrix at low cell densities and λ is the parameter which measures the force inhibition as a result of increasing cell density. For the densities with which we are concerned the traction force is approximately given with the cell stress tensor

σ_{cells} \approx τ c

.

The viscoelastic stresses we consider to be made up of elastic and viscous parts as described generally in the section on the mechanical theory. The stress–strain relation in such a complex tissue matrix is almost certainly nonlinear and plastic. There is still no experimental evidence which would allow us to postulate the actual form of the relation. Since many patterns result from relatively small deformations and cell density differences we make the assumption that for small strains, cell-matrix material forces can be modelled by a linear viscoelastic response [22]. The matrix stress tensor then consists of a viscous and an elastic component:

σ_{matrix} = σ_{viscous} + σ_{elastic}

with the viscous component of the stress proportional to the rate of change of the strain ϵ in the matrix:

σ_{viscous} = μ_{1} ϵ_{t} + μ_{2} θ_{t} I

where

θ = \nabla \cdot u

represents the dilation of matrix. Here the subscript t refers to differentiation with respect to time. The parameters μ₁ and μ₂ represent the bulk and shear viscosities of the matrix, respectively.

The elastic component of the stress is given by

σ_{elastic} = \frac{E}{1 + ν} (ϵ + \frac{ν}{1 - 2 ν} θ I)

where the Young's modulus E defines the stiffness of the matrix and the Poisson ratio ν measures the contraction of the matrix in one direction when it is stretched in a transverse direction.

In this application the difference is associated with the drag of the matrix across the dish. As the cells pull the matrix, it moves across the dish. Experiments indicate that some matrix fibrils remain attached to the dish, while the rest are dragged across the lower parts of the matrix. The net effect on the matrix surface due to the fibril attachments to the dish, is a resistant force. In this two-dimensional model we treat such resistance as a viscous drag:

F_{anchoring} = - s \frac{u_{t}}{h}

where h(x,y,t) (mm) represents the thickness of the matrix (related to the ECM density ρ) and s is a measure of the strength of the resistance contributed by the attachment. We thereby assume that the resistance is proportional to the velocity

v = u_{t}

of matrix displacement.

Matrix thickness

Since the vertical stress σ_zz=0, we get a relation between the strain components in the three directions, ε_xx, ε_yy, ε_zz. From Hooke's law in three dimensions we have

σ_{zz} = \frac{E}{1 + ν} [(1 - ν) ϵ_{zz} + ν (ϵ_{xx} + ϵ_{yy})] = 0 .

From this relation we get

ϵ_{zz} = \frac{- ν}{1 - ν} (ϵ_{xx} + ϵ_{yy})

(A.1)

When there is a strain ε_zz in the z-direction, the thickness is calculated using h(x,y,t)=h₀(x,y) (1+ε_zz) from which we derive the relation giving the thickness h as a function of space and time:

h (x, y, t) = h_{0} (x, y) (1 + ϵ_{zz}) = h_{0} [1 - \frac{ν}{1 - ν} (ϵ_{xx} + ϵ_{yy})] \Rightarrow h (x, y, t) = h_{0} (1 - \frac{ν}{1 - ν} θ)

where the dilation θ=ε_xx+ε_yy.

Boundary conditions for the model equations

Again, being guided by the experiments, the matrix barely moves along the edge of the dish. We incorporate this into the model by assuming zero displacement as boundary conditions. Hence, for a square dish (square rather than circular simply for ease of numerical programming and reduction of computer time) of dimensions [ab]×[ab] the condition becomes:

u (x, y = a, t) = u (x, y = b, t) = u (x = a, y, t) = u (x = b, y, t) = 0

(A.2)

where u is again the matrix displacement. Cells remain in the dish so we have zero flux boundary condition for the cells:

J_{cells} = \frac{\partial u}{\partial t} c - \nabla \cdot (D (ϵ) c) = 0

where J_cells is the flux of cells.

The equations for cell conservation and balance of forces together constitute the model mechanism. The equations were solved with the above boundary conditions and initial conditions in cell density and matrix distribution in keeping with the experimental set-up and the results shown in Figs. 2 and 3 above.

Bibliographie

[1] J.D. Murray; D.C. Deeming; M.W.J. Ferguson Size-dependent pigmentation pattern formation in embryos of Alligator mississippiensis: time of initiation of pattern generation mechanism, Proc. R. Soc. Lond. B, Volume 239 (1990), pp. 279-293

[2] J.D. Murray Mathematical Biology, Springer-Verlag, Heidelberg, 1993

[3] J.D. Murray Mathematical Biology, Vol. II: Spatial Models and Biomedical Applications, Springer-Verlag, New York, 2003

[4] J. Folkman Clinical applications of research on angiogenesis, New Eng. J. Med., Volume 333 (1995), pp. 1757-1763

[5] M.S. O'Reilly; L. Holmgren; C. Chen; J. Folkman Angiostatin induces and sustains dormancy of human primary tumors in mice, Nat. Med., Volume 2 (1996), pp. 689-692

[6] A.M. Turing The chemical basis for morphogenesis, Phil. Trans. R. Soc. Lond. B, Volume 237 (1952), pp. 37-72

[7] J.D. Murray; G.F. Oster; A.K. Harris A mechanical model for mesenchymal morphogenesis, J. Math. Biol., Volume 17 (1983), pp. 125-129

[8] G.F. Oster; J.D. Murray; A.K. Harris Mechanical aspects of mesenchymal morphogenesis, J. Embryol. Exp. Morphol., Volume 78 (1983), pp. 83-125

[9] J.D. Murray; G.F. Oster Generation of biological pattern and form, IMA J. Math. Biol., Volume 19 (1984), pp. 265-279

[10] J.D. Murray; G.F. Oster Cell traction models for generating pattern and form in morphogenesis, J. Math. Biol., Volume 19 (1984), pp. 265-279

[11] L. Wolpert Positional information and pattern formation, Phil. Trans. R. Soc. Lond. B, Volume 295 (1981), pp. 441-450

[12] H. Meinhardt Models of Biological Pattern Formation, Academic Press, London, 1983

[13] H. Berg; E. Budrene Complex patterns formed by motile cells in E. coli, Nature, Volume 349 (1991), pp. 630-633

[14] D.E. Woodward; R. Tyson; M.R. Myerscough; J.D. Murray; E.O. Budrene; H.C. Berg Spatio-temporal patterns generated by Salmonella typhimurium, Biophys. J., Volume 68 (1995), pp. 2181-2189

[15] R.C. Tyson; S.R. Lubkin; J.D. Murray A minimal mechanism for bacterial pattern formation, Proc. R. Soc. Lond. B, Volume 266 (1998), pp. 299-304

[16] H.G. Othmer; P.K. Maini; J.D. Murray Mathematical Models for Biological Pattern Formation, Plenum Press, New York, 1993

[17] P.K. Maini; H.G. Othmer Mathematical Models for Biological Pattern Formation, Springer-Verlag, New York, 2000

[18] L. Wolpert The development of pattern and form in animals, Carolina Biol. Readers, Volume 1 (1977) no. 5, pp. 1-16

[19] A.K. Harris; P. Wild; D. Stopak Silicone rubber substrata: A new wrinkle in the study of cell locomotion, Science, Volume 208 (1980), pp. 177-179

[20] I. Ferrenq; L. Tranqui; B. Vailhé; P.Y. Gumery; P. Tracqui Modelling biological gel contraction by cells: Mechanocellular formulation and cell traction force quantification, Acta Biotheor., Volume 45 (1997), pp. 267-293

[21] S.W. Moore; R.E. Keller; M.A.R. Koehl The dorsal involuting marginal zone stiffens anisotropically during its convergent extension in the gastrula of Xenopus laevis, Development, Volume 121 (1995), pp. 3131-3140

[22] Y.C. Fung Biomechanics. Mechanical Properties of Living Tissues, Springer-Verlag, New York, 1993

[23] R. Thoma Untersuchungen über die Histogenese und Histomechanik des Gefassystems, Enkeverlag, Stuttgart, 1893

[24] O. Hudlick; M.D. Brown Physical forces and angiogenesis (G.M. Rubanyi, ed.), Mechanoreception by the Vascular Wall, Futura, Mount Kisco, NY, 1993, pp. 197-241 (chapter 10)

[25] T.C. Skalak; R.J. Price The role of mechanical stresses in microvascular remodeling, Microcirculation, Volume 3 (1996) no. 2, pp. 143-165

[26] R.B. Vernon; J.C. Angello; M.L. Iruela-Arispe; T.F. Lane; E.H. Sage Reorganization of basement membrane matrices by cellular traction promotes the formation of cellular networks in vitro, Laboratory Investigation, Volume 66 (1992), pp. 536-547

[27] R.B. Vernon; S.L. Lara; C.J. Drake; M.L. Iruela-Arispe; J.C. Angello; C.D. Little; T.N. Wight; E.H. Sage Organized type I collagen influences endothelial patterns during ‘spontaneous angiogenesis in vitro’: Planar cultures as models of vascular development, In Vitro Vasc. Dev., Volume 31 (1995), pp. 120-131

[28] D. Manoussaki; S.R. Lubkin; R.B. Vernon; J.D. Murray A mechanical model for the formation of vascular networks in vitro, Acta Biotheor., Volume 44 (1996) no. 3/4, pp. 271-282

[29] J.D. Murray; D. Manoussaki; S.R. Lubkin; R.B. Vernon A mechanical theory of in vitro vascular network formation (C.D. Little; V. Mironov; E.H. Sage, eds.), Vascular Morphogenesis: In Vivo, In Vitro and In Mente, Birkhäuser, Boston, 1998, pp. 173-188

[30] Vascular Morphogenesis: In Vivo, In Vitro and In Mente (C.D. Little; V. Mironov; E.H. Sage, eds.), Birkhäuser, Boston, 1998

[31] J. Cook, Mathematical Models for Dermal Wound Healing: Wound Contraction and Scar Formation, PhD thesis, University of Washington, 1995

[32] B. Lee; L. Mitchell; G. Buchsbaum Rheology of the vitreous body. Part I: Viscoelasticity of human vitreous, Biorheology, Volume 29 (1994), pp. 521-533 (a) (b) B. Lee, L. Mitchell, G. Buchsbaum, Rheology of the vitreous body. Part II: Viscoelasticity of bovine and porcine vitreous Biorheology, 31, 1994, pp. 327-338

[33] V.H. Barocas; A.G. Moon; R.T. Tranquillo The fibroblast-populated collagen microsphere assay of cell traction force. Part 2: Measurement of the cell traction parameter, J. Biomech. Eng., Volume 117 (1995), pp. 161-170

[34] M.S. Kolodney; R.B. Wysolmerski Isometric contraction by fibroblasts and endothelial cells in tissue culture: a quantitative study, J. Cell Biol., Volume 117 (1992) no. 1, pp. 73-82

[35] G.W. Scherer; H. Hdach; J. Phalippou Thermal expansion of gels: A novel method for measuring permeability, J. Non-Cryst. Solids, Volume 130 (1991), pp. 157-170

[36] J.H. Hoying; S.K. Williams Measurement of endothelial cell migration using an improved linear migration assay, Microcirculation, Volume 3 (1996) no. 2, pp. 167-174

[37] T.L. Jackson; S.R. Lubkin; S.R. Siemens; N.O. Kerr; P.D. Senter; J.D. Murray Mathematical and experimental analysis of localization of anti-tumor anti-body-enzyme conjugates, Br. J. Cancer, Volume 80 (1999), pp. 1747-1753

Commentaires - Politique