1 Introduction
Human-induced mortality remains one of the main factors driving large carnivore populations to extinction [1–3]. Large carnivores can kill domestic and game animals, and for some species can threaten humans. They can be viewed as competitors for resources or can be targeted as trophies and, as a consequence, many species have been facing widespread persecution.
For instance, the French Pyrenean brown bear population underwent a dramatic decline during the past century through overhunting or direct persecution. In 1900 there were 150 bears in the Pyrenean range [4], whereas in 1990, the population had collapsed to less than 10 individuals in the Western Pyrénées [5]. In 1996 and 1997 the French government managed the experimental reintroduction of 3 bears (2 females and 1 male) originating from Slovenia [6] to create a new sub-population in the Central Pyrénées. One of the females was later accidentally killed [7] but the reintroduced sub-population has since grown, and a dispersing male has reached the endemic Western Pyrenean sub-population [7]. However, the future of the bear in the Pyrénées is far from secured. The fact that the bear is a charismatic species makes that the question of further reinforcement or how large a viable bear population should be remains controversial and needs to be addressed based on a rigorous approach. This requires the development of a bear-specific demographic model that we propose to address here. Demographic models or population viability analyses (PVA) are mathematical descriptions of species' life cycles over time [8]. They are now a widely used tool in endangered species conservation and their usefulness lies in comparing management strategies and exploring consequences of different assumptions on population dynamics [9]. Conservation biology owes much of its credibility to demographic modeling [10] and insights gained from modeling should never be dissociated from the model assumptions [11]. Indeed, results are better interpreted qualitatively rather than quantitatively and should not be used to determine a numerical value of a minimum viable population size or of a probability of reaching extinction [12].
In this paper, we build and analyse deterministic and stochastic stage-structured models to study the dynamics and viability of the Pyrenean brown bear population. We evaluate the need for further augmentation and try to define how many females or males – if any – should be released in order to secure the long term future of this population.
2 Methods
2.1 Bear biology
In Europe, female and male brown bears reach sexual maturity between 3.5 to 5 years old. Mating occurs in June–July and a male may accompany a female for up to two weeks. The young are born from January to March. The litter size ranges from 1 to 4, but 2 is most common and interbirth interval is most frequently 3 years. Under most circumstances, brown bears live as lone individuals, except for females accompanied by their cubs. Brown bears are distributed in overlapping home ranges and male home ranges are larger than those occupied by females. The Pyrenean brown bear population presently hosts 11 individuals dispatched into 2 sub-populations (Fig. 1). The Western sub-population consists of 1 female and 5 males [5,13] whereas the Central population consists of 2 females and 1 male [7]. Furthermore, 2 males have dispersed from the Central to Eastern Pyrénées in an area where no females are available (Quenette, unpubl. data).
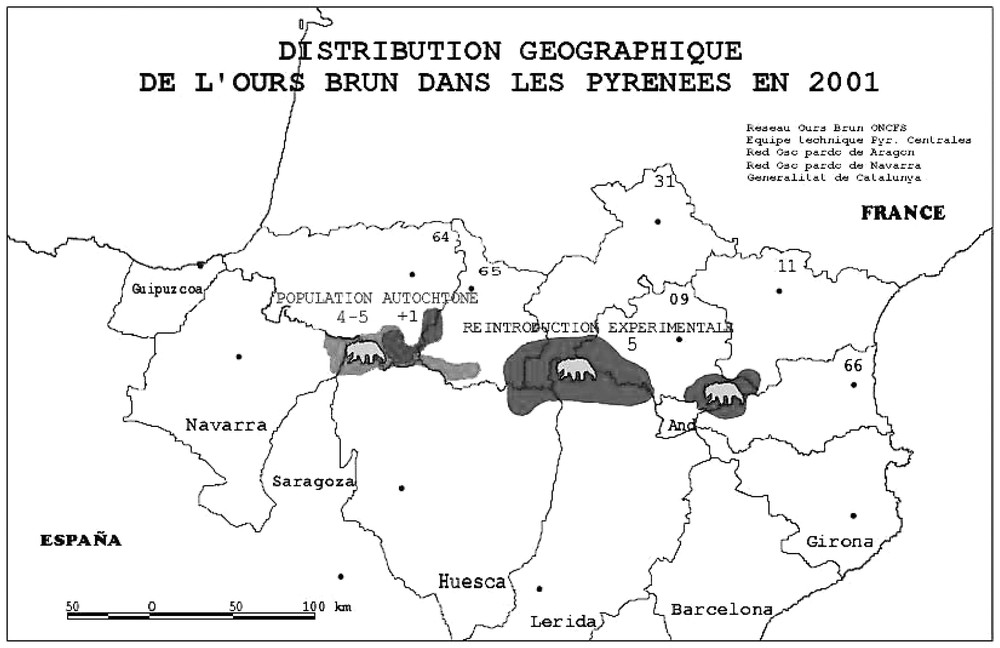
Present distribution of the brown bear in the Pyrénées.
2.2 Model structure and simulations
The population is divided into several stages defined by sex and age. Bears can be cubs (0–12 months), juveniles (12–24 months), subadults (24–36 and 36–48 months) or breeders (>48 months) for both sexes. Age at first reproduction is therefore 4 years. Transitions between classes are explained hereafter and shown on the life cycle graph (Fig. 2).
- (1) Surviving female juveniles become subadults 1.
- (2) Surviving male juveniles become subadults 1.
- (3) Surviving female subadults 1 become subadults 2.
- (4) Surviving male subadults 1 become subadults 2.
- (5) Surviving female floaters 2 become breeding females.
- (6) Surviving male floaters 2 become breeding males.
- (7) Surviving breeding females keep the same status.
- (8) Surviving breeding males keep the same status.
- (9) Surviving breeding females give birth to female cubs that become juveniles.
- (10) Surviving breeding females give birth to male cubs that become juveniles.
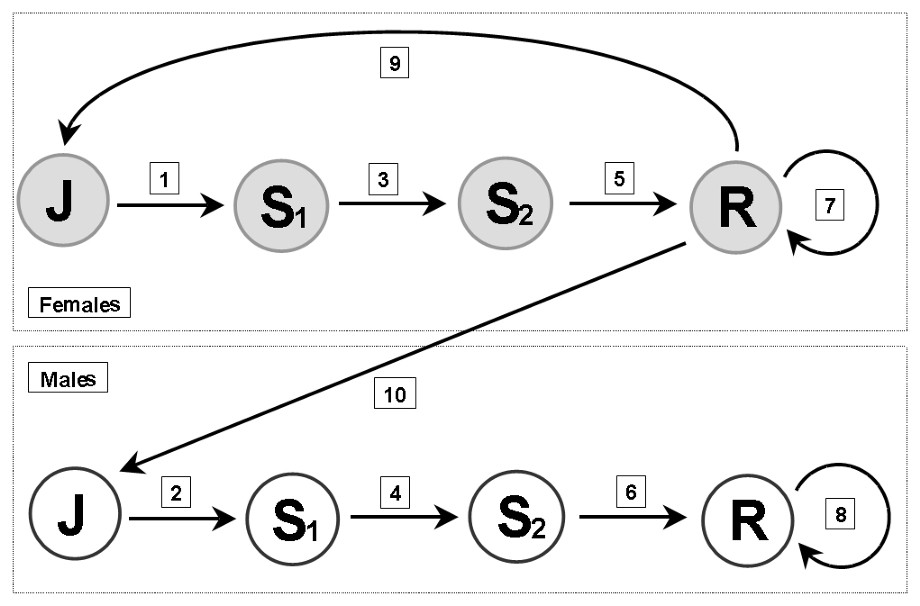
Life cycle graph for a bear stage-structured population. J: juveniles, S1: subadult, S2: subadult, R: reproducing individuals. See text for arrow details.
We assess the effects of releasing bears on population persistence with emphasis on number and sex of released bears. We try to identify a strategy that would maximize population persistence with the lowest number of released bears. We selected the smallest number of released bears that would lead to an extinction probability lower than 5% and investigate the best sex-ratio for this number. We study the impact of delaying in time the implementation of this optimal strategy. We model the Pyrenean bear population spatial structure and a possible indirect Allee effect [15] by considering augmentation strategies for the 2 existing sub-populations rather than for the whole metapopulation. We hypothesize that connections were null between the 2 sub-populations. A male has shown to be able to disperse from the Central to the Western sub-population [7] but since we cannot estimate the probability that a young male reaches the other sub-population or a part of the range where no females are available, we ignore this possibility. Moreover, since females are the limiting sex in the population and are most often philopatric [16,17], we believe our assumptions are conservative.
All analyses and simulations are performed with the computer program ULM (Unified Life Models) [18,19] that allows one to handle any time-discrete stage-structured population model. ULM has already been used to model the population dynamics of several carnivore species such as grizzly bears Ursus arctos horribilis [20], arctic foxes Alopex lagopus [21], Iberian lynxes Lynx pardinus [22] and wolves Canis lupus [23].
2.3 Demographic parameters
Since no accurate estimation of Pyrenean brown bear survival parameters was available, we define 4 scenarios, denoted by S0 to S3 from pessimistic to optimistic, that involve different combinations of parameter values (Table 1). Cubs have the lowest survival probabilities to account for the effect of predators, starvation and accidental deaths. An analysis of mortality for 150 cubs in the Cantabrican Cordillera between 1982 and 1991 yielded a mean cub mortality rate of 0.4 [24]. Survival probabilities of subadults, especially males, appear to be slightly lower than those of breeding bears: subadults travel through unknown areas, are not familiar with prey distribution, can be killed by resident bears and suffer a higher human induced mortality because of conflicts with humans. Reproducing bears have the highest survival. We estimate these survivals from several European and North American studies [24,25]. Mean litter size is 1.6 in the Western Spanish population [26] and 1.9 in Italy [27]. In the Eastern Spanish population (Cantabrican Cordillera), mean litter size was 2.3 cubs, whereas for reintroduced bears in Austria [28] and France (Quenette, unpubl. data) it was 2.6. Interbirth interval is usually between 3 and 5 years [24], despite cycles of 2 years have been observed [29]. We fix mean litter size at 2.1 and interbirth interval at 3 years. We keep the primary sex-ratio fixed at 0.5.
Model parameters for various scenarios and associated asymptotic growth rate λ
| Parameter | Scenario | |||
| S0 | S1 | S2 | S3 | |
| Female & male cub survival | 0.575 | 0.6 | 0.625 | 0.65 |
| Female & male juvenile survival | 0.775 | 0.8 | 0.825 | 0.85 |
| Male subadult survival | 0.775 | 0.8 | 0.825 | 0.85 |
| Female subadult survival | 0.825 | 0.85 | 0.875 | 0.9 |
| Female & male breeder survival | 0.875 | 0.9 | 0.925 | 0.95 |
| Litter size | 2.1 | 2.1 | 2.1 | 2.1 |
| λ | 0.975 | 1.006 | 1.039 | 1.071 |
3 Results
3.1 Bear future in the Pyrenean range
Asymptotic growth rate λ computation shows that a brown bear population increases under our S1, S2 and S3 scenarios but decreases under the more pessimistic one S0 (Table 1). The pessimistic scenario gives a 2.5% decline per year whereas the most optimistic used gives a 7.1% increase per year. Elasticities are larger for breeder survival (Table 2). Elasticities for all other class survival rates and litter size are far lower. We confirm through λ level curve computations [14] that the great importance of elasticity to breeder survival extends to parameter space and is not restricted to the local parameter value. The impact of removing a single bear on λ is the largest if this bear is a breeding female (Table 3).
Elasticities computed for a population under median scenario S2
| Parameter | Elasticity |
| Male cub survival | 0.137 |
| Male juvenile survival | 0 |
| Male subadult 1 survival | 0 |
| Male subadult 2 survival | 0 |
| Male breeder survival | 0 |
| Female cub survival | 0.137 |
| Female juvenile survival | 0.104 |
| Female subadult 1 survival | 0.098 |
| Female subadult 2 survival | 0.098 |
| Female breeder survival | 0.845 |
| Litter size | 0.122 |
Left eigenvector (corresponding to reproductive values) computed for a population under median scenario S2
| Class | Reproductive value |
| Male juveniles | 0 |
| Male subadult 1 | 0 |
| Male subadult 2 | 0 |
| Male breeders | 0 |
| Female juveniles | 0.1808 |
| Female subadult 1 | 0.2277 |
| Female subadult 2 | 0.2704 |
| Female breeder | 0.3211 |
3.2 Minimum viable population size
We compute probabilities of extinction within 100 years for several carrying capacities and under our 4 demographic scenarios (Fig. 3). A population in scenario S0 reaches extinction with high probabilities irrespectively of carrying capacity, whereas a population in scenario S3 nearly never goes extinct for a carrying capacity as small as 12 bears. For intermediate scenarios S1 and S2, probabilities of extinction are lower than 5% for carrying capacities greater than 40 and 20, respectively.
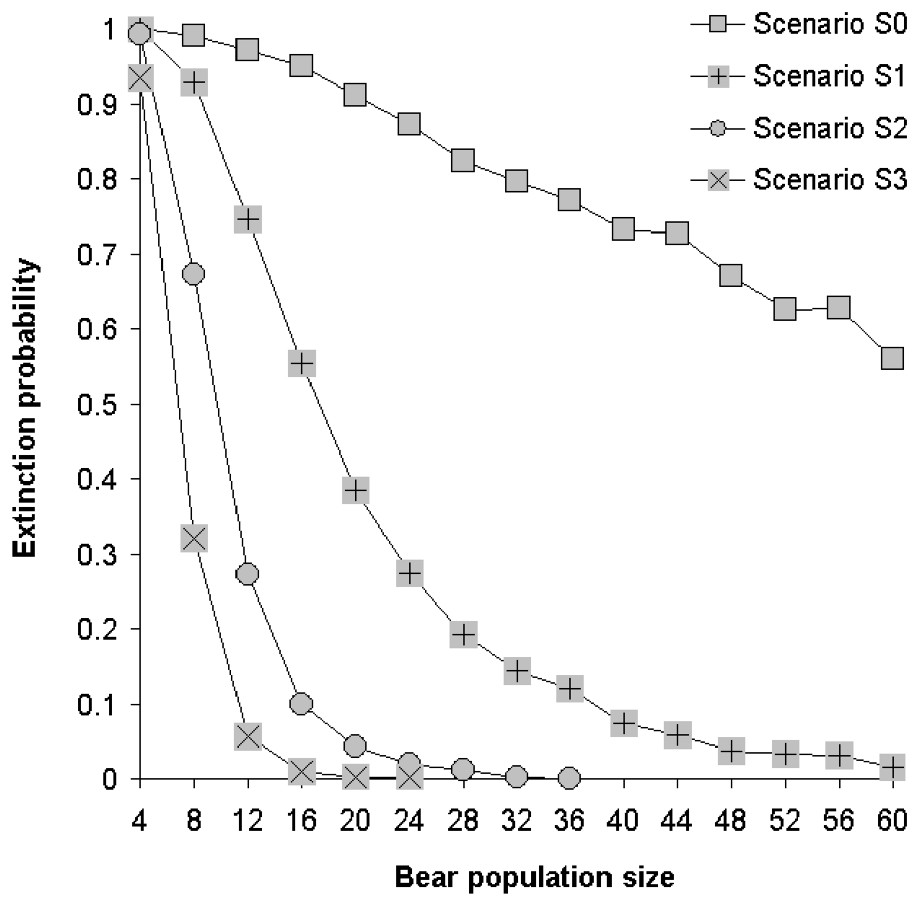
Extinction probabilities within 100 years as a function of population size assuming an initial settlement at carrying capacity.
3.3 Reinforcement strategies
Our computations reveal that not releasing any bear in these sub-populations would likely lead them to very high extinction risks. For the Western sub-population, keeping the extinction probability at low levels would mean releasing at least 5 bears (5 females/0 male, Fig. 4) for scenario S2, whereas the Central sub-population would require at least 6 bears (but 4 females/2 males, Fig. 5). These augmentations would be more efficient if they were carried out in the near future, i.e. releasing the same number of bears in 10 or 15 years would not prevent both of these sub-populations from reaching higher level of extinction probabilities (Figs. 6 and 7). Considering the best scenario, S3, changes only the numerical value of the smallest number of bear required, but does not change the fact that augmentations are needed in the near future.
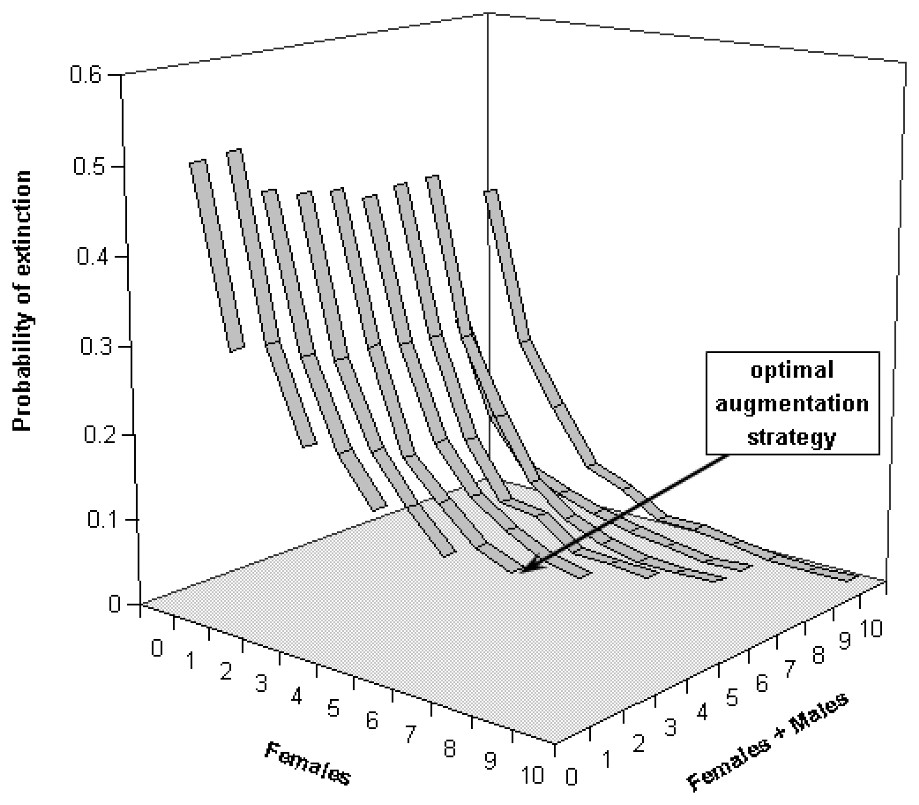
Extinction probabilities within 50 years for the Western Pyrenean bear sub-population as a function of number of released bears and number of released females in scenario S2.
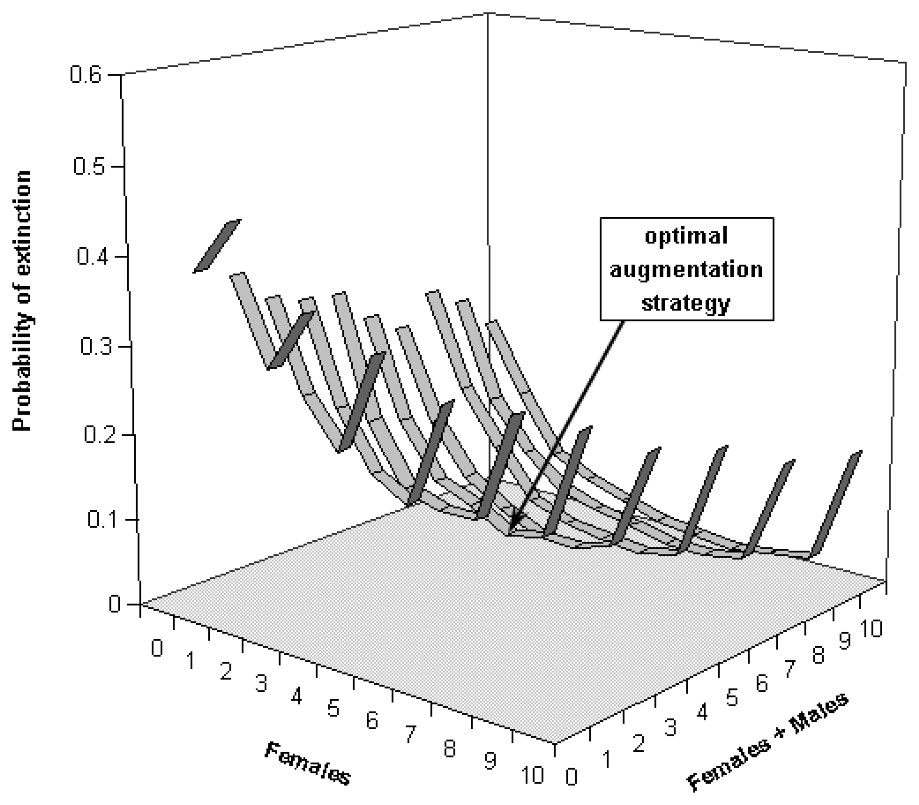
Extinction probabilities within 50 years for the Central Pyrenean bear sub-population as a function of number of released bears and number of released females in scenario S2.
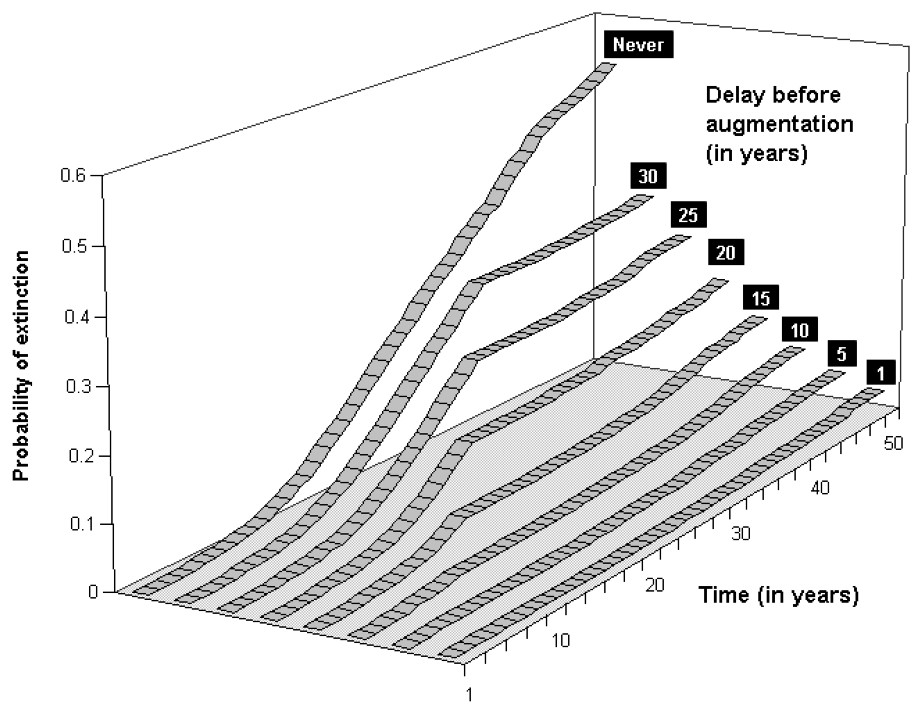
Extinction probabilities within 50 years for the Western Pyrenean bear sub-population in an optimal augmentation strategy (5 females/0 male) and scenario S2 as a function of time for various delays in releasing individuals.
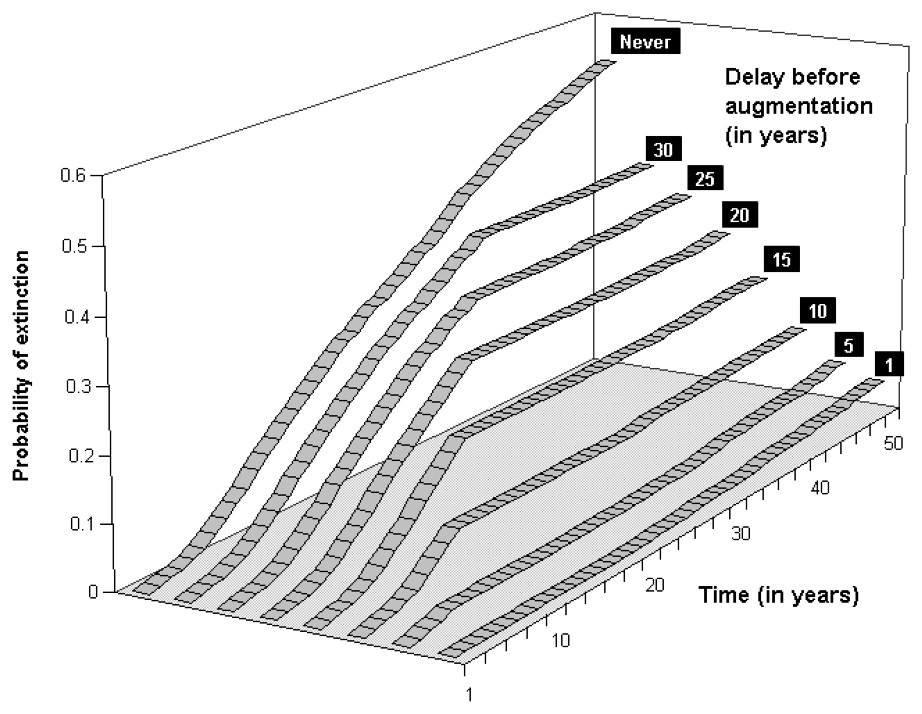
Extinction probabilities within 50 years for the Central Pyrenean bear sub-population in an optimal augmentation strategy (4 females/2 males) and scenario S2 as a function of time for various delays in releasing individuals.
4 Discussion
Our results show that even small bear populations can persist provided their demographic parameters remain high, but less favorable scenarios would require larger population sizes. Population persistence is more sensitive to breeder survival than to any other parameters. When focusing specifically on the present Pyrenean brown bear population, our results reveal that this population is unlikely to persist unless more bears are released. These bears should be mainly females and be released in both sub-populations and in the near future.
Our analysis relies on several important assumptions.
- (1) Individuals in a given class all have the same demographic parameters and could not be differentiated, which is an inherent assumption of stage-structured population models.
- (2) Cub survival is independent of mother age and senescence is not explicitly considered. Taking a breeding bear survival rate of 0.925 under scenario S2 (0.95 under scenario S3) yields an expected breeding expectancy of 13.3 years (20 years under scenario S3).
- (3) We do not model interbirth interval reduction when a litter dies. However, the reduced elasticity of λ to litter size suggests this is unlikely to change our conclusions.
- (4) We do not model possible infanticide by subadult males, which has recently been shown to be potentially detrimental to population survival [20,30,31]. However, this phenomena is most likely to occur in highly hunted populations, which is not the case in the Pyrénées.
- (5) Model parameters are kept constant during simulation (implying no habitat change).
- (6) We ignore catastrophes and genetic stochasticity because data are to scarce to incorporate these factors into our model. Reed et al. [12] have suggested that PVA start with simple models and use an approach that data can support and no data were available on the impact of catastrophes on European bear populations. Beissinger & Westphal [10] suggested that PVA should mix genetic and demographic currencies sparingly and that, given the lack of information on the number of lethal equivalent in most populations, it may be useful to concentrate on measurable demographic parameters. Wiegand et al. [24] reviewed the issue of incorporating genetics into a bear PVA and concluded that we do not yet have the data and understanding to include genetics quantitatively in brown bear or grizzly bear models.
Our study has major implications in terms of conservation recommendations. It shows that unless an augmentation program is launched, the Pyrenean brown bear population is expected to go extinct. Moreover, delaying further such a program would be risky in term of probability of extinction. It is fortunate that the expertise to reintroduce bears has been developed several years ago during the experimental program and this should make actions we recommend easier to perform in the near future. The brown bear is protected by the 92/43/EEC directive known as “Habitat Directive” as a strictly protected species (Annex IV) requiring special protected areas (Annex II). The Pyrenean population is considered in a very critical status by the “Action Plan for Conservation of the Brown bear in Europe” [34] which includes among the required actions the augmentation of the Pyrenean population. Releasing bears into previously extirpated or quasi-extinct populations is now a strategy that has been successfully implemented in Austria [28] and is being carried out in Italy [36]. A range wide bear conservation program on the Pyrénées should not be detrimental to other ongoing wildlife or ecosystem conservation programs [35]: bear predation on ungulates is rather low [37,38] and bears have no negative impact on forest or alpine ecosystem dynamics [38–40].
While our research has provided information regarding the demographic aspects of a reinforcement program, it is now widely recognized that carnivore conservation, especially planned return of larger ones, is a multidisciplinary task [41] requiring a collaborative approach between biologists, economists and sociologists. For the Pyrenean brown bear, some of the core issues are conflict with sheep farming, forestry and road use, and the human dimension. The last has shown to be particularly critical in large carnivore conservation and refers to the concept of social carrying capacity [42]. Indeed, projects of restoration of large carnivores have often to deal with the level of acceptation by local populations which can be highly variable both among the different social groups (hunters, farmers, hikers, local elected representatives, workers in tourist industry, craftsmen) and within a social group (Quenette, unpubl. data). In fact, bear augmentation strategies to which our modeling approach has contributed precision, will be a success only if people who live with and near bears every day become convinced that cohabiting with bears is possible.
Acknowledgements
This study was funded in part by the French Ministère de l'Education Nationale, de la Recherche et des Technologies, Action Concertée Incitative “Jeunes Chercheurs 2001” awarded to Regis Ferrière, and by the European Research Training Network ModLife (Modern Life-History Theory and its Application to the Management of Natural Resources), funded through the Human Potential Programme of the European Commission (Contract HPRN-CT-2000-00051). Bear reintroduction in the Central Pyrénées were carried under an agreement between the French Government and European Commission through the Life Projects B4-3200/93/772 and B4-3200/96/518. We thank J. Swenson for very useful comments on an earlier version of this the manuscript and P. Genovesi, A. Greth and F. Moutou for providing useful documents and wildlife technicians L. Chayron, P. Cluzel, S. Déjean, D. Dubreuil, E. Dubarry, J. Troietto and J. Morscheidt in charge of radiotracking bears in Central Pyrenees.


