1 Introduction
Functional imaging studies of sensory and cognitive pathways have confirmed and extended previous neuroanatomical and psychological findings. The physiological basis of the functional imaging signal has been of less interest than the localization of psychological representations. Recently, however, interest in the neurophysiological nature of the imaging signals is increasing as experiments succeed in directly relating the signals to brain energy consumption and neuronal work. The importance of cerebral energetics is underlined by the well-known findings that the relatively small brain, ∼2% of the human weight consumes ∼20% of its oxygen. The function of this energy, derived from the oxidation of glucose, which had been the subject of much controversy, has recently been resolved experimentally [1,2] and theoretically [3], showing that brain energy primarily supports neuronal firing and neurotransmitter cycling.
Experimental explorations of these thermodynamic measurements of brainwork were initiated by 13C in vivo NMR experiments which followed the 13C label from glucose through the tricarboxylic acid (TCA) cycle and the cycling path of neurotransmitter glutamate. The study of neuroenergetics by 13C nuclear magnetic resonance (NMR) has been extended by the calibration of functional imaging signals, which have provided independent, well-resolved, values of energetics [4–6]. The basis of functional magnetic resonance imaging (fMRI) established by these experiments suggest neurophysiological alternatives to the psychological interpretation of brain function that had been obtained from most imaging experiments. Furthermore, as we shall show, the quantitative biophysical relations between brain energy and neuronal activity provide an encouraging physical approach to unanswered questions of brain consciousness.
Glucose oxidation is the main cerebral energy-producing pathway and was the first cerebral pathway explored by 13C NMR in vivo. Modern studies of the relation between the delivery of glucose to the brain by blood flow and its metabolism started with Roy and Sherrington [7] who suggested the existence of “an automatic mechanism by which the blood supply of any part of the cerebral tissue is varied in accordance with the activity of the chemical changes which underlie the functional activation of that part”. This hypothesis proposed a tight coupling between blood flow, energetics, and neuronal functions, which continues to be our subject of study.
Early whole brain studies [8] determined cerebral metabolic rates of glucose (CMRglc) and oxygen (CMRO2) consumption, in conjunction with cerebral blood flow (CBF). They were expanded to determine localized changes during stimulation by Louis Sokoloff, who pioneered autoradiographic methods for localized neuroimaging in animal models. A radioactive glucose analog, (14C-2-deoxyglucose), was infused to measure localized changes in CMRglc, [9], while another autoradiographic method [10], measured localized changes in CBF. These quantitative methods refined the quantitative concept of neurovascular coupling by linking increases in glucose consumption, to changes in blood flow and neuronal activity. Invasive autoradiographic methods were extended to human studies by the non-invasive method of positron emission tomography (PET). 19F-fluoro-deoxyglucose was developed as a radioactive tracer to measure changes in CMRglc [11,12], CBF was measured by use of 15O-water [13] and changes in CMRO2 were measured by 15O oxygen consumption [14].
PET functional studies were reinforced and extended by the discovery of fMRI [15]. This method depends on the effects of paramagnetic deoxyhemoglobin upon the NMR transverse relaxation times of nearby water protons in the tissue [15]. Since the oxygen level in the blood determines the fraction of hemoglobin in the deoxygenated state, the image contrast was termed as blood oxygenation level dependent (BOLD) [16]. The BOLD fMRI method has experimental advantages over the PET method including better contrast-to-noise ratio as well as higher spatial and temporal resolution. Furthermore fMRI is readily measured by slight adaptation of clinical MRI scanners, which while expensive to purchase, are available in most clinical settings. Its non-invasive nature and the fact that it does not require radioactive tracers (which are necessary for PET experiments) give fMRI many advantages in neurobiological studies (for a review, see [17]). After the initial demonstration of the BOLD method in the human brain [18–21], the cognitive neuroscience community immediately embraced the method.
Functional imaging methods can measure neurophysiological parameters separately, e.g., specific PET methods can determine CBF, CMRglc, or CMRO2. On the other hand, in the popular BOLD measurements the signal changes (ΔS%) are functions of ΔCBF% and ΔCMRO2% with a small contribution from ΔCBV% (for a review, see [22]). Because of its dependence upon several independent variables, quantitative interpretation of fMRI measurements has required sustained experimental research over the past decade. The usual fMRI experiments intend merely to localize the responses to sensory or psychological tasks regardless of their neurophysiological bases. However the biophysical goal of fMRI studies has been to derive the fundamental energetic parameter CMRO2 from BOLD experimental results. This has recently been accomplished by combining several independent MRI measurements (e.g., CBF and CBV) with the BOLD signal. These parameters when used to interpret BOLD data can derive values of ΔCMRO2% (for a review, see [6]) and thereby connect fMRI results with the developing body of information that relates CMRO2 to neuronal activity [23,24].
The most established and quantitative relation between CMRO2 and neuronal activity has come from in vivo 13C magnetic resonance spectroscopy (MRS) studies in rats and humans [25,26]. Since the resonance frequency of NMR observable nucleus (e.g., 1H, 13C, 31P, 15N) depends on its chemical environment within the molecule, MRS can be used to detect small biomolecules in vivo. While 1H MRS is commonly used for identification and concentration of metabolites in vivo (e.g., aspartate, γ-amino butyric acid (GABA), glucose, glutamate, glutamine, and lactate), 13C MRS has provided a unique window to cerebral metabolism. The non-radioactive, stable, 13C isotope has a natural abundance of 1.1% so that, after the infusion of 13C-enriched substrates, MRS can measure the rates of isotopic incorporation into brain metabolites, and thereby metabolic fluxes.
The parameters of neurotransmission and neuroenergetics determined by these combined NMR methods have provided a biophysical basis for interpreting functional imaging and, more importantly, have allowed us to reformulate the nature of brain activity. In this review, we first summarize 13C NMR findings that in the cerebral cortex glutamate neurotransmission, which is a quantitative measure of neuronal activity and has been shown [3] to be involved in the work of moving ions across the cell membrane, is directly coupled with neuroenergetics (i.e., energy consumed). These results are then shown to support a model that correlates neuronal/glial cycling of neurotransmitter glutamate with glucose oxidation. In a separate, confirmatory set of experiments BOLD fMRI signals were converted to ΔCMRO2% which were compared with single electrode measurements of spiking frequencies in activated voxels, thereby providing a parallel relationship between energy consumption and brainwork. The implications of these results for the interpretation of functional imaging experiments and for the nature of brain function are then discussed. We have taken advantage of the certainties obtained from these biophysical studies to explore some generally inaccessible aspects of brain function.
2 Relationship between neuroenergetics and neurotransmitter flux
13C MRS provides a unique window on cerebral metabolism in vivo [25] allowing assignment of 13C resonances with high spectral resolution from specific positions within molecules, e.g., glucose, glutamate, glutamine, GABA, aspartate. Since the natural abundance of the 13C isotope is only 1.1%, the sensitivity of 13C MRS can be enhanced by using 13C enriched substrates [25]. Intravenous infusion of enriched 13C-labeled glucose allows the subsequent appearance of the 13C label in specific products of cerebral glucose metabolism to be measured in rats and humans by real time NMR spectra (Fig. 1).
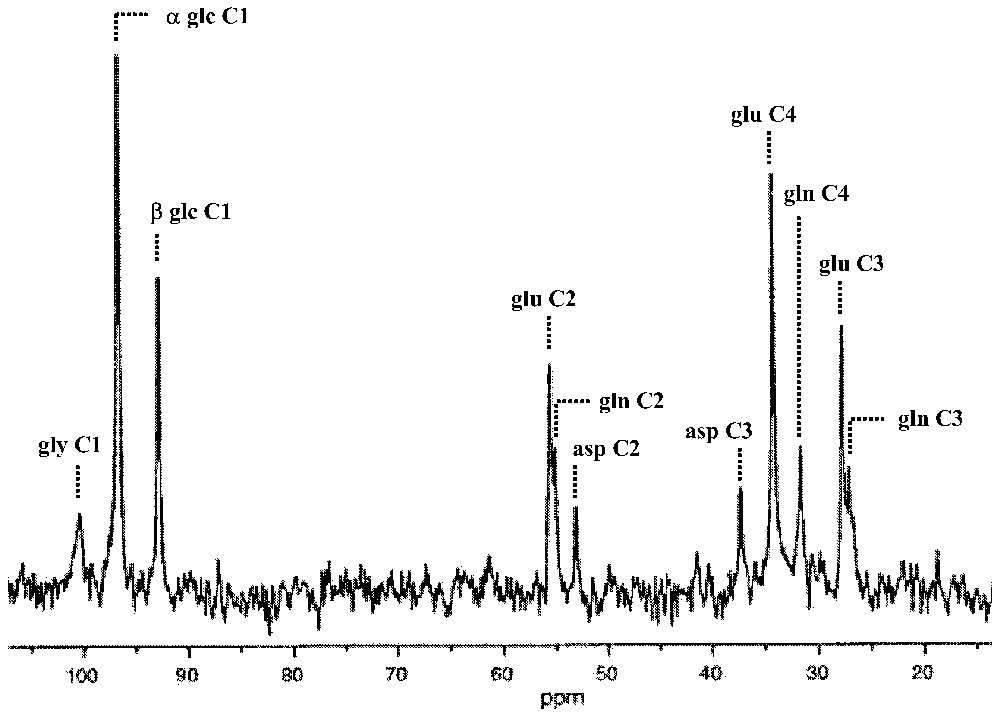
Time-dependent appearance of 13C label into specific products of glucose metabolism as a consequence of intravenous infusion of [1-13C]glucose. In the mammalian brain, there are two major ‘sinks’ for the 13C label: glutamate and glutamine pools. The in vivo spectrum was obtained at 7 T from a localized gray matter volume (300 μl; 10 min average) of an α-chloralose anesthetized rat after approximately 2 h of infusion. Abbreviations: asp, aspartate; glc, glucose (α and β anomers); gly, glycogen; glu, glutamate; gln, glutamine. Adapted from [6].
In early 13C MRS brain measurements the 13C flow from [1-13C]glucose to [4-13C]glutamate was used to determine the flux through the TCA cycle (VTCA) from which both CMRglc(ox) and CMRO2 could be determined (Fig. 2) [27–29]. The infusion of [1-13C]glucose leads to 13C flow down the glycolytic pathway to pyruvate from which the label enters the TCA cycle flowing through the small α-ketoglutarate pool (in μM range). The α-ketoglutarate pool rapidly exchanges with the large glutamate pool (in mM range) so that the kinetics of 13C label appearance depends upon the turnover of the combined pool, i.e., mainly glutamate. Thus VTCA can be determined by the kinetic equations of 13C label flow into the C4 glutamate as measured by 13C MRS. The best-fit of the metabolic model to the rise of C4-glutamate 13C fractional enrichment during steady state [1-13C]glucose infusion allowed VTCA to be calculated (Fig. 2). Values of CMRglc(ox) and CMRO2 in the non-stimulated brain obtained by this non-invasive approach agreed with previous measurements [30–34], so that by the mid 1990's this in vivo 13C MRS method of measuring CMRO2, and therefore energy consumption, was well established.
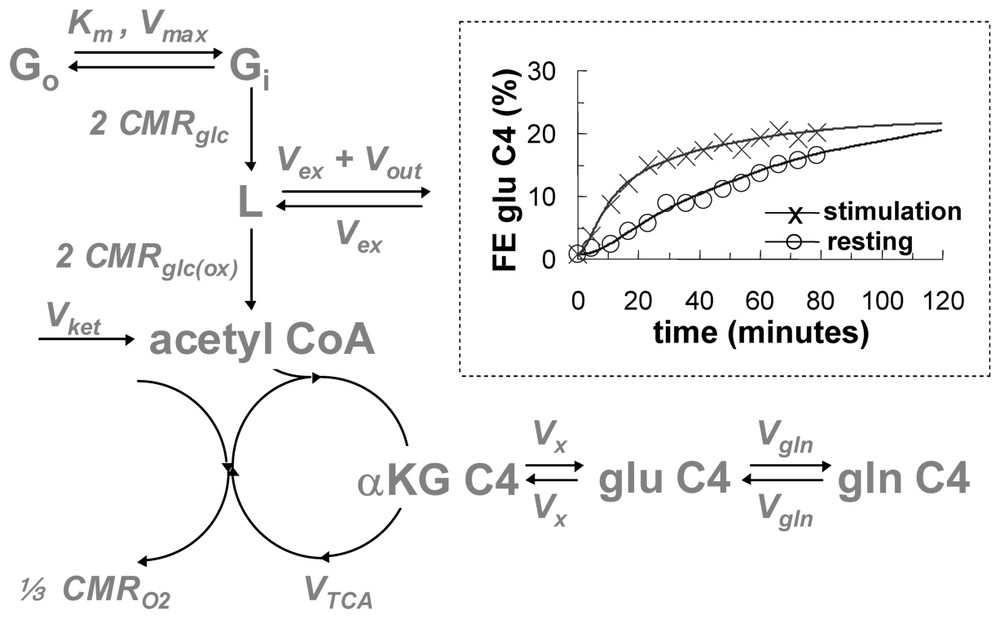
A schematic of the metabolic model for isotopic mass balance at steady state (see [30,31] for details). The [1-13C]glucose in plasma (Go) and brain (Gi) exchange via Michaelis–Menten kinetics, where Km and Vmax are the half-saturation concentration for transport and the maximum transport rate, respectively. The 13C label flows through glycolytic intermediates, which have negligible concentrations and arrives at a pool consisting of both pyruvate C3 and lactate C3 (represented by L, which has a concentration of 1.5 μmol g−1). There are two sources of 12C entrance into the TCA cycle: exchange of blood-brain pyruvate and lactate pool (Vex) and the ketone body flux (Vket), both of which dilute the 13C fractional enrichment (Vdil=Vex or Vket) of intermediates. The efflux at L (Vout) causes some 13C label to be lost to blood. The 13C label enters the acetyl CoA pool at a rate of 2 CMRglc(ox) prior to its entry into the TCA cycle. The 13C label enters the TCA cycle and labels α-ketoglutarate C4, αKG C4, and glutamate C4, glu C4 (12.0 μmol g−1). These two pools are in rapid isotopic exchange, Vx, where Vx/VTCA⪢1. There is an exchange between glutamate C4 and glutamine C4, gln C4 (6.2 μmol g−1), at a rate of Vgln (where Vgln/VTCA ranges from 1/4 to 1). CMRO2 is equal to . Inset: 13C turnover fractional enrichment (FE) of glutamate C4 data from anesthetized rat brain (symbols) and best fits of the metabolic model (lines) for steady-state conditions of resting (circle) and stimulation (cross) obtained by 1H[13C] MRS at 7 T (24 μl; 5 min average). The comparison demonstrates that VTCA is significantly increased during forepaw stimulation (0.3 ms pulses; 2 mA amplitude; 3 Hz) of the rat with α-chloralose anesthesia. Adapted from [6,33].
At that time, due to technical improvements, it became possible to measure in the human brain in vivo the 13C label flow into glutamine from glutamate [35]. From these data a high rate of glutamine synthesis was measured [31]. Glutamine is an intermediate in the proposed cycling of glutamate. Thus the ability to follow in time the 13C label flow into glutamate and subsequently into glutamine by 13C MRS in vivo opened glutamate neurotransmitter cycling to quantitation. The glutamate neurotransmitter cycle (Fig. 3) was originally proposed by [36] and [37] from 14C and 15N studies of rat brains. Additional evidence arose from enzyme and vesicle localization as well as isolated cell studies in the late 1980s and 1990s (for reviews, see [38,39]). However, the importance of this pathway in vivo was not known because of conflicting evidence from studies of brain slices [40] and other in vitro preparations [41] which suggested that the fraction of glucose flow leading to glutamine synthesis is low. In the glutamate neurotransmitter cycle model (Fig. 3), the action potential initiates the pre-synaptic release of vesicularized glutamate into the synaptic cleft. Once released, it diffuses across the gap until it is recognized by glutamate receptors on the postsynaptic surface. There it triggers the subsequent postsynaptic potential changes. The majority of released glutamate is not taken up by the pre-synaptic terminal but instead diffuses through the membranes of the surrounding astrocyte into which it is co-transported with Na+. The astrocytic enzyme glutamine synthetase then converts glutamate to glutamine consuming one ATP and one ammonia. Glutamine is transported across the astrocytic membrane, through the intracellular space, into the neuron, where the enzyme glutaminase reconverts it to glutamate. The glutamate is repackaged into vesicles where it is once again ready to restart the cycle. The first identification of both glutamate and glutamine turnover by 13C MRS was in the human brain at the rather low field of 2.1 T [35]. As higher magnetic fields of 4 T and 7 T are becoming available spectral resolution and sensitivity have both improved [42,43].
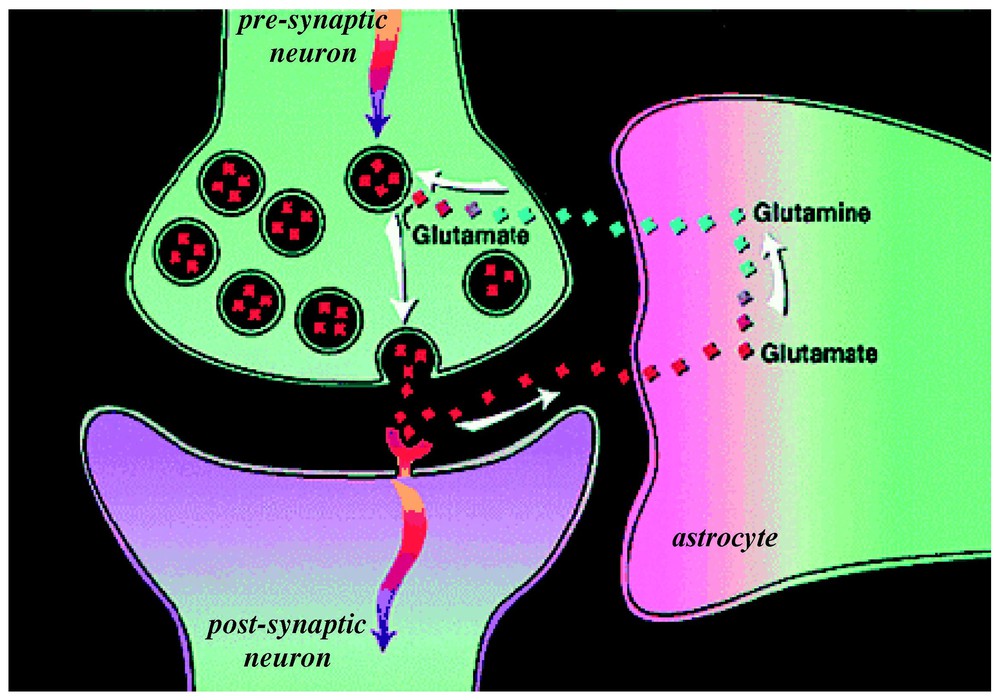
A model of glutamate–glutamine neurotransmitter cycling between neurons and astrocytes (for a review, see [52]). The rate of glutamate-to-glutamine cycle (Vcyc) has been quantitated by 13C MRS (for a review, see [25,26]). Action potentials or spikes (shown by curved arrows) reach the pre-synaptic terminal to initiate the release of vesicular glutamate into the synaptic cleft. This activates the glutamate receptors in the post-synaptic neuron, which is a step required in the propagation of spiking activity to the adjacent neuron (in an all-or-none manner). The extracellular glutamate is removed rapidly by Na+-coupled transport into astrocytes, where it is converted into glutamine. The synthesized glutamine then passively diffuses back to the neuron, and after re-conversion to glutamate, is repackaged into vesicles. Modified from [73].
Soon after these first experiments on human subjects, the easily manipulated rat model was exploited to expand the understanding of the interactions of the different rates in vivo (for a review, see [25]). The relative rates of neuronal glucose oxidation (CMRglu(ox)) and glutamate cycling (Vcyc) were measured over a wide range of brain activity in the rat [1]: deeply anesthetized conditions (pentobarbital), moderate depth of anesthesia (α-chloralose), and lightly anesthetized conditions (morphine). Simultaneous measurements of the 13C flow into glutamate and of the subsequent flow into glutamine were converted into CMRglu(ox) and Vcyc, respectively. Fig. 4 and Eq. (1) summarize the results:
| (1) |
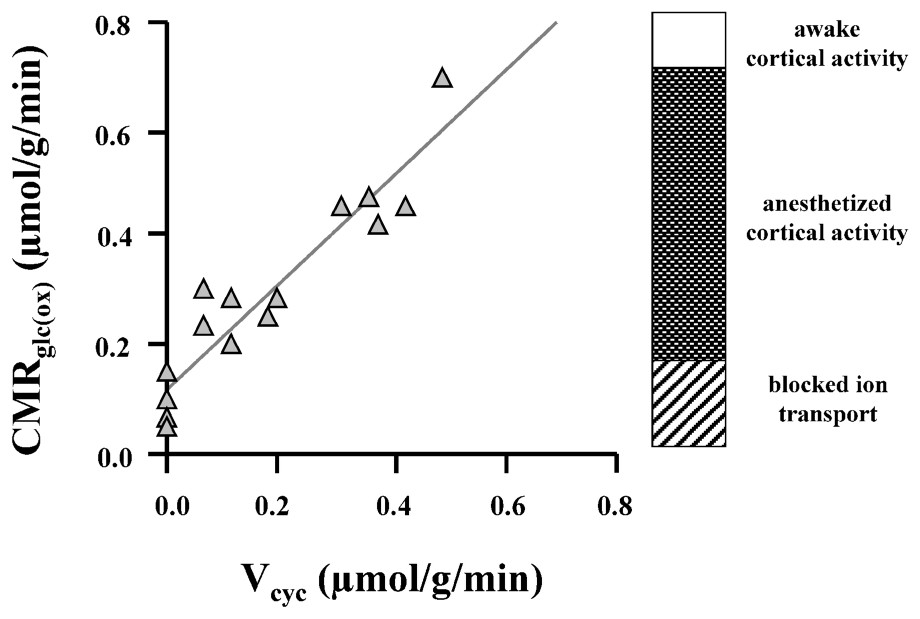
Relationship between Vcyc and CMRglc(ox) established from experimental results of 13C MRS experiments at 7 T [1], where rats were moderately anesthetized (with morphine and α-chloralose) to isoelectric conditions (high-dose pentobarbital). The best-fit line is given by Eq. (1) (in units of μmol g−1 min−1), which suggests that each mole of neurotransmitter glutamate cycling requires the oxidation of one mole of glucose. The awake, resting state has CMRglc(ox) of approximately 0.8 μmol g−1 min−1, which means that under this condition ∼80% of the resting energy consumption is dedicated to events associated with Vcyc. Modified from [1].
This high level of brain activity in the absence of specific stimulations is a novel neuroscientific finding from these experiments. Its implications are discussed below. Third, the slope of the CMRglu(ox) and Vcyc curve is ∼1. (For clarity of presentation of data in Fig. 4, the measured value of VTCA has been converted into CMRglu(ox) assuming stoichiometries of the idealized brain metabolism where the only carbon source is glucose and it is all oxidized). The slope of unity means that for every additional glucose molecule oxidized one glutamate is released as a neurotransmitter and cycled through glutamine. This stoichiometry along with the dominant role of glutamatergic processes in cortical energy metabolism allows changes in glutamate neurotransmitter flux to be approximately determined from measured changes in oxygen consumption, with a more precise relationship awaiting incorporation of glial and GABAergic neuroenergetics as a function of neuronal activity.
3 13C MRS support for coupling between neuroenergetics and neurotransmission
From studies of glial cells in suspension, Pellerin and Magistretti [51] related glutamate uptake to lactate production. Coupled with the results of Eq. (1), this eventually led to a proposed coupling in vivo between compartmented neuroenergetics, provided by glial glycolysis and neurotransmitter glutamate uptake [52]. The stoichiometry between glucose breakdown, metabolized to lactate, and glutamate uptake would be 1:1 as determined by ATP production and usage. A single glucose would produce two ATP equivalents non-oxidatively, one of which would restore the Na+/K+ gradient used to clear one glutamate while the second ATP would energize glutamine synthesis from NH3 and glutamate by glutamine synthetase (see Fig. 5). This 1:1 stoichiometry proposed between glucose consumption and glutamate was actually observed in vivo by the 13C MRS experiments as shown in Figs. 4 and 5 and Eq. (1). Therefore, at steady state, the stoichiometries of glycolysis agreed with the glial need for two ATP equivalents per glutamate. In the model glial lactate diffuses to the neurons where, proceeding via pyruvate, it would be oxidized to generate the larger fraction of the ATP. The in vivo results in Eq. (1), linking neuronal glucose oxidation to glutamate neurotransmission are consistent with the stoichiometries of the model and provided the strongest evidence that the model describes the in vivo events. These proposals have been reviewed quantitatively lately [25,26,52], and although some details remain unsettled, still the major aspects are supported by experiments.
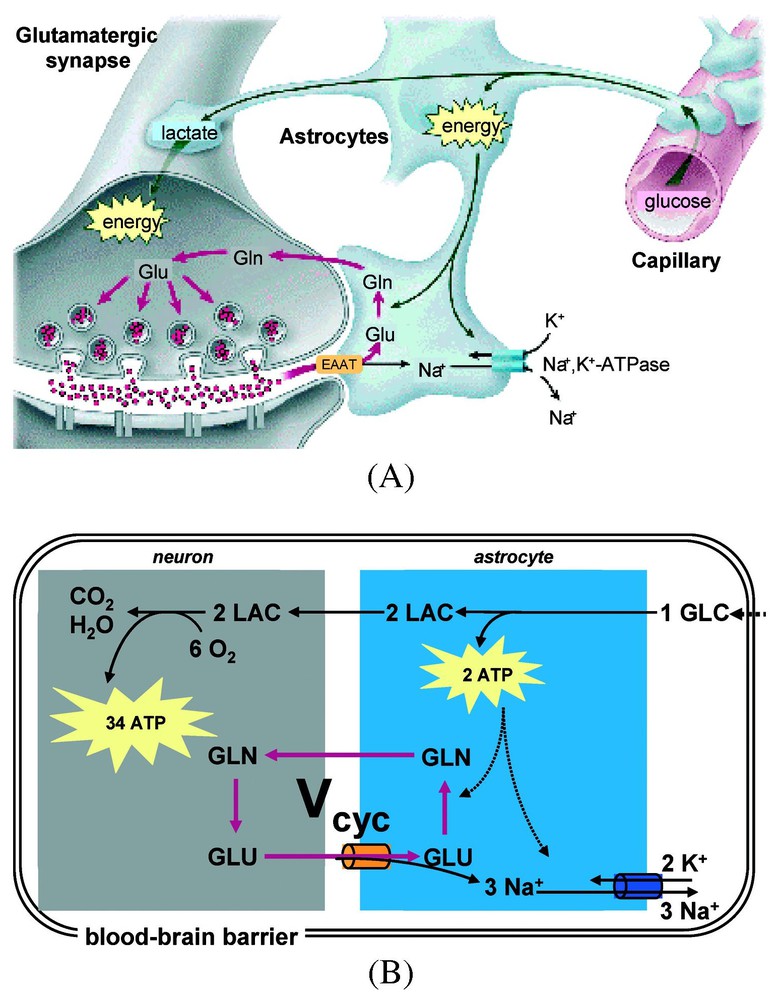
A model of stoichiometric coupling between Vcyc and CMRglc(ox) (for a review, see [52]). (A) The cytological association between capillaries and cellular compartments (astrocytes, and neurons) in the mammalian brain provide the framework for the century-old hypothesis of neurovascular coupling [7], which suggests that local neuronal activity is coupled with glucose utilization and blood flow. (B) The energy-requiring processes associated with neuronal activity maintain resting cell membrane potential, where the active Na+–K+ pump utilizes energy (i.e., ATP) to restore equilibrium Na+ and K+ concentrations in extracellular and intracellular compartments. The measured stoichiometry in Fig. 4 and Eq. (1) is consistent with the use of 2 ATP molecules in the astrocyte per molar oxidation of glucose. The dominant energy (∼80%) use in the neuron is connected with events associated with recycling the glutamate. Abbreviations: Vcyc, rate of glutamate neurotransmitter cycle; GLC, glucose; LAC, lactate; GLU, glutamate; and GLN, glutamine. Modified from [52].
4 Relationship between neuroenergetics and neural spiking frequency
The frequency of neuronal spiking measured by extracellular recordings is considered to be the ‘gold standard’ of brain activity [53]. Extracellular microelectrode recordings can report the activity of a small group of neurons near the electrode tip (<1 μm). Although neuronal firing is only one of the electrical signals that can be recorded extracellularly, it provides easily identifiable signals in vivo because they are short-lived, and have relatively high signal-to-noise ratio. Consequently, their different spike shapes can be assigned to different neurons in an ensemble [53–56].
Our most recent study [2] as well as prior studies [57–61] have shown in different ways that the stimulation-induced neuronal activity (as measured by electroencephalogram, local field potentials, or spiking activity) is spatially colocalized with the BOLD response. However, the existence of a quantitative relationship has been controversial, with findings in primates supporting a relationship between BOLD signal and average spike rate [60] as well as with local field potentials [61]. Recently, Logothetis and co-workers [61] compared these methods simultaneously in the anesthetized monkey brain at 4.7 T. Logothetis et al. concluded that changes in the BOLD signal represent the neuronal input because they observed a high correlation between the time-courses of BOLD signal and local field potentials, with a slightly weaker correlation with the time-courses of spiking activity. The time-course of local field potentials is believed to reflect mainly the neuronal input because they represent the weighted sum of the changing membrane potentials in the dendritic branch and the soma as a consequence of spiking from neighboring neurons. However since the input and output signals are not entirely distinct in a neuronal ensemble [53,62], it may be premature to link the fMRI signal to either the input or output of the system simply due to a better correlation with the BOLD time-course over several seconds.
Rees et al. [60] attempted to relate the stimulation-induced BOLD signal in humans with the spiking rate in non-human primates. They suggested that a ∼1% change in the BOLD signal at 1.5 T in humans corresponds to ∼9 Hz change in the spiking rate per neuron in region V5 of the non-human primate visual cortex, but reported (as have other groups [63]) large differences in this proportionality constant in other brain regions. These variations may largely reflect regional variations in the biophysical determinants of BOLD contrast [17,22] rather than fundamental differences in the coupling between energy metabolism and electrical activity.
The relationship found in our recent study [2], where we have related changes in neuroenergetics to spiking frequencies, has the advantage over previous studies of not depending upon the complex biophysical and technical fMRI parameters (e.g., field strength or pulse sequence) and statistical determinants of BOLD contrast.
In our recent study [2], the energy consumption CMRO2 obtained from calibrated BOLD images [4–6] was correlated with the spiking frequencies (ν) of 72 assigned neurons in layer 4 of the rat brain (Fig. 6). This provided an independent test of the coupling between energy metabolism and neurotransmitter release previously suggested by 13C MRS experiments (Eq. (1)). The extracellular electrodes identified specific spikes by their electrical properties (e.g., spike amplitude, duration, latency, etc.) and the spiking frequencies of these individual, identified neurons were measured under different experimental conditions. The spiking activities from 72 neurons in the somatosensory cortex were identified and each was followed under four conditions in the same experiment: two levels of α-chloralose anesthesia, each level with and without forepaw stimulation.
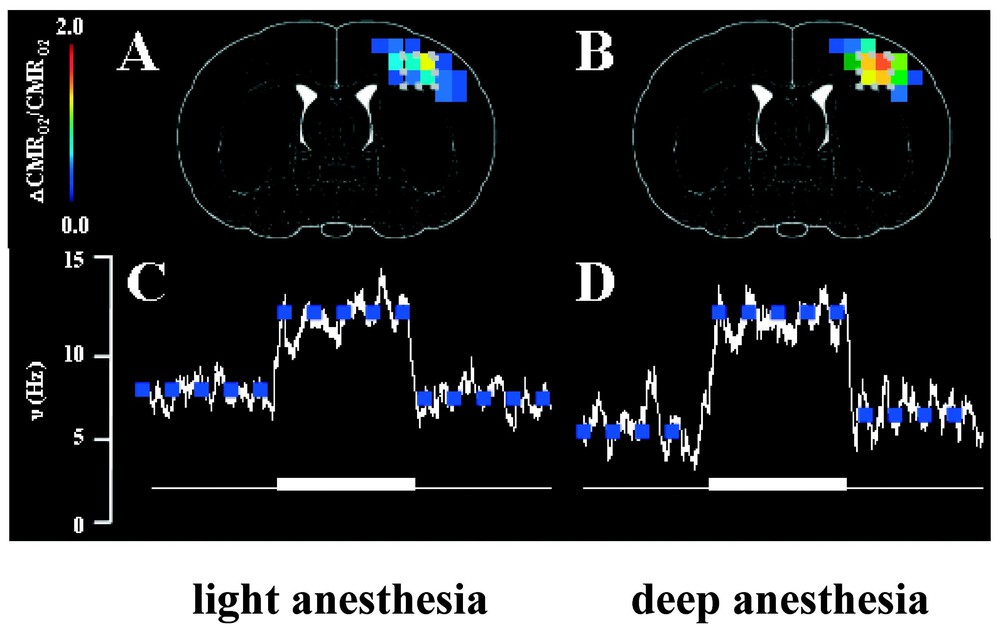
Localized changes in energy metabolism (CMRO2) and spiking frequency (ν) of a neuronal ensemble in the contralateral rat cortex induced by forepaw stimulation. In each case, the fMRI and electrophysiology measurements were made in each rat first under high basal activity (light anesthesia) then under low basal activity (deep anesthesia), achieved with two different doses of α-chloralose. The ΔCMRO2/CMRO2 maps (overlaid on stereotaxic coordinates from Paxinos and Watson, 1997) were determined from calibrated BOLD [6], whereas the Δν/ν values were extracted from extracellular recordings [2]. Approximately 92% of all microelectrode penetrations (in layer 4) identified at least two discrete neurons from the spike analysis. No significant stimulation-induced changes in ν and CMRO2 were observed in the ipsilateral side (data not shown).
In the α-chloralose anesthetized rat during forepaw stimulation the integrated values of Δν% was correlated with total ΔCMRO2% over a range of activity (Fig. 6), with the finding that:
| (2) |
| (3) |
In addition to the correlation between ν and CMRO2 information is available from the firing rates of the 72 different neurons whose performance was followed through the four conditions. The firing histograms (Fig. 7) show a different distribution in the two unstimulated states with more activity at the low frequencies in deeper anesthesia, in conformity with the lower average frequency in this condition. The coupling between Δν%=ΔCMRO2% enables these average frequencies to be converted to absolute energies by converting to CMRO2 values [65]. The firing frequencies of the individual neurons are affected by the stimulation – for example, in the more deeply anesthetized animals upon stimulation ∼60% of the individual firing rates increase, ∼30% decrease and ∼10% were unchanged. Different changes from the other anesthetized baseline lead to the important result that the histograms of the two stimulated states are indistinguishable. Furthermore in the stimulated states the data show that to a first approximation neurons in the ensemble go to the same firing frequency during stimulation, although as shown their firing rates generally differ in the two baseline conditions (FH, private communication).
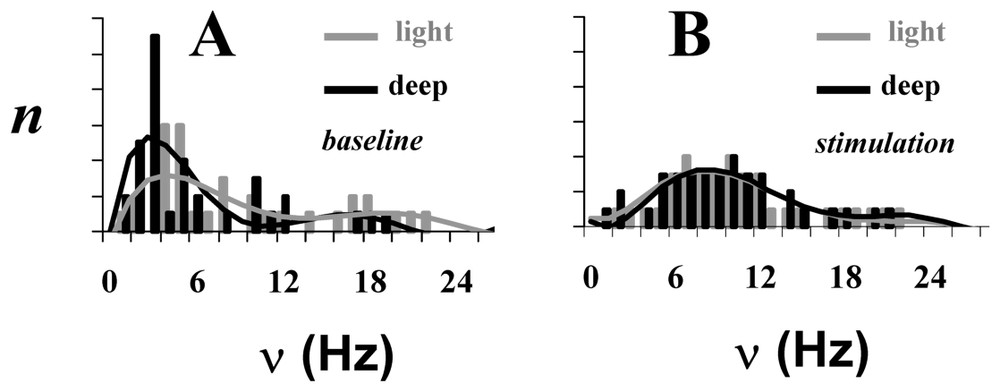
The neuronal activity patterns, as reflected by spiking frequency (ν), of a small ensemble (72 neurons) from the somatosensory cortex in α-chloralose anesthetized rats for four different conditions: (A) two baseline conditions and (B) two stimulated conditions. Each bar in the histogram represents averaged value of ν for that rat for the baseline (gray) and stimulated (black) conditions. There is a significant difference between spiking frequency distributions in the two baseline conditions (p<0.01), whereas upon stimulation the spiking frequency distributions become similar (p>0.25). Adapted from [2].
From a general knowledge of neuroanatomical connections we expect that neurons in the somatosensory cortex will be connected not only to sensory inputs (via the thalamus) but also to other brain regions – in particular other cortical regions. The resulting somatosensory firing will be the resultant of these two kinds of inputs indicated in the schematic Fig. 8. These results show that under deep α-chloralose anesthesia levels reduced activity is maintained by the anesthetic everywhere in the brain outside of the sensory cortex [2,32,66], so that predominantly the somatosensory cortical voxels are dominated by the stimulus-evoked activity.
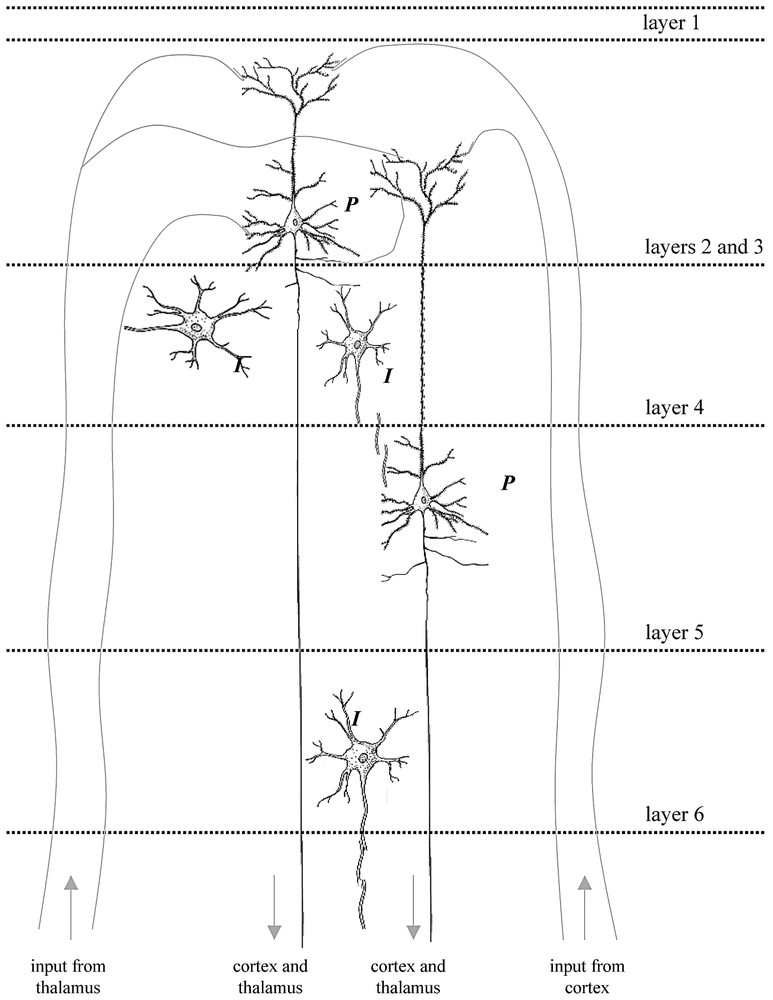
The placement of microelectrodes in layer 4 of the rat cortex [2] allowed measurement of the output of the major excitatory efferent neurons in the somatosensory cortex, i.e., the large pyramidal cells (P), which receive inputs from the thalamus as well as other regions of the cortex via afferent fibers. Small inter-neurons (I) also make local circuits with pyramidal neurons across different layers. Thus the spiking frequency measured for the ensemble represents the output due to combined inputs from cortico-cortical and thalamo-cortical connections. Under the anesthetized conditions of these experiments the sensory input to the cerebral cortex induced large changes in neurophysiological parameters (see Fig. 6). The speculative reason for this observation is due to reduced activities from neighboring brain regions (i.e., cortico-cortical connections) caused by anesthesia, which in turn allows the sensory input from the forepaw (i.e., thalamo-cortical connections) to be detected with greater significance. Future experiments in measuring either of these connections to the activated region in the cerebral cortex in greater detail (i.e., across different layers of the cortex) will provide greater insight into the interplay of population voting amongst the neuronal ensemble in sensing a particular stimulus [81]. The digitally drawn images of the neurons were inspired by cartoons from Kandel et al. [53].
The present experiments can be expanded by modifying the experimental protocols. In the present extracellular recordings, the electrodes were placed so as to select activities of neurons in layer 4, many of which form thalamo-cortical connections [67]. Additional experiments can explore the firing rates of other cortical layers, with primary connections to neighboring brain regions. Furthermore, the dominance of sensory stimulation can be reduced by decreasing magnitude of the electrical stimulus. Finally, contributions from the rest of the brain to the somatosensory voxels could be modified either globally, as stated by changing the anesthesia or somewhat regionally by selective interventions (e.g., competing stimuli activating the same region).
5 Contributions of non-oxidative energetics to a primarily oxidative brain
The constant relationship between oxidative neuroenergetics and glutamatergic neurotransmission (Fig. 4), observed at and below the awake state, appears inconsistent with an early finding from PET studies [68,69], which reported a much greater increase in ΔCMRglc% than ΔCMRO2% during stimulation. The functional studies of awake humans measuring changes in CMRglc, CMRO2, and CBF by PET reported ∼50% increase in CMRglc and CBF versus ∼5% increase in CMRO2. The authors proposed that stimulated activity was supported by anaerobic glycolysis. This posed the question as to whether neuroenergetic mechanisms were different above and below the non-stimulated, awake level of activity. Although subsequent PET and NMR experiments did not find such an extreme inequality of essentially no increase in CMRO2 (for a review, see [70,71]) they did qualitatively support an inequality between ΔCMRglc% and ΔCMRO2% upon stimulation. Although under all conditions glucose oxidation because of its greater yield, is the main ATP producing pathway, the small but definite contributions from non-oxidative sources (where lactate is the end product) under stimulation cannot be ignored. In fact, such an imbalance of glucose and oxygen uptake has long been known for the extreme stimulation experiment in seizures, where it has been accompanied by high lactate levels [72].
Obviously an additional mechanism was needed, one that reconciles the stimulus-induced increase in CMRglc over CMRO2 with idealized stoichiometries of glucose oxidation. The greater localized increase of glucose uptake over oxygen consumption during stimulation can be resolved by a recent proposal for the dynamic use of brain energy [70,71]. The energy requirement following a single firing event – which includes the action potential, neurotransmitter release and recycling, and associated excitatory (or inhibitory) postsynaptic potentials and which take several milliseconds – is high because of the immediate need for glutamate clearance (by astrocytic uptake) from the extracellular space. This rapid need for energy following each firing event cannot be met by the slow oxidative breakdown of glucose. Under conditions of slow firing rates, phosphocreatine and ATP reserves are presumably able to provide an adequate temporal energy buffer following each firing event. However during rapid firing this reserve is not able to support the rapid energy requirements (needed for rapid glutamate clearance) following bursts of spikes. In analogy with the energy sources for muscular contraction [73], it has been proposed that the intense short term requirements for power required by these bursts of neuronal activity must be produced by rapid non-oxidative glycolysis or glycogenolysis [70,71]. Averaged over the relatively long times of steady state the energy is essentially all supplied by oxidation of glucose, with the non-oxidative contributions serving as a temporal buffer.
As a consequence of the need to meet the temporal requirements of bursts of energy during increased activity, more lactate is produced (presumably in the astrocyte) than is needed (presumably in the neuron) for oxidation (Fig. 5). To meet the power requirements at the millisecond time scale of neuronal firing, and to the extent that the stoichiometric oxidation of glucose shown in Fig. 5 is the energy supply, the excess lactate is effluxed across the blood-brain barrier by mono-carboxylic acid transporters. Because excess lactate is effluxed, this proposal allows the energetics of glucose oxidation and glutamate cycling to be maintained during stimulation despite the apparent uncoupling between the input function CMRO2 and CMRglc, since the extra brain glucose is effluxed as lactate [74].
The unique feature of this proposal is that the increased CMRglc reflects power needs, i.e., the rate of energy consumption rather than steady-state energy needs. This role for non-oxidative metabolism allows steady state energy measurements to provide insights into rapid millisecond events. Although brain stoichiometry, as measured by inputs, departs from that expected by glucose oxidation, it does not mean that the organism is functioning inefficiently because the lactate effluxed can, as proposed by the lactate shuttle [70,74] be oxidized elsewhere.
6 Total neuronal activity supports cerebral function
For technical reasons, fMRI generally measures increments in regional brain activity. The ease of measuring incremental activity by functional imaging has been consonant with the widespread view that increments represent the modular energy required for functional activity [75]. Our findings that these signals arise from differences in total neuronal populations do not contradict such localizations. However the high level of brain activity during non-stimulated conditions observed in the 13C MRS experiments has raised questions about interpreting cerebral function exclusively in terms of such incremental activity [75]. Using energy as the measure of neuronal activity, the size of stimulus-induced incremental activity in awake human experiments is smaller than the basal activity. In anesthetized animals the size of incremental activities depend on depth of anesthesia and can be larger [23] but still are generally smaller than the baseline. The focus on the magnitude of incremental activity neglects contributions of activity at the basal level [76] and can be misleading. For example, if ΔCMRO2% in a localized region for one cognitive task is 1% (a typical value at 3 T) and for another task it is 2%, it would be misleading to conclude that twice the neuronal activity is required in the second task. Since approximately 75% of CMRO2 is associated with neuronal activity in humans [44,46] a more accurate conclusion would be an increase in neuronal activity from 76/75 to 77/75 of the baseline value.
Consequences of the large baseline activity (determined by 13C MRS studies) [1,44,46,77] for interpreting neuroimaging data have been discussed previously [76]. This interpretation explained the negative signals, observed with fMRI and PET, which at that time had been considered an anomaly [78,79], from the assumption that baseline activity was negligible. On the basis of high baseline brain activity [77] negative signals in a localized region were readily interpreted as a stimulated reduction in regional activity [76]. More recently, the existence and the importance of significant neuronal activity during non-stimulated conditions as a special property of certain brain regions (based on a meta-analysis of neuroimaging data) has been recognized by Gusnard and Raichle [80]. However in contrast to the 13C MRS measurements of a ubiquitous high resting neuronal activity, Gusnard and Raichle have proposed the existence of specific localized activity at rest in limited cortical regions. Their assignment follows from their finding that negative difference signals occur in certain regions to which they attribute high cognitive activities at rest. Their postulated “baseline” activity also differs in kind from the widespread high activities determined from the 13C experiments in that they claim a psychological basis (the negative signal change is consistent with the anticipated difference in activity between two psychological states) rather than a quantitative neuroenergetic basis for the existence and identification of baseline activity. We now discuss how the high baseline activity provides an approach to brain function that goes beyond the Posner and Raichle [75] interpretation of fMRI, to uncovering previously inaccessible brain activities.
7 The restless brain
The functional integrity of the brain depends on a collection of active cells, which are continuously transferring and processing information. Our studies have established the relationship between neuroenergetics and neurotransmission most quantitatively in animal models but similar results fit the available human data [25,26]. Our major findings can be summarized as follows:
- (1) To a first order changes in energy consumed are stoichiometrically coupled to the flux of glutamate/GABA neurotransmission and the rate of neuronal firing over a wide range of cortical activity, i.e., ΔCMRO2%≈Δν%≈ΔVcyc%.
- (2) In the awake non-stimulated condition (i.e., baseline activity), more than three quarters of the energy is devoted to neuronal activity.
- (3) To these conclusions we add the hypothesis that consciousness, related to the individual's subjective awareness, tracks the total degree of baseline activity and energy metabolism.
8 Implications for functional imaging
These results allow new neurophysiological and neuronal interpretations of contemporary functional imaging experiments. Two possible interpretative pathways of the experimental protocols are shown in a schematic presentation (Fig. 9). As indicated by the top line, the signal S, measured in a functional imaging experiment is often interpreted to provide insight into brain functioning M. The signals may derive from sensory experiments, or from more psychologically based protocols, but in either case they are interpreted in terms of a psychological model to elucidate brain function directly. The insights provided by this pathway are presumably responsible for the popularity of functional imaging experiments. However, from our viewpoint the main explanatory pathway is diagrammed in the lower lines. In that approach, the fMRI or PET functional imaging experiments can be used to determine the neurophysiological parameters (NP) of brain energy consumption, most conveniently expressed as CMRO2. Our results have shown that the values of CMRO2 determine neuronal activity (N), expressed either as neurotransmitter cycling, Vcyc, or neuronal spiking frequencies, ν. This explanatory pathway provides approaches to the questions of brain function M, which have neuroenergetic starting assumptions and reach different conclusion about the brain than those used in the psychological approach represented by S→M.

Schematic relationship between the neuroimaging signal (S) and mental processes (M). In the usual experimental plan and interpretation, which is influenced by psychology and cognitive neuroscience, a direct relationship between S and M is assumed, as represented by the upper Psychology pathway (dotted line). While the definition of M is based on psychology, the experimentally derived S serves to localize and quantitate the brain activity identified with the process. The lower Neuroscience pathway, assumes that M has a molecular and cellular basis, which is broken into three steps leading to S. The signal, S, in fMRI or PET experiments, is primarily a measure of the neurophysiological parameters (NP) of CMRglc, CMRO2, or CBF, as shown by the gray line. The relation between (NP) the neurophysiological measure of energy consumption and neuronal activity (N), which is shown by the dark line, has been clarified by the 13C MRS [1] and electrophysiology [2] experiments. These recent findings allow measurements of S to be converted into measures of N, which places us squarely facing the unsolved ‘hard’ problem of neuroscience, i.e., what is the relationship between M and N (dashed line)? Adapted from [76].
9 Neuronal basis of baseline and incremental signals
The 13C MRS experiments (as well as fluoro-deoxy-glucose (FDG) experiments by PET) can separately measure either baseline or incremental signals that represent activities of a very large population of neurons. Electrophysiological brain studies have suggested that the collaboration amongst a large number of neurons, firing at different frequencies, is crucial for encoding information in the brain (for a review, see [81]). The idea that a certain number of neurons in a cortical region respond to a given stimulus (i.e., population voting) is not new. It was suggested long ago by E.D. Adrian, who observed that touch causes discharges in several nerve fibers, with relative intensities that map the stimulus onto the cortex (for a review, see [64]). Information is more likely to be encoded in the brain by neuronal populations than by actions of individual neurons (for a review, see [82]) because typically each cell responds to more than one stimulus variable (e.g., intensity, frequency, etc.), and an individual cell cannot distinguish amongst these different stimulus variables. Since the response profiles of neurons are different, and a single neuron does not participate in just one type of function, the firing of a single cell by itself does not provide a meaningful basic code for information processing (for reviews, see [54,55]).
Our recent fMRI studies combined with electrophysiology [2,83], which measured the firing rates of a neuronal population and their energy consumption, correlated the population voting of 72 neurons with the averaged energetics (Fig. 7). Energy consumption and firing rates increase proportionately (Fig. 6). The population changes during stimulation created these contributions to the energy from an average of neuronal responses. The histograms of firing rates (Fig. 7) provide more specific information by depicting the redeployment of the same neurons under different stimulated and non-stimulated conditions. While this redistribution of the population voting is measured as an increment by neuroimaging techniques, the total population energies in the two conditions are represented by the integrated activities of the populations. The increment, therefore, is only conceptually separable from the total activity by comparing total activities of the population in two states. Viewed as a general redeployment of neuronal firing frequencies, the integrated signal from a region can increase, decrease, or remain unchanged as shown by the observed difference signals. The distributions of firing rates during non-stimulated conditions vary with the depth of anesthesia (Fig. 6). However, during the particular strong sensory stimulation in our experiments, the distributions of firing rates are characteristic of that state, regardless of the starting baseline activity (Fig. 7).
The 13C MRS measurements of high resting baseline activity are the sum of energy consuming connections measured in the voxel between neurons of different types (Fig. 8). In addition to local inter-neurons the synaptic activity in a voxel responds to connections with the rest of the brain [62]. These remote neuronal connections, which support the de-localized aspects of brain activity, contribute to the measures of total activity. Finally during stimulation the somatosensory cortex has direct input from the sensory neurons – an input that can be varied in the experiment. The resting unstimulated neuronal activity, which arises from local and distal neurons, is reduced by anesthesia both inside and outside of the somatosensory region. Upon stimulation of the anesthetized rat, the total neuronal activity inside the somatosensory voxels increased whereas total neuronal activity outside the stimulated region remained low [33,66,84]. Thus the forepaw stimulation introduces neuronal activity to the somatosensory cortex, but since the rest of the brain continues to show low activity (Fig. 6), its transmission to the somatosensory region remains low. This conforms to our observation that under strong stimulation the neuronal population as judged by the neuronal histograms (Fig. 7) is the same at our two levels of anesthesia so that it responds mainly to the sensory input. In a non-anesthetized functional experiment the situation may be different. In the non-anesthetized awake brain at rest, the forepaw stimulation raises the total neuronal activity only slightly [34,83]. Preliminary results, extending the α-chloralose experiments of Smith et al. [2], using a lighter level of anesthesia, have shown departures from the histogram of population ascribed to sensory stimulation (FH, private communication) suggesting that the remainder of the brain is beginning to contribute significantly. The interplay between contributions from localized and de-localized neuronal connections is measured by these experiments, with the promise that experiments varying the parameters of sensory input, anesthesia depth and the cortical level probed will provide additional insight to important questions of brain organization.
The pattern of neuronal firing, specific down to the level of individual neurons, is created, in these stimulated conditions, by the stimulus. The change in total energy upon a stimulus, detected, as the difference signal, S, is a determinant of the signal usually reported in an fMRI experiment. The usual assumption of an fMRI experiment, i.e., S reflects an involvement of that localized activity, is consistent with these neuronal results and is the basis of the usefulness of the differencing signals. The signals reflect an integrated, localized change in neuronal activity caused by the stimulus, but they do not measure the amount of activity that supports the stimulus. They measure the differences between that regional activity in the two states differenced.
This kind of differencing represents a paradigmatic scientific experiment. A psychological or cognitive hypothesis is proposed that a task will change brain activity in a localized region and it is observed to do so. In contrast, when considering the total or baseline brain activity such a formal structure of cause and effect is not available. The total level, at rest being identified as the baseline level – without any specific controlled sensory input – is accepted as having no objective cause. There are no psychological or cognitive concepts that can be postulated to cause this activity. We would not consider it scientifically valid to hypothesize that the brain, at rest, was engaged in or dedicated to a particular, identifiable activity, e.g., memory, love or computing. Without a causal claim, the baseline activity contrasts with the difference activity, where an orchestrated event is postulated to cause the difference signals measured.
10 Consciousness and baseline activity
In agreement with authoritative efforts to review and define consciousness we have no exact definition to propose. We do propose, however, that most discussions would accept consciousness as a feeling similar to awareness that humans normally possess when they are awake and which they lose when they are in a state of deep anesthesia, i.e. flat EEG. How does this restless neuronal activity measured in the absence of specified external stimuli, relate to subjectivity and to consciousness? Our results offer quantitative relations between, and empirical definitions of, brain observables that change continuously between these limits. These observables are the rate of energy consumption evaluated by CMRO2 and the rate of neuronal signaling measured by neuronal firing, ν, and neurotransmitter release Vcyc. Over a wide range of brain activity, the percentage changes in these parameters are equal (Figs. 4 and 6). Fractional changes in energy consumption are accompanied by equal fractional changes in these two functional descriptions of neuronal work.
Previous PET measurements have reported that glucose metabolism decreases with deepening anesthesia for several anesthetics (for a review, see [85]). These reductions are generally global although small regional differences are found. Titrating human glucose consumption with isoflurane, halothane and propofol anesthetics “to the point of unresponsiveness” the whole brain rates of glucose metabolism measured by PET were decreased by 40%, 46%, and 55% respectively [85–87]. These decreases in metabolic activity were “believed to reflect the reduced synaptic activity”, as judged by various EEG variables. Our relationships now establish this connection with great certainty, so that the readily available measurements of glucose metabolism can definitely be interpreted as linked to neuronal firing. Hence, along the pathway of deepening anesthesia, upon reaching about one half the normal brain firing rates, the subjects reached “the point of unresponsiveness.” Therefore there is an approximately quantitative correlation between some commonly accepted qualities used to describe consciousness and the magnitude of neuronal firing. While these correlation have been further refined by taking advantage of the spatial resolution of functional imaging methods [87], we attend here to the way in which the first order correlation between the averaged level of brain activity is related to the existence of consciousness, a correlation which could be followed by associating different levels of consciousness with levels of neuronal activity. The decreases of the baseline activity with deepening anesthesia and the accompanying loss of consciousness establishes the importance of the high baseline activity. It is connected, in ways that we are only now able to start exploring, with the unspecified aspects of consciousness. In the differencing methods of functional imaging baseline activities are discarded, only the differences between two cognitive states being retained. In this respect the differencing imaging methodology parallels the assumptions of cognitive psychology, in which, as has been shown [88–90], consciousness is often neglected.
11 Philosophical and neurophysiological structures
Our separation of brain activities into a differencing activity and a baseline or total activity, where the former arises from a cognitive task and the latter from wide unspecified internal brain connections finds a parallel in David Chalmers' philosophical analysis of brain activity or consciousness. Chalmers has suggested that consciousness could profitably be divided into ‘easy’ and ‘hard’ problems [91]. Easy problems would be those that can be addressed objectively, such as the studies of sensory or cognitive tasks that are evaluated in functional imaging experiments by the difference signal. Hard problems that would help to explain subjective experience, he suggests are beyond our present ability to formulate. These subjective experiences, we suggest, are expressed in the totality of neuronal activity, whose causal connections also, at present, cannot be formulated in causal terms. We propose that the present approach offers an experimental entry for exploring these unknown areas of subjective brain activity.
A relevant neuroscientific framework for relating localized and widespread activities has been offered and developed by Dehaene and colleagues [92]. The participation of large neuronal populations in function was assumed from measurements of electrical activity in awake and asleep humans [93]. The authors have more recently conceptually divided neuronal activity into a specific localized response to brain tasks (e.g., forepaw stimulation) interacting with a more de-localized response that modulates and controls the specific response. They define the de-localized activity as a global workspace that can “potentially interconnect multiple distributed and specialized brain areas in a coordinated, though variable manner, and whose intense mobilization might be associated with a subjective feeling of conscious effort.” [92]. The authors propose the global workspace to be active when, in addition to the specific modules, a stimulus interacts with other brain regions.
The concept of “global workspace” as the neural underpinnings of consciousness had been developed by Baar [94]. In his view a conscious state has wide access to neuronal information. This model is being actively advanced and applied to experimental results. Dehaene [95] has explored how advances in “psychological and neuropsychological research” have led to “a new comprehension of the neural underpinnings of consciousness.” Dehaene [95] starts from conscious states readily identified by introspection in daily lives or by psychological tests. After recognizing the caution that must be exercised in such introspective findings they plan to “systematically distinguish mental states that subjects label as ‘conscious’ from other states.” Dehaene [95] and co-workers [92] implement this approach by utilizing much of the recent experimentation by fMRI and more traditional methods. We have accepted this overall model of the global workspace but have referenced different findings, such as the changes of consciousness during anesthesia and the magnitude of baseline activity to support identification of the global workspace with consciousness. Moreover our empirical basis is provided by the quantitative measurements of the work done by neuronal firing and neurotransmitter fluxes and the coupled neuroenergetics measured by oxygen consumption. Our approach falls short of explaining the living world features of consciousness as discussed by psychology. It says nothing, in everyday terms, about the nature of intention or memory or the other great activities of mind. However it does provide quantitative information about the total neuronal activity and it begins to reduce that activity to components that can be studied separately from a limited scientific perspective. Our scientific basis of the neuroscience of proposed global workspace is thermodynamics, work and energy, and while it does not provide the scope covered by cognitive psychology it does provide an understanding with the sturdiness of definite physical knowledge.
Since the baseline activity measured from layer 4 in our studies (Fig. 7) is comprised of signals from local inter-neurons as well as from distant neurons, primarily thalamic [53,62,67], the large baseline activity could therefore be identified as input from, and connections to, other neurons including those in regions of the global workspace. The widespread decrease of baseline activity in the anesthetized state reflects a decrease in global activity. Because outside the somatosensory cortex the brain remains at low anesthetized activity during stimulation, connections to the global workspace should be reduced during stimulation in the anesthetized state compared to the non-anesthetized state. Therefore the high neuronal activity observed in the somatosensory cortex presumably is caused primarily by sensory neurons, which is consistent with the almost identical histograms of the stimulated state (Fig. 7) at both levels of anesthesia. In these assignments of total energetics and activities, the experiments described in this paper can provide quantitative measures to help separate contributions from local and global responses.
Differencing methods in functional imaging have be used with a computer module view of brain in which undefined baseline activities can be totaly neglected. In contrast, several neuroscientists have developed models of brain activity that include baseline activities in ways that are consistent with the high activities that we have quantitatively measured, as described above. The need for substantial unfocused neuronal activity for the service of even sensory responses was suggested by the brilliant experiment of Grinvald and colleagues [96]. Starting with the recognition that “cortical neurons are spontaneously active in the absence of external input even in primary sensory areas”, they studied the correlations between single-unit recordings and real-time optical imaging. While interpreting their data, they concluded by suggesting that “in the absence of stimulation the cortical network wanders through various states represented by coherent firing of different neuronal assemblies” and that a stimulus pushes the network into a particular activated assembly. Analogously, the elegant temporal synchronization of neuronal responses on which Singer's conclusion are based has led to the conclusion: “Of the many responses of VI those that become synchronized best will be particularly effective in influencing neurons in higher areas [97].” This hypothesis recognizes the large neuronal activity in the absence of stimulation and includes that activity in proposals about brain function.
In a similar view, emphasizing the importance of neuronal oscillations Llinas [98] starts from the view, “that nervous system function may actually operate on its own, intrinsically, and that sensory input modulates rather than informs this intrinsic system”. The interaction between sensory cues and the high existing brain activity allows a larger view of brain function. In contrast to localized computer-like modules, Llinas has proposed that synchronized firing of thalamo-cortical connections in a highly active brain play an important role in defining the subjective self. Our 13C NMR results, in agreement with the assumptions of these brain scientists about the importance of high baseline activities, provide measures of the magnitudes of such unstimulated activity and thereby provide a quantitative basis for analysis.
Finally, a word about philosophers' advice. Chalmers has suggested that scientists might do well to look for an understanding of the hard problem by starting with cognitive studies of related qualities such as awareness. He says [91]: “Consciousness and cognition do not float free of one another but cohere in an intimate way.” This direction has been studied by many respected cognitive scientists and it forms the basis of Dehaene's interpretation of the global workspace. Starting with difference functional imaging signals, some have looked for interactions between the signals found for example: from the effects in the visual response of attention being paid to nearby stimuli [99] while others have taken correlations between difference signals in different brain regions [100]. These attempts to extend the meaningfulness of fMRI beyond the assumptions of cognitive psychology are in accord with Chalmers' feelings that cognitive conceptualizations provide a good starting point for studying related subjectivities. But we have chosen a different direction to study the ‘hard’ problem, a direction that starts with hard, reliable assumptions based on physical knowledge. We have measured the relationship between energy consumption and the activity of local and distributed neurons. Our starting points have been quantitative and unambiguous and the questions they ask have been answered with ‘hard’ data. From the secure position these results have generated, we have proposed to advance slowly, but sure-footedly, towards the exploration of previously inaccessible neuronal functions.
Acknowledgements
We gratefully acknowledge grant support from the National Institutes of Health [DK-27121 (RGS), NS-037203 (FH), DC-003710 (FH), MH-067528 (FH), NS-32126 (DLR)], National Science Foundation [DBI-9730892 (FH), DBI-0095173 (FH)], and James S. McDonnell Foundation (FH).


