Dynamin recruitment by clathrin coats: a physical step?

Jean-Baptiste Fournier; Paul G. Dommersnes; Paola Galatola

doi:10.1016/S1631-0691(03)00096-9

Biological modelling / Biomodélisation

Dynamin recruitment by clathrin coats: a physical step?
[Recrutement des dynamines par les puits recouverts de clathrines : une étape physique ?]

Présenté par : Michel Thellier

Jean-Baptiste Fournier ¹ ; Paul G. Dommersnes ¹ ; Paola Galatola ²

¹ Laboratoire de physico-chimie théorique and FR CNRS 2438 « Matière et Systèmes complexes », ESPCI, 10, rue Vauquelin, 75231 Paris cedex 05, France
² LBHP, université Paris-7—Denis-Diderot and FR CNRS 2438 « Matière et Systèmes complexes », case 7056, 2, place Jussieu, 75251 Paris cedex 05, France

Comptes Rendus. Biologies, Volume 326 (2003) no. 5, pp. 467-476.

Résumés

Anglais
Français

Recent structural findings have shown that dynamin, a cytosol protein playing a key-role in clathrin-mediated endocytosis, inserts partly within the lipid bilayer and tends to self-assemble around lipid tubules. Taking into account these observations, we make the hypothesis that individual membrane-inserted dynamins imprint a local cylindrical curvature to the membrane. This imprint may give rise to long-range mechanical forces mediated by the elasticity of the membrane. Calculating the resulting many-body interaction between a collection of inserted dynamins and a membrane bud, we find a regime in which the dynamins are elastically recruited by the bud to form a collar around its neck, which is reminiscent of the actual process preempting vesicle scission. This physical mechanism might therefore be implied in the recruitment of dynamins by clathrin coats.

Des donnés structurales récentes ont montré que la dynamine, une protéine du cytosol qui joue un rôle clé dans l'endocytose clathrine-dépendante, s'insère partiellement dans la bicouche membranaire et tend à s'auto-assembler autour de tubules lipidiques. En tenant compte de ces observations, nous faisons l'hypothèse que les dynamines impriment localement une courbure cylindrique dans la membrane. Cette empreinte peut engendrer des forces élastiques de longue portée. En calculant l'interaction multi-corps entre un ensemble de dynamines insérées dans la membrane et une capsule endocytotique, nous trouvons un régime dans lequel les dynamines sont recrutées élastiquement par la capsule pour former un collier autour de son cou, ce qui rappelle le processus précédant la scission des vésicules d'endocytose. Ce mécanisme physique pourrait donc être impliqué dans le recrutement des dynamines par les capsules de clathrine.

Métadonnées

Reçu le : 2002-05-27
Accepté le : 2003-01-28
Publié le : 2003-05-01

PMID

DOI : 10.1016/S1631-0691(03)00096-9

Keywords: endocytosis, clathrin, dynamin, membrane inclusions interactions
Mot clés : endocytose, clathrine, dynamine, interactions entre inclusions membranaires

Affiliations des auteurs :

Jean-Baptiste Fournier ¹ ; Paul G. Dommersnes ¹ ; Paola Galatola ²

¹ Laboratoire de physico-chimie théorique and FR CNRS 2438 « Matière et Systèmes complexes », ESPCI, 10, rue Vauquelin, 75231 Paris cedex 05, France
² LBHP, université Paris-7—Denis-Diderot and FR CNRS 2438 « Matière et Systèmes complexes », case 7056, 2, place Jussieu, 75251 Paris cedex 05, France

@article{CRBIOL_2003__326_5_467_0,
     author = {Jean-Baptiste Fournier and Paul G. Dommersnes and Paola Galatola},
     title = {Dynamin recruitment by clathrin coats: a physical step?},
     journal = {Comptes Rendus. Biologies},
     pages = {467--476},
     publisher = {Elsevier},
     volume = {326},
     number = {5},
     year = {2003},
     doi = {10.1016/S1631-0691(03)00096-9},
     language = {en},
}

TY  - JOUR
AU  - Jean-Baptiste Fournier
AU  - Paul G. Dommersnes
AU  - Paola Galatola
TI  - Dynamin recruitment by clathrin coats: a physical step?
JO  - Comptes Rendus. Biologies
PY  - 2003
SP  - 467
EP  - 476
VL  - 326
IS  - 5
PB  - Elsevier
DO  - 10.1016/S1631-0691(03)00096-9
LA  - en
ID  - CRBIOL_2003__326_5_467_0
ER  -

%0 Journal Article
%A Jean-Baptiste Fournier
%A Paul G. Dommersnes
%A Paola Galatola
%T Dynamin recruitment by clathrin coats: a physical step?
%J Comptes Rendus. Biologies
%D 2003
%P 467-476
%V 326
%N 5
%I Elsevier
%R 10.1016/S1631-0691(03)00096-9
%G en
%F CRBIOL_2003__326_5_467_0

Jean-Baptiste Fournier; Paul G. Dommersnes; Paola Galatola. Dynamin recruitment by clathrin coats: a physical step?. Comptes Rendus. Biologies, Volume 326 (2003) no. 5, pp. 467-476. doi : 10.1016/S1631-0691(03)00096-9. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/S1631-0691(03)00096-9/

Version originale du texte intégral

1 Introduction

In eukaryotic cells, membranes of different organelles are functionally connected to each other via vesicular transport. Formation of transport vesicles from invaginated buds of the plasma membrane is called endocytosis [1]. In clathrin-mediated vesiculation, vesicle formation starts with the assembly on the donor membrane of a highly organized ‘coat’ of clathrins [2], which acts both to shape the membrane into a bud and to select cargo proteins [3–7]. The mechanism by which an invaginated clathrin-coated bud is converted to a vesicle (scission) involves the action of a cytoplasmic GTPase protein called dynamin [6,8]. Dynamins form oligomeric rings at the neck of deeply invaginated membrane buds and induce scission [9,10]. How exactly dynamin is recruited and how the scission actually occurs remains unclear [11,12]. In this paper we propose that dynamin recruitment by clathrin coats could be driven by long-ranged physical forces mediated by the membrane curvature elasticity.

Cryo-electron microscopy has recently revealed the detailed structure of the clathrin coats at 21-Å resolution [2]. Clathrin units, also called ‘triskelions’, have a star-like structure with three legs. Initially solubilized into the cytoplasmic fluid, they self-assemble onto the membrane surface into a curved, two-dimensional solid scaffold. The latter is a honeycomb made of hexagons and pentagons (geometrically providing the curvature) the sides of which are built by the overlapping legs of the clathrin triskelions. In the plasma membrane, clathrins usually interact with ‘adaptor’ transmembrane proteins, which also serve to select cargo proteins. However, it has been shown that clathrin coats can readily self-assemble onto protein-free liposomes [13,14].

Dynamin is known to be solubilized in the cytosol as tetramers, and to aggregate in low-salt buffers into rings and spirals [9]. Dynamin also self-assembles onto lipid bilayers, forming helically striated tubules that resemble the necks of invaginated buds (tube diameter ≃50 nm) [10]. Addition of GTP induces morphological changes: either the tubules constrict and break [15], or the dynamin spiral elongates [16]. These findings suggest that the scission of clathrin-coated buds is produced by a mechanochemical action [16,17].

At the earlier stages of the budding process, dynamins already strongly interact with bilayer membranes. Indeed, in vivo studies showed that dynamin binds acidic phospholipids in a way that is essential to its ability to form oligomeric rings on invaginated buds [18–22]. Using a model lipid monolayer spread at the air-water interface, it was shown that dynamins actually penetrate within the acyl region of the membrane lipids [23]. This finding was recently confirmed by the three-dimensional reconstruction of the dynamin structure by cryo-electron microscopy at 20 Å resolution [24]: dynamins form T-shaped dimers the ‘leg’ of which inserts partly into the outer lipid leaflet.

It was long ago suggested [25,26] that particles inserted within bilayers should feel long-range interactions mediated by the elasticity of the membrane. Indeed, a protein penetrating within a bilayer and binding its lipids – such as dynamin – may in general produce a local membrane curvature (see Fig. 1). Because of the very nature of the curvature elasticity of fluid membranes, this deformation relaxes quite slowly away from its source, and the presence of another inserted particle produces an interference implying an interaction energy [25]. This holds as long as the separation between the inclusions is smaller than the characteristic length $ξ_{σ} = \sqrt{κ / σ}$ , where $κ ≃ 60 k_{B} T$ is the bending rigidity of the membrane and σ is the tension of the membrane. At separations larger than ξ_σ, the membranes flattens out and the interaction vanishes exponentially. Note that the membrane tension is not a material constant like κ; it is an effective force per unit area, which is most probably biologically regulated [27] and is usually of the order of 10⁻² to 10⁻⁵ times the surface tension of ordinary liquids [27,28]. At this point, anticipating on our model for the clathrin-dynamin system, let us state that we shall formally assume σ=0 in this paper, which amounts to assuming that the relevant distances between the inclusions (i.e., the distance between the neck of the clathrin bud and the dynamins) are smaller than ξ_σ. This means that our model should rather apply to weakly tense membranes, e.g., $σ ≃ 10^{- 3} mJ m^{- 2}$ , for which ξ_σ≃400 nm (which is quite larger than the typical size of the clathrin buds ≃80 nm). Although the actual value of σ in the vicinity of clathrin buds is unknown, such a small tension agrees with recent measurements on biological membranes (erythrocytes membranes interacting with their cytoskeleton) [28]. In the case of stronger tensions, we expect our results to hold nonetheless, the dynamins being ‘captured’ when their Brownian diffusion brings them at a distance from the bud less than ξ_σ.

Fig. 1
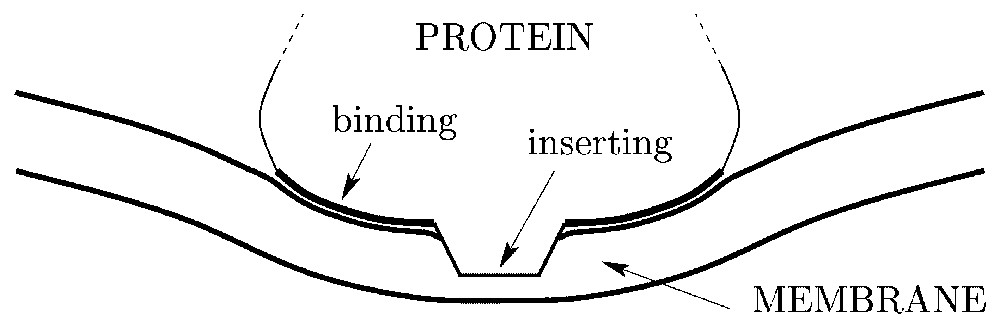
Schematic representation of a cytosol protein partly inserting within a lipid bilayer and inducing a local membrane curvature via a binding region.

The first detailed calculation of the membrane-mediated interaction was performed for two isotropic particles each locally inducing a spherical curvature [29,30]. The interaction was found to be repulsive, proportional to the rigidity κ of the membrane and to the sum of the squares of the imposed curvatures; it decays as R⁻⁴, where R is the distance between the particles. The case of anisotropic particles producing non-spherical membrane deformations is even more interesting, since their collective action on the membrane is expected to have nontrivial morphological consequences [31–33]. The local deformation of a membrane actually involves two distinct curvatures, associated with two orthogonal directions (as in a saddle or in a cylinder). Recent calculations showed that the interaction between two anisotropic inclusions is very long-ranged and decays as R⁻² [34–36]. It is always attractive at large separations and favors the orientation of the axis of minor curvature along the line joining the particles [35]. Note that these elastic interactions prevail at large separations, since they are of much longer range than other forces, such as van der Waals or screened electrostatic interactions.

2 Model

Among the above informations, let us outline the three points that are essential for our model. (i) Clathrin coats are solid scaffolds that rigidly shape extended parts of the membrane into spherical caps. (ii) Dynamins are solubilized proteins that partly insert within the membrane bilayer. (iii) Inserted membrane hosts that imprint a local membrane curvature interact with long-range forces of elastic origin.

We therefore build the following model. We consider a clathrin-coated bud as being a membrane patch bearing a constant, fixed spherical curvature. Technically, we shall build the bud by placing a large number of point-like spherical curvature sources at the vertex of a hexagonal lattice (see Fig. 2). Within the present formalism, this is the simplest way to define a rigid, almost non-deformable, spherically curved zone. Since the dynamins will not penetrate the bud, we expect that our results will not depend on whether the bud is geometrically enforced (which would be conceptually simpler but technically harder here) or built by an inclusion array. Note that the shape of the neck around the clathrin bud will result from the minimization of the total energy, and will therefore not be enforced artificially.

Fig. 2
Piece of a model membrane showing a clathrin coated bud and the imprints of inserted dynamins.

Because dynamins partly insert within the membrane and seem to accommodate cylindrical curvature, we model them as sources locally imprinting a cylindrical curvature. We place a large number of such ‘dynamins’ on a membrane in the presence of an artificial bud as described above (Fig. 2), and we study whether the latter will recruit or not the dynamins through elastic long-range forces.

2.1 Long-range elastic interactions between many membrane inclusions

The elastic interaction between N isotropic or anisotropic membrane hosts can be calculated from first principles [35,37–39]. The membrane is described as a surface which is weakly deformed with respect to a reference plane. Without this assumption, analytical calculations are virtually impossible. An obvious consequence is that we can accurately describe only weakly invaginated buds; nevertheless, we expect that our results will hold qualitatively for strongly invaginated buds. The membrane hosts are described as point-like sources bearing two curvatures c₁ and c₂, associated with two orthogonal directions. These values represent the two principal curvatures that the hosts imprint on the membrane through their binding with the membrane lipids (assuming the binding region is itself curved). For instance, a spherical impression corresponds to c₁/c₂=1, a cylindrical impression corresponds to c₁/c₂=0, and a saddle-like impression corresponds to c₁/c₂=−1. This over-simplified model actually contains the essential ingredients responsible for the long-range elastic interactions between membrane inclusions: for protein hosts of a size comparable to the thickness of the membrane, it yields accurate interactions for separations as small as about three times the particles size. Note that the curvature actually impressed by a particle could be affected by the vicinity of another inclusion, we shall however neglect this effect for the sake of simplicity (strong binding hypothesis).

The point-like curvature sources describing the membrane hosts diffuse and rotate within the fluid membrane, because of the forces and torques exerted by the other membrane hosts and of the thermal agitation $k_{B} T$ . We parameterize the orientation of a particle by the angle θ that its axis of minor curvature, i.e., the axis associated with min(|c₁|,|c₂|), makes with the x-axis, in projection on the (x,y) reference plane. Given N inclusions with specified positions x_i and y_i, orientations θ_i, and curvatures c_1i and c_2i, for i=1…N, we calculate the shape of the membrane satisfying the N imposed point-like curvatures and we determine the total elastic energy of the system. We thereby deduce the N-body interaction between the hosts F_int(…,x_i,y_i,θ_i,c_1i,c_2i,…). The mathematical details of this procedure are sketched in Appendix A.

2.2 Pairwise interactions

Before studying the collective interaction between model dynamins and clathrin coats, let us describe how point-like spherical and cylindrical sources interact pairwise (in the absence of membrane tension, as discussed in Section 1).

The membrane distortion produced by two inclusions modeled as point-like spherical curvature sources is shown in Fig. 3a. Each inclusion appears as a small spherical cap away from which the membrane relaxes to a flat shape. As evidenced by the plot of the interaction energy (see Fig. 3a), such spherical inclusions repel one another. Calling κ the bending rigidity of the membrane, a the thickness of the membrane (which is comparable to the size of the inclusions), c the curvature set by the inclusions and R their separation, our calculation gives (see Appendix A):

F_{cl - cl} (R) ≃ 8 π κ a^{2} c^{2} {(\frac{a}{R})}^{4}

(1)

for the the asymptotic interaction at large separations, in agreement with previous works [29,34,35]. Note that the plot given in Fig. 3a corresponds to the exact interaction within our model, not to the asymptotic expression (1).

Fig. 3
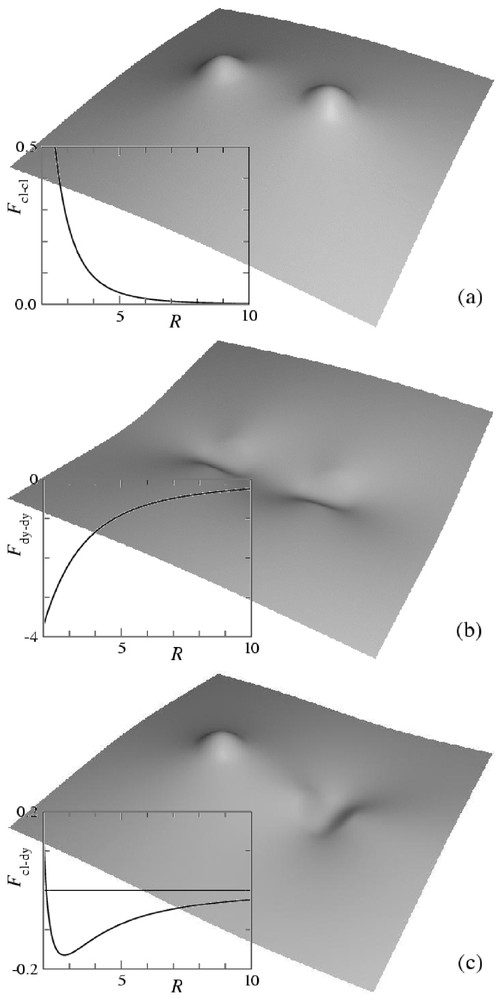
Shape of a membrane distorted by two inclusions imprinting local curvatures and interaction energy as a function of separation. Distances are rescaled by the membrane thickness a and energies by $κ a^{2} c^{2}$ . (a) Spherical inclusions of curvature c; (b) cylindrical inclusions of curvature c; (c) spherical inclusion of curvature c and cylindrical inclusion of curvature $0.2 c$ . The shapes are calculated from equation (A.13), the interaction energies from equation (A.12).

The membrane distortion produced by two inclusions modeled as point-like cylindrical curvature sources is shown in Fig. 3b. Each inclusion appears as a small cylindrical cap away from which the membrane relaxes to a flat shape. The interaction between two such hosts depends on their relative orientation. The minimum energy is found when the axes of the cylinders are parallel to the line joining the inclusions. As evidenced by the plot of the interaction energy (see Fig. 3b), the interaction is then attractive. It therefore turns out that two such hosts produce a weaker membrane deformation when they are close to one another than when they are far apart. As described in [35], when their curvature is strong enough, such inclusions tend to aggregate and to form linear oligomers. Their asymptotic interaction energy is given by

F_{dy - dy} (R) ≃ - 8 π κ a^{2} c^{2} {(\frac{a}{R})}^{2}

(2)

It decays as R⁻², hence it is of longer range than (1).

Finally, we show in Fig. 3c the membrane distortion produced by the interaction between a spherical source and a cylindrical one. The latter is oriented in the direction that minimizes the energy. As evidenced by the plot of Fig. 3c, the interaction is attractive at large separations and repulsive at short separations, with a stable minimum configuration at a finite distance. Calling c the curvature set by the cylindrical inclusion and c′ the one set by the spherical inclusion, our calculations give the asymptotic interaction

F_{cl - dy} (R) ≃ - 4 π κ a^{2} c c' {(\frac{a}{R})}^{2}

(3)

We may therefore expect that dynamins will be attracted by clathrins coats; however, owing to the non-pairwise character of the interaction [35], it is necessary to actually perform the corresponding many-body calculation. It is also necessary to check whether thermal agitation will or will not disorder the inclusions.

3 Collective interactions between model dynamins and clathrin buds

As described in Section 2, we build a model clathrin-coated bud by placing in a membrane N_cl point-like spherical inclusions of curvature c_cl on a hexagonal array with lattice constant b. Here, we have chosen N_cl=37 and $b = 3 a$ . By changing the curvature c_cl, we can adjust the overall curvature of the clathrin scaffold, thereby simulating the growth of a vesicular bud. We then add N_dy=40 point-like cylindrical sources of curvature c_dy modeling inserted dynamins.

To study the collective behavior of this system under the action of the multibody elastic interactions (see Section 2.1) and of thermal agitation, we perform a Monte Carlo simulation. The details of the simulations are given in Appendix B. To prevent unphysical divergences of the elastic interaction energy, it is necessary to introduce a hardcore steric repulsion preventing two inclusions to approach closer than a distance d. Since the size of the inclusions imprints is of the order of the membrane thickness a, we have chosen $d = 2 a$ . Actually, at such microscopic separations, other short-ranged interactions intervene, the details of which are still unknown. Here, we disregard them, since our interest lies in the mechanism by which the recruitment process and the formation of dynamin collars is driven. In a later stage, which we do not model here, dynamin rings are further stabilized by bio-chemical interactions [11].

The results of the Monte Carlo simulations are summarized in the phase diagram of Fig. 4, in terms of the curvatures c_cl and c_dy of the clathrins and dynamins imprints, respectively. Here, we have chosen to span c_cl between 0 to $0.2 a^{- 1}$ : for a lattice constant $b = 3 a$ and assuming a≃40 Å, this corresponds for the clathrin-coated bud to a maximum curvature of radius $ρ ≃ b / (a c_{cl}) ≃ 60 nm$ . Since our clathrin patch has seven spherical sources on its diameter, the size of the bud is $7 b ≃ 85 nm$ . These values are typical for clathrin-mediated endocytosis [6]. For the dynamins, we have spanned c_dy between $0.1 a^{- 1}$ and $0.4 a^{- 1}$ , which corresponds to a maximum curvature of the imprint ≃0.1 nm⁻¹. As for the membrane bending rigidity, we have taken $κ = 60 k_{B} T$ , since for biological membranes at room temperature κ lies between 50 and $100 k_{B} T$ [40,41].

Fig. 4
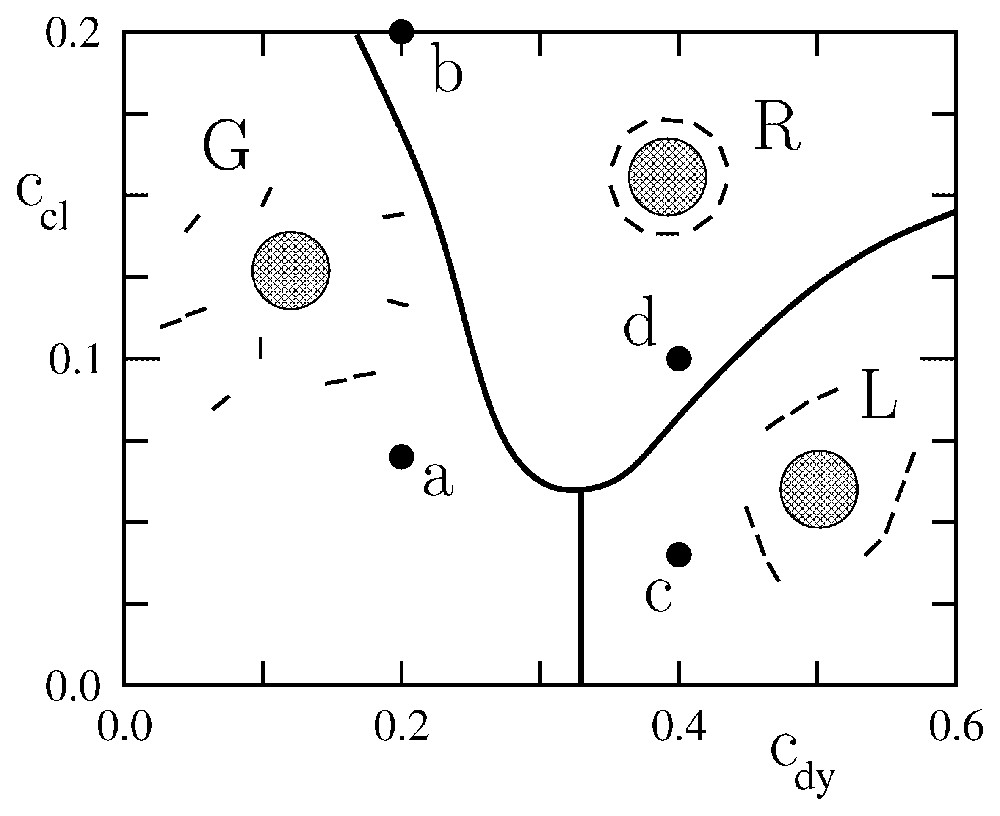
Phase diagram representing the typical equilibrium configurations of a system of model dynamins in the vicinity of a curved clathrin scaffold. c_dy and c_cl are the curvatures associated with the dynamins and clathrins, respectively, in units of the inverse membrane thickness a. In region G, the dynamins form a ‘gas’ non interacting with the clathrin scaffold. In region L, the dynamins form a system of linear oligomers non interacting with the clathrin scaffold. In region R, the dynamins form a ring around the clathrin scaffold, which is reminiscent of real endocytosis.

The phase diagram displays three regimes (see Fig. 4): a state in which the dynamins are disordered in a gas-like fashion (G), a state in which the dynamins form linear oligomers that do not interact with the clathrin bud (L), and a state in which the dynamins form a ring around the clathrin bud (R). In region (R), due to the shallowness of the dynamin imprints, the system is disordered by thermal agitation. Increasing the curvature of the dynamin imprints increases the elastic attraction between the dynamins (see Fig. 3b) and leads to the formation of linear oligomers (L). These oligomers wrap around the clathrin bud when the latter is sufficiently developed (R). Typical snapshots corresponding to the four points (a), (b), (c), (d) in Fig. 4 are shown in Fig. 5. Note that in Fig. 5b the dynamin collar is rather ‘gaseous’ due to the weakness of the dynamins' imprints, while in Fig. 5d the ring is tight and well ordered. (See also Fig. 6.)

Fig. 5
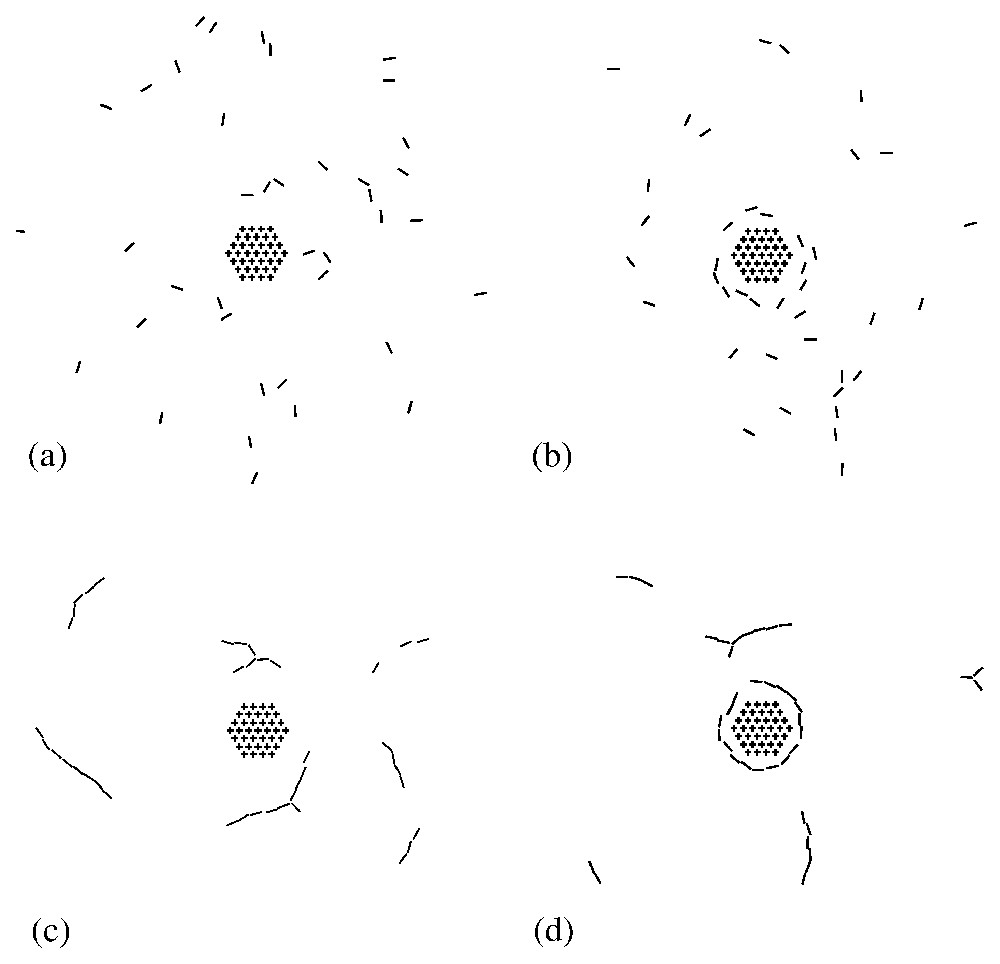
Typical snapshots showing the equilibrium arrangement of model dynamins (bars) in the vicinity of the clathrin scaffold (hexagonal array). The figures (a), (b), (c) and (d) refer to the corresponding points in the phase diagram of Fig. 4.

Fig. 6
Membrane shape corresponding to point (d) in Figs. 4 and 5, showing the self-assembly of a ring of dynamins around a clathrin bud.

It is difficult within the present paper to discuss the nature of the boundaries between the different ‘phases’ displayed in Fig. 4. Because we are considering a rather small (thermodynamically speaking) number of dynamins, and because they are under the influence of a localized curvature field, the transition lines between the various regions of Fig. 4 are actually broad. Attempting to describe them as first- or second-order transition lines should not be meaningfull.

4 Conclusion

In this paper, we have shown that if membrane-inserted dynamins produce cylindrical imprints and if the latter are sufficiently curved, then the resulting long-range forces mediated by the membrane elasticity are strong enough to overcome Brownian motion and bring them into a collar around the neck of a clathrin bud. Of course, simple diffusion could also bring dynamins around clathrin buds, and their binding into a ring could be the result of specific biochemical interactions. However, if a cylindrical imprint can speed up this process, then evolution may have selected it.

To test this model, one might look experimentally for linear oligomers of dynamins (see Fig. 5c). However, since ‘gaseous’ rings are also possible (see Fig. 5b), the existence of such linear aggregates may not be necessary. It would be more interesting to directly check, e.g., by cryo-electron microscopy, the shape of the dynamin region that penetrates within the membrane.

Finally, note that our model is obviously over-simplified: (i) many other integral proteins float around dynamins, (ii) dynamins may interact with various lipidic domains within the bilayer, (iii) the membrane may have a spontaneous curvature due to its asymmetry, (iv) fluctuations are not only thermal but also active, and hence could be larger than we estimate, and (v) large values of the membrane tension could shorten the range at which the dynamins are recruited (see Section 1). Nonetheless, we believe that our model correctly captures the effects of the anisotropic elastic interactions.

Acknowledgements

We acknowledge fruitful discussions with R. Bruinsma, F. Jülicher, F. Képès, J.-M. Delosme, B. Goud, P. Chavrier, V. Norris, and J.-M. Valleton.

Appendix A Many-body interactions between point-like curvature sources

Let us outline the derivation of the interaction between N anisotropic point-like sources that locally imprint a curvature on the membrane. As explained in the text, such constraints modelize a wide class of membrane inclusions, including transmembrane and cytosol proteins partly inserted within the membrane.

For small deformations u(x,y) with respect to the (x,y) plane, the free energy associated with the curvature elasticity of a membrane is given by [42]:

F_{el} = \frac{κ}{2} \int d x d y {(\nabla^{2} u)}^{2}

(A.1)

Indeed, for small deformations, the Laplacian ∇²u(r) is equal to the sum of the membrane's principal curvatures at point r=(x,y). The material parameter κ is the bending rigidity.

Determining the shape of the membrane in the presence of inclusions at positions r_α imprinting local curvatures requires minimizing the elastic energy (A.1) with local constraints on the membrane curvature tensor. In the small deformation limit, the elements of the latter are given by the second spatial derivatives of the membrane shape: u_,xx(r), u_,xy(r) and u_,yy(r). Introducing $3 N$ Lagrange multipliers Λ_ij^α to enforce the curvature constraints, the Euler–Lagrange equation corresponding to the constrained minimization is

\nabla^{2} \nabla^{2} u (r) = \sum_{α = 1}^{N} [Λ_{xx}^{α} δ_{, xx} (r - r_{α}) + Λ_{xy}^{α} δ_{, xy} (r - r_{α}) + Λ_{yy}^{α} δ_{, yy} (r - r_{α})]

(A.2)

where δ(r) is the two-dimensional Dirac's delta and a comma indicates derivation. By linearity, the solution of this equation is

u (r) = \sum_{μ = 1}^{3 N} Λ_{μ} Γ_{μ} (r)

(A.3)

where the Λ_μ's and Γ_μ's are the 3N components of the column matrices

Λ = (\begin{matrix} Λ_{xx}^{1} \\ Λ_{xy}^{1} \\ Λ_{yy}^{1} \\ Λ_{xx}^{2} \\ ⋮ \end{matrix}), Γ (r) = (\begin{matrix} G_{, xx} (r - r_{1}) \\ G_{, xy} (r - r_{1}) \\ G_{, yy} (r - r_{1}) \\ G_{, xx} (r - r_{2}) \\ ⋮ \end{matrix})

(A.4)

and

G (r) = \frac{1}{16 π} r^{2} \ln r^{2}

(A.5)

is the Green function of the operator ∇²∇², satisfying the equation ∇²∇²G(r)=δ(r).

We introduce a column matrix K containing the values of the 3N constraints

K = (\begin{matrix} u_{, xx} (r_{1}) \\ u_{, xy} (r_{1}) \\ u_{, yy} (r_{1}) \\ u_{, xx} (r_{2}) \\ ⋮ \end{matrix})

(A.6)

With u(r) given by equation (A.3), enforcing the constraints yields the following equation for the Lagrange multipliers:

\sum_{ν = 1}^{3 N} M_{μ ν} Λ_{ν} = K_{μ}

(A.7)

where the 3N×3N matrix M is given by

M = (\begin{matrix} 𝗆_{11} & 𝗆_{12} & \dots & 𝗆_{1 N} \\ 𝗆_{21} & 𝗆_{22} & ⋮ \\ ⋮ & ⋱ & ⋮ \\ 𝗆_{N 1} & \dots & \dots & 𝗆_{NN} \end{matrix})

(A.8)

in which the

𝗆_{α β}

's are N² matrices of size 3×3 defined by

𝗆_{α β} = (\begin{matrix} G_{, xxxx} (r_{β α}) & G_{, xxxy} (r_{β α}) & G_{, xxyy} (r_{β α}) \\ G_{, xxxy} (r_{β α}) & G_{, xxyy} (r_{β α}) & G_{, xyyy} (r_{β α}) \\ G_{, xxyy} (r_{β α}) & G_{, xyyy} (r_{β α}) & G_{, yyyy} (r_{β α}) \end{matrix})

(A.9)

where r_βα=r_α−r_β. Setting

r_{α} - r_{β} = r_{β α} [\cos θ_{α β} \hat{x} + \sin θ_{α β} \hat{y}]

(A.10)

yields explicitely

𝗆_{α β} = \frac{1}{4 π r_{β α}^{2}} (\begin{matrix} \cos (4 θ_{α β}) & \sin (2 θ_{α β}) & - \cos (4 θ_{α β}) \\ - 2 \cos (2 θ_{α β}) & \cdot [2 \cos (2 θ_{α β}) - 1] \\ \sin (2 θ_{α β}) & - \cos (4 θ_{α β}) & - \sin (4 θ_{α β}) \\ \cdot [2 \cos (2 θ_{α β}) - 1] & - \sin (2 θ_{α β}) \\ - \cos (4 θ_{α β}) & - \sin (4 θ_{α β}) & \cos (4 θ_{α β}) \\ - \sin (2 θ_{α β}) & + 2 \cos (2 θ_{α β}) \end{matrix})

(A.11)

Integrating equation (A.1) by parts and taking into account the constraints yields the elastic energy

F_{el} = \frac{1}{2} κ K^{t} M^{- 1} K

(A.12)

where K^t is the transpose of K. From equations (A.3) and (A.7), the equilibrium shape of the membrane is given by

u (r) = K^{t} M^{- 1} Γ (r)

(A.13)

When α=β, $𝗆_{α β}$ as given by equation (A.11) diverges: indeed equation (A.1) correctly describes the membrane elastic energy only for distances r≳r₀, where r₀ is of the order of the membrane thickness. It is therefore necessary to introduce a high wavevector cutoff r₀⁻¹ in the theory. From the definition of the Green function G(r), we deduce, in Fourier space

G_{, xxxx} (r) = \int \frac{d^{2} q}{{(2 π)}^{2}} \frac{q_{x}^{4} e^{i q \cdot r}}{q^{4}}

(A.14)

Hence, introducing the cutoff, we obtain

G_{, xxxx} (0) = \underset{0}{\int^{r_{0}^{- 1}}} \frac{q d q}{{(2 π)}^{2}} \underset{0}{\int^{2 π}} d θ \cos^{4} θ = \frac{3}{32 π r_{0}^{2}}

(A.15)

and similarly for the other elements of the matrix (A.9). With the above prescription, we obtain

𝗆_{α α} = \frac{1}{32 π r_{0}^{2}} (\begin{matrix} 3 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 3 \end{matrix})

(A.16)

As an illustration, let us consider the case of two identical isotropic inclusions, each prescribing the curvature c. Then

K^{t} = (c, 0, c, c, 0, c)

(A.17)

and, from equations (A.12), (A.8), (A.11), and (A.16), with r₁₂=R, the interaction energy is

F_{el} = \frac{512 π κ {(r_{0} c)}^{2}}{{(\frac{R}{r_{0}})}^{4} + 8 {(\frac{R}{r_{0}})}^{2} - 32}

(A.18)

in which we have discarded a constant term. Setting r₀=a/2, we indeed obtain the leading asymptotic interaction (1). This special choice for r₀ allows to match the result of Goulian et al. [29], which was obtained from multipolar expansions. It should be noted that the interaction given by equation (A.18) is exact within the present formalism (for r larger than ≃a), whereas multipolar expansions can only give in analytical form the leading asymptotic orders.

When many inclusions are present, the matrix M and its inverse, which determines the interaction energy through equation (A.12), can be easily calculated numerically once the positions of the inclusions are defined.

Appendix B Monte Carlo simulations

The Monte Carlo simulation that we perform employs the standard Metropolis algorithm [43]. For given positions and orientations of the particles representing the dynamins, the energy is numerically calculated from equation (A.12). At each Monte Carlo step, we perform a Metropolis move consisting in either a translation or a rotation of one arbitrarily chosen dynamin particle. The amplitude of the moves is adjusted in order to keep an average acceptance rate of 50%. We confine the dynamins inside a circular box (of radius $80 a$ ) centered around the clathrin lattice, which is kept fixed. To take into account the hard-core repulsion (see Section 3), we simply reject any move bringing two particles closer than the minimum approach distance d (here $2 a$ ). Note that in this simulation the membrane is not discretized: the interaction energy that we use fully takes into account the elasticity of the membrane.

Bibliographie

[1] H. Lodish; A. Berk; S.L. Zipursky; P. Matsudaira; D. Baltimore; J.E. Darnell Molecular Cell Biology, W.H. Freeman & Co, New York, 1999

[2] C.J. Smith; N. Grigorieff; B.M. Pearse Clathrin coats at 21-angstrom resolution: a cellular assembly designed to recycle multiple membrane receptors, EMBO J., Volume 17 (1998), pp. 4943-4953

[3] B.M.F. Pearse; M.S. Robinson Clathrin, adapters, and sorting, Annu. Rev. Cell Biol., Volume 6 (1990), pp. 151-171

[4] J.E. Rothman Mechanism of intracellular protein transport, Nature, Volume 372 (1994), pp. 55-63

[5] R. Schekman; L. Orci Coat proteins and vesicle budding, Science, Volume 271 (1996), pp. 1526-1533

[6] M. Marsh; H.T. McMahon Cell biology – The structural era of endocytosis, Science, Volume 285 (1999), pp. 215-220

[7] K. Takei; V. Haucke Clathrin-mediated endocytosis: membrane factors pull the trigger, Trends Cell Biol., Volume 11 (2001), pp. 385-391

[8] S.L. Schmid; M.A. McNiven; P. De Camilli Dynamin and its partners: a progress report, Curr. Opin. Cell Biol., Volume 10 (1998), pp. 504-512

[9] J.E. Hinshaw; S.L. Schmid Dynamin self-assembles into rings suggesting a mechanism for coated vesicle budding, Nature, Volume 374 (1995), pp. 190-192

[10] K. Takei; P.S. McPherson; S.L. Schmid; P. De Camilli Tubular membrane invaginations coated by dynamin rings are induced by GTP-Gamma-S in nerve-terminals, Nature, Volume 374 (1995), pp. 186-190

[11] J.E. Hinshaw Dynamin and its role in membrane fission, Annu. Rev. Cell Dev. Biol., Volume 16 (2000), pp. 483-519

[12] D. Danino; J.E. Hinshaw Dynamin family of mechanoenzymes, Curr. Opin. Cell Biol., Volume 13 (2001), pp. 454-460

[13] K. Takei; V. Haucke; V. Slepnev; K. Farsad; M. Salazar; H. Chen; P. De Camilli Generation of coated intermediates of clathrin-mediated endocytosis on protein-free liposomes, Cell, Volume 94 (1998), pp. 131-141

[14] K.M. Huang; K. D'Hondt; H. Riezman; S.K. Lemmon Clathrin functions in the absence of heterotetrameric adaptors and AP180-related proteins in yeast, EMBO J., Volume 18 (1999), pp. 3897-3908

[15] S.M. Sweitzer; J.E. Hinshaw Dynamin undergoes a GTP-dependent conformational change causing vesiculation, Cell, Volume 93 (1998), pp. 1021-1029

[16] M.H.B. Stowell; B. Marks; P. Wigge; H.T. Mc Mahon Nucleotide-dependent conformational changes in dynamin: evidence for a mechanochemical molecular spring, Nat. Cell Biol., Volume 1 (1999), pp. 27-32

[17] B. Marks; M.H.B. Stowell; Y. Vallis; I.G. Mills; A. Gibson; C.R. Hopkins; H.T. Mc Mahon GTPase activity of dynamin and resulting conformation change are essential for endocytosis, Nature, Volume 410 (2001), pp. 231-235

[18] P.L. Tuma; M.C. Stachniak; C.A. Collins Activation of dynamin GTPase by acidic phospholipids and endogenous rat-brain vesicles, J. Biol. Chem., Volume 268 (1993), pp. 17240-17246

[19] J.P. Liu; K.A. Powell; T.C. Sudhof; P.J. Robinson Dynamin-I is a Ca²⁺-sensitive phospholipid-binding protein with very high affinity for protein-kinase-C, J. Biol. Chem., Volume 269 (1994), pp. 21043-21050

[20] H.C. Lin; B. Barylko; M. Achiriloaie; J.-P. Albanesi Phosphatidylinositol (4,5)-bisphosphate-dependent activation of dynamins I and II lacking the proline/arginine-rich domains, J. Biol. Chem., Volume 272 (1997), pp. 25999-26004

[21] Y. Vallis; P. Wigge; B. Marks; P.R. Evans; H.T. Mc Mahon Importance of the pleckstrin homology domain of dynamin in clathrin-mediated endocytosis, Curr. Biol., Volume 9 (1999), pp. 257-260

[22] A. Lee; D.W. Frank; M.S. Marks; M.A. Lemmon Dominant-negative inhibition of receptor-mediated endocytosis by a dynamin-1 mutant with a defective pleckstrin homology domain, Curr. Biol., Volume 9 (1999), pp. 261-264

[23] K.N.J. Burger; R.A. Demel; S.L. Schmid; B. de Kruijff Dynamin is membrane-active: lipid insertion is induced by phosphoinositides and phosphatidic acid, Biochemistry, Volume 39 (2000), pp. 12485-12493

[24] P.J. Zhang; J.E. Hinshaw Three-dimensional reconstruction of dynamin in the constricted state, Nat. Cell Biol., Volume 3 (2001), pp. 922-926

[25] H. Gruler Chemoelastic effect of membranes, Z. Naturforsch. C, Volume 30 (1975), pp. 608-614

[26] H. Gruler; E. Sackmann Long-range protein–protein interaction in membranes, Croat. Chem. Acta, Volume 49 (1977), pp. 379-388

[27] C.E. Morris; U. Homann Cell surface area regulation and membrane tension, J. Membr. Biol., Volume 179 (2001), pp. 102-179

[28] N. Gov; A.G. Zilman; S.A. Safran Cytoskeleton confinement of red blood cell membrane fluctuations (2002) | arXiv

[29] M. Goulian; R. Bruinsma; P. Pincus Long-range forces in heterogeneous fluid membranes, Europhys. Lett., Volume 22 (1993), pp. 145-150

[30] J.-B. Fournier; P.G. Dommersnes Long-range forces in heterogeneous fluid membranes – Comment, Europhys. Lett., Volume 39 (1997), pp. 681-682

[31] Y. Bouligand Geometry and topology of cell membranes (J.-F. Sadoc, ed.), Geometry in condensed matter physics, World Scientific, Singapore, 1990, pp. 193-229

[32] J.-B. Fournier Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions, Phys. Rev. Lett., Volume 76 (1996), pp. 4436-4439

[33] V. Kralj-Iglič; V. Heinrich; S. Svetina; B. Žekš Free energy of closed membrane with anisotropic inclusions, Eur. Phys. J. B, Volume 10 (1999), pp. 5-8

[34] J.M. Park; T.C. Lubensky Interactions between membrane inclusions on fluctuating membranes, J. Phys. I, Volume 6 (1996), pp. 1217-1235

[35] P.G. Dommersnes; J.-B. Fournier N-body study of anisotropic membrane inclusions: membrane mediated interactions and ordered aggregation, Eur. Phys. J. B, Volume 12 (1999), pp. 9-12

[36] T. Chou; K.S. Kim; G. Oster Statistical thermodynamics of membrane bending-mediated protein–protein attractions, Biophys J., Volume 80 (2001), pp. 1075-1087

[37] K.S. Kim; J.C. Neu; G.F. Oster Many-body forces between membrane inclusions: a new pattern-formation mechanism, Europhys. Lett., Volume 48 (1999), pp. 99-105

[38] K.S. Kim; J. Neu; G. Oster Effect of protein shape on multibody interactions between membrane inclusions, Phys. Rev. E, Volume 61 (2000), pp. 4281-4285

[39] P.G. Dommersnes; J.-B. Fournier The many-body problem for anisotropic membrane inclusions and the self-assembly of ‘saddle’ defects into an ‘egg-carton’, Biophys. J., Volume 83 (2002), pp. 2898-2905

[40] J.B. Song; R.E. Waugh Bending rigidity of SOPC membranes containing cholesterol, Biophys. J., Volume 64 (1993), pp. 1967-1970

[41] H. Strey; M. Peterson Measurement of erythrocyte-membrane elasticity by flicker eigenmode decomposition, Biophys. J., Volume 69 (1995), pp. 478-488

[42] W. Helfrich Elastic properties of lipid bilayers – Theory and possible experiments, Z. Naturforsch. C, Volume 28 (1973), pp. 693-703

[43] N. Metropolis; A.W. Rosenbluth; M.N. Rosenbluth; A.H. Teller; E. Teller Equation of state calculations by fast computing machines, J. Chem. Phys., Volume 21 (1953), pp. 1087-1092

Commentaires - Politique