Abridged English version
1 Introduction
Age estimation from skeletal indicators is of major interest for both past and actual populations. Concerning children, several methods have already been established on the basis of dental maturation processes. Some of them are using the dental eruption sequence, while others are based on measurements and calculations. Nevertheless, the majority of these methods suffer from lack of precision and inter-observer variability. The aim of this work is to propose a probabilistic approach and to compare two methods of age estimation (discriminant functions and Bayesian approach), which can both be applied during clinical or radiological examinations. Our method is simply based on the count of erupted teeth, which is known to be almost independent from environmental factors, and on the classification into age groups.
2 Material and methods
2.1 Apprenticeship sample
The apprenticeship sample was constituted in the dental care service of a hospital in Marseilles (France). This sample was composed by 810 radiographs, belonging to 397 males (49%) and 413 females (51%). The mean age in the global sample is 12.63 and range was 6.10 to 21.08. The selected individuals had no missing teeth and the first molar was erupted. Intra- and inter-observer tests revealed no significant differences to the threshold of 5%. The count of the erupted teeth was realised by two different observers in order to validate the methodology. The radiological criterion used to state tooth eruption was the fact that the line passing by the crown's cusps was higher than the line joining the cemento-enamel junctions of the mesial and distal borders of the adjacent teeth. The number of germs corresponding to Demirjian's A level (mineralised crown) was also taken into account. The determination score for germs, following the Demirjian's methodology, and emerged teeth was established on the 16 mandibular teeth seen in 25 and 15 X-ray pictures for intra- and inter-observer tests respectively. The studied variables were age (AGE), the number of upper and lower permanent incisors (INCSUPDEF and INCINFDEF), cuspids (CANSUPDEF and CANINFDEF), bicuspids (PMSUPDEF and PMINFDEF), first molars (MSIXSUP and MSIXINF), second molars (MDOUZESUP and MDOUZEINF), wisdom teeth (DSSUP and DSINF), as well as upper and lower deciduous (INCSUPTEMP and INCINFTEMP), cuspids (CANSUPTEMP and CANINFTEMP), molars (MSUPTEMP and MINFTEMP), and the number of present germs except wisdom teeth, and the number of wisdom teeth (GERMES and DSGERMES, respectively).
2.2 Discriminant functions
The ages in the global sample were discretised according to legal age limits, i.e., 13, 16, and 18 years old. For each threshold, four Fisher's linear functions were established depending on the variables kept by stepwise ascending discriminant analysis. In order to establish the models, we sequentially proposed to analyse all variables (models 13/C, 16/C, 18/C), all the variables except that of germs (models 13/SG, 16/SG, 18/SG), maxillary variables except that of germs (13/MAX, 16/MAX, 18/MAX), mandibular variables, except that of germs (models 13/MD, 16/MD, 18/MD).
2.3 Bayesian approach
The learning sample was utilised as reference database for the calculation of the posterior probability to belong to a specific age group. We conducted our study following two age-assessment strategies: first, we classified the children into 1-year age groups (ranging 6 to 21 years old); then, we used legal age groups (< 13, between 13 and 16, between 16 and 18, > 18 years old).
2.4 Test sample
The test sample was composed by the panoramic radiographs of 290 children. This test sample was different from the learning sample, since it was coming from two dental care services: 190 originating from Marseille and 100 from Dijon. The mean age was 12.11 years old, ranging from 6.56 to 20.23. These X-rays belonged to 143 males (49.3%) and 147 females (50.7%).
2.5 Data analysis
The chronological ages were calculated with Epi-Info® (CDC/ENSP).
Fisher's linear functions were obtained by stepwise ascending discriminant analysis on Systat 8.0® (SPSS Inc.).
Bayesian approach results were obtained using Excel 2000® (Microsoft) to automate the database management and calculations.
For each child, we obtained the probability to belong to a specific age group, defined as above or below chosen threshold (13, 16, or 18 years old) with Fisher's linear functions and Bayesian approach, too.
This age estimation was then compared to real age and the accuracy of the prediction was assessed in percentages.
3 Results
The discriminant approach gave more than 90% of good prediction for the three used thresholds (13, 16, 18). Since the Bayesian approach did not allow a better classification score than 85%.
1 Introduction
La détermination de l'âge à partir d'estimateurs squelettiques est une problématique anthropobiologique qui s'applique à la fois aux populations du passé et aux populations actuelles. Ses enjeux concernent la paléodémographie, l'archéologie, la médecine et l'odontologie légale, tant pour le sujet vivant que pour l'identification individuelle de restes. Chez l'enfant, différentes méthodes d'estimation de l'âge ont été proposées à partir de l'analyse des modes de maturation dentaire. Cela passe par l'utilisation de planches comme celles d'Ubelaker [1], qui schématisent et résument les séquences types d'éruption à différents âges clés. On peut également appliquer des méthodes de calcul comme la méthode Demirjian littérale ou simplifiée, plus ou moins fiable suivant les populations et limité au plafond des 16 ans [2–6]. Néanmoins, on se heurte au problème de la précision de l'estimation, dû à la méthode employée, mais aussi aux observateurs [7–9]. Des diagrammes pour lecture de l'âge ou des âges moyens d'éruption ont même été proposés [10–13]. Il a été démontré qu'il est meilleur de se baser sur un phénomène à courte période, comme l'éruption dentaire [14,15]. De plus, les facteurs environnementaux influent moins sur le développement dentaire que sur le développement physique général, tandis que les séquences d'éruption dentaire chez l'enfant sont largement indépendantes de l'influence du milieu et que le comptage des dents présentes en bouche peut procurer une estimation relativement précise non biaisée de l'âge, meilleure que la mesure de la taille, équivalente à la méthode Demirjian [16–18]. Le but de notre travail est de proposer deux types d'outils statistiques prédictifs de l'estimation de l'âge chez l'enfant : les fonctions discriminantes de Fisher et l'approche bayésienne automatisée.
2 Matériel et méthodes
2.1 Échantillon d'apprentissage
Un échantillon d'apprentissage a été constitué dans un service hospitalier d'odontologie, comprenant 810 radiographies panoramiques de 397 garçons (49,0 %) et 413 filles (51,0 %), de 12,63 ans de moyenne d'âge, compris entre 6,10 et 21,08 ans. Les sujets retenus étaient indemnes de dents absentes pour extractions ou agénésies ou de dents trop délabrées et présentaient une première molaire définitive en place. La faisabilité de l'attribution des scores selon la méthode Demirjian a été vérifiée ; les 16 dents mandibulaires de 25 et 15 radiographies panoramiques ont été cotées respectivement pour une comparaison intra-observateur et inter-observateurs : aucune différence significative n'a été mise en évidence entre les séries de cotations (tests t). Néanmoins, par précaution, le nombre de chaque type de dents émergées sur radiographie a été relevé simultanément par deux observateurs. Le critère d'émergence radiologique d'une dent a été défini par le fait que la ligne passant par les pointes cuspidiennes de sa couronne devait dépasser la ligne joignant les jonctions émail-cément mésiale et distale de la ou des dents adjacentes. Le nombre de germes présents a été également relevé. Le germe était réputé présent au stade de minéralisation de la couronne, c'est-à-dire au stade A de Demirjian. Pour améliorer la précision de l'estimation de l'âge que n'offre pas suffisamment Ubelaker, nous avons choisi de distinguer les variables dentaires pour chaque type de dents (incisives, canines, prémolaires), déciduales et permanentes, maxillaires et mandibulaires ; les molaires permanentes, ayant des séquences d'éruption plus spécifiques, ont été individualisées (1res molaires, 2es molaires, dents de sagesse). En définitive, les variables de l'étude ont été l'âge (AGE), le nombre d'incisives supérieures et inférieures définitives (INCSUPDEF et INCINFDEF), de canines supérieures et inférieures définitives (CANSUPDEF et CANINFDEF), de prémolaires supérieures et inférieures (PMSUP et PMINF), de 1res molaires supérieures et inférieures définitives (MSIXSUP et MSIXINF), de 2es molaires supérieures et inférieures définitives (MDOUZESUP et MDOUZEINF), de dents de sagesse supérieures et inférieures (DSSUP et DSINF), d'incisives supérieures et inférieures temporaires (INCSUPTEMP et INCINFTEMP), de canines supérieures et inférieures temporaires (CANSUPTEMP et CANINFTEMP), de molaires supérieures et inférieures temporaires (MSUPTEMP et MINFTEMP), de germes présents, excepté ceux des dents de sagesse (GERMES), et de germes de dents de sagesse présents (DSGERMES).
2.1.1 Modèles discriminants
L'échantillon a été ordonné, en fonction de l'âge réel des enfants, en deux classes d'âge selon les seuils 13, 16 et 18 ans. Pour chaque seuil, des modèles de fonctions linéaires de Fisher ont été obtenus par fonctions discriminantes à triage pas à pas ascendant, la méthode de sélection des variables étant la minimisation de la variance résiduelle ; à chaque étape, la variable qui minimise la somme des carrés des variations non expliqués entre les groupes est sélectionnée avec le critère d'introduction F, fixé à p=0,05. Suivant les variables de départ proposées, nous obtenons quatre modèles, à partir de toutes les variables (modèles 13/C, 16/C, 18/C), à partir de toutes les variables, sauf celles concernant les germes (modèles 13/SG, 16/SG, 18/SG), à partir des variables maxillaires, sauf celles concernant les germes (modèles 13/MAX, 16/MAX, 18/MAX), à partir des variables mandibulaires sauf celles concernant les germes (modèles 13/MD, 16/MD, 18/MD). Ces modèles permettront de prédire la probabilité a priori d'appartenance d'un enfant à une classe d'âge, c'est-à-dire s'il se situe au-dessus ou en dessous du seuil considéré de 13, 16, ou 18 ans (Tableaux 1–3).
Fonctions linéaires de Fisher et pourcentages de classement en fonction du seuil de 13 ans
| Variables | Classes d'âge | |||||||
| retenues dans | < 13 ans | > 13 ans | ||||||
| le modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle |
| 13/C | 13/SG | 13/MAX | 13/MD | 13/C | 13/SG | 13/MAX | 13/MD | |
| Constante | −111,398 | −111,398 | −0,995 | −7,776 | −112,712 | −112,712 | −5,642 | −12,997 |
| CANSUPDEF | 1,170 | 1,170 | 1,107 | 1,964 | 1,964 | 1,898 | ||
| MSIXSUP | 110,332 | 110,332 | 108,68 | 108,608 | ||||
| MDOUZESUP | 0,535 | 0,535 | 0,347 | 2,922 | 2,922 | 2,764 | ||
| DSSUP | 1,840 | 1,840 | −4,542×10−2 | 2,514 | 2,514 | 1,505 | ||
| CANINFTEMP | 7,732 | 8,317 | ||||||
| PMINF | 4,041 | 4,870 | ||||||
| MDOUZEINF | 0,929 | 2,351 | ||||||
| DSINF | −3,260 | −3,260 | −0,139 | −1,978 | −1,978 | 1,534 | ||
| % d'enfants | 73,8 | 73,8 | 72,8 | 73,3 | 94,0 | 94,0 | 94,0 | 91,7 |
| bien classés | ||||||||
| % d'erreurs de | 26,2 | 26,2 | 27,2 | 26,7 | 6,0 | 6,0 | 6,0 | 8,3 |
| classement |
Fonctions linéaires de Fisher et pourcentages de classement en fonction du seuil de 16 ans
| Variables | Classes d'âge | |||||||
| retenues dans le | < 16 ans | > 16 ans | ||||||
| modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle |
| 16/C | 16/SG | 16/MAX | 16/MD | 16/C | 16/SG | 16/MAX | 16/MD | |
| Constante | −115,578 | −111,725 | −110,563 | −1,324 | −114,168 | −111,235 | −111,178 | −6,348 |
| CANSUPTEMP | 4,158 | 3,752 | ||||||
| MSIXSUP | 110,631 | 111,014 | 109,862 | 107,861 | 108,165 | 107,909 | ||
| MDOUZESUP | 3,614 | 1,810 | 1,729 | 4,944 | 3,159 | 3,141 | ||
| DSSUP | 2,547 | 1,466 | −1,108 | 3,758 | 2,918 | 2,348 | ||
| CANINFTEMP | ||||||||
| PMINF | 0,992 | 1,226 | ||||||
| MDOUZEINF | −7,773×10−2 | 0,742 | ||||||
| DSINF | −3,552 | −4,450 | −4,526×10−2 | −0,319 | −0,987 | 4,089 | ||
| DSGERMES | 1,192 | 0,895 | ||||||
| % d'enfants | 98,4 | 98,0 | 98,0 | 99,2 | 43,2 | 45,9 | 29,7 | 37,8 |
| bien classés | ||||||||
| % d'erreurs de | 1,6 | 2,0 | 2,0 | 0,8 | 56,8 | 54,1 | 70,3 | 62,2 |
| classement |
Fonctions linéaires de Fisher et pourcentages de classement en fonction du seuil de 18 ans
| Variables | Classes d'âge | |||||||
| retenues dans | < 18 ans | > 18 ans | ||||||
| le modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle | Modèle |
| 18/C | 18/SG | 18/MAX | 18/MD | 18/C | 18/SG | 18/MAX | 18/MD | |
| Constante | −111,583 | −111,076 | −0,644 | −0,805 | −112,391 | −112,235 | −6,637 | −6,953 |
| MSIXSUP | 110,213 | 110,408 | 107,480 | 107,589 | ||||
| MDOUZESUP | 1,661 | 2,272 | 1,121 | 2,637 | 2,976 | 2,033 | ||
| DSSUP | 1,889 | 1,360 | 3,662×10−2 | 4,584 | 4,291 | 5,085 | ||
| MDOUZEINF | 1,286 | 1,909 | ||||||
| DSINF | −3,150 | −3,756 | −1,626×10−2 | 0,160 | −0,176 | 4,993 | ||
| DSGERMES | 0,732 | 0,406 | ||||||
| % d'enfants | 97,4 | 97,4 | 97,8 | 97,1 | 62,5 | 68,8 | 62,5 | 50,0 |
| bien classés | ||||||||
| % d'erreurs | 2,6 | 2,6 | 2,2 | 2,9 | 37,5 | 31,3 | 37,5 | 50,0 |
| de classement |
Par exemple, en présence de données maxillaires uniquement, l'application des deux formules suivantes :
- • −110,563+(109,862×nombre de 1res molaires définitives maxillaires émergées) + (1,729×nombre de 2es molaires définitives maxillaires émergées) − (1,108×nombre de dents de sagesse maxillaires émergées) pour l'appartenance à la classe d'âge inférieure à 16 ans ;
- • −111,780+(107,909×nombre de 1re molaires définitives maxillaires émergées) + (3,141×nombre de 2es molaires définitives maxillaires émergées) + (2,348×nombre de dents de sagesse maxillaires émergées) pour l'appartenance à la classe d'âge supérieure à 16 ans ; permettra de situer l'enfant expertisé par rapport à ce seuil, en fonction de l'équation ayant obtenu le score le plus élevé.
2.1.2 Approche bayésienne
L'échantillon d'apprentissage a constitué la base de données aux calculs bayésiens de probabilité a posteriori d'appartenance à un intervalle d'âge. Nous avons choisi de pratiquer l'étude selon deux rangements, d'une part, en fonction de classes d'un an, entre 6 et 21 ans, d'autre part, en classes dites légale, c'est-à-dire classes d'âge en dessous de 13 ans, entre 13 ans inclus et 16 ans, entre 16 ans inclus et 18 ans, et égal ou au-dessus de 18 ans. La probabilité a posteriori est proportionnelle à la probabilité a priori multipliée par le maximum de vraisemblance : le modèle bayésien fait un comparatif de la fréquence de chaque caractère dans chaque classe d'âge avec tous les individus de la base de données, dans notre cas l'échantillon d'apprentissage, qui représente les valeurs possibles de référence [19,20]. Nous avons utilisé pour cela un progiciel, conçu au laboratoire, qui nous a permis d'automatiser les relevés des variables par individu de l'échantillon de validation et, à partir de la base de données constituée par les enfants de l'échantillon d'apprentissage, d'obtenir les probabilités d'appartenance aux classes d'âge considérées pour l'échantillon test. La procédure pour chaque sujet était la suivante : sur écran, tout d'abord choix de l'intervalle de classes d'âge souhaité (classes d'un an ou classes « légales »), et de l'âge initial du balayage de la séquence des classes ; ensuite saisie des valeurs de chaque variable. La probabilité a posteriori était obtenue, en temps réel, par classes d'âge en données numériques et en diagrammes en bâtons (Fig. 1). Le logiciel permet également d'accepter des données incomplètes en l'absence d'information pour certaines variables (pour une dent : son absence ; pour les germes : l'absence de radiographie à disposition). En effet, nous pouvons désactiver certaines variables qui ne seront plus prises en compte dans la base de données. Le logiciel calculera ainsi les probabilités a posteriori comme si elles n'avaient jamais existé ; toutefois, cela diminuera sensiblement la qualité des prédictions, en se privant du pouvoir prédictif de départ. Il est à noter que pour notre étude nous n'avons pas eu recours à des données incomplètes.
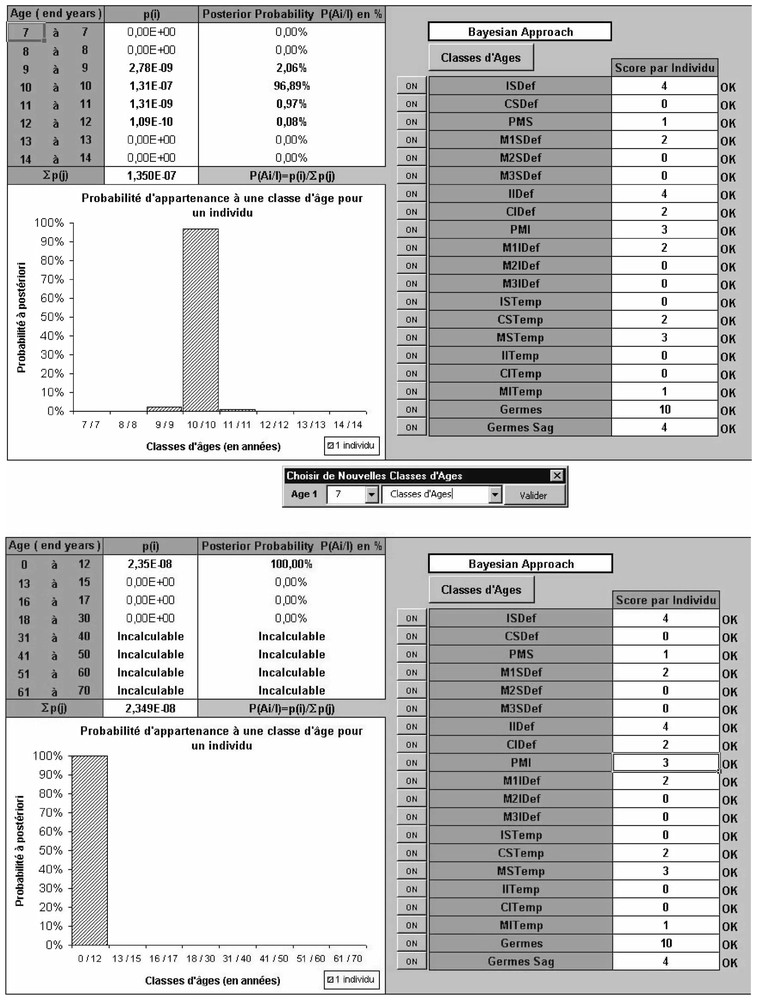
Interface du progiciel d'approche bayesienne selon les classes d'âges de 1 an (en haut) et selon les classes dites légales (en bas). Note: on lit que l'enfant se situe pour l'écran supérieur entre 9 et 12 ans (p=2,06+96,89+0,97+0,08=100%) et pour l'écran inférieur en dessous de 13 ans (p=100%).
2.2 Échantillon de test
Un échantillon de test a été constitué, comprenant 290 enfants, différents de l'échantillon d'apprentissage, d'âge connu, fréquentant deux services hospitaliers d'odontologie (190 à Marseille, 100 à Dijon), d'une moyenne d'âge de 12,11 ans, compris entre 6,56 et 20,23 ans, composée de 143 garçons (49,3 %) et de 147 filles (50,7 %).
2.3 Analyse des données
Les âges réels connus des enfants des échantillons ont été calculés en années et en décimales sur le logiciel EPI INFO® (CDC/ENSP).
Le dépouillement des radiographies panoramiques a permis d'estimer pour chaque enfant une probabilité a priori d'appartenance à une classe d'âge selon les modèles discriminants, en fonction de la distribution à deux classes, aux seuils de 13, 16 et 18 ans, et une probabilité a posteriori d'appartenance à un intervalle d'âge en fonction des deux classements d'âge établis selon l'approche bayésienne (soit en classe de 1 an, soit en 3 classes : < 13 ans, compris entre 13 et 16 ans, compris entre 16 et 18 ans, > 18 ans).
Après quoi, le pourcentage de bien classés (et d'erreurs) par rapport à l'âge réel connu a été calculé pour les différents modèles aux différents seuils, et pour les approches bayésiennes.
Le seuil de 5 % a été fixé pour le triage pas à pas ascendant des variables dans les différents modèles discriminants ; les fonctions linéaires de Fischer ont été obtenues avec le logiciel Systat 8.0® (SPSS).
La probabilité a posteriori à 100 % a été retenue pour les prédictions bayésiennes ; le progiciel, permettant les calculs automatisés, a été conçu à partir du logiciel Excel® (Microsoft).
3 Résultats
3.1 Modèles discriminants
Les fonctions de Fisher obtenues quels que soient les modèles permettent d'obtenir des prédictions de bien classés au-dessus du seuil de 13 ans, entre 91,7 et 94 %, au-dessous du seuil de 16 ans, entre 98 et 99,2 %, et au-dessous du seuil de 18 ans, entre 97,1 et 97,8 %. En revanche, les erreurs de classement en dessous du seuil de 13 ans et au-dessus des seuils de 16 et 18 ans sont très importantes, respectivement supérieures à 26, 54, 31 %.
3.2 Approche bayesienne
La prédiction selon les classes d'âge d'un an a permis de prédire correctement l'appartenance à un intervalle d'âge de 86,5 % des enfants. Par le rangement en classes légales, on a atteint 85,2 % d'enfants bien classés.
4 Discussion–conclusion
L'estimation de l'âge est un problème fondamental en anthropologie biologique, où l'odontologie propose des réponses. En effet, le développement dentaire est une bonne source d'indication de l'âge chez l'enfant [21] ; l'éruption gingivale fait partie du développement dentaire, elle sert d'estimateur de l'âge. Les modèles discriminants proposés selon le rangement en deux classes permettent de répondre aux questions du franchissement du seuil de 13 ans et du non-franchissement des seuils de 16 et 18 ans, avec un taux de bon classement supérieur à 90 % ; l'approche bayesienne automatisée propose une appartenance à une classe d'âge avec un bon classement inférieur à 85 %.
Nous offrons donc la possibilité de proposer, quelle que soit la situation envisagée, c'est-à-dire existence ou pas de radiographies panoramiques, présence de restes squelettiques incomplets maxillaires ou mandibulaires, la probabilité d'appartenance à une classe d'âge en fonction du seuil d'âge choisi. La mise au point de ces protocoles de détermination d'âge chez l'enfant permet d'offrir une nouvelle approche originale, en proposant une nouvelle méthode probabiliste couvrant la période de 6 à 20 ans. Elle présente un complément à la méthode d'Ubelaker [1]. Elle permet tout à la fois de satisfaire aux contraintes des médecins légistes en ce qui concerne la question du franchissement des seuils de responsabilité pénale par les enfants mis en cause, et de fournir aux anthropologues une transcription lisible des qualificatifs d'immature, d'enfant ou de jeune adulte. Ceci permet de répondre aux interrogations des autorités judiciaires et policières sur l'âge de l'enfant vivant ou décédé, et des anthropologues sur l'âge de l'enfant au décès à partir de restes de populations du passé.


