1 Introduction
There is growing evidence that future research on neural systems and higher brain functions will be a combination of classical (sometimes called reductionist) neuroscience with the more recent nonlinear science. This conclusion will remain valid despite the difficulties in applying the tools and concepts developed to describe low dimensional and noise-free mathematical models of deterministic chaos to the brain and to biological systems. Indeed, it has become obvious in a number of laboratories over the last two decades that the different regimes of activities generated by nerve cells, neural assemblies and behavioral patterns, their linkage and their modifications over time cannot be fully understood in the context of any ‘integrative’ physiology without using the tools and models that establish a connection between the microscopic and the macroscopic levels of the investigated processes.
Part I of this review [1] was focused on briefly presenting the fundamental aspects of nonlinear dynamics, the most publicized aspect of which is chaos theory. More fundamental text books can also be consulted by mathematically oriented reader [2–5]. After a general history and definition of this theory we described the principles of analysis of time series in phase spaces and the general properties of dynamic trajectories as well as the ‘coarse-grained’ measures, which permit a process to be classified as chaotic in ideal systems and models. We insisted on how these methods need to be adapted for handling biological time series and on the pitfalls faced when dealing with non stationary and most often noisy data. Special attention was paid to two fundamental issues.
The first was whether, and how, one can distinguish deterministic patterns from stochastic ones. This question is particularly important in the nervous system where variability is the rule at all levels of organization [6] and where for example time series of synaptic potentials or trains of spikes are often qualified as conforming to Poisson distributions on the basis of standard inter event histograms (see also [7]). Yet this conclusion can be ruled out if the same data are analyzed in depth with nonlinear tools such as first or second order return maps and using the above-mentioned measures confronted with those of randomly shuffled data called surrogates. The critical issue is here to determine if intrinsic variability, which is an essential ingredient of successful behavior and survival in living systems, reflects true randomness or if it is produced by an apparently stochastic underlying determinism and order. In other words how can the effects of ‘noise’ be distinguished from those resulting from a small number of interacting nonlinear elements. In the latter case they also appear as highly unpredictable but their advantage is that they can be dissected out and the physical correlates of their interacting parameters can be identified physiologically.
The second issue concerned the possible benefits of chaotic systems over stochastic processes, namely of the possibility to control the former. Theoretically such a control can be achieved by taking advantage of the sensitivity of chaotic trajectories to initial conditions and to ‘redirect them’, with a small perturbation, along a selected unstable periodic orbit, toward a desired state. A related and almost philosophical problem, which we will not consider further, is whether the output of a given organism can be under its own control as opposed to being fully determined by ‘in-principle-knowable causal factors’ [6]; The metaphysical counterpart of this query consists in speculating, as did number of authors, about the existence and nature of free-will [8,9]...
In the present part II of this review, we will critically examine most of the results obtained at the level of single cells and their membrane conductances, in real networks and during studies of higher brain functions, in the light of the most recent criteria for judging the validity of claims for chaos. These constraints have become progressively more rigorous particularly with the advent of the surrogate strategy (which however can also be misleading (references in [1])). Thus experts can easily argue that some early ‘demonstrations’ of deterministic chaos founded on weak experimental evidence were accepted without sufficient analysis [9]. But this is only one side of the story. Indeed we will see that the tools of nonlinear dynamics have become irreplaceable for revealing hidden mechanisms subserving, for example, neuronal synchronization, periodic oscillations and also for studies of cognitive functions and behavior viewed as dynamic phenomena rather than processes that one can study in isolation from their environmental context.
The history of the search for chaos in the nervous system, of its successes and its errors, and of the advent of what has become neurodynamics is truly fascinating. It starts in the 1980s (see [10]) with the observation that when rabbits inhale an odorant, their EEGs display oscillations in the high-frequency range of 20–80 Hz that Bressler and Freeman [11] named ‘gamma’ in analogy to the high end of the X-ray spectrum! Odor information was then shown to exist as a pattern of neural activity that could be discriminated whenever there was a change in the odor environment or after training. Furthermore the ‘carrier wave’ of this information was aperiodic. Further dissection of the experimental data led to the conclusion that the activity of the olfactory bulb is chaotic and may switch to any desired) perceptual state (or attractor) at any time. To compensate for experimental limitations the olfactory bulb was then simulated by constructing arrays of local oscillators interconnected by excitatory synapses that generated a common waveform. The inclusion of inhibitory cells and synapses facilitated the emergence of amplitude fluctuations in the waveform. Learning could strengthen the synapses between oscillators and favored the formation of Hebbian nerve cell assemblies in a self-regulatory manner which opened new ways of thinking about the nature of perception and of storing ‘representations’ of the outside world.
This complementary, experimental and theoretical approach of Freeman and his collaborators was similar to that of other authors searching for chaos, during the same period, in the temporal structure of the firing patterns of squid axons, of invertebrate pacemaker cells and of temporal patterns of human epileptic EEGs. We will show that regardless of today's judgment on their hasty conclusions and naive enthusiasm that relied on ill-adapted measures for multidimensional and noisy systems these precursors had amazingly sharp insights. Not only were their conclusions often vindicated with more sophisticated methods but they blossomed, more recently, in the form of the dynamical approach of brain operations and cognition.
We have certainly omitted several important issues from this general overview which is largely a chronological description of the successes, and occasional disenchantments, of this still evolving field. One can mention the problem of the stabilization of chaos by noise, of the phylogeny and evolution of neural chaotic systems, whether or not coupled chaotic systems behave as one and the nature of their feedbacks, to name a few. These issues will most likely be addressed in depth in the context of research on the complex systems, to which the brain obviously belongs.
2 Subcellular and cellular levels
Carefully controlled experiments during which it was possible to collect large amounts of stationary data have unambiguously demonstrated chaotic dynamics at the level of neurons systems This conclusion was reached using classical intracellular electrophysiological recordings of action potentials in single neurons, with the additional help of macroscopic models. These models describe the dynamical modes of neuronal firing and enable a comparison of results of simulations with those obtained in living cells. On the other hand and at a lower level of analysis, the advent of patch clamp techniques to study directly the properties of single ion channels did not make it necessary to invoke deterministic equations to describe the opening and closing of these channels which show the same statistical features as random Markov processes [12,13], although deterministic chaotic models may be consistent with channel dynamics [7,14,15].
It is generally believed that information is secured in the brain by trains of impulses, or action potentials, often organized in sequences of bursts. It is therefore essential to determine the temporal patterns of such trains. The generation of action potentials and of their rhythmic behavior are linked to the opening and closing of selected classes of ionic channels. Since the membrane potential of neurons can be modified by acting on a combination of different ionic mechanisms, the most common models used for this approach take advantage of the Hodgkin and Huxley equations (see [16–18] as first pioneered and simplified by FitzHugh [19] in the FitzHugh–Nagumo model [20]).
Briefly, knowing the physical counterpart of the parameters of these models, it becomes easy to determine for which of these terms, and for what values the firing mode of the simulated neurons undergoes transformations, from rest to different attractors, through successive bifurcations. A quick reminder of the history and the significance of the mathematical formalism proposed by Hodgkin and Huxley and later by other authors is necessary for clarifying this paradigm.
2.1 Models of excitable cells and of neuronal firing
2.1.1 The Hodgkin and Huxley model
It is the paving-stone upon which most conductance-based models are built. The ionic mechanisms underlying the initiation and propagation of action potentials have been beautifully elucidated by applying to the squid giant axon the voltage clamp technique, in which the membrane potential can be displaced and held to a new value by an electronic feedback (for a full account see [21–23]). As shown in Fig. 1A, it was found that the membrane potential of the axon is determined by three conductances, i.e. gNa, gK and gL, which are placed in series with their associated batteries VNa, VK and VL and in parallel with the membrane capacitance C. Before activation the membrane voltage, V, is at rest and the voltage-dependent channels permeable to sodium (Na+) and potassium (K+), which can be viewed as closed. Under the effect of a stimulation, the capacitor is led to discharge so that the membrane potential is shifted in the depolarizing direction and due to the subsequent opening of channels, a current is generated. This current consists in two phases. First sodium moves down its concentration gradient thus giving rise to an inward current and a depolarization. Second, this transient component is replaced by an outward potassium current and the axon repolarizes (Fig. 1B).
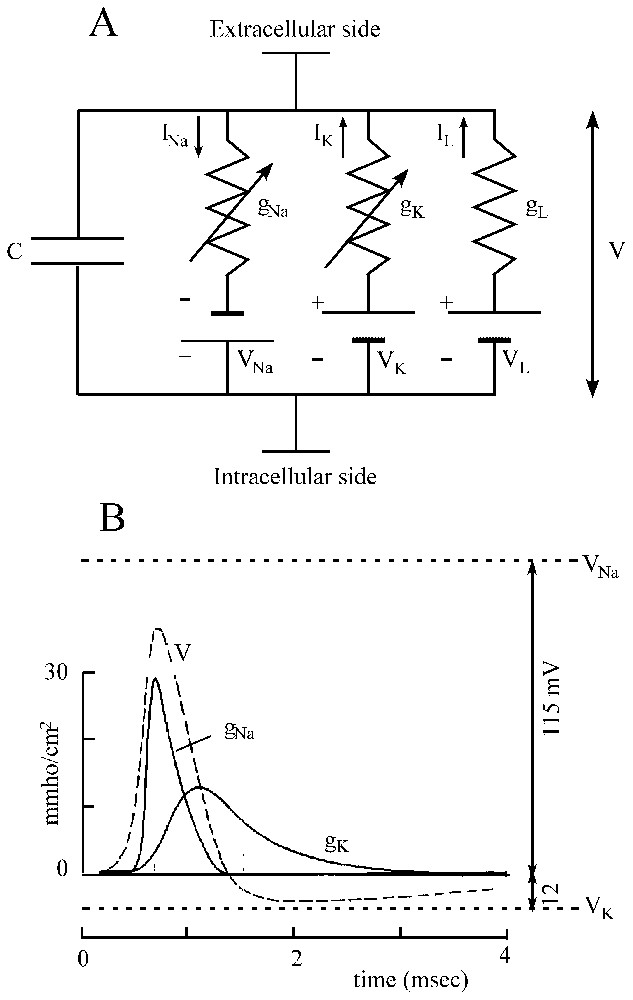
Ionic currents involved in the generation of action potentials. (A) Equivalent circuit of a patch of excitable membrane. There are two active conductances gNa and gK, and a third passive ‘leak’ conductance gL which is relatively unimportant and which carries other ions, including chloride. Each of them is associated to a battery and is placed in parallel with the capacitance C (see text for explanations). Vertical arrows (labeled I) point the direction of the indicated ionic currents. (B) Theoretical solution for a propagated action potential (V, broken line) and its underlying activated conductances (gNa and gK), as a function of time; note their good agreement with those of experimentally recorded impulses. The upper and lower horizontal dashed lines designate the equilibrium potential of sodium and potassium, respectively. (Adapted from [21], with permission of the Journal of Physiology.)
To describe the changes in potassium conductances Hodgkin and Huxley assumed that a channel has two states, open and closed, with voltage-dependent rate constants for transition between them. That relation is formally expressed as,
| (1) |
Fitting the experimental data to this relationship revealed where gK is the maximal conductance. Thus it was postulated that four particles or sensors need to undergo transitions for a channel to open. Similarly, for the sodium channel, it was postulated that three events, each with a probability m, open the gate and that a single event, with a probability (1−h) blocks it. Then
| (2) |
| (3) |
| (4) |
The Hodgkin and Huxley model has been, and remains extremely fruitful for the studies of neurons as it reproduces with great accuracy the behavior of excitable cells such as their firing threshold, steady state activation and inactivation, bursting properties, bistability, to name a few of their characteristics. For example it has been successfully used, with some required adjustments of the rate constants of specific conductances, to reproduce the action potentials of cardiac cells (whether nodal or myocardial) and of cerebellar Purkinje cells (for details about authors and equations, see [26]). However, its implementation requires an exact and prior knowledge of the kinetics of each of the numerous conductances acting in a given set of cells. Furthermore the diversity of ionic currents in various cell types coupled with the complexity of their distribution over the cell, implies that number of parameters are involved in the different neuronal compartments, for example, in dendrites (see [23,27]). This diversity can preclude simple analytic solutions and further understanding of which parameter is critical for a particular function.
To avoid these drawbacks and to reduce the number of parameters, global macroscopic models have been constructed by taking advantage of the theory of dynamical systems. One can then highlight the qualitative features of the dynamics shared by numerous classes of neurons and/or of ensemble of cells such as their bistability, their responses to applied currents or synaptic inputs, their repetitive firing and oscillatory processes. This topological approach yields geometrical solutions expressed in term of limit cycles, basins of attraction and strange attractors, as defined in [1]. For more details, one can consult several other comprehensive books and articles written for physiologists [18,28,29].
2.1.2 The FitzHugh–Nagumo model: space phase analysis
A simplification of the Hodgkin and Huxley model is justified by the observation that, changes in the membrane potential related to (i) sodium activation, and (ii) sodium inactivation and potassium activation, evolve during a spike on a fast and slow time course, respectively. Thus the reduction consists of taking two variables into account instead of four, a fast (V) and a slow (W) one, according to:
| (5) |
| (6) |
An important aspect of the FitzHugh–Nagumo formalism is that since it is a two-variable model it is well suited for phase plane studies in which the variables V and W can be shown as functions of time (however, it can be noted that although models based on Hodgkin and Huxley equations can generate chaos, single two dimensional FitzHugh–Nagumo neurons cannot). These plots called ‘phase plane portraits’ provide a geometrical representation, which illustrates qualitative features of the solution of differential equations. The basic relationships were derived by Van der Pol [30] who was interested in nonlinear oscillators and they were first applied to the cardiac pacemaker [31]. It is therefore not surprising that this model was used later on to study the bursting behavior of neurons, sometimes linked with the Hodgkin and Huxley equations in the form of a mosaic, as proposed by Morris and Lecar [32] to describe the excitability of the barnacle muscle fiber (see [18]). Specifically, when an appropriate family of currents is injected into the simulated ‘neurons’ the behavior of the evoked spike trains appears in the phase space to undergo a transition from a steady state to a repetitive limit cycle via Hopf bifurcations which can be smooth and unstable (supercritical, Fig. 2A) or abrupt (subcritical, Fig. 2B), or via homoclinic bifurcations, i.e. at saddle nodes and regular saddles (not shown, see [33]), with the possible hysteresis when the current I varies from one side to the other of its optimal values (Fig. 2C).
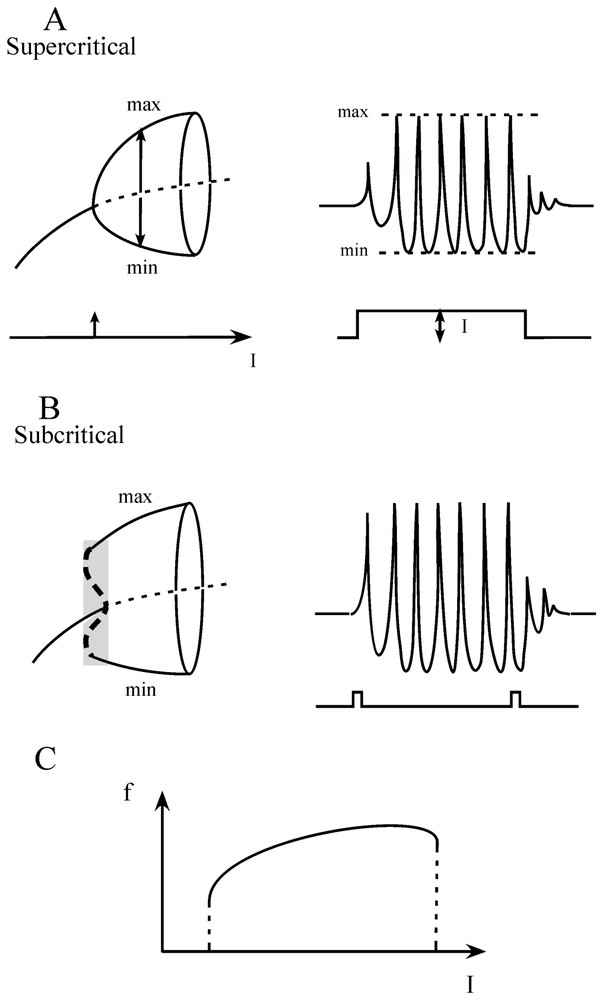
Transitions from a steady state to an oscillatory firing mode. (A) Left. Diagram bifurcation of a supercritical Hopf bifurcation. The abscissa represents the intensity of the control parameter, in this case an ‘intracellularly applied current’, I. The ordinate is the membrane potential. The repetitive firing state is indicated by the maximal (max) and minimal (min) amplitudes of the oscillations. Note that for a critical value of I (arrow) the system shifts from a steady state to an oscillatory mode (solid curve) on either side of an unstable point (dashed line). Right. Corresponding firing pattern of a neuron (upper trace) produced by a current, I, of constant intensity (lower trace). (B) Left. Same presentation as above of events in the case of a subcritical Hopf bifurcation. The stable oscillatory branch is preceded by an unstable phase (vertical dashed line in shaded area) during which the steady state and the oscillations coexist. Right. Current pulses of low amplitude can reset the oscillations during this unstable state (bistability). (C) Plot of the frequency of firing (f, ordinate) versus the intensity of the applied current (I, abscissa). (Adapted from [33], with permission of the MIT Press.)
2.1.3 Definitions
A few definitions of some of the events observed in the phase space become necessary. Their description is borrowed from Hilborn [34]. A bifurcation is a sudden change in the dynamics of the system; it occurs when a parameter used for describing it takes a characteristic value. At bifurcation points the solutions of the time-evolution equations are unstable and in many ‘real’ systems (other than mathematical) these points can be missed because they are perturbed by noise. There are several types of fixed points (that is of points at which the trajectory of a system tends to stay). Among them nodes (or sinks) attract close by trajectories while saddle points attract them on one side of the space but repel them on the other (see also Section 6.1 for the definition of a saddle). There are also repellors (sources) that keep away nearby trajectories. When for a given value of the parameter, a point gives birth to a limit cycle it is called a Hopf bifurcation, a common bifurcation, which can be supercritical if the limit cycle takes its origin at the point itself (Fig. 2A) or subcritical if the solution of the equation is at a finite distance (Fig. 2B) due to amplification of instabilities by the nonlinearities [35]. To get a feeling for what are homoclinic and heteroclinic bifurcations and orbits one has to refer to the invariant stable (insets) and unstable (outsets) manifolds and to the saddle cycles which are formed by trajectories as they head, according to strict mathematical rules, toward and away from saddle points, respectively (for more details see [1] and Section 6.1). Specifically, a homoclinic intersection appears on Poincaré maps when a control parameter is changed and insets and outsets of a saddle point intersect; there is a heteroclinic intersection when the stable manifold of one saddle point intersects with the stable manifold of another one. Once these intersections occur they repeat infinitely and connected points form homoclinic or heteroclinic orbits that eventually lead to chaotic behavior.
2.1.4 The Hindmarsh and Rose model of bursting neurons
This algorithm becomes increasingly popular in neuroscience. It is derived from the two-variable model of the action potential presented earlier by the same authors [36], which was a modified version of the FitzHugh–Nagumo model and it has the important property of generating oscillations with long interspike intervals [37,38]. It is one of the simplest mathematical representation of the widespread phenomenon of oscillatory burst discharges that occur in real neuronal cells. The initial Hindmarsh and Rose model has two variables, one for the membrane potential, V, and one for the the ionic channels subserving accommodation, W. The basic equations are:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Despite some limitations in describing every property of spike-bursting neurons, for example the relation between bursting frequency and amplitude of the rebound potential versus current observed in some real data [40], the Hindmarsh and Rose model has major advantages for studies of: (i) spikes trains in individual cells, and (ii) the cooperative behavior of neurons that arises when cells belonging to large assemblies are coupled with each other [40,41].
First, as shown in Fig. 3A, and depending on the values of parameters in the equations above, the neurons can be in a steady state or they can generate a periodic low-frequency repetitive firing, chaotic bursts or high-frequency discharges of action potentials (an example of period-doubling of spike discharges of a Hindmarsh and Rose neuron, as a function of the injected current is illustrated in Fig. 14 displayed in Part I of this review [1]).
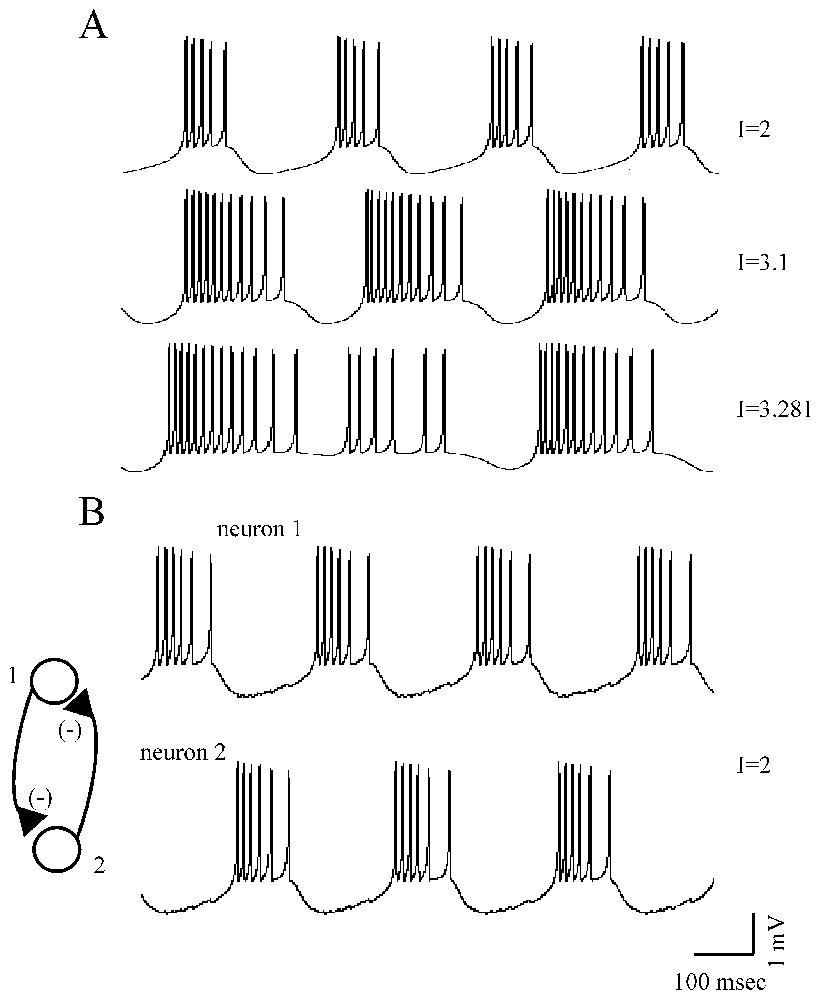
Different firing patterns of Rose and Hindmarsh neurons. (A) For increased values of an injected current, I (as indicated, from top to bottom), the model cell produced short, long and irregular (chaotic) bursts of action potentials. (B) Example of out of phase sequences of bursts generated by two strongly reciprocally coupled inhibitory neurons (after Faure and Korn, unpublished).
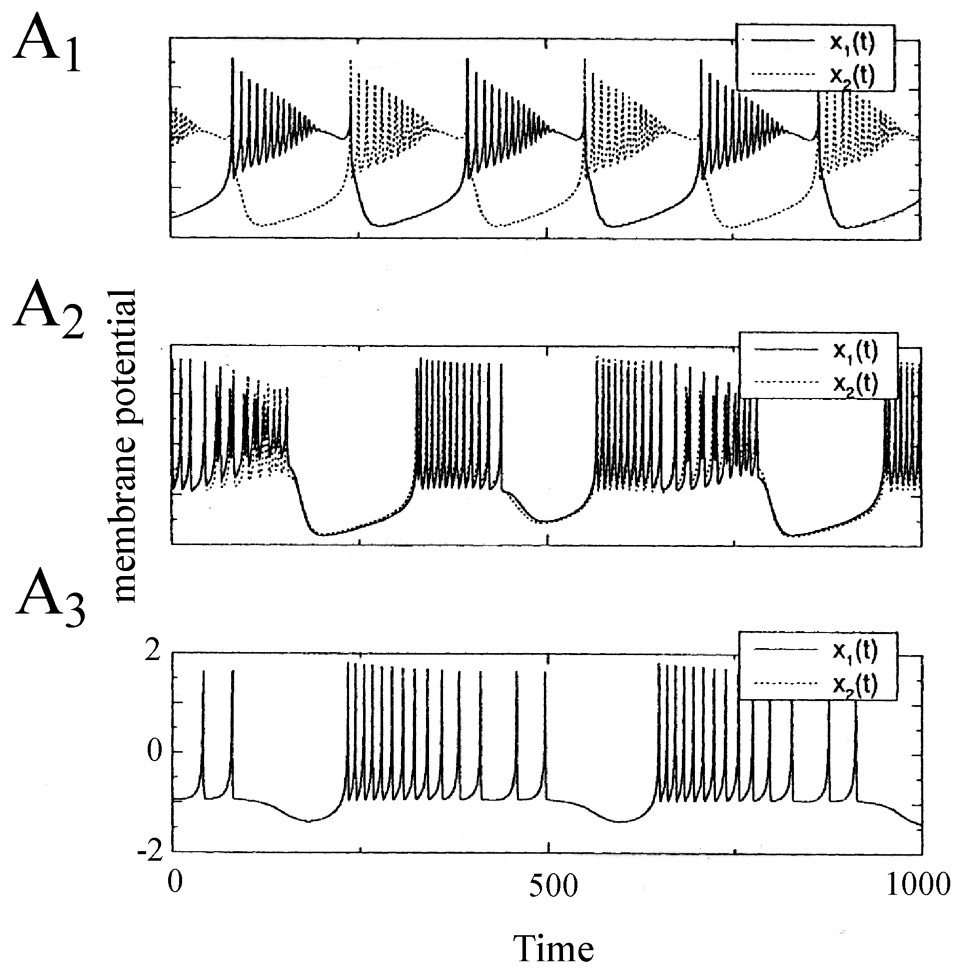
Synchronization of two electrically coupled Rose and Hindmarsh neurons. The membrane potentials x1(t) and x2(t) are in antiphase for a low value of the coupling parameter ε which is a conductance of the ‘wire’ connecting them (A1, ε=0.02). As this parameter is increased, the synchronization is incomplete and nearly in phase (A2, ε=0.4) and it is finally complete and in phase (A3, ε>0.5). (From [40], with permission of Neural Computation.)
Second, Rose and Hindmarsh neurons can be easily linked using equations accounting for electrical and/or chemical junctions (the latter can be excitatory or inhibitory) which underlie synchronization in theoretical models as they do in experimental material (references in [39]). Such a linkage can lead to out of phase (Fig. 3B) or to in phase bursting in neighboring cells or to a chaotic behavior, depending on the degree of coupling between the investigated neurons.
2.2 Experimental data from single cells
2.2.1 Isolated axons
The nonlinear behavior of axons and the potential for deterministic chaos of excitable cells have been well documented both experimentally and with extensive theoretical models of the investigated systems. The results obtained with intracellular recordings of action potentials in the squid giant axon are particularly convincing. Specifically, by changing the external concentration of sodium (Na), it is possible to produce a switch from the resting state to a state characterized by (i) self sustained oscillations and (ii) repetitive firing of action potentials that mimic the activity of a pacemaker neuron (Fig. 4A). The resting and oscillatory states were found to be thermodynamically equivalent to an asymptotically stable equilibrium point and a stable limit cycle, respectively, with an unstable equilibrium point between them (Fig. 4B). Simulations based upon modified Hodgkin and Huxley equations successfully predicted the range of external ionic concentrations accounting for the bistable regime and the transition between the unstable and the stable periodic behavior via a Hopf bifurcation [42,43].
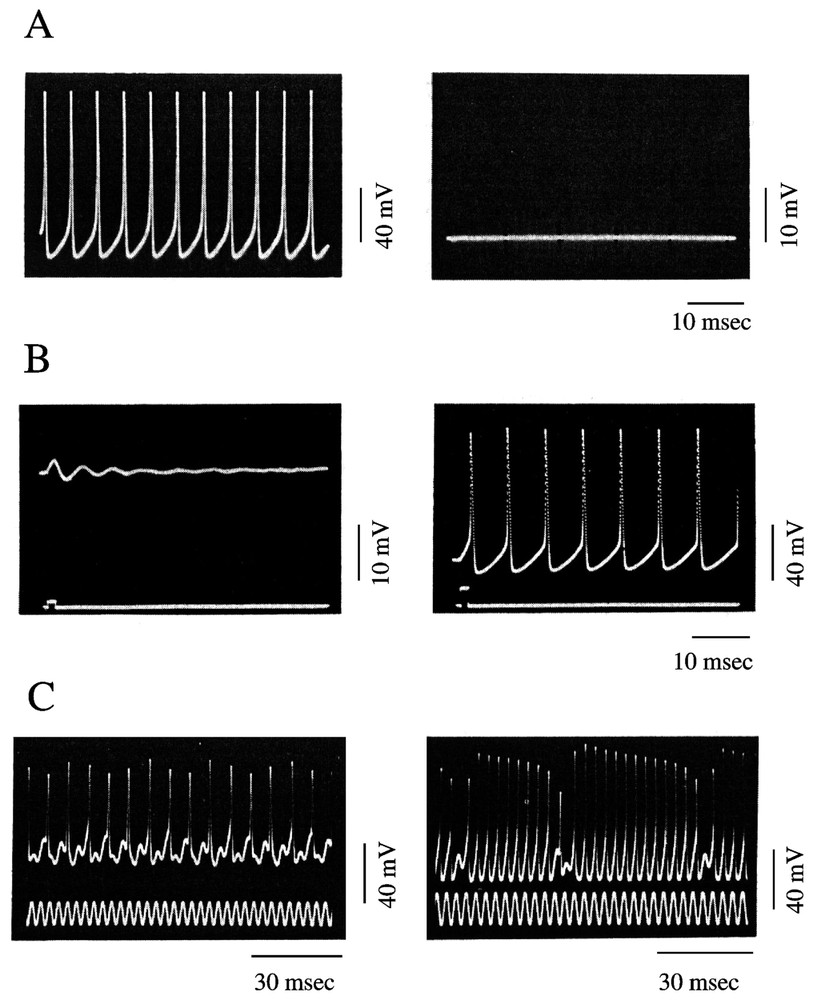
Periodic and non-periodic behavior of a squid giant axon. (A) Periodic oscillations (left) and membrane potential at rest (right) after exposure of the preparation for 0.25 and 6.25 min to an external solution containing the equivalent of 530 and 550 mM NaCl, respectively. (B) Bistable behavior of an axon placed in a 1/3.5 mixture of NSW 550 mM NaCl. Note the switch from subliminal (left) to supraliminal (right) self-sustained oscillations, produced by a stimulating pulse of increasing intensity. (C) Chaotic oscillations in response to sinusoidal currents. The values of the natural oscillating frequency and the stimulating frequency (fn) were 136 and 328 Hz (left) and 228 and 303 Hz (right). In each panel, the upper and lower traces represent the membrane potential and the activating current, respectively. (A and B are modified from [42], C is from [44], with permission of the Journal of Theoretical Biology.)
Extending their work on the squid giant axon, Ahira and his collaborators [43,44] have studied the membrane response of both this preparation and a Hodgkin and Huxley oscillator to an externally applied sinusoidal current with the amplitude and the frequency of the stimulating current taken as bifurcation parameters. The forced oscillations were analyzed with stroboscopic and Poincaré plots. The results showed that, in agreement with the experimental results, the forced oscillator exhibited not only periodic but also non-periodic motions (i.e. quasi-periodic or chaotic oscillations) depending on the amplitude and frequency of the applied current (Fig. 4C). Further, several routes to chaos were distinguished, such as successive period-doubling bifurcations or intermittent chaotic waves (as defined in Part I, [1]).
With a somewhat similar rationale, Hayashi and Ishizuka [45] used as a control parameter a dc current applied intracellularly through a single electrode to study the dynamical properties of discharges of the membrane of the pacemaker neuron of a marine mollusk, Onchidium verraculatum. Again, a Hodgkin and Huxley model did show a sequence of period-doubling bifurcations from a beating mode to a chaotic state as the intensity of the inward current was modified. The different patterns shared a close similarity with those observed experimentally in the same conditions (Fig. 5A1–A3).
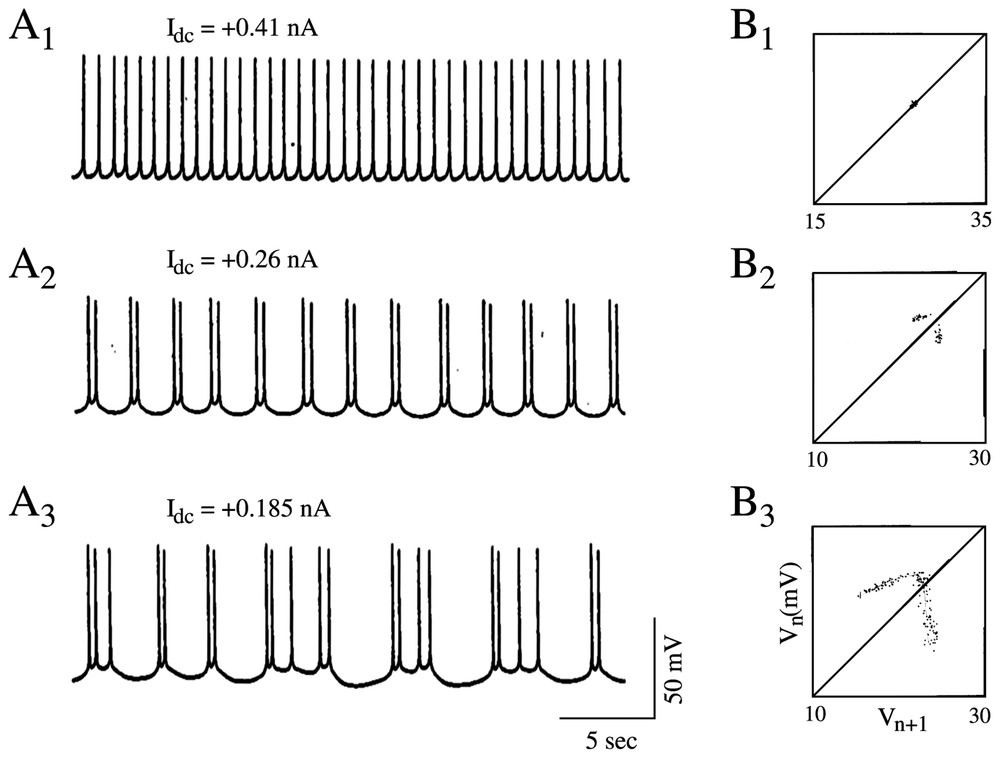
Discharge patterns of a pacemaker neuron caused by a dc current (A1–A3) representative samples of the recorded membrane potential. (B1–B3) One-dimensional Poincaré maps of the corresponding sequence of spikes constructed using the delay method (see [1] for explanations). (A1–B1) Regular discharges of action potentials. (A2–B2) Periodic firing with two spikes per burst. (A3–B3) Chaotic bursting discharges. (Adapted from [45], with permission of the Journal of Theoretical Biology.)
Another and interesting report by Jianxue et al. [46] showing that action potentials along a nerve fiber can be encoded chaotically, needs to be mentioned. ‘Spontaneous’ spikes produced by injured fibers of the sciatic nerve of anaesthetized rats were recorded and studied with different methods. Spectral analysis and calculations of correlation dimensions were implemented first, but with limited success due to the influence of spurious noise. However other approaches turned out to be more reliable and fruitful. Based on a study of interspike intervals (ISI), they included return (or Poincaré) maps (ISI(n+1) versus ISI(n); Fig. 5B1–B3) and a nonlinear forecasting method combined with gaussian scaled surrogate data. Conclusions that the time series were chaotic found additional support in the calculations of Lyapunov exponents after adjusting the parameters in the program of Wolf et al. [47], which is believed to be relatively insensitive to noise.
2.2.2 Chaos in axonal membranes: comments
General self criticism by Aihiara et al. [44] as to which ‘chaos’ with dimensions of the strange attractors between 2 and 3 in their experiments was observed under rather artificial conditions is important. This criticism applies to all forms of nonlinear behavior reported previously: in every instance the stimulations, whether electrical or chemical, were far from physiological. However chaotic oscillations can be produced by both the forced Hodgkin and Huxley oscillator and the giant axon when a pulse train [44] or a sinusoidal current [43] are used. This already implies that, as will be confirmed below, nonlinear neuronal oscillators connected by chemical or electrical synapses can supply macroscopic fluctuations of spike trains in the brain.
2.3 Single neurons
It is familiar to electrophysiologists that neuronal cells possess a large repertoire of firing patterns. A single cell can behave in different modes i.e. such as a generator of single or repetitive pulses, bursts of action potentials, or as a beating oscillator, to name a few. This richness of behavioral states, which is controlled by external inputs, such as variations in the ionic environment caused by the effects of synaptic drives and by neuromodulators, has prompted number of neurobiologists to investigate if, in addition to these patterns, chaotic spike trains can also be produced by individual neurons. If so, such spike trains would become serious candidate neural codes as postulated previously for other forms of signals thought to play a major role as information carriers in the nervous system [48,49]. Analytical ‘proof’ that this hypothesis is now well grounded has been presented for the McCulloch and Pitts neuron model [50].
Puzzled by the variability of activities in the buccal-oral neurons of a sea slug Pleurobranchae californica, Mpitsos et al. [51] recorded from individual cells with standard techniques and analyzed the responses generated in deafferented preparations in order to study the temporal patterns of signals produced by the central nervous system itself. The recorded cells, called BCN (for buccal-cerebral neurons) were particularly interesting since they can act as either an autonomous group or as part of a network that produces coordinated rhythmic movements of all buccal-oral behaviors. Several criteria of chaos were apparently satisfied by the analysis of the spike trains. These tests included the organization of the phase portraits and Poincaré maps which revealed attractors with clear expansions and contractions between space trajectories, positive Lyapunov exponents (assessed with the program of Wolf et al. [47]) and relatively constant correlation dimensions. The authors recognized however the limitations of these conclusions since their time series were quite short and often non-stationary. In addition surrogates were not used in their study.
Chaotic regimes were described with mathematical models of neuron R15 of another mollusk, Aplysia Californica, but their reality has only been confirmed directly with recordings from the actual cell. Neuron R15 had been known for long to fire in a normal, endogeneous, bursting mode [52] and in a beating (i.e. tonic) mode if a constant depolarizing current is injected onto the cell or if the sodium potassium pump is blocked. These activities were first mimicked qualitatively by Plant and Kim [53] with the help of a modified version of the Hodgkin and Huxley model. When implemented further for additional conductances and their dynamics by Canavier et al. [54–56], the algorithms predicted different modes of activity and, more importantly, that a chaotic regime exists between the bursting and beating modes of firing. That is, chaotic activity could well be the result of intrinsic properties of individual neurons and need not be an emergent property of neural assemblies. Furthermore the model approached chaos from both regimes via period doubling bifurcations. It was also suggested that these as well as other modes of firing, such as periodic bursting (bursts of spikes separated by regular periods of silence) correspond, in a phase space, to stable multiple attractors (Fig. 6A1–A3 and B1–B3). These attractors coexisted at given sets of parameters for which there was more than one mathematical solution (bistability). Finally, it was predicted that variations in external ionic concentration (of sodium or calcium), transient synaptic inputs and modulatory agents (serotonin) can switch the activity of the cell from one stable firing pattern to the other.
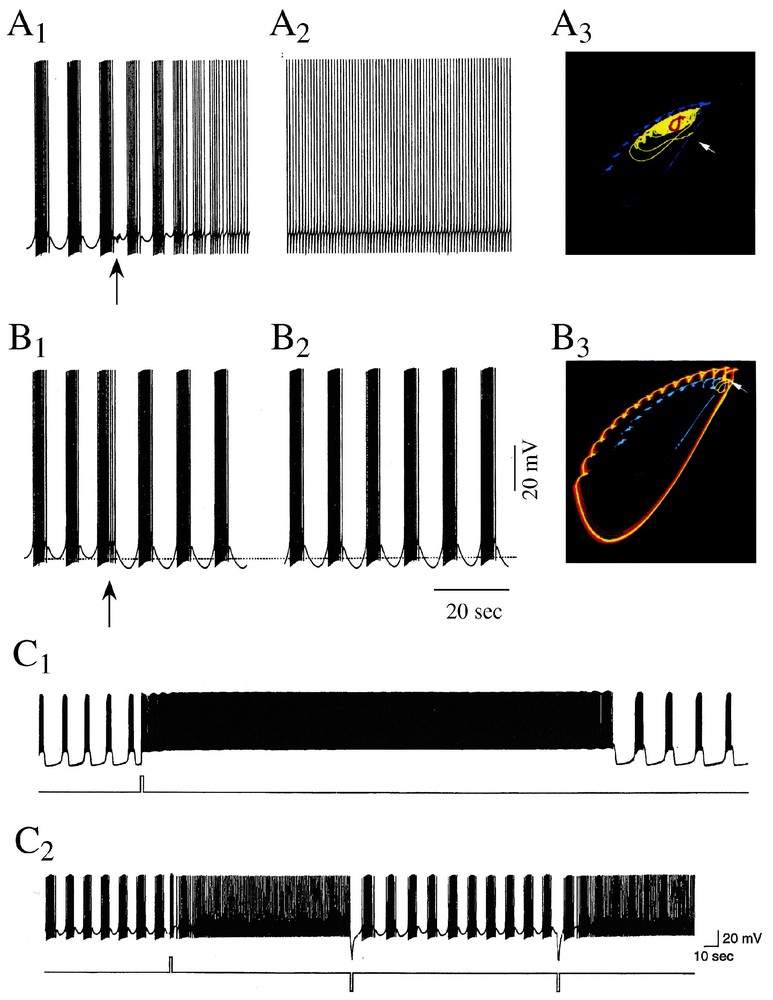
Sensitivity of bursts to external stimuli. (A1–A3 and B1–B3) Control of model responses. (A1–A3) A short (1 s, 4 Hz) train of ‘synaptic’ inputs (arrow) delivered immediately after a burst (A1) induces after a brief initial transient a transition to a beating mode (A2) which persists during an hour. In the phase plane projection (A3), the original pattern is shown in cyan and the final attractor is in red. (B1–B3) Identical initial conditions as in A1, but the stimulus that is delivered earlier (B1) induces a prolonged shift into a new mode of firing (apparently chaotic according to the authors) (B2). In the corresponding phase plane (B3), the initial attractor is cyan and the final one is magenta. (C1–C2) Bistability in a intracellularly recorded R15 neuron. Shift of the cell from a bursting to a beating mode of activity. (C1) A brief current pulse (bottom) delivered during an interburst hyperpolarization is followed by a sustained beating after which the spiking activity returns to the original bursting pattern. (C2) Successive transitions between identical bursting and beating episodes (above), whether current pulses (bottom) are in the depolarizing or the depolarizing direction. (A1–B3 from [56]; C1–C2 from [60], with permission of the Journal of Neurophysiology.)
Experiments confirmed these prophecies in part. For example, transitions between bursting and beating had already been observed in R15 in response to the application of the blocker 4-aminopyridine (4-AP), suggesting that potassium channels may act as a bifurcation parameter [57]. Also transitions from beating to doublet and triplet spiking and finally to a bursting regime were described in response to another K+ channel blocker, tetraethyl ammonium which, in addition to this pharmacological property, was credited to induce ‘chaotic-like’ discharges in identified neurons of the mollusc Lymnae Stagnalis [58,59]. More critically, recordings from R15 were performed by Lechner et al. [60] to determine whether multistability is indeed an intrinsic property of the cell and if it could be regulated by serotonin. It was found that R15 cells could exhibit two modes of oscillatory activity (instead of eight in models) and that brief perturbations such as current pulses induced abrupt and instantaneous transitions from bursting to beating which lasted from several seconds to tens of minutes (Fig. 6C1 and C2). In presence of low concentrations of serotonin the probability of occurrence of these transitions and the duration of the resulting beating periods were gradually increased.
The contribution of ionic channels in the dynamic properties of isolated cells has been demonstrated by important studies of the anterior burster (AB) neuron of the stomatogastric ganglion of the spiny lobster, Pancibirus Interruptus. In contrast to ‘constitutive’ bursters, which continue to fire rhythmic impulses when completely isolated from all synaptic input, this neuron is a ‘conditional’ burster, meaning that the ionic mechanisms that generate its rhythmic firing must be activated by some modulatory input. It is the primary pacemaker neuron in the central pattern generator (see Section 3.2) for the pyloric rhythm in the lobster stomach. With the help of intracellular recordings, Harris–Warrick and Flamm [61] have shown that the monoamines dopamine, serotonin and octopamine convert silent AB neurons into bursting ones, the first two amines acting primarily upon Na+ entry and the latter on the calcium currents, although each cell can burst via more than one ionic channel (see also [61,62]). These experimental results were exploited on by Guckenheimer et al. [63] who characterized the basic properties of the involved channels in a model combining the formulations of Hodgkin and Huxley, and of Rinzel and Lee [64]. Specifically, changes in the intrinsic firing and oscillatory properties of the model AB neuron were correlated with the boundaries of Hopf and saddle-node bifurcations on two dimensional maps for specific ion conductances. Complex rhythmic patterns, including chaotic ones, were observed in conditions matching those of the experimental protocols. In addition to demonstrating the efficacy of dynamical systems theory as a means for describing the various oscillatory behaviors of neurons, the authors proposed that there may be evolutionary advantages for a nerve cell to operate in such regions of the parameter space: bifurcations then locate sensitive points at which small alterations in the environment result in qualitative changes in the system's behavior. Thus, using a notion introduced by Thom [65] the nerve cell can function as a sensitive signal detector when operating at a point corresponding to an ‘organizing center’.
The above mentioned studies met a rewarding conclusion when Abarbanel et al. [40] analyzed the signals produced in the isolated LP cells from the lobster stomatogastric ganglion. The data consisted of intracellularly recorded voltage traces from neurons subjected to an applied current of different amplitudes. As the intensity of the current was varied, the pattern of firing shifted via bifurcations, from a periodic (Fig. 7A and B) to a chaotic like (Fig. 7C–E) structure. The authors could not mathematically distinguish chaotic behavior from a nonlinear amplification of noise. Yet, several arguments strongly favored chaos, such as the robust substructure of the attractors in Fig. 7C and D. The average mutual information and the test of false nearest neighbors allowed to distinguish between noise (high-dimensional) and chaos (low-dimensional). This procedure was found to be more adequate than the Wolf method which is only reliable for the largest exponents.
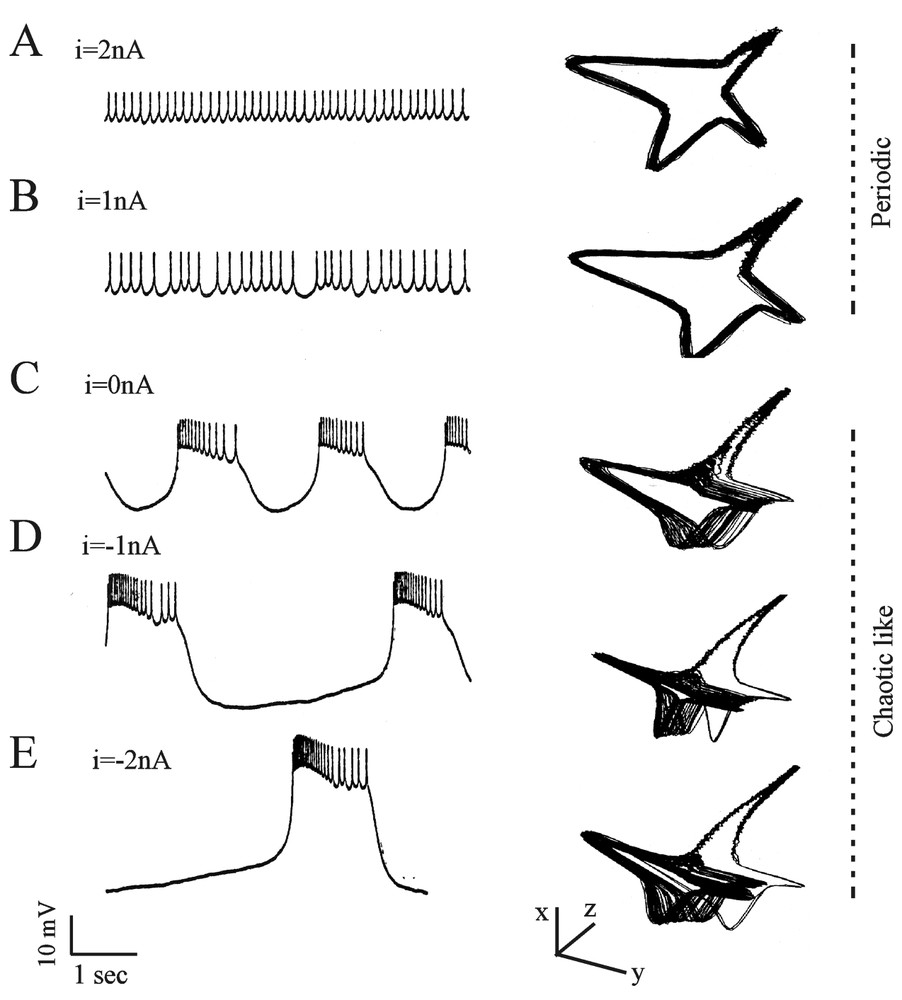
Dynamic changes of the membrane potential of a LP neuron. Left column: intracellularly monitored slow oscillations and spikes in the presence of the indicated values of directly applied currents. Right column: corresponding state phase reconstructions obtained with the time delay method (see text for explanations). The original coordinates are rotated so that the fast spiking motion takes place in the x–y plane and the slow bursting motion moves along the z-axis. (Modified from [40], with permission of the Journal of Neurophysiology.)
Recent investigations on isolated cells have shown that dynamical information can be preserved when a chaotic input, such as a ‘Rössler’ signal, is converted into a spike train [66]. Specifically, the recorded cells were in vitro sensory neurons of rat's skin subjected to a stretch provided by a Rössler system, and, for the sake of comparison, to a stochastic signal consisting of phase randomized surrogates. The determinism of the resulting inter spike intervals (monitored in the output nerve) was tested with a nonlinear prediction algorithm, as described in [1]. The results indicated that a chaotic signal could be distinguished from a stochastic one (Fig. 8). That is, and quoting the authors, for prediction horizons up to 3–6 steps, the normalized prediction error (NPE) value for the stochastically evoked ISI series were all near 1.0, as opposed to significantly smaller values for the chaotically driven ones. Thus sensory neurons are able to encode the structure of high-dimensional external stimuli into distinct spike trains.
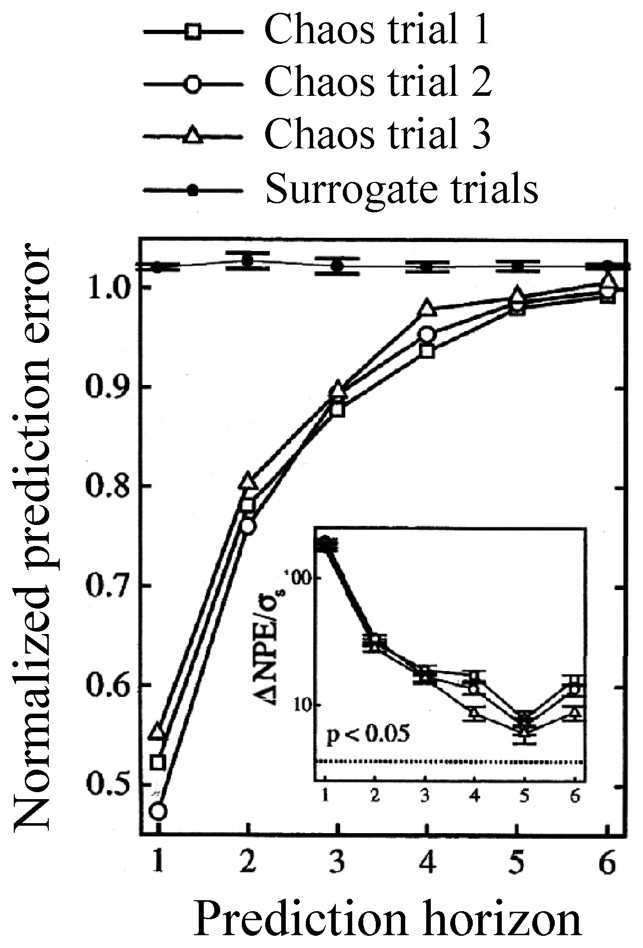
Normalized prediction error as a function of the predicted horizon for chaotic and random (surrogate) signals, in a sensory neuron. An embedding dimension of three was used, significance was assessed with two-tailed tests. Inset: results from the statistical analysis: σs is the standard deviation of the normalized prediction error (NPE) for the surrogate trials; dashed line: significance level corresponding to the indicated p value. (From [66], with permission of the Physical Review Letters.)
Although based on studies of non isolated cells recorded in vitro, another report can be mentioned here, at least, as a reminder of the pitfalls facing the analysis of large neuronal networks with nonlinear mathematical tools. It represents an attempt to characterize chaos in the dynamics of spike trains produced by the caudal photoreceptor in the sixth ganglion of the crayfish Procambarus clarkii subjected to visual stimuli. The authors [67] rely on the sole presence in their time series of first order unstable periodic orbits statistically confirmed with gaussian surrogates, despite evidence that this criterion alone is far from convincing [68].
3 Pairs of neurons and ‘small’ neuronal networks
A familiar observation to most neurobiologists is that ensembles of cells often produce synchronized action potentials and/or rhythmical oscillations. Experimental data and realistic models have indicated that for some geometrical connectivity of the network (closed topologies) and for given values of the synaptic parameters linking the involved neurons, the cooperative dynamics of cells can take the form of a low dimensional chaos. Yet a direct confirmation of this notion, validated by unambiguous measures for chaos, has only been obtained in a limited sample of neural circuits. In principle, as noted by Selverston et al. [69], network operations depend upon the interactions of numerous geometrical synaptic and cellular factors, many of which are inherently nonlinear. But since these properties vary among different classes of neurons, it follows that although often taken as an endpoint by itself a ‘reductionist’ determination of their implementation can be useful for a complete description of network's global activity patterns. So far, such a detailed analysis has only been achieved successfully in but a few invertebrate and lower vertebrate preparations.
3.1 Principles of network organization
In an extensive review of the factors that govern network operations, Getting [70] remarked that individual conductances are not as important as the properties that they impart. Instead, he insists on two main series of elements. The first defines the ‘functional connectivity’. It includes the sign (excitatory or inhibitory) and the strength of the synaptic connections, their relative placement on the postsynaptic cell (soma or dendritic tree) and the temporal properties of these junctions. The second, i.e. the ‘anatomical connectivity’ determines the constraints on the network and ‘who talks to whom’. Despite the complexity and the vast number of possible pathways between large groups of neurons, several elementary anatomical building blocks which contribute to the nonlinearity of the networks can be encountered in both invertebrate and vertebrate nervous system. Such simple configurations have mutual (or recurrent) excitation (Fig. 9A) which produces synchrony in firing, and reciprocal (Fig. 9B) or recurrent (Fig. 9C) inhibitions which regulate excitability and can produce patterned outputs. Recurrent cyclic inhibition corresponds to a group of cells interconnected by inhibitory synapses (Fig. 9D), and it can generate oscillatory bursts with as many phases as there are cells in the ring [71]. In addition cells can be coupled by electrical junctions either directly (Fig. 9E) or by way of presynaptic fibers (Fig. 9F). Such electrotonic coupling favors synchrony between neighboring and/or synergistic neurons [72].
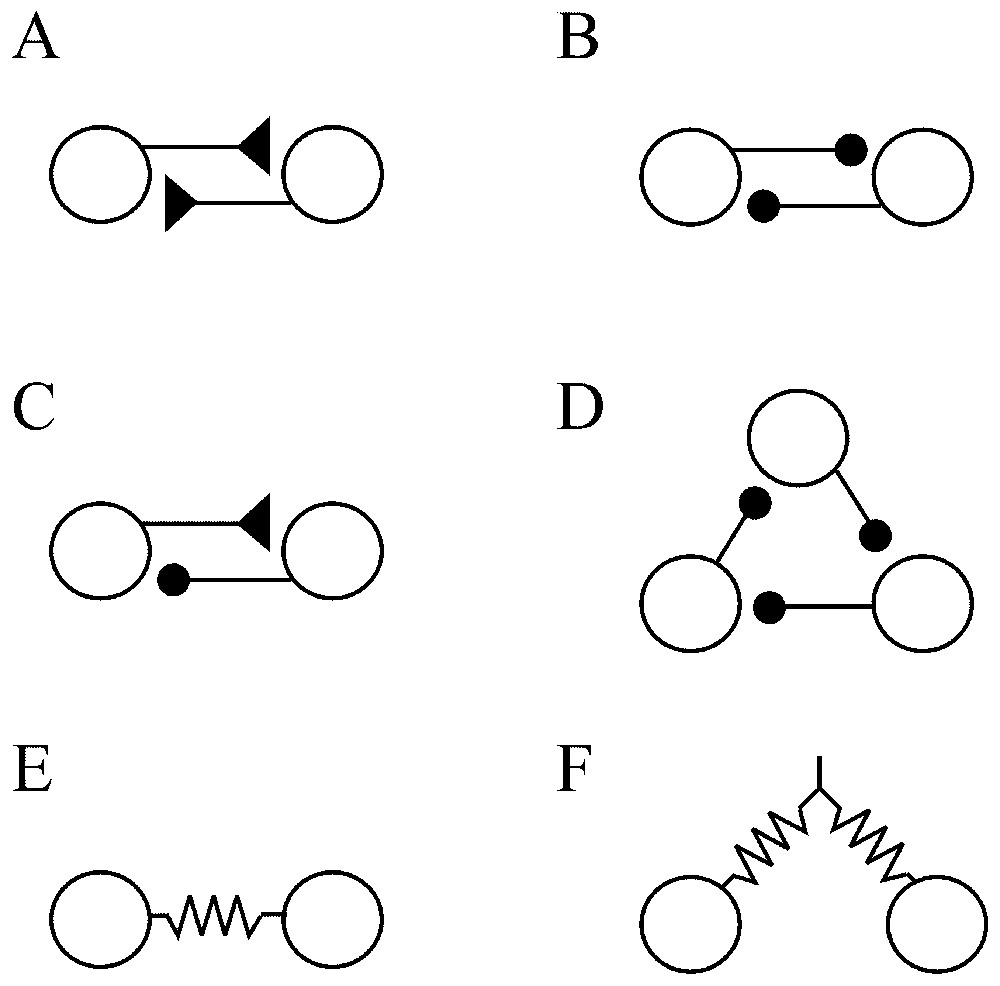
Simple ‘building blocks’ of connectivity. (A) Recurrent excitation. (B) Mutual inhibition. (C) Recurrent inhibition. (D) Cyclic inhibition. (E) Coupling by way of directly opposed electrotonic junctions. (F) Electrical coupling via presynaptic fibers. Symbols: triangles and dots indicate excitatory and inhibitory synapses, respectively; resistors correspond to electrical junctions.
A number of systems can be simplified according to these restricted schemes [73], which remain conserved throughout phylogeny. As described below, such is the case in the Central Pattern Generators (CPGs) involved in specific behaviors that include rhythmic discharges of neurons acting in concert when animals are feeding, swimming or flying. One prototype is the lobster stomatogastric ganglion [74], in which extensive studies have indicated that (i) a single network can subserve several different functions and participate in more than one behavior, (ii) the functional organization of a network can be substantially modified by modulatory mechanisms within the constraints of a given anatomy, and (iii) neural networks acquire their potential by combining sets of ‘building blocks’ into new configurations which however, remain nonlinear and are still able to generate oscillatory antiphasic patterns [75]. These three features run contrary to the classical view of neural networks.
3.2 Coupled neurons
When they are coupled, oscillators, such as electronic devices, pendula, chemical reactions, can generate nonlinear deterministic behavior (Refs. [7,76]) and this property extends to oscillating neurons, as shown by models (Fig. 10) and by some experimental data.
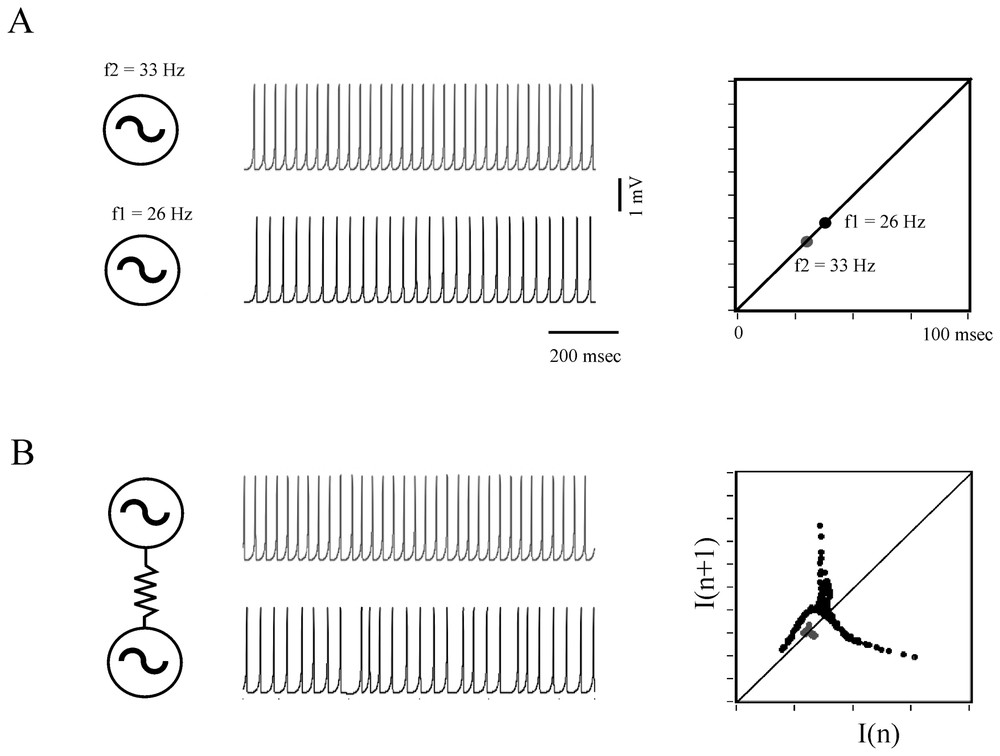
Determistic behavior of coupled formal neurons. (A) Two excitable cells modeled according to Rose and Hindmarsh generate periodic action potentials at the rate of 26 and 33 Hz, respectively (left) and each of these frequencies is visualized on a return map (right). (B) Same presentation as above showing that when the neurons are coupled, for example by an electrotonic junction, their respective frequency is modified and the map exhibits a chaotic-like pattern. Note the driving effect of the faster cell on the less active one. (After Faure and Korn, unpublished.)
Makarenko and Llinas [77] provided one of the most compelling demonstration of chaos in the central nervous system. The experimental material, i.e. guinea-pig inferior olivary neurons was particularly favorable for such a study. These cells give rise to the climbing fibers that mediate a complex activation of the distant Purkinje cells of the cerebellum. They are coupled by way of electrotonic junctions, and slices of the brainstem which contain their somata can be maintained in vitro for intracellular recordings. Subthreshold oscillations resembling sinusoidal waveforms with a frequency of 4–6 Hz and an amplitude of 5–10 mV were found to occur spontaneously in the tested cells and to be the main determinant of spike generation and collective behavior in the olivo-cerebellar system [78]. Nonlinear analysis of prolonged and stationary segments of those oscillations, monitored in single and/or in pairs of IO neurons was achieved with strict criteria based on the average mutual information, calculation of the global embedding dimensions and of the Lyapunov exponent. It unambiguously indicated a chaos with a dimension of ∼2.85 and a chaotic phase synchronization between coupled adjacent cells which presumably accounts for the functional binding of theses neurons when they activate their cerebellar targets.
Rather than concentrating on chaos per se, Elson et al. [79] clarified how two neurons which can individually generate slow oscillations underlying bursts of spikes (that is spiking bursting and seemingly chaotic activities) may or may not synchronize their discharges when they are coupled. For this purpose they investigated two electrically connected neurons (the pyloric dilatators, PDs) from the pyloric CPG of the lobster stomatogastric ganglion (STG). In parallel to the natural coupling linking these cells, they established an artificial coupling using a dynamic clamp device that enabled direct injections of, equal and opposite currents in the recorded neurons, different from to the procedure described in [80], in that they used an active analog device which allowed the change in conductivity, including sign, and thus varied the total conductivity between neurons. The neurons had been isolated from their input as described in Bal et al. [81]. The authors found that with natural coupling, slow oscillations and fast spikes are synchronized in both cells despite complex dynamics (Fig. 11A). But in confirmation of earlier predictions from models [40], uncoupling with additional negative current (taken as representing an inhibitory synaptic conductance) produced bifurcations and desynchronized the cells (Fig. 11B). Adding further negative coupling conductance caused the neurons to become synchronized again, but in antiphase (Fig. 11C). Similar bifurcations occurred for the fast spikes and slow oscillations, but at a different threshold for both types of signals. The authors concluded from these observations that the mechanism for the synchronization of the slow oscillations resembled that seen in dissipatively coupled chaotic circuits [82] whereas the synchronization of the faster occurring spikes was comparable to the so-called ‘threshold synchronization’ in the same circuits [83]. The same experimental material and protocols were later exploited by Varona et al. [87,91] who suggested, after using a model developed by Falke et al. [84], that slow subcellular processes such as the release of endoplasmic calcium could also be involved in the synchronization and regularization of otherwise individual chaotic activities. It can be noted here that the role of synaptic plasticity in the establishment and enhancement of robust neural synchronization has been recently explored in details [85] with Hodgkin and Huxley models of coupled neurons showing that synchronization is more rapid and more robust against noise in case of spike timing plasticity of the Hebbian type [86] than for connections with constant strength.
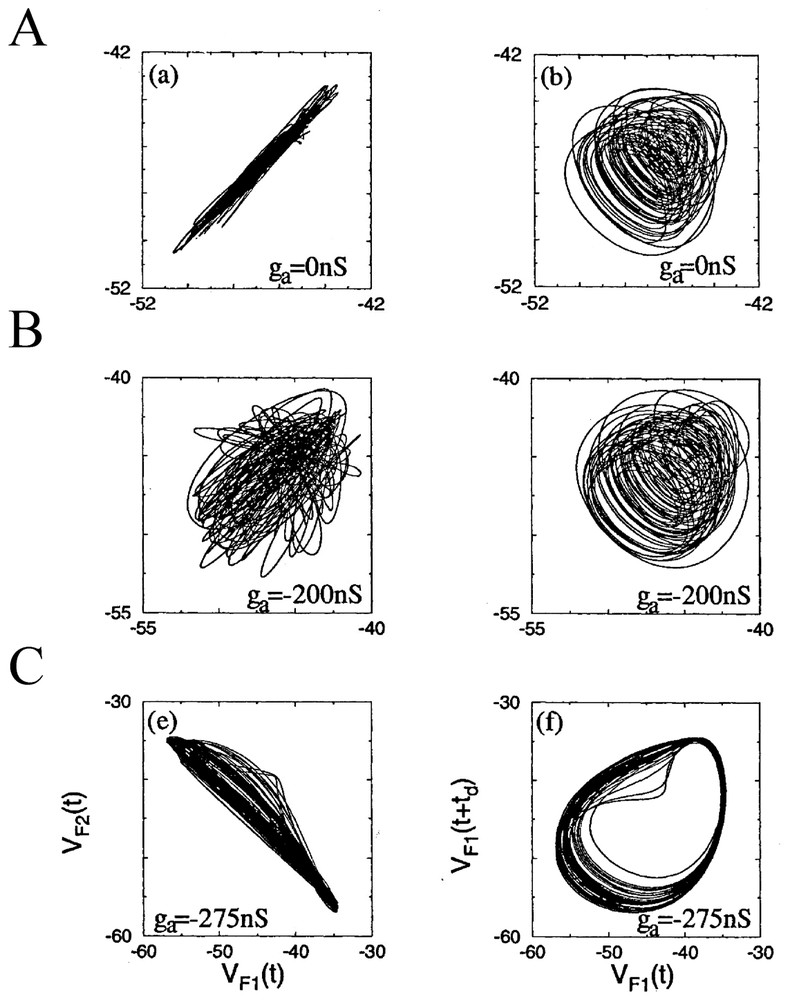
Phase portraits of the slow oscillations in two coupled PD neurons as a function of the indicated external conductance ga. The projections on the two planes of variables VF1(t), VF2(t) in the left column, that is of the low-pass filtered (5 Hz) of the membrane potential V of cells 1 and 2 and of VF1(t), VF1(t+td) in the right column characterize the level of synchrony of bursts in the neurons, and the complexity of the bursts dynamics, respectively. (From [79], with permission of the Physical Review Letters.)
Conversely, isolated, non regular and chaotic neurons can produce regular rhythms again once their connections with their original networks are fully restored. This was demonstrated by Szucs et al. [87] who used an analog electronic neuron (EN) that mimicked firing patterns observed in the lobster pyloric CPG. This EN was a three degree of freedom analog device that was built according to the model of Hindmarsh and Rose. When the anterior burster (AB) which is one of the main pacemakers of the STG was photoinactivated and when synaptic connections between the cells were blocked pharmacologically, the PD neurons fired irregularly (Fig. 12A1 and A2) and nonlinear analysis indicated high-dimensional chaotic dynamics. However, synchronized bursting, at a frequency close to that seen in physiological conditions, appeared immediately after bidirectional coupling was established (as with an electrotonic junction) between the pyloric cells and the EN, previously set to behave as a replacement pacemaker neuron (Fig. 12B1). Furthermore switching the sign of coupling to produce a negative conductance that mimicked inhibitory chemical connections resulted in an even more regular and robust antiphasic bursting which was indistinguishable from that seen in the intact pyloric network (Fig. 12B2). These data confirmed earlier predictions obtained with models suggesting the regulatory role of inhibitory coupling once chaotic cells become members of larger neuronal assemblies [88,89].
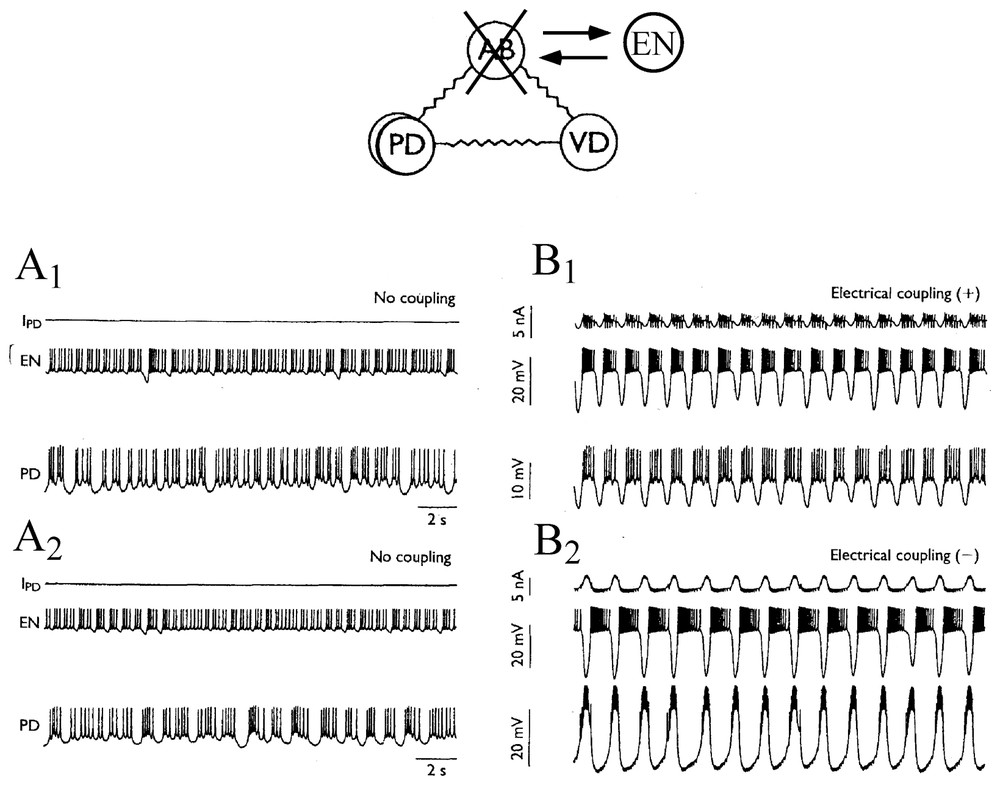
Connecting an electronic neuron to isolated neurons via artificial synapses restores regular bursting. Above: experimental setup. The pyloric pacemaker group of the lobster consists in four electronically coupled neurons. These are the anterior burster (AB), which organizes the rhythm, two coupled pyloric dilatator (PD) and the ventral dilatator (VD). Here AB is replaced by an electrotonic neuron (EN), set to behave in a state of chaotic oscillations. (A1–A2) Neurons disconnected exhibit chaotic discharges of action potentials. (B1–B2) Generation of a bursting pattern in the mixed network after coupling the cells. IPD is the current flowing into PD from EN. Note that the bursts are in phase, or out of phase, in EN and PD depending whether the coupling conductance is positive (B1) or negative (B2), respectively. (Adapted from Szucs et al. [87], with permission of NeuroReport.)
The LP neuron receives strong inhibitory inputs from three electrically coupled pacemaker neurons of the STG. These are the anterior burster (AB) and two pyloric dilator (PD) cells. As shown above, this setting had already been exploited by Elson et al. [79] to strengthen the notion that the intrinsic instabilities of circuit neurons may be regulated by inhibitory afferents. Furthermore, in control conditions [90], the spontaneous bursts generated by the LP neuron are irregular, as illustrated by the superimposed traces of Fig. 13A. However forcing inhibitory inputs had a strong stabilizing effect. When the latter were activated at 65 Hz the bursts were relatively stable and periodic and their timing and duration were both affected (Fig. 13B). This means that inhibition is essential in small assemblies of cells for producing the regulation of the chaotic oscillations prevalent in the dynamics of the isolated neurons (see also [91]). Equally important is that in confirmation, when cells were isolated from all their synaptic inputs their ‘free-running’ activity resembled that of a typical nonlinear dynamic system showing chaotic oscillations with some additive noise, a property that could account for the exponential tail of their computed variance (Fig. 13C).
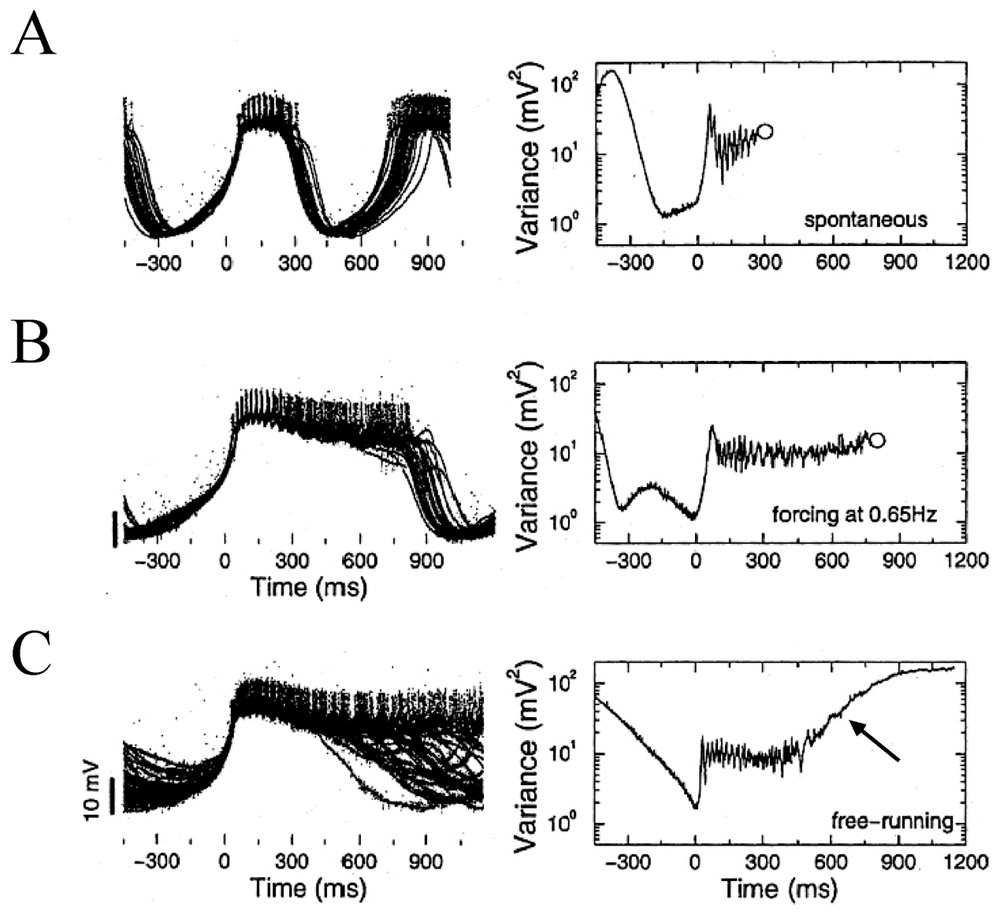
Control of bursting by inhibitory inputs in a LP neuron. Left column: superimposed traces, with individual bursts (n∼30% of a total of 165) sweeps are aligned at time 0 ms which corresponds to the point of minimum variance. Negative times indicate the hyperpolarizing phase preceding each burst's onset. Right column: variance as a function of time between the voltage traces calculated fom the entire sample of recordings in each condition. (A–C) See text for explanations. Open circles mark the mean time of burst termination. The arrow in C signals the exponential tail of the plot (from Elson et al. [90], with permission of the Journal of Neurophysiology).
3.3 Lessons from modeling minimal circuits (CPGs)
The role of the different forms of coupling between two chaotic neurons has been carefully dissected by Abarbanel et al. [40] in studies based on the results obtained with the Hindmarsh and Rose model. Although the values of some of the coupling parameters may be out of physiological ranges, interesting insights emerged from this work: for a high value of the coupling coefficient ε, synchronization of identical chaotic motions can occur. This proposition has been verified for coupling via electrical synapses (Fig. 14A1–A3) with measurements of the mutual information and of Lyapunov exponents. Similarly, progressively higher values of symmetrical inhibition, or of excitatory coupling, lead to in phase and out of phase synchronization of the bursts of two generators which can then exhibit the same chaotic behavior as one. This phenomenon is called ‘chaotic synchronization’ [82,92]. The authors extended these conclusions to moderately ‘noisy’ neurons and to non symmetrically and non identical coupled chaotic neurons.
Sensory dependent dynamics of neural ensembles have been explored by Rabinovich et al. [93] who described the behavior of individual neurons present in two distinct circuits, modeled by conductance based equations of the Hodgkin Huxley type. These formal neurons belonged to an already mentioned ‘CPG’, the STG (Section 3.2) and to coupled pairs of interconnected thalamic reticular (RE) and thalamo cortical (TC) neurons that were previously investigated by Steriade et al. [94]. Although the functional role played by these networks is very different (the latter passes information to the cerebral cortex), both of them are connected by antagonistic coupling (Fig. 15A1 and A2). They exhibit bistability and hysteresis in a wide range of coupling strengths. The authors investigated the response of both circuits to trains of excitatory spikes with varying interspike intervals, Tp, taken as simple representations of inputs generated in external sensory systems. They found different responses in the connected cells, depending upon the value of Tp. That is, variations in interspike intervals led to changes from in-phase to out-of-phase oscillations, and vice-versa (Fig. 15B1 and B2). These shifts happened within a few spikes and were maintained in the reset state until a new input signal was received.
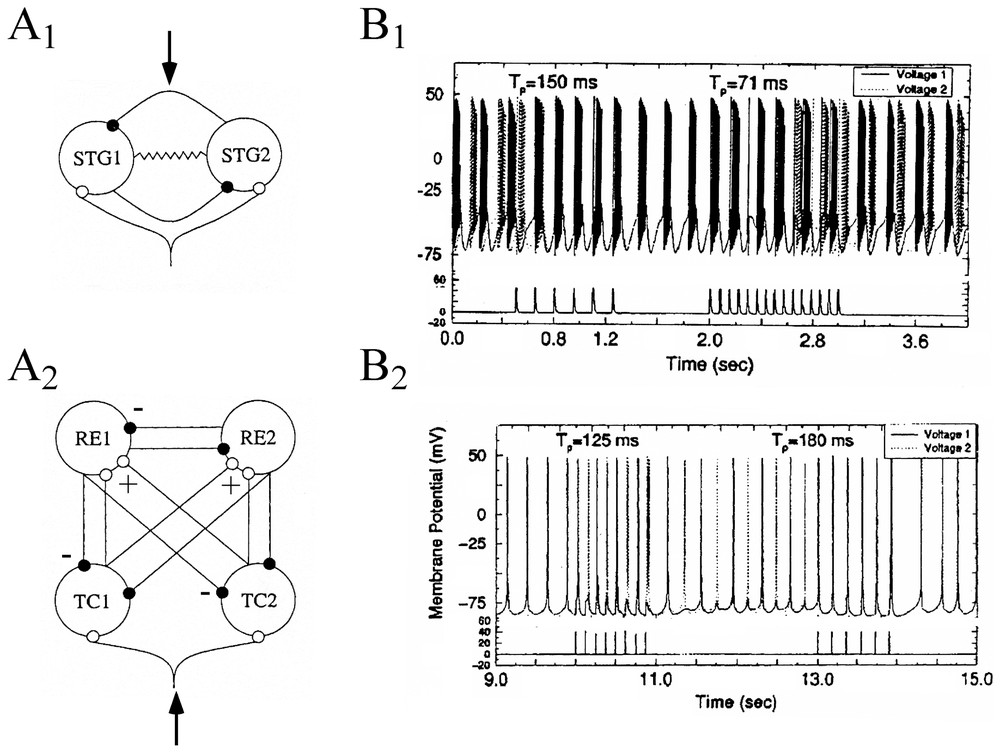
Responses of formal circuits to train of excitatory inputs. (A1–A2) Diagrams of the STG circuits (A1) and of the thalamo-cortical network (A2). Solid and empty dots indicate inhibitory and excitatory coupling connections. The resistor symbol in the CPG denotes a gap junction between the two neurons. External signals were introduced at loci indicated by arrows. (B1–B2) Time series (upper traces) showing the effect of external forcing by 1-s period trains of spikes (lower traces) at the indicated interspike intervals (Tp), in the CPG (B1) and in the RE-TC (B2) circuits. Action potentials from each of the two cells are indicated by solid and dashed vertical lines, respectively. (Adapted from [93], with permission of Physical Review E.)
Since bistability occurs in the CPG when there are two distinct solutions to the conductance-based equations within a given range of electrical coupling [93], the authors further investigated the range of the strength of the inhibitory coupling over which the RE–TC cells act in the same fashion. It turned out that there were two distinct phase portraits in the state space, each one for a solution set (Fig. 16). Here they illustrate two distinct attractors, and the one that ‘wins’ depends on the initial conditions of the system. The two basins of attraction are close to each other, supporting the fact that a switch between them can be easily produced by new spike trains. This behavior corresponds to what the authors call ‘calculation with attractors’ [91].
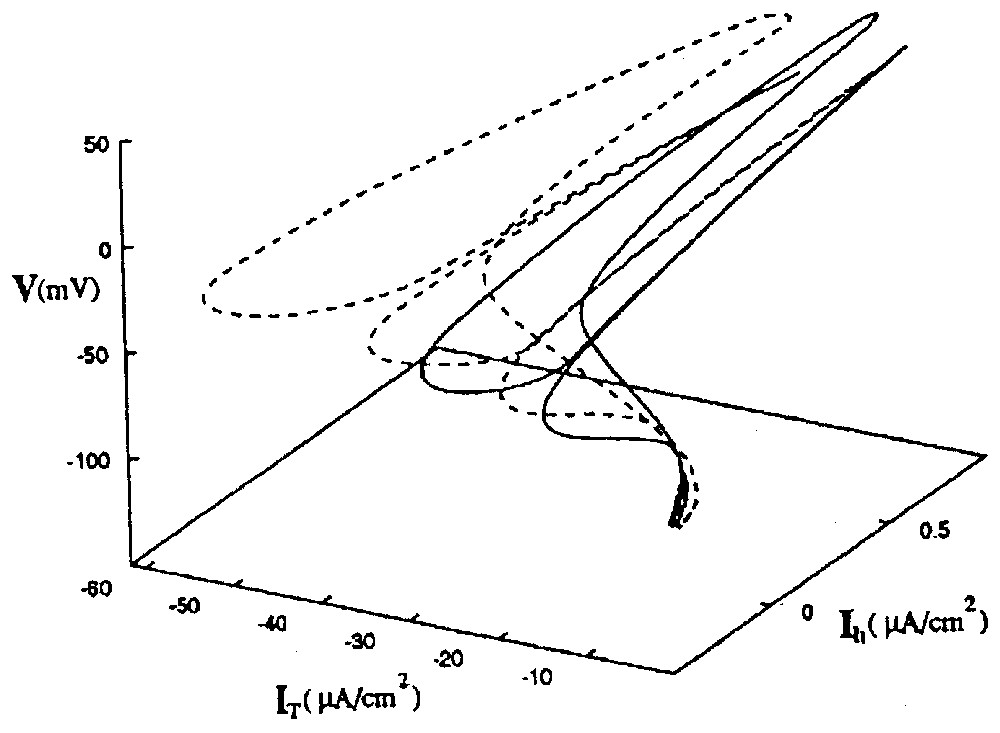
State space portrait of two coexisting attractors of the RE–TC system. The solid line is the orbit in [V(t),IT(t),Ih(t)] space of the in-phase oscillations. The dotted line is the path taken in the same state space by the out of phase oscillations. Note that the two attractors are close to each other, supporting the notion that spike trains with appropriate intervals can induce transitions between them. Abbreviations: V membrane potential, IT and Ih: activation and inactivation of ionic channels. (From [93], with permission of Physical Review E.)
Larger cortical assemblies aimed at mimicking cortical networks were also modeled in order to characterize the irregularities of spike patterns in a target neuron subjected to balanced excitatory and inhibitory inputs [95]. The model of neurons was a simple one, involving two state units sparsely connected by strong synapses. They were either active or inactive if the value of their inputs exceeded a fixed threshold. Despite the absence of noise in the system, the resulting state was highly irregular, with a disorderly appearance strongly suggesting a deterministic chaos. This feature was in a good agreement with experimentally obtained histograms of firing rates of neurons in the monkey prefrontal cortex.
3.4 Comments on the role of chaos in neural networks
Most of the above reported data pertain to CPGs in which every neuron is reciprocally connected to other members of the network. This is a ‘closed’ topology, as opposed to an ‘open’ geometry where one or several cells receive inputs but do not send output to other ones, so that there are some cells without feedback. This case was examined theoretically by Huerta et al. [96] using a Hindmarsh and Rose model. Taking as a criterion the ability of a network to perform a given biological function such as that of a CPG, they found that although open topologies of neurons that exhibit regular voltage oscillations can achieve such a task, this functional criterion ‘selects’ a closed one when the model cells are replaced by chaotic neurons. This is consistent with previous claims that (i) a fully closed set of interconnections are well fit to regularize the chaotic behavior of individual components of CPGs [41] and (ii) real networks, even if open, have evolved to exploit mechanisms revealed by the theory of dynamical systems [97].
What is the fate of chaotic neurons which oscillate in a regular and predictable fashion once they are incorporated in the nervous system? Rather than concentrate on the difficulties of capturing the dynamics of neurons in three or four degrees of freedom Rabinovich et al. [89] addressed a broader and more qualitative issue in a ‘somewhat’ opinionated fashion. That is, they asked how is chaos employed by natural systems to accomplish biologically important goals, or, otherwise stated, why ‘evolution has selected chaos’ as a typical pattern of behavior in isolated cells. They argue that the benefit of the instability inherent to chaotic motions facilitates the ability of neural systems to rapidly adapt and to make transitions from one pattern to another when the environment is altered. According to this viewpoint, chaos is ‘required’ to maintain the robustness of the CPGs while they are connected to each other, and it is most likely suppressed in the collective action of a larger assembly, generally due to inhibition alone.
4 Neural assemblies: studies of synaptic noise
In all central neurons the summation of intermittent inputs from presynaptic cells, combined with the unreliability of synaptic transmission produces continuous variations of membrane potential called ‘synaptic noise’ [98]. Little is known about this disconcerting process, except that it contributes to shape the input–output relation of neurons (references in [99,100]). It was first attributed to a ‘random synaptic bombardment’ of the neurons and the view that it degrades their function has remained prevalent over the years [101]. More important, it has been commonly assumed to be stochastic [102–104] and is most often modeled as such [95,105,106]. Therefore the most popularized studies on synaptic noise have mostly concentrated on whether or not, and under which conditions, such a Poisson process contributes to the variability of neuronal firing [107–109]. Yet recent data which are summarized below suggest that synaptic noise can be deterministic and reflect the chaotic behavior of inputs afferent to the recorded cells. These somewhat ‘unconventional’ studies were motivated by a notion which has been and remains too often overlooked by physiologist, i.e. that at first glance, deterministic processes can take the appearance of stochasticity, particularly in high-dimensional systems. This question is addressed in details in [1]. As will be shown in the remaining sections of this review, this notion brings about fundamental changes to our most common views of mechanisms underlying brain functions.
4.1 Chaos in synaptic noise
Conventional histograms of the time intervals separating synaptic potentials and/or currents comprising synaptic noise suggest random distributions of this measure. However since a chaotic process can appear stochastic at first glance (see [1]), the tools of nonlinear dynamics have been used to reassess the temporal structure of inhibitory synaptic noise recorded, in vivo, in the Mauthner (M-)cell of teleosts, the central neuron which triggers the animal's vital escape reaction.
Several features of chaos were extracted from the differentiated representation of the original time series (Fig. 17A). Recurrence plots obtained with the time delay method already suggested the existence of non random motion [110]. Return (or Poincaré) maps were also constructed with subsets of events selected according to their amplitude by varying a threshold θ (Fig. 17B) and plotting each interval (n) against the next one (n+1). As θ was progressively lowered, the maps first disclosed a striking configuration which took the form of a triangular motif, with its apex indicating a dominant frequency, fp, of the inhibitory post-synaptic potentials that build up synaptic noise (Fig. 17C1). Subtracting events associated with fp in the initial time series further revealed at least three populations of IPSPs of progressively smaller amplitudes having in consecutive return maps, distinct periodicities πp,πs,πt (Fig. 17C1 and C2), all in the so-called gamma range commonly observed in higher vertebrates. Two series of observations were compatible with chaotic patterns, (i) mutual interactions and correlations between the events associated with these frequencies were consistent with a weak coupling between underlying generating oscillators and, (ii) unstable periodic orbits (Fig. 17D) as well as period 1, 2 and 3 orbits (see also Section 6.1) were detected in the return maps [39]. The notion of a possible ‘chaos’ was strengthened by the results of measures such as that of the % of determinism and of the Kolmogorov–Sinai entropy [111] combined with the use of surrogates, which confirmed the nonlinear properties of synaptic noise (Fig. 17E).
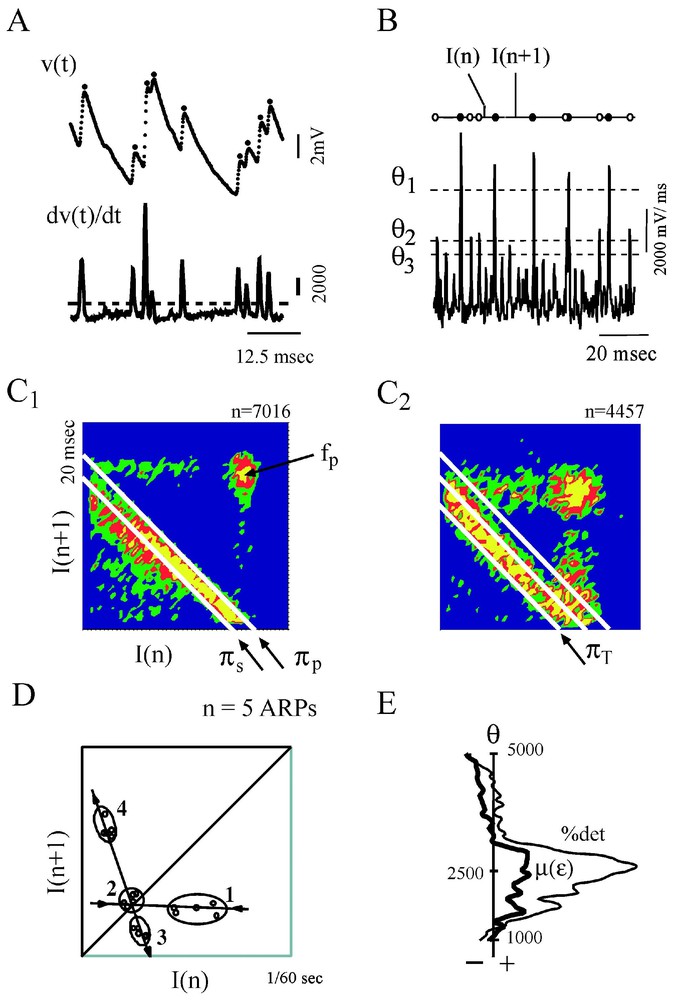
Evidence for non random patterns in the synaptic noise of a command neuron. (A) Consecutive IPSPs observed as depolarizing potentials (dots) recorded at a fast sweep speed (V(t), above) and their derivative (dV/dt, below). The dashed line delineates the background instrumental noise. (B) Derivative of a segment of synaptic noise, recorded at a slow sweep speed: fast events, each corresponding to an IPSP were selected by a threshold θ, having different values (from top to bottom θ1,θ2,θ3); intervals between each selected event, are labeled I(n) and I(n+1). (C1–C2) Return maps constructed with events selected by θ2, i.e. above a level corresponding to an intermediate value of the threshold. The density was calculated by partitioning the space in 50×50 square areas (i.e. with a resolution of 0.42×0.42 ms) and by counting the number of points in each of these boxes. Areas in blue, green, red and yellow indicate regions containing less than 4 points, between 4 and 8, 8 and 12 or more points, respectively. (C1) The principal and secondary periods, πP=16.25 ms and πS=14.4 ms fit the highest density of points at the lower edge of the triangular pattern. (C2) A third period, πT=13.3 ms is unmasked at the base of another triangle obtained after the events used to construct C1 have been excluded. (D) Unstable period orbits (n=5) with stable and unstable manifolds determined by sequences of points that converge towards, and then diverge from, the period-1 orbit (labeled 2), in the indicated order. (E) Variations of the significance level of two measure of determinism, the %det and μ(ε), as a function of θ (see [1] for definitions). The vertical dashed line indicates a confidence level at 2e−5 after comparison with surrogates (A–D) form. (Modified from [39], with permission of the Journal of Neurophysiology.)
A model of coupled Hindmarsh and Rose neurons, generating low-frequency periodic spikes at the same frequencies as those detected in synaptic noise (Fig. 18A) produced return maps having features similar to those of the actual time series providing, however, that their terminal synapses had different quantal contents (Fig. 18C1 and B1 versus C1 and B2). In these simulations the quantal content varied in the range determined experimentally for a representative population of the presynaptic inhibitory interneurons which generate synaptic noise in the M-cell [112]. The involvement of synaptic efficacies in the transmission of dynamical patterns from the pre- to the postsynaptic side was verified experimentally, taking advantage of the finding that the strength of the M-cells inhibitory junctions are modified, in vivo, by long-term tetanic potentiation (LTP), a classical paradigm of learning that can be induced in teleosts by repeated auditory stimuli. It was found (not illustrated here) that this increase of synaptic strength enhances measures of determinism in synaptic noise without affecting the periodicity of the presynaptic oscillators [39].
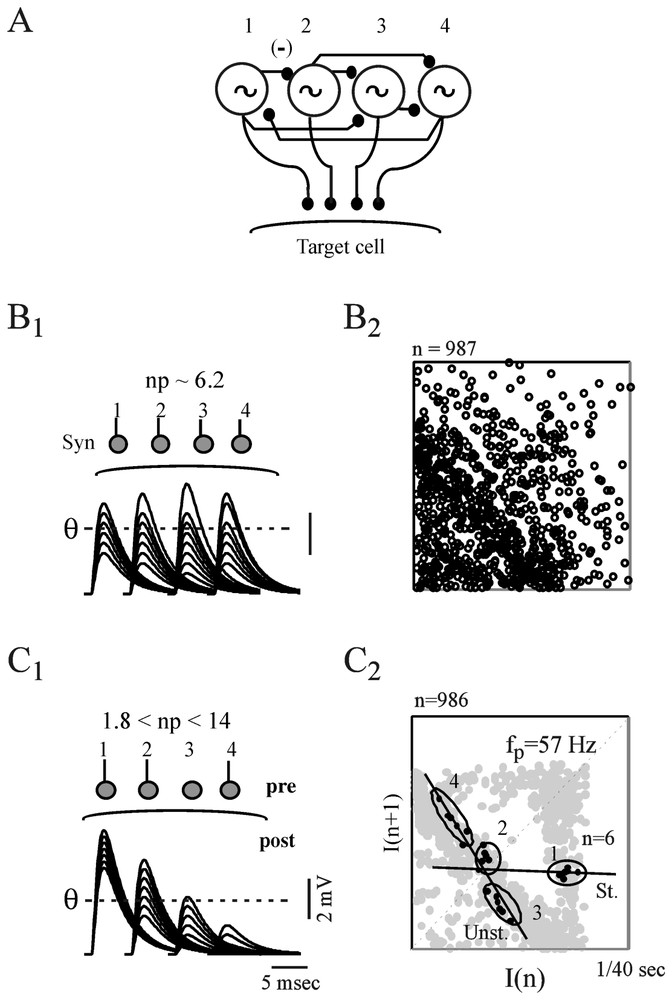
Contribution of synaptic properties to the transmission of presynaptic complex patterns. (A) Modeled Hindmarsh and Rose neurons (labeled 1 to 4), coupled by way of inhibitory junctions and set to fire at 57, 63, 47 and 69 Hz, respectively. (B1–B2) Analysis of postsynaptic potentials produced by uniform junctions. (B1) Top. Same neurons as above implemented with terminal synapses having different releasing properties but the same quantal content, np. Bottom. Superimposed IPSPs generated by each of the presynaptic cells and fluctuating in the same range. As a consequence they are equally selected by the threshold, θ. (B2) The resulting return map appears as random. (C1–C2) Same presentation as above but, terminal synapses now have distinct quantal contents. Thus θ detects preferentially IPSPs from oscillators 1 and 2 (C1) and the corresponding map exhibits a triangular pattern centered on the frequency of the larger events (C2). Note also the presence of UPOs (n=6). (From [39], with permission of the Journal of Neurophysiology.)
4.2 ‘Chaos’ as a neural code
The nature of the neural code has been the subject of countless speculations (for reviews, see [113–115]) and, despite innumerable schemes, it remains an almost intractable notion (for a definition of the term and its history, see [116]). For example, it has been proposed [48,117–119] that the coding of information in the Central Nervous System (CNS) emerges from different firing patterns. As noted by Perkel [49] ‘non classical’ codes involve several aspects of the temporal structure of impulse trains (including burst characteristics) and some cells are measurably sensitive to variations of such characteristics, implying that the latter can be ‘read’ by neurons (review in [120]). Also, a rich repertoire of discharge forms, including chaotic ones, have been disclosed by applying nonlinear analysis (dimensionality, predictability) to different forms of spike trains (references in [121]). Putative codes may include the rate of action potentials [104,122], well defined synchronous activities of the ‘gamma’ type (40 Hz), particularly during binding [123] and more complex temporal organization of firing in large networks [124,125]. The role of chaos as well as the reality of a code ‘itself’ will be further questioned in Section 8.3.
Relevant to this issue, it has been suggested that chaos, found in several areas of the CNS [67,126], may contribute to the neuronal code [95,127–129]. But the validation of this hypothesis required a demonstration that deterministic patterns can be effectively transmitted along neuronal chains. Results summarized in the preceding section indicate that, surprisingly, the fluctuating properties of synapses favor rather than hamper the degree to which complex activities in presynaptic networks are recapitulated postsynaptically [39]. Furthermore, they demonstrate that the emergence of deterministic structures in a postsynaptic cell with multiple inputs is made possible by the non-uniform values of synaptic weights and the stochastic release of quanta.
4.3 Stochastic resonance and noise
The emerging concept in neurosciences of stochastic resonance (SR), which assigns a useful role to random fluctuations, must be mentioned. It refers to a cooperative phenomenon in nonlinear systems, where an intermediate level of activity improves the detection of subthreshold signals (and their time reliability [130]) by maximizing the signal-to-noise ratio (references in [131]). The theory of SR has mostly been developed with the simplifying assumption of a discrete two state model [132,133]. It is described as the consequence of interactions between nonlinearity, stochastic fluctuations and a periodic (i.e. sinusoidal) force [134] and it applies to the case of integrate-and-fire models (references in [135]). The basic concepts underlying this process are illustrated in Fig. 19A and B.
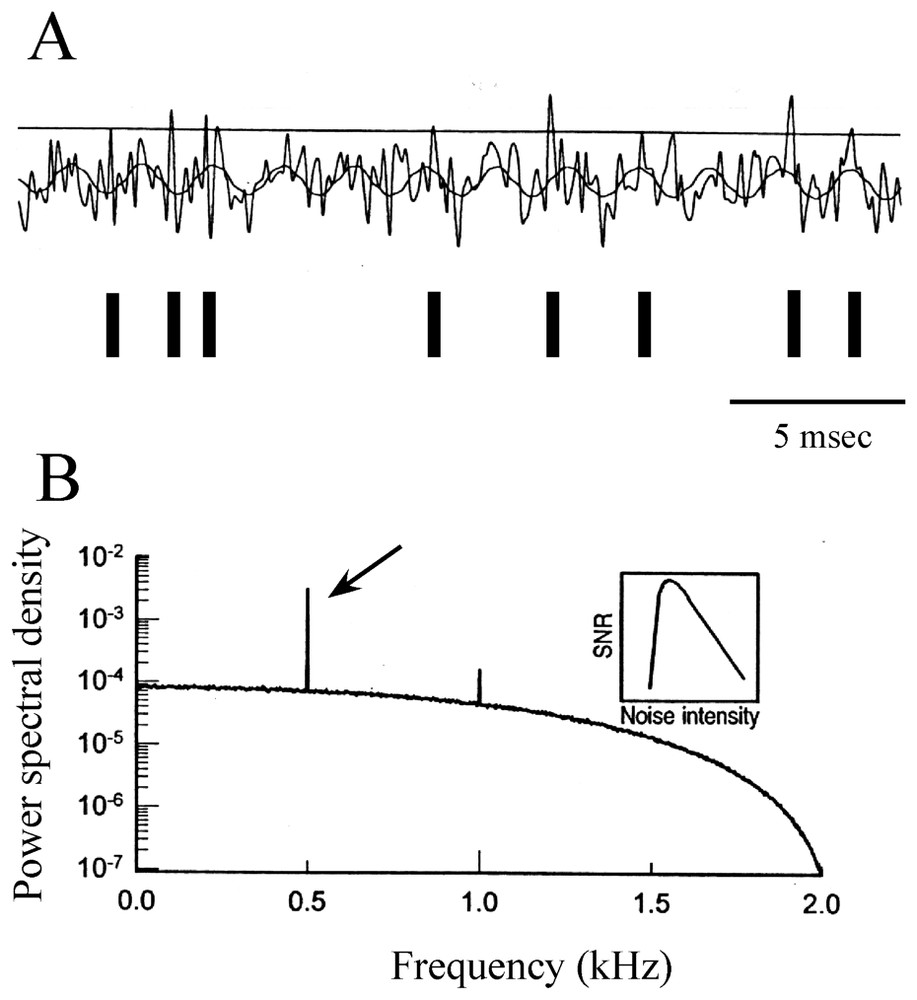
Modulation of a periodic signal by stochastic resonance. (A) Modeled subthreshold sinusoidal signal with added Gaussian noise. Each time the sum of the two voltages crosses the threshold (horizontal line) a spike is initiated (above) and a pulse is added to the time series, as indicated by vertical bars (below). (B) Power spectrum density (ordinates) versus signal frequency (abscissae), with a sharp peak located at 0.5 kHz (arrow). Inset: signal to noise ratio (SNR-ordinates) as a function of noise intensity (abscissae) showing that the ability to detect the frequency of the sine wave is optimized at intermediate values of noise. (Modified from [131], with permission of Nature.)
Data from several experimental preparations have confirmed that SR can influence firing rates in sensory systems, such as crayfish [136] and rat [137] mechanoreceptors, the cercal sensory apparatus of paddlefish [138], and frog cochlear hair cells [139]. It can also play a positive role in rat hippocampal slices [140] and in human spindles [141], tactile sensation [142] and vision [143]. SR is also likely to occur at the level of ionic channels [144] and it could favor synchronization of neuronal oscillators [145].
Several aspects of SR call for deeper investigations, particularly since noise, a ubiquitous phenomenon at all levels of signal transduction [146], may embed nonrandom fluctuations [147]. Enhancement of SR has been demonstrated in a Fitzhugh–Nagumo model of neuron driven by colored (1/f) noise [148], while periodic perturbations of the same cells generate phase locking, quasiperiodic and chaotic responses [149]. In addition, a Hodgkin and Huxley model of mammalian peripheral cold receptors, which naturally exhibits SR in vitro, has revealed that noise smooths the nonlinearities of deterministic spike trains, suggesting its influence on the system's encoding characteristics [150]. A SR effect termed ‘chaotic resonance’ appears in the standard Lorentz model in the presence of a periodic time variation of the control parameters above and below the threshold for the onset of chaos [151]. It also appears in the KIII model [152] involving a discrete implementation of partial differential equations. Here noise not only stabilizes aperiodic orbits, since an optimum noise level can also act as a control parameter, that produces chaotic resonance [153] which is believed to be a feature of self organization [153]. Finally SR has been reported in a simple noise-free model of paired inhibitory-excitatory neurons, with piece-wise linear function [154].
5 Early EEG studies of cortical dynamics
An enormous amount of efforts has been directed in the last three decades towards characterizing cortical signals in term of their dimension in order to ascertain chaos. However, with time, the mathematical criteria for obtaining reliable conclusions on this matter became more stringent, particularly with the advent of surrogates aimed at distinguishing random from deterministic time series [155]. Therefore despite the astonishing insights of their authors, who opened new avenues for research, the majority of the pioneer works (only some of which will be alluded to below), are outdated today and far from convincing.
5.1 Cortical nets
Most of the initial investigations have relied upon the analysis of single channel electroencephalographic (EEG) signals, with attempts to estimate dimension with the Grassberger–Procaccia algorithm, the average pointwise dimension [156], the Lyapunov exponent, the fractal dimension [157] or the mutual information content [158]. But in addition to the conflict between the requirement of long time series and the non-stationarity of actual data, serious difficulties of such measures (such as artefacts or possible misinterpretations) have been pointed out [159,160]. That is, refined tests comparing measures of segments of EEGs led to the conclusion [160] that the actual data could not be distinguished from gaussian random processes, pending support of the view that EEGs are linearly filtered noise [161], either because they are not truly chaotic or because they are high dimensional and determinism is difficult to detect with current methods. This rather strong and negative statement was later on moderated by evidence that, as pointed out by Theiler [155], despite the lack of proof for a low-dimensional chaos, a nonlinear component is apparent in all analyzed EEG records [160,162–167]. This notion is illustrated in Fig. 20, where recordings obtained from a human EEG, were analyzed with a method that combined the redundancy approach (where the redundancy is a function of the ‘Kolmogorov–Sinai’ entropy [166]) with the surrogate data technique. The conclusion of this study was that, at least, nonlinear measures can be employed to explore the dynamics of cortical signals [168]. This view has been strongly vindicated by later investigations ([169], see Section 6.2.2).
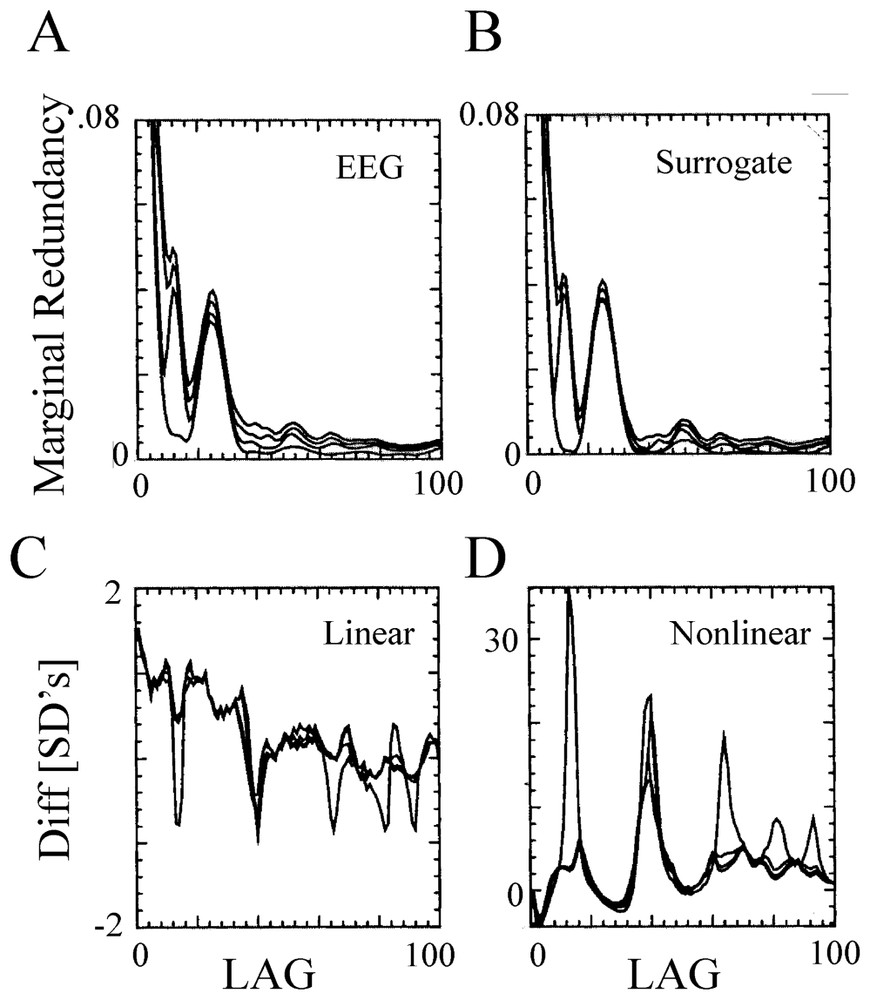
Nonlinearity of human EEG. (A,B) Redundancy assessed on a 90 s recording session (during the sleep state) at one location of the scalp (A), and on its surrogates (B), as a function of the time lag. The four curves in each panel correspond to a different embedding dimension, n=2 to 5 (from bottom to top). Note the lack of qualitative differences between the tests computed from the EEG and its surrogates. (C–D) Linear (C) and nonlinear (D) redundancy statistics for the same EEG record. Note that several highly significant differences (tens of SDs) were detected in the nonlinear statistics in contrast with the low difference in the linear ones. Note also the different scales, in C and D. (From [166], with permission of Biological Cybernetics.)
5.2 Experimental background
Freeman and his collaborators took advantage of the relative simplicity of the olfactory bulb electrogenesis and of the ability to insert arrays of electrodes in this structure in conscious rabbits, to (i) search for EEG patterns during odor recognition and discrimination, and (ii) investigate the effects of learning. Both were expected to stabilize the distribution of the recorded electrical activities. In presence of a learned odor, a distinctive pattern was observed on the entire bulbar surface, suggesting that each neuron in this structure participated in every discriminative response [170,171]. Furthermore a mathematical model of the bulb was constructed with nonlinear differential equations [172,173], possibly because dimensionality could not be measured due to limited data sets. It generated time series that resembled the surface EEG obtained experimentally (for details, see Section 7.1). These belonged to four classes which are illustrated in Fig. 21A, namely, (i) total silence, as in deep anaesthesia, (ii) a ‘normal’ state, with fast and desynchronized traces, which were recorded in waking but unmotivated animals, suggesting a chaotic activity with a correlation of 5.5 (in the model) and 5.9 (in the experimental data), (iii) in reaction to a learned odor, the EEG was characterized by inspiratory bursts of oscillations that disappeared during expiration and simulations suggested that this state corresponds to a limit cycle attractor [173] that was specific to a given odor, with a dimension decreasing from 2.3 to 1.13 during its presentation. That is, this irregular pattern was interrupted by oscillatory bursts following activation of the olfactory receptors. Finally, (iv) a last type of activity resembled that of an epileptic seizure; it occurred after an intense electrical simulation of the lateral olfactory tract, and it had a dimension of ∼2.6 in both experimental and simulated data [174]. The corresponding attractor was toroidal shaped. The authors believed that the shift from one state to the next could occur abruptly, via bifurcations, and they concluded that when placed in a given learned input ‘domain’, the neural system has a tendency to generate a qualitatively distinctive form of ordered behavior that emerges from a chaotic background state [127].
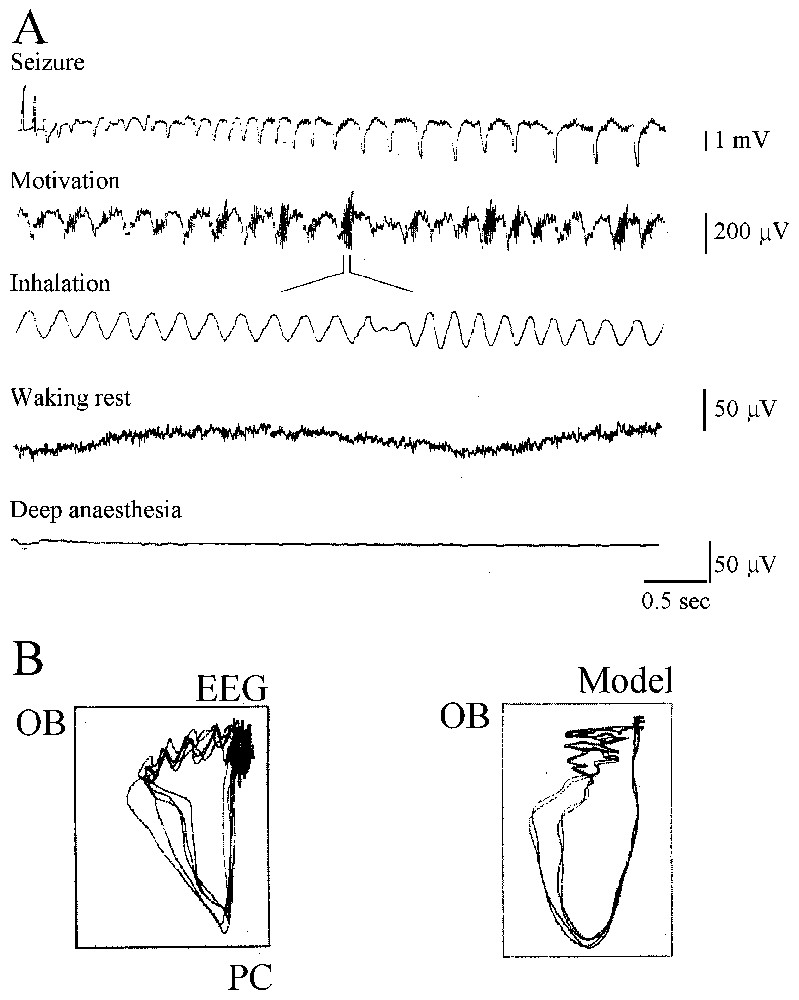
Dynamical states identified in the rat olfactory bulb by EEG recordings. (A) From bottom to top. Recordings obtained in the indicated behavioral phase (see text for explanations). (B) Comparison of attractors computed using experimental data (left) and using a model (right) from the prepyriform cortex (CP) and the olfactory bulb (BO), suggesting a torus. Note that although related, the two maps are not identical. (From [173], with permission of Biological Cybernetics.)
Other analysis of experimental data include those of Rapp et al. [175], who reported low-dimensional firing rates of (sometime injured) neurons in the anaesthetized squirrel monkey and of Röschke and Basar [176], who observed low (within 4 to 5) correlation dimensions of slow waves recorded with chronically implanted electrodes in the auditory cortex, the hippocampus and the reticular formation of sleeping cats. Studies of extracellularly recorded spike trains obtained in the optic tectum of awake pigeon [177] and in the thalamus and substantia nigra of anaesthetized rats [178] suggested chaos, with evidence that sensory (auditory) stimulations strongly affected the ‘chaotic’ behavior in the latter preparation. ‘High-dimensional’ nonlinear structures of interspike intervals with predictability were reported in nigral dopaminergic neurons [179].
5.3 First struggles with human data
Babloyantz and her collaborators [180] were the first to study the human EEG with the tools of nonlinear dynamics that they applied to recordings obtained during sleep. Chaos was assumed on the basis of low dimensions (4–5) and positive Lyapunov exponents computed during stages 2 and 4, characterized by α and γ waves, respectively. In contrast, no attractor was detected in the awake state or during the rapid eye movement (REM) phases of sleep. Numerous reports followed this observation but they were liable to strong criticisms despite the fact that the number of subjects examined increased and the algorithms as well as comparative statistics became more rigorous [181]. Conflicting conclusions were also obtained relative to (i) whether dimension is higher when eyes are opened than when they are closed and α rhythm is more pronounced [182–184], and (ii) defining a ‘resting’ state in the sole presence of a low dimensionality [185,186]. On the other hand, results obtained with a variety of tasks cutting across different sensory modalities and various states of attention supported the idea that nonlinear analysis is a valid approach for characterizing aspects of brain dynamics that cannot be seen with classical spectral methods (references in [168]; see also [187,188]).
5.4 Pathological processes and chaos
Although models of neural networks had already indicated that bifurcation sequences were involved in transitions from steady states to chaotic activities [189], the first dimensional analysis of an epileptic (petit mal) EEG was, again, provided by Babloyantz [190] who postulated the existence of a chaotic attractor being the direct consequence of the “deterministic nature of brain activity”. Phase portraits of attractors was constructed (Fig. 22), and measures of the dimensionality (which was low), of the Lyapunov exponent, evaluation of the autocorrelation function and comparisons of the derived values with those of ‘normal’ EEGs seemed to be in agreement with the author's conclusions. This work was followed by investigations of human epileptic EEGs [191,192] and rat [193] with measures of Lyapunov exponents and of the correlation dimensions, which suggested the emergence of chaotic attractors during seizures.

Human epileptic seizure activity. The illustrated petit mal episode, lasting ∼5 s, was the longest and the least contaminated by noise during a 24 hour recording session. Channels 1 and 3, which measured potential drops between the frontal and parietal regions of the scalps, were used to construct the space phase trajectories and for further analysis (see text) suggesting chaotic-like components in the signals. Inset: phase portrait constructed with channel 1. (Adapted from [190], with permission of the Proceedings of the National Academy of Sciences (USA).)
Investigations of other diseases such as Creutzfeld–Jakob, schizophrenia and finnitus were inconclusive (see details in [168]) but they reinforced the belief in ‘dynamical diseases’ [7] and a potential usefulness of a nonlinear approach for diagnostic purposes (see also Section 6.3.2).
6 Recent approaches of cortical dynamics
Despite serious pitfalls and limitations that have been dissected out in several reports [164,194–196], studies of brain signals have greatly benefited from the method of surrogate-data testing for nonlinearity [155]. As detailed in Part I of this review [1] the basic principle here is that nonlinearity can be established by a comparison of a nonlinearity measure of the data on the one side and of a collection of surrogate data sets on the other side, the latter sharing the data's linear properties but otherwise being random [196]. Although the null hypothesis for linearity of this test can still be rejected by noisy or intrinsically unstable time series [197], the availability of surrogates opened a new era in the studies of signals generated by single neurons and/or by neuronal assemblies.
6.1 Unstable periodic orbits
An alternative to conventional measures of chaos has been to search in the reconstructed space phase or in return maps for geometric figures called unstable periodic orbits (UPOs) which constitute the skeleton of chaotic systems [198,199]. Chaotic trajectories wander endlessly around unstable fixed points in sequence of close approaches to, and departures from them, along characteristic directions called stable and unstable manifold, respectively. The structure of this dynamics is known mathematically as that of a ‘saddle point’. This analogy refers to the behavior of a ball placed on a saddle. Specifically, if placed at its center the ball will remain there until a small perturbation displaces it to one side or the other, but always in the transverse direction towards one of the stirrups (unstable manifold). Conversely, if the ball is placed in front or the back of the saddle, it will roll along the center line (stable manifold) towards the unstable equilibrium point located at the center of the saddle. This simple metaphor, which was proposed by Weiss et al. [200] helps to understand a basic property of chaotic systems: due to their critical sensitivity to initial conditions, they can be controlled by an external minimal perturbation [200–202]. Several methods are available for this purpose [203] and they all take advantage of the fact that a chaotic trajectory can be stabilized on a desired orbit or otherwise stated, that the ‘ball’ can be pushed back to the center of the saddle, near an unstable equilibrium point (see also Fig. 17 of Faure et al. [1]).
Thus, theoretically, one could detect chaos in natural systems, by using (i) the search for UPOs, and (ii) chaos control techniques, as pioneered in arrhythmic cardiac tissue by Garfinkel et al. [204]. Such a control was successfully achieved in rat hippocampal slices exposed to high external K+ perfusion which triggered irregular burst discharges of pyramidal cells, occurring at irregular intervals and resembling epileptic interictal spike foci [126]. The bursts became increasingly periodic following electrical stimulations of the Schaffer collaterals at frequencies determined by previous identification of unstable fixed points using extracellularly recorded time series converted into first return maps which exhibited well defined UPOs. An inverse procedure termed ‘anticontrol’ was also effective in moving the system away from these orbits and reduced its periodicity.
The Schiff et al. [126] interpretation of their data has been strongly challenged by Christini and Collins [205]. Implementation of the Fitz–Nagumo model allowed these authors to demonstrate that chaos criteria of the form used in [126] could be reproduced by a noise-driven, non chaotic neuronal system. They obtained similar results when they applied chaos control to a single stochastic system, suggesting that this procedure can be applied to a wider range of experimental systems than previously assumed.
Statistically significant evidence (as demonstrated with surrogates) of the existence of UPOs has been obtained in time interval scatter plots of spike discharges of the caudal photoreceptor of the crayfish [67]. Rules for a strict definition of UPOs were in fact established in this preparation where their presence was taken as an indicator of low dimensional dynamics. They were also found in the inhibitory synaptic noise of the teleost M-cell [110] and in periodic bursts of action potentials recorded with EMGs in intact swimming lampreys, or with suction electrodes during lamprey's fictive swimming [206]. In addition UPOs were carefully tested against surrogates in series of time intervals between successive spike discharges recorded with EEG electrodes on the scalp of a patient suffering from epileptic focal seizures [207]. The recordings were taken in three consecutive experimental conditions, i.e. at rest, and during the performance of a visual or an auditory discrimination task requiring a finger response. Only one UPO was detected at rest whereas two specific ones emerged, in a striking one to one association, following a given sensory stimulus presentation (visual or auditive). Finally, So et al. [208] applied the transform technique previously described by them (which uses the local dynamics of the system such that the transformed data are concentrated about distinct UPOs and identify complex higher period orbits) to (i) single cell and (ii) network burst firing activity recorded in rat hippocampal slices as well as to (iii) digitized human EEG, collected from epileptic patients. They were able to unravel the ‘hierarchy’ of low periodic orbits (Fig. 23A and B) present in dynamical systems [209,210] and to establish that the estimated dynamics near the UPOs have predictive properties, thus confirming that close trajectories near them have similar behavior (Fig. 23B).
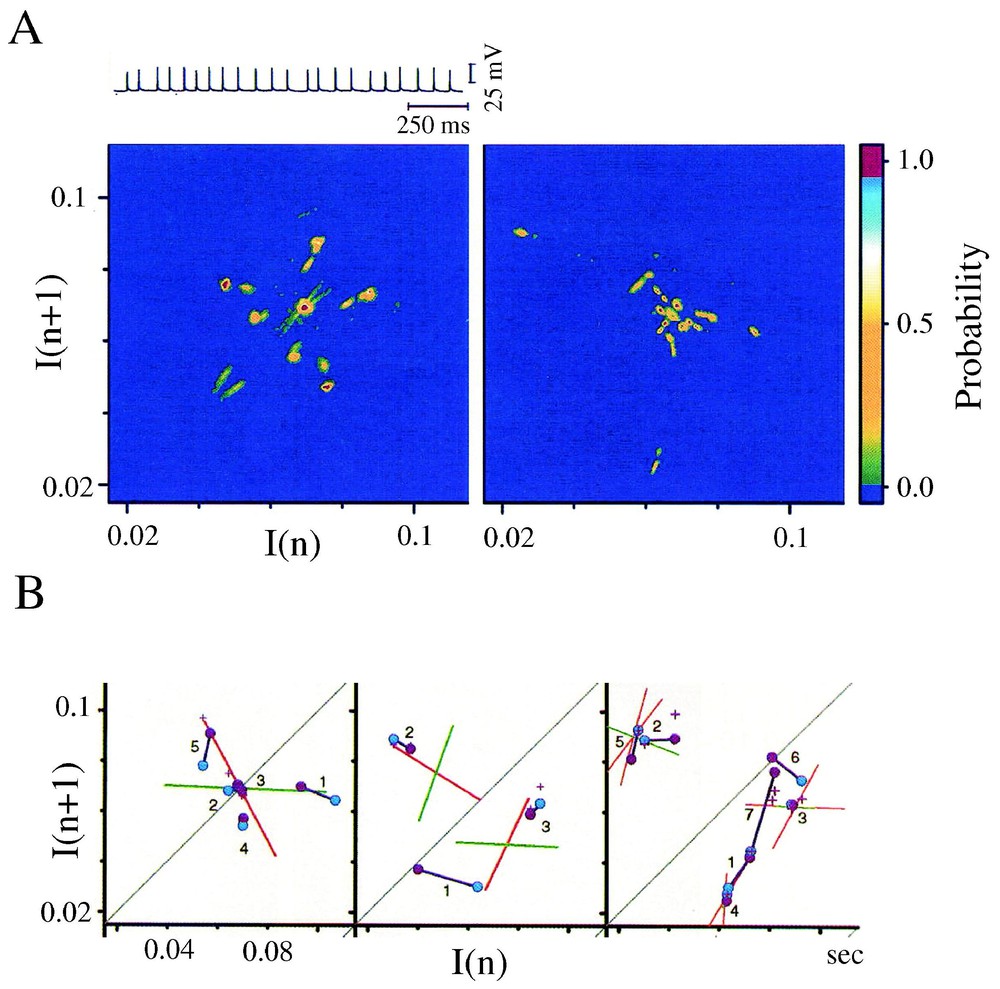
Hierarchy of UPOs from a single hippocampal cell. (A) Above: Sample recorded sweep with consecutive action potentials. Below: return maps with a family of period-2 (left) and period-3 (right) orbits. Colors indicate probability of the transform data density being outside the distribution of maximum peaks observed from 100 transformed surrogate densities. The most significant spots, with probability ⩾0.95 are shown in red; note the presence of two of them (out of 6 possible period-2 orbits) and of three (out of 5 possible -3 orbits) strongly significant ones (B) Local dynamics around three representative orbits. They are illustrated by green and red lines, which indicate their stable and unstable manifolds, respectively. From left to right: period-1, -2, and -3 orbits. Deviations between pairs of representative trajectories are plotted in successive time steps and indicated by connecting lines. Symbols = ▵, initial points; ∘ subsequent steps; + predicted positions. (Adapted from [129], with permission of The Biophysical Journal.)
6.2 Period-doubling bifurcations
Some neuronal systems can undergo transitions from a steady state to an oscillatory firing mode (Fig. 2) or from producing periodic to bursting clusters of action potentials (Figs. 5 and 6). And a universal evidence of chaos is provided by complete sequences of period-doubling cascades, as first evidenced by Feigenbaum [211] references in [1]. This ‘road’ to chaos can be induced by injecting intracellularly various intensities of DC currents which act as a ‘control parameter’, as in the case of the squid giant axon illustrated in Fig. 4. Similarly, noise-mediated oscillators contained in the electrosensory organs of the paddlefish Polydon Spathula can be forced to generate nearly periodic spiking patterns, with frequency locking in different modes, by external periodic and electric fields [212]. More physiological stimuli, such as sensory inputs, can act in the same way and produce profound changes in the behavior of ‘integrative’ structures of the brain.
A striking example of this scheme is found in the work of Crevier and Meister [213] who subjected the retina of the larval tiger salamander and the human visual system to flicker patterns of varying frequency and contrasts and recorded in vivo the accompanying electro retinograms (ERG). They found that “during rapid flicker, the eye reports to the brain only every other flash of light”. Retinal ganglion cells, fire spikes on alternating flashes, resulting in period-doubling bifurcation in visual processing. Specifically, at slow frequency, a volley of spike was observed at both the onset and offset of each flash. As frequency increased above 4 Hz, the ‘on’ volley disappeared (Fig. 24A1) and above 9 Hz, every other flash was followed by a volley of action potentials whereas the intervening ones failed to elicit a response (Fig. 24A2). Another bifurcation occurred at 12 Hz with no more than 1 response every 4 stimulations. Finally, above 15 Hz, a seemingly chaotic pattern was recognized in the ERG and in the nerve fibers (Fig. 24A3). More strikingly, the entire population of retinal cells acted in synchrony rather than ‘choosing’ flashes independently of each other. At higher frequencies, this ‘synchronous period-doubling’ reversed until the signal was again periodic for values >30 Hz (Fig. 24B1). The authors observed a similar scenario when they varied the contrast of the flashes, while keeping the frequency constant (Fig. 24B2).
Synchronous period-doubling of responses of the salamander retina. (A1–A3) In each panel recordings of the ERG (above) and optic nerve fibers (middle) to uniform flash stimuli (below) delivered at the indicated frequencies. Filled circles designate response magnitude; note that the response amplitude repeats on every cycle (A1), every two cycles (A2) and becomes chaotic (A3) as the stimulus frequency increases from 4 to 15 Hz (B1–B2). Bifurcation plots of ERG amplitude as a function of flash frequency at constant contrast (B1) and as a function of contrast at constant flash frequency. (C1–C3) Period-doubling in a model of nonlinear feedback where ‘input impulses’ are scaled by a variable gain g(y) that depends on the time constant τ of the decay of the amplitude B of a preceding impulse (C1). Bifurcation plots of the model output pulse amplitude displayed as in B1 and B2, are shown in C2 and C3, respectively. (Adapted from [213], with permission of the Journal of Neurophysiology.)
Accelerating sequences of period-doubling lead to chaotic regimes in neural models [54] and many nonlinear systems that exhibit such a behavior contain some form of negative feedback by which responses affect the subsequent ones. Thus Crevier and Meister constructed a single model of nonlinear feedback where the peak amplitude of the ERG was taken to be proportional to the amplitude of the light flash, C, and to a gain factor, g(y) (Fig. 24C1). With just two parameters (i.e. gain and its exponential decay τ as a function of the recent response), the predicted bifurcation plots matched the approximate locations of the experimental branch points for both flash frequency (Fig. 24C2) and contrast (Fig. 24C3). This confirmed experimental evidence that the critical feedback interactions require only cone photoreceptors and off-bipolar cells.
The possible mechanisms of this period-doubling (which may involve synaptic and/or presynaptic conductances) remain unclear and one can also note that the chaotic sequences of the bifurcation plots were not fully characterized with measures of chaos. Finally, Canavier and Meister demonstrated an analogous regime of period doubling in human ERGs occurring between 30 and 70 Hz. When measured by the power in the subharmonic components of flash frequencies the degree of period-doubling of the human visual evoked potentials was even greater in the latter than in the ERGs. The authors further suggested that this process is related, at the retinal level, with illusionary flicker patterns.
6.3 Epileptic activities and electroencephalograms
EEGs represent the integral output of a large number of neurons, with complex underlying dynamics or, otherwise stated, of subsystems with numerous degrees of freedom. In addition, the presence of noise of unknown origin makes it hopeless to reinterpret the data within the frame of chaos theory. This was conclusively demonstrated by Theiler [214] who reexamined a published case of an epileptic EEG that had previously yielded ‘evidence’ of chaos. The measures (Lyapunov exponent and correlation dimension) turned out to be closely matched by surrogates. Accordingly most authors failed to demonstrate ‘true’ chaos in the resting brain on the basis of EEG recordings that are barely distinguishable from those of linearly filtered noise [166,215–218].
6.3.1 Epilepsy and chaos-indicators
Despite the above mentioned difficulties in characterizing EEGs which ruined initial hopes (see also Section 5.3), epilepsy continued to be considered as a privileged material for ascertaining chaos because it is a widely recognized model of neuronal synchronization and it is commonly believed that seizure episodes are characterized by bifurcations to system states of low complexity [219,220]. In line with this notion, a number of available data indicate that decreasing dimensionality is an essential characteristic of sensory information processing [221]. The complexity of the EEG is decreased during the P3 event-related potential in a task dependent and area specific way [222], as shown with the method of ‘point-correlation’ dimension, [223] which is capable of tracking changes in epochs with non stationary features. Thus, whatever their conclusions about ‘chaos’ per se, results of studies of animal and human epileptic brains deserve particular attention because they brought a new light to the relevance of nonlinear tools for comparative studies, (i.e. state by state), of neuronal dynamics. This concept is further discussed in Section 8.4.
Finally, epileptic bursts were produced in the CA3 region of the rat hippocampal slices exposed to a K+ enriched extracellular medium by electrical stimulations of the mossy fiber inputs. Time series of the evoked field potentials were analyzed and the conclusion was that of ‘undoubted’ evidence for chaos [224]. These were bifurcations leading to a chaotic state, strange attractors in the tri-dimensional phase space, positive Lyapunov exponents estimated using the Wolf's algorithm and non-invertible strobomaps with unstable fixed points (Fig. 25A1 and A3). In addition the phase diagrams delineated regions with several values of phase-locking and irregular responses having features of intermittency (Fig. 25B). Given the strength of these findings it is unfortunate that the authors did not validate their conclusions with surrogates, particularly since Schiff et al. [225] had not long before applied tests for determinism to time series of population spikes also monitored in the rat CA3 region in presence of a high K+ medium; three tests had been applied (an adapted version of the local flow approach, a local dispersion and a nonlinear prediction), and in all instances the surrogates pleaded in favor of stochasticity.
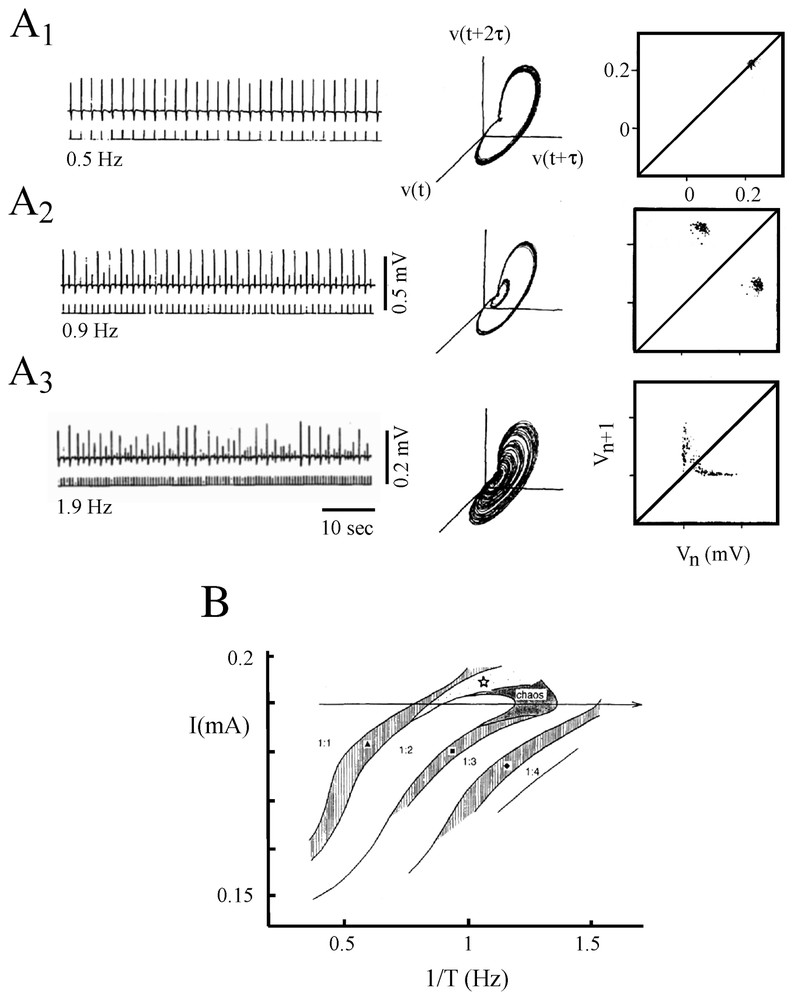
‘Chaotic’ responses of epileptiform bursts. (A1–A2) Left. Sample recordings of field potentials evoked in a slice of the CA3 region (upper traces) by a mossy fiber stimulation and successive current pulses (lower traces) of constant amplitude and duration. Note the amplitude fluctuations of the responses, with a 1:1 (A1) a 1:2 (A2) phase locking and a chaotic pattern (A3) when the intervals between pulses were 0.5, 0.9 and 1.9 Hz, respectively. Middle. Attractors reconstructed from the corresponding time series of 40 s each (delay time: τ=10 ms). Right. One dimensional strobmaps constructed with 71, 201 and 201 evoked responses; the maps show a non-invertible function and a slope at their fixed points more negative than −1. (B) Phase diagram of the field potentials responses. In areas marked 1:n, one burst occurs each n=1,2,3,4 current pulses and in the regions marked by a filled triangle, a square and by a diamond, intermittency occurs. In the area signaled by a star, the responses are not deterministic (abscissa: inverse of the interpulse intervals, 1/T; ordinate: amplitude of the current pulses, I). (Adapted from [224], with permission of Brain Research.)
6.3.2 Prediction of epileptic seizures
Past efforts to identify systematic changes in the preictal to ictal EEG with linear measures [226,227] were resurrected with the presumptions that such recordings have nonlinear properties. This finding prompted numerous groups to search for preseizure patterns that could precede the onset of electrical and/or clinical manifestations of the disease and help localize the epileptic locus [193,219,220,228–238]. As expected, several nonlinear measures, particularly the effective correlation dimension, Deff, and the Lyapunov exponents, can help ‘anticipate’ the occurrence of seizures up to about twenty minutes before their onset. These results were taken as justifying hopes that one can construct an ‘in vivo warning device’ that could help control drug-resistant epilepsies. On the experimental side, intracellular recordings of neurons from guinea pig CA3 hippocampal slices indicated that the slow depolarization, which precedes the critical ‘paroxysmal depolarizing shift’, is accompanied by clear modifications of Deff in some models of epilepsies (i.e. induced by xanthine or penicillin) whereas a similar loss of complexity could not be detected in low-veratridine models [239]. However as in the case of other complex functions and syndromes, different reports have tempered this optimism. For example, warnings were given about artifacts that appear at high value of the correlation integral and erroneous interpretations of the phase randomization of the data encountered during a study where only one out of six seizures yielded ‘high-quality’ attractors [240]. Furthermore, careful comparisons of methods (power spectral density, cross correlation, principal components analysis, phase correlation, wavelet packet analysis, correlation integral and mutual prediction) for detecting, in intracranially recorded EEGs, the earliest dynamical changes leading to seizures, found no predictive advantages of the nonlinear over the linear ones, and wisely warranted ‘addressing the problem from a variety of viewpoints’ [241]. A rather similar conclusion had been reached by Schreiber [197] who used the reversibility test in one case of epilepsy and found no definite proof for chaos despite the ‘rejection’ of the null hypothesis by surrogates.
7 Dynamics of large scale networks
7.1 Possible role of chaos
Application of the tools and concepts of nonlinear dynamics to studies of the neural correlates of ‘higher’ brain functions have motivated several hypothesis regarding biological attractors and their role in information processing, perception, motor behavior, memory and cognition. These functions involve enormous populations of cells and multiple positive as well as negative feedbacks. These features, together with the striking variability of the signals obtained by recording neuronal activity [242] have been taken as arguments favoring the notion that the dynamics of the nervous system are nonlinear, and even chaotic. This hypothesis has continued to attract numerous researchers despite unconvincing experimental results (since there are no definite tests for chaos when it comes to analyzing multidimensional and fluctuating biological data ([9], see also [1])). Also, there have been suggestions that, rather than chaotic, some experimental series may be better described using other terms (1/f long-range scaling, fractal, multifractal) which, however, have no clear implications with respect to underlying mechanisms [9].
A number of formal models with dynamic and/or chaotic properties have served as analogs for, and as alternatives to, physiological networks. Their efficiency in pattern recognition, storing and retrieval, and their effectiveness, for example in employing Cantor sets for coding information have been the subject of extensive research, based on various mathematical tools [10,89,95,114,243–250]. Yet, none of these descriptions fully capture the features of complex systems. As this highly specialized field is rapidly evolving, the most relevant propositions of only some of these models will be considered.
The first, and perhaps strongest advocates of chaos in the brain, namely Freeman and his collaborators, have replicated features of the EEG of the olfactory system and its dynamics (see also Section 5.2) including during perceptual processing and recognition of a known odor, or learning of a new one [127,173,174,251–255]. Their model of the olfactory bulb, denoted KIII is composed of nonlinear ordinary differential equations (ODEs) with feedback delay. Each ODE stands for a neural mass, having either an excitatory or inhibitory output to the ODEs with which it connects. Connected mutually inhibitory or excitatory pairs mimic populations of similar neurons that form one structure (called KI). A KII set of excitatory or inhibitory KI sets portrays one of the relay stations of the olfactory system (i.e. the olfactory bulb, the anterior olfactory nucleus and the prepyriform cortex, respectively). Both basal and stimulated states were mimicked and the results were compared with actual recordings from rats and rabbits, using amplitude histograms, power spectra, attractor reconstruction, visual inspection of traces and correlation. ‘With proper settings’ the model yielded sustained chaotic activity that was indistinguishable from that of background EEG of the resting animals. Furthermore, with stimulations, it produced ‘bursts’ of oscillations that forced the system through a change from the aperiodical basal state to a more periodic pattern similar to that observed during inhalation (see also Fig. 21).
These experiments led Freeman's group to postulate specific roles of chaos in memory and brain functions and to apparently refute the classical views of information processing and of representations advocated by connexionist neuroscientists. Rather, internal states would correspond to low dimensional attractor with multiple ‘wings’ [255–257]. According to this scheme, the central part of the attractor is its basal chaotic activity. It provides the system with a ‘ready state’ and each of the wings may be either a near-limit cycle or a broad band chaos which stands for many templates or neural cell assemblies. Pattern recognition is then considered as the transition from one wing to another, whereas a novel input (with no template) activates the system to a non-reproducible near-limit cycle wing, or a new broad band. The scale invariance of the system and its independence of the initial conditions at the transitions enable the system to classify an uninterrupted sequence of stimuli. That is, and taking a specific example, a chaotic well provides an escape from an established attractor so that an animal can recognize an odorant as novel with no greater delay than for any known sample with, however, the freedom to maintain its activity while building the new attractor [127]. Therefore chaos confers the system with a deterministic ‘I don't know’ state within which new activity patterns can emerge.
The strong and weak points of the model have been repeatedly debated by the authors themselves and by others. It is interesting that the main uncertainties concerning the ‘physiological’ requirements of the algorithm that were postulated at the onset of this work [127] have been validated for a large part by recent electrophysiological studies. These were (i) excitation of the periglomerular cells by each other and to mitral cells [258], (ii) mutual inhibitory interneurons in the olfactory bulb [259] and cortex, and, (iii) mutual excitatory connections among mitral cells in the bulb [260]. Conversely, it is now demonstrated that, contrary to earlier beliefs of the authors [255] inhibitory synapses can undergo changes with learning.
The endless controversy about the respective virtues of chaotic models versus the connectionnist ones, developed by others [249,261–266] remains unsolved. According to Freeman [127] the connectionnist algorithms tend to be ‘pattern completion devices’ the successful task of which can only be achieved when interactions between units are appropriately weighted. Therefore, chaotic systems would be well designed for preventing convergence and for an easy ‘destabilization’ of their activity by a novel input (odor). They could also be ideally fit for accommodating the neural networks with a new and still unlearned stimulus. In an extension of this model, and to account for phase modulations of chaotic waves in the EEG gamma range, the term of intervening ‘mesoscopic’ domains, extending over large areas of the cortex, has been borrowed by Freeman from physics [10,152].
7.2 More about olfaction and neural networks: winnerless competition
Working primarily on the processing of olfactory information at the first two stages of its transformation, that is at the level of the receptors and their postsynaptic targets, G. Laurent and his collaborators saught to understand how the brain solves the double and contradictory task of recognizing odors as unitary percepts (in a synthetic sense) and categorizing them (with the ability to recognize, in a noisy environment, small differences between odors). Their credo was that these early olfactory circuits (and other sensory networks as well) should be viewed as a system and that our current thinking about sensory integration in terms of ‘responses’ following a stimulus is too often linear and passive: one should rather consider them as active and internal processes where a major role is devoted to the dynamics of the brain circuits themselves [267,268]. Specifically, two objectives are accomplished in parallel by the nervous system. The first is to create ‘through spatio-temporal patterns of neuronal activation’ a large coding space in which representational clusters which allow the storage and recall of unpredictable ‘items’ can spread. The second is to confer stability to this space in the face of noise and to optimize it [267].
This group's research has been focused on the dynamical properties of individual and ensembles of neurons firing in response to odor presentations, in vivo, in both insects (locusts Schistocerca Americana) and zebrafish (Danio Rerio). In insects, the neurons are, the antennal (AL) or olfactory lobe projection neurons (PN), which are activated by the olfactory receptor neurons (ORNs), and whose signals (triggered by odorants in broad and overlapping peripheral regions) are transmitted to the mushroom body (a center for learning and memory). The ALs and PNs are organized according to the same anatomical principles as the olfactory bulb and the mitral-tufted cells of vertebrates, respectively. In addition, local GABAergic inhibitory neurons, i.e. periglomerular or granule cells (GCs) in vertebrates and local neurons (LNs) in insects can act on local or distant connections between the ORNs and mitral cells, or their equivalents in other species.
According to these authors, several dynamical properties of the olfactory system justify the choice of the so-called winnerless competition model, which will be defined below. First, as in other species (references in [267]) it was found that individual odors evoke complex temporal response patterns in many (but not all) of the insect PNs [269] and in zebrafish MCs [270]. The responses differ across odors for a given neuron and across neurons for a given odor thereby causing, in each case, the formation of specific neural assemblies. Fig. 26A1 illustrates these findings and shows that, in addition, some neurons respond by a period of inhibition preceding a delayed spiking. All these responses were stable and reliable following repeated stimulations (Fig. 26A2). They were superimposed on one of several epochs of the oscillations of the extracellular local field potential (LFP) that signals a coherent and synchronized population activity (Fig. 26B), with reproducible and reliable periods of phase-locking for each neuron. But unlike the firing pattern in individual units, the oscillation frequency (20–30 Hz) are independent of odor identity. One way to summarize these data is to consider [271] that overall the macroscopic oscillation is caused by a stimulus-specific ‘message’ which is distributed in space (the odor-singular sets of synchronized cells) and in time (the periods when the cells synchronize and desynchronize in an odor-particular manner), reflecting the fact that the odor representation in the olfactory bulb is distributed and combinatorial. Clustering (correlation) followed by declustering of cells during odor representation changes continuously throughout a stimulus in a manner that progressively reduces the similarities between ensembles coding for related odors [270].
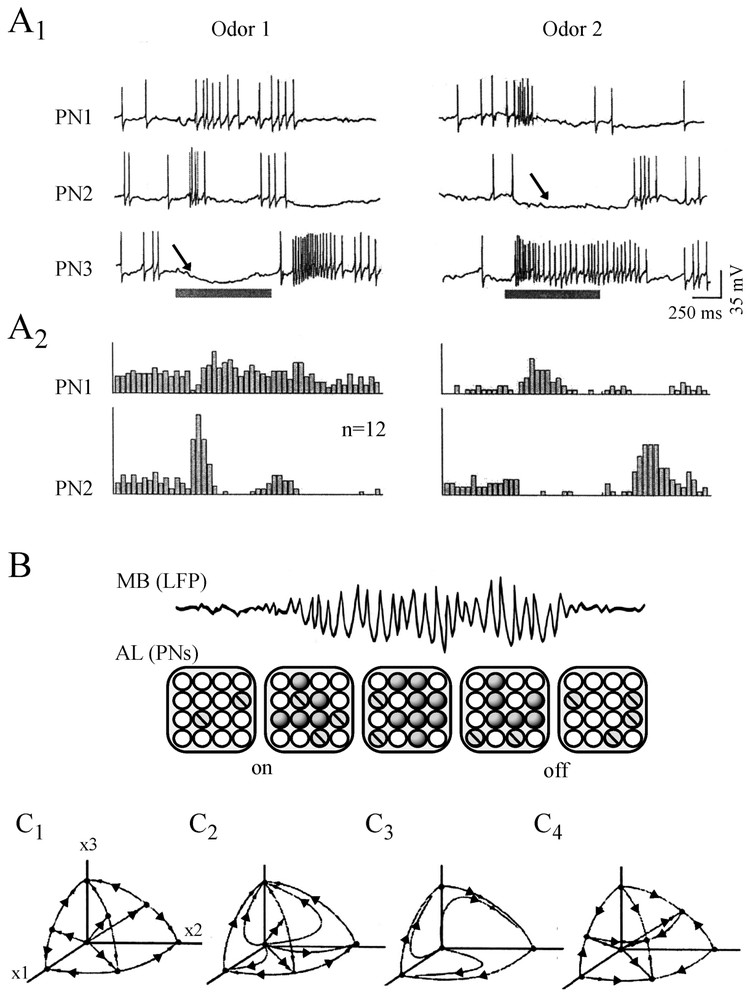
Odor-evoked responses and their behavior in the phase state. (A1–A2). Firing patterns of three simultaneously recorded locust PNs labeled 1 to 3. (A1) Spike discharges and inhibitory postsynaptic potentials (arrows) evoked by the presentation of two different odors, at times indicated by the horizontal bars. (A2) Reliability and specificity of these dynamic responses shown by the poststimulus time histograms of successive events in PN1 and PN2 (n=12 successive trials). (B) Hypothesis for odor coding in the olfactory system. Above. Local field potential (LFP) in the mushroom body (MB). Below. Temporal changes in activity of 16 projection neurons (PNs circles) in the antennal lobe (AL). PN can be silent or inhibited (white), spiking but not synchronized (barred) or active and phase-locked with the LFP (dark). Note that in response to an odor pulse (on) the LFP oscillations are caused by ensembles of synchronized cells. (C1–C4) Schematic illustrations in a 3D phase space of four types of dynamical behavior produced by systems with symmetrical (C1) or assymmetrical (C2–C4) coupling. (C1) multistability (C2) weak competition (C3) winner take all (C4) winnerless competition (see text). (Modified from, A1, A2: [275], with permission of Neuron; B: [271], with permission of the Journal of Neuroscience; C1–C4: [267], with permission of the Annual Review of Neuroscience.)
Secondly, synaptic inhibition plays a major role in the patterning of the odor-evoked neural assemblies. Experimental evidence indicates that blocking the fast inhibition mediated by LNs with GABA antagonists abolishes the oscillatory synchronization [272–274] without however affecting the slow phases of inhibition observed before, during and after bursting in individual neurons or impairing the ability to discriminate stimuli. Accordingly, simulations with a Hodgkin and Huxley type model [275,276] clarified the respective roles of the fast and still unidentified slow inhibitory mechanisms in forming the dynamical PN assemblies illustrated in Fig. 26A1 and A2.
A common nonlinear model of olfactory processing is that of coding with attractors, or Hopfield nets [263,277], where each odor is represented by an autonomous and specific attractor. Each one has its own basin of attraction and is created through training with a stimulus which modifies a particular set of connections in the olfactory bulb until a steady state is obtained. The resulting picture of this process is that of several coexisting attractors in a multistable system, as illustrated in Fig. 26C1. It was argued [267] that although the Hopfield systems are dynamic, they become static after convergence and furthermore they have hard capacity limits. On the other hand, Freeman's models do not ‘explicitly’ take into consideration individual neurons or network topology. Thus another classical paradigm, called the ‘winnerless competition model’ (WLC), is advocated by G. Laurent and his collaborators [268,278].
Like other nonlinear models, WLC is based on simple nonlinear equations of the Lotka–Volterra type where (i) the functional unit is the neuron or a small group of synchronized cells and (ii) the neurons interact through inhibitory connections. Several dynamics can then arise, depending for a large part on the nature of this coupling and the strength of the inhibitory connections. If the connections are symmetrical, and in some conditions of coupling [267,278], the system behaves as a Hopfield network (Fig. 26C1) or it has only one favored attractor if all the neurons are active (Fig. 26C2). If the connections are only partly asymmetrical, one attractor (which often corresponds to the activity of one neuron) will emerge in a ‘winner-takes-all’ type of circuit (Fig. 26C3). Finally a ‘weakly chaotic’ WLC arises when all the inhibitory connections are nonsymmetrical; then, the system, with N competitive neurons, has different heteroclinic orbits (see Section 2.1.3) in the phase space (Fig. 26C4). In this case, and for various values of the inhibitory strengths, the system's activity ‘bounces off’ [267] between groups of neurons: if the stimulus is changed, another orbit in the vicinity of the heteroclinic orbit becomes a global attractor. In such a manner, WLC encodes many stimuli: the capacity of an N node Hopfield network is N/7, while that of a WLC network is e(N−1)!. Furthermore the latter is strongly dissipative (i.e. it quickly forgets its initial state) and represents information by transient orbits rather than by attractors, per se.
Rabinovich et al. [278] implemented a WLC with nine FitzHugh–Nagumo neurons having synaptic inhibitory currents modeled by first order kinetics. Their numerical simulations indicated that the network produced firing patterns which were different for different stimuli in the mimicked PNs and in manners that was furthermore consistent with those observed experimentally [267,269,279]. Full information about the inputs (their ‘representation’) was found in the output sequences. In dynamical terms, the WLC networks “produce identity-temporal or spatio-temporal coding” in the form of deterministic trajectories moving along heteroclinic orbits that connect saddle fixed points or limit cycles as in the phase space. These ‘saddle states’ correspond to the activity of specific neurons or groups of cells, with sequential switching from one state to another. The advantages of this model are global stability, sensitivity of the dynamics to the forcing stimulus, insensitivity to noise and a larger capacity than that of other classical models.
The same chaotic model has been hypothesized to be at the origin of the hunting behavior of a mollusk Clione Limacina. This predator is a gastropod which lacks a visual system and finds its prey during a search behavior characterized by a circular motion whose plane and radius change in a chaotic-like manner [280] that produces random changes of direction in the gravitational field. Clione has been used extensively for studies of basic mechanisms underlying orientation and locomotion (references in [281,282]). It swims by using rhythmical oscillations (about 1 Hz) of two wings and its direction in a three dimensional space is governed by the bending of its tail (Fig. 27A). When swimming, it maintains a vertical (head up) position [281]. Driven by signals from gravity sensing organs, the statocysts, the network causes correction to deviations from this position by producing flexions of the tail. The statocyst (which contains a stone-like structure statolith) has an internal wall with about ten mechanoreceptors (SRNs) that are excited by the statolith. The SRNs send axons to the pathways controlling wing and tail motions [283] and they form a network in which a fraction of them (30%) are coupled with GABAergic inhibitory nonsymmetrical connections.
Winnerless competition between sensory neurons. (A) Above: spatial orientation of free swimming Cliones. Body profiles during passive sinking (a and b) and when locomotion is resumed (c and d). Below: drawings of the animal excited by a contact with its prey (e) and swimming against the bottom (f). Note that a, b, e and c, d, f, are dorsal and lateral views of Clione, respectively. (B) Schematic representation of the model network with six sensors receptor neurons (SRNs) and the inhibitory connections (thicker lines indicate stronger ‘synaptic’ strengths). (C) Computer-modeled time series of activities in the SRNs (labeled to ) under the action of the hunting neuron (dimensionless units). (D) Three-dimensional projection in the phase space of the activities in neurons a2, a4 and a6, which were linked by the strongest inhibitory connections. (A from [283], with permission of the Journal of Neurophysiology; B, C and D: adapted from [280], with permission of Chaos.)
The direction of movement or orientation of Clione changes in time in an irregular and unpredictable manner as the animal searches for its food, the small mollusk Limacina helicina [284] which triggers this behavior. Two large cells, the cerebral hunting neuron (CHNs) excite the RSNs and control the activation of the networks. That is, the behavior can be caused by (i) external sensory stimulations, or (ii) internal signals via the CHNs. The intrinsic mechanism, which is essential to the model of Varona et al. [280], was analyzed during in vitro experiments, which showed that the isolated nervous system can indeed produce fictive hunting behavior and generate chaotic like-motor outputs to the tail muscle [278].
The model comprises a statocyst with six SRNs having Lotka–Volterra-type dynamics and inhibitory connections (Fig. 27B). Depending on the latter, the system can exhibit the several dynamics illustrated in Fig. 26C1–C4. However, based on experimental data, it was reasonable to assume that the inhibitory connections are asymmetrical, three of them being strong, three others moderate, and the rest weak.
When there was no activation of the sensory neurons, the statolith induced a high rate of firing in one of them (that may organize the head-up position) and the others were quiet. But the winnerless competition between sensory neurons could override the effects of the statolith for given stimulations of the CHNs. The neurons then displayed a chaotic behavior with activities switching among the receptors (Fig. 27C and D) and with positive Lyapunov exponents. These results support the notion that in the presence of a prey, the SRN network generates new information, i.e. chaotic outputs with positive Kolmogorov–Sinaı̈ entropy, which can organize via the motoneurons the apparently random hunting behavior of Clione [280].
7.3 Chaotic itinerancy
In a series of important articles, Tsuda and his collaborators give critical arguments that favor the notion of chaos in the brain and that it participates in perception and memory. Their demonstration is based on mathematical models of associative memories constructed according to their knowledge of the anatomy of the neural circuits of the cerebral cortex and the hippocampus, as described by Szentagothai [285,286].
Similar to those of McCulloch and Pitts [287], the formal neurons of [288] have two states, +1 (firing) and −1 (reset). If the neuron exceeds the threshold at a given time, it fires with a probability p, which is independent of the activity level and is otherwise set to zero, for convenience. The network is made of pyramidal (excitatory) and stellate or basket (inhibitory) cells; the former send fibers to all the pyramidal cells whereas the latter make only synaptic contacts with one of them (Fig. 28A). A Hebbian synaptic learning is assumed. More generally, this non-equilibrium model consists of two blocks I and II containing a recurrent net and positive feedback connections whose strengths are fixed, and they differ only by the addition of a negative feedback connection in block II.
Transitions between states through chaotic itinerancy. (A) Architecture of the system for associative memory. Shaded triangles and large circles denote pyramidal and stellate neurons respectively; synapses are symbolized by small filled circles (see text for explanations). (B) Schematic representation of a chaotic itinerancy. The trajectory wanders among attractor ruins; it is attracted by one of them but it leaves it via an unstable direction toward another attractor. (C–D) Two-dimensional view of classical attractors, illustrating from left to right (in C), fixed points, a limit cycle and chaotic orbits, and, (in D), a ‘ruin’ attractor where the dynamical orbits approach a fixed point but then escape from it; this fixed point can be considered as a ruin of a Milnor attractor. (A from [290], with permission of Neural Networks; B and D from Tsuda, 200, with permission of Behavioral and Brain Sciences.)
The successive recalls of stored memories and the consequences of the interplay between the dynamical system and noise were systematically studied. Two types of noise were implemented. One, (called dendritic), results from electric currents randomly leaking from neighboring cells. The other is equivalent to the synaptic noise produced by quantal release of synaptic vesicles (whether spontaneous or spike-triggered) by incoming fibers, as defined in Section 4.1; it was injected in the network to produce a ‘stochastic renewal of dynamics’, since in this model a neuron does not always fire when the sum of the inputs crosses the threshold. Rather, at that point in time, either a threshold dynamics is selected or the previous dynamics is used again. This results [289] in an iterated function system (IFS). The overall dynamics is determined by the instability of the IFS which is due, in this type of network, to the reset caused by specific inhibitory neurons.
Depending on pre-determined probabilities the emerging dynamics was that of a ‘chaotic intermittency’ (Fig. 28B) either between attractors in the usual sense (fixed points, limit cycles, tori or strange attractors – see Fig. 28C) or, due to the activation of the inhibitory neurons (particularly in the block II), between ‘exotic’ Milnor attractors [290,291].
Chaotic itinerancy is a particular form of transitions between states and of chaotic behavior. It has been proposed as a universal class of high dimensional dynamical systems after it was found in a model of neural dynamics. As explained by Tsuda [248,291], in a multi-state high dimensional system, each state corresponds to an attractor but in the case of weak instability, only a ‘trace’ of it remains in the system and unstable directions appear in its neighborhood. Once destabilized, it becomes an attractor ‘ruin’ (Fig. 28D), which is related to a Milnor attractor. Milnor attractors may possess unstable manifolds and a system can escape from them as a consequence of small perturbations. This nice feature may not be sufficient to make them biologically relevant [292] but it is important to note that chaotic itinerancy has been reported in vivo preparations [257,293]. Therefore the model can be used, according to Tsuda [291] for the interpretation of cognitive processes, particularly given some of its striking properties. These include the retention of information [294], the capability to learn and recognize patterns [288], and the ability to simultaneously process learning and recall [295].
In thermodynamic models such as that of Hopfield [263], external noise is essential for helping a system to escape local minima (references in [99]) and to undergo transitions in the landscape between peaks and valleys (Fig. 29A). In Tsuda's model, instability is intrinsic to the system (Fig. 29B). This represents an interesting challenge in brain studies. Specifically, it could be important to determine whether, and how, chaotic behavior is generated by noise, as in the case of the ‘noise-induced order’ and chaos of Matsumoto and Tsuda [296]. That is, even if a low-dimensional chaos (as it is strictly defined by mathematicians), does not exist in the nervous system, the interplay of the latter with noise could be responsible for a topologically and functionally similar behavior.
Schematic illustration of the difference between transitions produced by chaotic itinerancy and by addition of external noise in an attractor landscape. (A) In a formal model, noise allows the system escape local minima; as the noise level increases so does the probability of a jump between energy levels. (B) In chaotic itinerancy, the instability is intrinsic to the system and transitions from one orbit to the next are autonomous (from [291]).
Another issue raised by Tsuda [291] is (again) that of coding of information in neural sets, particularly in the hippocampus and in olfactory networks driven by a chaotic input. Such ‘chaos-driven contracting’ systems possess attractors represented by so-called SCND functions (for singular-continuous but nowhere differentiable). These functions which can be viewed [297,298] as ‘fractal images’ with Cantor sets, related to the formation of “episodic memory and primitive thought processes” [291]. It has been predicted that they will be found in the membrane potential of inhibitory neurons driven by chaotic afferents [297]. Despite their attractiveness, these proposals are still grounded on mathematical perspectives alone and one can wonder to what extent they are implemented neurologically [299]. On the other, hand elegant studies [300] strongly advocate that chaos intermittency and coding could be more effective in solving the ‘binding’ problem during perception and attention rather than, as believed by so many authors, spike coincidence and neural oscillations.
8 General conclusions
The reluctance of many physiologists to adopt chaos theory has been justified, at least, in part, by evidence that there still is a large gap between the use of topological profiles in a state space to characterize a neural system or function and their use to identify the underlying physical correlates. One has to recognize indeed that so far, the main application of nonlinear systems in neurobiology have been to reconstruct, from a single measurement of the membrane voltage, a ‘proxy’ state space description [301] that gives access to the number of ‘degrees of freedom’, i.e. of dynamical variables involved in the studied process. This strategy gives however a firm experimental basis to the size (that is the degrees of freedom) of the models describing this process [301] and one must bear in mind that this approach has proved quite successful for understanding the dynamics of higher brain functions, as will be discussed below.
8.1 Reality of ‘neurochaos’
As other complex systems the brain is constructed along several overlapping spatial (here anatomical) hierarchies. These range from molecules and neurons to small and large networks. Also, it operates within a broad range of time scales, including milliseconds (spikes and synaptic potentials duration), seconds (networks operations), hours and more (LTP). Probably relating to this multiplicity of scales, chaos has been reported at almost all levels of the CNS that is in invertebrate neurons and spinal giant axons, in central pattern generators, vertebrate olivary and hippocampal neurons, in the olfactory bulb, and at the level of the human brain. Therefore it has been proposed [248] to designate this class of chaotic phenomena under the term ‘neurochaos’. Yet, as repeatedly noted in this review, clear and convincing demonstrations that there is chaos in the nervous system are still scarce because the results of specific measures of invariants such as Lyapunov exponents, entropy, correlation integrals [1] become less reliable as one investigates progressively higher levels of the neural hierarchy and high-dimensional biological systems.
This paucity of firm experimental foundations has been compensated for by theoretical studies most often originating from modified (but still realistic) Hodgkin–Huxley equations which have predicted and/or confirmed neurochaos. These studies helped to dissect its underlying components (coupled neuronal oscillators and synchronized clusters of cells) and to obtain modifications of the membrane potential including bifurcations and trains of bursting spikes similar to those recorded from the living brain. Several mechanisms at the origin of neurochaos have been considered [173,248,291,302]. Among them the most common are (i) the presence of slow channels or of a delay (refractory period) that affect the input–output relation of neurons, (ii) feedback and coupling between excitatory and inhibitory drives at the cellular level or in the design of networks, (iii) neuronal circuits behaving as damped nonlinear oscillators [173], and (iv) the more theoretical noise-induced chaos already mentioned in Section 4.3 of this review (references in [248]). Strictly speaking, chaos has been unambiguously demonstrated but in a few and privileged cases only, particularly given the presence of bifurcations, at the axonal and single cell levels (Sections 2.2 and 2.3) and at pairs of coupled neurons or in small circuits (Section 3.2).
In contrast, if viewed in a broader perspective than just the identification of chaos as strictly defined mathematically, the use of nonlinear tools has been quite fruitful at both extremes of the scale or complexity during investigations of neural functions.
8.2 Functions of inhibition in chaotic systems
At the elementary or ‘reductionist’ level we have learned a few lessons. One is a confirmation of the critical role played by inhibitory processes on the dynamics of neuronal assemblies. Inhibitory interneurons couple other neurons, both anatomically and functionally, and therefore they participate in the shaping of dynamical assemblies and/or oscillators that can generate chaos. This has been demonstrated (i) in the case of the presynaptic neurons that produce in the Mauthner cell the non random components of its inhibitory synaptic noise (Section 4.1), (ii) in hippocampal and olfactory systems, where inhibition is essential for the formation of clusters of oscillatory cells, for their transitions to new states along their road to chaos and for the temporal patterning of activity in neural assemblies or the formation of dynamic ‘memories’ (Sections 5.2 and 7.2), as well as (iii) the dynamics and the resetting of models of higher brain functions (Section 7.3). Inhibition has opposite effects in invertebrate's CPGs where it contributes to the stabilization of the spontaneous chaotic oscillations that prevail in the behavior of isolated neurons: this chaotic behavior disappears once the cells are reembedded in the entire network (Sections 3.2 and 3.3).
Another lesson is that, as shown in CPGs and in the olfactory bulb, neither a neuron, nor a cell assembly, is designed to serve a single purpose. Rather, they can implement several functions depending upon the internal states of the brain and the constraints placed upon it by environmental factors.
8.3 Chaos, information theory and the neural code
In a more global and ‘integrative’ perspective, nonlinear studies may seriously challenge some of our strongest beliefs in neurosciences. In addition there could be considerable benefits for the nervous system to choose chaotic regimes given their wide range of behaviors and their aptitude to quickly react to changing conditions [1].
Important recent progress has been made in studies of the relationship between chaos and information theory, i.e. the possible role of chaotic dynamics in ‘information’ processing and coding in the brain (see also Section 4.2). This issue was already raised by pioneers in the early eighties [303–307] and subsequent theoretical studies have suggested that a dynamic preservation of information in the brain can be achieved in the presence of chaotic activities in neurons as well as in coupled chaotic systems [248]. Specifically, and although the Lyapunov exponents and other measures of invariants such as entropy indicate a loss of information or unidirectional transmission, information is preserved by a process named information-mixing whereby at least part of this information survives from one time step to the next, even if most of its contents included in previous digits or sequences has been lost.
Particular attention has been paid, with the help of information theory, to the description and quantification of the nature and quality of information in linear and nonlinear (but not in chaotic) neurons and in neuronal networks [301,308–311], see also [312]. A major concern has been to assess rigorously the relationship between a stimulus set and the subsequent neural response and to characterize the behavior of dynamic systems under continuously varying input conditions. This problem had been considered to be quite difficult since identical stimuli can yield variable trains of spikes in the recorded axons [311]. Further developments based on the Wiener–Volterra methods for measuring response functions have been obtained [212] during investigations aimed at clarifying how the brain recovers (i.e. ‘decodes’) information about events in the world transmitted (or ‘coded’) by spike trains. Such studies are certainly fundamental for our understanding of the nonlinear input–output functions that prevail in the nervous system [301], although the question has also been raised whether there truly is a need for decoding and binding instead of simply recreating distinct sets of states of dynamical assemblies ([313], see also below). Finally information theoretic methods have proven useful for identifying system nonlinearities and for the validation of nonlinear models and their expectations [310].
8.4 Representation of the outside world
Chaos theory is the most spectacular branch of dynamical systems theory which may prove, in a near future, to be a most fruitful avenue for understanding brain operations and higher functions. Both theories are based on the use of the same nonlinear tools and language, starting with constructing a phase space that provides a topological description of the system under scrutiny and of its behavior (see [1]). Dynamical theory is a serious and almost irreducible challenge to the computational framework still favored by the majority of neuroscientists who believe that neuronal networks are internally organized to function as ‘computational’ devices [314–316].
The notion that the brain is a device that generates outputs resulting from transformations of its inputs (or symbolic messages) according to given rules (or algorithms) dates back to the first models of neurons by McCulloch and Pitts [287], the advent of Wiener's cybernetics [317] and Shannon's information theory [318]. In its simplest version this view states that the sensory organs deliver messages to the nervous system which ‘computes’ the appropriate output after series of manipulations carried out in successive and arbitrary time steps. The assumption that the nervous system acts as a machine, or as a ‘digital brain’ has been pursued by numerous studies aimed at solving the coding problem and by decades of modeling of neural networks (often of the connectionist type). Representative models of this kind take the form of layers of neuron-like elements that are trained to deal with numerical input–output transformations; here the critical factors are the network's architecture and the learning algorithms [316,319–322]. Cognitive and decision-making ‘computational’ processes are treated as a succession of calculations of the value of each alternative outcome, or choice, after which the system (or the brain) ‘chooses’ the best value out of all possible ones. A rather static and passive idea of internal representations that would be ‘carved’ in the brain by actions of the outside world is inherent to this traditional belief: some symbols encode (or ‘represent’) information, and a given input is systematically associated to a specific output The related models have a variety of anatomo-functional architectures and they use synaptic and cellular constraints such as Hebb's rules or conditions for LTP induction to produce increases of synaptic efficacy that are required for creating novel representations in neural nets.
Serious objections have been advanced against computationalism. They posit that the brain and the cognitive system are not computers that can be neatly divided in distinct modules, each of which accounts for a different symbol-processing task and communicates its solution to other modules [323]. In contrast and rather than manipulating frozen and formal representational units at whatever level (it can be a spike code or an architecture), the nervous system evolves continuously and in real time in conjunction with changes in the surrounding world. A pioneer of this way of thinking has been Freeman [127] for whom studies on the patterns generated by the olfactory system (and how) was a necessary prelude for understanding the higher order processes by which “they are assembled into Gestalts in the larger apparatus of the forebrain” [10]. In contrast to man-made systems designed to perform particular tasks, the brain would rely on self-organized (and chaotic) processes to generate relevant activity patterns and perception would be a creative course of actions “rather than a look-up table of imprinted data”. Similarly, the more recent dynamical systems theory seeks to understand the unfolding of cognitive processes over time and to identify what external and internal factors influence this unfolding [314].
As documented by van Gelder and Port [324], dynamicists are concerned with the behavior of large ensembles of neurons. Whereas classical neurobiologists focus their attention on single cells or on small networks, dynamicists construct low-dimensional models suggesting that the CNS is a single system with numerous (and interactive) state variables. When it is analyzed with the mathematical tools of dynamics, the behavior of such an ensemble is the totality of its overall states ie that of a sequence of points that delineate attractors, trajectories and bifurcations and various geometrical landscapes in the phase space. Remarkably, all the components of the system are modified at the same time and according to well-defined rules. This evolution must be understood as a process during which changes depend on forces that (i) operate within the system, and (ii) are best described with differential equations. Inputs cease to uniquely determine the internal state of the brain they merely perturb its intrinsic dynamics and in this context the term ‘representation’ no longer applies to the well-defined cast of an internal or external scenario but rather may include internal dynamical states (as they have been defined above namely attractors, limit cycles and so on…).
The history and the main principles of the theory of dynamical systems their connections with other fields of neuroscience and, more recently with the self-organization and emergence of new patterns in the so-called complex systems can be found in several reports and books [324–328]. This theory has quickly proven successful for dealing with, for example, neural circuits [18], the control of movement [329,330], language [331], perception and action [332], cognition [322,333,334], operations leading to decision-making [335] and for the successful implementation of autonomous agents (references in [314]).
The relations between chaos theory and the dynamical systems theory receive increasing attention. As pointed out by van Gelden and Port [324] when they mention the work of Pollack [336] on the structure of natural languages (in their introductory chapter to the book Mind as Motion), “there has been fascinating initial explorations of the idea that highly distinctive kinds of complexity in cognitive performance, such as the productivity of linguistic capacities, might be grounded in chaotic or near chaotic behavior”. Similar remarks certainly apply to Chaotic Itinerancy (see Section 7.3): as explained in [248] implementation of this model was preceded by the introduction of Coupled Map Lattices (CMLs) by Kaneko [337–339] for the studies of spatio-temporal chaos. A CML is a dynamical system with discrete time steps (‘maps’), localized (‘lattice’) and a continuous state. It consists of dynamical elements like, for example, neurons on a lattice which interacts (is ‘coupled’) with other sets of elements. It can display switching between clusters of activity that have been interpreted as equivalent to ‘choosing’ among several perspectives in a sensory field [340].
Despite obvious progress, numerous and fundamental topics remain under discussion. Among them, and in addition to those mentioned in the course of this review, Werner [116] notes “whether problems generally classified as undecidable can be approached by means of chaotic processors. Would computing with chaos be capable of dealing with mathematically undecidable functions? What kind of functionality might chaotic regimes have? Can they outperform non-chaotic regimes?…” These questions are close to those raised by Tsuda (references in [248]) when he proposes that there is a chaotic “Hermeneutics of the Brain” that allows us to ‘know’ the activity of the nervous system and that the ways we recognize the latter as well as the outside world are both interpretative. This view, which was inspired by Marr's theory [341] of the internal representation of visual information with symbols, means that the brain does not directly map its environment nor free itself from it. Rather it interprets symbols or states produced within it, and chaotic dynamic systems are well fit for this purpose. The brain not only perceive but it also creates new realities, this is why it is an hermeneutic device [342]. This possible interface between logic and the self-organization of symbol sequences has been considered elsewhere [305,343] (references in [288]).
Acknowledgements
We thank H. Abarbanel (Institute for Nonlinear Science, University of San Diego, La Jolla) and D.S. Faber (Department of Neuroscience, Einstein College of Medicine, Bronx, N.Y.) for their critical reading of the manuscript and for their precious scientific comments and R. Miles (INSERM, EMI 224, Cortex et Épilepsie, CHU Pitié-Salpétrière) for his generous help and patient assistance. This work was supported in part by the Defense advance Projects Agency (DARPA) contract No. 66001-00-C-8012.


