Version française abrégée
1 Introduction : le concept d'émergence
Les notions d'émergence ou de propriétés émergentes sont souvent employées pour rendre compte de phénomènes observés en sciences expérimentales. On considère que des phénomènes tels que les cellules de Bénard en thermodynamique, les constructions et les comportements des insectes sociaux (l'intelligence de la fourmilière est la somme de la stupidité de toutes les fourmis [1]), les déplacements collectifs de vols d'oiseaux ou de bancs de poissons et même le système immunitaire [2] présentent un caractère émergent, tout comme des phénomènes sociaux ou économiques (embouteillages, synchronisation des applaudissements), ou le comportement des systèmes informatiques (circulation de l'information sur l'Internet, systèmes multi-agents, automates cellulaires... [3]). Des phénomènes complexes tels que l'apparition de la vie sur terre, l'évolution de nouvelles espèces ou la structure de la pensée cognitive sont considérés comme des phénomènes typiques d'émergence [4]. Depuis quelques années, ce concept prend une importance certaine dans les sciences du vivant, de la cognition, en intelligence artificielle. Mais rares sont les aventuriers qui se risquent à le définir [5].
Par définition, l'émergence est l'état de ce qui émerge, à savoir qui dépasse le niveau moyen, retient l'attention, sort du lot... Nous retrouvons alors le concept de saillance, utilisé pour la reconnaissance des formes [6]. La notion d'émergence apparaît également dans l'assertion Le tout est plus que la somme de ses parties (contre-pied du principe Le tout est la somme des parties, attribué à Aristote), qui évoque également des mécanismes de non-linéarité ou d'interaction. L'émergence est classiquement définie comme l'apparition d'un système qui ne peut pas être prédit ou expliqué à partir des conditions antécédentes [7]. Selon Georgé [2], le système ne doit et ne peut pas contenir explicitement la connaissance du but du système (i.e. de la fonction émergente) et les moyens d'y arriver. Van de Vijver [8] rappelle que l'émergence est un processus par lequel de nouvelles structures et fonctions font leur apparition. L'émergence renvoie à ce qui apparaît comme nouveau, inattendu, irréversible et significatif, ou est tel à cause de l'impossibilité de l'expliquer de manière réductive. Certaines de ces définitions présentent un caractère négatif évident, ce qui ne rend pas le concept d'émergence très lisible. Les propriétés d'imprévisibilité ou de nouveauté qui caractérisent l'émergence présentent un aspect temporel incompatible avec une définition absolue. Pour certains, la notion d'émergence ne répond pas à la rigueur scientifique : Une chose sort d'une autre, sans être à proprement parler produite ou causée par elle. La notion est pour le moins obscure [9].
D'après Nesle, le terme d'auto-organisation désigne l'émergence spontanée et dynamique d'une structure spatiale, d'un rythme ou d'une structure spatio-temporelle (se développant dans l'espace et le temps) sous l'effet conjoint d'un apport extérieur d'énergie et des interactions à l'œuvre entre les éléments d'un système considéré [10]. Selon Ricard [11], si un système présente un nombre de degrés de liberté ou une entropie supérieurs à l'union des sous-systèmes qui le composent, il est alors défini comme un système émergent ou complexe, ces deux termes étant alors équivalents. Dans l'exposé sur l'émergence proposé par l'équipe SMAC et J.-P. Georgé [2,3], la notion d'émergence est caractérisée par des propriétés telles que la nouveauté, l'auto-organisation, l'irréductibilité, l'interdépendance des niveaux, mais n'est pas définie formellement, même dans un cadre strictement informatique.
Cariani [12] définit l'émergence comme le processus par lequel de nouvelles structures ou fonctions se mettent à exister. Il distingue l'émergence combinatoire où la nouveauté provient de nouvelles combinaisons d'éléments préexistants et l'émergence créatrice, où la nouveauté naît de la création de nouveaux genres d'éléments. Bonabeau et Dessalles [13] distinguent deux autres types d'émergence : l'émergence de structures de degré plus élevé EHS, et l'émergence relative à un modèle ERM. Le premier type se produit quand un phénomène apparaît à un niveau à partir de constituants et de processus définis et en place à un niveau inférieur , et quand les propriétés de sont difficiles ou impossibles à déduire des propriétés des constituants et des processus de . Suivant la seconde définition, il y a émergence quand le comportement d'un système naturel ne peut plus être expliqué par un modèle de ce système (il dévie ou bifurque des prédictions du modèle), et un nouveau modèle est nécessaire. En considérant que les modèles scientifiques jouent le rôle de détecteurs conceptuels, les auteurs montrent que ERM est un cas particulier de EHS.
Trop souvent, le concept d'émergence a été utilisé de façon, sinon abusive, en tout cas dans un contexte scientifique flou rendant sa compréhension et son utilisation difficile[2]. Dans cet article, nous allons présenter un modèle mathématique de morphogenèse et montrer sous quelles conditions des patrons de complexité supérieure peuvent émerger de ce modèle. L'ambition de cette contribution est de proposer, dans le contexte relativement limité de ce modèle, une définition plus rigoureuse du concept d'émergence.
2 Le système dynamique
Nous définirons un modèle comme l'implémentation d'un système (tel que le système de Turing ou le système simple de Meinhardt précisé ci-dessous) dans une structure cellulaire statique ou dynamique.
Le système simple de Meinhardt (modèle 3.1 de 1982 [14], équation 2.1b de 1995–2003 [15]) fait intervenir deux agents : l'activateur A et l'inhibiteur H. Ce modèle fait partie de la classe des modèles de Gierer–Meinhardt [16,17], qui sont eux-mêmes des modèles de Turing. Les deux agents interagissent dans chacune des cellules du système et diffusent entre les cellules voisines. L'évolution au cours du temps des concentrations a et h est définie par les équations :
Ce système comporte sept paramètres : s (valeur fixe du substrat), et (production de base de l'activateur et de l'inhibiteur), et (taux d'élimination de l'activateur et de l'inhibiteur) et et (coefficients de diffusion de l'activateur et de l'inhibiteur).
L'état d'équilibre d'une cellule du système est défini, en absence de diffusion avec les cellules voisines, par l'équation du 3e degré :
Cette équation est résolue numériquement en ne retenant que la racine non complexe.
Ce système dynamique est simulé numériquement sur la base du système itératif valeur de pour un pas de temps Δt.
Dans les simulations effectuées, les valeurs des paramètres sont , , , , , et . On a et le temps d'évolution est fixé à 500 cycles, soit 5000 itérations. À l'équilibre, et .
Les différentes simulations et les figures présentées ont été réalisées à l'aide du programme Meincell1 rédigé en Scilab [18,19] et en Ada95 sous Windows.
3 Pavage de quasi-carrés
La structure dans laquelle est implémenté le système est composée de cellules disposées selon un pavage régulier.
Nous définirons un quasi-carré comme un rectangle dont les longueurs des cotés sont a et tels que . Ce sous-ensemble comprend les rectangles pas trop aplatis. On y trouve en particulier les carrés et les rectangles d'or () [20].
L'opération D qui consiste à diviser un quasi-carré dans le sens de sa plus grande longueur est interne dans l'espace des quasi-carrés. Un quasi-carré de rapport donnera deux quasi-carrés de rapport , puis quatre quasi-carrés de rapport . Il apparaît donc que l'opérateur D2 ne modifie pas la forme . Par exemple, si nous partons d'un carré, nous retrouverons un carré toutes les deux divisions. L'application de l'opération D à un quasi-carré donne deux quasi-carrés de même rapport (principe des formats A0, A1, A2, …).
Chaque quasi-carré du pavage a les adresses de ses quatre voisins selon le voisinage de Von Neuman. Ces adresses sont utilisées lors du processus de diffusion. Un algorithme spécifique permet de mettre rapidement à jour les adresses des quasi-carrés voisins au cours du processus de division.
4 Implémentation dans une structure statique
La structure statique consiste en une matrice de cellules quasi-carrées. Cette structure peut comprendre entre cellules et cellules. Chaque cellule est reliée à ses quatre cellules voisines, à l'exception des cellules de bord (trois voisines) et des coins (deux voisines).
Au départ, toutes les cellules sont placées à l'état d'équilibre . Pour provoquer l'évolution du système, la valeur de l'inhibiteur de la première cellule (située au coin supérieur gauche) est multipliée par deux .
À partir du coin supérieur gauche, on voit apparaître des arcs de cercles concentriques régulièrement espacés (Fig. 1A–C). Chacun de ces arcs se discrétise ensuite en pics régulièrement espacés. Nous avons un motif périodique qui se répète de façon identique indépendamment des dimensions (nombre de cellules) de la structure statique.
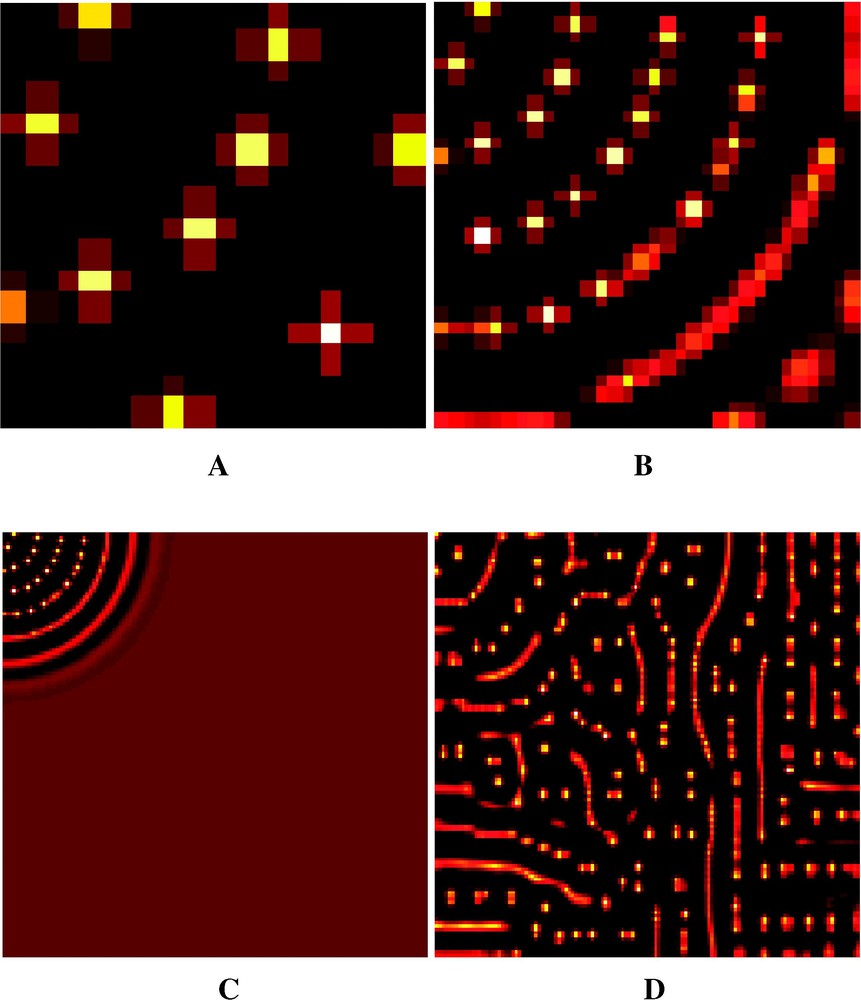
Evolution of the Meinhardt system. This figure represents, for each cell, the values of activator according to a hot color range (black = lower value, white = higher value). Time = 500 cycles with step time 0.1. (A) Static structure 16×16=256 cells. (B) Static structure 32×32=1024 cells. We notice the arc-of-circle patterns whose centre is the upper left corner. (C) Static structure 128×128=16 384 cells. The system, initiated at the upper left corner of the cell matrix, has not achieved its expansion on the whole structure. (D) Dynamic structure from 8×4=32 to 128×128=16 384 cells, with a doubling of the cells number every 50 cycles. We notice the aperiodicity and the phenotypic complexity of the pattern.
Evolution du modèle de Meinhardt. Cette figure représente pour chaque cellule les valeurs de l'activateur selon une gamme de couleurs chaudes (noir = valeur inférieure, blanc = valeur supérieure). Temps = 500 cycles par pas de 0.1. Fig. 1A (en haut à gauche) : structure statique de 16×16=256 cellules. Fig. 1B (en haut à droite) : structure statique de 32×32=1024 cellules. On voit la structure en arcs de cercle centrés sur le coin supérieur gauche. Fig. 1C (en bas à gauche) : structure statique de 128×428=16 384 cellules. Le système, initié au coin supérieur gauche de la matrice de cellules, n'a pas achevé son expansion sur la totalité de la structure. Fig. 1D (en bas à droite) : structure dynamique de 8×4=32 à 128×128=16 384 cellules avec un doublement du nombre de cellules tous les 50 cycles. On remarquera la non-périodicité et la complexité phénotypique du patron obtenu.
5 Implémentation dans une structure dynamique
Dans le contexte de la structure dynamique, le nombre de cellules passe de 32 à 16 384 cellules. Pour chaque valeur de temps multiple de 50 cycles, chaque cellule quasi-carrée se divise en deux cellules filles dans le sens de sa plus grande longueur. Les cellules filles conservent les mêmes valeurs d'activateur et d'inhibiteur que leur cellule mère. Les paramètres du modèle, les conditions initiales et les conditions temporelles d'évolution du modèle sont identiques à celles utilisées précédemment dans le cas de la structure statique.
Dans le cas du système dynamique évoluant dans une structure dynamique (SD)2 [21], nous observons des motifs (Fig. 1D) de nature très différente de ceux observées dans les structures statiques (Fig. 1A–C).
6 Discussion
6.1 Le modèle SD2
La seule différence de contexte entre les Fig. 1A–C et 1D réside dans la modification dynamique du nombre de cellules au cours de la simulation dans le second cas. Le nombre total de calculs effectués pour l'implémentation du système de Meinhardt dans la structure dynamique (16 368 000 opérations élémentaires) est strictement compris entre ceux effectués pour l'implémentation dans la structure statique cellules (160 000 opérations élémentaires) et ceux relatifs à cellules (81 920 000 opérations élémentaires), qui induisent des structures périodiques.
La structure périodique observée dans la Fig. 1A–C est relativement simple à décrire sous la forme d'arcs de cercles équidistants et de la réduction de ces arcs en points équidistants. La structure du patron de la Fig. 1D est bien plus difficile à décrire et exprime un degré de complexité apparente nettement supérieur. Cette complexité a été obtenue en jouant sur le coté temporel de la simulation. En effet, un délai plus important entre les deux premières multiplications cellulaires aurait donné au système le temps d'atteindre son équilibre périodique, et ainsi de suite. De même, un délai très court entre les multiplications n'aurait pas permis au système d'évoluer. Dans la simulation présentée, le patron complexe de la Fig. 1D présente un caractère temporel provisoire, et l'évolution du système figé dans la configuration statique cellules tendra vers un patron périodique comparable à celui de la Fig. 1C.
Nous interprétons la complexité de la Fig. 1D comme le résultat de l'interaction entre deux mécanismes plus simples, qui opèrent à des vitesses différentes. La distance est mesurée en nombre de cellules, et le temps en nombre de cycles de calcul.
Le premier mécanisme est une vitesse constante de propagation du système dans la structure. Dans le cas d'une structure statique, par exemple celle représentée sur la Fig. 1C, en effectuant un affichage tous les 75 cycles, on voit apparaître un nouvel arc de cercle, situé en moyenne à 6,4 cellules du précédent. En première approximation, on peut considérer que cette vitesse dépend uniquement de la valeur du coefficient de diffusion de l'inhibiteur.
Le second mécanisme est la multiplication régulière dans le temps (tous les 50 cycles) du nombre de cellules. Cela se traduit par une augmentation exponentielle de la distance moyenne de deux cellules de la structure dynamique.
Dans le cas d'une structure dynamique, ce second mécanisme contrarie de plus en plus le premier qui tend à ramener à vitesse constante le système à l'équilibre.
Si la multiplication cellulaire est arrêtée à un moment donné, le système reviendra progressivement à un équilibre de nature périodique dans l'espace. Sinon, le système tendra à l'infini vers un état qui pourra être qualifié à la fois de chaotique et de fractal au sens large. Dans le contexte biologique de la morphogenèse, le nombre de cellules suit dans le temps une loi logistique avec au début une croissance exponentielle suivie à la fin d'une stabilisation. À un moment donné, la synthèse des substances qui induisent la formation des patrons est interrompue, et comme ces substances sont transformées en d'autres substances, le système se fige dans un état intermédiaire plus ou moins proche de l'équilibre. C'est cela qui permet aux zèbres et aux tigres d'avoir leurs raies et aux panthères et aux girafes d'avoir leurs taches. Comme le souligne Lesne [10], les structures auto-organisées sont hors d'équilibre, car parcourues de flux de matière et d'énergie.
Bien que non prévisibles au niveau de l'examen du modèle, les patrons complexes obtenus présentent un caractère totalement déterministe. À chaque simulation basée sur les mêmes valeurs de paramètres, on retrouve le même patron, de la même manière que pour les modèles qui simulent le chaos. Si la position et la longueur de chaque pic de la Fig. 1D sont imprévisibles a priori, le patron présente des constantes : par exemple, les distances entre pics sont du même ordre que les distances entre les arcs de cercle de la Fig. 1C.
6.2 Le concept d'émergence
Le patron apériodique présenté sur la Fig. 1D répond manifestement à la définition de l'émergence créatrice de Cariani [12]. Dans le cadre de la définition ERM de Bonabeau et Dessalles [13], la notion d'émergence est relative à un contexte théorique et à un résultat expérimental non prédit par cette théorie.
Dans le contexte de la théorie thermodynamique des systèmes fermés, l'implémentation d'un système simple de Meinhardt, caractérisé par des valeurs identiques des coefficients de diffusion de l'activateur et de l'inhibiteur dans une structure statique donnera un patron uniforme, parfaitement cohérent avec la théorie. Si, à présent, le modèle simple de Meinhardt considéré plus haut est implémenté, nous observons l'émergence d'un patron périodique non prévu par la théorie.
Dans le contexte de la théorie de Turing ou de la dynamique des systèmes ouverts, un tel résultat est prédit et il n'y a plus émergence. Dans ce même contexte théorique, l'implémentation du même système de Meinhardt dans une structure dynamique induit l'émergence d'un patron apériodique non prévu par la théorie. La simplicité du modèle de morphogenèse, d'une part, et l'extrême simplicité du processus de développement cellulaire, d'autre part, ne permettent pas de prédire la complexité de la Fig. 1D : c'est l'aspect inattendu de l'émergence.
Il reste alors à envisager la construction d'un nouveau cadre théorique plus général, qui intègrera les précédents et prédira le patron apériodique observé, et réduira le caractère émergent des observations.
Il est important de noter que, dans tous les cas, le système demeure qualitativement identique, et que la quantité de calculs mise en jeu reste comparable. L'émergence d'un patron de complexité supérieure n'est pas directement induite par un nombre plus élevé de calculs. L'émergence ERM de Bonabeau et Dessalles [13] peut être interprétée par le fait que le formalisme utilisé par le modèle est insuffisant pour décrire les structures spatiales et temporelles formées à partir de ce modèle.
6.3 Complexité et émergence
Il apparaît ici que la modélisation des patrons complexes introduit deux notions différentes de complexité :
- – la complexité génotypique du modèle, qui peut se mesurer par le nombre de paramètres du modèle, par le nombre d'instructions algorithmiques, ou par le nombre de calculs élémentaires qu'il est nécessaire d'effectuer pour obtenir un patron donné ;
- – la complexité phénotypique du patron, qui se mesure en termes d'organisation, par exemple en négentropie [23], propre à quantifier les phénomènes de complexification que montrent nombre de processus vitaux.
En général, pour modéliser un patron phénotypiquement plus complexe, on construira un modèle génétiquement plus complexe. L'objet de la modélisation est alors d'optimiser le rapport des deux complexités, en faisant mieux que le simple hasard. Par exemple, il est toujours possible de modéliser n'importe quel patron défini sous la forme d'une matrice de cellules (ou pixels), par la simulation de tous les patrons possibles en faisant varier tous les états qu'une cellule peut prendre. Pour une matrice de n cellules à deux états (noir/blanc), il y a patrons possibles, donc calculs élémentaires.
Une première approche consiste à raisonner avec un modèle constant, de complexité génotypique plus ou moins grande, et à maximiser la complexité phénotypique. On cherche alors à faire émerger du modèle les patrons les plus complexes possibles, comme dans la discussion ci-dessus du concept d'émergence. Il y aura émergence chaque fois qu'un patron de complexité phénotypique supérieure sera modélisé. La difficulté de cette approche réside dans la mesure de la négentropie, qui peut dépendre de l'arbitraire de l'observateur.
La seconde approche, équivalente en théorie, consiste à raisonner avec un patron constant, de complexité phénotypique plus ou moins grande, et à minimiser la complexité génotypique. On cherche alors à ajuster différents modèles avec le patron donné, en recherchant le modèle le plus simple possible (principe de parcimonie). Tout modèle qui permet de générer ce même patron avec moins de calculs présente un progrès. Il y aura émergence chaque fois qu'un nouveau modèle de plus faible complexité génétique permettra de générer ce même patron. Le seul facteur arbitraire réside dans l'adéquation de l'ajustement entre le patron simulé par le modèle et le patron de référence. Il est possible de quantifier cette adéquation en mesurant la distance des deux patrons selon une métrique donnée et en la comparant à une valeur seuil fixée a priori.
Cette dernière définition réduit considérablement le rôle de l'observateur introduit par différents auteurs dans leur définition de l'émergence [5,12,13,22]. À la différence de Ricard [11], l'émergence définie ci-dessus ne se réduit pas à la complexité, bien qu'elle y soit fortement liée. Enfin, et à la différence de toutes les propositions antérieures, tout phénomène pouvant être qualifié d'émergent au sens de notre définition peut être invalidé (falsifiable au sens de Popper).
1 Introduction: the concept of emergence
The notions of emergence or emergent properties are often used to qualify phenomena observed in experimental sciences. Phenomena such as the Bénard cells in thermodynamics, the buildings and behaviours of social insects (the intelligence of ants' nest is the sum of the stupidities of all ants [1]), collective moving of flying birds or fish shoals, as the immune system [2] present an emergent character, just as social or economic phenomena (traffic jam, applause synchronization) or the behaviour of computer systems (information traffic in Internet, multi-agent systems, cellular automates, ... [3]). Complex phenomena such as the appearance of life on Earth, the evolution of new species or the structure of cognitive thought are often considered as instances of some emergent higher structure [4]. For some years, this concept takes more and more importance in biological sciences, cognitive sciences, artificial intelligence. But few are the adventurers who dare to define it [5].
By definition, emergence is the state of what is emerging, standing higher than the medium level, retaining attention, or appearing different... We have here the concept of salientness (the René Thom's saillance) used in pattern recognition [6]. The notion of emergence also appears in the maxim The whole is more than the sum of the parts (opposite of the principle The whole is the sum of the parts attributed to Aristotle) also evoking mechanisms of non-linearity or interaction. The emergence is classically defined as the appearance of a system that cannot be predicted or explained from the previous conditions [7]. According to Georgé [2], the system must not and cannot explicitly contain the knowledge of the aim of the system (i.e. the emerging function) and the ways to reach it. Van de Vijver [8] recalls that emergence is a process where new structures and functions appear. Emergence refers to what appears as new, unexpected, irreversible and significant, or is such because it is not possible to explain it in a reductive way. Some of these definitions present an obvious negative character, which do not lead to a very legible concept. Properties of unpredictability or novelty present a temporal character incompatible with an absolute definition. For some authors, the notion of emergence does not correspond to scientific rigor. A thing comes from another one, without being made or caused by it strictly speaking. The notion is obscure at the very least [9].
According to Nesle, the term auto-organization refers to the spontaneous and dynamical emergence of a spatial structure, a rhythm, or a spatiotemporal structure (evolving in space and time) under the joint effects of an exterior supply of energy and interactions working between the elements of the system considered [10]. Following Ricard [11], if a system presents a number of degrees of freedom or entropy greater than the sum of its sub-systems, then it is defined as an emergent or complex system, the two words being equivalent. In the presentation of the SMAC group and of J.-P. Georgé [2,3], the notion of emergence are characterized by properties of novelty, auto-organization, irreducibility, level interdependency, but is not positively defined, even in a strictly computer frame.
Cariani [12] defines emergence as the process by which new structures and functions come into being. He distinguishes the combinatoric emergence wherein novelty arises by new combinations of pre-existing elements and the creative emergence wherein novelty arises by de novo creation of new kinds of elements. Bonabeau and Dessalles [13] distinguish two other kinds of emergence: emergence of higher level structures EHS, and emergence relative to a model ERM. The first kind occurs when a phenomenon appears at a level out of constituents and processes defined and taking place at a lower level , and when the properties of are difficult or impossible to deduce from the properties of the constituent units and processes of . Following the second definition, there is emergence when a natural system's behaviour can no longer be explained by a model of that system (it deviates or bifurcates from the predictions of the model) and requires a new model. In considering that scientific models play the role of conceptual detectors, the authors show that ERM is a special case of EHS.
Too often, the concept of emergence has been used in an improper way or in a fuzzy scientific context leading to a difficult understanding and use[2]. In the present paper, we introduce a mathematical model of morphogenesis and we show under which conditions patterns of higher complexity can emerge from this model. The ambition of this contribution is to propose a more rigorous definition of the concept of emergence in the relatively limited context of this model.
2 The dynamic system
We define a model as the implementation of a system (such as the Turing system or the simple system of Meinhardt specified below) into a static or dynamic cellular structure.
The simple system of Meinhardt (model 3.1 of 1982 [14], Eq. 2.1b of 1995–2003 [15]) integrates two agents: the activator A and the inhibitor H. This model belongs to the class of the Gierer–Meinhardt models [16,17], themselves being Turing models. The two agents interact in each cell of the system and diffuse between the next cells. The temporal evolution of the concentrations a and h is defined by the equations:
This system is characterized by seven parameters: s (fixed value of the substrate), and (base productions of activator and inhibitor), and (elimination rates of activator and inhibitor) and and (diffusion coefficients of activator and inhibitor).
The equilibrium state of a cell of the system is defined, without diffusion between next cells, by the third-degree equation:
Retaining the non-complex root numerically solves this equation.
This dynamic system is numerically simulated on the basis of the iterative system value of for a temporal step Δt.
In the simulations performed, the values of the parameters are , , , , , and . We have and the temporal variation is fixed to 500 cycles, i.e. 5000 iterations. At equilibrium, and .
The different simulations and the figures were realized using the program Meincell1 written in Scilab [18,19] and Ada95 under Windows OS.
3 Paving of almost-squares
The structure where is implemented the system is built up with cells placed in a regular paving.
An almost-square is defined as a rectangle which lengths of sides are a and such as . This subset includes not too much flat rectangles, in particular squares and golden rectangles () [20].
The operation D consisting in dividing an almost-square along its higher lengthwise is internal in the space of almost-squares. An almost-square characterized by the ratio gives two almost-squares of ratio , then four almost-squares of ratio . Then, it appears that the operator D2 does not modify the shape . For instance, if the original figure is a square, a square will be found every two divisions. When applied to an almost-square , the operation D preserves the ratio (principle of the formats A0, A1, A2, ...).
Each almost-square of the paving keeps the addresses of its four neighbours, following a Von Neuman neighbourhood. These addresses are used to apply the diffusion process. A specific algorithm rapidly updates the addresses of an almost-square and of its neighbours when it divides.
4 Implementation in a static structure
The static structure consists in a matrix of almost-square cells. This structure can be made of to cells. Each of these cells is connected to its four neighbours, except the edge cells (three neighbours) and the corner cells (two neighbours).
Initially, all cells are at equilibrium state . To induce the evolution of the system, the inhibitor value of the first cell (at the upper left corner) is twice as much as the equilibrium value .
From the upper left corner, concentric and regularly spaced out arc of circles (Fig. 1A–C). Then each of these arcs is discretized into regularly spaced out peaks. This forms a periodic pattern identically repeated regardless of the dimensions (number of cells) of the static structure.
5 Implementation in a dynamic structure
In the context of a dynamic structure, the number of cells goes from 32 to 16 384 cells. Every 50-cycles temporal period, each cell is divided into two daughter cells following its higher length. The daughter cells have the same activator and inhibitor values as their mother cell. The parameters of the model, initial conditions and temporal conditions are identical to those previously used with the static structure.
For the dynamic system evolving in a dynamic structure (DS)2 [21], we observe patterns (Fig. 1D) presenting a nature very different from those observed for static structures (Fig. 1A–C).
6 Discussion
6.1 The DS2 model
The single contextual difference between Fig. 1 A–C and 1D lies in the dynamic modification of the number of cells () during the simulation for the second case. The total number of computations performed in the implementation of the Meinhardt system in the dynamic structure (16 368 000 elementary operations) is strictly bounded by those performed in the implementation in the static structure cells (160 000 elementary operations) and cells (81 920 000 elementary operations), which produce periodic patterns.
The periodic patterns observed in Fig. 1A–C are simple to describe in terms of equidistant arcs of circles and of reduction of these arcs of circles into equidistant points. The structure of the pattern presented in Fig. 1D is much more difficult to describe and clearly expresses a visibly higher level of complexity. This complexity was obtained by playing on the temporal character of the simulation. Indeed, a higher delay between the two first divisions should allow the system to reach its periodic equilibrium, and so on. Likewise, a very short delay between divisions should not allow the system to evolve. In the simulation presented, the complex pattern of Fig. 1D presents a provisional temporal character, and the evolution of the system frozen in the static -cell configuration should tend towards a periodic pattern similar to the one of Fig. 1C.
We interpret the complexity of Fig. 1D as the result of the interaction between two simpler mechanisms, which operate at different speeds. The distance is measured in number of cells, and the time in number of cycles of computation.
The first mechanism is a constant speed of diffusion of the system in the structure. In the case of a static structure, for instance the one represented in Fig. 1C, by making a display every 75 cycles, a new arc of circle appears, located at 6.4 cells on average from the previous one. In first approximation, this speed depends only on the value of the diffusion coefficient of the inhibitor.
The second mechanism is the regular multiplication with time (every 50 cycles) of the number of cells. The consequence is an exponential increase of the mean distance between two cells of the dynamic structure.
In the case of a dynamic structure, this second mechanism impedes more and more the first one, which tends towards the system to return to the equilibrium state at constant speed.
If, at a given moment, the cell multiplication is stopped, the system will progressively return to a periodical equilibrium state in space. If not, the system will ad infinitum tend towards a state that can be at the same time described as chaotic and fractal in a large sense. In the biological context of morphogenesis, the number of cells follows along time a logistic law, with an exponential increase at the beginning followed by stabilization at the end. At a given moment, the synthesis of the compounds that induce the pattern formation is stopped, and as these compounds are transformed into other compounds, the system is frozen at an intermediate state more or less close to the equilibrium state. This mechanism allows zebras and tigers to get their stripes and panthers and giraffes their spots. As stressed out by Lesne [10], the auto-organized structures are out of equilibrium, because floods of matter and energy cross them.
Although unpredictable at the level of model examination, the complex patterns obtained present a wholly determinist character. For each simulation based upon the same parameter values, the same pattern is found again, as for models simulating chaos. If the position and length of each peak of Fig. 1D is a priori unpredictable, the pattern presents constants: for instance, the distances between peaks is in the same order of magnitude as the distances between arcs of circles in Fig. 1C.
6.2 The concept of emergence
The aperiodic pattern presented in Fig. 1D obviously corresponds to the creative emergence of Cariani [12]. In the context of the definition ERM of Bonabeau and Dessalles [13], the notion of emergence is relative to a theoretical context and to experimental results that are not predicted by this theory.
In the context of the thermodynamic theory of closed systems, implementing a simple system of Meinhardt characterized by identical values of diffusion coefficients of activator and inhibitor in a static structure will provide a uniform pattern, wholly consistent with the theory. Now, if the above Meinhardt system is implemented, we observe the emergence of a periodic pattern unpredicted by the theory.
In the context of the theory of Turing or of the thermodynamic of open systems, such a result is predicted, and there is no more emergence. In this same theoretical context, the implementation of the same system of Meinhardt into a dynamic structure induces the emergence of an aperiodic pattern unpredicted by the theory. The simplicity of the model of morphogenesis, on the one hand, and the extreme simplicity of the process of cellular development, on the other hand, are not able to predict the complexity observed in Fig. 1D: this is the unexpected side of emergence.
Then, a new more general theoretical frame has to be built up, which will integrate the previous ones, predict the aperiodic patterns observed, and reduce the emergent character of observations.
It is important to note that in all cases, the system remains qualitatively identical, and that the amount of computations involved is comparable. The emergence of a pattern with a higher complexity is not directly induced by a higher number of computations. The ERM emergence of Bonabeau and Dessalles [13] can be interpreted by the fact that the formalism used in the model is inadequate to describe the spatial and temporal structures generated by this model.
6.3 Complexity and emergence
It appears here that modelling of complex patterns introduces two different notions of complexity:
- – the genotypic complexity of the model, which can be measured by the number of parameters of the model, the number of algorithmic instructions or of elementary computations required to get a given pattern;
- – the phenotypic complexity of the pattern, measured in terms of organization, for instance in negentropy [23], likely to quantify the phenomena of complexification shown by many vital processes.
Usually, in order to model a phenotypically more complex pattern, a genotypically more complex model will be built. Then, the object of modelling consists in optimizing the ratio of the two complexities, making better than the simple random. For instance, any pattern defined under the form of a matrix of cells (or pixels) can always be modelled by simulating all possible patterns, varying all states a cell can take. For a two states (black/white) n-cell matrix, there are possible patterns, then elementary computations.
A first approach consists in reasoning with a constant model, characterized by a more or less higher genotypic complexity, and to maximize the phenotypic complexity. Then the aim is to make emerge the more complex patterns from the model, as in the above discussion about the concept of emergence. There will be emergence each time a pattern of a higher phenotypic complexity will be modelled. The difficulty of this approach lies in the measure of negentropy, which can depend on the arbitrary of the observer.
The second approach, equivalent in theory, consists in reasoning with a constant pattern, characterized by a more or less higher phenotypic complexity, and to minimize the genotypic complexity. Then the aim is to fit different models with the given patterns, in searching the simplest model (principle of parsimony). Any model able to fit this same pattern with less computation will present a progress. There will be emergence each time a new model with a lower genetic complexity generates this same pattern. The only arbitrary factor lies in the appropriateness of fit between the pattern simulated by the model and the reference pattern. It is possible to quantify this appropriateness by measuring the distance between the two patterns according to a given metric and comparing it with an a priori fixed threshold value.
This definition considerably reduces the role of the observer introduced by different authors in their definition of emergence [5,12,13,22]. Unlike Ricard's definition [11], the above-defined emergence is not reduced to complexity, although tightly linked to it. Finally, at the difference of all previous propositions, every phenomenon that can be qualified of emergent in the sense of our definition can be invalidated (falsifiable in the sense of Popper).


