Primary sequences of proteins from complete genomes display a singular periodicity: Alignment-free <i>N</i>-gram analysis

Jan P. Radomski; Piotr P. Slonimski

doi:10.1016/j.crvi.2006.11.001

Biochemistry / Biochimie

Primary sequences of proteins from complete genomes display a singular periodicity: Alignment-free N-gram analysis
[La séquence primaire des protéines de génomes complètement séquencés présente une périodicité singulière : analyse sans alignement fondée sur la fréquence des bigrames]

Présenté par : Jean Rosa

Jan P. Radomski ¹ ; Piotr P. Slonimski ²

¹ Interdisciplinary Centre for Mathematical and Computational Modelling, Warsaw University, Pawińskiego 5A, Bldg. D, 02106 Warsaw, Poland
² Centre de génétique moléculaire du CNRS & université Pierre-et-Marie-Curie (Paris-6), 91190 Gif-sur-Yvette, France

Comptes Rendus. Biologies, Volume 330 (2007) no. 1, pp. 33-48.

Résumés

Anglais
Français

A method is proposed to represent and to analyze complete genome sequences (52 species from procaryotes and eukaryotes), based upon n-gram sequence's frequencies of amino acid pairs (bigrams), separated by a given number of other residues. For each of the species analyzed, it allows us to construct over-abundant and over-deficient occurrence profiles, summarizing amino acid bigram frequencies over the entire genome. The method deals efficiently with a sparseness of statistical representations of individual sequences, and describes every gene sequence in the same way, independently of its length and of the genome sizes. The frequency of over-abundant and over-deficient occurrences of bigrams presents a singular periodicity around 3.5 peptide bonds, suggesting a relation with the alpha helical secondary structure.

Nous avons développé une méthode d'analyse des séquences, dite des bigrames (n-tuples avec $n = 2$ ), représentant les 400 combinaisons des 20 acides aminés, séparées par un nombre variable de liaisons peptidiques. Un ensemble de 52 génomes, procaryotes et eucaryotes, a été étudié. Une analyse statistique approfondie permet de dégager, pour chaque génome, un profil caractéristique de combinaisons d'acides aminés significativement surreprésentées ou sous-représentées. La fréquence de ces déviations présente une périodicité de 3,5 liaisons peptidiques, ce qui suggère une relation avec l'hélice alpha de la structure secondaire.

Métadonnées

Reçu le : 2006-10-19
Accepté le : 2006-11-07
Publié le : 2006-12-01

PMID

DOI : 10.1016/j.crvi.2006.11.001

Keywords: Alignment-free, N-gram analysis, Singular periodicity
Mot clés : Analyse sans alignement, Périodicité singulière

Affiliations des auteurs :

Jan P. Radomski ¹ ; Piotr P. Slonimski ²

¹ Interdisciplinary Centre for Mathematical and Computational Modelling, Warsaw University, Pawińskiego 5A, Bldg. D, 02106 Warsaw, Poland
² Centre de génétique moléculaire du CNRS & université Pierre-et-Marie-Curie (Paris-6), 91190 Gif-sur-Yvette, France

@article{CRBIOL_2007__330_1_33_0,
     author = {Jan P. Radomski and Piotr P. Slonimski},
     title = {Primary sequences of proteins from complete genomes display a singular periodicity: {Alignment-free} {\protect\emph{N}-gram} analysis},
     journal = {Comptes Rendus. Biologies},
     pages = {33--48},
     publisher = {Elsevier},
     volume = {330},
     number = {1},
     year = {2007},
     doi = {10.1016/j.crvi.2006.11.001},
     language = {en},
}

TY  - JOUR
AU  - Jan P. Radomski
AU  - Piotr P. Slonimski
TI  - Primary sequences of proteins from complete genomes display a singular periodicity: Alignment-free N-gram analysis
JO  - Comptes Rendus. Biologies
PY  - 2007
SP  - 33
EP  - 48
VL  - 330
IS  - 1
PB  - Elsevier
DO  - 10.1016/j.crvi.2006.11.001
LA  - en
ID  - CRBIOL_2007__330_1_33_0
ER  -

%0 Journal Article
%A Jan P. Radomski
%A Piotr P. Slonimski
%T Primary sequences of proteins from complete genomes display a singular periodicity: Alignment-free N-gram analysis
%J Comptes Rendus. Biologies
%D 2007
%P 33-48
%V 330
%N 1
%I Elsevier
%R 10.1016/j.crvi.2006.11.001
%G en
%F CRBIOL_2007__330_1_33_0

Jan P. Radomski; Piotr P. Slonimski. Primary sequences of proteins from complete genomes display a singular periodicity: Alignment-free N-gram analysis. Comptes Rendus. Biologies, Volume 330 (2007) no. 1, pp. 33-48. doi : 10.1016/j.crvi.2006.11.001. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2006.11.001/

Version originale du texte intégral

1 Introduction

In an intriguing article, Damashek [1] described an automatic classification of a whole library of texts with the aid of calculated n-grams. The resulting vector representation of documents, together with a simple Euclidean distance measure, allowed for each document to be placed into a proper semantic context, not only as to its language origin, but also to put it into a correct thematic contextual class. Similar searches, for near exact sequence matches, are performed frequently in large-scale sequencing projects of comparative genomics. However, the traditional sequence distances require sequence alignment (either pairwise or multiple), and therefore are not directly applicable to the problem of whole genome phylogeny, where events such as rearrangements (gene/chromosome/genome) make the full-length alignments inapplicable. Nevertheless, the vast majority of methods used up to date to compare complete genomes are based upon techniques of local alignment of two or more DNA, or protein sequences. These methods are very successful for the phylogenetic studies of gene/protein families or superfamilies, and even for the phylogenies of complete genomes, when the evolutionary divergence between taxons is not too great. However, when genetic recombination, shuffling and various mechanisms responsible for genome fluidity and dynamics are predominant (as in phylogenies of deep-rooted taxons), comparisons based upon sequence alignments alone fail to extricate a large body of phylogenetic signals. For example, in a comparison of the Aeropyrum pernix genome with the Ureoplasma urealiticum one, only a very small fraction of protein sequences of the first genome can be aligned with those of the second genome ( $114 / 3499 = 3 %$ ). Thus, the genetic recombination and, in particular, genetic shuffling are at odds with sequence comparison by alignment, which assumes conservation of contiguity between homologous segments: the alignment approach overlooks well-documented long-range interactions, and also the relative fluidity resulting from recombination with shuffling of conserved segments without loss of function.

A variety of theoretical approaches are being used to derive alignment-free methods that overcome this limitation. The issue of quantifying the similarity between biological sequences is of paramount importance, and even more, so as the difficulty in defining a metric for sequences' dissimilarity is also present in the analysis of natural language texts, thus both areas can be synergistic. There are many algorithms for searching genetic databases for biologically significant similarities in biological sequences. Past research has shown that word-based search tools are computationally efficient and can find similarities or dissimilarities invisible to other methods. The characteristic family of word-based dissimilarity measures, that define distance between sequences, can be computed by simultaneously comparing the frequencies of all subsequences of n adjacent letters (i.e., n-words, n-grams, k-tuples, the actual names given in the literature can differ; however, they all describe the same concepts and approaches) in sequences. Applications to real data demonstrate that currently used word-based methods rely mostly on Euclidean distance; however, other distance measures can be used as well, perhaps leading to a significant improvement.

The earliest work systematizing the use of n-tuple counts for sequence comparison [2–4] used the difference between two DNA sequences by the squared Euclidean distance between their transition matrices. Daeyaert et al. [5] have studied unaligned sequences characteristics of the amino acid composition of n-tuples (i.e. doublets, triplets, quadruplets, etc.), investigating the performance of two statistics (termed commonality and specificity) derived from n-tuple counts.

Distribution regimes for the number of k-word matches between two random sequences observed when comparing two sequences and counting the number of k-letter words the two sequences have in common were analyzed by Karlin [6] and Lippert et al. [7]. The rigorous study of the statistical distribution revealed three asymptotic regimes, including compound Poisson and normal. The compound Poisson distribution arises when the word size k is large, and the word matches are rare. The normal distribution arises when the word size is small and the matches are common. However, when the word size is small and the letters are uniformly distributed, the anticipated limiting normal distribution does not always occur. In this situation, the uniform distribution provides the exception to other letter distributions. Therefore a naive ‘one distribution fits all’ approach could easily create serious errors in estimating significance.

Stuart et al. [8] presented a method for generating gene and species phylogenies from whole genomes, using short-character string matches not placed within explicit alignments. The singular value decomposition of a sparse tetrapeptide frequency matrix was used to represent the proteins of organisms uniquely as vectors in a high-dimensional space. Muller and Koonin [9] have used a principal component analysis (PCA) to classify DNA sequences, by translating sequences into vectors that represent their word content. They tested the approach with several datasets of genomic DNA, and were able to classify introns and exons with an accuracy of up to 96%. Alignment-free metrics, until very recently, have not been an object of a comparative study. The classification accuracy of word composition metrics was reviewed [10,11], together with a new definition of distance between protein sequences – the W-metric, which bridges alignment metrics, such as scores produced by the Smith–Waterman algorithm [12], and methods based solely on k-tuple composition. Although alignment methods resulted in very good classification accuracy at the family and superfamily levels, the alignment-free distances were as good as alignment algorithms when sequence similarity was smaller, such as for recognition of fold or class relationships. Edgar [13] used word statistics for the discovery of local similarities and the estimation of evolutionary distance by identifying k-mers common to two sequences. The ability of compressed amino acid alphabets to extend these techniques to distantly related proteins was also investigated. Distance measures derived from k-mer counting were found to correlate well with percentage identity derived from sequence alignments. Compressed alphabets were seen to improve performance in local similarity discovery, but no evidence was found for improvements when applied to distance estimates.

None of the studies discussed so far have dealt with the comparison of complete genomes using alignment-free techniques, although some did refer to such a possibility. The major obstacle stems from the very sparse statistics resulting while using n-grams of longer lengths (already for tetrapeptides, the number of possible combinations of 4-grams from 20-letter alphabet is much larger than that actually observed for proteins of an average 300 residues). Also, the longer the n-grams used, the less the method can be termed truly alignment free. The very first approach, which can be considered as analyzing complete genomes by alignment-free methods, takes the idea to its extreme – Kreil and Ouzounis [14] used amino acid compositions deduced from six archea, 19 bacterial species, and two eukaryotes to build a phylogenetic tree of species correlated with the optimal living temperatures of their environment. Their method takes into account, not only homologous proteins, but also proteins unique to particular species. Radomski and Slonimski [15] have used to a small extent, the bigram analysis of a set of ribosomal protein sequences to develop the notion of the genomic style of proteins. Rosato et al. [16] also analyzed the thermal dependencies of 15 proteomes, using the concept of n-grams with a spacer, and described some observed anomalies in n-gram distribution at certain spacer lengths.

On the other hand, already in 1967, the notion of the expectancy-rectified frequencies of bigrams with spacer (s) – i.e. the observed frequency of occurrence of the s-pair of amino acids $f^{s} (i j)$ compared to the expected frequency of such s-pair occurrence $f^{s} (i) f^{s} (j)$ – was introduced by Krzywicki and Slonimski [17], who have shown that for certain spacer length statistically highly significant deviations are present in proteins, albeit due to the small number of sequences available at that time, judged by the present-day standards, the idea had to wait a long time for further developments.

2 The concepts and the methods used

When compared to a language text, an average genetic sequence is relatively short. The mean length of proteins oscillates at about 350 residues (see, e.g., in Table 1). Therefore, calculating the set of n-grams for a such short string of amino acids will lead to a vector representation, which is severely sparse, especially for higher n-grams lengths, and hence to very poor statistics. To alleviate this problem, we propose here a hybrid approach. Namely, to compute counts of all amino acid pairs – separated by sub-sequences of differing length, the actual composition of these spacer sub-sequences will be neglected. However, when such partial counts are used as a composite set, a poor statistic problem is not any longer a hindering obstacle, and the complete information about particular n-gram frequencies profile is preserved, albeit in a distributed and convoluted form.

	Species	Abbr.	Sequences	Length	Mean
1	Aeropyrum pernix	AerPe	2 689	642 607	239
2	Agrobacterium tumefaciens	AgrTu	4 554	1 473 418	323
3	Aquifex aeolicus	AquAe	1 520	483 613	318
4	Archaeoglobus fulgidus	ArcFu	2 404	667 175	278
5	Arabidopsis thaliana	AThal	25 546	11 143 776	436
6	Bacillus halodurans	BacHa	4 060	1 191 293	293
7	Bacillus subtilis	BacSu	4 093	1 220 624	298
8	Borrelia burgdorferi	BorBu	850	284 466	335
9	Buchnera sp	Buchn	563	185 207	329
10	Campylobacter jejuni	CamJe	1 628	510 671	314
11	Caulobacter crescentus	CauCr	3 729	1 211 419	325
12	Caenorhabditis elegans	CEleg	17 083	7 730 583	453
13	Chlamydia muridarum	ChlMu	907	324 168	357
14	Chlamydophila pneumoniae AR39	ChlPn	1 108	364 543	329
15	Chlamydia trachomatis serD	ChlTr	892	312 510	350
16	Clostridium acetobutylicum	CloAc	3 666	1 134 524	310
17	Deinococcus radiodurans	DeiRa	2 930	903 345	308
18	Escherichia coli O157H7	EColi	5 352	1 614 338	302
19	Haemophilus influenzae	HaeIn	1 707	523 355	307
20	Halobacterium sp	HaloB	2 050	585 593	286
21	Helicobacter pylori 26695	HelPy	1 562	498 658	319
22	Lactococcus lactis	LacLa	2 258	668 470	296
23	Methanococcus jannaschii	MetJa	1 714	486 267	284
24	Methanobacterium thermoautotrop	MetTh	1 866	529 023	284
25	Mycoplasma genitalium	MycGe	479	175 115	366
26	Mycobacterium leprae	MycLe	1 605	537 654	335
27	Mycoplasma pneumoniae	MycPn	676	239 568	354
28	Mycoplasma pulmonis	MycPu	779	290 681	373
29	Mycobacterium tuberculosis CDC1551	MycTu	4 175	1 330 978	319
30	Neisseria meningitidis MC58	NeiMe	2 020	587 940	291
31	Pasteurella multocida	PasMu	2 008	666 797	332
32	Porphyromonas gingivalis	PorGi	2 226	660 580	296
33	Pseudomonas aeruginosa	PseAe	5 559	1 867 388	336
34	Pyrococcus abyssi	PyrAb	1 761	536 824	305
35	Pyrococcus horikoshii	PyrHo	2 060	572 271	278
36	Rickettsia conorii	RicCo	1 374	339 125	247
37	Rickettsia prowazekii	RicPr	832	278 929	335
38	Sinorhizobium meliloti	SinMe	3 336	1 051 050	315
39	Staphylococcus aureus Mu50	StaAu	2 708	805 807	298
40	Streptococcus pneumoniae Tigr4	StrPn	2 088	595 476	285
41	Streptococcus pyogenes	StrPy	1 695	517 888	306
42	Sulfolobus solfataricus	SulSo	2 968	843 129	284
43	Sulfolobus tokadai	SulTo	2 826	755 676	267
44	Synechocystis PCC6803	Syny3	3 164	1 034 287	327
45	Thermoplasma acidophilum	TheAc	1 478	456 589	309
46	Thermotoga maritima	TheMa	1 842	584 266	317
47	Thermoplasma volcanium	TheVo	1 522	453 778	298
48	Treponema pallidum	TrePa	1 031	352 431	342
49	Ureaplasma urealyticum	UreUr	611	228 980	375
50	Vibrio cholerae	VibCh	3 283	1 161 898	304
51	Xylella fastidiosa	XylFa	2 759	744 871	270
52	Saccharomyces cerevisiae	Yeast	6 200	2 897 330	467

	Sum/mean		157 796	55 256 952	350

The method involves several steps (although, depending on the actual purpose at hand, not all the chain will be always necessary). For completeness sake, we present them here sequentially, to facilitate understanding.

Step one involves counting occurrences of the particular amino acid pairs as follows. For the given genome sequence V, and the all spacer lengths, λ, in order to calculate observed values of a given amino acid pair ( $a_{k}$ , $a_{l}$ ), for each species i, first we need to construct a series of square matrices $N_{i}^{λ}$ . Each element of every matrix $N_{i}^{λ}$ contains the counted sum of all specific ( $a_{k}$ , $a_{l}$ ) pairs separated by a string of length λ of other residues present in this sequence. Using a sliding window of the length $λ + 2$ , and starting at the position m, we would scan the whole sequence V, calculating elements of the matrix by the formula:

N_{i}^{λ} (a_{k}, a_{l}, n) = \sum_{m = 1}^{M - λ - 1} f (a_{k}, a_{l}, λ, m)

(1)

where M is the sequence's n length, and

f (a_{k}, a_{l}, λ, m) = {\begin{matrix} 1, & if V (m) = a_{k} and \\ V (m + λ + 1) = a_{l} \\ 0, & otherwise \end{matrix}

Obviously, when $λ = 0$ one has a dipeptide (and a tripeptide for $λ = 1$ ; tetrapeptide for $λ = 2$ , etc.). Note, that since these are ordered counts, each starting at the protein's N-terminus, the amino acid pair, e.g., Phe–Ala is not identical to the amino acid pair Ala–Phe, and thus the matrices $N_{i}^{λ}$ are not symmetrical.

Step two – the null hypothesis. It is well known that various proteins have large differences in their amino acid composition. Therefore, the actual abundance of any amino acid pair in a given protein has to be compared with the one predicted by the null hypothesis, which states there are no constrains whatsoever in the occurrence of any amino acid pair, i.e. their occurrence is random, and depends solely on the amino acid composition of a given protein. Therefore, the expected value, $P_{i}^{λ} (a_{k}, a_{l,} n)$ , of finding the given amino acids pair ( $a_{k}, a_{l}$ ) separated by λ residues in a protein sequence n of the species i, can be calculated according to the formula:

P_{i}^{λ} (a_{k}, a_{l}, n) = S_{i}^{a_{k}} (n) \cdot S_{i}^{a_{l}} (n) \cdot L_{i}^{λ} (n)

(2)

for the genome i, the

L_{i}^{λ}

is sum of the lengths of all specific segments

a_{k} λ a_{l}

, present in the sequence n, and the sum of all frequencies,

S^{a} (n)

, of the sequence's n amino acids a, equals 1, that is:

\sum_{a = 1}^{20} S_{i}^{a} (n) = 1

It needs to be stressed, although it is obvious as all sequences differ by both length and their composition, that the expected value of

P_{i}^{λ}

must be calculated separately for each protein in a particular genome.

Step three: the measure of deviation from the null hypothesis for any species i can be expressed as a ratio of the two values: the $N_{i}^{λ}$ and the $P_{i}^{λ}$ . Given the observed (as described in step one), and expected (described in the step two) values of finding any amino acid pair ( $a_{k}, a_{l}$ ) separated by λ residues in all sequences of species i, one can calculate their ratio, as a sum running through all sequences n of a given genome:

R_{i}^{λ} (a_{k}, a_{l}) = \log {\sum_{n} \frac{N_{i}^{λ} (a_{k}, a_{l}, n)}{P_{i}^{λ} (a_{k}, a_{l}, n)}}

(3)

The $R_{i}^{λ}$ values can be considered as a measure of how much any particular ( $a_{k} λ a_{l}$ ) frequency deviates from the expected: based on the frequencies of amino acids $a_{k}$ , and $a_{l}$ . It must be stressed that the calculated $R_{i}^{λ}$ values will account for both occurrences of the over-abundant situations, as well as the over-deficient amino acid pairs. Accordingly, each kind of occurrence must be treated separately to obtain meaningful results. Whichever the case, in order to extricate the observations significantly deviating from the bulk of all ratios $R_{i}^{λ}$ , it is useful to consider only the values larger than a predefined threshold, e.g., larger than one, two or three standard deviations. Also, it is important to note that this method of the $R_{i}^{λ}$ calculation eliminates any bias due to the different sizes of compared genomes and lengths of protein sequences, which was still present in both the $N_{i}^{λ}$ and the $P_{i}^{λ}$ matrices. We will denote all such $R_{i}^{λ}$ matrices, after passing them through the standard deviation threshold, by $O_{i}^{λ}$ , and call them species-occurrence matrices.

Additionally, we can count how often any two species i and j display co-occurrence of such anomalous effects for a given ( $a_{k}, a_{l}$ ) pair of amino acids. This step involves summing-up all co-occurrences of the same ( $a_{k}, a_{l}$ ) pair of amino acids between the two occurrence matrices $O_{i}^{λ} (a_{k}, a_{l})$ , and $O_{j}^{λ} (a_{k}, a_{l})$ for the corresponding species i and j, which yields a series of the square matrices $C^{λ}$ of co-occurrence. Again these matrices are not symmetrical, as the upper triangles will contain the positive, and the lower triangles will contain the negative co-occurrence counts, respectively. At the same time, we need to know also the corresponding sums of all positive, $S p^{λ}$ , and negative, $S n^{λ}$ , co-occurrences, in order to calculate expected species co-occurrence matrices $E p^{λ}$ (and $E n^{λ}$ ) as follows:

E p^{λ} (i, j) = \frac{S p_{i}^{λ} \cdot S p_{j}^{λ}}{400}

(4)

The factor of 400 corresponds to all possible amino acids combinations. The respective elements $E n^{λ} (i, j)$ of the negative co-occurrence matrices are calculated in the same manner.

And finally we arrive at how to calculate the species co-occurrence difference matrices:

D p^{λ} = C p^{λ} - E p^{λ}

(5)

3 The results

Table 1 contains the names of all 52 species used in the present study, together with their abbreviations, the number of genes/sequences, their total length and the average, species specific, sequence length. The range of spacer, λ, lengths used here varied from 0 to 18 (already at about $λ = 12 – 14$ , there were only small variations visible, see below, so the higher values of λ are included here for comparison purpose only).

3.1 Distributions

It is of primary interest to see the shape of the distribution and to verify whether there would be any statistically significant deviations. For 52 species, 400 amino acid pairs, and 19 spacer lengths, we have almost 400 thousands observations. Notice, that calculation of $R_{i}^{λ}$ eliminates any bias due to the length and number of proteins present in a genome. Fig. 1 shows the histogram (at bin width of 0.001) of the sum of the results obtained. It is immediately apparent that the mono-modal bell-shaped curve, closely resembling a normal distribution, is not ideally symmetrical, as there are slightly more negative then positive values present. A thin white line at the left slope is a mirror image of the right slope, and it can be seen that this minor lack of symmetry concerns all ranges of values.

Fig. 1
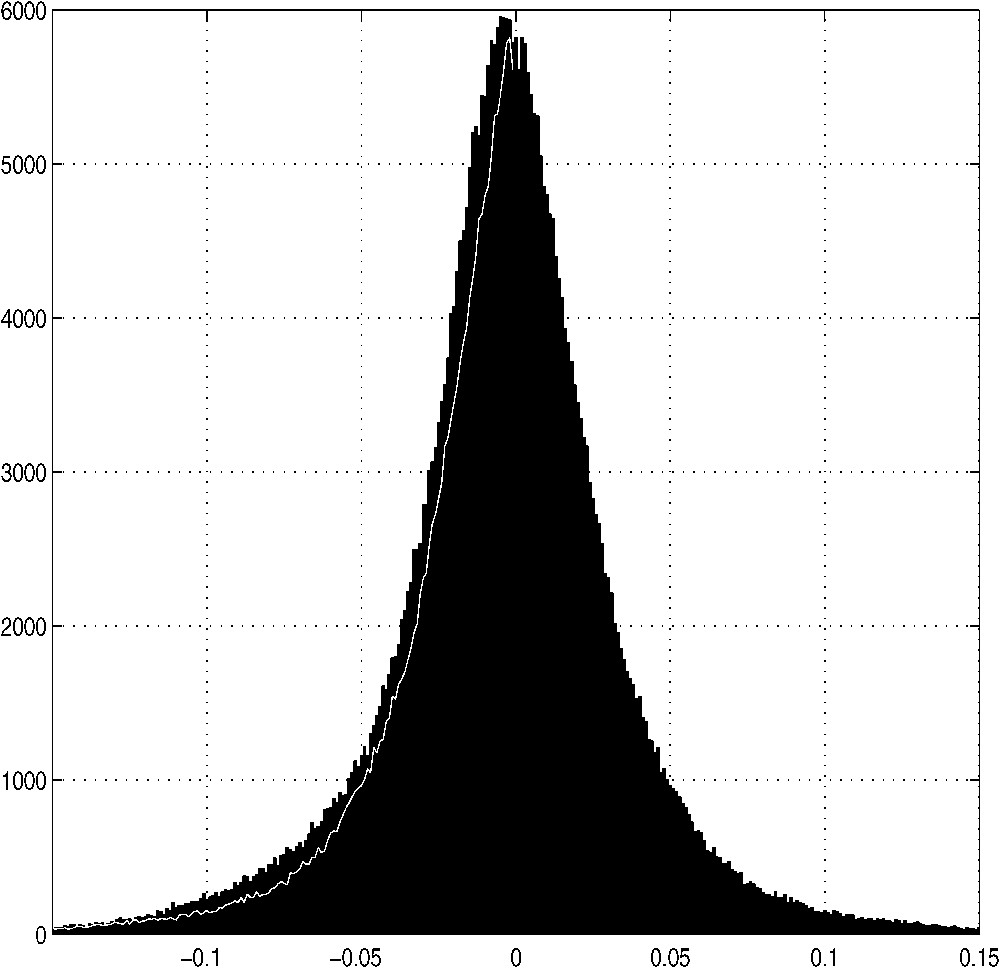
Distribution of all the bigrams analyzed. The value of the ratio $R_{i}^{λ}$ (Eq. (3)) is plotted in intervals of 0.001 (abscissa) and the corresponding number of occurrences is shown in ordinals, based upon analysis of 395 200 bigrams of different kinds (19 spacer lengths, and 400 amino acid pairs) from complete genomes of 52 species (see Table 1).

The source of this dissymmetry is immediately obvious upon comparing distributions for all species involved. In Fig. 2, there are examples of distributions for the three archea: AerPe, ArcFu, and SulTo (first row), the three eubacteria: AgrTu, ChlMu, and VibCh (middle row), and finally all the three eukaryotes present: AThal, CEleg, and Yeast (bottom row). It can be seen that for the three eukaryotes, their distributions are all shifted systematically towards negative values, and approximately by the same amount. As eukaryotic sequences constitute about 31% of all sequences analyzed, their influence is quite substantial, although the negative shift is less pronounced for all sequences together, than for any of the three eukaryotes separately. At present, we are unable to comment upon this observation, and perhaps a few more complete eukaryotic genomes need to be analyzed by the method described, before any firm conclusions can be drawn. For all archea, most notably for AerPe, distributions are also broader, than for both the bacterial (the distribution for AgrTu being very narrow, perhaps the most narrow of all 52 genomes), and the eukaryotic species analyzed.

Fig. 2
Examples of distribution of bigrams from different species. The value of the ratio $R_{i}^{λ}$ (Eq. (3)) and the corresponding number of occurrences are plotted as in Fig. 1 for nine individual complete genomes. Note that each genome has 7600 different kinds of bigrams (400 amino acid pairs, and 19 spacers).

The most interesting characteristics of the monomodal, bell-shaped curve of Fig. 1 are, however, its deviations from a normal distribution. The extreme tails of the observed distribution are more pronounced than expected from normal. For instance, the $R_{i}^{λ}$ values deviating from mean by more than three standard deviations (STD) represent 1.42% of the whole (for a Gaussian distribution: 0.27%), whereas the $R_{i}^{λ}$ values comprised within ±1 STD represent 84.3% (normally distributed: 68.3%). This means there are $4545 [= 395 200 \times (1.42 - 0.27 %)]$ occurrences of $R_{i}^{λ}$ values, which are exceptional in comparison with a normal distribution. The analysis of these singular $R_{i}^{λ}$ occurrences constitutes the main body of the present article. They correspond to the two classes of bigrams: over-abundant (or over-represented) amino acid pairs, and over-deficient (under-represented) amino acid pairs.

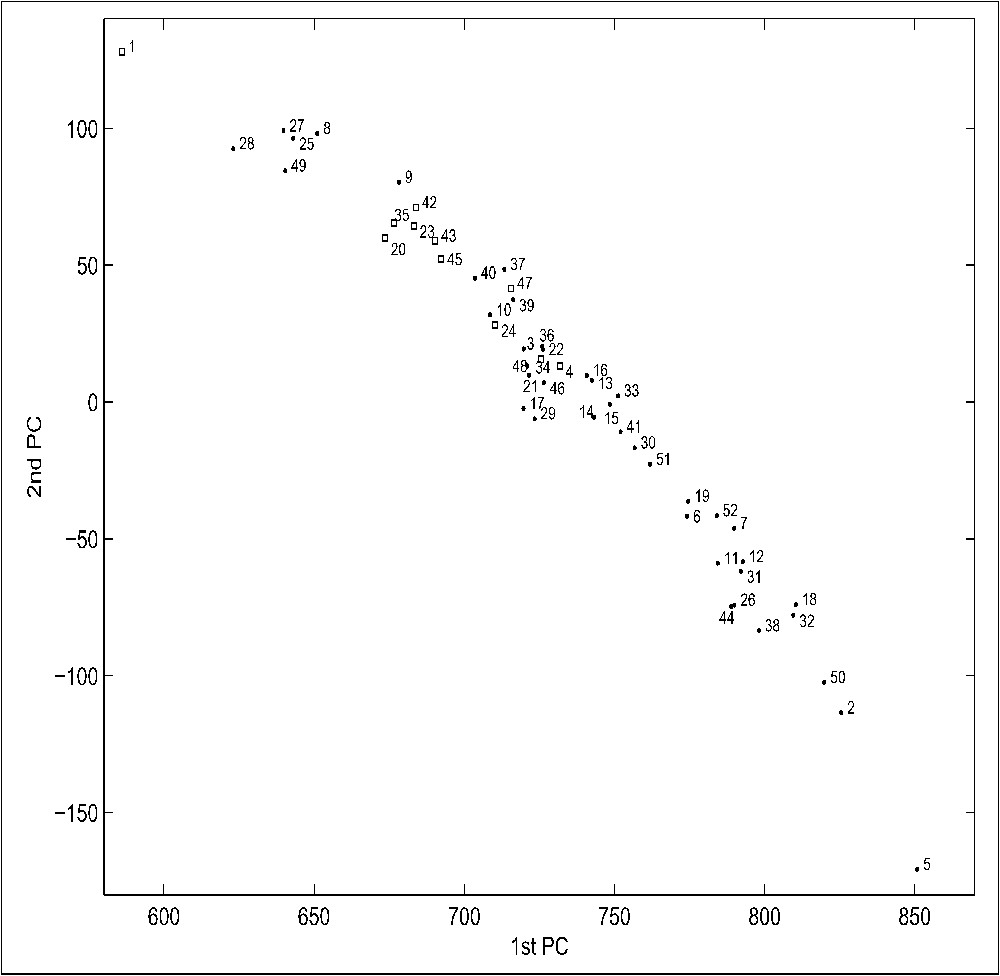
As an attempt to substantiate the above observations, at least semi-quantitatively, we performed a principal-component analysis (PCA) of the 52 histogram vectors (bin width of 0.001). The first three principal components covered almost 98.7% of the whole information variance present in this set (the first PC: 97.67%, the second PC: 0.71%, and the third PC: 0.28%). The scatter plots of the first PC vs. the second PC, of the first PC vs. the third PC, and the second PC vs. the third PC are shown on Figs. A1a, A1b and A1c (Figs. A1–A3 can be found in the web-available supplementary material), respectively. While it remains always a subject of interpretation when one attempts to attribute an explanatory meaning to a particular set of PCs, it seems reasonable to propose the following. The first PC and the second PC together correspond to the vertical extent of each histogram, and to the histogram's ‘steepness’ (AThal and AgrTu, points numbered on all panels of Fig. A1 as 5 and 2, respectively), or its antinomy ‘broadness’ (AerPe, points numbered 1 on all panels). And the third PC could well stem from the histogram's shift to the left or to the right of the central position (CEleg and Yeast, points 12 and 52 on all panels, being most shifted towards negative values, while PorGi and MycLe, points numbered 32 and 26 on all panels, are least shifted (Figs. A1b and A1c). Such an interpretation agrees very well with all the individual histogram cases (cf. Fig. 2). To check whether the first PC of the above analysis is affected by the particular genome size, and if so to what extent, we normalized all histogram vectors such that the vertical axes were now spanning the range between 0 and 1, and then performed the PCA on the new set as well. Again the first three principal components covered more than 98.6% of the whole information variance present in the normalized set (the first PC: 97.65%, the second PC: 0.73%, and the third PC: 0.24%). Exactly the same interpretation as for the primary histogram set holds for the normalized PCA results; so much so that the respective genomes occupy qualitatively the same positions, in relation to each other, although the overall appearance is somewhat changed. Notably, the PCA plots corroborate that eukaryotes are indeed negatively shifted, which is most pronounced for CEleg, and Yeast (points 12 and 52 on all panels), as well as being rather separated from all other species (Figs. A1b and A1c). Of the whole set of 52 species analyzed, the AThal (points numbered 5 on all panels) displays the steepest distribution (the distribution of AgrTu, points numbered 2 on all panels, is steepest amongst bacteria), whereas that of AerPe (points numbered 1 on all panels) is the most broad, indicating substantial deviations from the null hypothesis for this archeon, for both the over-abundant, and the over-deficient regions.

It is perhaps also noteworthy (Fig. A1a), that after AerPe, the more broad distributions are characteristic also for the smallest genomes of the set: BorBu (8), Buchn (9), MycGe (25), MycPn (27), MycPu (28), and UreUr (49). Then follows the rest of archean genomes (all archea are marked as squares on all Fig. A1 plots), together with the two hyper-thermophilic bacteria AquAe (3), and TheMa (46), and then all remaining bacteria. Should we have only an isolated case like that of AerPe, then perhaps a lateral gene transfer might be indicated as a possible source of the genome broad distribution. However, as it is being followed by all small genomes of the set analyzed, which because of their very smallness could hardly be all subjects of a more pronounced massive horizontal exchange than other, bigger microbial genomes, the actual reason remains unclear. Especially as all remaining archea have relatively broad distributions too. We believe that ‘broadness’ of the distribution reflects the intra species diversity of protein sequences of a genome. In that sense, AerPe sequences would be the most diverse in between themselves, and on the contrary, AThal sequences would be least diverse, since these two species occupy the two extremes of the PCA component PC1 vs. component PC2 plot (Fig. A1a). Obviously, these two species have in their genomes numerous protein sequences that are so different that by classical comparison methods they could be only assigned to the ‘maximum’ of diversity (e.g., the Blast $E_{value}$ close to 1, in a pairwise comparison). The alignment free approach we use here would allow us to disentangle, within this ‘maximum’ of diversity, several subclasses, and to relate them to different species.

Interestingly, the broadness of diversity is quite large not only in AerPe (whose genome is deeply rooted and rather difficult to place in a classical species tree), which has a quite large genome for a prokaryote, but also in the smallest genomes like mycoplasmas or UreUr. Therefore, if one hypothesizes that the AerPe broadness of diversity results from horizontal transfer of numerous genes, one would have to evoke a similar mechanism for a large fraction of genomes of the smallest, semi-parasitic eubacteria as well.

There are also striking differences between distributions for different spacer lengths. The example histograms of such distributions for the sum of all 52 species analyzed are given in Fig. 3 – the value of the ratio $R_{i}^{λ}$ (Eq. (3)) and the corresponding number of occurrences are plotted as in Figs. 1 and 2, for the different spacer lengths. Note that there are 20 800 ( $400 \times 52$ ) different kinds of bigrams for each spacer. The more broad distributions are observed for dipeptides, and then with increasing λ they are getting steeper and steeper. Again, as it is the case for the whole set and for individual eukaryotic genomes, a notable negative shift can be observed for $λ = 2, 3, 6, 7, 10$ , and 13, although with the increasing spacer lengths these discrepancies are getting less and less pronounced.

Fig. 3
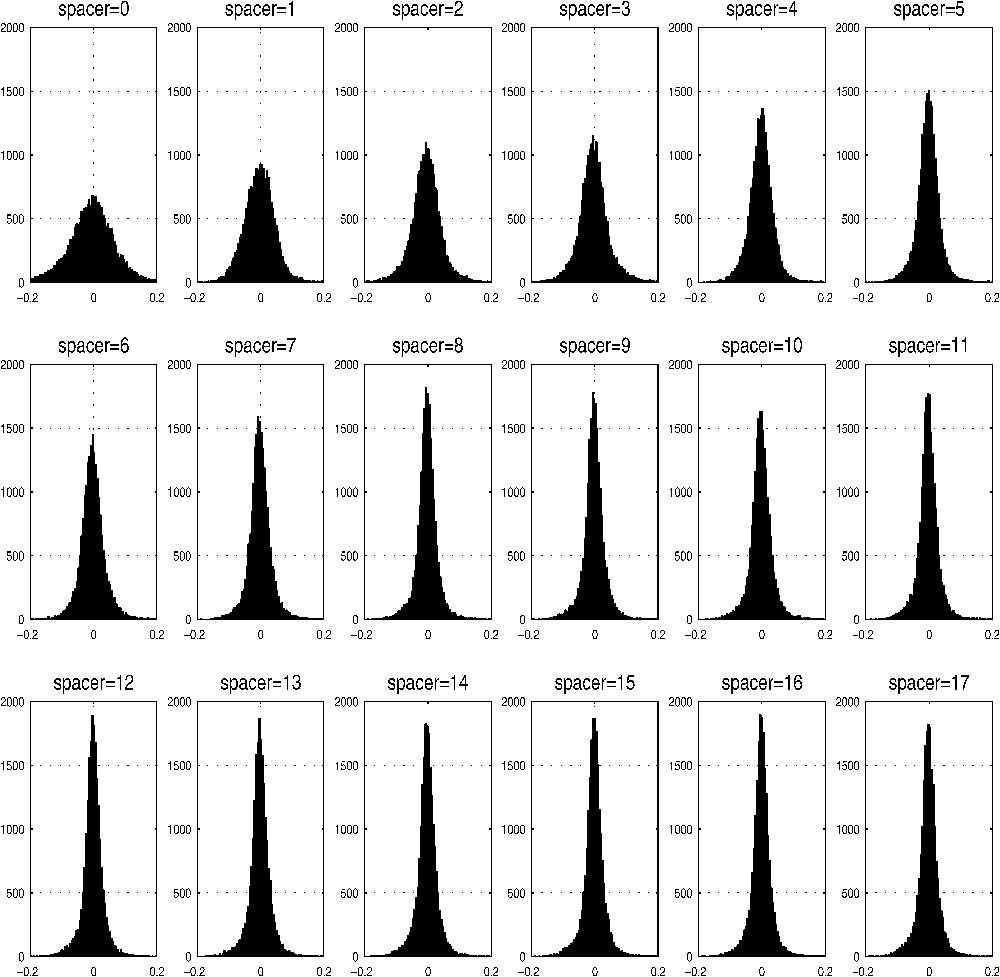
Example of distribution of bigrams for different spacer lengths, as the sum for all 52 species analyzed. The value of the ratio $R_{i}^{λ}$ (Eq. (3)) and the corresponding number of occurrences are plotted as in Figs. 1 and 2 for the different spacer lengths and for all 52 genomes analyzed. Note, that for each spacer there are 20 800 (400×52) different kinds of bigrams.

3.2 Periodicity

For the 52 species, and 19 spacer lengths, each calculated for 400 amino acid pairs, there are 395 00 individual data points. One can ask what are the mean, variance and standard deviation of the whole set, or for each particular genome. However, it is perhaps much more interesting to examine deviations and regularities occurring for the individual amino acid pairs constituting peptide ends at various λ, and the differences or similarities concerning each and all of 52 genomes.

In Fig. 4, there are plots of the number of observations exceeding two standard deviations (estimated separately for all 52 species, and for each amino acid pair at a given λ) for the over-abundant, and the over-deficient occurrence situations, summed up for each λ. It can be seen that for $λ = 2$ up to $λ = 8$ , the slight negative shift, already mentioned above, is readily visible. The number of over-deficient situations (triangles) is greater than that of over-abundant ones (circles) in this range to a much greater extent, although the effect is present at almost every λ value. The greatest differences are present for the spacer lengths 2 and 3, and also 6. The sum of both effects (squares) is also plotted at the top. The periodic character of significant deviations coincides to a very high extent for both the over-abundant and the over-deficient cases, and these oscillations are highly intriguing. If one considers the summed-up plot (squares), there are several ridges at $λ = 1, 3, 6, 10, 13$ and 17, separated by valleys at $λ = 2, 5, 8, 12$ , and 16. The remaining λ values are of intermediate character. With the exception of the valley at $λ = 2$ , all other occurrences fit in well with their respective character between ‘deficient’ and ‘abundant’ cases; thus the actual character of the data point at $λ = 2$ warrants perhaps a further investigation. However, as these points behave for the current set of 52 genomes, one can state that the ridges are spaced intermittently at the intervals of three and four peptide bonds. The most obvious explanation would be that the effect is caused by the prevalence of alpha helical conserved 3-D protein motifs, since the 3.5-periodicity is the characteristic feature of the α helix. However, although it is generally believed that such alpha helices are prevalent, there are also other structural 3-D motifs, also quite abundant, most notably the beta sheets and beta barrels, whose effect should be to obscure, rather than to enhance the periodicity observed here. On the other hand, it might be argued that while the other 3-D motifs should influence the outcome as well, their summary effects might cancel each other, and thus the only remaining strong signal will be that of the alpha helices (and possibly also beta sheets).

Fig. 4
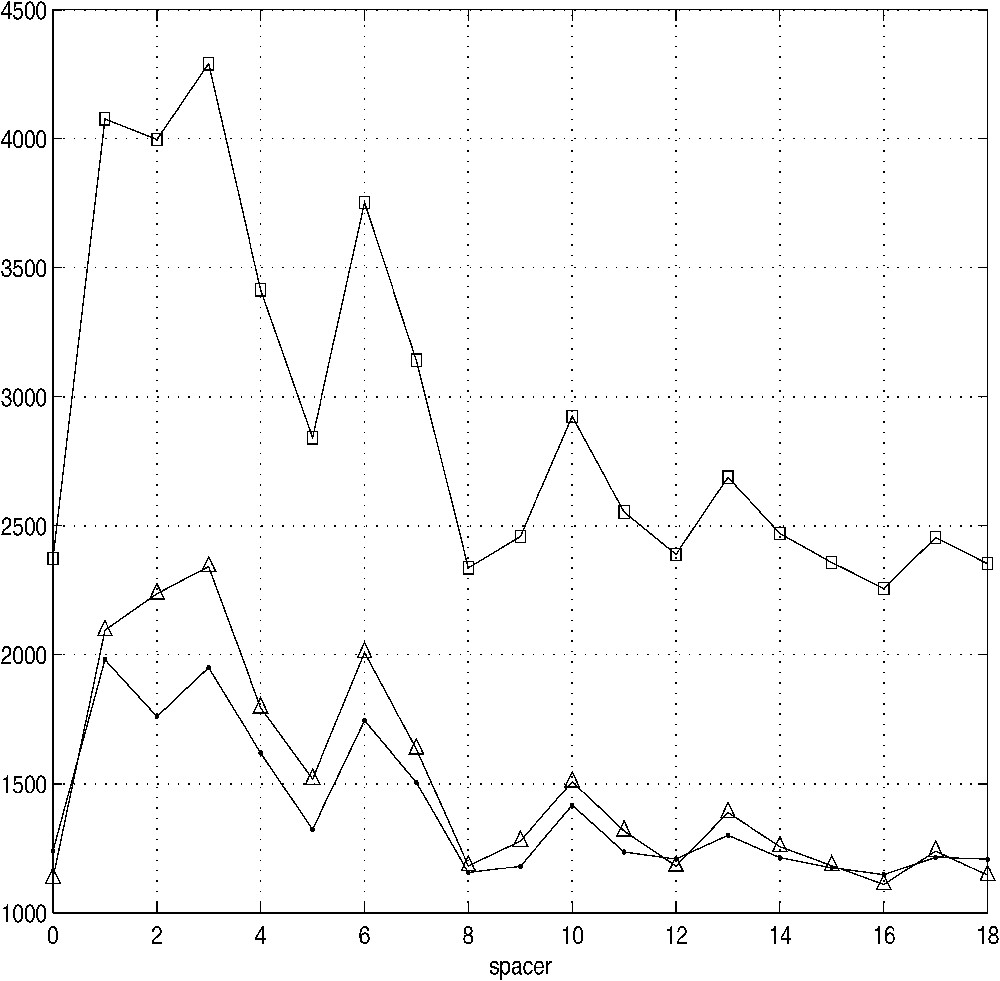
Periodic behaviour of over-abundant and over-deficient cases for all amino acid pairs, summarized for all 52 species. The summed-up occurrences of over-deficient cases (triangles) and of over-abundant cases (circles) for all amino acid pairs and all 52 species show the overall effect of the value of the ratio $R_{i}^{λ}$ (Eq. (3)) exceeding two standard deviations, and its dependence upon the spacer length λ. The top curve (squares) shows the additive effect of both over-deficient and over-abundant cases.

Examination of the effects, shown in Fig. 4 for the summed up influences of each λ value, and all 52 complete genomes, can also be done individually for each of the 52 species under study. Many such examples are depicted in Figs. 5 and A2, comparing the behaviours of all three eukaryotes: Yeast, CEleg, and AThal (panels 5a, 5b, and 5c respectively from top to bottom – for consistency reasons the numbering of all panels in Figs. 5 and A2 is continuous: marked in small letters a–p), eight bacteria: BacSu (5d), AgrTu (5e), ChlMu (5f), ChlPn (5g), ChlTr (5h), HelPy (A2n), BorBu (A2o), and TrePa (A2p), as well as five archea: ArcFu (A2i), MetTh (A2j), PyrAb (A2k), SulTo (A2l), and AerPe (A2m). For the most species not shown in Figs. 5 and A2, the overall behaviour of their periodic ridges and valleys usually follows the same patterns shown and described in Fig. 4, that is the prominent peaks at the $λ = 3, 6, 10$ , and 13, and the corresponding valleys at the $λ = 4 – 5, 8 – 9, 11 – 12$ , etc. In particular, for all six remaining archean species (data not shown): HaloB, MetJa, PyrHo, SulSo, TheAc, and TheVo, their patterns match some or at least one pattern displayed by archea in Figs. 5 and A2. Also for the bacterial species: AquAe, BacHa, CamJe, CloAc, DeiRa, EColi, HaeIn, LacLa, NeiMe, PasMu, RicCo, SinMe, StrPy, TheMa, and XylFa, the overall periodicity scheme looks ‘typical’. However, all three (ChlMu, ChlPn, and ChlTr, Figs. 5f, 5g, and 5h, respectively) display distinctly variant patterns with the very prominent ridge at the $λ = 1$ value, with the peaks at $λ = 3, 6, 10$ much less pronounced; the same variant can be also observed for the PorGi, and Syny3. Another, rather striking difference is distinctly visible for the HelPy (Fig. A2n), which, alone in the whole set of the 52 species, shows a very different behaviour for dipeptides ( $λ = 0$ ), also the usual valley at $λ = 4$ turns to a peak, especially for the over-abundant occurrence situations (bottom curve, circles). BorBu (Fig. 6o) TrePa (Fig. A2p), while quite similar to each other, also differ from the other species. At the same time, BorBu is also to some extent similar to many other small genomes of comparable size, like MycGe, MycPn, and MycPu. Very distinct, and quite dissimilar from any other genome, is the pattern displayed by the archeon AerPe (Fig. A2m).

Fig. 6
The comparison examples of summed-up distributions of the individual amino acid pairs for the over-deficient and the over-abundant cases, and the spacer-length values λ=5 and λ=6. The summed-up (for all 52 species analyzed) occurrences of over-deficient (left column) and of over-abundant (right column) cases for all amino acid individual pairs show the overall effect of the spacer-length values λ=5 (top row) and λ=6 (bottom row). Only situations for values of the ratio $R_{i}^{λ}$ (Eq. (3)) exceeding two standard deviations were considered. The area of each square is proportional to the magnitude of the effect, and additionally they are colour coded such that the increase is depicted from deep blue (smallest) through green (medium) towards dark red (largest). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

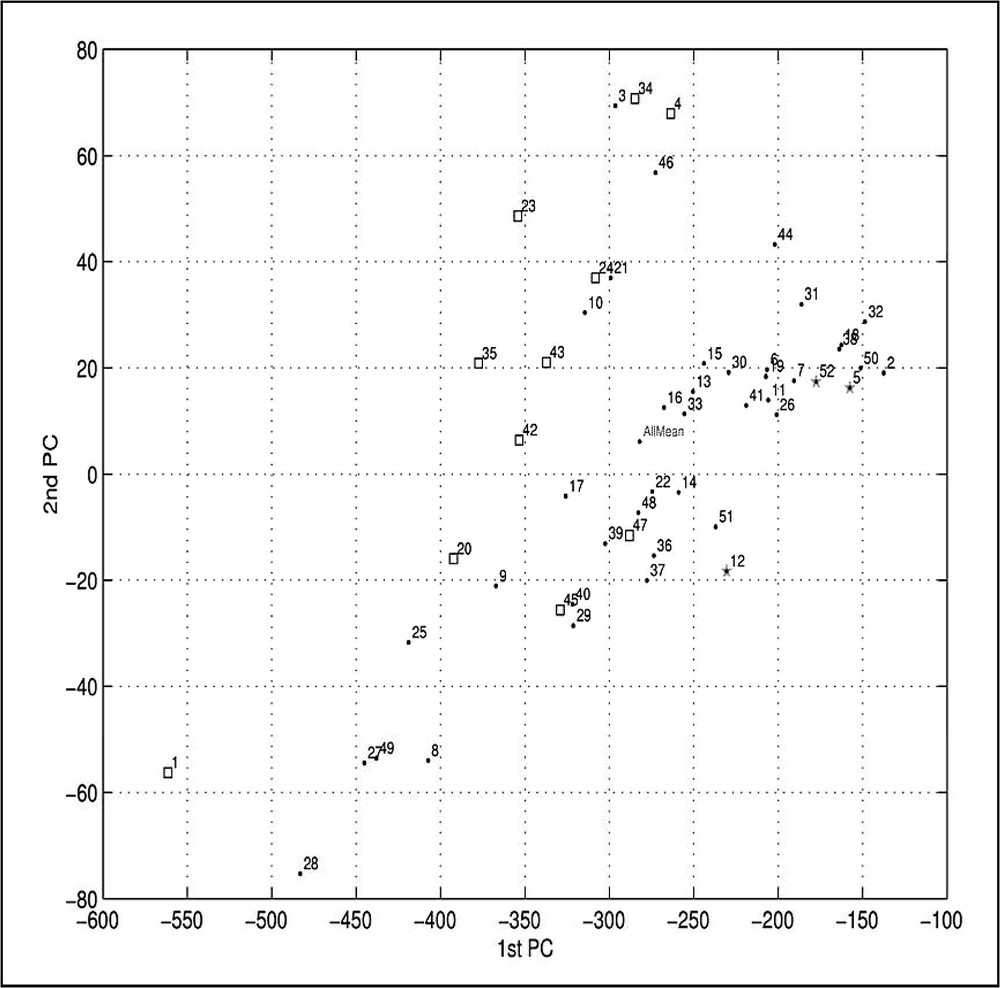
To better illustrate relationships between various patterns of periodicity shown by the different species, we have again used Principal-Component Analysis scatter plots. In Fig. A3a, the results show the plot of the first PC vs. the second PC obtained after performing PCA on the periodicity vectors for all 52 species constructed as a sum of over-deficient and over-abundant occurrence situations exceeding two standard deviations (the same data has been shown already as the top curves in Figs. 5 and A2), together with the corresponding mean vector for all species together (the top curve in Fig. 4, divided by 52). In Fig. A3b, the results show the corresponding plot of the first PC vs. the third PC. The first three principal components covered almost 99.3% of the whole information variance present in the set of 53 periodicity vectors (first PC: 97.67%, second PC: 1.19%, third PC: 0.40%). The point near the ( $0, 0$ ) coordinates on the both panels of Fig. A3, marked as AllMean corresponds to the top curve in Fig. 4, and can be interpreted as the average periodicity patterns of all 52 species taken together. The numbering for all species in Fig. A3 is the same as in Table 1. It is readily visible that AerPe (A3a, number 1, square) is indeed very different from all other species. The same can be said about HelPy (A3b, number 21, circle). All three chlamydias: ChlMu, ChlPn, and ChlTr (A3b, numbers 13, 14, and 15, circles) are also grouped close to each other. On both panels, the three eukaryotes (numbers 5, 12, and 52, stars) are close to each other, and are placed rightmost of other species. There are two distinct, diagonally oriented, groups clearly visible in Fig. A3a. The first one encompasses all but two (TheAc: number 45, and TheVo: number 47, which are both members of the second group) archea; four small eubacteria: MycGe, MycPn, MycPu, and UreUr (numbers 25, 27, 28, and 49, respectively), and also three larger eubacteria: CamJe, HelPy, and TheMa (numbers 10, 21, and 46). The second group comprises all but three remaining bacteria (which are members of an intermediary, and also discernible group situated in between: BorBu – number 8, Buchn – number 9, and DeiRa – number 17), and all eukaryotes.

It is also interesting to compare the individual amino acid pair's distributions for given λ values. The nature of the peak at $λ = 3$ , as shown in Fig. 5, is not entirely clear because the position of this particular peak may be actually located at $λ = 2$ . For this reason, we have visualized the behaviour of the AA pairs for both the over-deficient and the over-abundant occurrence situations, and for $λ = 5$ (Figs. 6a and 6b, top row), and $λ = 6$ (Figs. 6c and 6d, bottom row), that is for the big peak and its adjacent valley. The size of each square is proportional to the corresponding value of the sum of all occurrences, when the value of the particular ratio $R_{i}^{λ}$ (Eq. (3)) exceeded two standard deviations, for a given amino acid pair, and a particular value of the spacer length λ, that is the thresholds are the same as in Fig. 4. The behaviour of various AA pairs are strikingly different, not only between the same AA pair at the different λ values, or between the over-deficient and the over-abundant occurrence situations at the same spacer length, but particularly in the case when all conditions are exactly the same, and when only the AA pairs differ. For obvious reasons, the behaviour of a given amino acid pair can be either neutral (most common situation), although, as can be observed here, there are surprisingly many cases when it exceeds the value of two standard deviations from expectancy, or over-deficient, or over-abundant; but it cannot be both – so, in a sense, panels 6a and 6b, or panels 6c and 6d does form complementary pairs. Much more interesting is to compare panels 6a with 6c, or panels 6b with 6d, respectively. Remembering that for $λ = 5$ there is a valley in Fig. 4, whereas for $λ = 6$ we observe a peak, it is intriguing to note that for both situations, the observed effects are of qualitatively of the same nature for both valleys and peaks, with differences only in their quantities. Hence, we can see a roughly diagonal concentration of more numerous observations exceeding two standard deviations for both panels 6a and 6c, or 6b and 6d, corresponding to over-deficiency and over-abundance respectively. The effect is much more pronounced for peaks (e.g., $λ = 3, 6, 10$ , etc.) than for valleys ( $λ = 2, 5, 8$ , etc.); nevertheless, it can be explained as the concentration of either hydrophobic–hydrophobic (e.g., Leu–Leu, or Phe–Phe pairs) or hydrophylic–hydrophylic bigrams (e.g., Glu–Glu, or Glu–Lys pairs) for the over-abundant occurrence situations (right column in Fig. 6), and the concentration of either hydrophylic–hydrophobic (e.g., Glu–Leu pair) or hydrophobic–hydrophylic (e.g., Leu–Asp pair) bigrams for the over-deficient occurrence situations (left column in Fig. 6). The most striking comparison is that of the two orthogonal diagonals at $λ = 6$ , where the hydrophilic–hydrophilic and the hydrophobic–hydrophobic amino acid pairs are over-abundant, while the hydrophilic–hydrophobic and the hydrophobic–hydrophilic ones are over-deficient (compare Figs. 6c and 6d).

4 Discussion and conclusions

The method we propose here, to represent and analyze sequences of complete genomes, by using n-gram-based frequencies of amino acid pairs separated by a given number of other residues, allows us to:

(a) deal with a sparseness of statistical representation of resulting n-gram descriptors for individual gene sequences;
(b) describe every gene sequence in the same way, independently of its length;
(c) compare whole genomes in the same manner, notwithstanding given genome size;
(d) finally to compare qualitatively even deeply rooted taxons, without the necessity of utilizing even a single sequence alignment.

Using this approach, we show first of all that the n-gram-based analysis allows the classification of various taxons into the most intra-genome, but inter-protein diverse species on the one hand, and to the intra-genome and inter-protein most homogenous species, on the other one. To the first class belong the archeon Aeropyrum pernix and small bacteria like Mycoplasmas, Borrelia burgdorferi and Ureaplasma urealyticum, while to the second class belong the eukaryote Arabidopsis thaliana and eubacteria like Vibrio cholerae and Agrobacterium tumefaciens. The continuous spectrum of other taxons lies between these two extremes (Fig. A1a). This classification is neither related to the G+C content of the genome, nor to the classical tripartite tree of life [18]. We think that it describes the heterogeneity/homogeneity of protein sequences and protein structures within the species, and evolutionary constrains that either lead to the maintenance of extreme diversity or streamline the species to more homogeneity. In the genomes that have to cope with all the functions necessary for an independent (or quasi independent) life, in a minimum of genome size, the diversity will be extreme, while in larger genomes functionally specialized for certain types of life, the inter-protein diversity would decrease due to successive duplications and extensions of sequences, like in Agrobacterium and Arabidopsis. If this hypothesis is correct, the recently sequenced genome of Paramecium would be placed at the lower rightmost part of the Fig. A1a PCA scatter plot.

The subsequent PCA analysis (Fig. A3), utilizing the summed up over-abundant and over-deficient occurrence profiles of each species, leads to a very similar classification: again Aeropyrum and small eubacteria occupy one end of the PCA first and second components' space, while Agrobacterium, Arabidopsis and Vibrio cholerae are located at the opposite extreme (Fig. A3a). However, additional information is gained by comparing these two PC analyses. While in Fig. A1a the vectors summarize the diversity of sequences in proteome, in Fig. A3a the vectors represent the form of amplitude changes in oscillations of summed up over-abundant and over-deficient occurrences, depicted individually in panels of Figs. 5 and A2. The more homogeneous proteomes have more conspicuous oscillations than the more heterogeneous ones (compare pronounced oscillations of Arabidopsis, panel 5c, and Agrobacterium, panel 5e, with the more flat oscillations of Aeropyrum pernix, panel A2m, and Borrelia burgdorferi, panel A2o).

The relationship between individual amino acid pairs and the distance separating two members of the pair also leads to interesting results. We do not attempt here to describe the detailed behaviour of all 19 spacer lengths and all the 400 amino acid pairs. However, as shown in Fig. 6, there are striking differences in the abundance of the occurrence pairs of similar amino acids (hydrophobic–hydrophobic, and hydrophilic–hydrophilic) as opposed to the abundance of dissimilar pairs (hydrophilic–hydrophobic, and hydrophobic–hydrophilic), the first ones being overrepresented at the oscillation peaks (Figs. 4, 6, and 7), while the second ones are generally under-represented. The peaks correspond to the $λ = 3, 6, 10 \dots$ and therefore to the distances of 4, 7, 11… peptide bonds. This immediately suggests that the oscillations observed at the level of whole genomes may result from the periodic nature of the α helical proteins with their basic frequency of 3.5 peptide bonds.

Fig. 7
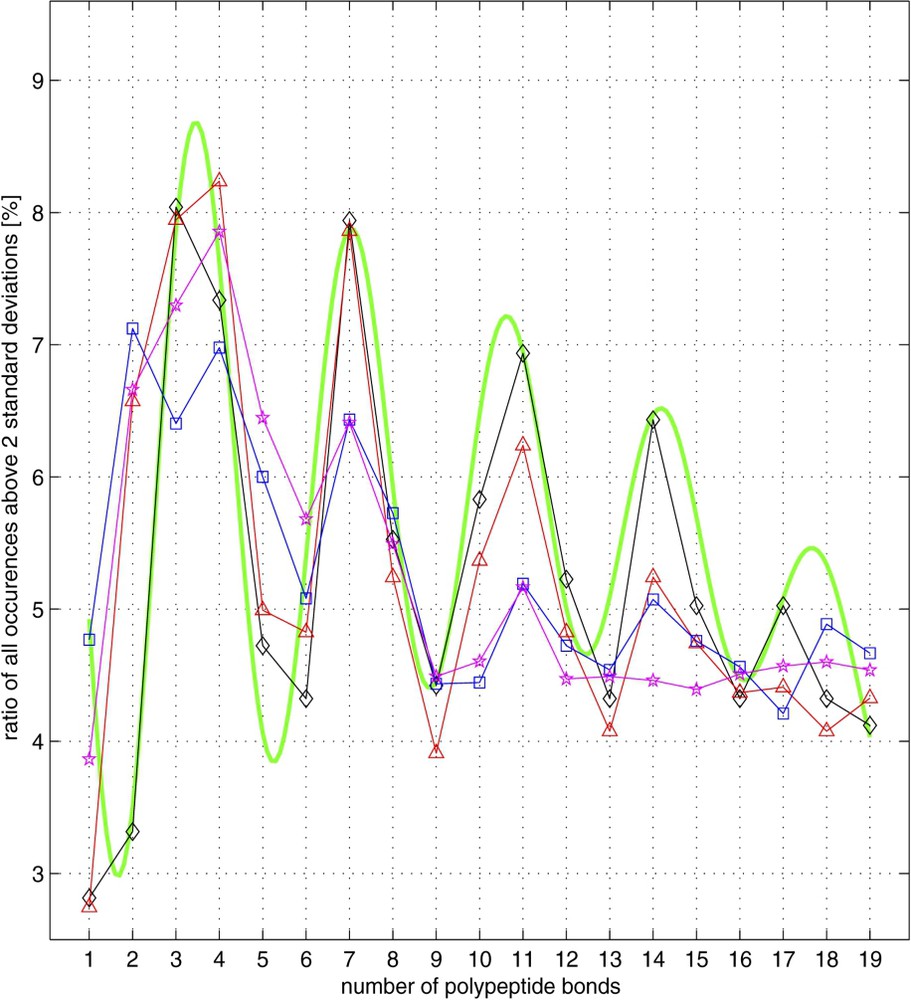
Summary of the periodicity data for all 52 species. The summed-up occurrences of the over-deficient, together with the over-abundant cases for all amino acid pairs, presenting the overall effect of the value of the ratio $R_{i}^{λ}$ (Eq. (3)) exceeding two standard deviations. Shown as ratios [in percent] of occurrences for a given polypeptide chain length, divided by the sum of all such occurrences. The lines are for: CEleg (diamonds, black line), all three eukaryotes together (triangles, red line), all eleven archea together (stars, magenta line), and all 38 bacterial species together (squares, blue line). For comparison purposes, an exponentially dampened sinusoid, with periodicity of 3.5, and the functional form given by the equation: $f (τ) = A_{1} e^{ψ τ} \sin (ω τ) - A_{2} e^{ϕ τ} + B$ , and $A_{1} = 4$ , ψ=−0.095, $A_{2} = 0.01$ , ϕ=0.26, B=6.1; ω=1.75, is also plotted (green line). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

If our hypothesis, according to which the observed periodicity is connected with the relative abundance of the α helical fragments in certain genomes when compared to others, is correct, then the genome of CEleg (Fig. 5b) would code for proteins statistically more rich in α helical structures than genome of BorBu (Fig. A2o), for example. There are two possible statistical interpretations:

– either in the genome of CEleg, there are many more proteins rich in α helices, such proteins being relatively absent in the genome of BorBu;
– or, although such α helical motifs might be prevalent in BorBu, there are other structural 3-D motifs, also quite abundant, most notably the β sheets and β barrels, whose effect should act to obscure, rather than to enhance the periodicity observed.

Therefore, the relative prevalence of different structural motifs would influence observed diversity of the periodicity patterns described here (Figs. 5a and A2p). It has been observed [19–22] that the periodicity of the DNA sequence, with about 10 to 11 bp per turn, is prevalent in a number of both eukaryotic and prokaryotic genome sequences. These periodicities are generally interpreted as resulting from physical properties of DNA chain, reflecting chromatin structure and its various aspects in different kingdoms of archea and bacteria. It has been envisaged that the 10–11 bp DNA sequence periodicity might stem from the “correlations in the corresponding protein sequences due to the amphipatic character of α helices” [21]. Also, another type the DNA sequence periodicity of 6 bp have been correlated [20] with the β sheet protein sequence structural motif. However, more recent work [23] argues in favour of the idea that the 10–11-bp DNA sequence periodicity is not related to the protein structure, since it appears concentrated in the intergenic regions of the E. coli genome.

Here we observe periodicity with a basic frequency of 3.5 peptide bonds (Fig. 7), together with its multiplicity of 7, 10.5, 14, etc., resulting from the over-representation of specific pairs of similar amino acids (e.g., Leu–Leu), together with the under-representation of the corresponding dissimilar amino acid pairs (e.g., Leu–Asp). This amino acid periodicity of whole genomes, when translated to the DNA level would give 10.5 bonds periodicity ( $3.5 \times 3 = 10.5$ ); therefore, we believe that in the DNA sequence periodicity of 10–11 bp, the α helical structure of proteins encoded by DNA plays a mayor role. The most important conclusion of our work concerns the cause of the observed periodicity of oscillation revealed by the bigram analysis of complete proteomes. Depending on the genome studied, this periodicity is more or less conspicuous (compare various panels in Figs. 5 and A2). However, also when summing up the analyzed genomes (whether all eleven archeas, or all thirty eight eubacteria, etc.), the periodicity of 3.5 peptide bonds is always quite apparent and striking (Fig. 7). This idea is further developed in the accompanying article [24], demonstrating that 11-bp periodic oscillations of nucleotide sequence are localized in the genomic ORFs, and are more pronounced in genes coding for alpha rich proteins than in those coding for proteins devoid of such secondary structures.

Acknowledgements

J.P.R. was partially supported from the KBN grants 115/E-343/S/BST-1076/ICM/2005 and 115/E-343/BW-1703/ICM/2005. P.P.S. is Professor Emeritus (active) of University Paris-6. We would like to thank Dr C.J. Herbert from CGM for looking over English.

Supplementary material

Fig. A1
Principal component analysis of the distribution histogram vectors for 52 species. The first three principal components covered almost 98.7% of the whole information variance present in this set (the first PC: 97.67%, the second PC: 0.71%, and the third PC: 0.28%). Scatter plots of the first PC vs. the second PC (panel A), the first PC vs. the third PC (panel B), and the second PC vs. the third PC (panel C). The species are numbered, next to the corresponding points, as listed in Table 1.

Fig. A2
The summarized periodic behaviour of over-abundant and over-deficient cases for all amino acid pairs, shown for selected species. The summed-up occurrences of over-deficient (triangles) cases, and of over-abundant (circles) cases for all amino acid pairs and some individual species (**A2i** – ArcFu, **A2j** – MetTh, **A2k** – PyrAb, **A2l** – SulTo, **A2m** – AerPe, **A2n** – HelPy, **A2o** – BorBu, **A2p** – TrePa) show the overall effect of the value of the ratio $R_{i}^{λ}$ (Eq. (3)) exceeding two standard deviations, and its dependence upon the spacer length λ. The top curve (squares) shows the addictive effect of both over-deficient and overabundant cases. Clearly, while for the most species the individual curves are very much alike the shapes depicted in Fig. 4, there are also quite a few exceptions, most notably for the two spirochetes BorBu and TrePa, HelPy, and archeon AerPe.

Fig. A3
Principal-Component Analysis of the periodicity vectors for 52 species. The first three principal components covered almost 99.3% of the whole information variance present in this set (the first PC: 97.67%, the second PC: 1.19%, and the third PC: 0.40%). Scatter plots of the first PC vs. the second PC (panel a), the first PC vs. the third PC (panel b). The species are numbered, next to the corresponding points, as listed in Table 1.

Bibliographie

[1] M. Damashek Gauging similarity via n-grams: text sorting, categorizing and retrieval in any language, Science, Volume 267 (1995), pp. 843-848

[2] B.E. Blaisdall A measure of the similarity of sets of sequences not requiring sequence alignment, Proc. Natl Acad. Sci. USA, Volume 83 (1986), pp. 5155-5159

[3] B.E. Blaisdall Effectiveness of measures requiring and not requiring prior sequence alignment for estimating the dissimilarity of natural sequences, J. Mol. Evol., Volume 29 (1989), pp. 526-537

[4] B.E. Blaisdall Average values of a dissimilarity measure not requiring sequence alignment are twice the averages of conventional mismatch counts requiring sequence alignment for computer generated system model, J. Mol. Evol., Volume 29 (1989), pp. 538-547

[5] F. Daeyaert; H. Moereels; P.J. Lewi Classification and identification of proteins by means of common and specific amino acid n-tuples in unaligned sequences, Comp. Meth. Progr. Biomed., Volume 56 (1998), pp. 221-233

[6] S. Karlin Statistical significance of sequence patterns in proteins, Curr. Opin. Struct. Biol., Volume 5 (1995), pp. 360-371

[7] R.A. Lippert; H.Y. Huang; M.S. Waterman Distributional regimes for the number of k-word matches between two random sequences, Proc. Natl Acad. Sci. USA, Volume 99 (2002), pp. 13980-13989

[8] G.W. Stuart; K. Moffett; S. Baker Integrated gene and species phylogenies from unaligned whole genome protein sequences, Bioinformatics, Volume 18 (2002), pp. 100-108

[9] H.M. Muller; S.E. Koonin Vector space classification of DNA sequences, J. Theor. Biol., Volume 223 (2003), pp. 161-169

[10] S. Vinga; J.S. Almeida Alignment-free sequence comparison, Bioinformatics, Volume 19 (2003), pp. 513-523

[11] S. Vinga; R. Gouveia-Oliveira; J.S. Almeida Comparative evaluation of word composition distances for the recognition of SCOP relationships, Bioinformatics, Volume 20 (2004), pp. 206-215

[12] T.F. Smith; M.S. Waterman Identification of common molecular subsequences, J. Mol. Biol., Volume 147 (1981), pp. 195-197

[13] R.C. Edgar Local homology recognition and distance measures in linear time using compressed amino acid alphabets, Nucl. Acids Res., Volume 32 (2004), pp. 380-384

[14] D.P. Kreil; C.A. Ozounis Identification of thermophylic species by the amino acid compositions deduced from their genomes, Nucl. Acids Res., Volume 29 (2001), pp. 1608-1615

[15] J.P. Radomski; P.P. Slonimski Genomic style of proteins: concepts, methods and analysis of ribosomal proteins from 16 microbial species, FEMS Microbiol. Rev., Volume 25 (2001), pp. 425-435

[16] V. Rosato; N. Pucello; G. Giuliano Evidence for cysteine clustering in thermophylic proteomes, Trends Genet., Volume 18 (2002), pp. 278-281

[17] A. Krzywicki; P.P. Slonimski Formal analysis of protein sequences. I. Specific long range constraints in pair associations of amino acids, J. Theor. Biol., Volume 17 (1967), pp. 136-158

[18] C.R. Woese; O. Kandler; M.L. Wheelis Toward a natural system of organisms: Proposal for the domains archaea, bacteria and eucaria, Proc. Natl Acad. Sci. USA, Volume 87 (1990), pp. 4576-4579

[19] M.I. Kanehisa; T.Y. Tsong Hydrophobicity and protein structure, Biopolymers, Volume 19 (1980), pp. 1617-1628

[20] V.B. Zhurkin Periodicity in DNA primary structure is defined by secondary structure of the coded protein, Nucl. Acid Res., Volume 9 (1981), pp. 1963-1971

[21] H. Herzel; O. Weiss; E.N. Trifonov 10–11-bp periodicities in complete genomes reflect protein structure and DNA folding, Bioinformatics, Volume 15 (1999), pp. 187-193

[22] P. Worning; L.J. Jensen; K.E. Nelson; S. Brunak; D.W. Ussery Structural analysis of DNA sequence: evidence for lateral gene transfer in Thermotoga maritima, Nucl. Acid Res., Volume 28 (2000), pp. 706-709

[23] S. Hosid; E.N. Trifonov; A. Bolshoy Sequence periodicity of Escherichia coli is concentrated in intergenic regions, BMC Mol. Biol., Volume 5 (2004), pp. 14-20

[24] P.P. Slonimski Periodic oscillations of the genomic nucleotide sequences disclose major differences in the way of constructing homologous proteins from different procaryotic species, C. R. Biologies, Volume 330 (2007) no. 1

Commentaires - Politique