Systems biology and the origins of life? Part II. Are biochemical networks possible ancestors of living systems? Networks of catalysed chemical reactions: Non-equilibrium, self-organization and evolution

Jacques Ricard

doi:10.1016/j.crvi.2010.10.004

Résumé

The present article discusses the possibility that catalysed chemical networks can evolve. Even simple enzyme-catalysed chemical reactions can display this property. The example studied is that of a two-substrate proteinoid, or enzyme, reaction displaying random binding of its substrates A and B. The fundamental property of such a system is to display either emergence or integration depending on the respective values of the probabilities that the enzyme has bound one of its substrate regardless it has bound the other substrate, or, specifically, after it has bound the other substrate. There is emergence of information if $p (A) > p (A| B)$ and $p (B) > p (B| A)$ . Conversely, if $p (A) < p (A| B)$ and $p (B) < p (B| A)$ the system is integrated. The first condition is likely to occur if the system is far from quasi-equilibrium. Moreover, in such systems, emergence results in an increase of the energy level of the ternary EAB complex that becomes closer to the transition state of the reaction, thus leading to the enhancement of catalysis. Hence a drift from quasi-equilibrium is, to a large extent, responsible for the production of information and enhancement of catalysis. Non-equilibrium of these simple systems must be an important aspect that leads to both self-organization and evolutionary processes. These conclusions can be extended to networks of catalysed chemical reactions. Such networks are, in fact, networks of networks, viz. meta-networks. In this formal representation, nodes are chemical reactions catalysed by poorly specific proteinoids, and links can be identified to the transport of metabolites from proteinoid to proteinoid. The concepts of integration and emergence can be applied to such situations and can be used to define the identity of these networks and therefore their evolution. Defined as open non-equilibrium structures, such biochemical networks possess two remarkable properties: (1) the probability of occurrence of their nodes is dependant upon the input and output of matter in, and from, the system and (2) the probability of occurrence of the nodes is strictly linked to their degree of connection. The higher this degree of connection and the higher is their probability of occurrence. These conclusions are in clear disagreement with the static descriptions of the so-called scale-free metabolic networks.

1 Introduction

In the accompanying article [1], we have outlined the fact that any living organism is able to reproduce, to display some sensitivity to a time-arrow, to possess an identity and to evolve. In the previous paper, it was shown that three of these features were already met in apparently simple physical systems, namely encapsulated catalysed chemical reactions. In this Note we intend to discuss the last point, namely to decide whether or not a network of chemical reactions can display some sort of evolution. Indeed one cannot think of evolution in classical neo-Darwinian terms for these tentative prebiotic systems were not supposed to display any real mutation followed by its selection. Nevertheless, one can think of some sort of self-organization process followed by the selection of structures that possess a functional advantage. As in the previous Note [1], the mathematical developments of Section 2 can be omitted on first reading by those unfamiliar with these developments.

2 Prebiotic systems are non-equilibrium dynamic structures able to self-organize and to evolve

Biochemical networks of present day cells can tentatively be considered models of prebiotic systems. These collective structures are, in fact, dynamic open systems that receive molecules from the external milieu, transform these molecules and release some of the corresponding products outside the system. Hence such tentative prebiotic systems could have been networks of connected and encapsulated primordial enzyme reactions. It is no doubt of functional interest, in this perspective, to discuss some of the properties of these systems. An important property of networks of enzyme reactions is that any of these reactions is per se a network with its own nodes and links. Hence, exactly as metabolic networks of present day living cells, the tentative prebiotic systems could be considered networks of networks, or meta-networks. It is therefore of interest to study some of the dynamic properties of enzyme reactions in this perspective.

2.1 Enzyme reactions as simple biochemical networks

This Section can be omitted on a first reading.

From a phenomenological viewpoint, enzyme reactions as they take place today, are basically of two different types called the sequential and the substitution types. Most enzyme reactions usually involve two substrates, or sometimes three. In the so-called sequential process, the enzyme binds all the substrates before releasing the products. Alternatively, in the substitution mechanisms, the enzyme binds a substrate, releases the corresponding product, then binds the second substrate before releasing the last product. We are going, in the following, to discuss the sequential mechanism, which is, by far, the most important. In the case of an enzyme E that binds sequentially the two substrates A and B before releasing the products P and Q, the general situation is depicted in Fig. 1 and implies that the enzyme binds either A or B first and the other substrate, B or A, afterwards. In this perspective the enzyme can bind A first then B, or B first and then A. For that reason the process is called sequential random. A limiting situation is obtained when the free enzyme binds one substrate only, for instance A but not B. B can be bound to the enzyme only after E has bound A. Then the process is called ordered sequential, (Fig. 1). This model is a limiting case of the general one.

Fig. 1
A and B. Sequential binding of substrates and release of products to, and from, enzyme E. In A, it is assumed that the binding of substrates A and B to the enzyme takes place randomly. In B it is postulated that the binding of the substrates follows a compulsory order.

Let us consider the sequential random enzyme process described in Fig. 1A. One can derive the general expression of the probabilities that the enzyme has bound A, B, or both A and B. One finds the general expressions

p (A) = \frac{K_{1} [A] (1 + K_{3} [B]) + u_{E A}}{1 + K_{1} [A] + K_{3} [B] + K_{1} K_{2} [A] [B] + u_{E A} + u_{E B} + u_{E}}

(1a)

p (B) = \frac{K_{3} [B] (1 + K_{4} [A]) + u_{E B}}{1 + K_{1} [A] + K_{3} [B] + K_{1} K_{2} [A] [B] + u_{E A} + u_{E B} + u_{E}}

(1b)

p (A, B) = \frac{K_{1} K_{2} [A] [B]}{1 + K_{1} [A] + K_{3} [B] + K_{1} K_{2} [A] [B] + u_{E A} + u_{E B} + u_{E}}

(1c)

In these expressions the u's represent the shifts between the standard quasi-equilibrium and the actual non-equilibrium (steady-state) of the system. In Eqs. (1a)–(1c) the constants K₁, K₂,… are the ratios k₁/k₋₁, k₂/k₋₂…, of rate constants. The shifts between the standard quasi-equilibrium and the actual non-equilibrium of the system are shown to be expressed as

u_{E A} = \frac{k k_{1} [A] (k_{- 3} + k_{4} [A])}{k_{- 3} k_{- 4} (k_{- 1} + k_{2} [B]) + k_{- 1} k_{- 2} (k_{- 3} + k_{4} [A])}

(2a)

u_{E B} = \frac{k k_{3} [B] (k_{- 1} + k_{2} [B])}{k_{- 3} k_{- 4} (k_{- 1} + k_{2} [B]) + k_{- 1} k_{- 2} (k_{- 3} + k_{4} [A])}

(2b)

u_{E} = \frac{k (k_{- 1} + k_{2} [B]) (k_{- 3} + k_{4} [A])}{k_{- 3} k_{- 4} (k_{- 1} + k_{2} [B]) + k_{- 1} k_{- 2} (k_{- 3} + k_{4} [A])}

(2c)

One can notice that the u's are of necessity positive and that they introduce non-linear terms in the expression of p(A), p(B) and p(A,B). Moreover, simple inspection of kinetic scheme of Fig. 1A suggests that the binding of A and B to the enzyme may interact, leading in turn to the increase, or decrease, of the corresponding information (2a)–(2c). One may express in quantitative terms the emergence, or integration, of information through the relation

i (A : B) = \log \frac{p (A |B)}{p (A)} = \log \frac{p (B |A)}{p (B)}

(3)

If i(A:B) adopts negative values which implies that $p (A) > p (A |B)$ and $p (B) > p (B |A)$ the system is emergent. If it is the converse that is occurring, the system is integrated (3).

In order to check the validity of this idea one can derive, for instance, the expression of $p (A |B)$ and one finds

p (A |B) = \frac{K_{4} [A]}{1 + K_{4} [A] + u_{E B}^{*}}

(4)

where

u_{E B}^{*} = u_{E B} / K_{3} [B]

. The expression of

u_{E B}^{*}

is then

u_{E B}^{*} = \frac{k k_{- 3} (k_{- 1} + k_{2} [B])}{k_{- 3} k_{- 4} (k_{- 1} + k_{2} [B]) + k_{- 1} k_{- 2} (k_{- 3} + k_{4} [A])}

(5)

and the ratio

p (A |B) / p (A)

assumes the form

\frac{p (A |B)}{p (A)} = \frac{K_{4} [A] + K_{1} K_{4} {[A]}^{2} + K_{3} K_{4} [A] [B] + K_{1} K_{2} K_{4} {[A]}^{2} [B] + N (u)}{K_{1} [A] + K_{1} K_{4} {[A]}^{2} + K_{3} K_{4} [A] [B] + K_{1} K_{2} K_{4} {[A]}^{2} [B] + D (u)}

(6)

In this expression N(u) and D(u) show the role played by the non-equilibrium in the emergence, or integration, of the system. If N(u) = D(u) = 0 then the system is at thermodynamic equilibrium. Under these conditions of thermodynamic equilibrium, if K₄ > K₁, which implies from the first principle of thermodynamics that K₂ > K₃, the system is integrated. If alternatively, K₁ > K₄ and K₃ > K₂ the system is emergent. Emergence, however, can be enhanced if the system is away from thermodynamic equilibrium, that is if N(u) ≠ 0 and D(u) ≠ 0 (4)–(6). These non-equilibrium functions assume the form

N (u) = K_{4} [A] u_{E A} + K_{4} [A] u_{E B} + K_{4} [A] u_{E}

(7a)

D (u) = u_{E A} + K_{4} [A] u_{E A} + K_{1} [A] u_{E B}^{*} + K_{1} K_{2} [A] [B] u_{E B}^{*} + u_{E A} u_{E B}^{*}

(7b)

The function u_E which appears in the expression of N(u) can be rewritten in terms of either u_EA, u_EB or u^*_EB for one has

u_{E} = \frac{k_{- 1} + k_{2} [B]}{k_{1} [A]} u_{E A} = \frac{k_{- 3} + k_{4} [A]}{k_{3} [B]} u_{E B} = \frac{k_{- 3} + k_{4} [A]}{k_{- 3}} u_{E B}^{*}

(8)

Expression (7a), (7b) can be rewritten as

N (u) = K_{4} [A] u_{E A} + \frac{K_{4}}{K_{1}} \frac{k_{- 1} + k_{2} [B]}{k_{- 1}} u_{E A} + K_{3} K_{4} [A] [B] u_{E B}^{*}

(9)

or as

N (u) = K_{4} [A] u_{E A} + K_{3} K_{4} [A] [B] u_{E B}^{*} + K_{4} [A] \frac{k_{- 3} + k_{4} [A]}{k_{- 3}} u_{E B}^{*}

(10)

Non-equilibrium conditions, viz. conditions that maximize the values of the u's, will increase the degree of emergence if D(u) − N(u) > 0. Alternatively, they will increase the degree of integration if D(u) − N(u) < 0. Hence the value of the difference D(u) − N(u) is essential to determine how non-equilibrium alters integration, or emergence (8)–(10). The expression of D(u) − N(u) can be written under either of the following equivalent forms:

D (u) - N (u) = (1 - \frac{K_{4}}{K_{1}} \frac{k_{- 1} + k_{2} [B]}{k_{- 1}}) u_{E A} + K_{1} [A] u_{E B}^{*} + u_{E A} u_{E B}^{*}

(11a)

D (u) - N (u) = u_{E A} + K_{1} [A] (1 - \frac{K_{2}}{K_{3}} \frac{k_{- 3} + k_{4} [A]}{k_{- 3}}) u_{E B}^{*} + u_{E A} u_{E B}^{*}

(11b)

The difference D(u) − N(u) will be positive and large if

K_{1} ≫ K_{4} and k_{- 1} ≫ k_{2} [B]

(12a)

K_{3} ≫ K_{2} and k_{- 3} ≫ k_{4} [A]

(12b)

Under these conditions the expressions of the u's reduce to

u_{E A} = \frac{k}{k_{- 2} + k_{- 4}} K_{1} [A]

(13a)

u_{E B} = \frac{k}{k_{- 2} + k_{- 4}} K_{3} [B]

(13b)

u_{E B}^{*} = \frac{k}{k_{- 2} + k_{- 4}}

(13c)

and the expression of D(u) − N(u) simplifies to

D (u) - N (u) = u_{E A} + K_{1} [A] u_{E B}^{*} + u_{E A} u_{E B}^{*}

(14)

It appears from this expression that departure of the system from quasi-equilibrium of necessity increases the value of the difference D(u) − N(u) (14). The larger the u values and the greater is the difference D(u) − N(u). It results from this conclusion that departure of the system from quasi-equilibrium of necessity increases its emergent character [2].

The situation is completely different if

K_{4} > > K_{1} and k_{2} [B] > > k_{- 1}

(15a)

K_{2} > > K_{3} and k_{4} [A] > > k_{- 3}

(15b)

Under these conditions the difference D(u) − N(u) reduces to

D (u) - N (u) = (1 + u_{E B}^{*} - \frac{K_{4}}{K_{1}} \frac{k_{2} [B]}{k_{- 1}}) u_{E A}

(16)

which is likely to adopt negative values owing to the fact that K₁ is very small relative to K₄ and k₋₁ very small relative to k₂[B]. Hence drifting the system away from quasi-equilibrium tends to increase its integrated character (16).

A similar reasoning can be applied to the kinetic scheme of Fig. 1B. The present situation is thus a limiting one in which the binding of B to the free enzyme is negligible. As previously, the probability of occurrence of the EA complex, p(A), can be expressed in terms of equilibrium concentrations plus u terms that express the deviation of the system from pseudo-equilibrium conditions. One has then

p (A) = \frac{K_{1} [A] + K_{1} K_{2} [A] [B] + u_{E A}}{1 + K_{1} [A] + K_{1} K_{2} [A] [B] + u_{E A} + u_{E}}

(17a)

p (B) = p (A, B) = \frac{K_{1} K_{2} [A] [B]}{1 + K_{1} [A] + K_{1} K_{2} [A] [B] + u_{E A} + u_{E}}

(17b)

p (B| A) = \frac{K_{2} [B]}{1 + K_{2} [B] + u_{E A}^{*}}

(17c)

with

u_{E} = \frac{k}{k_{- 2}} + \frac{k K_{2} [B]}{k_{- 1}}

(18a)

u_{E A} = \frac{k}{k_{- 2}} K_{1} [A]

(18b)

u_{E A}^{*} = \frac{k}{k_{- 2}}

(18c)

One can now derive the expression of $p (B |A) / p (B)$ . If this ratio is larger than one, the system is integrated (18a)–(18c). If alternatively the ratio is smaller than one the system is emergent. The expression of the ratio $p (B |A) / p (B)$ is

\frac{p (B |A)}{p (B)} = \frac{1 + K_{1} [A] + K_{1} K_{2} [A] [B] + u_{E A} + u_{E}}{K_{1} [A] + K_{1} K_{2} [A] [B] + K_{1} [A] u_{E A}^{*}}

(19)

If the system is close to equilibrium, i.e. if the u's are close to zero then

\frac{p (B |A)}{p (B)} = \frac{1 + K_{1} [A] + K_{1} K_{2} [A] [B]}{K_{1} [A] + K_{1} K_{2} [A] [B]} > 1

(20)

Far away from quasi-equilibrium one has

D (u) - N (u) = - \frac{k}{k_{- 2}} - \frac{k K_{2} [B]}{k_{- 1}} < 0

(21)

Hence it follows that a sequential ordered system can only be integrated and that a drift from quasi-equilibrium increases the extent of integration.

2.2 Thermodynamic significance of the concepts of integration and emergence

The thermodynamic and kinetic scheme of Fig. 1A allows one to analyse and understand the thermodynamic significance of the concepts of integration and emergence. Let us assume first that the binding of A to the enzyme does not interfere with that of B and conversely. In such a situation one should have

K_{1} = K_{4} and K_{2} = K_{3}

(22)

In going from state E to state EAB one can follow two different pathways but the free energy difference between the initial and the final states is independent of the pathway (Fig. 2).

Fig. 2
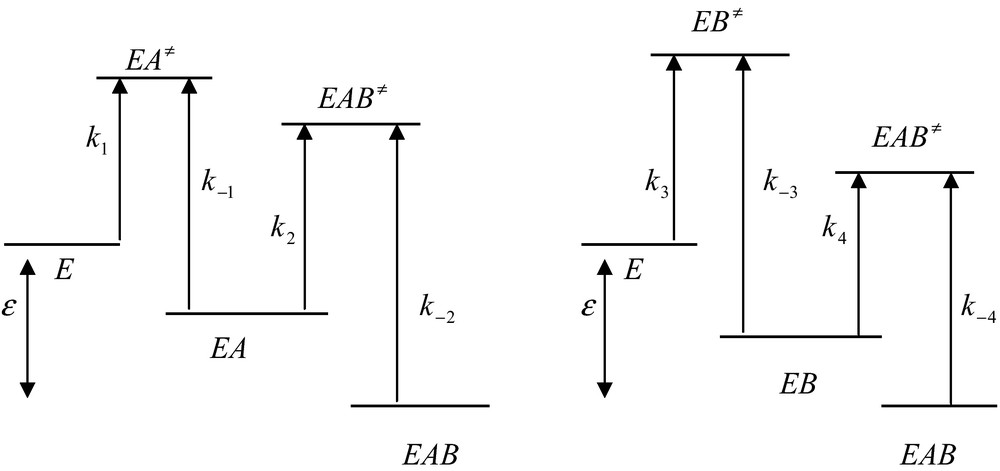
Free energy profiles for the random and independent binding on a protein of two ligands, A and B. In this process, k₁ = k₄, k₋₁ = k₋₄, k₂ = k₃ and k₋₂ = k₋₃. The global free energy difference, ɛ, between the initial and the final sates is the same for the two processes. For simplicity, the free energy differences between the ground and the transition states are depicted by the corresponding rate constants.

Upon going from a stable state to another stable state one has to overcome an energy barrier corresponding to a transition state (for example, EA^≠). According to the classical transition state theory, the corresponding rate constant, for instance k₁, depends upon the value of the corresponding free energy, $Δ G_{1}^{\neq}$ , required to reach the transition state EA^≠. This classical relationship is [3]

k_{1} = \frac{k_{B} T}{h} \exp (- Δ G_{1}^{\neq} / R T)

(23)

where k_B, h, R and T are the Boltzmann constant, the Planck constant, the gas constant and the absolute temperature, respectively. It follows from relation (23) that the higher the free energy $Δ G_{1}^{\neq}$ and the lower the value of the corresponding rate constant.

Now let us assume that the system is integrated, then one has

K_{2} > K_{3} and k_{2} [B] > k_{- 1}

(24a)

K_{4} > K_{1} and k_{4} [A] > k_{- 3}

(24b)

The free energy profiles for the binding of A to E and B to E will not be affected relative to the situation described in Fig. 2. However, the free energy profiles pertaining to the binding of B to EA and A to EB will be different from those of Fig. 1. Moreover the fact that relations (24a) and (24b) hold implies that the energy level of the ternary EAB state is lower than that of the same ternary state obtained in the absence of any interaction for the binding of A and B to the enzyme. It then follows that integration of the system results in a decrease of the energy level of the ternary EAB complex (Fig. 3).

Fig. 3
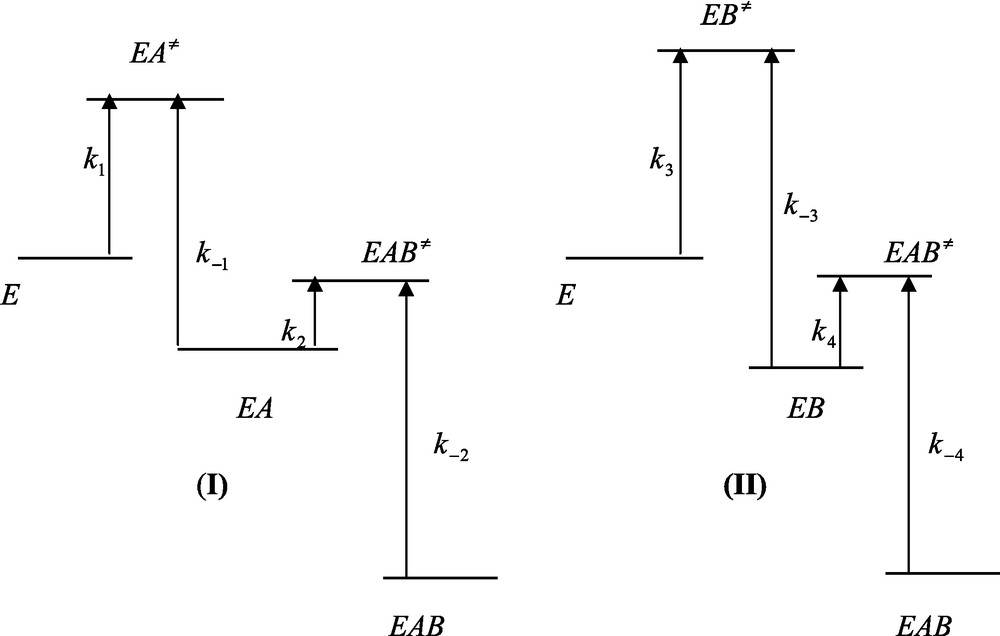
Free energy profiles of ligand binding to a protein in the case of an integrated system. **(I)** Relationship k₂[B] > k₋₁ is fulfilled. **(II)** Relationship k₄[B] > k₋₃ is fulfilled. In **(I)** and **(II)** relationships K₂ > K₃ and K₄ > K₁ are fulfilled. Care must be taken that rate constants are related to the corresponding free energy barrier that separate the ground and the transition states by equation (23) of the main text. This means that the larger the free energy difference between the ground and the transition states and the smaller is the corresponding rate constant. Integration is characterized by a decrease of the final free energy level (EAB) relative to the initial one (E).

In the case of emergence, the free energy profiles of Fig. 4 should be altered as to be antagonistic to that shown in Fig. 2. The peaks pertaining to the binding of A and B to the free enzyme E remain unchanged whereas the peaks pertaining to the binding of A and B to the EB and EA complexes should be modified as the relationships

K_{3} > K_{2} and k_{- 1} > k_{2} [B]

(25a)

K_{1} > K_{4} and k_{- 3} > k_{4} [A] apply.

(25b)

Fig. 4
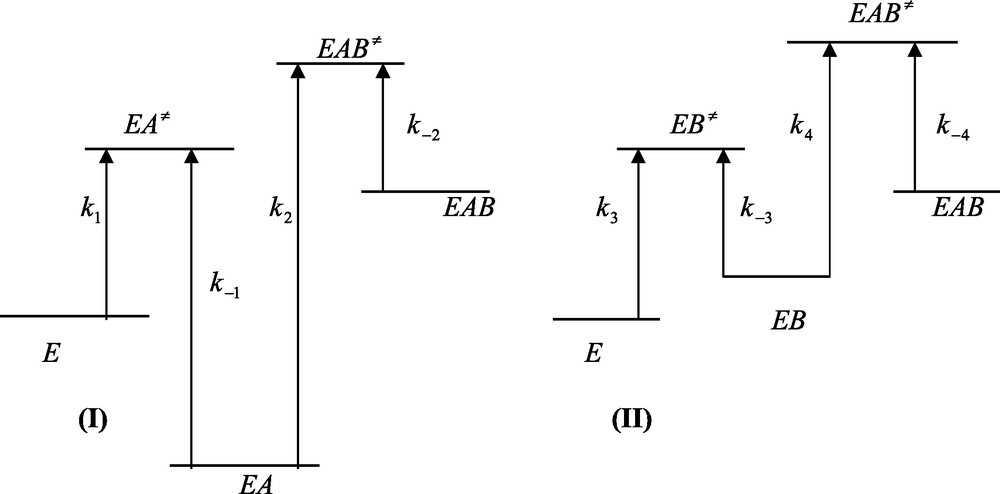
Free energy profiles of ligand binding to a protein in the case of an emergent system. **(I)** Relationship k₋₁ > k₂[B] is fulfilled. **(II)** Relationship k₋₃ > k₄[A] is fulfilled. In **(I)** and **(II)** relationships K₃ > K₂ and K₁ > K₄ are fulfilled. Care must be taken that the larger the free energy difference between the ground and transition states and the smaller is the corresponding rate constants. Emergence is characterized by an increase of the final state (EAB) relative to the initial one (E).

The corresponding energy profiles are depicted in Figure 4. Relationships (25a) and (25b) imply that the ternary EAB complex possess a higher energy level than those of the binary EA and EB complexes. Hence, contrary to what is obtained for integration, emergence means that the interaction between the two binding processes results in emergence of energy upon going from the state of the free enzyme E up to the state of the ternary EAB complex.

A limiting situation is obtained for ordered sequential mechanisms where one of the pathways, for instance E ↔ EB ↔ EAB, is lacking. This is likely to occur if the free energy barrier that separates the EB complex from the free enzyme is too high. In that case, one should have k₋₃ > > k₃, K₃ ≈ 0 and K₂ > > K₃. As free energy is a state function, it follows that K₄ > > K₁. Hence, in agreement with the kinetic results presented above, the system cannot be emergent. It is integrated.

As previously mentioned, occurrence of emergence, or of integration, relies upon the sign and the value of the difference D(u) − N(u). If this difference is positive and large, the system is emergent. Under these conditions, relations (12a) and (12b) apply and the u values are not negligible. This means that the system is away from quasi-equilibrium. Moreover, relationships (12a) and (12b) show that the energy level of the ternary EAB complex is higher than that of the other stable states. This point has an important implication. It means that the ternary EAB state, owing to non-equilibrium conditions, comes close to the transition state EX^≠. As expected, this means that the catalytic constant k is large. It follows that the enzyme becomes more efficient. In other words emergence, for an enzyme reaction, means enhancement of catalytic activity. To a large extent, emergence is due to the lack of thermodynamic equilibrium of the system.

A symmetrical situation takes place for an integrated enzyme network. Away from thermodynamic equilibrium, the difference D(u) − N(u) assumes negative values. Relationships (15a) and (15b) apply and the free energy level of the ternary EAB complex is lower than that of the free enzyme state E. Such a situation has an immediate consequence. It implies that the catalytic constant is small and therefore that the enzyme is a poor catalyst.

We are now in the position of defining the identity of an enzyme reaction, or of a network of enzyme reactions, through the sequence of Aristotelian information of the various steps and through the degree of emergence, or integration, generated by the interaction of ligands bound to proteins. Such sequence is no doubt characteristic of a reaction profile and, perhaps, as specific as a succession of base pairs in DNA. Moreover one could expect that such structures could display random alterations that could increase, or decrease, the performances of the system. “Favourable” changes should lead to networks that, after some time could become dominant relative to less “favoured” systems. In other words, some kind of selection could have been exerted upon these catalytic networks leading, from sequential ordered systems, to sequential random ones.

3 Networks of catalysed chemical reactions

It has already been outlined that it is probably not unsound to consider that the first prebiotic systems could have been encapsulated networks of catalysed chemical reactions. In this perspective, it is logical to consider that metabolic networks of present day living systems should display some similarities with these tentative prebiotic networks and could be considered models of these networks. Such prebiotic networks should possess the following features that can also be found in present day metabolic networks:

As outlined above, a biochemical network can be considered a network of networks, or a meta-network for each node is itself a network. This situation is likely to be associated with a time hierarchy in the overall system, the steps of substrate binding and release to and from the catalyst being much faster than the transfer of a metabolite from catalyst to catalyst. This condition is likely to be fulfilled in most cases in such a way it is sensible to consider each catalysed reaction a macro-state, or a node, of the system. Within each macro-state one can distinguish different micro-states which correspond to the free catalyst and the various complexes it may form with the substrates. The probability that catalyst E_i has bound, for instance, substrate A_i is

p {(A_{i})}_{E i} = \frac{[E_{i} A_{i}] + [E_{i} A_{i} B_{i}]}{Y_{i}}

(26)

where

Y_{i} = [E_{i}] + [E_{i} A_{i}] + [E_{i} B_{i}] + [E_{i} A_{i} B_{i}]

(27)

Similarly the probability that the network, considered as a whole, has bound substrate A_i is

p {(A_{i})}_{N} = \frac{[E_{i} A_{i}] + [E_{i} A_{i} B_{i}]}{Y_{T}}

(28)

where

Y_{T} = Y_{1} + Y_{2} + Y_{3} + .. .

(29)

It follows from relations (26) and (28) that the relationship between $p {(A_{i})}_{E i}$ and $p {(A_{i})}_{N}$ is

p {(A_{i})}_{N} = p (Y_{i}) p {(A_{i})}_{E i}

(30)

where p(Y_i) is the probability of occurrence of node Y_i in the meta-network. If substrate A_i is specific for enzyme E_i, viz. if it binds to enzyme E_i only, then the conditional probability that E_i has bound A_i, given it has already bound B_i, is the same whether E_i is isolated or included in the network sequence. Then one has

p {(A_{i} |B_{i})}_{E i} = p {(A_{i} |B_{i})}_{N}

(31)

and it becomes possible to define functions $h {(A_{i})}_{N}$ and $h {(A_{i} |B_{i})}_{N}$ as

h {(A_{i})}_{N} = - \log [p (y_{i}) p {(A_{i})}_{E i}]

(32)

h {(A_{i} |B_{i})}_{N} = - \log p {(A_{i} |B_{i})}_{N}

(33)

Hence the amount of Aristotelian information released, or consumed, at the level of node Y_i is

I {(A_{i} : B_{i})}_{N} = h {(A_{i})}_{N} - h (A_{i} |B_{i})_{N} = \log \frac{p (A_{i} |B_{i})_{E i}}{p {(A_{i})}_{E i}} - \log p (Y_{i})

(34)

This expression is equivalent to

I {(A_{i} : B_{i})}_{N} = I {(A_{i} : B_{i})}_{E i} - \log p (Y_{i})

(35)

It then appears that the Aristotelian information released, or consumed, at the level of a node is equal to the intrinsic Aristotelian information of that node, considered in isolation, plus a term that expresses how this node is integrated in the network. The second contribution is in fact a measure of the effect of context of this node on its information. Hence the mean Aristotelian information per node of the meta-network can be written as

< I (A_{i} : B_{i}) > = \sum_{i} p (Y_{i}) I (A_{i} : B_{i})_{E i} - \sum_{i} p (Y_{i}) \log p (Y_{i})

(36)

The first term of the right-hand side of this expression represents the mean contribution of the Aristotelian information of the micro-states in a set of unconnected macro-states. The second term, called topological information, expresses how the connections of the macro-states contribute to the mean information of the whole system. This contribution is dependent upon the topology of the network made up of these macro-states each of them having a probability p(Y_i) dependent upon the network topology. Expression (36) provides a good criterion for the identity of the meta-network exactly as a DNA sequence allows one to characterize a living organism (Fig. 5).

Fig. 5
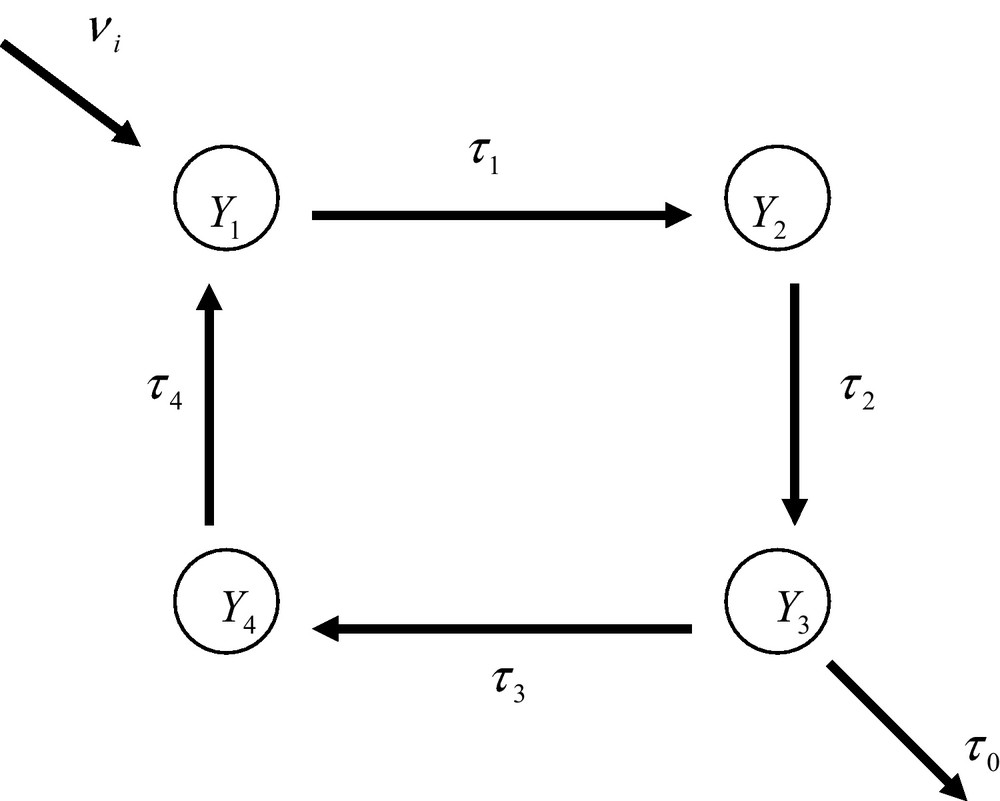
An ideal regular open metabolic network. The nodes Y₁,..., Y₄ are the individual enzyme reactions. The τ’s are the apparent transition constants (see main text). The system is open and displays an input and output of matter.

In order to illustrate how a meta-network is organized, it is of interest to consider, as an example, the simple ideal situation of a regular open system made up of four enzyme reactions (Fig. 5). As already outlined previously, the transition constant, τ_i, between two macro-states is defined from the product of the probability of occurrence, p(A_i, B_i), of the ternary complex, E_iA_iB_i, the catalytic constant, k_i, and the apparent diffusion constant, $k_{i}^{D *}$ . One has then [5]

τ_{i} = k_{i} k_{i}^{D *} p (A_{i}, B_{i})

(37)

In this expression,

k_{i}^{D *}

and p(A_i, B_i) are mathematically defined as

k_{i}^{D *} = k_{i}^{D} \frac{\partial [S_{i}]}{\partial x}

(38)

and

p (A_{i}, B_{i}) = \frac{K_{1 i} K_{2 i} [A_{i}] [B_{i}]}{1 + K_{1 i} [A_{i}] + K_{3 i} [B_{i}] + K_{1 i} K_{2 i} [A_{i}] [B_{i}] + u_{E A} + u_{E B} + u_{E}}

(39)

In expression (38) $k_{i}^{D}$ is the real diffusion constant and ∂[S_i]/∂ x the concentration gradient of substance S_i. In the case of the network shown in Fig. 6, the differential equations that describe the dynamics of the macro-states are

\frac{d p (Y_{1})}{d t} = \frac{ν_{i}}{Y_{T}} + τ_{4} p (Y_{4}) - τ_{1} p (Y_{1})

\frac{d p (Y_{2})}{d t} = τ_{1} p (Y_{1}) - τ_{2} p (Y_{2})

(40)

\frac{d p (Y_{3})}{d t} = τ_{2} p (Y_{2}) - (τ_{3} + τ_{0}) p (Y_{3})

\frac{d p (Y_{4})}{d t} = τ_{3} p (Y_{3}) - τ_{4} p (Y_{4})

Fig. 6
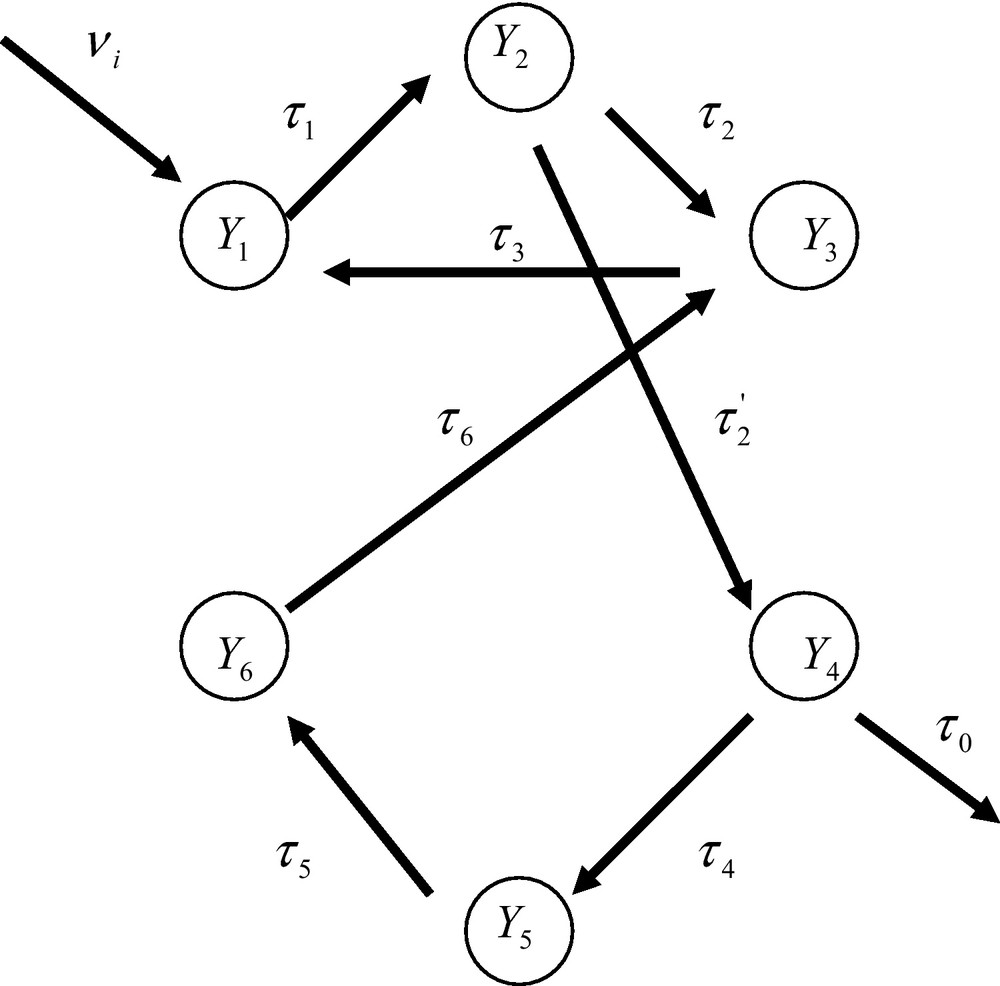
A fuzzy-organized network of enzyme reactions. The probability of occurrence of the nodes (the enzyme reactions) depends upon their degree of connections.

Moreover a conservation equation should hold for the probabilities of occurrence of the macro-states, namely

p (Y_{1}) + p (Y_{2}) + p (Y_{3}) + p (Y_{4}) = 1

(41)

Under steady state conditions, differential equations degenerate into algebraic expressions. Moreover, under these conditions, the input and output rates should be equal viz.

\frac{ν_{i}}{Y_{T}} = τ_{0} p (Y_{3})

(42)

Three steady state equations plus the conservation equation are sufficient to allow the derivation of the expression of the probabilities of occurrence of the macro-states. Substituting the third steady state equation by the conservation equation allows one to write

[\begin{array}{c} τ_{1} & - τ_{2} & 0 & 0 \\ 0 & τ_{2} & - (τ_{0} + τ_{3)} & 0 \\ 0 & 0 & τ_{3} & - τ_{4} \\ 1 & 1 & 1 & 1 \end{array}] [\begin{array}{c} p (Y_{1}) \\ p (Y_{2}) \\ p (Y_{3}) \\ p (Y_{4}) \end{array}] = [\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}]

(43)

Solving this Cramer system yields

p (Y_{1}) = \frac{τ_{2} τ_{3} τ_{4} + τ_{0} τ_{2} τ_{4}}{τ_{1} τ_{2} τ_{3} + τ_{1} τ_{2} τ_{4} + τ_{1} τ_{3} τ_{4} + τ_{2} τ_{3} τ_{4} + τ_{0} τ_{2} τ_{4} + τ_{0} τ_{1} τ_{4}}

p (Y_{2}) = \frac{τ_{1} τ_{3} τ_{4} + τ_{0} τ_{1} τ_{4}}{τ_{1} τ_{2} τ_{3} + τ_{1} τ_{2} τ_{4} + τ_{1} τ_{3} τ_{4} + τ_{2} τ_{3} τ_{4} + τ_{0} τ_{2} τ_{4} + τ_{0} τ_{1} τ_{4}}

(44)

p (Y_{3}) = \frac{τ_{1} τ_{2} τ_{4}}{τ_{1} τ_{2} τ_{3} + τ_{1} τ_{2} τ_{4} + τ_{1} τ_{3} τ_{4} + τ_{2} τ_{3} τ_{4} + τ_{0} τ_{2} τ_{4} + τ_{0} τ_{1} τ_{4}}

p (Y_{4}) = \frac{τ_{1} τ_{2} τ_{3}}{τ_{1} τ_{2} τ_{3} + τ_{1} τ_{2} τ_{4} + τ_{1} τ_{3} τ_{4} + τ_{2} τ_{3} τ_{4} + τ_{0} τ_{2} τ_{4} + τ_{0} τ_{1} τ_{4}}

It appears from these results that the transition constant of the output, τ₀, plays a part in the expression of the probability of occurrence of the nodes and that they tend to increase the probability of the nodes located up-stream the output of the network. It would then be incorrect to consider the network a closed, isolated, system.

Let us consider now the fuzzy-organized system of Fig. 6 where the nodes are enzyme reactions. The reasoning followed previously allows one to derive the expressions of the probabilities of occurrence of the nodes. One finds

p (Y_{1}) = \frac{τ_{3} τ_{5} τ_{6} (τ_{4} + τ_{0}) (τ_{2} + τ_{2}^{'})}{Δ} p (Y_{2}) = \frac{τ_{1} τ_{3} τ_{5} τ_{6} (τ_{4} + τ_{0})}{Δ}

p (Y_{3}) = \frac{τ_{1} τ_{2} τ_{5} τ_{6} (τ_{4} + τ_{0}) + τ_{1} τ_{2}^{'} τ_{4} τ_{5} τ_{6}}{Δ} p (Y_{4}) = \frac{τ_{1} τ_{2}^{'} τ_{3} τ_{5} τ_{6}}{Δ}

(45)

p (Y_{5}) = \frac{τ_{1} τ_{2}^{'} τ_{3} τ_{4} τ_{6}}{Δ} p (Y_{6}) = \frac{τ_{1} τ_{2}^{'} τ_{3} τ_{4} τ_{5}}{Δ}

with

Δ = τ_{5} τ_{6} (τ_{4} + τ_{0}) (τ_{1} τ_{3} + τ_{1} τ_{2} + τ_{2} τ_{3} + τ_{2}^{'} τ_{3}) + τ_{1} τ_{2}^{'} (τ_{3} τ_{4} τ_{5} + τ_{3} τ_{4} τ_{6} + τ_{3} τ_{5} τ_{6} + τ_{4} τ_{5} τ_{6})

(46)

In these open systems the probability of occurrence of any node cannot be arbitrarily defined. It is in fact defined by the topology of the network considered as a collective entity. Any probability of occurrence of a node depends upon the number of pathways leading to that node. As we shall see in the next Section these conclusions imply a dramatic change of our views about the mode of description of metabolic networks subjected to the thermodynamics of open systems.

4 Discussion

Even simple enzyme reactions display some kind of behaviour that can be considered an evolutionary process. Obviously, this type of evolution is not of neo-Darwinian type for there is, in a catalysed chemical reaction, no random mutation of the structure of a genetic material that is to be selected by the external milieu. The type of evolution we are referring to is based on some kind of self-organization of the system. Of particular interest in this perspective are the physical processes that lead to the emergence, or enhancement, of catalytic activity. This situation may occur if the enzyme displays random binding of its two substrates (see Fig. 1), viz. the enzyme should bind its substrates in either order. Emergence can occur even if the system is close to equilibrium provided that

K_{1} > K_{4} and K_{3} > K

(47)

The degree of emergence, however, cannot be very large under these sole conditions. As a matter of fact the extent of emergence can be considerably amplified if the system is far away from thermodynamic equilibrium. As shown in Section 2.1, this implies that the u values are not negligible and then simple relationships (47) should be replaced by

K_{1} > K_{4} and k_{- 3} > k_{4} [A]

(48a)

K_{3} > K_{2} and k_{- 1} > k_{- 2} [B]

(48b)

To a large extent it is a drift from equilibrium that is responsible for the enhancement, or the emergence of the catalytic function.

A number of enzymes do not display random binding of their susbstrates, viz. the substrates bind to the protein following a compulsory order. In that case, and whatever the system is close to a steady state, or not, it can only display integration. The concept of emergence is important for it implies that owing in part to non-equilibrium conditions it has thermodynamic implications. It has been shown in particular in Section 2.2 that conditions (48a) and (48b) imply that the free energy level of the ternary enzyme-substrates EAB state should be higher than that of the free enzyme itself. The higher the energy level of the EAB state and the closer it should be to that of the EAB^≠ transition state. From a thermodynamic viewpoint this implies that the free energy barrier, which has to be overcome during catalysis, is reduced. It then appears that in the case of an enzyme process the term emergence means emergence, or enhancement, of a catalytic process. Hence it is tempting to consider that non-equilibrium self-organization of simple catalytic processes could have been the basis of their evolution.

In fact, the networks we have been referring to are not only isolated enzyme reactions but even more networks of enzyme reactions, which we have called meta-networks. In such a system, each node (also called macro-state) is in fact an enzyme reaction connected to other reactions according to a certain topology. In this model description, the links connecting the nodes correspond to the transfer of metabolites from catalyst to catalyst. The distinction we have made between macro- and micro-states is fully justified if there is a time-hierarchy in the system, which is likely to be the case, as the time-scale of the events taking place during the enzyme reaction are much faster than the migration of metabolites from catalyst to catalyst. In this model description, any macro-state is characterized by several micro-states that represent the successive states of a catalyst interacting with its substrates. The information of a node of such meta-network is the sum of the individual informations of the corresponding micro-states plus a topological information that expresses how the global network topology affects the information of one of its nodes.

The model description of networks of biochemical reactions raises the general question of the best description of such networks. Recently a number of authors [6–14] have discussed the organization and functional properties of networks in a completely different perspective. This description, implicitly or explicitly, postulates that there exists a general mode of formal representation of networks whatever their nature. In this perspective, for instance, one could describe and analyse in the same manner networks of social relationships in a human society, for instance, and metabolic networks as well [6–14]. This is quite an optimistic claim for metabolic networks are subjected to thermodynamics whereas networks of social relationships are not. Sequencing genomes of living systems has allowed one to identify their genes, proteins and metabolites. Today databases offer this information. On this basis, it is possible to construct a graph of which the nodes are the metabolites and the links the chemical reactions that connect them. Using this mode of network description, Barabasi and his colleagues [11,13,14] have concluded that real networks, and in particular biochemical networks, are scale-free. This means that a large number of nodes are poorly connected whereas a small number of them, called “hubs”, appear highly connected.

This mode of network description is purely static and does not tell anything about the real probability of occurrence of the nodes. Moreover it does not take account of the fact that a network of catalysed chemical reactions should comply with the laws of thermodynamics. In this perspective, such system should possess the following properties:

• it should be considered an open system with an input and an output of matter;
• the free energy change upon going from a node to another one should be the same regardless the pathway thus leading to some constraints between the corresponding rate constants;
• it is not possible to define the degree of connexion of a node independently of its probability of occurrence. It is then clear that these thermodynamic requirements are not taken into account in Barabasi's description of metabolic networks [11]. The very fact there could exist highly connected nodes with a poor probability of occurrence is hardly compatible with the fact, already mentioned, that the probability of occurrence of a node is directly related to its degree of connexion. Probability of occurrence and degree of connexion cannot be considered independent variables. In this perspective, it might seem surprising that a metabolic network, which should comply with the laws of thermodynamics of open systems, could be described, in the same manner as, for instance, the film actor collaboration network [8] which has little to do with thermodynamics…

Last, the author of the present articles would like to stress again that the scenario proposed for the origins of life is conjectural. However, these conjectures are physically sound and therefore worth being explored together with other possibilities [15].