Chemotaxis with directional sensing during <i>Dictyostelium</i> aggregation

Rui Dilão; Marcus J.B. Hauser

doi:10.1016/j.crvi.2013.10.008

Biophysics/Biophysique

Chemotaxis with directional sensing during Dictyostelium aggregation

Rui Dilão ^1,² ; Marcus J.B. Hauser ³

¹ Non-Linear Dynamics Group, IST, Department of Physics, avenue Rovisco Pais, 1049-001 Lisbon, Portugal
² Institut des hautes études scientifiques, 35, route de Chartres, 91440 Bures-sur-Yvette, France
³ Abteilung Biophysik, Institut für Experimentelle Physik, Otto-von-Guericke-Universität Magdeburg, Universitätsplatz 2, 39106 Magdeburg, Germany

Comptes Rendus. Biologies, Volume 336 (2013) no. 11-12, pp. 565-571.

Résumé

We show that the chemotactic movements of colonies of the starving amoeba Dictyostelium discoideum are driven by a force that depends on both the direction of propagation (directional sensing) of reaction-diffusion chemotactic waves and on the gradient of the concentration of the chemoattractant, solving the chemotactic wave paradox. It is shown that the directional sensing of amoebae is due to the sensitivity of the cells to the time variation of the concentration of the chemoattractant combined with its spatial gradient. It is also shown that chemotaxis exclusively driven by local concentration gradient leads to unstable local motion, preventing cells from aggregation. These findings show that the formation of mounds, which initiate multicellularity in Dictyostelium discoideum, is caused by the sensitivity of the amoebae due to three factors, namely, to the direction of propagation of the chemoattractant, to its spatial gradient, and to the emergence of cAMP “emitting centres”, responsible for the local accumulation of the amoebae.

Métadonnées

Reçu le : 2013-06-14
Accepté le : 2013-10-09
Publié le : 2013-11-01

PMID

DOI : 10.1016/j.crvi.2013.10.008

Mots clés : Chemotaxis, Directional sensing, Dictyostelium, Chemotactic wave paradox

Affiliations des auteurs :

Rui Dilão ^{1, 2} ; Marcus J.B. Hauser ³

¹ Non-Linear Dynamics Group, IST, Department of Physics, avenue Rovisco Pais, 1049-001 Lisbon, Portugal
² Institut des hautes études scientifiques, 35, route de Chartres, 91440 Bures-sur-Yvette, France
³ Abteilung Biophysik, Institut für Experimentelle Physik, Otto-von-Guericke-Universität Magdeburg, Universitätsplatz 2, 39106 Magdeburg, Germany

@article{CRBIOL_2013__336_11-12_565_0,
     author = {Rui Dil\~ao and Marcus J.B. Hauser},
     title = {Chemotaxis with directional sensing during {\protect\emph{Dictyostelium}} aggregation},
     journal = {Comptes Rendus. Biologies},
     pages = {565--571},
     publisher = {Elsevier},
     volume = {336},
     number = {11-12},
     year = {2013},
     doi = {10.1016/j.crvi.2013.10.008},
     language = {en},
}

TY  - JOUR
AU  - Rui Dilão
AU  - Marcus J.B. Hauser
TI  - Chemotaxis with directional sensing during Dictyostelium aggregation
JO  - Comptes Rendus. Biologies
PY  - 2013
SP  - 565
EP  - 571
VL  - 336
IS  - 11-12
PB  - Elsevier
DO  - 10.1016/j.crvi.2013.10.008
LA  - en
ID  - CRBIOL_2013__336_11-12_565_0
ER  -

%0 Journal Article
%A Rui Dilão
%A Marcus J.B. Hauser
%T Chemotaxis with directional sensing during Dictyostelium aggregation
%J Comptes Rendus. Biologies
%D 2013
%P 565-571
%V 336
%N 11-12
%I Elsevier
%R 10.1016/j.crvi.2013.10.008
%G en
%F CRBIOL_2013__336_11-12_565_0

Rui Dilão; Marcus J.B. Hauser. Chemotaxis with directional sensing during Dictyostelium aggregation. Comptes Rendus. Biologies, Volume 336 (2013) no. 11-12, pp. 565-571. doi : 10.1016/j.crvi.2013.10.008. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2013.10.008/

Version originale du texte intégral

1 Introduction

Chemotaxis is the phenomenon in which cells or microorganisms direct their movement as a response to the local variation of the concentration of some chemical substance. For example, in colonies of Dictyostelium discoideum (Dd), localised groups of starving amoebae initiate the production of cyclic adenosine monophosphate (cAMP) that spreads in space as reaction-diffusion travelling chemical waves. In the vicinity of these spontaneously formed cAMP emission centres, the amoebae sense cAMP and direct their chemotactic movements towards the initiation centres [1]. Near these centres, amoebae rotate around a spontaneously formed hole (i.e. a zone depleted from cells), where the cell density increases locally to form aggregates (Fig. 1). At a later stage of development, aggregates are transformed into a simple multicellular organism with two main kinds of differentiated cells [2]. This is one of the simplest known mechanisms of transition from colonies of unicellular to multicellular organisms. For a detailed description of Dictyostelium aggregation and open questions on the involved biochemical mechanisms, see [2–4].

Fig. 1
Aggregation of a colony of Dictyostelium discoideum towards a spontaneously formed aggregation “centre”. Near the aggregation centre, amoebae begin to rotate around a spontaneously formed hole. This hole is characterised by a depletion of cells. (Data from Christiane Hilgardt [25]).

Experimental observations show that Dd cells move towards a region where cAMP chemical waves are produced, and the speed of cells is proportional to the slope or gradient of the concentration of cAMP [1,5]. On the other hand, it has been observed that cells move as long as the gradient is positive, when measured along the direction of the wave source [2,6]. “When the slope reverses, Dd cells stop moving and await for the next wave.” [2, p. 101] This fact shows that the chemotactic cell response cannot solely be determined by the local cAMP gradient [7].

Here, we investigate whether the force that drives the chemotaxis of Dd cells is solely proportional to the gradient of the chemotactic substance or whereas it also depends on the direction of propagation (directional sensing) of the time varying chemotactic signal.

If the chemotactic substance is produced at a localized source and disperses monotonically along space, the question of directional sensing is meaningless. However, if the chemoattractor propagates along space as periodically repeating wave, the hypothesis that the chemotactic motion of cells is driven by a local concentration gradient implies that the existence of a periodic variation in time of the direction of motion of the cells. This simple gradient hypothesis induces motion of the amoebae in the direction opposed to the source of the chemotactic signal, leading, asymptotically in time, to dispersive motion, preventing the amoebae from aggregation (Appendix A). This oscillatory behaviour in the aggregation pattern of Dictyostelium discoideum has never been observed and this effect is called the chemotactic wave paradox [7,8].

In the experimentally oriented literature, it is implicitly assumed that Dd cells are sensitive to the direction of propagation of the cAMP wave [9–12]. On the other hand, in simulation studies, it is generally assumed that cell chemotaxis is only driven by the sensitivity of the cells to the gradient of the chemotactic substance [13–17], and directional sensing is not included in models. Early studies have shown that the amoebae motility is also sensitive to temporal gradients [18]. However, sensitivity to temporal gradients have never been considered in mathematical models of Dictyostelium aggregation. One of the results we derive here (Appendix A) is that the introduction of directional sensing leads to the sensitivity to the temporal gradient of the chemoattractant.

Since we are interested in unravelling the importance of the effects of the gradient and of the directional sensing in the Dd aggregation phenomena, we will let the cells propagate in a cAMP concentration field with a prescribed dynamics. In this paper, we omit some well-known properties of Dd aggregation, like the fact that Dd amoebae produce and relay cAMP upon sensing of an external concentration of the chemoattractant [19], and the phenomenon of streaming [2]. While the production and relay of cAMP is necessary for the establishment of a gradient field of cAMP, these effects are independent of the mechanisms responsible for chemotaxis and directional sensing.

2 Chemotaxis with directional sensing

We denote by $X (x, y, t)$ the local concentration of some chemotactic substance. The equation of motion of an amoeba under the influence of a chemoattractant has the form:

m \ddot{\vec{r}} = - λ \dot{\vec{r}} + \vec{F} (X (x, y, t))

(1)

where, as usual, the dots represent time derivatives,

\vec{r} = (r_{x}, r_{y})

are the spatial position coordinates of the amoeba, λ is a damping coefficient, m is the mass of the amoeba and

\vec{F}

represents a generic chemotactic force field. The term

- λ \vec{r}

describes the damped motion of the cells and has been measured experimentally, [20].

As it is shown in the Appendix A, the direction dependent chemotactic force field is:

\vec{F} = \{\begin{array}{l} \vec{g r a d} X if sign (\frac{\partial X}{\partial t}) > 0 \\ \vec{0} if sign (\frac{\partial X}{\partial t}) \leq 0 \end{array}

(2)

Introducing (2) into (1), the equations of motion of an amoeba under the influence of the chemotactic signal $X (x, y, t)$ are:

(i) if $sign (\frac{\partial X}{\partial t}) > 0$ ,

\{\begin{array}{l} m {\ddot{r}}_{x} & = & - λ {\dot{r}}_{x} + μ \frac{\partial X}{\partial x} \\ m {\ddot{r}}_{y} & = & - λ {\dot{r}}_{y} + μ \frac{\partial X}{\partial y} . \end{array}

(3)

(ii) if

sign (\frac{\partial X}{\partial t}) \leq 0

,

\{\begin{array}{l} m {\ddot{r}}_{x} & = & - λ {\dot{r}}_{x} \\ m {\ddot{r}}_{y} & = & - λ {\dot{r}}_{y} . \end{array}

(4)

The equations of motion (3)–(4) have been derived under the assumption that amoebae are sensitive to the direction of propagation of a chemotactic wave, together with the condition that if the slope of the gradient reverses sign, there is no chemotactic motility.

To describe the spatial variation of the chemoattractant $X (x, y, t)$ , we consider the Ginzburg–Landau reaction-diffusion equation [21]:

\{\begin{array}{l} \frac{\partial X}{d t} & = & ν \bar{X} - β \bar{Y} + ({\bar{X}}^{2} + {\bar{Y}}^{2}) (a \bar{X} - b \bar{Y}) + D_{X} Δ X \\ \frac{\partial Y}{d t} & = & β \bar{X} + ν \bar{Y} + ({\bar{X}}^{2} + {\bar{Y}}^{2}) (a \bar{Y} + b \bar{X}) + D_{Y} Δ Y \end{array}

(5)

where

\bar{X} = X - X^{*}

,

\bar{Y} = Y - Y^{*}

,

Δ = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}

is the two-dimensional Laplace operator,

D_{X}

and

D_{Y}

are the diffusion coefficients, and ν, β, a, b, X^*, and Y^* are parameters. The functions X and Y represent chemical variables. In bounded two-dimensional domains with zero-flux boundary conditions, if ν > 0 and a < 0, the reaction-diffusion equation (5) has a homogeneous and unstable spatially extended steady state with constant values,

X (x, y, t) = X^{*}

and

Y (x, y, t) = Y^{*}

. A local perturbation of this unstable spatial steady state leads to spatial oscillations of X and Y. For these parameter values, the ordinary differential equation part of equation (5) (

D_{X} = D_{Y} = 0

) has a limit cycle in the

(X, Y)

phase space with radius

r = \sqrt{- ν / a}

.

All the equations are written in dimensional form and, in the following, we use the CGS system of units.

For ν > 0 and a < 0 and particular choices of the initial conditions, the numerical solutions of the Ginzburg–Landau reaction-diffusion equation (5) in bounded domains and with zero-flux boundary conditions produce wave-like target (i.e. concentric) and spiral propagating patterns [21], similar to the ones observed in the early phase of aggregation of Dd colonies. Therefore, in order to investigate numerically the aggregation properties of the model equations (3)–(4), we have integrated numerically equation (5) in a circular region inside a square of side length $N d x = 600 \times d x$ . We have considered zero-flux boundary conditions on the circular region, and the parameter values considered were ν = 1 s^-1, β = 0.5 s^-1, a = –1 cm⁴/(s mol²), b = 1 cm⁴/(s mol²), $D_{X} = D_{Y} = 0.000001$ cm²/s, $X^{*} = Y^{*} = 1.5$ mol/cm², dt = 0.005 s and $d x = \sqrt{6 D_{X} d t} = 0.000173$ cm [22].

In Fig. 2, we show the time evolution of 1000 amoebae, calculated from (3)–(4), coupled with the chemotactic signal $X (x, y, t)$ , propagating as a reaction-diffusion spiral wave emanating from the central region of the two-dimensional domain. The chemotactic signal $X (x, y, t)$ has been calculated with equation (5). The spiral wave has been induced by perturbing four contiguous lattice sites with X and Y taking values on the limit cycle of the diffusion-free Ginzburg–Landau equation (5) [21,22]. The values of the variables X and Y for these four sites have a phase advance of $π / 2$ in phase space. Initially, the amoebae move towards the central region of the circular domain and, after a transient time, all the cells rotate near the tip of the spiral, forming a ring as shown in Fig. 2d. The radius of the ring is related to the diffusion coefficients of X and Y, i.e. the radius increases with increasing diffusion coefficients.

Fig. 2
(Color online) Time evolution of the position of $1000$ amoebae in a two-dimensional circular domain, calculated with equations (3)–(4), for (a) t = 0 s, (b) t = 40 s, (c) t = 60 s and (d) t = 80 s. Green spots represent amoebae positions. Red and blue correspond to regions of high and low local concentrations of the chemoattractant X, respectively. The chemotactic signal is a reaction-diffusion spiral wave originated at the central point (emission centre) of the two-dimensional domain and has been calculated with equations (5). The parameters of the dynamics of the amoebae are m = 0.0001 g, λ = 0.0001 g/s and μ = 0.00001 g cm²/s². The parameters associated with the dynamics of the chemotactic signal are described in the text.

Comparing the numerical simulation of Fig. 2d with the aggregation patterns of Dd cells in Fig. 1, we conclude that the rotating ring pattern of Dictyostelium discoideum colonies is similar to the rotating ring pattern obtained in these simulations. This suggests that the hole observed in Fig. 2d is due to the rotation of the tip of the reaction-diffusion spiral wave associated with the dynamics of the chemoattractant X. Chemotactic models without the directional sensing condition, introduced in (3)–(4), would lead to a non-aggregative behaviour as in the case of the simulation in Fig. 3 of Appendix A.

Fig. 3
Position of one amoeba as a function of time according to equations [7] (a) and [11]–[12] (b). The initial position of the amoeba has been set to x₀ = 2 with zero initial speed. The parameters of the simulations are, A = 0.02, c = 0.5, m = 1 and λ = 0.5. From these numerical simulations, we conclude that the sensitivity to the gradient and to the direction of propagation (case b) explains cell movements towards the origin of coordinates, as observed in experiments.

For the chosen parameter values, the circular region of the simulations of Fig. 2 has the diameter, $d = 600 \times d x = 0.1039$ cm, and the wave length of the cAMP spiral wave, which is approximately $0.1039 / 6 = 0.017$ cm (compared with [2], pp. 130, Fig. 8.15). Assuming that an amoeba, initially at the periphery of the circular domain, reaches the annular region after t = 80 s, as simulations have shown, the order of magnitude of the amoeba speed is $v = d / (2 \times 80) = 0.00064$ cm/s = 6.4 μm/s. The wave length of the cAMP wave and the speed of the amoebae are within the orders of magnitude of the observed values [1]. In this simple calibration, the simulation time relates with the real time of the motion of amoebae by a scaling constant also affecting m, λ and the chemoattractant concentration.

We have also tested the amoeba motion in the presence of a concentric chemotactic waves or target waves, generated by the Ginzburg–Landau equation (5). In this case, the amoebae move towards the centre of the circular domain, accumulating near the wave initiation centre (Fig. 4). The target wave pattern was generated from a spatially uniform initial condition on the unstable steady state $(X = X^{*}, Y = Y^{*})$ with a small perturbation at the centre of the circular region. After reaching the region of the initial perturbation, all the amoebae stop moving.

Fig. 4
(Color online) Time evolution of the position of 1000 amoebae in a two-dimensional circular domain, calculated with equations (3)–(4), for (a) t = 0 s, (b) t = 40 s, (c) t = 60 s and (d) t = 80 s. Green spots represent amoebae positions. Red and blue correspond to regions of high and low local concentrations of the chemoattractant X, respectively. The chemotactic signal propagates as a reaction-diffusion target wave originated at the central point of the two-dimensional domain (emission centre) and has been calculated with equations (5). All the amoebae accumulate in the emission centre the chemotactic target wave (d). The parameters of the amoeba dynamics (3)–(4) are m = 0.0001 g, λ = 0.0001 g/s and μ = 0.00001 g cm²/s². The parameters associated with the dynamics of the chemotactic signal are described in the text.

To understand the role of the cAMP emission centres in Dd aggregation, in Fig. 5, we show the distribution of 1000 amoebas at time t = 80 s, calculated from a random initial distribution of the chemotactic signal $X (x, y, t)$ and of the amoebae. From this simulation, we conclude that if the chemoattractant is not produced from emission centres, there are no aggregation movements towards localised spatial regions. In order to have aggregation towards a finite number of localised spots, the chemotactic signal must be initiated in the emission centres. Other simulations have shown that if the aggregation centres are within a short distance, the interference between the reaction-diffusion waves destroy the process of aggregation. This simulation shows that the spontaneously formed cAMP emission centres, are necessary for the aggregation and formation of the slime mould and the subsequent multicellularity process.

Fig. 5
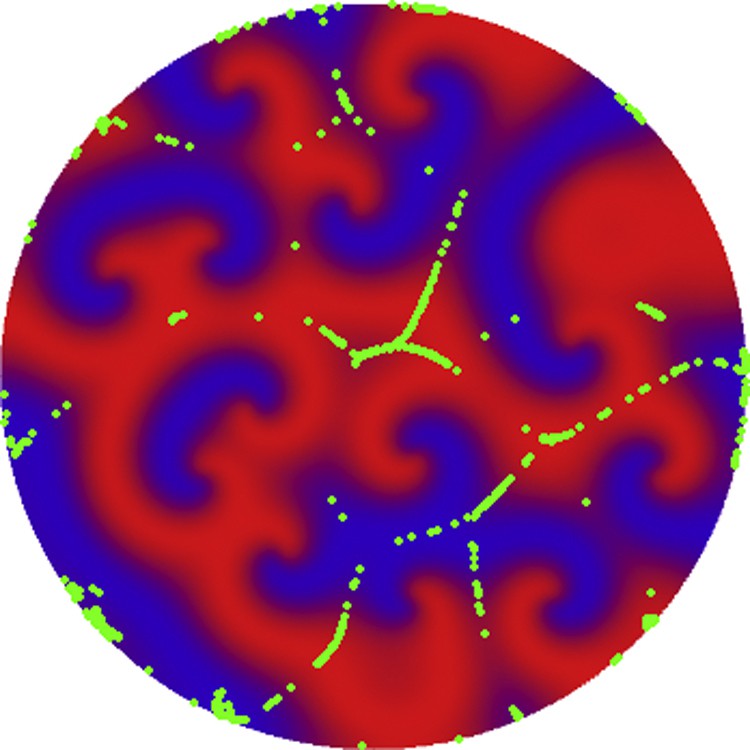
(Color online) Distribution of $1000$ amoebae at time t = 80 s. In these simulation the chemoattractant has a random distribution along the two-dimensional domain. The initial distribution of amoebas is similar to the one in Fig. 4(a), and the parameters of the chemotactic signal and of the amoeba are the same as in Fig. 4. In this case, no emission centres are formed and no Dd aggregation occurs.

3 Discussion

From the model just described, we conclude that the typical circular ring pattern found in the aggregation of Dd colonies is explained by the sensitivity of the amoebae to the direction of propagation and to the gradient of the chemoattractant, together with the spiral shape of the propagating chemoattractant signal. In other models without directional sensing [23], spiral chemoattractant waves do not produce this rotating motion of the Dd cells. This dynamic effect is at the origin of the multicellularity and of the formation of the mould [2], prior to the emergence of the Dd slug.

The sensitivity of amoebae to the gradient of concentration is due to the large number of cAMP receptors (of the order of 50,000) distributed along the plasmic membrane of amoebae [2]. The density of occupation of the cAMP receptors along the amoeba's external membrane is a sensor for the gradient of chemoattractant, being at the origin of the motility of the cells against the chemotactic gradient. Dd amoebae can detect a 1% difference in concentration of the chemoattractant between the front and the back of the cells [5,24]. This spatial information together with the local sensitivity of the cells to the time variation of the concentration of chemoattractant, determines the directional sensing of amoebae. If the local concentration of chemoattractant decreases, the binding rate of cAMP to its receptors also decreases, justifying the sensitivity of the cells to the time variation of the concentration of chemoattractant, in agreement with observations [18].

These biological mechanisms explain why amoebae are sensitive to the temporal and spatial derivatives of the chemotactic field, explaining the stop moving condition, as observed in the Dd aggregation [6,12]. On the other hand, our simulations results are consistent with the polarization effects observed in the amoebae during aggregation [11]. We have concentrated this investigation on the roles of the cAMP gradient and directional sensing, solving the well-known chemotactic wave paradox [8]. Consequently, in the present approach, we did not consider other well-known effects observed in the aggregation of Dd colonies as streaming [2,13], and cAMP production by amoebae [19].

Disclosure of interest

The authors declare that they have no conflicts of interest concerning this article.

Acknowledgments

We would like to thank Christiane Hilgardt for helpful discussions. We would like to thanks the comments of one of the anonymous reviewers of this paper. Travel support by the European Science Foundation research network program FUNCDYN (Functional Dynamics in Complex Chemical and Biological Systems) is gratefully acknowledged. The first author would like to thank IHÉS, where the final version of this paper has been prepared.

Appendix A

We consider a chemotactic substance distributed along a one-dimensional domain. We assume that the concentration of this substance evolve in time and space as a one-dimensional travelling wave, symmetrically along the positive and the negative x-directions. This centrally symmetric wave is generated at the point x = 0 and has radial propagation speed c > 0. To simplify, we assume that the concentration of the chemotactic substance propagates according to the wave type law:

ϕ (x, t) = \{\begin{array}{l} A (1 - \cos (c t - | x |)), i f | x | \leq c t \\ 0, i f | x | > c t \end{array}

(6)

where

A

is the concentration amplitude, and

t \geq 0

.

At time t = 0, we consider an immobile amoeba at position x₀ > 0. Assuming that the response of the amoeba to the chemotactic signal is solely proportional to its gradient, as it is generally assumed in the literature [13,15,16], the one-dimensional equation of motion of the amoeba is:

m \ddot{x} = - λ \dot{x} + \frac{\partial ϕ}{\partial x}

(7)

where λ is a damping constant and x(t) is the position of the amoeba at time t. Equation (7) describes the chemotactic response of an amoeba without directional sensing.

To implement directional sensing in the model equation (7), we now introduce vectorial notation. The effect of the chemoattractant $ϕ (x, t)$ on the amoebae is assumed to be described by the force:

\vec{F} = (\frac{\partial ϕ}{\partial \vec{n}}) \vec{n} = (\frac{\partial ϕ}{\partial x}) n_{x} \vec{n}

(8)

where

\vec{n} = n_{x} e_{x}

is the direction of propagation of the chemical wave. In this one-dimensional case,

n_{x} = \pm 1

and e_x is the usual direction versor. As the wave (6) propagates radially from the origin of coordinates x = 0, if x > 0, then,

n_{x} = + 1

. If x < 0, then n_x = –1. To introduce the directional sensitivity of the amoeba, we assume that the amoeba moves towards the origin x = 0 when it senses a positive slope of the gradient, measured in the negative x-direction (

\frac{\partial ϕ}{\partial x} < 0

). The amoeba stops moving when the slope of the gradient reverses sign. Therefore, the response of the amoeba to the chemical signal with directional sensing is described by the effective force:

\vec{F} = F e_{x} = \{\begin{array}{l} (\frac{\partial ϕ}{\partial x}) n_{x} \vec{n} = (\frac{\partial ϕ}{\partial x}) n_{x}^{2} e_{x} = (\frac{\partial ϕ}{\partial x}) e_{x}, \\ i f (\frac{\partial ϕ}{\partial x}) n_{x} < 0 \\ 0 e_{x}, i f (\frac{\partial ϕ}{\partial x}) n_{x} \geq 0 . \end{array}

(9)

In order to determine a closed form for the direction versor n_x, we consider the scalar wave field, $ϕ (x, t) = \cos (c t - x)$ , where c is a positive constant, $| x | \leq c t$ and $x, t \in R$ .

As c > 0, the scalar field $ϕ (x, t)$ propagates in the positive x-direction and, for each fixed t = t₁, we can have two cases: (i) if, $\frac{\partial ϕ}{\partial x} |_{t = t_{1}} < 0$ , then, $\frac{\partial ϕ}{\partial t} |_{t = t_{1}} > 0$ , (ii) if, $\frac{\partial ϕ}{\partial x} |_{t = t_{1}} > 0$ , then, $\frac{\partial ϕ}{\partial t} |_{t = t_{1}} < 0$ . Therefore, in both cases, $sign (\frac{\partial ϕ}{\partial x} \frac{\partial ϕ}{\partial t}) < 0$ , where $sign (x) = 1$ for x > 0, and $sign (x) = - 1$ for x < 0.

Assume now that the scalar field propagates in the negative x-direction, that is, c < 0. (i) If, $\frac{\partial ϕ}{\partial x} |_{t = t_{1}} < 0$ , then, $\frac{\partial ϕ}{\partial t} |_{t = t_{1}} < 0$ . (ii) If, $\frac{\partial ϕ}{\partial x} |_{t = t_{1}} > 0$ , then, $\frac{\partial ϕ}{\partial t} |_{t = t_{1}} > 0$ . Therefore, in both cases, $s i g n (\frac{\partial ϕ}{\partial x} \frac{\partial ϕ}{\partial t}) > 0$ .

So, the direction of propagation of the one-dimensional scalar field $ϕ (x, t)$ is:

n_{x} = - sign (\frac{\partial ϕ}{\partial x} \frac{\partial ϕ}{\partial t}) .

(10)

Introducing (10) into (9), the effective force on the amoeba is:

\vec{F} = F e_{x} = \{\begin{array}{l} (\frac{\partial ϕ}{\partial x}) e_{x}, i f - sign (\frac{\partial ϕ}{\partial t}) < 0 \\ 0 e_{x}, i f - sign (\frac{\partial ϕ}{\partial t}) \geq 0 . \end{array}

(11)

Hence, the equation describing the motion of the amoeba is:

m \ddot{x} = - λ \dot{x} + F

(12)

where

F

is given by (11). Equation (12), together with (11), describes the chemotactic force on the amoeba, taking into account directional sensing.

In Fig. 3, we show the time evolution of the position of a cell with initial condition x₀ = 2 and x = 0, calculated with equations (7) and (11)–(12), respectively, and chemotactic field (6). Initially, the cell is immobile. For $t \geq x_{0} / c = 2 / c$ , the movement of the amoeba is equally described by the two model equations and the amoeba starts to move in the direction of the point x = 0. For the case of simple chemotaxis, the motion is described by equation (7). For larger values of t, the he slope of the chemoattractant concentration changes sign and the amoeba reverses the direction of motion. In this case, the motion of the amoeba is oscillatory and numerical simulations show that the cell slowly deviates from the origin of coordinates. Asymptotically in time, the position of the amoeba goes away from the source of the chemoattractant. A simple linear analysis shows that equation (7) is linearly unstable around the phase space fixed point $(x = 0, \dot{x} = 0)$ .

In contrast, using model equation (12), with the force (11), amoebae direct their motion towards the origin of coordinates, where the source of the chemoattractant is located.

The simulations in Fig. 3 show that a model based on equation (11)–(12) describes the observed motility in the aggregation of Dictyostelium discoideum colonies. On the other hand, the model based on equation (7) shows that wave driven chemotaxis without directional sensing leads to divergent motion.

For wave propagation in two-dimensional domains, the directional sensing condition in (11) and the direction versor (10) are simply generalised. As the gradient is normal to the level curves of a surface, in two space dimensions, the normalized direction of propagation is then:

\begin{array}{l} \vec{N} = & - & \frac{|\frac{\partial ϕ}{\partial x}|}{∥\vec{grad} ϕ∥} signal (\frac{\partial ϕ}{\partial x} \frac{\partial ϕ}{\partial t}) {\vec{e}}_{x} \\ - & \frac{|\frac{\partial ϕ}{\partial y}|}{∥\vec{grad} ϕ∥} signal (\frac{\partial ϕ}{\partial y} \frac{\partial ϕ}{\partial t}) {\vec{e}}_{y} \\ = & - \frac{1}{∥\vec{grad} ϕ∥} \frac{\partial ϕ}{\partial x} signal (\frac{\partial ϕ}{\partial t}) {\vec{e}}_{x} \\ - & \frac{1}{∥\vec{grad} ϕ∥} \frac{\partial ϕ}{\partial y} signal (\frac{\partial ϕ}{\partial t}) {\vec{e}}_{y} \end{array}

and $|\vec{N}| = 1,$ provided $∥\vec{grad} ϕ∥ 0 .$

Bibliographie

[1] F. Alcantara; M. Monk Signal propagation during aggregation in the slime mould Dictyostelium discoideum, J. Gen. Microbiol., Volume 85 (1974), pp. 321-334

[2] R.H. Kessin Dictyostelium, Evolution, Cell Biology and the Development of multicellularity, Cambridge University Press, 2001

[3] Hilgardt C.; J. Čejková; M.J.B. Hauser; ŠevčíkováF H. Streamless aggregation of Dictyostelium in the presence of isopropylidenadenosin, Biophys. Chem., Volume 132 (2008), pp. 9-17

[4] P.N. Devreotes; S.H. Zigmond Chemotaxis in eukaryotic cells: a focus on Leukocytes and Dictyostelium, Annu. Rev. Cell. Biol., Volume 4 (1988), pp. 649-686

[5] L. Song; S.M. Nadkarnia; H.U. Bödeker; C. Beta; A. Bae; C. Franck; W.J. Rappel; W.F. Loomis; E. Bodenschatz Dictyostelium discoideum chemotaxis: thresholds for directed motion, Eur. J. Cell Biol., Volume 85 (2006), pp. 981-989

[6] K. Tomchik; P. Devreotes Adenosine 3′-5′-monophosphate waves in Dictyostelium discoideum: a demonstration by isotope dilution-fiuorography, Science, Volume 212 (1981), pp. 443-446

[7] T. Höfer; P.K. Maini; J.A. Sherratt; M.A.J. Chaplain; P. Chauvet; D. Metevier; P.C. Montes; J.D. Murray A resolution of the chemotactic wave paradox, Appl. Math. Lett., Volume 7 (1994), pp. 1-5

[8] R.D. Soll; D. Wessels; A. Sylwester The motile behavior of amoebae in the aggregation wave in Dictyostelium discoideum (H.G. Othmer; P.K. Maini; J.D. Murray, eds.), Experimental and Theoretical Advances in Biological Pattern Formation, NATO ASI series A, Vol. 259, Plenum Press, 1993

[9] C. Janetopoulos; R. Firtel Directional sensing during chemotaxis, FEBS Lett., Volume 582 (2008), pp. 2075-2085

[10] C.A. Parent; B.J. Blacklock; W.M. Froehlich; D.B. Murphy; P.N. Devreotes G protein signaling events are activated at the leading edge of chemotactic cells, Cell, Volume 95 (1998), pp. 81-91

[11] A. Samadani; J. Mettetal; A. van Oudenaarden Cellular asymmetry and individuality in directional sensing, Proc. Natl. Acad. Sci. USA, Volume 103 (2006), pp. 265-289

[12] K.F. Swaney; C.-H. Huang; P. Devreotes Eukaryotic chemotaxis: a network of signaling pathways controls motility, directional sensing, and polarity, Annu. Rev. Biophys., Volume 39 (2010), pp. 11549-11554

[13] J. Dallon; H. Othmer A discrete cell model with adaptive signaling for aggregation of Dictyostelium discoideum, Philos. Trans. Roy. Soc. Lond. B, Volume 352 (1997), pp. 391-417

[14] E. Keller; L. Segel Initiation of slime mold aggregation viewed as an instability, J. Theor. Biol., Volume 26 (1970), pp. 399-415

[15] J. Murray Mathematical Biology, Springer-Verlag, Berlin, 1989

[16] S. Nagano Diffusion-assisted aggregation and synchronization in Dictyostelium discoideum, Phys. Rev. Lett., Volume 80 (1988), pp. 4826-4829

[17] C. van Oss; A.V. Panfilov; P. Hogeweg; F. Siegert; C.J. Weijer Diffusion-assisted spatial pattern formation during aggregation of the slime mould Dictyostelium discoideum, J. Theor. Biol., Volume 181 (1996), pp. 203-213

[18] B. Varnum; K.B. Edwards; D.R. Soll Dictyostelium amebae alter motility differently in response to increasing versus decreasing temporal gradients of cAMP, J. Cell Biol., Volume 101 (1985), pp. 1-5

[19] A. Goldbeter; L. Segel Unified mechanism for relay and oscillation of cyclic AMP in Dictyostelium discoideum, Proc. Natl. Acad. Sci. USA, Volume 74 (1977), pp. 1543-1547

[20] H.U. Bödeker; C. Beta; T. Frank; E. Bodenschatz Quantitative analysis of random ameboid motion, Europhys. Lett., Volume 90 (2003), p. 28005

[21] R. Dilão; A. Volford Excitability in a model with a saddle-node homoclinic bifurcation, Discrete Contin. Dyn. Syst. B, Volume 4 (2004), pp. 419-434

[22] R. Dilão; J. Sainhas Validation and calibration of models for reaction-diffusion systems, Int. J. Bifurcat. Chaos, Volume 8 (1998), pp. 1163-1182

[23] D. Kessler; H. Levine Pattern formation in Dictyostelium via the dynamics of cooperative biological entities, Phys. Rev. E, Volume 48 (1993), pp. 4801-4804

[24] S.H. Zigmond Ability of polymorphonuclear leukocytes to orient in gradients of chemotatic factors, J. Cell Biol., Volume 75 (1977) no. 2, pp. 606-616

[25] C. Hilgardt, Biologische Variabilität bei der Musterbildung von Dictyostelium, PhD Thesis, Otto-von-Guericke-Universität Magdeburg, 2010.

Commentaires - Politique