1 Introduction
Gethsemane is the place located at the foot of the Mount of Olives, now within the city of Jerusalem. In a farm place (χωρίον) called Gethsemane (Γɛθσημανί) takes place the scene of the prayer of Jesus before his death [1]. Regarding the name “Gethsemane” (Γɛθσημανɛι), the etymology most plausible is from Geth-shamena’ (Latin: torcular olei), where geth would come from gath, i.e. “press”, while the second term shamena could be the plural from Hebrew and Aramaic sēmān (signs or omens) or from the Hebrew šemen (oil) [2]. The Dalman [3] considers “oil press” most probable than “press of signs or omens” as the word's etymology.
Biblical passages, writings and witnesses from those who visited the Gethsemane in the centuries represent the sources to which we refer in this study to contextualize the historical presence of the olive tree in this important place for Christianity.
By comparing the data of different Gospels, we come to know that the place where Jesus goes after the last dinner is “the Mount of Olives” (Luke 29,39), “on the other side of Cèdron stream” (John 18,1,2), while Matthew (26,36) and Mark (14,32) identify this place with “Gethsemane”. To the biblical terminology refer both Eusebio Pamphili of Caesarea (ca. 260–339 AD) in the Onomasticon (295 AD), and Sofronio Eusebio Girolamo (347–420 AD) in De situ et nominibus locorum Hebraicorum (390 AD), both of them speaking in fact of “Mount of Olives” and “Gethsemane” (www.getsemani-it.custodia.org). Surprisingly, until then we do not find the binomial “olive”/“Gethsemane Hortus”. It is therefore of a certain interest to see how we arrived to that pairing of terms.
The first reference to the presence of olive trees in the Gethsemane is only in the 15th century, when the Dominican friar Felix Fabri, reporting his travel to Jerusalem between 1480 and 1483, wrote “[…] we went down into the valley, crossed the brook to the farm at Gethsemane, and there sat down in shade under the olive trees, and breakfasted merrily together” [4]; olive trees, in his description, restore pilgrims with their shadow, even if they do not give sacredness to the place.
So the historical–literary sources leave a void of about 1400 years; that is the time during which the olive trees of Gethsemane are not mentioned. The hypotheses explaining this silence are twice. The first one is that maybe olive trees did not exist anymore. Titus Flavius Josephus (Jerusalem 37–Rome 100) narrates that, during the siege of Jerusalem, Titus Flavius Vespasianus ordered his soldiers to level the land by destroying vegetable gardens, plantations and fruit trees [5]. The facts narrated by Titus Flavius Josephus are likely to have taken place some hundreds of meters to the north with respect to Gethsemane, so they should not have interested the olive trees in question.
A second hypothesis is that maybe the olive trees did exist, but were not considered important in the overall frame because there was not yet a culture of landscape. Gethsemane thus was considered only as a “place” without considering the different botanical species present there. From the 16th century onwards, the olive trees are present in the literature and are positioned in the Garden of Gethsemane. Giovanni Zuallardo writes in 1586 more detailed information: “This garden has still some very old olive trees: but it is divided in different parts, as much for the path as for the enclosures” [6]. The author offers also a drawing containing six trees within a trapezoidal fence and other four down the road within a triangular fence (Fig. 1).
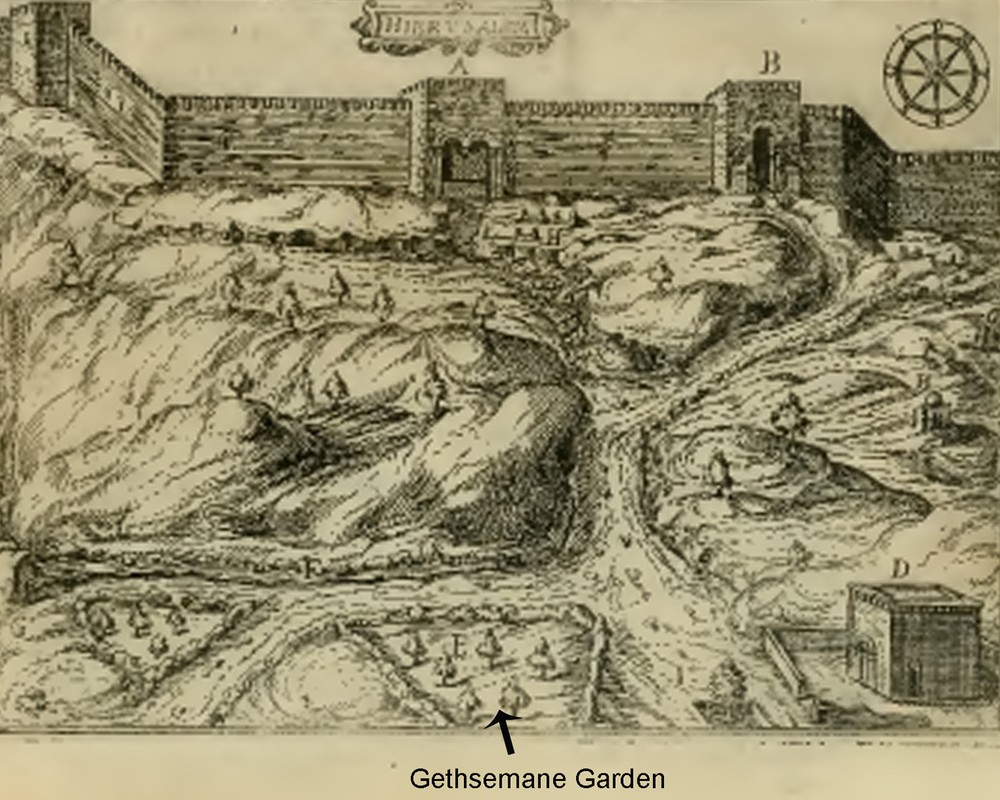
(Color online.) An illustration of Jerusalem with the Garden of Gethsemane (arrow). In G. Zalluardo, 1586 [6].
In the 17th century, there have been numerous references to both the presence of the olive trees and their number: the Franciscan friar Francesco Quaresmi, in his Elucidatio Terrae Sanctae of 1632, writes: “The vegetable garden of Gethsemane is full of many and very old olive trees”; Eugenio Roger in 1631 and Bernardino Surio in 1644 write that nine plants are present [7].
Later on, the number of olive trees was reduced to eight, as the today's ones, as Father Michel Nau, who visited the place in 1674, narrates: “Il reste huit arbres fortunés du nombre, à ce qu’on dit, de ceux qui étoient-là, du temps du Sauveur” (“there remain eight fortunate trees in number, according to what people say, of those that were there at the time of the Savior”) [7].
Until today, the reality of the eight plants of the vegetable garden of Gethsemane, guarded and protected by the Franciscan fathers, did not undergo significant changes with respect to the above-quoted historical sources.
It appears therefore of some interest to know something more about those trees, that have been conserved for so long time, likely because they were in some way a memory of what happened in Christian history.
Classical approaches to the identification of olive germplasm are based on morphological and biometric characters [8], and more recently on DNA analysis, based on molecular markers such as RAPD, AFLP, and SSR. These markers were largely used to solve problems of identity and to estimate genetic diversity in Olea europaea [9–11]. Morphological and molecular analyses are becoming complementary tools for olive germplasm characterization [12].
The aim of the present work was therefore to study those ancient eight olive trees growing in the Gethsemane Garden in Jerusalem, using morphological, morphometric, and ultrastructural observations. Molecular analyses were also conducted to evaluate the degree of relationship between individual plants.
2 Materials and methods
2.1 Plant materials
The plant material consisted of the eight ancient olive trees preserved in the Hortus Gethsemani (31°46′47′′N; 35°14′22′′E; Fig. 2).

(Color online.) The Garden of Gethsemane nowadays, with the ancient olive trees.
2.2 Morphometric study
The morphological characterization of the accessions was accomplished by recording for each accession a list of morphological descriptors selected by the International Olive Council [13]. Fifty samples of leaves, fruits, endocarps, and pollen grains were randomly taken for each of the eight accessions.
Fully expanded leaves were collected in summer from the current year's growing shoots, and the leaf length (LL, cm), leaf width (LW, cm) and the leaf shape index, calculated as a leaf length/width ratio (LL/LW ratio), were recorded. Leaf area (LA, cm2) was evaluated using the WD3WinDIAS Leaf Image Analysis System (Delta-T Devices Ltd, Cambridge, UK).
Fruits were collected at maturity, and the linear dimensions (length FL, cm, width FW, cm) were measured with a caliper, and the fruit length/width ratio (FL/FW ratio) calculated in turn. Endocarp length (EL, cm), width (EW, cm), length/width ratio (EL/EW ratio) were also recorded. Number (NG) and width of grooves (WG, mm) were measured at 2 mm from the base.
Pollen grains were analyzed by measuring the polar axis (PP, μm), the equatorial diameter (EP, μm), the distance between the furrow edge (DFP, μm), and the size index, which is the result of the multiplication between the polar axis and the equatorial diameter divided by 100: . Fresh pollen grains and endocarps were analyzed using the Fei Quanta 200 Environmental Scanning Electron Microscope (ESEM, QUANTA 200, Fei Corporation, The Netherlands) operating at 1 Torr.
2.3 Molecular analysis
Total genomic DNA was extracted from fresh leaves using the DNeasy plant mini kit (Qiagen, Hilden, Germany). Leaves collected from different canopy areas allowed us to prepare two biological replicates for each individual tree. Quality and quantity of DNA were verified by standard spectrophotometry (ND-100 spectrophotometer, NanoDrop Technologies, Wilmington, DE, USA) and visualized on agarose gel. The DNA was analyzed at 14 microsatellite DNA loci (DCA-18, UDO-043, DCA-09, GAPU-103A, DCA-16, DCA-17, DCA-03, GAPU-101, DCA-07, DCA-14, GAPU-71B, DCA-15, DCA-05, EMO-90), selected for their high discriminating capacity according to Baldoni and coworkers [14]. Fragments amplified by PCR were separated by capillary electrophoresis using either an ABIPrism 3730 DNA analyzer (Applied Biosystems) or the LIZ 500 size standard to size alleles and a Megabace (General Electric) and the Et400-R size standard (Amersham Biosciences) to compare the data with those of the paper cited above.
2.4 Data analysis
The traits examined were evaluated for their quantitative variables: mean, minimum value, maximum value, maximum value/minimum value ratio, range, standard deviation (SD), and coefficient of variation (CV%). The collected data were also analyzed by using univariate (ANOVA) and multivariate analysis of variance (principal component analysis and clustering analysis). ANOVA were performed using a statistical software package (Statgraphics Plus, version 5.1 for Windows).
Principal component analysis (PCA) is the most common technique for carrying out explorative analysis and for data dimensionality reduction. It combines the original variables linearly by characterizing each object in order to produce a set of new variables. These new variables, which are referred to as principal components (PC), have the following properties:
- • they are mutually uncorrelated (orthogonality);
- • the first PC (PC-1) has the greatest variance among all possible linear combinations of the starting variables;
- • the PCn has the largest variance among all linear combinations of the starting variables that are orthogonal to PC-1… PC(n − 1).
This means that high-order PCs have little variance and little weight in characterizing the objects; they can thus be disregarded with little loss of information. In PCA, each object is characterized by a vector of K scores, where K is the number of retained component. It is then possible to explore the data structure in the object space by studying a limited number of 2D scatterplots, i.e. score plots. The coefficients that give the weight of each variable in the build-up of a PC are called loadings.
Therefore, each variable is characterized by a vector of K loadings. This makes it possible to study correlations among variables by looking at 2D scatterplots (the loading plots). Cluster analyses were utilized in order to investigate the similarity between the accessions. In our case, data processing was performed using the NIPALS algorithm and the Unscrambler X® software (CAMO, Oslo, Norway).
3 Results and discussion
3.1 Phenotypic analysis
The descriptive statistical analysis values for each of the quantitative traits are reported in Table 1. The coefficients of variation (CV) of the characters varied between 1.71 and 20.60%; the lowest CV values were observed for the polar axis (PP), while the highest were observed for leaf area (LA) (Table 1). The number grooves showed a CV of 14.40% and width grooves scored 13.40%, while the remainder of the traits showed values under 13.0%. Eight out of the 17 traits analyzed showed values next to 12.0%, and five out of these had values below 6.50%. A lower CV was instead observed for pollen characters (PP, PE, P/E ratio and SI) (Table 1). The low CV values measured for characters and the minimum difference between minimum and maximum values are the reflection of the least variation between accessions for the characters analyzed.
Basic statistic parameters of the analyzed morphometric characters.
| Characters | Mean | Max | Min | Range | SD | CV (%) |
| LL (cm) | 4.95 | 6.40 | 4.00 | 2.40 | 0.60 | 12.00 |
| LW (cm) | 1.16 | 1.50 | 0.90 | 0.60 | 0.14 | 12.10 |
| LL/LW | 4.30 | 5.82 | 3.00 | 2.82 | 0.54 | 12.50 |
| LA (cm2) | 4.54 | 6.81 | 2.83 | 3.98 | 0.94 | 20.60 |
| PP (μm) | 27.40 | 28.10 | 26.40 | 1.64 | 0.47 | 1.71 |
| EP (μm) | 17.30 | 18.00 | 16.30 | 1.79 | 0.52 | 2.98 |
| PP/EP | 1.58 | 1.70 | 1.47 | 0.24 | 0.05 | 3.31 |
| SI (PP × EP/100) | 4.74 | 5.05 | 4.27 | 0.78 | 0.20 | 4.16 |
| DEP (μm) | 9.80 | 11.00 | 8.98 | 2.02 | 0.59 | 6.06 |
| FL (cm) | 1.99 | 2.50 | 1.20 | 1.30 | 0.25 | 12.50 |
| FW (cm) | 1.26 | 1.60 | 0.80 | 0.80 | 0.16 | 12.80 |
| FL/FW | 1.59 | 2.00 | 0.92 | 1.08 | 0.18 | 10.70 |
| EL (cm) | 1.68 | 2.15 | 1.10 | 1.05 | 0.21 | 12.50 |
| EW (cm) | 0.72 | 0.90 | 0.48 | 0.42 | 0.09 | 12.60 |
| EL/EW | 2.33 | 3.33 | 1.64 | 1.69 | 0.27 | 11.80 |
| NG (n) | 8.02 | 12.00 | 5.00 | 7.00 | 1.16 | 14.40 |
| WG (mm) | 0.24 | 0.30 | 0.18 | 0.12 | 0.03 | 13.40 |
The average values of leaf length (LL) and leaf width (LW) were 4.95 and 1.16 cm, respectively, and the leaves LL/LW ratio varied between 5.82 and 3.00, with a mean of 4.30 (Table 1). The evaluated plants showed the same leaf shape, the leaves were elliptical and of medium-to-small size (Fig. 3a). The average value of leaf area (LA) was 4.54 cm2 and varied between 6.81 and 2.83 cm2; the highest LA was observed in plant 6 while the lowest value was displayed by plant 5 (data no shown).

(Color online.) (a) Leaf; (b) fruits; (c) ESEM micrograph of endocarp grooves; (d) endocarps; (e) ESEM micrograph of pollen grain morphology and exine pattern.
The average values of FL and FW were 1.99 cm and 1.26 cm, respectively. The mean ratio FL/FW varied between 2.00 and 0.92 and averaged 1.59. FL/FW ratio described the fruit shape and we observed a uniform fruit shape for the Gethsemane eight plants. The fruit samples of the eight plants had similar pomological traits, showed an oblong shape, were small and symmetrical, and their epicarp colour was dark violet (Fig. 3b).
The endocarp (Fig. 3c and d) had a mean length (EL) and width (EW) of 1.68 and 0.72 cm, respectively, and the mean ratio EL/EW was 2.33 (Table 1). The mean of grooves per stone (NG) was 8.02 (CV = 14.40%) and their number varied from 5 to 12. The average value of the grooves width (WG) was 0.24 mm with CV 13.40% (Table 1). The endocarp samples had similar pomological traits; were of intermediate size, weakly asymmetric, oblong, with a corrugated surface, and superficial, regular grooves.
The average values of PP and EP were 27.40 μm (CV = 1.71%) and 17.30 μm (CV = 2.98%), respectively, while the ratios of the PP over EP averaged 1.58, ranging from 1.70 to 1.47. The average value of size index of pollen (SI) was 4.74 (CV = 4.16%) and ranged between 5.05 and 4.27 (Table 1). Pollen grains were isopolar, monadic, prolate, trizonocolpate, with a reticulate exine (Fig. 3e).
The matrix of morphological characters was processed using principal component analysis, in order to detect any sub-clustering within the ensemble of Gethsemane olive trees. Because the population of Gethsemane plants is very small, this analysis has an indicative value, and only generic conclusions can be drawn.
The first thing that should be noted is that the variance explained by the first two PCs, 69%, is relatively low (Table 2), and there is not a very strong difference between the variances explained by PC-1 (42%) and PC-2 (27%). This happens because few strong correlations exist among the traits, and suggests that a sensible part of data variance could be due to random causes. Fig. 4 is the loading plot, which express the importance of each morphologic character in the calculation of PCs. Variables farther from the centre have greater importance, and if a variable has a large (positive or negative) projection along an axis, it is important for the corresponding PC. The plot shows that there are no variables having a dominant role in the model. The heaviest loads for PC-1 are those linked to the dimensions of fruit and endocarp, but also to pollen (EP and DEP). The heaviest loads for PC-2 come instead of leaf dimensions and of EL/EW ratio.
PC loading and proportion of total variation associated with the first two axes of PCA.
| Characters | PC loading | |
| PC-1 | PC-2 | |
| LL (cm) | –0.19 | –0.37 |
| LW (cm) | –0.09 | –0.42 |
| LL/LW | –0.23 | –0.11 |
| LA (cm2) | –0.16 | –0.41 |
| PP | 0.08 | 0.24 |
| EP | 0.27 | 0.20 |
| PP/EP | –0.25 | –0.07 |
| DEP | 0.30 | 0.01 |
| FL (cm) | –0.29 | 0.20 |
| FW (cm) | –0.36 | 0.14 |
| FL/LW | 0.30 | 0.08 |
| EL (cm) | –0.23 | 0.36 |
| EW (cm) | –0.28 | 0.19 |
| EL/EW | –0.10 | 0.41 |
| NG (n) | –0.32 | 0.01 |
| WG | –0.32 | 0.08 |
| Variance proportion | ||
| Accumulated (%) | 42 | 27 |
| Cumulative (%) | 42 | 69 |
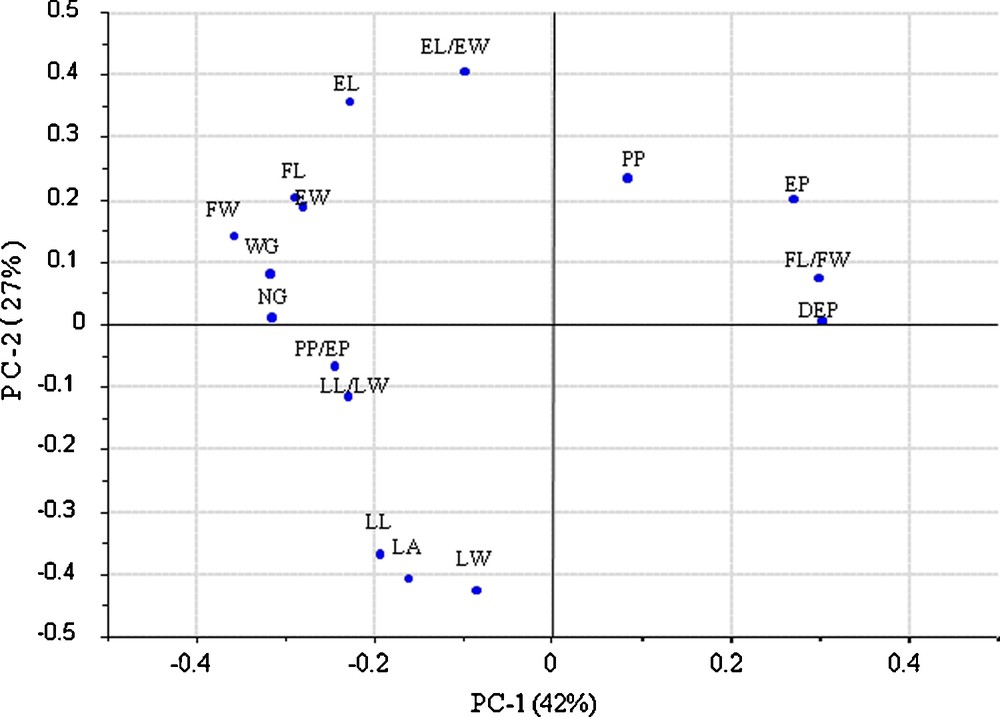
Loadings of the first two principal components.
The scores of the first two principal components are plotted in Fig. 5 together with Hotelling T2 ellipse, which marks the threshold for outlier detection at the 5% significance level. All samples are well within the threshold and no clear outlier was observed. Also, the representative points of plants are distributed quite uniformly. Apparent sub-groups can be seen in the plot, but they are probably due to random variations and are quite common in such small ensembles. Kolmogolov–Smirnof normality tests have been carried on each PC, and their outcomes are summarized in Table 3. In both cases, no significant deviation from normal distribution were detected at the 5% level; this means that any apparent sub-grouping could be due to random causes.
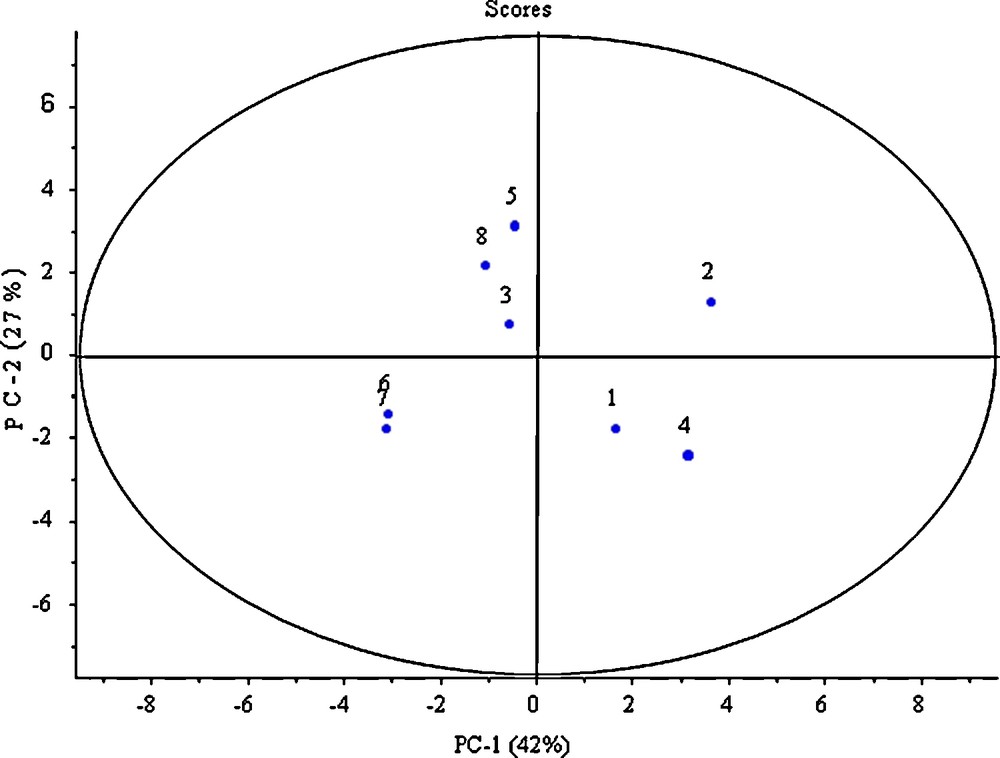
Scores of the first two principal components. The ellipse is the Hotelling T2 threshold for outlier detection. All points lie well within the borderline.
Kolmogorov–Smirnov test at the 5% significance level.
| Variable | PC-1 | PC-2 |
| K–S statistics | 0.197 | 0.248 |
| Critical value at the 5% level | 0.289 | 0.289 |
| P-value | 0.88 | 0.64 |
| Normality | Supported | Supported |
Although PCA did not detect strong differences among Gethsemane trees, it could be interesting to perform a hierarchical cluster analysis within the PC-1–PC-2 sub-space. This allows us to individuate easily the closest siblings for each plant. This analysis was carried out using Euclidean distance and average linkage, and produced the dendrogram in Fig. 6.
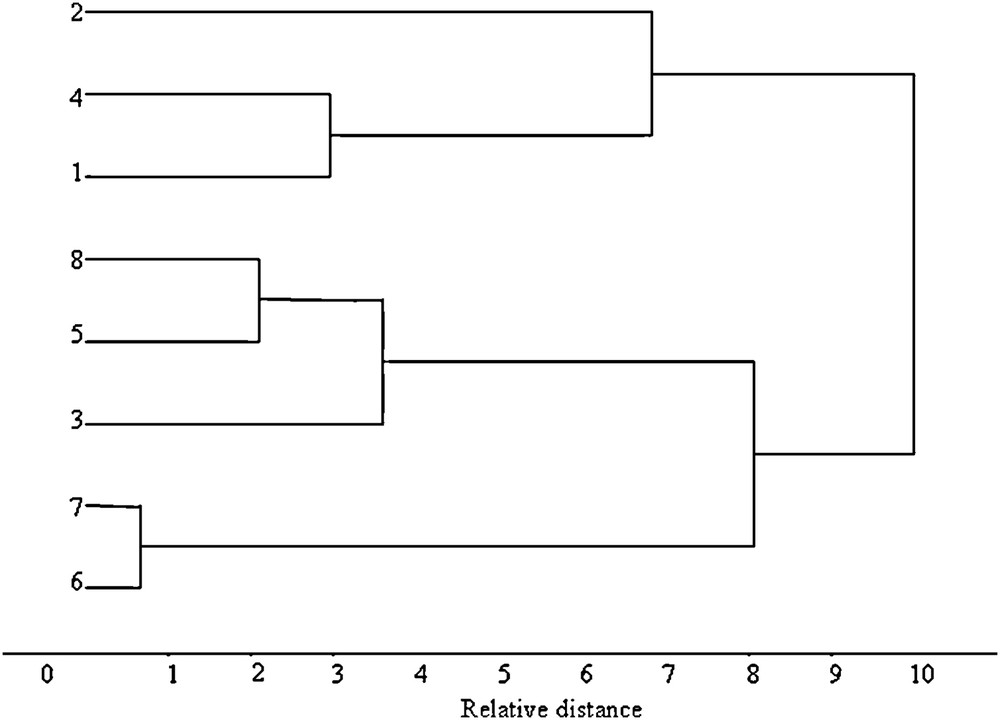
Dendrogram of hierarchical cluster analysis, based on Euclidean distance and average linkage.
The dendrogram show that the family of Gethsemane trees has two main branches; one made of plants 1, 2 and 4, and the other by the other five plants. A careful examination of the PCA model shows that the most peculiar traits of plants 1, 2 and 4 consist of small FW and EL, and high DEP. These variables are plotted in Figs. 7 and 8, where one can see the two main branches of the Gethsemane family.

Scatterplot of fruit width (FW) vs endocarp length (EL).
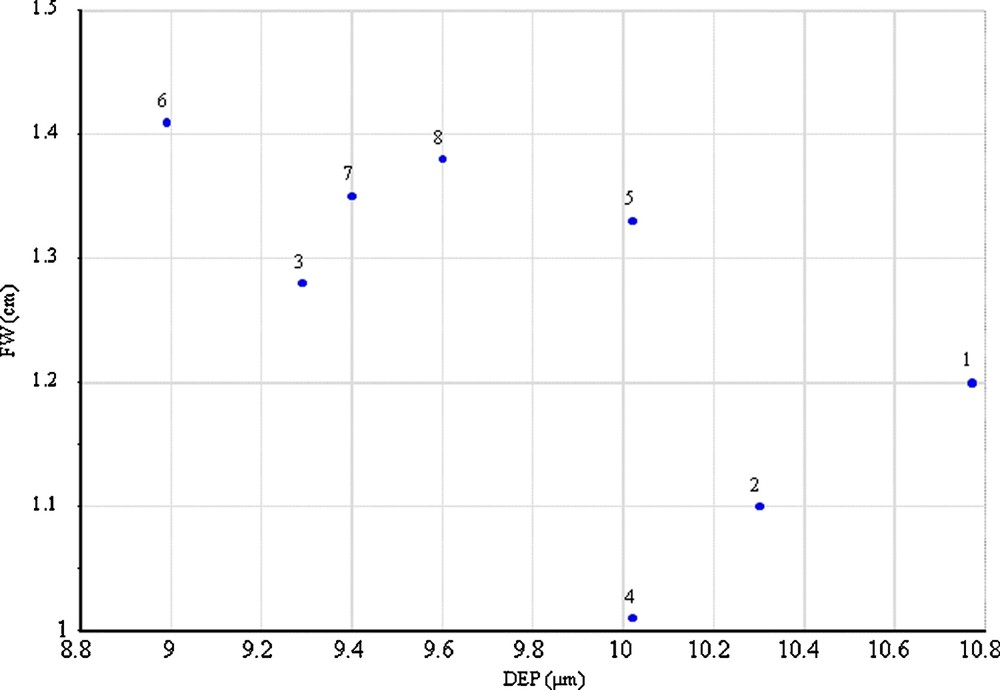
Scatterplot of fruit width (FW) vs distance between the furrow edge (DEP).
3.2 Molecular analysis
As far as molecular analysis is concerned, the eight olives showed the same profile at the 14 microsatellites loci analyzed (Table 4). We could therefore consider that the eight olive trees belong to the same genotype, provided that the probability of identity by chance over all loci analyzed calculated for the allelic frequencies reported by Baldoni et al. [14], could be as low as 1,39901 × e−13 for unrelated genotypes. We tried to identify synonymy for our genotype in the public database of olive cultivars (www.oleadb.it) where the molecular profile of cultivars is reported for 13 out of the 14 SSR markers analyzed, and we could not find any synonymy with cultivars recorded, even after the allele sizes were tentatively harmonized according to the list of allele sizes displayed for each marker.
Allelic profile of the olive trees of the Gethsemane Garden at 14 SSR loci (numbers represent the fragment size in base pairs of the two alleles of each SSR locus). When the second allele is missing, the individual could be either homozygous or heterozygous, with a null allele.
| Microsatellite DNA loci |
Fragment size (bp) |
| UDO-043 | 212–216 |
| DCA-3 | 243–247 |
| DCA-5 | 204– |
| DCA-7 | 149–165 |
| DCA-9 | 172–194 |
| DCA-14 | 185–191 |
| DCA-15 | 246–266 |
| DCA-16 | 124–126 |
| DCA-17 | 113–179 |
| DCA-18 | 177– |
| GAP-U71B | 121–124 |
| GAP-U101 | 191–199 |
| GAP-U103A | 150–174 |
| EMO-90 | 184–186 |
4 Conclusion
Historical memories on the Garden of Gethsemane and the description of the eight olive trees that are preserved in the garden have provided the first results for the characterization of these “notable trees”. They are special trees because they are very old, probably among the oldest of the species in the world, and because they have witnessed important historical events. The natural ecosystem of the Garden of Gethsemane and the olive trees are full part of the culture and spirituality of many peoples.
Combining the results of the different analyses carried out with the present work, we could conclude that the eight olive trees of the Gethsemane Garden in Jerusalem have been propagated from a single genotype, and the differences displayed at the morphological and morphometric analyses are either due to mutations accumulated during the trees’ long standing (approximately nine centuries, Dr. Mauro Bernabei, pers. comm.) or to their position in the garden.
Disclosure of interest
The authors declare that they have no conflicts of interest concerning this article.


