1 Introduction
Since the pioneering work of Volterra [1] and Lotka [2] in the mid-1920s, there has been increasing interest in investigating the dynamical behaviors of predator–prey models in both ecology and mathematical ecology [3–11]. In particular, one of the important dynamical predator–prey behaviors, such as periodic phenomena and bifurcation has become even more interesting [6–10,12–24]. In 1980, Freeman [25] proposed a most popular predator–prey model with Michaelis–Menten-type functional response:
| (1) |
Considering that in many situations, predators must search and share or compete for food, Arditi and Ginzburg [3] introduced and studied the following ratio-dependent-type functional response model:
| (1.2) |
Since the functional response depends on the predator density in a different way, Hassel and Varley [26] reconstructed the predator–prey model with Hassell–Varly-type functional response, which takes the following form:
| (1.3) |
| (1.4) |
| (1.5) |
| (1.6) |
In this paper, we will devote our attention to investigating the properties of a Hopf bifurcation of system (1.6), that is to say, we shall take the delay τ as the bifurcation parameter and show that when τ passes through a certain critical value, the positive equilibrium loses its stability and a Hopf bifurcation will take place. Furthermore, when the delay τ takes a sequence of critical values containing the above critical value, the positive equilibrium of system (1.6) will undergo a Hopf bifurcation. In particular, by using the normal form theory and the center manifold reduction due to Faria and Maglhalaes [28], the formulae for determining the direction of Hopf bifurcations and the stability of bifurcating periodic solutions are obtained. In addition, the existence of periodic solutions for τ far away from the Hopf bifurcation values is also established by means of the global Hopf bifurcation result of Wu [29].
In order to obtain the main results of our paper, throughout this paper, we assume that the coefficients of system (1.6) satisfy the following condition:
H1
am2 + cd − cr > 0, r > d
This paper is organized as follows. In Section 2, the stability of the positive equilibrium and the existence of a Hopf bifurcation at the positive equilibrium are studied. In Section 3, the direction of Hopf bifurcation and the stability of bifurcating periodic solutions on the center manifold are determined. In Section 4, numerical simulations are carried out to illustrate the validity of the main results. In Section 5, some conditions that guarantee the global existence of the bifurcating periodic solutions to the model are given. Biological explanations and some main conclusions are drawn in Section 6.
2 Stability of the equilibrium and existence of the local Hopf bifurcation
In the section, by analyzing the characteristic equation of the linearized system of system (1.6) at the positive equilibrium, we investigate the stability of the positive equilibrium and the existence of the local Hopf bifurcations occurring at the positive equilibrium.
Considering the biological meaning, we only study the property of a unique positive equilibrium (i.e., coexistence equilibrium). It is easy to see that under the hypothesis (H1), system (1.6) has a unique positive equilibrium
Let
| (2.1) |
Then, we obtain the linearized system of (2.1)
| (2.2) |
| (2.3) |
In order to investigate the distribution of roots of the transcendental equation (2.3), the following Lemma stated in [30] is helpful.
Lemma 2.1.[30]For the transcendental equation
Regarding τ as the parameter, we can apply Lemma 2.1 to (2.3), which is a special case of
Obviously, if m1n2 ≠ m2n1, then, λ = 0 is not a root of (2.3). For τ = 0 the characteristic equation (2.3) becomes:
| (2.4) |
It is easy to see that Eq. (2.4) have two negative real roots if the following condition:
H2
m1 + n2 < 0, m1n2 − m2n1 > 0
Multiplying eλτ on both sides of (2.3), it is obvious to obtain:
| (2.5) |
For ω0 > 0, iω0 is a root of (2.5) if and only if
| (2.6) |
Separating the real and imaginary parts of (2.6), we get:
| (2.7) |
If the condition (H2) holds, we can easily check that cosω0τ ≠ 0. Then, it follows from (2.7) that:
| (2.8) |
From the second equation of (2.7), we can easily obtain:
| (2.9) |
From (2.7), we know that (2.3) has a simple pair of purely imaginary roots ±iω0 at
Let
Assume that
H3
Then, the following transversality condition holds.
Proof. Differentiating the equation (2.3) with respect to τ leads to:
When τ = τk, iω0 is a purely imaginary root of (2.3). We then easily get:
| (2.10) |
From (2.7), we have:
Hence,
Under the condition (H3), we know that
Applying Lemma 2.1, we obtain the following results: Lemma 2.3. If (H1), (H2) and (H3) are satisfied, then
(i) if
(ii) if τ = τ0, all roots of Eq. (2.3) except ±iω0 have negative real parts;
(iii) if τ ∈ [τk, τk+1) for k = 0, 1, 2, ..., Eq. (2.3) have 2 (k + 1) roots with positive real parts.
Spectral properties of Eq. (2.3) immediately lead to the properties of the zero solutions to system (2.2), and equivalently, of the positive equilibrium E∗ for system (1.6).
Theorem 2.4.Suppose that (H1), (H2) and (H3) are satisfied. Then, the positive equilibrium E∗of system(1.6)is asymptotically stable when
3 Direction and stability of the Hopf bifurcation
In the previous section, we have obtained conditions for Hopf bifurcations to occur when τ = τk. In this section, we will employ the algorithm of Faria and Maglhalaes [28] to compute explicitly the normal forms of system (1.6) on the center manifold. After that, we will investigate the direction of the Hopf bifurcation and stability of the bifurcating periodic orbits from the positive equilibrium E∗ of system (1.6) at these critical values of τk. We know that Eq. (2.3) has a pair of purely imaginary roots ±iω0 when τ = τk and system (1.6) undergoes a Hopf bifurcation from E∗. Let μ = τ–τk, then μ = 0 is the Hopf bifurcation value of system (1.6).
Throughout this section, we refer to Faria and Maglhalaes [28] for the meaning of the notations involved.
Normalizing the delay τ by the time-scaling t → t/τ, then the system (2.1) can be rewritten as a functional differential equation in
| (3.1) |
Let u = (u1(t), u2(t))T, then, system (3.1) can be rewritten in the following vector form:
| (3.2) |
Obviously, L(τ) is a continuous linear function mapping
| (3.3) |
In fact, we can choose
| (3.4) |
| (3.5) |
From Lemma 7.1.1 in Hale [32], we know that
| (3.6) |
| (3.7) |
For
| (3.8) |
| (3.9) |
Consider the complex coordinates and still denote
Also, the two eigenvectors Ψ1, Ψ2 of A* corresponding to the eigenvalues iω0τk, –iω0τk, respectively, construct a basis Ψ = (Ψ1, Ψ2)T of the adjoint space P* of P and
Thus,
Take the enlarged phase space C by considering the space
Thus, we have the decomposition BC = P⊕Kerπ. Using the decomposition
| (3.10) |
| (3.11) |
| (3.12) |
In what follows, we first define the operators
| (3.13) |
In particular,
By (3.10), we have
| (3.14) |
Noting that L(μ) = μ / τkL(τk), we have
| (3.15) |
| (3.16) |
Since the second-order terms in (μ, x) on the center manifold are given by
| (3.17) |
| (3.18) |
In the following, we shall compute the cubic term
However, the terms
From (3.1) and (3.2) and from (3.18) we can easily see that
Therefore, we have
From (3.15), we have:
In view of the definition of
| (3.19) |
From (3.19), we can easily obtain:
Thus, we obtain:
In what follows, we shall compute
| (3.20) |
| (3.21) |
Thus, from (3.20), we obtain
Therefore,
Since h110(θ) and h200(θ) for
Following [28], we know that h = h (θ; x1, x2, μ) is the unique solution in the linear space of homogeneous polynomials of degree 2 in 3 real variable (x, μ) = (x1, x2, μ) of the equation
| (3.22) |
| (3.23) |
Combining the definition (3.6) of the operator A(τ), we can obtain:
For the sake of simplicity, let:
| (3.24) |
Then, h0 can be evaluated by the system
| (3.25) |
| (3.26) |
In view of (3.14), (3.15), (3.25) and (3.26), we know that
| (3.27) |
| (3.28) |
Solving the Eq. (3.27) and (3.28), we have
| (3.29) |
| (3.30) |
| (3.31) |
| (3.32) |
| (3.33) |
Accordingly, the normal form (3.12) of (3.10) has the following form
The normal form (3.12) relative to P can be written in real coordinates (ω1, ω2) through the change of variables x1 = ω1 − iω2, x2 = ω1 + iω2. Setting ω1 = ρ cosν, ω2 = ρ sinν, then this form becomes
| (3.34) |
Summarizing the above analysis, we have the following result.
Theorem 3.1.The flow of Eq.(3.2)with μ = 0 on the center manifold of the origin is given by (3.34). Hopf bifurcation is supercritical if k1k2 < 0 and subcritical if k1k2 > 0. Moreover, the nontrivial periodic solution is stable if k2 < 0 and unstable if k2 > 0.
4 Numerical examples
In this section, we present some numerical results for some particular values of the parameters associated with the model system (1.6). We consider the system (1.6) with a = 1, b = 2, c = 0.3, m = 0.5, d = 0.8, r = 2. That is,
| (4.35) |
Then, the stability determining quantities for Hopf bifurcating periodic solutions are given by k1 = 0.1912, k2 = −0.1377. From Theorem 2.4, we know that the positive equilibrium
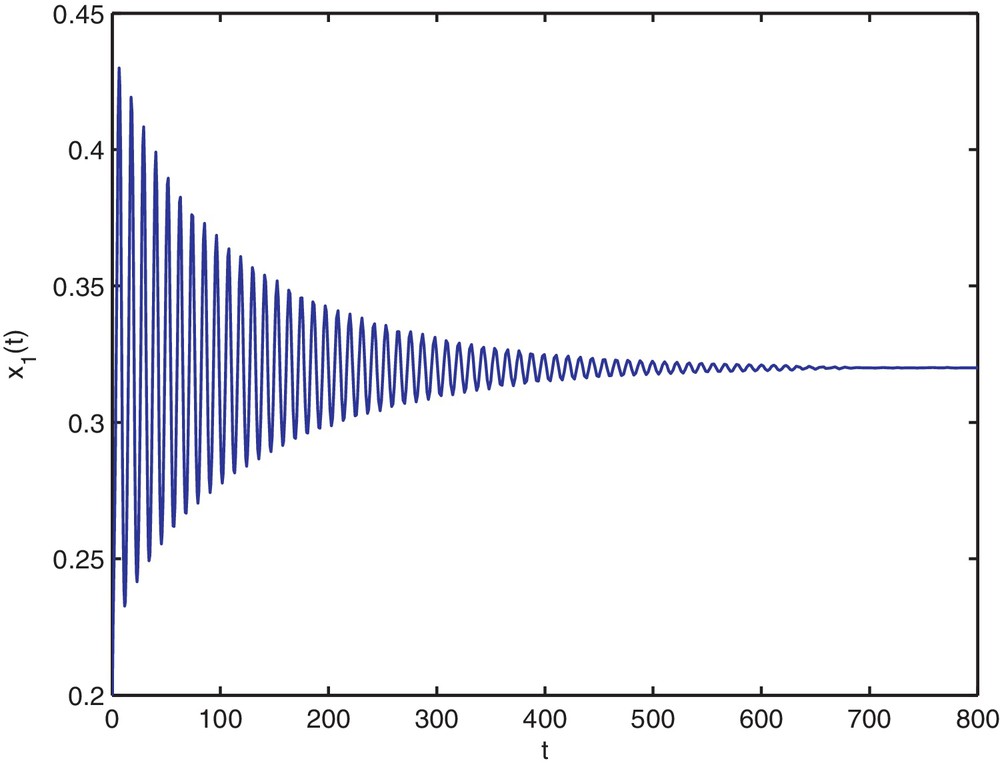
Trajectory portrait and phase portrait of system (4.35) with τ = 1.9 < τ0 ≈ 1.94. The positive equilibrium
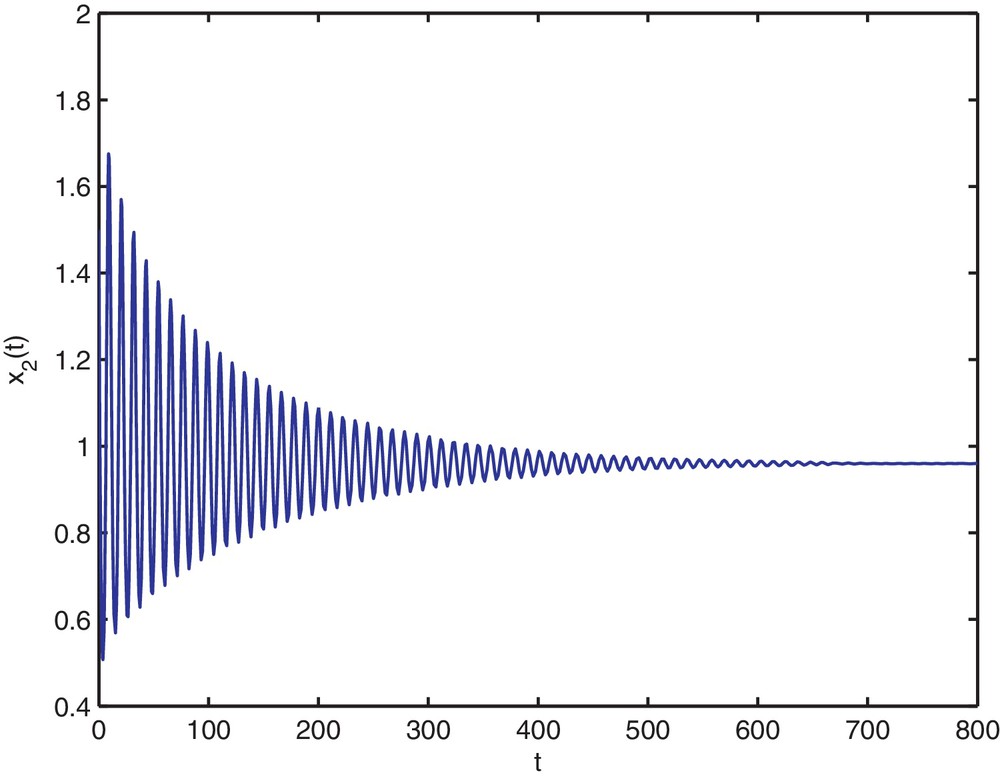
Trajectory portrait and phase portrait of system (4.35) with τ = 1.9 < τ0 ≈ 1.94. The positive equilibrium
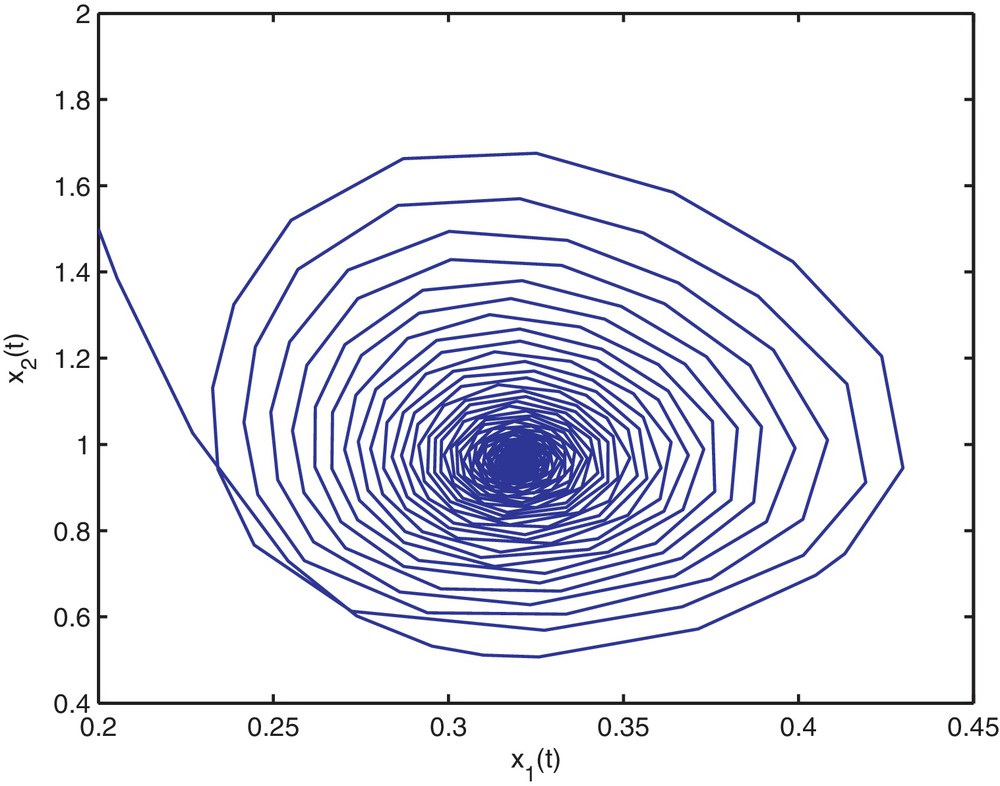
Trajectory portrait and phase portrait of system (4.35) with τ = 1.9 < τ0 ≈ 1.94. The positive equilibrium
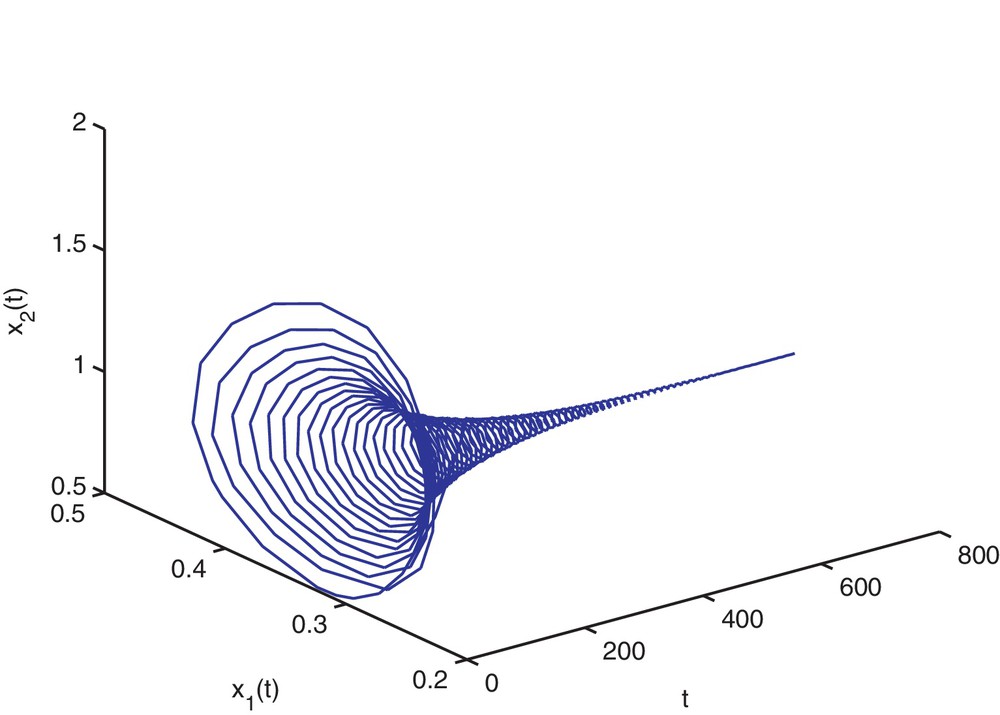
Trajectory portrait and phase portrait of system (4.35) with τ = 1.9 < τ0 ≈ 1.94. The positive equilibrium

Trajectory portrait and phase portrait of system (4.35) with τ = 2 < τ0 ≈ 1.94. Hopf bifurcation occurs from the positive equilibrium
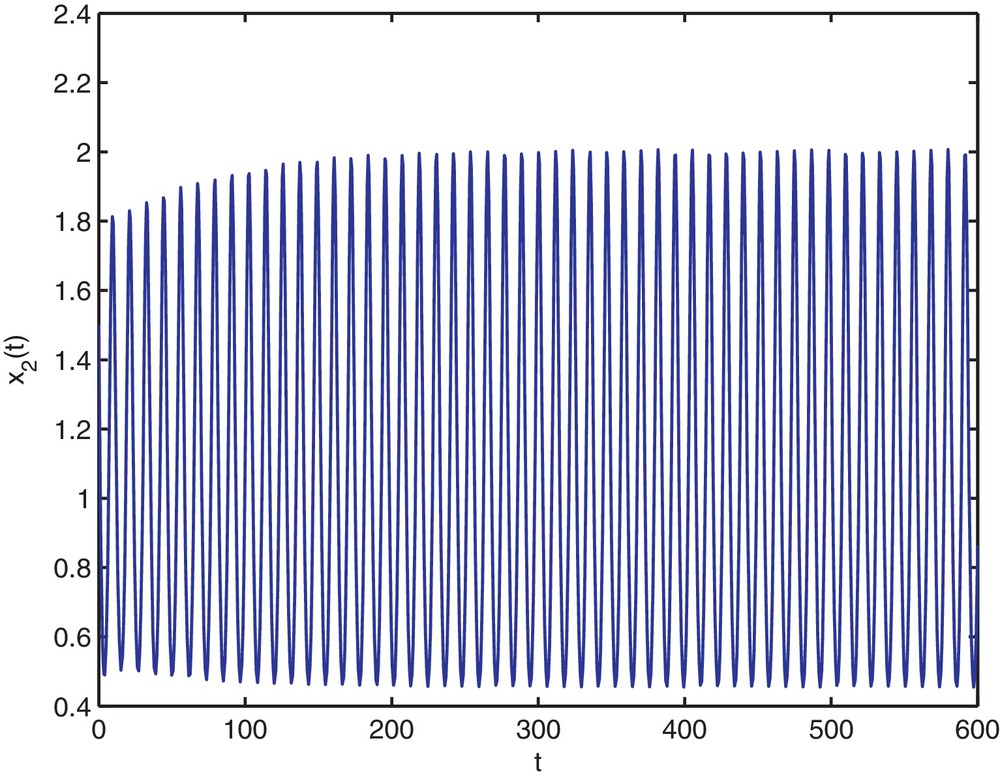
Trajectory portrait and phase portrait of system (4.35) with τ = 2 < τ0 ≈ 1.94. Hopf bifurcation occurs from the positive equilibrium
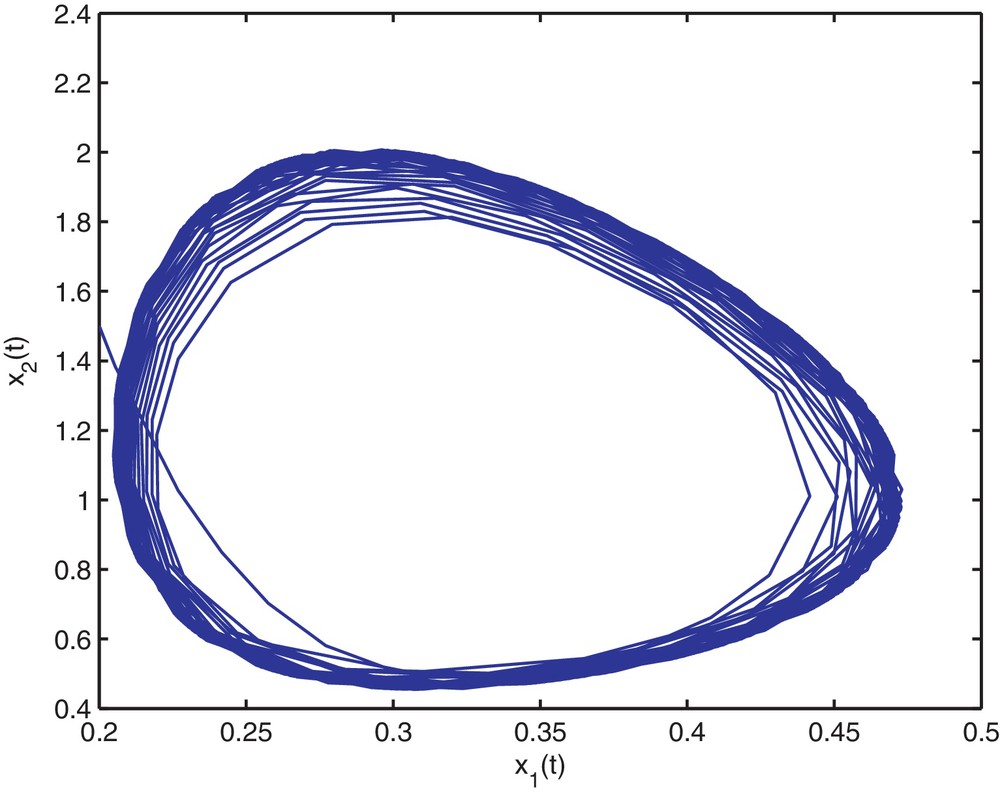
Trajectory portrait and phase portrait of system (4.35) with τ = 2 < τ0 ≈ 1.94. Hopf bifurcation occurs from the positive equilibrium

Trajectory portrait and phase portrait of system (4.35) with τ = 2 < τ0 ≈ 1.94. Hopf bifurcation occurs from the positive equilibrium
5 Global continuation of local Hopf bifurcations
In the earlier sections we have established that the model system (1.6) undergoes a Hopf bifurcation at
Throughout this section, we closely follow the notations in Wu [29]. For the simplification of notations, setting
| (5.1) |
Following the work of Wu [29], we need to define:
Let
For the benefit of the readers, we first state the global Hopf bifurcation theory due to Wu [29] for functional differential equations.
Lemma 5.1.
Assume that
(i)
(ii)
Obviously, if (ii) of Lemma 5.1 is not true, then
Lemma 5.2. If τ is bounded, then all periodic solutions to (1.6) is uniformly bounded.
Proof. Let
Thus,
| (5.2) |
Clearly,
Thus,
From the second equation of (1.6), we have
Then,
Therefore,
Applying the second equation of (1.6), we get
i.e.
It follows that
Thus, the possible periodic solutions lying in the first quadrant of (1.6) must be uniformly bounded. This completes the proof of Lemma 5.2.
Lemma 5.3.If a < d, r < c, then system (1.6) has nonconstant periodic solution with period τ.
Proof. Suppose for a contradiction that system (1.6) has a nonconstant periodic solution with period τ. Then, the following ordinary differential equations
| (5.3) |
Note that x-axis and y-axis are the invariable manifold of system (5.3) and the orbits of system (5.3) do not intersect each other. Thus, there are no solutions crossing the coordinate axes. On the other hand, consider that if system (5.3) has a periodic solution, then there must be an equilibrium in its interior, and that E0(0, 0) is located on the coordinate axis. Thus, we can conclude that the periodic orbit of system (5.3) must lie in the first quadrant.
In the sequel, we will prove that system (5.3) has no nonconstant periodic solution in the first quadrant.
Define
It is easy to show that D is an ultimately bounded region (or absorbing and positively invariant set) of system (5.3). Let
Then, a direct computation show that, for (x, y) ∈ D and a < d, r < c,
Thus, the Bendixson–Dulac criterion, together with the fact that D is an ultimately bounded region of (5.3), implies that (5.3) has no nontrivial periodic solutions, leading to a contradiction. Thus, the proof is complete.
Theorem 5.4.Assume that a < d, r < c. Let ω0 and τk (k = 0,1,2,…) be defined by (2.8) and (2.9), respectively. Then, for each τ > τk (k ≥ 1), system (1.6) has at least k periodic solutions.
Proof. Obviously,
By Lemma 2.2 and 2.3, there exists ɛ > 0, δ > 0 and a smooth curve λ: (τk – δ, τk + δ) → C such that
Let
By Theorem 3.3 of Wu [29], we conclude that the connected component
Thus,
Hence,
| (5.4) |
Now, we are in position to prove that the projection of
For the sake of contradiction, we suppose that the projection of
6 Conclusions and biological explanations
In this paper, we have investigated the local stability of the positive equilibrium



Vous devez vous connecter pour continuer.
S'authentifier