Abridged English version
The asymptotic value of a monotonous growth function can be accounted for in terms of either an internal- or endogenous-nature limit, which is characteristic of the biological variable investigated, or an external limit, which is determined by the environment. This question is considered here by reference to two kinds of theoretical growth models: (i) a global model, such as logistics, which is the archetype of sigmoidal growth functions, and (ii) a model of structured cell population.
The logistic model
In Eq. (1), the parameter K represents the boundary value. The instantaneous growth rate depends both on the present state of the variable and on the amount that remains to be acquired . The ‘achieved growth–remaining potential growth’ pair is equivalent to an agonistic component (with a positive effect) and to an antagonistic (with a negative effect) component pair. In ecology, the parameter K is generally interpreted in terms of the carrying capacity of the milieu, i.e. as a limit of an external nature. The models derived from Monod's model for bacteria growth are based upon the limiting role of an exogenous variable (the substrate), which is submitted to depletion. The parameter K may also refer to a genetic characteristic of the type of cell or organism investigated. The question of the interactions between the growing cell and its milieu is then raised as these interactions condition the boundary value [11,12].
Growth models for structured cell populations
The autocatalytic model (model II, Buis, 2003) [3] is used here in the following simple case: (i) three categories of cells (classes of functional equivalence): juvenile C1, mature C2 (the only cells that are able to divide), senescing or differentiated C3; (ii) asymmetry of cell divisions: . Two modalities are considered in relation with the nature of growth limitation.
External limitation: autocatalysis–competition model. In this case, the source or available substrate S involved in the autocatalysis process [4] is assumed to occur in limited amounts. The development of the model leads to Eq. (3) for the growth of the total population . This equation formally corresponds to a modified logistic equation, with a general form given by Eq. (4), which is a reformulation of the basic principle of Verhulst's logistic theory [5]. The agonistic component is not the present state of the total population ; it only represents its active fraction (non-senescing mature cells). The limit K is determined by the initial conditions, which strictly define the growth potential of the population: the inoculum and the amount of available source at the beginning of growth . In this case, the limitation is of an exogenous nature.
Internal limitation. When the source S is non-limiting, the model leads to growth of an exponential type. A parameter m, which is equivalent to a marker of the number of already completed divisions in the cell descent, can then be introduced to limit such an indefinite growth. With an assigned maximum value, the parameter m was used for the generation of sigmoidal growth curves for cell populations with growth governed by a context-free L-system [13]. In the absence of such a constraint, this type of system is characterized by a growth of the exponential or polynomial type [15]. Using the three preceding cell classes (C1, C2, and C3), the assumptions of the model then become the following.
(a) Two factors of endogenous limitation of growth are involved: (i) the occurrence of a senescence or differentiation process according to the transformation , which limits the number of cells that become able to divide, at each generation; (ii) the existence of a maximum number λ of divisions per cell lineage. For any mature cell , the value of m determines its generation capacity at any instant. For non-senescing cells, division can occur only if . Referring to the principle of asymmetry of cell divisions, any mitosis of a potentially active mature cell is accompanied with a change in the state of the daughter cells: (Fig. 1).
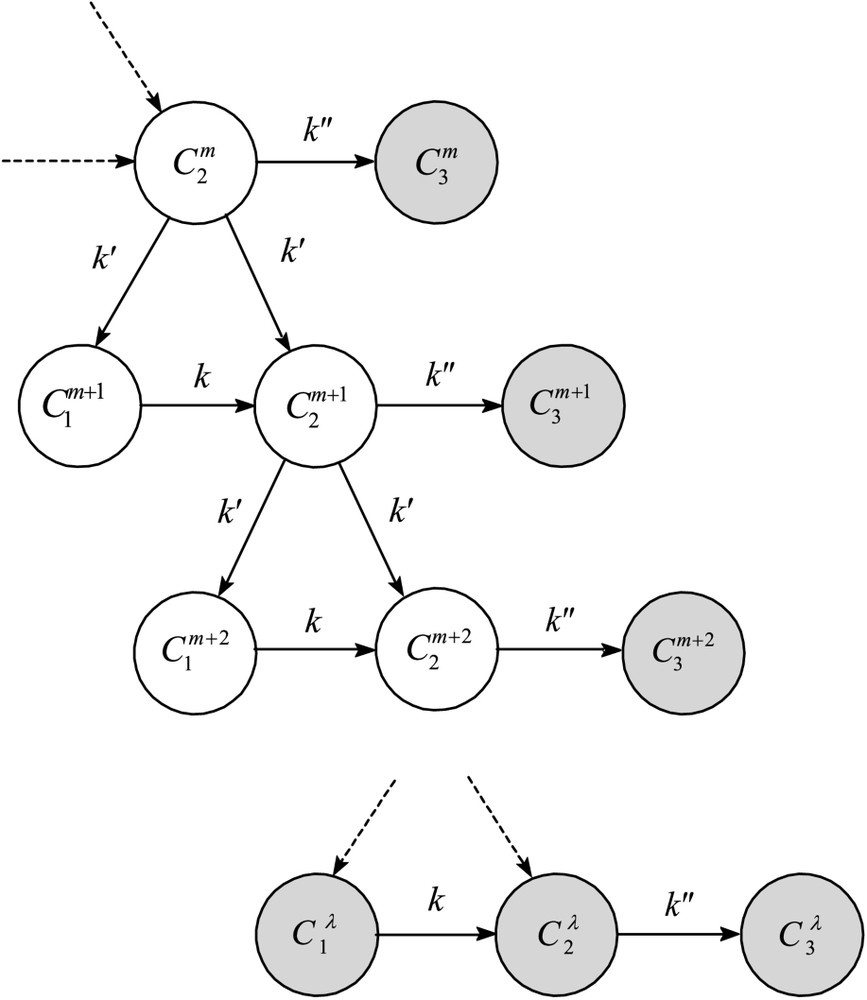
Modèle avec limitation du nombre de divisions. Graphe des transformations. : cellules juvéniles ; : cellules matures actives ; : cellules sénescentes. Le paramètre * en exposant désigne le nombre de divisions accomplies. Les cercles en grisé représentent les cellules ne se divisant plus.
(b) The transition rules are of a deterministic nature, according to the principle of cell automata (L-systems). The transformation is characterized by a transition coefficient , whereas the coefficients and of the transformations (senescence) and (division), respectively, are submitted to the condition .
The equivalence classes and the equations of the preceding model are modified consequently. The new model is investigated for two quite different cases: the duration of the cell enlargement–maturation prior to mitosis (‘life span’ or ‘generation time’), i.e. the number of juvenile cell states, may or may not vary during ontogenesis.
Ontogenesis-independent lifespan. The cell generation time is fixed for any pair of sister cells, irrespective of their occurrence in the genealogy. The system of equations is given in Eqs. (5) and (6). There is a stable, asymptotic steady state, without oscillations. The overall growth rate (Eq. (7)) is quite different from that in the equation with an external limit (Eqs. (3) or (4)) as the growth rate only depends on the present number of active matured cells. The asymptotic value is not explicit: it depends on parameters λ and as well as on the initial states . The model generates sigmoidal curves with asymmetry and shape variations with the parameters and the number of cell states (Fig. 2). The non-monotonic variation of the specific rate is to be noted. The temporal structure (singular points of ) [20] includes five phases and is thus different from that of logistics.
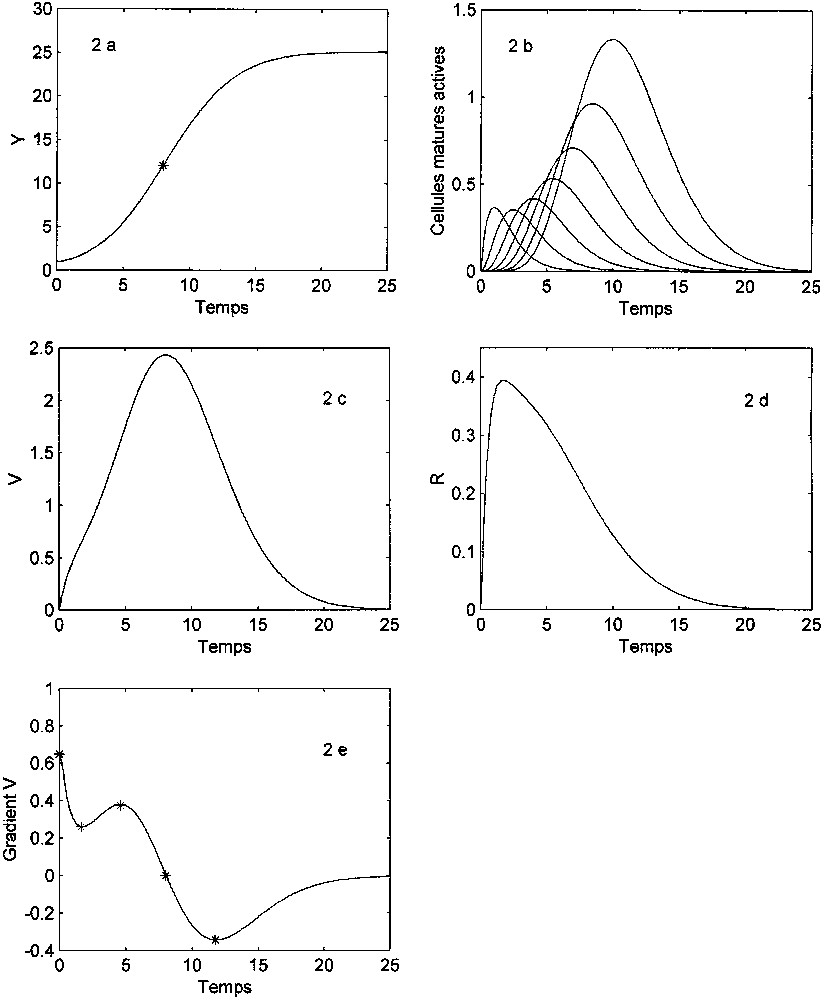
Limitation interne. Nombre maximal de divisions : λ=7. ; ; y(0)=(1,0,0). (a) Courbe de croissance de la population en nombre total de cellules Y(t). * : point d'inflexion (). Dissymétrie gauche : . (b) Évolution des effectifs des différentes catégories de cellules matures actives . Pour chaque courbe de gauche à droite, m varie de 0 à 6. (c) Vitesse de croissance absolue : . (d) Vitesse de croissance spécifique : . (e) Accélération de croissance (gradient de V). Les points singuliers * délimitent ici cinq phases (structure temporelle) [20].
Variable lifespan during ontogenesis. The number p of juvenile states, through which any cell must proceed before acquiring the mitotic capacity, varies in the course of time. More precisely, it depends not only on the initial state, but also on the progress of cell file development, i.e. on the number of divisions already achieved. Thus . Fig. 3 shows the kinetics of such a cell population, with and a linear relationship between p and m. The temporal structure includes six phases, with a non-monotonic variation of the specific rate R.

Limitation interne avec durée de maturation p variable au cours de l'ontogenèse p(m) (voir texte). Nombre maximal de divisions : λ=7 ; ; (pas de sénescence) ; y(0)=(1,0). Voir la légende de la Fig. 2. Dissymétrie droite : . Structure temporelle à six phases.
An alternative illustration is given in Fig. 4 in the case of an ontogeny with two phases: only one juvenile state for (cells subjected to 0, 1 or 2 mitoses), then three juvenile states for (cells dividing three times and more). The growth curve then does not display the classical sigmoidal shape, and the growth rate is characterized by two local maximum values.
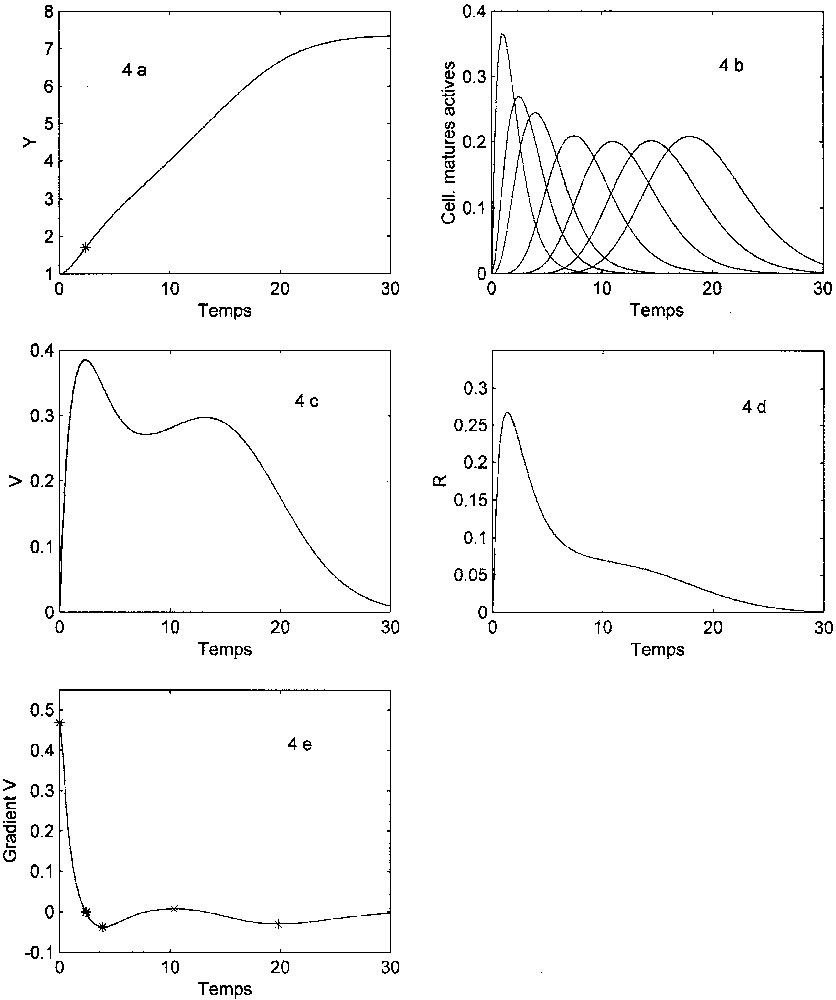
Limitation interne avec durée de maturation variable (deux stades ontogénétiques, voir texte). λ=7 ; ; ; y(0)=(1,0,0). Voir la légende de la Fig. 2. Dissymétrie droite : . Structure temporelle à cinq phases.
Conclusion
The use of the structured cell population model allows the significance of the asymptotic value of the growth curves to be assessed.
1. In the case of a limit of an external nature, the reformulation of the logistic equation, which is put forward, leads to the characterization of two kinds of growth potentiality: a carrying capacity, which is determined by the milieu, and a present potentiality, which is strictly determined by the active fraction of the population.
2. With an endogenous limitation, such as the maximum number λ of divisions per cell filiation, only the instantaneous active fraction determines the overall rate. The asymptotic value is implicit and depends on the initial conditions and on the values of the parameters. As a result, the growth curves generated by the model show a marked flexibility, with singularities in the variation of the absolute and specific rates. The global models do not account for the wide diversity of the experimental curves in every case. The interest of the concept of temporal structure as a basic kinetic property is also pointed out.
1 Introduction
De nombreux modèles univariés autonomes de croissance (à coefficients indépendants du temps) explicitent un terme, noté K, correspondant à la valeur limite (dite à saturation) de la variable analysée y. C'est le cas des fonctions classiques les plus utilisées, comme la logistique (simple ou généralisée), la fonction de Gompertz ou celle de Weibull, qu'il s'agisse d'effectifs, de dimensions, de poids ou de toute autre grandeur [1]. Du point de vue de la biologie théorique, il conviendrait que les hypothèses du modèle précisent le type de processus de limitation en jeu, en rapport avec la signification de ce paramètre K. D'autres modèles, au contraire, ne précisent pas cette valeur limite, comme celui de Bertalanffy, qui définit simplement la vitesse instantanée comme le bilan entre les processus d'anabolisme et de catabolisme, chacun de ceux-ci étant supposé être une fonction puissance de la variable y, sans aucune référence explicite à sa valeur limite.
À l'opposé de tels formalismes, qui peuvent être qualifiés de globaux, l'utilisation de modèles dits structurés permet une analyse beaucoup plus fine du phénomène de croissance. L'idée de structuration [2] est de portée très générale, ne s'appliquant pas seulement à une population d'individus ou de cellules, mais aussi à des entités diverses, telles qu'un organe ou un organisme considéré comme un ensemble unitaire de différents éléments physiquement associés. Sur la base de notre précédente analyse de la croissance de populations cellulaires structurées [3] selon le formalisme général des systèmes de transformation de Delattre [4], nous nous proposons un examen de cette notion de limite, d'une part en vue d'une interprétation améliorée de la logistique, archétype des modèles globaux, et d'autre part en distinguant les deux cas de limitation externe et de limitation interne.
2 Le modèle logistique
La théorie dite logistique est fondée sur l'équation de vitesse proposée par Verhulst [5] :
| (1) |
Sous sa forme multiplicative, la vitesse instantanée de croissance est fonction à la fois de l'état actuel de la variable et de la quantité restant à acquérir . Ce binôme – croissance accomplie, croissance potentielle restante – équivaut à un couple de deux composantes : un terme dit agoniste (à effet positif) et un terme dit antagoniste (à effet négatif), respectivement croissant et décroissant au cours du temps. D'un point de vue épistémologique, on peut l'exprimer par le binôme : « acte réalisé, acte en puissance », se référant au concept aristotélicien d'entéléchie, idée reprise, au début du XXe siècle et dans un tout autre contexte, par l'embryologiste Driesch, qui en faisait une « entité cachée » [6]. Rappelons que, sous son aspect purement mathématique, Lotka [7] a souligné clairement que l'équation de Verhulst représente, pour une fonction monotone, un « formalisme minimal » satisfaisant les deux contraintes d'annulation de la vitesse pour et pour en fin de croissance. Selon l'Éq. (1) sous sa forme additive, ceci revient à associer à l'équation de croissance exponentielle un terme inhibiteur de freinage de degré 2.
En écologie et en dynamique des populations, le paramètre K est interprété généralement comme la capacité biotique (carrying capacity) du milieu ou comme sa « résistance » à une croissance indéfinie. Cette interprétation classique repose sur la relation, tôt notée par Deschamps [8], entre la vitesse de croissance et la disponibilité du milieu en ressources, son équation étant strictement équivalente à celle de Verhulst [9]. Ce qui souligne le caractère externe de la limite postulée par la fonction logistique. Il en va de même avec d'autres modèles, comme celui de Monod pour la croissance bactérienne [10] qui, sous un autre formalisme, repose très explicitement sur le rôle limitant exercé par une variable exogène (substrat, nutriment) soumise à déplétion.
Dans ce même domaine une autre interprétation classique de l'équation logistique repose sur le bilan entre des processus de natalité et de mortalité. En réalité, ceci n'a de sens que sous la condition d'hypothèses complémentaires dûment identifiées. Ainsi Verhulst avait-il précisé avec soin que son équation, dans ses applications en démographie, supposait, comme première approximation, que les taux (ou vitesses spécifiques) de natalité et de mortalité étaient tous deux des fonctions linéaires de l'effectif total de la population. Ce qui n'est évidemment qu'un cas particulier de densité-dépendance.
Les diverses modifications apportées à la fonction logistique, en particulier celles de Pearl et de Richards [1], en introduisant des paramètres supplémentaires, apportent une flexibilité intéressante, qui fait défaut à la sigmoïde de Verhulst. Mais elles ne disent rien sur les possibles bases d'interprétation de la limitation de croissance.
De plus, il convient de noter que ce paramètre K peut recevoir une toute autre interprétation. Dans les cas de grandissement cellulaire ou de croissance organique, dimensionnelle ou pondérale, la signification de K est, pour une large part, d'ordre génétique, représentant, au moins en ordre de grandeur, la taille ou le poids caractéristique de l'espèce biologique considérée. Il s'agit alors implicitement d'une limitation de nature interne ou endogène. Au reste, un même modèle peut préciser dans ses hypothèses l'existence conjointe de ces deux sortes de limite. C'est le cas du modèle de Droop [11] qui, aux deux variables d'état de Monod (biomasse et nutriment), en ajoute une troisième correspondant à la quantité d'un élément limitant se trouvant stockée dans la cellule ( « quota intracellulaire ») et que l'on peut interpréter, au moins en partie, comme étant de nature endogène. Le principe d'une interaction entre une cellule en croissance et son environnement est développé par Falkner [12] avec son modèle d'adaptation physiologique. Appliqué aux relations entre la croissance de cyanobactéries et l'absorption de phosphate, ce modèle est basé sur l'existence d'un « processus d'information » permettant de détecter des fluctuations de l'environnement et d'y répondre par une modification de l'état de sous-systèmes cellulaires spécifiques (transporteur de phosphate notamment). En rapport avec notre présent travail, ceci peut s'interpréter comme une adaptation dynamique des processus de limitation endogène de croissance.
Outre cette question importante de limite, il faut s'interroger sur l'interprétation de l'équation logistique. La composante agoniste de l'Éq. (1) est supposée proportionnelle à la valeur de la variable sans tenir compte de sa structure. Ce qui suppose que tous les éléments de la population sont, au moins approximativement, dans un même état de croissance. Or, toute population, et plus généralement tout objet biologique, n'est évidemment pas un système homogène dont tous les éléments seraient dans un même état de croissance et dont la dynamique pourrait se réduire à la cinétique d'une variable unique comme un effectif global. En tant que modèle explicatif, il est nécessaire de revoir le fondement biologique exact de l'équation logistique.
3 Modèles de croissance de population cellulaire structurée
3.1 Limitation externe : modèle d'autocatalyse–compétition (Buis, modèle II) [3]
Rappelons que, sous sa forme la plus simple et en modifiant ici la numérotation des indices pour en faciliter la présentation, ce modèle repose sur les hypothèses suivantes : (i) existence de trois catégories de cellules (ou classes d'équivalence fonctionnelle) – juvéniles C1, matures C2 (seules aptes à se diviser), sénescentes ou en voie de différenciation C3 – ; (ii) existence d'une source ou substrat S en quantité limitée et formalisation du processus d'autocatalyse selon Delattre [4] ; (iii) dissymétrie des divisions cellulaires : . La courbe de croissance de la population totale est de type sigmoïde, mais, à la différence de la logistique simple, présente une dissymétrie variable. La vitesse instantanée de croissance globale est :
| (2) |
| (3) |
Notons que l'équation de vitesse de la population cellulaire totale (3) correspond formellement à une équation logistique modifiée dont la forme générale est :
| (4) |
À la différence du modèle logistique classique, la composante agoniste ne dépend que de la seule classe des cellules matures actives, tandis que la composante antagoniste reste inchangée. On associe ainsi, en un même modèle, le principe d'une structuration de la population et le principe proposé par la logistique d'un couple de composantes opposées, ce qui est évidemment plus satisfaisant que le recours artificiel à des paramètres supplémentaires (comme le paramètre de dissymétrie de la logistique généralisée), qu'on ne peut justifier biologiquement.
3.2 Limitation interne
Divers processus peuvent intervenir, tels que, par exemple, un mécanisme d'auto-intoxication du système biologique en croissance [8]. Envisageons ici une limitation d'ordre génétique, au sens d'une suite d'instructions programmées en fonction du type cellulaire. Soit la croissance d'une population structurée comme précédemment, mais en absence de compétition (c'est-à-dire la source externe S non limitante) et introduisons la condition d'une limitation λ du nombre de divisions par lignée cellulaire. Cette contrainte a été proposée par Lück et Lück [13] dans le cadre des L-systèmes [14] pour rendre compte des courbes de croissance sigmoïdes. On sait en effet qu'avec ces modèles discrets (automates cellulaires) de type D0L-système, les fonctions de croissance ne peuvent être asymptotiques, étant de type exponentiel, polynomial ou une combinaison des deux (théorème de Paz et Salomaa) [15]. En absence de toute sénescence ou différenciation, la croissance en nombre est toujours exponentielle et suit une relation de Fibonacci étendue : , où et désignent les durées de vie (lifespans) des deux cellules-sœurs [16]. Avec sénescence ou différenciation (existence d'un état inapte à la division), la croissance est polynomiale.
Il convient de modifier notre modèle précédent [3] selon les hypothèses suivantes, puisque la potentialité de croissance d'une cellule n'est plus seulement caractérisée par sa durée de vie (ou nombre d'états avant sa division, en fonction de son état initial) et par les coefficients usuels de transition entre classes. Comme précédemment, les symboles C1, C2 et C3 désigneront, respectivement, les cellules juvéniles, matures et sénescentes.
Hypothèses
(1) Les deux éléments de limitation endogène de croissance d'une population sont : (i) l'occurrence d'un processus de sénescence ou de différenciation (transformation , Fig. 1), qui limite, à chaque génération, le nombre de cellules devenant aptes à se diviser ; (ii) l'existence d'un nombre maximal λ de divisions par lignée cellulaire. Pour toute cellule de type , le nombre de mitoses précédemment accomplies dans la lignée détermine à tout instant sa capacité de génération : pour les cellules n'entrant pas en sénescence, il ne peut y avoir division que si . L'introduction de cette contrainte équivaut à postuler une sorte de compteur du nombre de divisions déjà effectuées, déterminant la potentialité mitotique restante. Cette condition correspond à l'existence d'un nombre donné de cellules tel que l'on observe chez certains organismes. C'est le cas, par exemple, du nématode Caenorhabditis elegans, qui possède exactement 1090 cellules somatiques dont on a décrit la filiation avec précision. En conservant le principe précédent de dissymétrie des divisions cellulaires, toute mitose de cellule mature s'accompagne d'un changement d'état des cellules-filles du type : , où m désigne le nombre de divisions déjà réalisées dans la lignée.
(2) Les règles de transition sont de nature déterministe, selon le principe des L-systèmes sans interaction (context free). Ceci conduit à modifier la théorie des systèmes de transformation basée sur des coefficients de transition fractionnaires [4 (Delattre, p. 24, axiome III ; Chauvet, axiome 5, p. 61)]. En effet, dans un modèle autonome déterministe, toute cellule change d'état à chaque itération temporelle. Nous posons donc, pour la transition cellule juvénile , un coefficient de passage . Cette transition sous-entend a priori un grandissement cellulaire et/ou une maturation. Le devenir d'une cellule mature correspondant à une bifurcation (soit division, soit sénescence), les coefficients de transition de ces deux processus, respectivement et , sont soumis à la condition : . Une cellule mature se divise ou se différencie, mais ne reste pas transitoirement à l'état mature, ce qui correspond à un principe de modèle « sans retard ». Notre modèle se distingue ainsi des systèmes usuels à compartiments tels que divers modèles de populations cellulaires structurées, qui, de plus, doivent préciser le rapport entre le grandissement cellulaire et le changement de classe. C'est le cas, par exemple, du modèle conservatif d'Arino [17], qui repose sur un schéma réactionnel différent du nôtre, où interviennent le substrat (développant le modèle archétype de Monod) et le « type » d'accroissement de la biomasse (soit « intra-classe », soit « hors classe »).
À propos des règles de transition, rappelons que Vitanyi [18] a proposé de formaliser le cursus de croissance d'un filament cellulaire selon deux phases successives : (i) une phase exponentielle strictement autonome correspondant à la grammaire d'un D0L-système (déterministe et sans interaction), (ii) une phase définie par une équation différentielle logistique. Opérant par itération, le D0L-système détermine la réécriture de la séquence cellulaire selon un « temps physiologique ». Au-delà d'un seuil correspondant à la diminution de nutriments, l'intervalle entre deux divisions successives devient variable en termes de « temps physique ». La principale difficulté réside dans la correspondance entre ces deux échelles de temps et dans sa justification.
(3) En conséquence de l'introduction du paramètre , la division cellulaire ne correspond plus à une autocatalyse stricto sensu. En effet toute mitose sur la classe de cellules ne s'accompagne pas, pour les produits, d'un retour sur cette classe (qui est la condition d'existence de l'autocatalyse [19]), mais d'une transition d'une classe m à une classe .
Nous modifierons en conséquence les classes d'équivalence fonctionnelle et le graphe des transformations (Fig. 1) ainsi que les équations de notre modèle précédent [3]. Pour simplifier, nous ferons abstraction de la source S, qui n'est plus ici une variable sujette à déplétion. Deux cas sont à considérer selon que la durée de grandissement – maturation cellulaire avant mitose ( « durée de vie » ou « temps de génération »), c'est-à-dire le nombre d'états cellulaires impliqués, est constant ou non au cours de l'ontogenèse des lignées cellulaires.
1. Durée de vie indépendante de l'ontogenèse
Dans ce cas, le temps de génération cellulaire est fixe pour toute paire de cellules-sœurs, quelle que soit leur occurrence dans la généalogie. Reprenons le cas précédent à trois catégories de cellules (juvéniles, matures, sénescentes). Toute cellule est notée , ; ), où j est l'indice d'état cellulaire, m le nombre de divisions déjà réalisées dans la lignée et λ le nombre maximal de divisions cellulaires, le nombre de classes étant de . Les variables dénommées ci-après désignent respectivement les nombres de cellules de la suite {.
Ainsi, pour les premières classes cellulaires, les transitions s'écrivent :
| (5) |
| (6) |
Les valeurs propres de la matrice des coefficients de ce système sont réelles négatives ou nulles. Il existe donc un état stationnaire stable asymptotique sans oscillations. Cette valeur limite correspond, soit aux différentes classes d'accumulation des cellules inactives (), soit, en absence de sénescence, à la classe terminale .
La vitesse de croissance de la population, en nombre total de cellules , est :
| (7) |
La vitesse de croissance globale ne dépend donc ici que du nombre de cellules matures actives. Cette expression est très différente de l'équation logistique, car elle ne comporte pas de terme explicite de limite. La valeur asymptotique est fonction : (i) de λ, (ii) du coefficient de sénescence , (iii) de l'état initial . En absence de sénescence ou de différenciation () et avec un état initial constitué uniquement de cellules ou (n'ayant encore subi aucune division), la valeur limite de l'effectif total est : . En cas de sénescence (), cette valeur asymptotique est donnée par l'intégration numérique de (6). La forme de la sigmoïde de croissance (en particulier sa dissymétrie) dépend des paramètres et λ ainsi que du nombre d'états cellulaires. La Fig. 2 correspond à ce modèle pour . Dans ce cas, on observe une légère dissymétrie gauche de la courbe de croissance totale de la population : (Fig. 2a). La courbe des variations de la vitesse absolue (Fig. 2c) n'a pas la forme « en cloche » habituelle du modèle logistique. Notons aussi la variation non monotone de la vitesse spécifique de croissance :
Sous forme discrétisée, le modèle a pour matrice de transition ( ; ) :
2. Durée de vie variable au cours de l'ontogenèse
Le temps de génération est une grandeur caractéristique de cinétique cellulaire. Il peut varier considérablement selon les conditions expérimentales, mais aussi, dans un environnement donné, au cours du développement d'une population cellulaire. Le nombre d'états juvéniles, par lesquels toute cellule doit passer avant l'acquisition de la capacité mitotique, est alors fonction du temps, posant : , p étant le nombre total d'états ou classes cellulaires. Plutôt qu'une dépendance temporelle directe, il est intéressant de relier p directement à l'ontogenèse de la lignée, dont le stade de développement peut être défini par le nombre de divisions déjà réalisées. Cette variation ontogénétique du temps de génération peut se schématiser comme suit, en conservant la même règle de dissymétrie des cellules-sœurs :
- • grandissement et maturation :
- • division :
- • sénescence : ;
La cinétique de la population cellulaire dépend essentiellement de λ et de cette fonction du temps de génération. Dans le cas d'une une relation linéaire croissante entre p et m, nous avons le système suivant :
La Fig. 3 donne un exemple avec . Cette cinétique est caractérisée par une structure temporelle à six phases, la croissance débutant par une phase très brève d'accélération positive croissante. Notons également la variation non monotone de .
Comme variante de cette dépendance temporelle de p, l'ontogenèse peut se dérouler en plusieurs phases successives, définies par le nombre d'états juvéniles, par exemple en deux phases respectivement à un et à trois états juvéniles. Les différentes classes cellulaires sont les suivantes :
- •
1re phase : (cellules ayant subi 0, 1 ou 2 mitoses), 1 seul état juvénile :
sénescence :
- •
2e phase : (cellules se divisant trois fois et plus), trois états juvéniles :
sénescence :
Un exemple est donné sur la Fig. 4. Dans ce cas, la courbe de croissance n'a plus la forme sigmoïde classique. Elle présente en effet une irrégularité locale (existence d'une « bosse » entre et ), caractéristique que l'on observe dans diverses courbes expérimentales. La variation de la vitesse globale de croissance n'est pas en forme de « cloche », mais présente deux maximums locaux nets. La structure temporelle présente la particularité de ne pas présenter de phase initiale d'accélération positive croissante.
Un tel type de modèle « flexible » peut donc présenter de nettes particularités dans la cinétique de l'effectif global de la population. Il faut souligner notamment les variations possibles, d'une part, de l'évolution de et, d'autre part, de la structure temporelle, avec une suite de phases, très différente du cas logistique classique à quatre phases (accélération positive croissante puis décroissante, accélération négative décroissante puis croissante). De fait, on observe assez souvent des structures temporelles variées lorsqu'on analyse en détail diverses données expérimentales de croissance.
Remarque. D'un point de vue formel, ce système peut présenter une alternative au modèle multilogistique (somme de plusieurs logistiques non synchrones). Nous avons utilisé celui-ci (sous sa forme bilogistique) pour rendre compte des constantes irrégularités présentées par les courbes de croissance des cellules cladomophores et pleuridiophores de l'algue rhodophycée Antithamnion plumula [22]. Dans ce cas, le principe était d'envisager une somme de deux ou plusieurs composantes, chacune étant afférente a priori à un élément physique donné de la cellule en cours de grandissement (comme les deux zones pariétales d'élongation observées chez Antithamnion defectum [23]). Tout différent, notre présent modèle se fonde sur la possibilité d'un changement ontogénétique des classes d'équivalence et des règles de transition. Nous avons là une dualité d'approche, que l'on peut dénommer respectivement d'ordre spatial (somme de composantes non synchrones pour un modèle multilogistique) et d'ordre temporel ou ontogénétique (variation des durées de maturation cellulaire pour un modèle structuré sur un ensemble d'états de croissance).
4 Conclusion
L'examen comparé de modèles autonomes globaux comme la logistique et de modèles structurés de populations cellulaires nous permet de préciser la notion, qui reste généralement implicite, de limite d'une cinétique de croissance monotone. La structuration est basée sur une suite d'états de croissance, incluant tout processus de sénescence ou de différenciation. La notion de classes d'état est à interpréter dans un sens très large, pouvant correspondre, soit à des états discrets, qualitatifs, soit à un grandissement, chaque classe de cellules juvéniles étant alors définie par un intervalle de dimensions ou de masse. Cette structuration est aisément extensible, sans modification majeure, à la prise en compte d'une mortalité cellulaire (système dit non conservatif).
(1) Dans le cas d'une limite de nature externe (ressources, substrat), nous proposons une reformulation de l'équation logistique de Verhulst. Cette nouvelle équation explicite deux sortes de capacités ou potentialités. À la capacité offerte par le milieu (la carrying capacity classique en dynamique des populations naturelles), il faut associer la potentialité actuelle réelle du système en croissance. Cette potentialité est déterminée par la fraction active du système (Éq. (4)). Seule apte à croître, cette fraction varie elle-même d'une manière non monotone en fonction des transitions entre classes d'éléments.
(2) Avec une limite de nature interne ou endogène, comme la limitation du nombre λ de divisions par lignée cellulaire, la fraction active instantanée de la population totale Y détermine seule la vitesse globale. La valeur limite est directement fonction des conditions initiales , du paramètre λ et de l'occurrence de processus de sénescence ou de différenciation. Différentes modalités cinétiques peuvent se présenter selon les particularités du graphe des transitions, notamment selon que le processus de grandissement–maturation cellulaire préalable à la division (temps de génération) varie ou non au cours de l'ontogenèse. Un tel modèle est susceptible de rendre compte de la diversité des courbes empiriques de croissance, qui ne sont pas toujours de forme strictement sigmoïde, du fait de particularités locales non négligeables. Celles-ci sont clairement explicitées par la notion de structure temporelle, souvent plus complexe que la structure classique de la logistique à quatre phases. La chronologie exacte des variations de l'activité de croissance ainsi révélée constitue une propriété fondamentale du processus de croissance.


