1 Introduction
The notion of global connectivity has played a useful role to understand the physical behavior of network glasses and amorphous thin-films. The idea emerged in an embryonic form in the early seventies as material properties 〚1〛 of the chalcogenides were examined as a function of composition. However, it was not until the early eighties that a theoretical foundation evolved with the recognition that bonding interactions in covalent glasses form a hierarchy, and that nearest-neighbor valence interactions can serve as Lagrangian constraints 〚2〛. This led to the evolution of a mean-field theory of elasticity 〚3〛 and the prediction 〚2, 3〛 of a solitary floppy to rigid phase transition in network glasses, when the number of such constraints/atom, nc, increases to 3. These counting algorithms permit enumerating nc in terms of the mean coordination number, r̄, of a network, and lead to a threshold value of at the rigidity transition first identified 〚2, 3〛 by J.C. Phillips and M.F. Thorpe.
In the past five years, new insights into elastic thresholds have emerged in chalcogenide glasses from theory 〚4〛 as well as experiments 〚5〛. Specifically, Temperature Modulated Differential Scanning Calorimetry and Raman scattering have revealed 〚5〛 not one (transition) but actually two rigidity transitions as discussed elsewhere. The two transitions define the limits of an intermediate phase 〚6〛 that separates the floppy from the stressed rigid phase. It has lead to a structure based classification of glasses in terms of their elastic response: floppy-intermediate-stressed rigid. The novelty as well as challenge of the intermediate phase here is that it is a non-mean-field phase. This new classification is having consequences in a number of diverse fields, including protein folding 〚7〛, phase diagrams of high-Temperature Superconductors 〚8〛, and the phase transition associated with NP-complete problem 〚9〛 in computer science.
Nanoscale phase separation effects can give rise to pronounced changes in physical properties of network glasses such as molar volumes 〚10〛 and optical band gap 〚11〛 near and 2.67. The central issue at hand then is, how are we to distinguish elastic effects from nanoscale phase separation ones? In this work we provide guidance on phase separation effects in glasses. Compositional trends in physical properties of the chalcogenides suggest that rigidity transitions effects are clearly separated from nanoscale phase effects for transitions observed near .
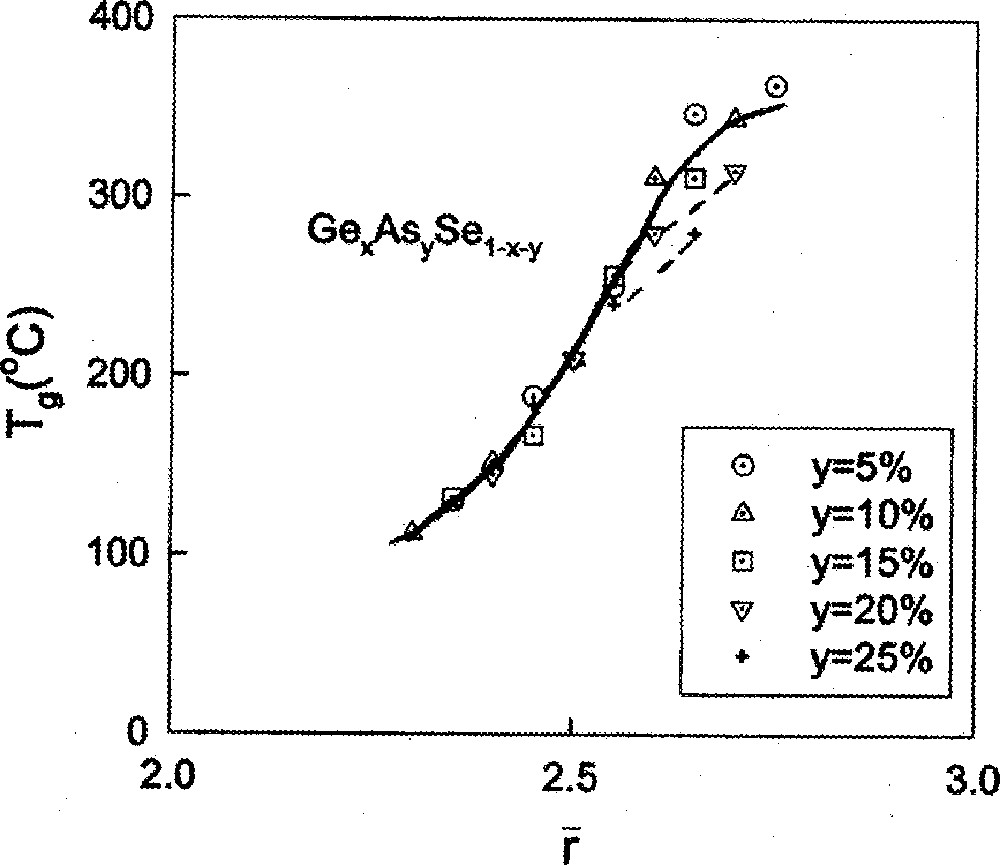
The use of the term nanoscale phase separation in this review is to denote networks that are, in general, partially polymerized with the size of the minority regions not to exceed 100 nm typically. Such glasses display a single glass-transition temperature Tg. These are to be contrasted from macroscopically heterogeneous glasses displaying bimodal Tgs in which the phases could extend to microns in size. This review is structured as follows. In section 2, we summarize ideas on the connection between Tg and network connectivity. In section 3, we provide thermal and spectroscopic evidence that shows As- and Ge–based stoichiometric chalcogenide glasses nanoscale phase separate near and 2.67, respectively. On the other hand, such effects are suppressed qualitatively due to chemical disorder in ternary (As or P)xGexSe1–2x glasses containing equal concentrations of the group IV and V elements. In these ternaries, rigidity transition effects are observed near , as discussed in sections 4 and 5, respectively. However, the molecular origin of physical anomalies near is better understood as due to nanoscale phase separation rather than a rigidity transition associated with a dimensionality change as has been proposed 〚12〛.
2 Nanoscale phase separation and threshold behavior of Tg
One usually estimates the global connectivity of a network in terms of its mean coordination number, r̄, by weighting the coordination numbers of constituent atoms in proportion to their concentrations in a network. Thus, for the case of the binary Asx(Se or S)1–x glasses, the mean coordination number r̄ becomes:
The linear increase in (equation (2)) suggests that the global connectivity of these binary glasses increases monotonically with x. The mathematical construction however does not insure that such is the case in these binary glasses at all x. How are we then to decide if the global connectivity of a glass network continues to increase, or does the network actually nanoscale phase separate at some threshold concentration of As? In principle, the direct answer would appear to be to examine the molecular structure of glasses in diffraction or electron microscopy measurements. Unfortunately, even in crystalline solids detection of nanoscale phase separation effects by structure methods has proved to be rather difficult. In the case of disordered systems the approach poses formidable challenges. An alternative but well-grounded approach comes from examining compositional trends in the glass-transition temperature, Tg(x). Although Tg of a glass is widely ascribed to kinetics 〚13〛 of cooling, the experimental fact remains that alloying or glass structure effects produce far larger changes in Tg than kinetic ones.
There is growing recognition that Tg is an excellent measure of global connectivity of a glass network. The idea forms the basis of stochastic agglomeration theory 〚14, 15〛, which permits calculating changes in Tg as a function of network cross-linking or chemical composition. The theory has successfully provided a formal derivation 〚15〛 of the Gibbs–Di Marzio phenomenological relation 〚16〛 that describes increases of Tg in polymers as a function of cross-linking. In the stochastic limit, the results of these combinatorial calculations are found to be in excellent agreement with results on the group IV selenides (Fig. 1). The observed slope, dTg/dx, in both SixSe1–x and GexSe1–x glasses at low x (< 0.10) where agglomeration effects are considered to be stochastic, is in excellent accord with the parameter-free value of this slope,
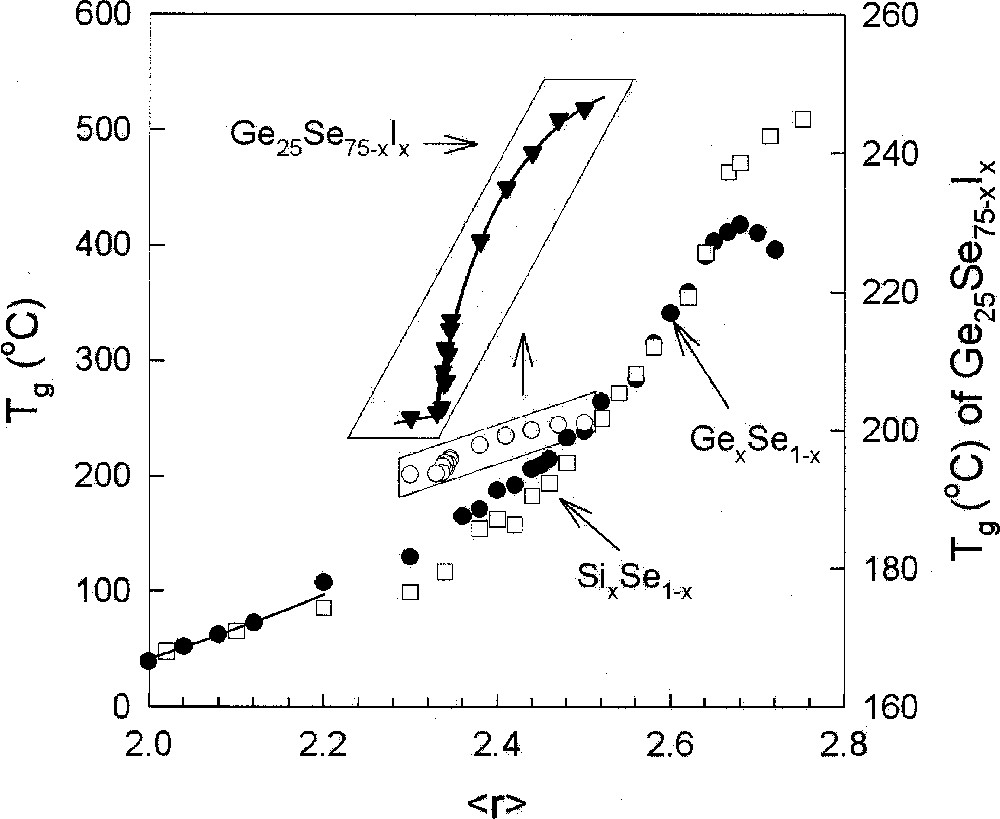
Compositional trends in Tg in binary SixSe1–x (□) and GexSe1–x glasses (•), and ternary Ge25Se75–xIx glasses (○ or ▾) plotted as a function of r, taken from refs 〚5〛, 〚54〛, and 〚58〛, respectively. The sharp decrease in Tg for the ternary (inset) occurs near r = 2.34, the rigidity transition.
Experiments on AsxSe1–x 〚17–19〛 (Fig. 2) and AsxS1–x 〚17, 20, 21〛 (Fig. 3) glasses show that in the 0 < x < 0.40 range, Tg(x) increases monotonically with x. We can understand the behavior in terms of the Se-chain network becoming progressively more connected as As-centered pyramidal units emerge. The process of cross-linking Se chains clearly saturates near x = 0.40. At higher x (> 0.40), Tgs are found to decrease progressively, suggesting that now the global connectivity of the glass network apparently decreases as the As content of the glasses increases. The As–As bonds that appear in the network at x > 0.38, apparently do not form part of the backbone of the network. Raman scattering experiments in both As–Se 〚22〛 and As–S 〚20〛 glasses show the evolution of As4Se4 and As4S4 monomers in corresponding glasses once x > 0.38. These monomers grow in concentration at the expense of the backbone of the network, thus lowering the connectivity of the network globally. We thus arrive at the notion that the microscopic origin for the reduction of Tg at x > 0.40 is nanoscale phase separation of the network. Indeed the existence of a threshold of Tg near x = 0.40 constitutes evidence of nanoscale phase separation in both these binary glasses.
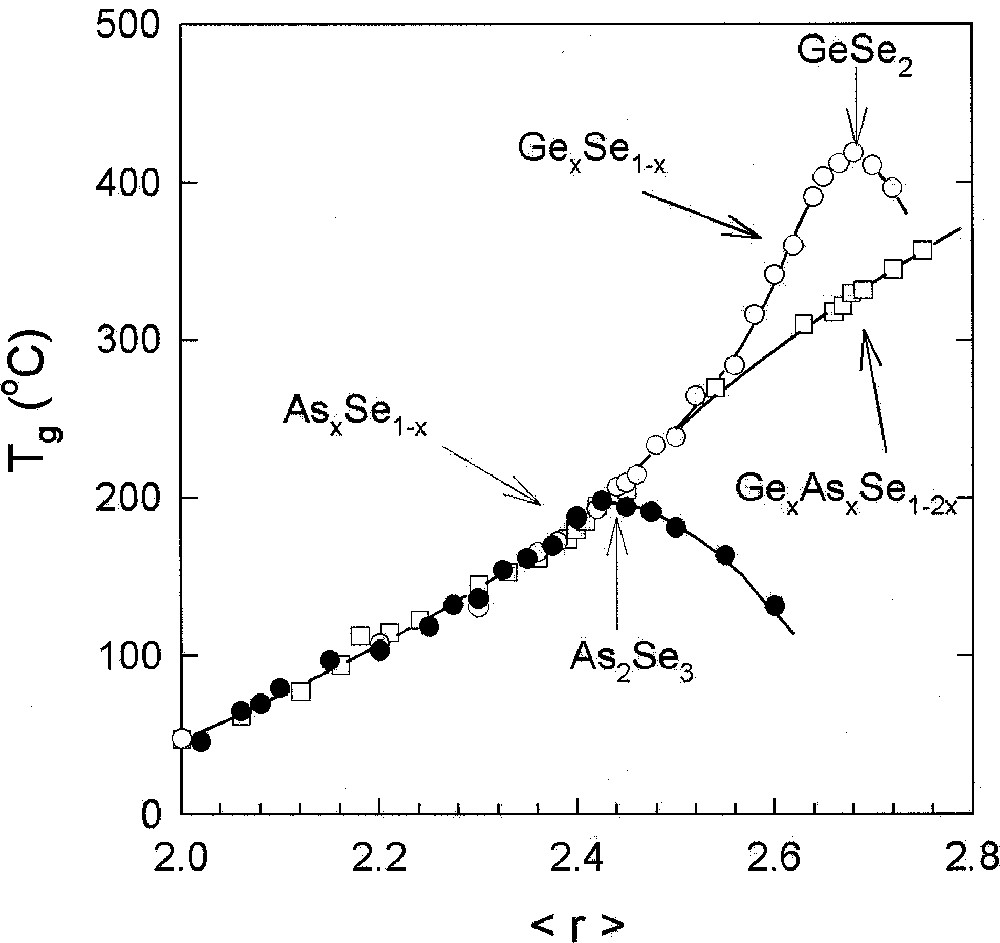
Compositional trends in Tg in AsxSe1–x (•), GexSe1–x (○) and AsxGexSe1–2x (□) glasses plotted as a function of r, the mean coordination number taken from refs 〚19〛, 〚54〛, and 〚39〛, respectively.
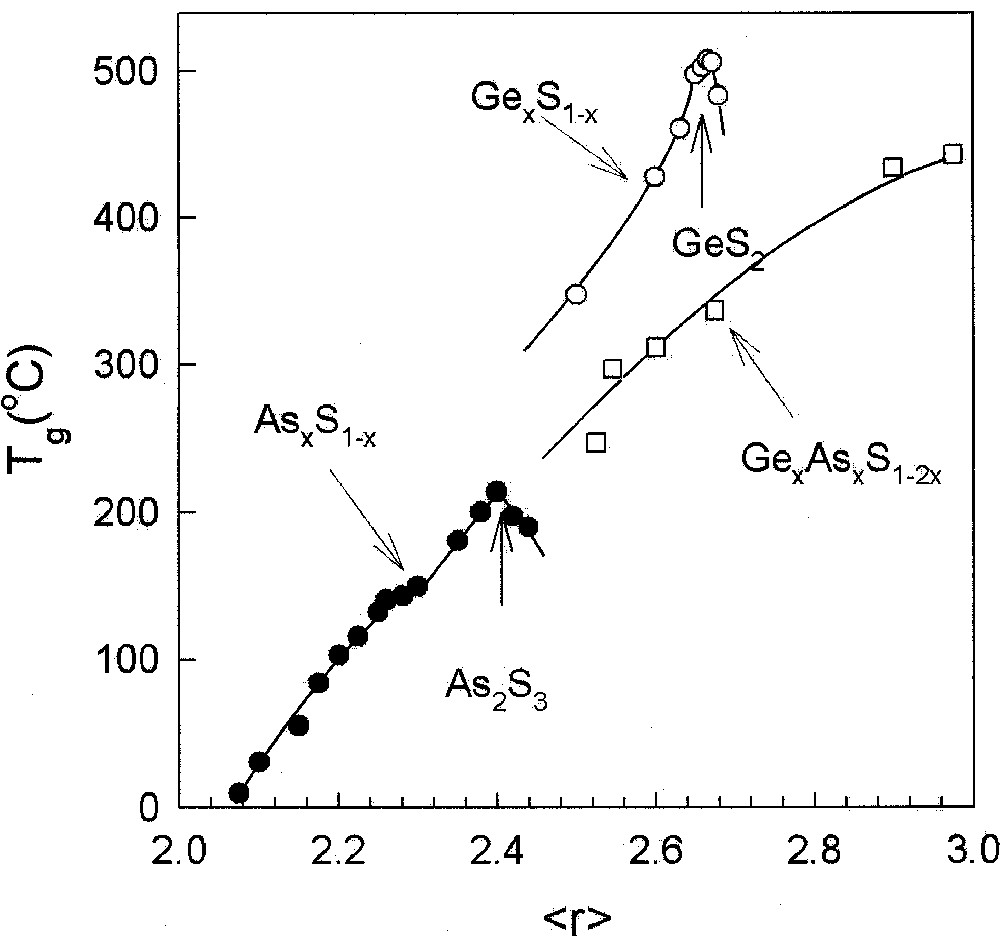
Compositional trends in Tg in AsxS1–x (•), GexS1–x (○) and AsxGexS1–2x (□) glasses plotted as a function of r, the mean coordination number taken from refs 〚20〛, 〚38〛, and 〚41〛, respectively. The Tg results on the ternary are from DSC measurements taken from ref. 〚41〛, while the other set of results are from MDSC.
A similar result is observed in binary PxSe1–x glasses 〚23, 24〛, where Tgs are found to increase in the 0 < x < 0.50 range and then to plummet rather sharply once x > 0.50 (Fig. 4) as P4Se3 monomers emerge in the glasses. Not only do Tgs decline to room temperature and below, but the glass forming tendency is found to nearly vanish near x = 0.57, when a crystalline molecular solid composed of P4Se3 cages is formed even upon a water quench of melts.
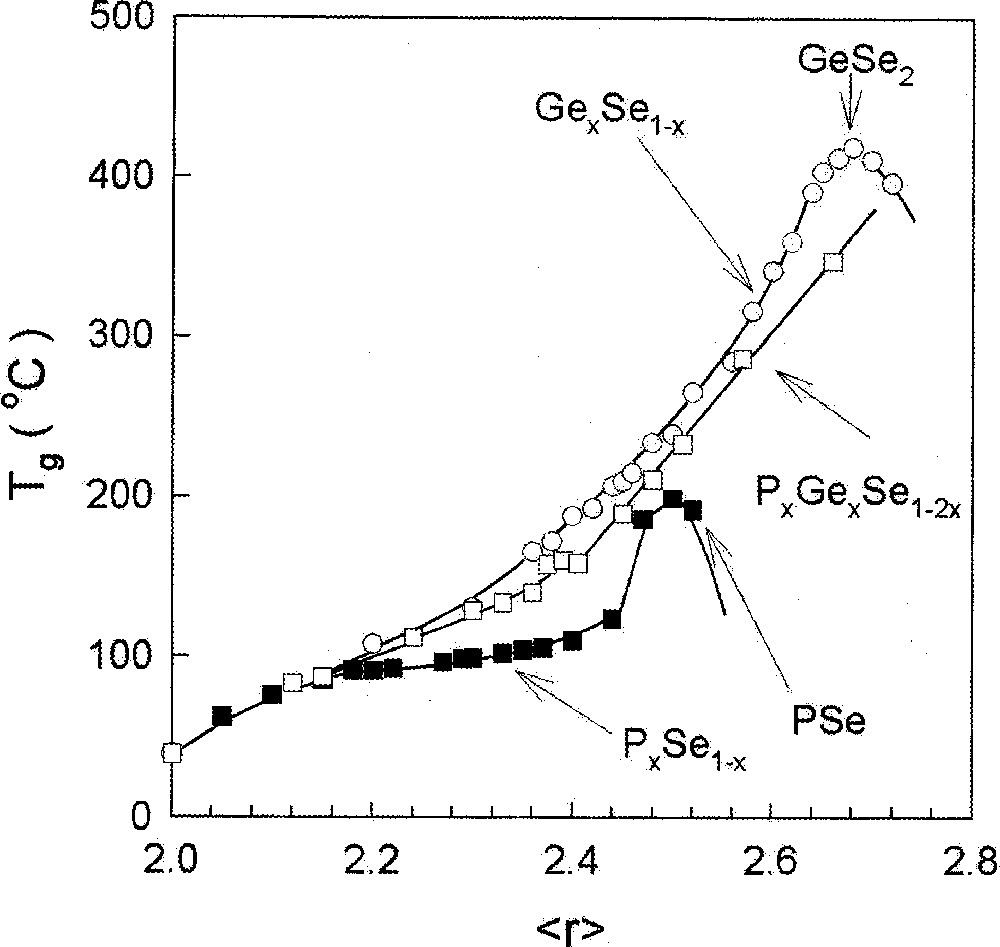
Compositional trends in Tg in PxSe1–x (■), GexSe1–x (○) and PxGexSe1–2x (□) glasses plotted as a function of r, the mean coordination number taken from refs 〚24〛, 〚54〛, and 〚43〛, respectively.
2.1 Tg and the role of chemical bond strengths
A correlation between compositional trends in Tg and average chemical bond strengths in chalcogenide glasses was noted by Tichy and Ticha 〚25〛. Chemical bond strengths play a scaling role in determining Tgs, when comparing networks having the same global connectivity (r̄), such as GeS2 with GeSe2, or As2S3 with As2Se3. However, such chemical considerations alone cannot account for the observed changes in Tg as a function of r̄, which are structure-related. Two examples would serve to make the case. In binary As–S glasses Tg(x) are found to increase 〚20〛 monotonically (Fig. 3) with x in the 0 < x < 0.40 range. Pauling single bond strength 〚26〛 of a S–S bond of 50.9 kcal mol–1 exceeds that of As–S single bond of 47.25 kcal mol–1. Indeed, if average bond strengths alone were to determine Tgs of AsxS1–x glasses as has been suggested 〚25〛, one would expect Tg to decrease with the As content x. On the other hand, the observed increase of Tg with x is precisely the behavior one expects as the S-chain network is progressively cross-linked by As resulting in an increase of the global connectivity in the 0 < x < 0.40 range.
Fig. 1 compares compositional trends in Tg in the Ge–Se binary 〚27〛 with the Si–Se one 〚28〛. The glaring difference between these trends is the presence of a threshold in Tg near x = 1/3 or in the Ge–Se binary, but the absence of it in the Si–Se binary. The Pauling single bond strength 〚26〛 of a Ge–Se bond exceeds that of a Ge–Ge bond by 11.5 kcal mol–1, while that of a Si–Se bond exceeds that of a Si–Si bond by 9.2 kcal mol–1. If average bond strengths alone were the factor controlling compositional trends in Tg, one would be hard pressed to understand why Tgs decline at x > 1/3 in the Ge–Se binary, but increase at x > 1/3 in the Si–Se binary, when weaker homopolar bonds (Si–Si, Ge–Ge) emerge in both systems.
The Tg trends above are precisely the ones expected if Ge–Ge bonds were to segregate 〚29〛 from the Ge–Se backbone to nucleate a separate Ge-rich nanophase, and thus lower the global connectivity, while Si–Si bonds were to form part 〚30〛 of the Si–Se backbone and increase its global connectivity, and thus Tg of the glasses. Si–Se melts at x > 1/3 possess astronomically high viscosities 〚30〛 understandably because of the fully polymerized nature of the underlying backbones. The case of the SixSe1–x binary glass system at x > 1/3, is the exception that proves the rule that Tgs are a good representation of network connectivity with chemical bond strengths playing the role of scaling these numbers between networks of similar global connectivities.
2.2 The vibration iso-coordination rule
Inelastic neutron scattering studies on ternary AsxGeySe1–x–y glasses have proved an elegant probe of the low frequency vibrational density of states (VDOS) 〚31, 32〛. The excitations in the 5 meV region are usually identified with floppy modes 〚32〛 in undercoordinated networks. Effey and Cappelletti have found 〚33〛 scattering strength of these excitations to be strictly controlled by the global connectivities of glasses as measured by their mean coordination number, , and to be independent of chemical compositions so long as . A parallel result was noted for vibrational lifetime of a H2O guest molecule in these glasses, which increased 〚34〛 monotonically with r̄, regardless of chemical composition. These results support the notion that at low r (< 2.4), the Se-rich glasses are fully polymerized and continue to be so as the group IV and V elements are added to increase global connectivity of the backbone.
A striking exception to this rule emerged in binary AsxSe1–x glasses at x = 0.6, for which the low frequency VDOS are found to be characteristic of a floppy glass () even though the chemical composition suggests a rigid glass (). In the neutron VDOS 〚32〛, sharp modes are observed between 10 and 20 meV. These modes have contributions from characteristic As-rich clusters (As4Se4 and As4Se3) and amorphous As, for which confirmation is given by FT-Raman measurements 〚22, 35, 36〛. The sharpness of the modes suggests that these As-rich clusters are decoupled from the backbone. The exception to the vibration isocoordination rule falls in line with the sharply reduced glass transition of this composition 〚32, 19〛. These results are consistent with nanoscale phase separation of this As-rich glass.
3 Stoichiometric binary chalcogenide glasses and nanoscale phase separation effects
The threshold behavior in Tg observed in binary GeySe1–y and AsxSe1–x glasses, near y = 1/3 and x = 2/5, respectively, as discussed in section 2, we therefore take as evidence for nanoscale phase separation of these stoichiometric glasses. Insights into the molecular structures responsible for this phase separation emerge from Raman and Mössbauer spectroscopy results 〚20, 29〛.
In binary Ge–Se glasses, Raman scattering measurements (Fig. 5a) show 〚29〛 evolution of a mode at 178 cm–1 first emerges 〚29〛 near a threshold composition of x = 0.32. The mode is identified with presence of ethanelike Ge2(Se1/2)6 units. In 119Sn Mössbauer spectroscopy (Fig. 5b), a non-tetrahedral site is found to first emerge near the same threshold of x = 0.32. The site is assigned to Sn present in ethanelike units. The slope, dTg/dx, decreases sharply once these non-tetrahedral local units first appear in the network. This is not a coincidence. The reduction in the slope dTg/dx, once these Ge–Ge bonds first appear in the glass suggests that these bonds do not form part of the backbone, in other words the ethanelike units form a separate nanophase from the backbone. The backbone here comprises of corner- and edge sharing tetrahedral Ge (Se1/2)4 units. A parallel result is found in GexS1–x glasses 〚37〛 near x = 0.32, as discussed in recent work 〚38〛.
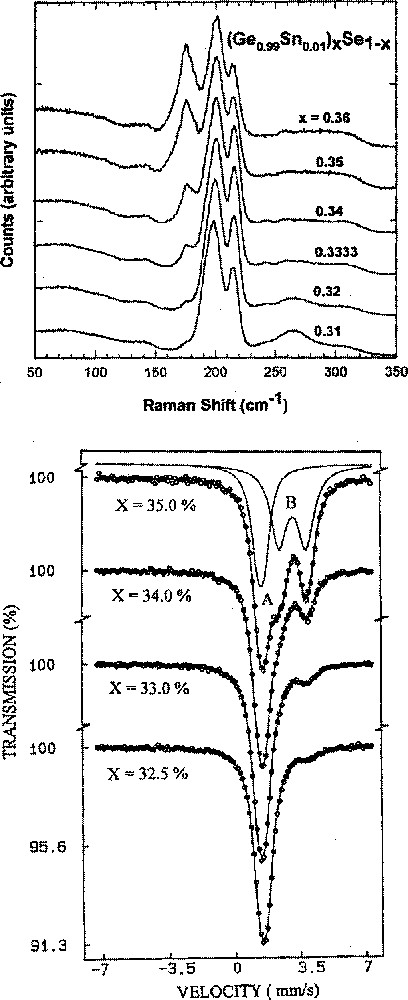
(a) Raman scattering (b) and 119Sn Mössbauer spectra of (Ge0.99Sn0.01)xSe1–x glasses showing respectively evolution of the 178–cm–1 mode and the B-site quadrupole doublet as a function of x starting from x = 0.32. Results taken from ref. 〚?〛. Both spectroscopic features are ascribed to ethanelike units populated in the network.
Raman scattering in AsxS1–x glasses near x = 2/5 taken from ref. 〚20〛 are reproduced in Fig. 6. Noteworthy in the lineshapes is the emergence of sharp modes labeled R once the As content exceeds approximately of 0.38. These modes are identified with Realgarlike modes, i.e. As4S4 monomers, that apparently nucleate in the binary glasses once x exceeds 0.38. The sharpness of these Realgar modes is due to the fact that these units are decoupled from the backbone, suggesting that the stoichiometric glass is nanoscale phase separated.

Ramanline deconvolution of bulk AsxS1–x glasses at indicated compositions showing modes of orpimentlike (○) and Realgarlike (R) phases taken from ref. 〚29〛. The spectra were obtained using 647-nm excitation in a macro-Raman configuration at room temperature.
4 Absence of nanoscale phase separation in ternary Gex(As or P)xSe1–2x glasses
The titled ternary glasses are of general interest because compositional trends in Tg(x) in these systems (Figs. 2 and 4) display a monotonic increase 〚39, 40〛 with x, even when . The behavior is in sharp contrast to the threshold in Tg observed 〚19, 29〛 in corresponding binary (As–Se, Ge–Se) glasses. A parallel Tg result is found 〚40〛 in the Ge–As–S ternary when compared to corresponding binary glasses (Fig. 3). In these ternary glass systems, there is an equal concentration of the group IV and V additives, which leads to a mix of As-centered pyramids with Ge-centered tetrahedra. The mix promotes chemical disorder and suppresses nanoscale phase separation effects even as the additive concentration increases as reflected in the monotonic increase of Tg. These glass systems are thus ideal to examine rigidity percolation effects.
The PxGexSe1–2x ternary displays compositional trends in Tg that show an almost linear increase in the range 〚42, 43〛 suggestive of increased global connectivity as a function of r̄ even at . Aspects of glass molecular structure that lead to such a behavior are currently less well understood. The P-centered structures in these glasses were probed in 31P NMR measurements 〚42〛. The subject is currently under investigation by Raman and Mössbauer spectroscopy measurements 〚43〛 that are providing valuable information on the nature of the Ge-centered and Se-centered structures. There are striking similarities as well as glaring differences in the structure of the P-based ternary glasses from the corresponding As-based ones. For example, in MDSC measurements of the P-based glasses, one observes a sub-Tg endotherm 〚43〛, which is not observed in corresponding As-based glasses. These aspects of structure are currently under investigation.
Vibrational temperatures of 119Sn sites in ternary As–Ge–Se glasses
We have examined Ge-centered local structures in the As-Ge–Se ternary in Raman scattering and 119Sn Mössbauer spectroscopy 〚44〛 measurements. In Raman scattering, one observes modes of corner-sharing and edge-sharing Ge(Se1/2)4 tetrahedra to emerge with increasing x. At higher x (x > 0.21) modes of ethanelike Ge–Ge units manifest in the lineshape. In Mössbauer spectroscopy 〚44〛, tetrahedral Sn sites (labeled A) appear in the Se-rich 0 < x < 0.18 glasses, but non-tetrahedral Sn-sites (labeled B) to first appear once x > 0.18 in Ge-rich glasses as shown in Fig. 7. These non-tetrahedral sites constitute signature of Ge–Ge bonds in the network 〚45〛. Simple counting arguments reveal that a chemical threshold occurs at xc = 0.182 above which Ge–Ge bonds are expected.
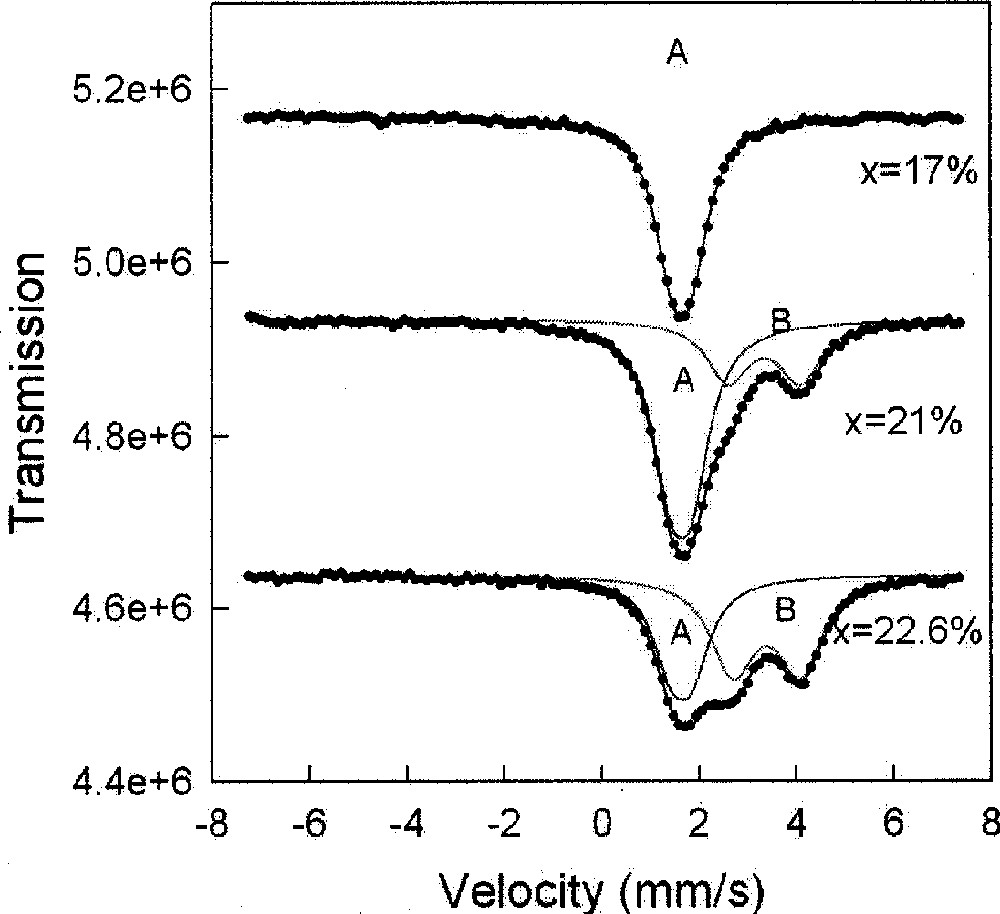
119Sn Mössbauer spectra of ternary GexAsxSe1–2x glasses at indicated compositions x, showing tetrahedrally coordinated Sn sites (A) and non-tetrahedral sites (B), when x > 0.18. The B sites represent signature of Ge–Ge bonds emerging in the network. Figure taken from ref. 〚29〛.
Lamb–Mössbauer factors of the A and B sites have been measured 〚44〛 by recording spectra of glasses at x > 0.18 as a function of temperature. From these results we obtain the vibrational temperature (effective Debye Temperature) of the A and B sites. Results of these experiments show that their vibrational temperatures are and i.e., about 15 K apart. We had performed similar measurements in binary GexSe1–x glasses earlier 〚32, 46〛, and found vibrational temperatures of these two sites, , and , to be 30 K apart in these nanoscale phase separated materials. Thus, vibrational temperatures of chemically inequivalent sites in nanoscale-phase separated glasses differ significantly more than in homogeneous glasses reflecting the intrinsic heterogeneity of the former systems.
5 Alloying behavior of Sb and As additives in chalcogenide glasses contrasted
New insights into the chemical alloying behavior of pnictide additives in chalcogenide glasses have emerged from the compositional variation of Glass-transition temperatures. In this section we discuss the alloying behavior of Sb and separately As in GexSe1–x glasses.
5.1 Glass-transition temperature variation in the GexSbySe1–x–y ternary
In an impressive set of measurements of Tg and molar volumes in the titled ternary, Mahadevan and Giridhar 〚47〛 found that the threshold behavior of near observed at y = 0, i.e., binary GexSe1–x glasses (Fig. 2), shifts rather systematically (Fig. 8a) to lower values of r̄ as the Sb content (y) of titled ternary glasses increases in the 0 < y < 0.25 range. The existence of this threshold shift suggests nanoscale phase separation must occur. For a trivalent pnictide on strictly chemical grounds, one can always write:

a. variation in ternary GexSbySe1–x–y glasses showing the threshold behavior in Tgs to systematically move to lower r̄ values as the indicated Sb concentrations (y) are increased. The figure is taken from ref. 〚47〛. b. The predicted variation in the threshold value of r̄ from a nanoscale phase separated model developed here and the observed threshold value of r̄ taken from ref. 〚47〛.
In the present case, however, the first and second terms on the right hand side of equation (4) describe, respectively, the Sb-rich nanophase that segregates from the base glass phase. Because of such separation, the base glass can nanoscale phase separate 〚29〛 when the Ge/Se stoichiometry ratio exceeds the threshold value of , i.e.:
Thus, for a given Sb content (y), equation (5) serves to define a critical mean coordination number:
5.2 Glass-transition temperature variation in the GexAsySe1–x–y ternary
A very different physical picture of alloying As as opposed to Sb in Ge–Se glasses emerges from Tg trends of the GexAsySe1–x–y ternary. The threshold behavior of Tgs so characteristic 〚29〛 of the base glass (Ge–Se) near , is no longer observed when as little as 5 atomic percent of As is alloyed, as shown in Fig. 9. The results of Fig. 9 taken from ref. 〚47〛 are based on the work of Borisova 〚48〛 and Frischat 〚49〛. These trends suggest that As(Se1/2)3 pyramids now mix on a molecular scale with corner- and edge-sharing Ge(Se1/2)4 tetrahedra, and suppress nanoscale phase separation of the backbone. Ge–Ge bonds must still form at high r̄, but they apparently do so as part of the main backbone, as noted earlier (section 4) for the case when x = y, in the Ge–As–Se ternary.
variation in ternary GexAsySe1–x–y glasses taken from the work of Z.U. Borisova 〚48〛.
With increasing As concentration y in the Ge–As–Se ternary, one also notes that the Tgs increase (Fig. 9), but more slowly with r near 2.67, i.e. the slope decreases. Important insights into the slopes dTg/dr emerge from the stochastic agglomeration theory 〚14〛, which relates these to the number of ways building blocks (tetrahedra and pyramids) can agglomerate. Specifically, if there are several types of building blocks that can couple in many ways, the underlying entropy of mixing increases, and the calculations reveal 〚50〛 the slope dTg/dr to invariably decrease. The pattern is also observed in binary glasses (Fig. 1), when one contrasts results on the two families of group IV selenides. For example, the slope near for SixSe1–x glass is less than for GexSe1–x glasses, probably because of a substantially larger concentration of edge-sharing tetrahedra in the Si-bearing glasses than in the Ge-bearing ones.
6 Rigidity transitions in network glasses
One of the success stories to emerge in glass science in the past two decades is the existence of elastic phase transitions as a function of connectivity of networks. These phase transitions have led to a structure based classification of glasses in terms of their elastic response 〚4, 6〛 as floppy-intermediate- stressed rigid.
6.1 Discovery of the intermediate phase
Although the existence of floppy and rigid phases was recognized starting in the mid eighties 〚32, 51, 52, 53〛, it was not until 1999 that experimental evidence for intermediate phases evolved 〚5, 28, 54〛. These phases evolve in between floppy (nc < 3) and stressed rigid (nc > 3) phases, and their widths provide a measure of the degree of self-organization of a glass network. The widths of Intermediate Phases are apparently controlled by local and medium range structures that are stress-free. These phases were first observed in Raman scattering experiments on IV–VI binary glasses 〚27, 28, 54〛, wherein mode frequency (squared) variations as a function of r̄ display distinct power-laws.
An important development in identification of intermediate phases has been the application of T-modulated Differential Scanning Calorimetry (MDSC) 〚55, 56〛. The method permits deconvoluting the heat flow endotherm near Tg into two parts, a reversing heat flow and a non-reversing heat flow. The reversing heat flow is the fraction of the heat flow that tracks the programmed T-modulations and shows a text book glass transition on a flat baseline, independent of the instrument baseline. It permits a reliable scan rate and thermal history independent measurement of Tg. All (MDSC) Tg results reported in Figs. 1–4 were obtained from the inflexion point of the reversing heat flow using a model 2920 unit from TA Instruments, Incorporated at 3 °C min–1 scan rate and 1 °C/100 s modulation rate. In these scans, the non-reversing heat flow signal usually displays a peak as a precursor to the actual glass transition. In fully relaxed samples, the area under the peak provides the latent heat of melting of a glass and will henceforth be noted as the non-reversing heat.
The novelty of the intermediate phase is that mean-field theories cannot access it 〚4〛. It is a rigid but stress-free phase of a glass. Glasses in the intermediate phase possess some very unusual physical properties including the near absence of a latent heat of melting. In other words, glasses (T < Tg) in these phases possess a configurational entropy that is nearly the same as in corresponding melts (T > Tg). This is revealed by the near absence of the non-reversing heat flow in MDSC measurements. Experiments on several glass systems have now been documented, and the results show the optical elastic thresholds to coincide 〚28, 54〛 with the thermal ones. To keep our discussion brief, we will therefore restrict to thermal thresholds, which can thus serve as a convenient probe of the rigidity transitions in glasses.
6.2 Thermally reversing windows in network glasses and rigidity transitions
Compositional trends of the non-reversing heat flow in binary SixSe1–x 〚28〛 and ternary Ge0.25S0.75–yIy 〚57〛 glasses appear in Fig. 10a. Noteworthy in these trends is the squarewell-like behavior observed in the binary glass. The intermediate phase here extends from xc(1) = 0.20, or to xc(2) = 0.26 or , with glass compositions at x < xc(1) reckoned as floppy, while those at x > xc(2) as stressed rigid. The situation is replicated in the companion GexSe1–x glasses as discussed 〚54〛 elsewhere.
Compositional trends of the non-reversing heat flow in (a) the SixSe1–x binary, the Ge0.25Se0.75–yIy ternary, and (b) the AsxSe1–x binary glasses, revealing thermally reversing windows of varying widths and centroid. These windows are identified with intermediate phases.
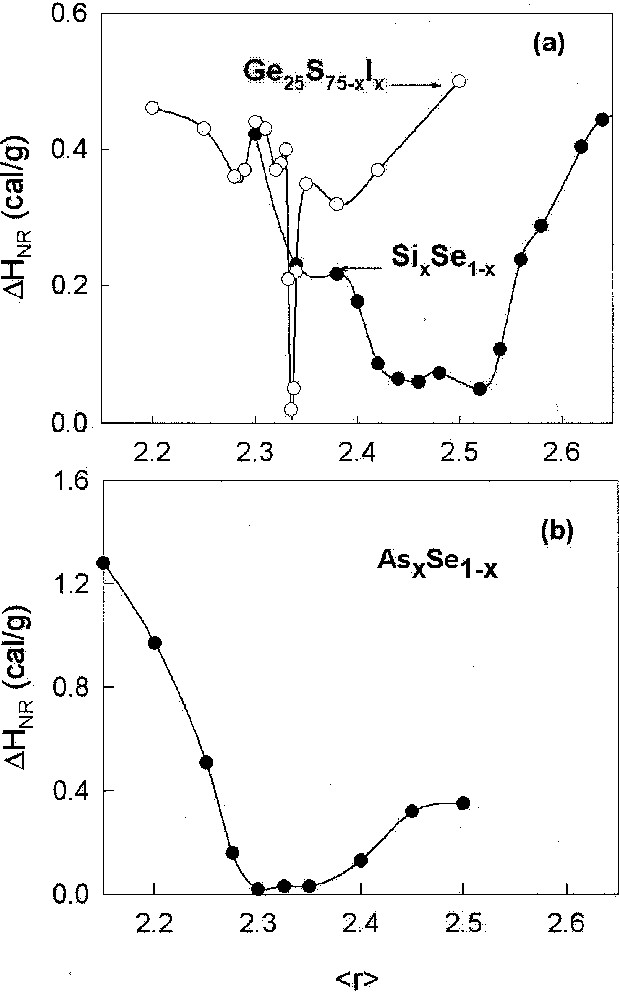
The case of the Ge–S–I ternary 〚57〛 is profound, because in this case the upper and lower bounds of the intermediate phase coincide, giving rise to a narrow peak in the non-reversing heat centered near r = 2.34. This is a remarkable result because it corresponds exactly to the value of r̄ where mean-field theory predicts the floppy to rigid transition to occur. A parallel circumstance occurs in the Ge–Se–I ternary 〚58〛. In Fig. 1, we note that Tgs in the Ge–Se–I ternary show a precipitous drop near , signaling the sharp rigid to floppy transition. The agreement between theory and experiment here is unparalleled in glass science. It raises the broader issue why does mean-field theory work so well in these ternary glasses when it completely breaks down in binary Ge–Se, and Si–Se glasses. The answer rests in the recognition that Iodine alloying randomly cuts S or Se bridges of the backbone, and the replacement inhibits the medium-range structure of the backbone in the form of rings to form. Constraint counting algorithms do not distinguish between S and Se in these glasses. Taken together, these results serve to demonstrate that the physical origin of the observed effects must indeed stem from rigidity effects.
Compositional trends in the non-reversing heat flow in binary AsxSe1–x glasses 〚19〛 appear in Fig. 10b. Here the intermediate phase is localized between c(1) = 0.27 or and xc(2) = 0.38 or . This is also a fascinating result because it opens new ground. The result is inconsistent 〚19, 59〛 with the conventional picture of only pyramidal As-centered local structures present in the molecular structure of these Se-rich glasses. The downshift of the window onset to that we have suggested 〚19〛 is consistent with inclusion of quasi-tetrahedral As-centered local Se=As(Se1/2)3 units in the structure of these glasses. In this case, MDSC measurements through the non-reversing heat flow have yielded a new feature of local structure that was apparently not recognized in earlier structure studies.
In all the three cases discussed above, it is noteworthy that rigidity transitions occur at ranges of r̄, below the regime where nanoscale phase separation effects manifest. These rigidity transitions are thus quite distinct from nanoscale phase separation effects.
6.3 The very special case of ternary AsxGexSe1–2x glasses
The glass-forming region 〚48〛 in the As–Ge–Se ternary appears in Fig. 11. The hashed marked region shows the opening of the intermediate phase in between the stressed rigid and the floppy phases. The region straddles compositions near shown as a broken tie-line connecting the binary compositions, GeSe4 with As2Se3. Also shown in Fig. 11 are the regions (shaded) of glass formation where nanoscale phase separation effects manifest. Such effects are largely localized along the binary rich compositions, and for that reason even ternary compositions that are either As-rich or Ge-rich display features characteristic of nanoscale-separated glasses.
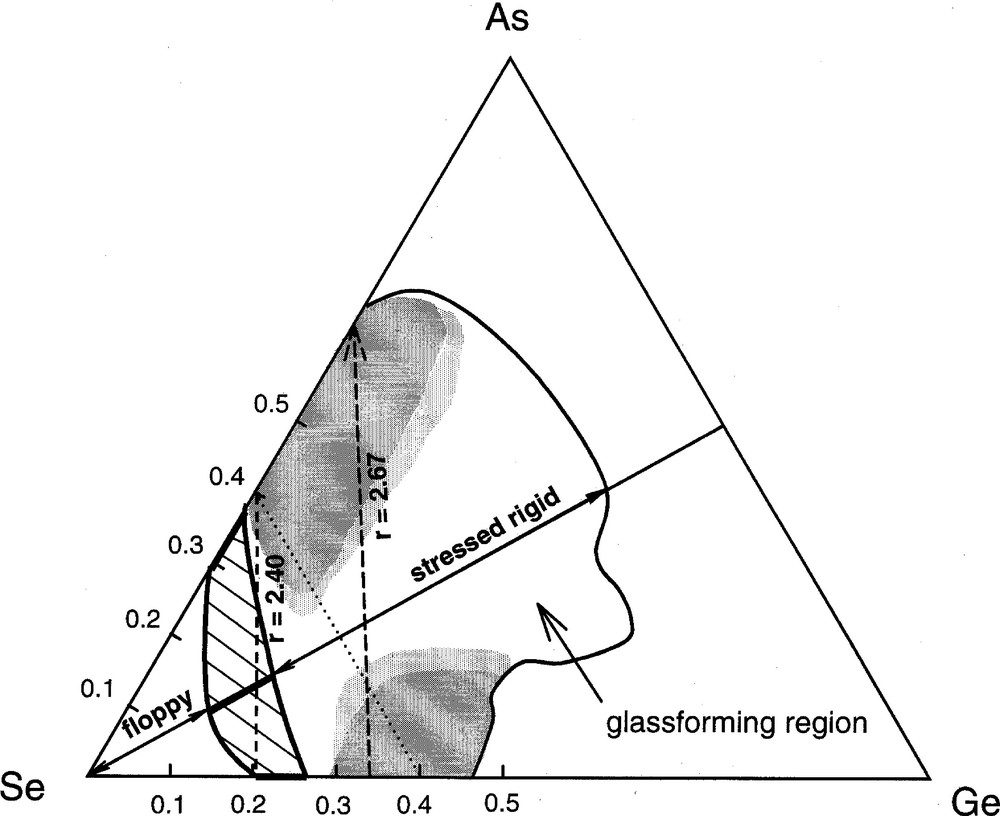
Glass-forming region in the As–Ge–Se ternary taken from ref. 〚48〛. The hashed marked region straddling the isocoordination line r = 2.4 represents the evolution of the intermediate phase in between the floppy (left) and the stressed rigid phase (right). The shaded regions reflect compositions where glass networks are viewed to be nanoscale phase separated. These regions overlap with the r = 2.67 isocoordination line near the Ge-rich and As-rich compositions. The dotted line describes the As0.4Se0.6 join to Ge0.4Se0.6.
Compositional trends in the non-reversing heat flow in ternary AsxGexSe1–2x glasses 〚39〛 appear in Fig. 12. The intermediate phase in this case extends from xc(1) = 0.10 or rc(1) = 2.30 to xc(2) = 0.155 or rc(2) = 2.46. This is a rather broad range, and it encompasses the intermediate phases of both the Ge–Se and the As–Se binary glasses. The width of the intermediate phase suggested from these thermal measurements, has recently been refined from the more precise Raman scattering measurements 〚44〛 and will be discussed in a forthcoming publication.
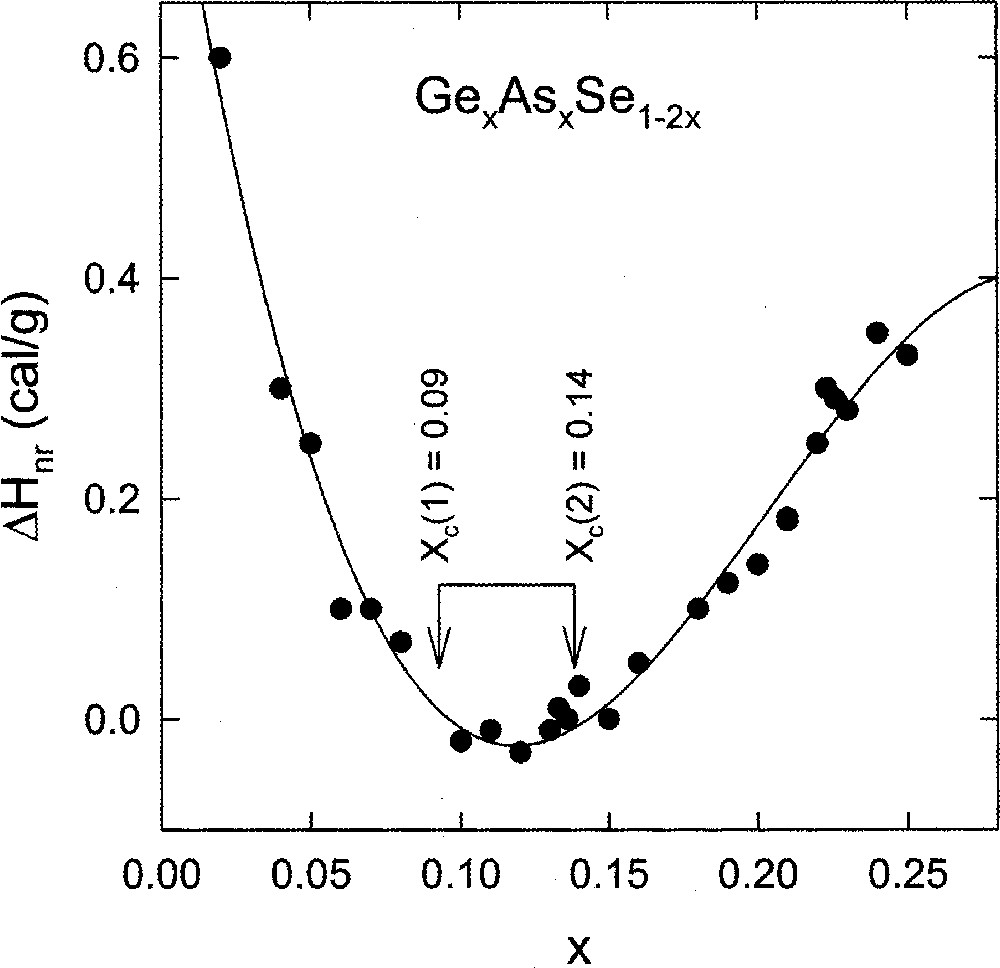
Compositional trends in non-reversing heat flow in ternary GexAsxSe1–2x glasses revealing a wide thermally reversing window with an onset near xc(1) = 0.09 or rc(1) = 2.27 and an end near xc(2) = 0.14 or rc(2) = 2.42. There is no evidence of any anomalies near r = 2.67 or x = 0.22.
6.4 Electrical and phonon transport in ternary GexAs0.40–xSe0.60 glasses
Several groups have examined thermal and electrical transport in ternary GexAs0.40–xSe0.60 glasses and amorphous thin films, and rather complete results are now available for discussion. To orient the reader, it might be well to mention that this ternary joins the two binary end member compositions, As0.40Se0.60 and Ge0.40Se0.60, and furthermore it intersects the GexAsxSe1–2x ternary (Fig. 11) of interest at right angles at x = 0.20. The line composed of points spans compositions in this ternary, as shown in Fig. 11. Thermal diffusivities, (α(x)), of bulk GexAs0.40–xSe0.60 glasses and their S-counterparts were examined over the 0 < x < 0.40 range by Velinov et al. 〚60〛. They showed α(x) to display a global minimum near x = 0.15 for the selenide glasses, and near x = 0.18 for the sulfide glasses. Dark electrical conductivities, σd(x), in carefully annealed selenide thin-films over the full range (0 < x < 0.40) of compositions were studied by Nesheva and Skordeva 〚61〛. Their results show a rather spectacular narrowly defined deep global minimum in σd(x) near x = 0.22.
The end member compositions of the GexAs0.40–xSe0.60 ternary are intrinsically nanoscale phase separated (Fig. 11). The molecular structure of Ge0.40Se0.60 glass inferred from Raman scattering and Mössbauer spectroscopy measurements has shown 〚46, 62〛 that it consists of two nanophases, an ethanelike phase and a distorted rocksalt phase. In section 2, we have discussed the case of nanoscale phase separation in As40Se60 glass. On the other hand, a glass composition at the midpoint, i.e., x = 0.20, which also forms part of the GexAsxSe1–2x ternary, is rather special because it is spatially homogeneous. The most natural interpretation of the global minima in both α(x) and σd(x) near x = 0.20, or is that it represents phonon and charge–transport localization in these fully polymerized networks. Carrier transport in glass compositions on either side of the global minimum is aided by the presence of internal surfaces in heterogeneous (nanoscale phase separated) structures. This is akin to increased diffusion of carriers at grain boundaries in a polycrystalline material as opposed to a single crystal. These results highlight the important role of glass structure morphology (homogeneous versus heterogeneous), on transport measurements, also noted earlier in work 〚63, 64〛 on chalcogenides.
The experimental evidence of a rigidity transition due to a dimensional regression from 2d to 3d, as suggested by Keiji Tanaka 〚12〛, would be best observed in a glass system, such as the GexAsxSe1–2x ternary where nanoscale phase separation effects are absent. Neither Raman scattering nor MDSC results provide evidence of anomalies near in the present ternary 〚39〛. The present results do not provide evidence of a rigidity transition due to a dimensionality change. Many of the glass systems where such an effect has been claimed 〚12, 47, 60, 61〛, upon close examination, are all found to be nanoscale phase separated 〚65〛. Finally, independent evidence for onset of nanophase separation in Ge–Se glasses at has been obtained by T-dependent Raman measurements recently 〚66〛. Neutron structure factors of GeSe2 glass 〚67〛 that have been analyzed by molecular dynamic simulations 〚68, 69〛 have to date not considered these nanoscale phase separation effects. Alternatively, structure studies on present ternary glasses that apparently do not phase separate, would appear to be rather attractive systems to investigate in future.
7 Concluding remarks
Compositional trends in Tg provide valuable insights into the molecular structure of network glasses. Ge–Se based glasses and their S counterparts, at low mean coordination number , are usually fully polymerized, but nanoscale phase separate at higher r̄ (> 2.60) glasses. As–Se based glasses and their S analogues are usually fully polymerized at , but nanoscale phase separate at higher r̄ (> 2.40). On the other hand, ternary GexAsxSe1–2x glasses containing equal concentrations of the group IV and group V additives are quite special, they appear to be fully polymerized to reasonably high values of r̄ (> 3.0) and are attractive systems to examine elastic thresholds in glasses. Raman scattering and T-modulated Differential Scanning Calorimetric measurements in such spatially homogeneous networks reveal in general the presence of two elastic thresholds near , but no evidence of a rigidity transition near that could be due to dimensionality change.
Acknowledgements
It is a pleasure to acknowledge discussions with M. Micoulaut, D. McDaniel and R. Kerner during the course of this work. The assistance of the late Professor Ernst Franke in providing facilities to synthesize glasses is acknowledged. This work is supported by US National Science Foundation grant DMR-01-01808.



