1 Introduction
Chalcogenide glasses are known to exhibit a variety of photoinduced phenomena 〚1, 2〛. Among those, the fluidity induced in As2S3 glass by intense subgap light with photons of ħω < Eg 〚3〛, where Eg is the Tauc optical gap, is the one of dramatic phenomena. Here, steady light illumination gives rise to prominent fluidity, which is comparable to that obtained above the glass-transition temperature. One may simply speculate that the temperature rise given by illumination is responsible for the fluidity. However, it is amply demonstrated that the phenomenon occurs through athermal processes, i.e. it is photo-electro-structural 〚3〛. Then, why can such less energetic photons provide the prominent macroscopic effect?
It is mentioned here that the fluidity in chalcogenide glasses can also be induced by other electronic excitations. For instance, electron beams accelerated at 10–30 kV induce appreciable fluidity in As2S(Se)3 and GeS2 glasses 〚4〛. On the other hand, negative tip voltages (about –5 V) in scanning tunneling microscopes seem to provide substantial fluidity in Cu–As–Se glasses 〚5〛. We may then assume that the electronic fluidity appears universally in chalcogenide glasses. Or, in a wider perspective, these fluidities may be regarded as kinds of electronic melting, which was predicted by Van Vechten et al. 〚6〛 and has been demonstrated recently for crystals in fs time scales (see, for instance 〚7〛). Accordingly, the photoinduced fluidity in chalcogenide glasses induced by mild excitation appears to be an important topic in electron-lattice instabilities.
In the present work, I will discuss the mechanism of the photoinduced fluidity. First, overall features are summarized, and then some ideas are proposed. Related studies reported by other researchers are also briefly reviewed.
2 Experimental
The sample most extensively studied was As2S3 glass. The glass is stable, and the optical bandgap Eg of ∼ 2.4 eV and the glass-transition temperature of ∼180 °C are suitable for investigating the photoinduced phenomenon. The sample forms are flakes, which are cut from annealed films free from substrates, and fibers. Details of fluidity measurements have been reported previously 〚3〛. In short, the time dependence of elongation behaviors of the samples exposed to simultaneous illumination and stresses is measured, from which the fluidity (the inverse of viscosity) can be evaluated.
Note that, for some purposes, the photoinduced fluidity has been evaluated through giant photoexpansion 〚8〛. This is because the fluidity experiment, mentioned above, is more or less difficult. On the other hand, the giant photoexpansion can be evaluated easily from resultant deformation profiles on glass surfaces. And this phenomenon is understood to appear through the photoinduced fluidity and the photoexpansive force, although the actual microscopic mechanism remains to be studied 〚9–13〛. Accordingly, the deformation can be regarded as a measure of the photoinduced fluidity, while it is affected by the magnitude of expansive forces.
3 Results
Fig. 1 shows a demonstration of the photoinduced fluidity. An As2S3 film with a thickness of 50 μm was prepared through vacuum evaporation, cleaved from a substrate, annealed at the glass-transition temperature, and then shaped into the form of, approximately, 0.2 mm by 2 mm in lateral dimensions. Next, one end (the left edge in Fig. 1) of the sample was pasted to a block, and the other end was stressed with a stick, which curved slightly the sample. And, as illustrated in (a), the sample was illuminated through a side surface by focused He–Ne laser light (ħω = 2.0 eV and 102 W cm–2). Then, after an exposure of 2 h, the sample bent segmentally as shown in (b). It is known that the penetration depth of 2.0-eV light into the sample is ∼1 cm. Therefore, we can assume that only an illuminated region along the light path becomes viscous, and the segmental structure is produced. Here, it should be underlined that such deformations cannot be produced using band gap light, because of limited penetration depths (≤ 10 μm). In addition, such spatially restricted fluidity could not be obtained by thermal methods, due to heat conduction.
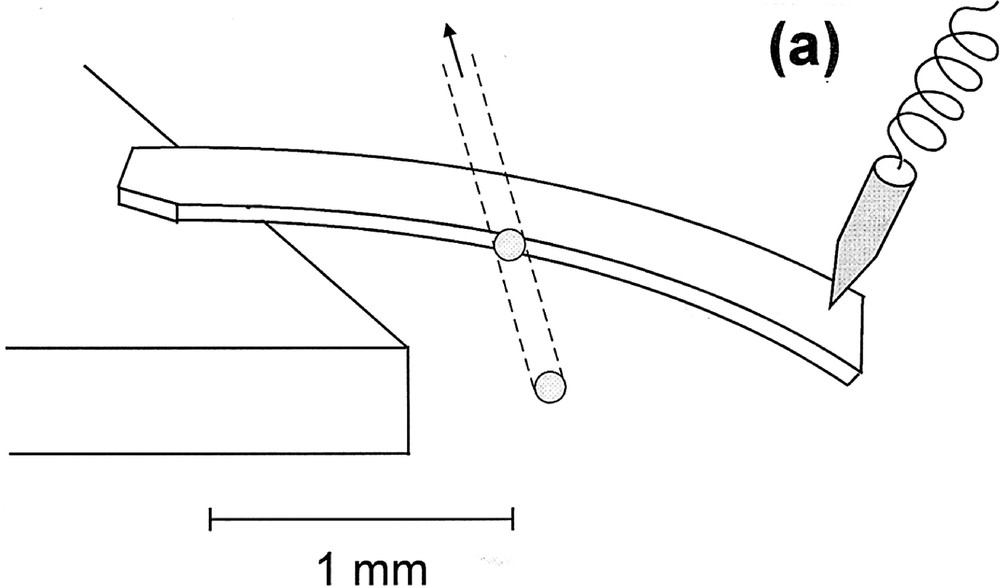
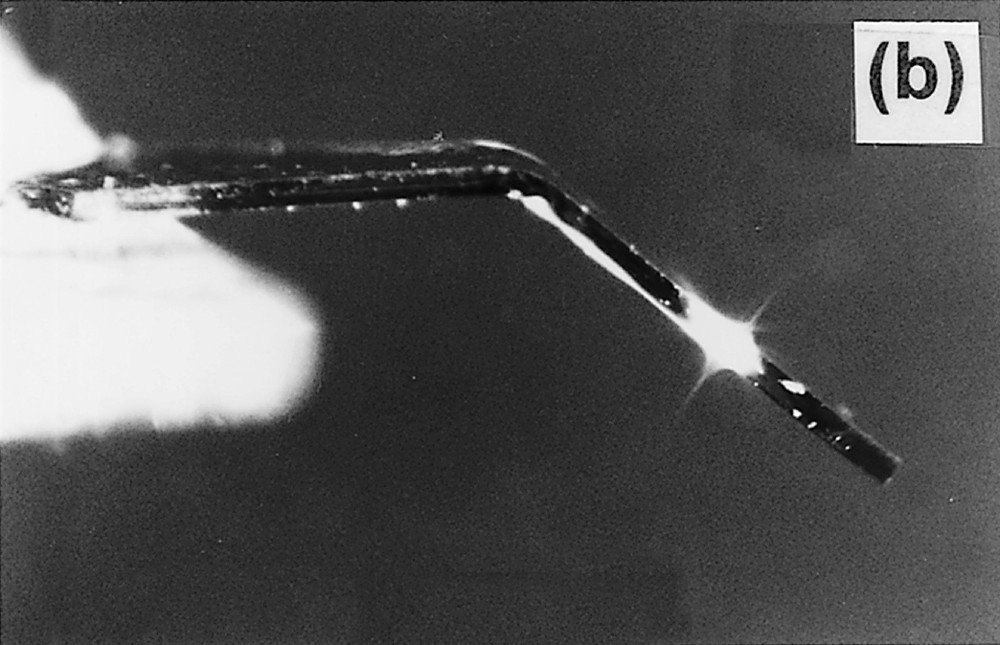
A demonstration of the photoinduced fluidity in an As2S3 flake: (a) shows an experimental illustration, and (b) the result.
Another example is shown in Fig. 2. The sample is an annealed As2S3 film with a thickness of 4 μm, and the central region has been illuminated by focused He–Ne laser light, with an intensity of 4 mW (∼104 W cm–2) for 10 min. The region expands, which is a manifestation of the giant photoexpansion 〚8〛. That is, this expansion occurs as a result of expansive forces and the fluidity of an illuminated volume. We here note that the surface of the expanding region is much smoother than that of the outer unilluminated area. That is, the roughness in the illuminated region is ∼3 nm, while that in the unilluminated region is ∼30 nm. This smoother surface is assumed to occur as a result of the photoinduced fluidity under surface tensions.
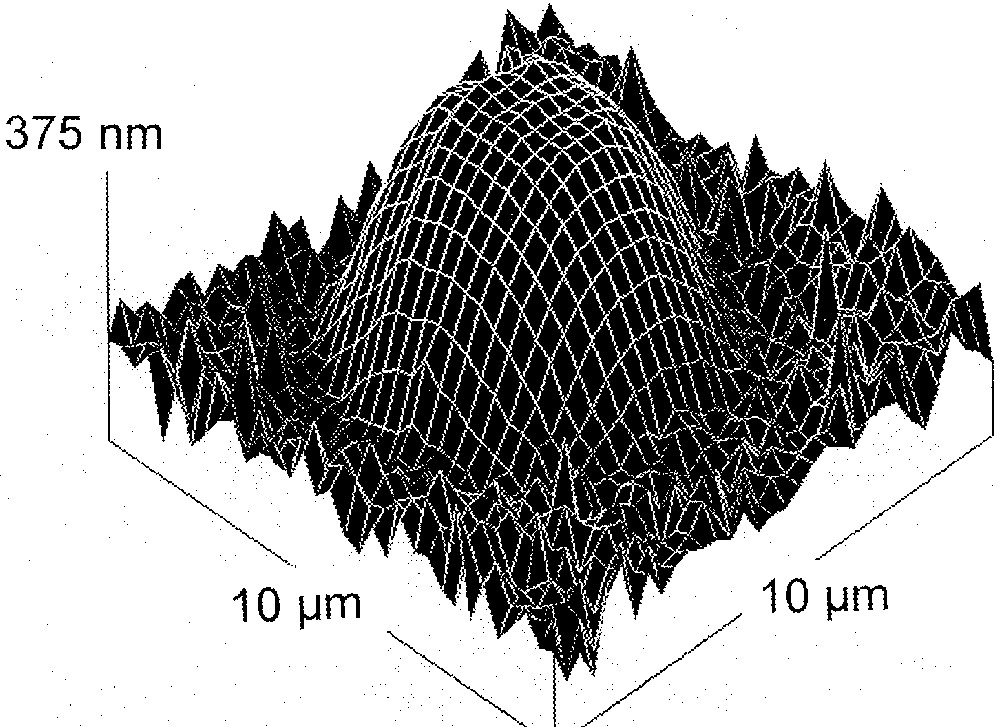
A giant photoexpansion appearing on an annealed As2S3 film. The surface is profiled using an atomic force microscope.
Fig. 3 shows the light-intensity dependence of elongation behaviors of As2S3 flakes having similar shapes under a stress of 440 N cm–2. The light intensity of 10 mW corresponds to an exposure of 102 W cm–2. Note that no elongation has been detected in the dark. Under illumination (a), we see familiar creep characteristics 〚14〛, which consist of transient responses (retarded elastic strain) and linear elongations (viscous strain). Then, from the linear regions, we can evaluate the viscosity η (the inverse of the fluidity), which is a measure of the photoinduced fluidity. (b) shows that this phenomenon becomes prominent when the light is more intense than ∼102 W cm–2. As shown in Fig. 2 and reported previously 〚8〛, the giant photoexpansion is prominent when the light is more intense than ∼103 W cm–2, which is similar to the threshold of the photoinduced fluidity. In contrast, it is demonstrated that weaker subgap illumination induces only optical changes, which are smaller than those induced by bandgap light 〚15〛.
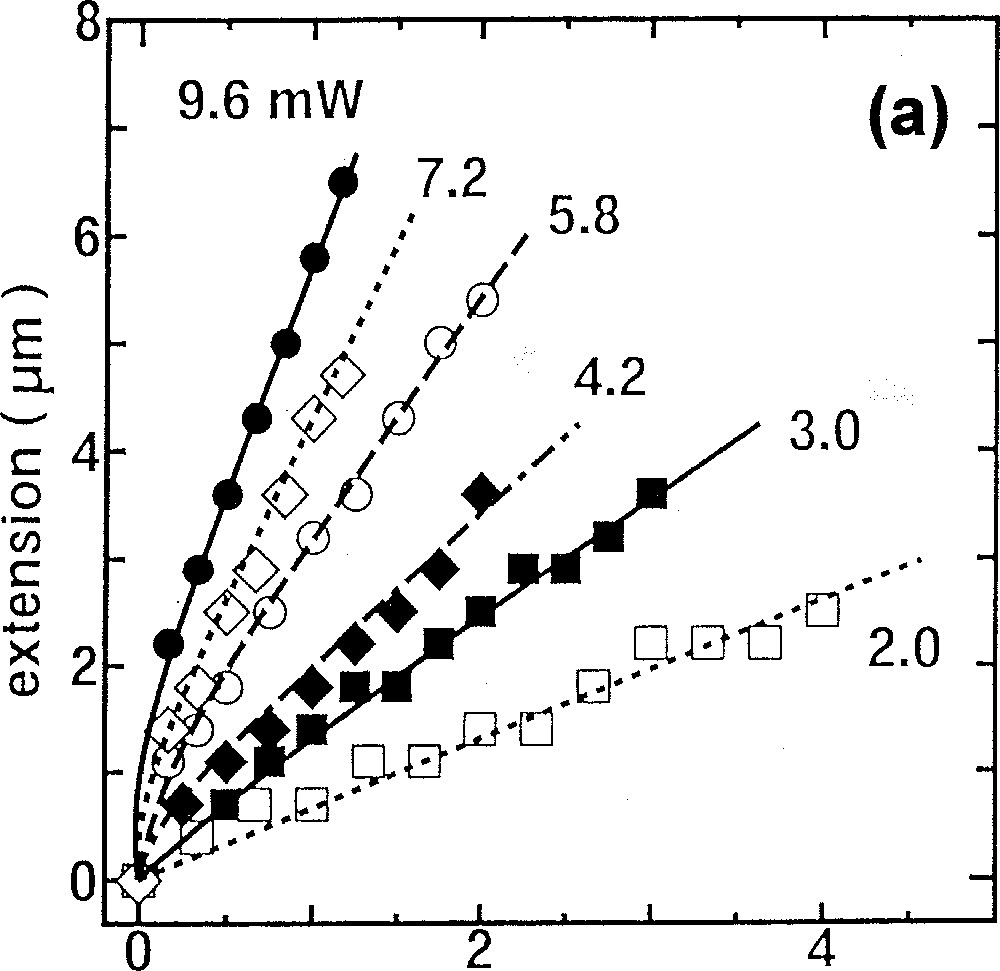
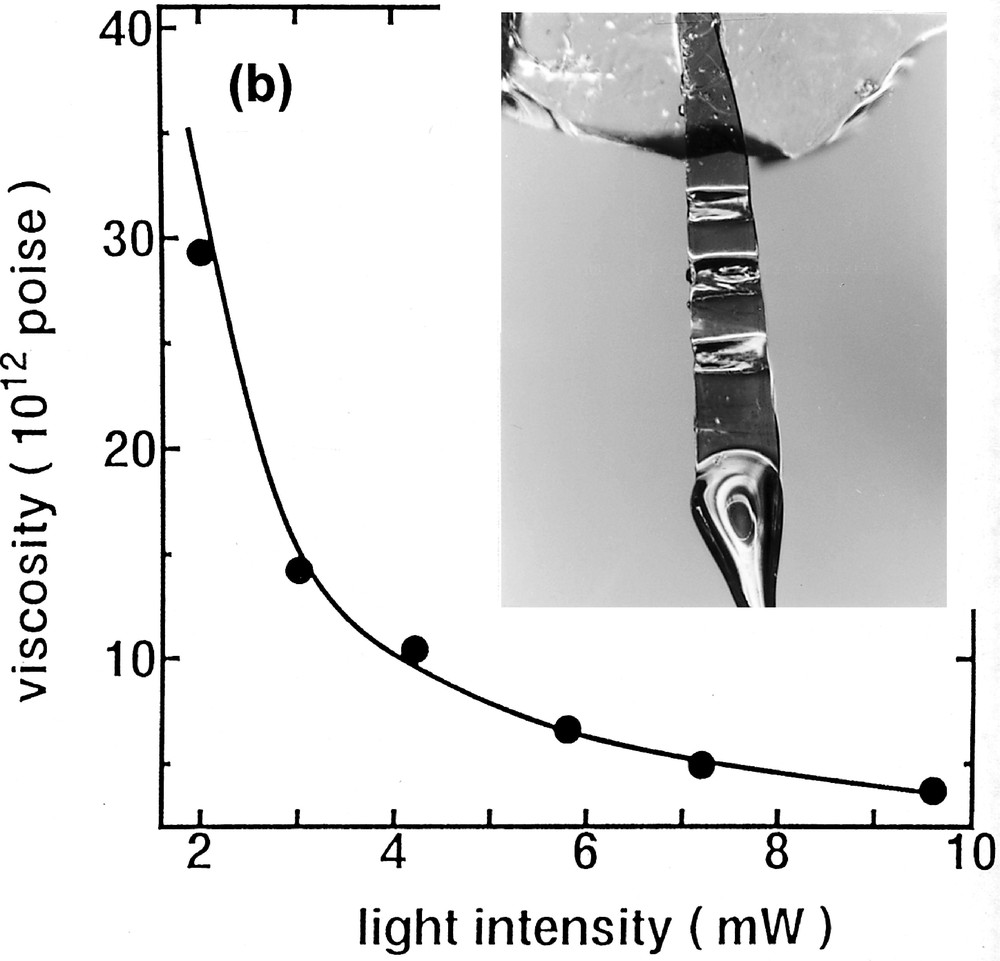
Light-intensity dependence of the photoinduced fluidity. The samples are As2S3 flakes with dimension of 50 μm, ∼0.2 mm, and ∼5 mm. (a) shows elongation behaviors, and (b) shows the viscosity η as a function of the light intensity and a photograph of a sample, which has been employed three times for the elongation measurements.
Fig. 4 shows the dependence on temperature at which an As2S3 flake is stretched. Here, the light intensity is fixed at 10 mW. We see that the elongation is, in general, faster at lower temperatures, which can be regarded as evidence of an athermal nature of the phenomenon. Because, if the temperature rise by light absorption were responsible, the elongation would become greater at higher temperatures. In detail, however, the curve at 322 K may be exceptional, which is probably influenced by the retarded elastic strain 〚14〛. The temperature dependence of viscosity (fluidity) is reproduced in (b) in comparison with the thermal behavior 〚3〛, which shows common temperature dependence. As reported previously 〚10, 13〛, the giant photoexpansion also becomes greater at lower temperatures.
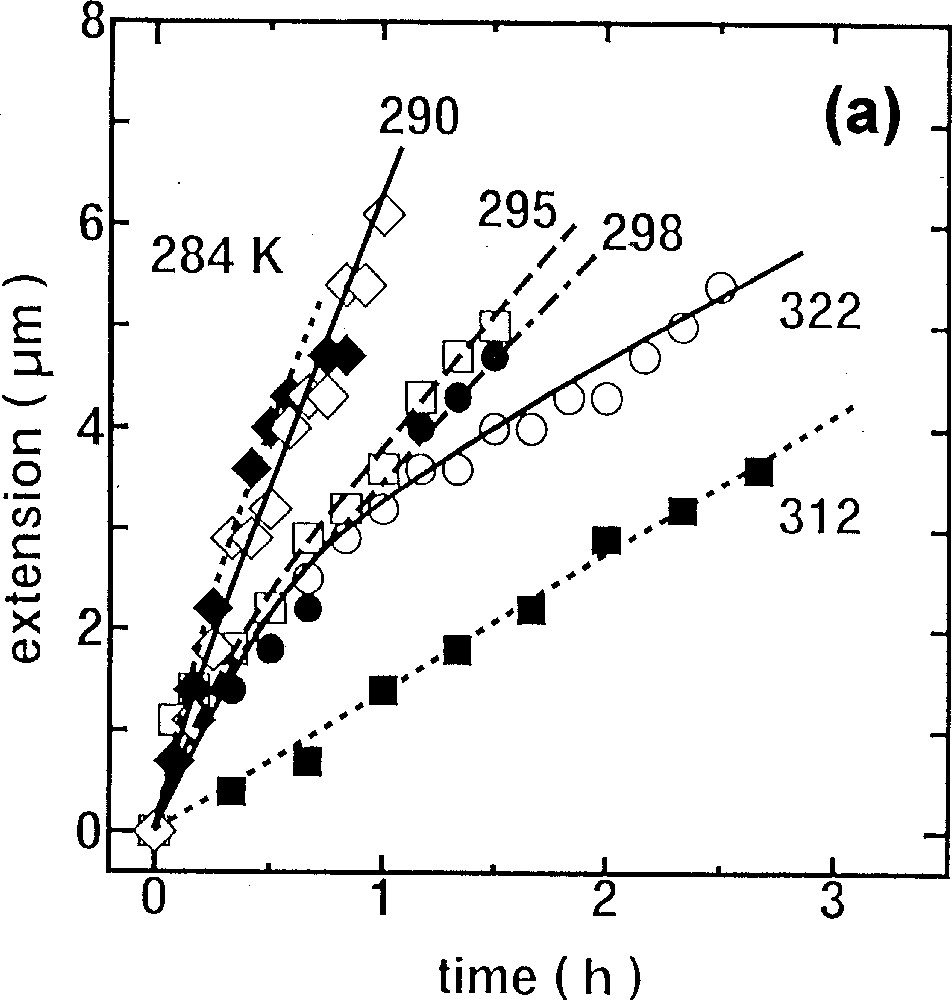
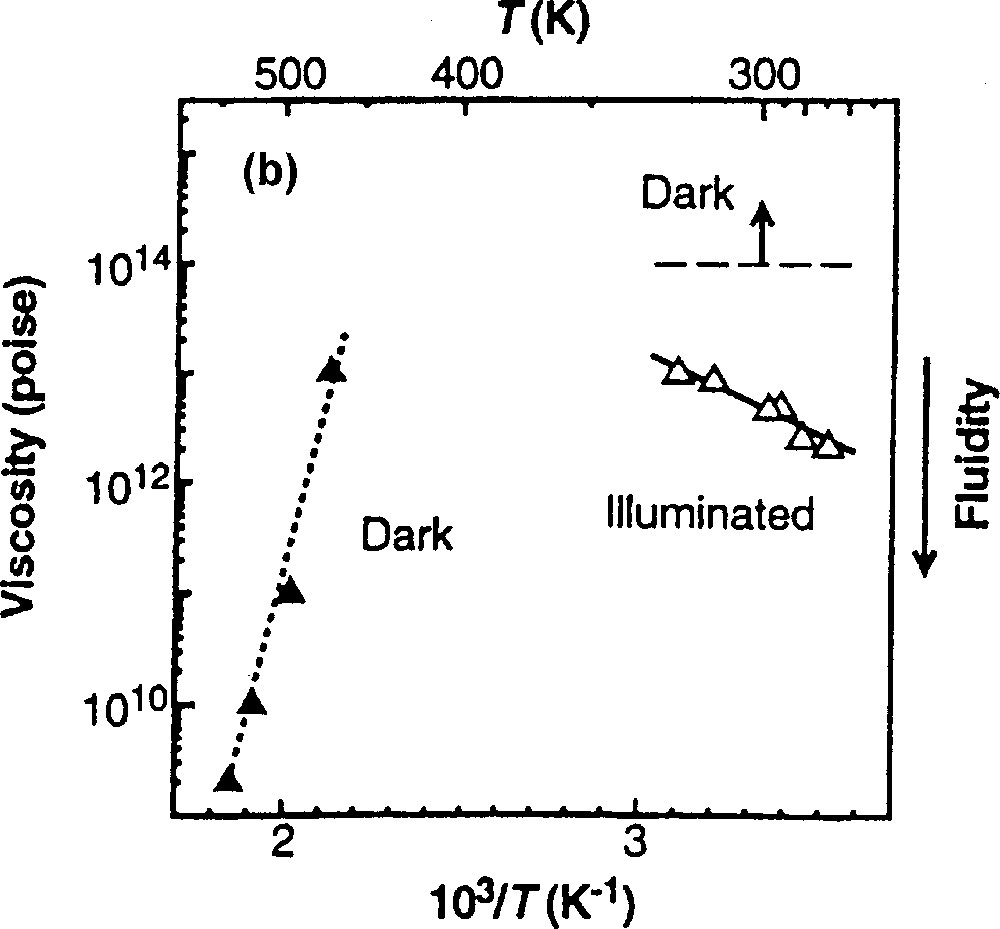
Temperature dependence of the photoinduced fluidity in As2S3 flakes. Experimental conditions are similar to those in Fig. 3. (a) shows elongation behaviors, and (b) summarizes the results 〚3〛, in which the dotted line gives the conventional thermal fluidity.
Three additional features should be noted: first, for the photoinduced fluidity, there exist some quantitative differences between the film and the fiber samples. Preliminary results shown in Fig. 5 suggest that the fiber exhibits appreciable dark fluidity, which is apt to mask the photoinduced fluidity. This dark fluidity seems to be much greater than that appearing in the bulk, which is plotted in Fig. 4b by a dotted line. Although the actual composition of the fiber is As37S63, not As40S60, it is difficult to ascribe this prominent dark fluidity to this composition difference, since the glass-transition temperatures are not largely different. Alternatively, it is suggested that amorphous structures in the fiber are oriented and defected, due to extrusion preparation methods 〚16, 17〛, and that such modified structures may be responsible for the different behavior. It seems that the behavior in the film gives intrinsic features, and accordingly, these have been investigated in more details.
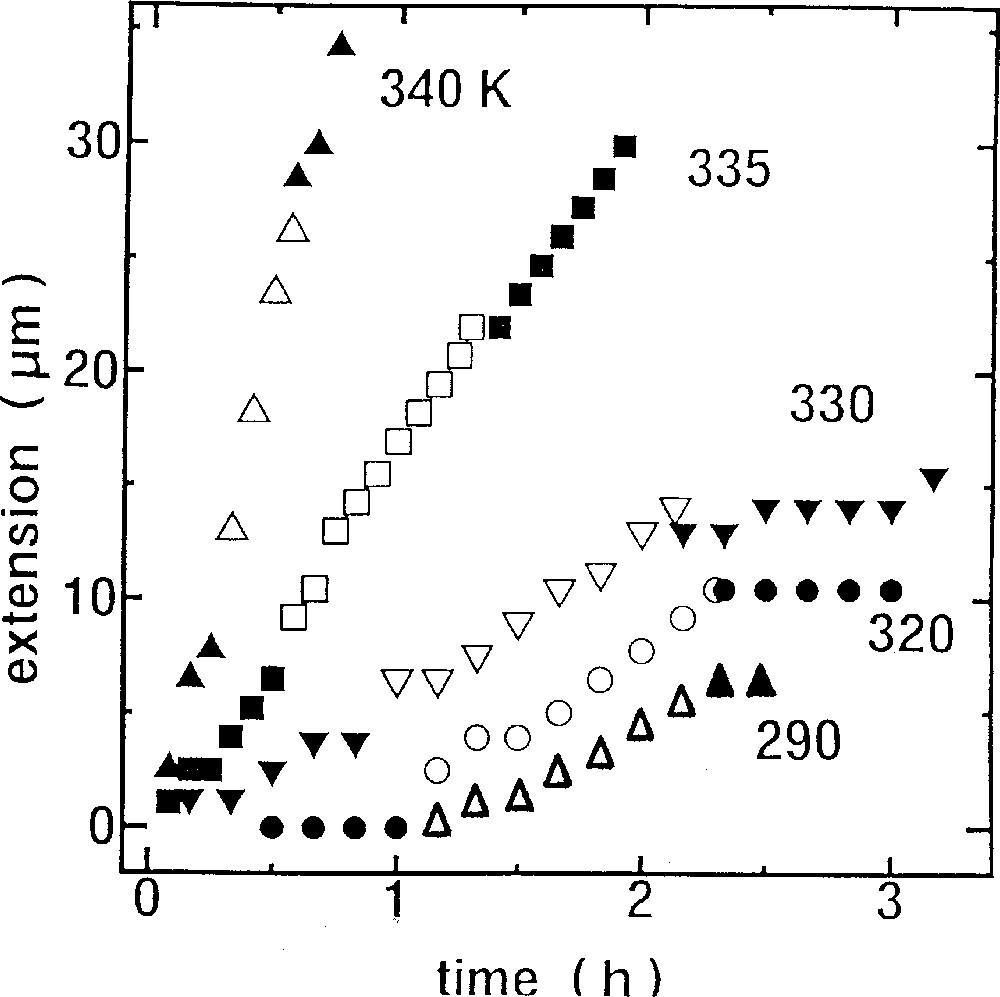
Temperature dependence of elongation behaviors in an As37S63 fiber (uncladded) with a diameter of 100 μm subjected to stress of 103 N cm–2. Light illumination is the same as that in Fig. 4.
Second, photoinduced fluidity has been examined for polyethylene and Pyrex glass using ultraviolet light sources. However, only thermal fluidity has appeared. At present, therefore, we can assume that the photoinduced fluidity is prominent only in chalcogenide glasses.
Third, spectral dependence has been investigated for the giant photoexpansion. This is because the penetration depth of light adds complicated factors to evaluations of the photoinduced fluidity. Then, it has been confirmed that the (giant) photoexpansion in As2S3 can be induced by light of ħ ω ≥ 1.9 eV 〚9, 12, 13〛. The minimal photon energy is located at the onset of the Urbach edge, which extends at 1.9–2.3 eV. Photoexpansions also appear in As2Se3 〚10, 18〛, GeS2 〚8, 10, 18〛, and GeSe2 〚unpublished〛 glasses, when exposed to Urbach-edge light (Se has not been examined, since it needs low-temperature experiments.) Note that, among these glasses, electrons are exceptionally more mobile than holes in GeSe2 〚19〛. Therefore, we can assume that Urbach-edge light can provide the photoinduced fluidity, irrespective of the conduction types.
4 Discussion
4.1 Mechanism
One of the reasons why the fluidity induced by Urbach-edge light is prominent can undoubtedly be sought into its long penetration depth extending up to ∼1 cm (see Fig. 6a). Accordingly, although light absorption is small (α ≥ 1 cm–1), this light can cause bulky effects. In contrast, the penetration depth of bandgap light (ħ ω ≥ Eg ≈ 2.4 eV) is shorter than ∼10 μm, which can produce some effects limited near the surface, provided that carrier diffusion is not responsible for the effects. However, why the less energetic light can give rise to such a drastic fluidity remains to be studied.
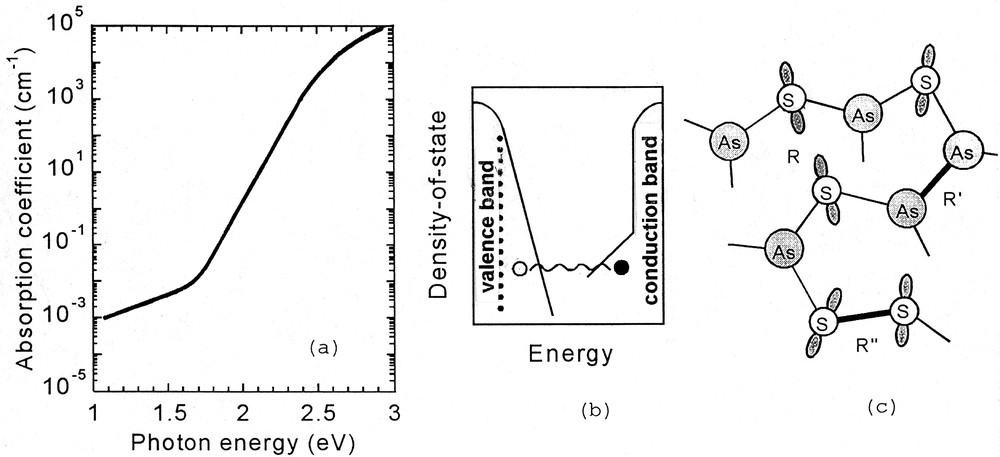
The optical absorption edge of As2S3 glass (a), the density-of-states (b), and related atomic structures (c) 〚20〛. Open and solid circles in (b) depict a hole and an electron, which are excited by subgap light.
Since the photoinduced fluidity is prominent under intense illumination, we may envisage a role of two-photon absorption. However, this possibility is excluded with the two reasons. One is based on the excitation spectrum of ħ ω ≥ 1.9 eV. If the two-photon absorption were responsible, the spectrum should extend to ∼ Eg/2 (≈ 1.2 eV). The other is the following: A recent study shows that the two-photon absorption becomes dominant when light is more intense than ∼107 W cm–2 〚20〛, which is substantially greater than the threshold, ∼102 W cm–2, of the photoinduced fluidity. These facts suggest that the one-photon absorption causes the phenomenon.
Since the photoinduced fluidity is produced by light in the Urbach-edge region, it is needed to understand its origin. That is, what kind of photoelectronic excitation occurs under the illumination? To get insight into the problem, I have studied the optical absorption spectrum, the density of states, and related atomic structures 〚19, 21–23〛. Fig. 6a shows the optical absorption edge in As2S3 glass, the overall feature being well known 〚2〛. From high- to low-absorption regions, there exist the so-called quadrature dependence of α ħ ω ∝ (ħ ω – Eg)2, where the Tauc gap Eg ≈ 2.4 eV, the exponential Urbach edge of α ∝ exp(ħ ω /EU), where EU ≈ 50 meV, and the weak absorption tail of α ∝ exp (ħ ω/EW), where EW ≈ 250 meV. Note that the recent As2S3, which has been purified for preparing optical fibers, shows the weak absorption tail reduced to α ≤ 10–2 cm–1 〚23〛.
I have proposed that the Urbach edge and the weak absorption tail are produced by the density of state and the atomic structure illustrated in Fig. 6b and c 〚22〛. The Urbach edge is assumed to arise from localized states above the valence band, since EU is nearly the same with the characteristic energy of the valence-band edge evaluated from transient photoconductivity 〚19〛. In addition, since the valence band is constructed with the lone-pair electron states of chalcogen atoms, it is reasonable to assume that the interaction such as R in Fig. 6c, which probably fluctuates from site to site, can give the states at the valence-band edge. On the other hand, several observations, e.g., the mid-gap position of Fermi levels 〚2〛 and resonant Raman-scattering spectra 〚22〛, suggest that the weak absorption tail is a manifestation of tail states below the conduction band, and that the antibonding states of As–As wrong bonds (R’ in Fig. 6c) seem to be responsible for the localized states.
Taking this idea into account, we can assume that the photoinduced fluidity occurs as follows: Urbach-edge light excites electrons and holes, which are localized at sites as R’ and R in Fig. 6c, respectively. Then, one or both of these bonds, possessing intra- and inter-molecular characters, are broken through processes presently unspecified, and the segmental-layer structure becomes fragmental. That is, the localized sites (R and/or R’), which act as ‘knots’ of the segmental structure, are released by photoelectronic excitations. Such atomic changes will appear as the macroscopic fluidity, if the material is subjected to stresses. Or, the fragments may remain to be charged positively and negatively. Such ionic structures may be less resistive to shear forces as the ionic crystal does 〚24〛.
This model offers plausible reasons why the photoinduced fluidity has not been observed in other materials such as polyethylene and Pyrex glass. Probably, structural knots do not exist in polyethylene, which has chain structures consisting of CH2 units. On the other hand, Pyrex glass contains too many knots due to three-dimensional continuous random network structures, and accordingly, the fluidity cannot appear.
Then, what is the role of intense Urbach-edge light? From the result shown in Fig. 3, we can estimate that the number of absorbed photons is ∼1020 s–1 cm–3, which produce trapped electrons and holes. Detrapping time of these carriers by thermal excitation is estimated to be ∼1 ms, depending upon the trap depth 〚13, 19, 25〛. Accordingly, the number of steadily trapped charges is ∼1017 cm–3, which is comparable to the density of the localized states. That is, we can envisage a situation, in which all the localized states are filled with carriers. Actually, the photocurrent appearing under intense subgap illumination 〚25〛 is assumed to be a manifestation of excess holes being detrapped. Therefore, under the intense illumination, most of all atomic knots can be released, and this situation causes the macroscopic fluidity. On the other hand, if the light is weak, the photoelectronic process occurs only at limited sites, which cannot influence the macroscopic fluidity.
I assume that the fluidity produced by bandgap illumination follows essentially the same process. In this case, illumination may excite free electrons and holes, while these will be trapped immediately into localized states. Then, the knot release will occur. However, the smaller penetration depth limits the phenomenon near the surface. In addition, intense bandgap illumination is likely to induce greater temperature rises. Therefore, the effect cannot be dramatic as that by subgap light.
On the other hand, the thermal fluidity in chalcogenide glasses can be induced through different processes. Unlike the photon excitation, the thermal energy enhances atomic vibrations in the whole system, in which the intermolecular bond is much weaker than the intramolecular. Accordingly, the intermolecular bond is likely to become more freely. Therefore, it is plausible that the slipping of layer molecules governs the thermal fluidity 〚26〛.
4.2 Related studies
It may be valuable to briefly review related studies reported after a pioneering observation by Vonwiller 〚27〛. For instance, Deryagin et al. demonstrate that microhardness in Se and As2Se3 decreases upon light illumination 〚28〛. Matsuda et al. 〚29〛 and Koseki and Odajima 〚30〛 show, using bimetallic samples consisting of chalcogenide films and mica layers, that structural relaxations become faster under illumination. Tagantsev and Nemilov employ a rod-bending method for investigations of photoviscous effects 〚31〛. Poborchii et al. report photomelting of Se at ∼80 K 〚32〛. However, in these studies, bandgap illumination is employed, or seems to be employed, and accordingly, the role of temperature rises may not be neglected 〚33〛. Photoelectronic effects are somewhat ambiguous.
More recently, some Raman-scattering studies on subgap excitations have been reported 〚34–36〛. However, these studies may neglect the role of intense subgap illumination. Therefore, the connection between these results and the photoinduced fluidity is not clear.
Several models have been proposed. Koseki and Odajima 〚30〛 and Fritzsche 〚1, 37〛 have proposed that atomic bond interchanges are induced by electronic excitations. In these models, they assume that the bond interchange occurs through photo-generation of defects. The concept may be essentially the same as the present one. Recent computer simulations demonstrate detailed dynamics 〚38–40〛. However, it seems that notable differences still exist between the real situation and the models treated in these computer simulations. For instance, the number of atoms in the simulations is still limited, and it is critical if we can get insights into macroscopic behaviors from these results.
On the other hand, Shimakawa et al. have proposed a novel idea 〚41, 42〛. They assume that photons excite electrons and holes, and holes diffuse away, taking the fact that holes are more mobile in most chalcogenide glasses 〚19〛. Then, layer clusters located in the illuminated region become negatively charged, and the Coulomb repulsion among the clusters exerts expansive forces and fluidity. That is, in the Shimakawas’ model, the photoexpansion and the fluidity can be explained in a coherent way. This model resembles that proposed for electron-beam induced modifications 〚4, 10〛. However, for light illumination, we may notice a problem. They implicitly assume that holes diffuse over the illuminated region, which can be a scale of ∼1 mm for light illumination. However, can the hole excited at low temperatures, e.g. 80 K, by subgap photons diffuse such a long distance?
Finally, it may be worth mentioning a possible relation between the photoinduced fluidity and the electronic melting proposed by Van Vechten et al. 〚6〛 and experimentally demonstrated for crystals using fs lasers by some researchers 〚7〛. Van Vechten et al. have predicted that if ∼1/10 of valence electrons in Si is excited, the lattice becomes fluid before the lattice temperature exceeds the melting temperature. That is, the electronic excitation causes direct bonding instability. This concept is applicable to the present case with some modifications. In the chalcogenide glass, due to the low-dimensional disordered structure, the needed excitation probably decreases (∼1017 cm–3). In addition, the lifetime (∼1 ms) of carriers in the localized states is considerably longer than that (∼10–8 s) in the band in crystals, and accordingly, the photoinduced fluidity can be provided by cw light. The essence, i.e. electronic excitations break atomic bonds, appears to be universal.
5 Final remarks
The photoinduced fluidity is assumed to be a manifestation of photoelectronic instability in low-dimensional chalcogenide-glass structures. Here, a photo-electro-structural change is crucial, and I believe that the photo-electronic process has been understood in some degree until now. However, the successive electro-structural process is still speculative. This is because the understanding of amorphous structures remains to be incomplete. In addition, it is difficult to connect theoretically and experimentally the atomic changes and the macroscopic fluidity in glasses.
For this problem, Raman and Brillouin scatterings may be useful tools. For instance, if the light intensity dependence of Brillouin scattering spectra can be measured using a He–Ne laser (1.96 eV) and As2S3 glass, the transverse sound may disappear under photoinduced fluid states. Or, if we can obtain Raman and Brillouin spectra simultaneously, the connection between the atomic and the macroscopic change may become clear.
With regard to applications, the photoinduced fluidity can be employed for microscopic shape manipulations of chalcogenide glasses. For instance, a shape modification of As2S3 fibers has been demonstrated previously 〚3〛. On the other hand, the giant photoexpansion has been employed to produce optical components such as microlenses 〚18, 43, 44, 45〛.
Acknowledgements
I thank Dr. T. Gotoh and my ex-students, H. Hisakuni and A. Saitoh, for their valuable assistance.


