1 Introduction
Water is a very good solvent for certain types of compound and, in many respects, oxidic glasses have very similar properties when in the molten state. It is because the detailed chemistry and physics of aqueous media have received so much attention, that in order to gain an understanding of glasses and glass melts comparisons with aqueous solutions are frequently made. Such comparisons can work very well. For example, metal ions dissolved in glass are often coloured similarly to their aqueous solutions, e.g. the (blue) Cu2+ ion, and their optical absorption spectra can be interpreted along similar lines. However, there are instances where attempted comparisons have very limited success, as in the creation of the ‘p-oxide’ scale which was originally intended as a measure of melt acidity or basicity analogous to the pH scale 〚1, 2〛.
It is possible to provide a somewhat superficial explanation for the success or otherwise of such comparisons, but a more detailed investigation is required if a fundamental understanding is to be achieved. An approach based on chemical bonding and structural considerations is presented here as a likely way forward for discerning to what extent the features of a glass melt can be compared with those of the aqueous medium.
2 Nature of the oxide(–II) species
In the H2O molecule and in most glasses, oxygen has the oxidation number of –2 being chemically combined as the oxide(–II) species. A remarkable property of oxide(–II) is its ability to exist so that the chemical bonding is ionic, covalent or metallic. For present considerations, we are concerned with the situation where the bonding is partly covalent, partly ionic.
This chemical ‘state’ is conveniently handled in terms of electronic polarisability, α, where the hypothetical modelling starts with all atomic species in the entirely ionic state. For example, a soda-lime-silica glass would be considered initially as composed of the ions Na+, Ca2+, Si4+ and O2–. The polarising effects of the cations are then taken into account, and this would result in much of the negative charge of the oxide(–II) ions being drawn off towards the Si4+ ions with the formation of Si–O polar covalent bonds. It makes sense to refer to oxide(–II) ‘atoms’ rather than ‘ions’, and these would retain substantial negative charge, interacting in an essentially electrovalent manner with the Na+ and Ca2+ cations. In effect, the chemical state of oxide(–II) is characterised by its state of polarisation, αO2-, and this is conveniently calculated from the refractive index and density of the glass 〚3–6〛.
Electronic polarisability can be thought of as the volume occupied by the electronic charge clouds of an atom or ion, although it is different from the atomic or ionic volume calculated from atomic or ionic radius 〚7〛 (it is of interest that if the ratio of polarisability to molar volume reaches a critical value, e.g. by the application of pressure, there is conversion into the metallic state 〚8〛). For oxide(–II), the polarisability can vary over a wide range. This property is unique to oxide(–II), and whereas α (in Å[sup3 ]) for e.g. F– or Cl– is more or less fixed at 1.04 and 3.66 respectively (Pauling values) 〚7〛, typical values for oxide(–II) are 1.41 in SiO2, 1.71 in MgO and 2.49 in CaO. The reason for this behaviour arises because of the dinegative charge borne by the O2– ion, which results in a much higher level of repulsion between the valence shell electrons than occurs for uninegative ions 〚3〛. As oxide(–II) becomes more ionic, the repulsion between the electrons increases and there is an increase in its polarisability. The electrovalent character of the bonding for a series of oxides, MaOb, increases with decreasing electronegativity of M, xM, and it follows that increasing 1/xM represents increasing ionicity of oxide(–II). The plot of αO2- against 1/xM (Fig. 1a) indicates how the polarisability is an indication of the extent of negative charge borne by the oxide(–II) species in the oxides designated.
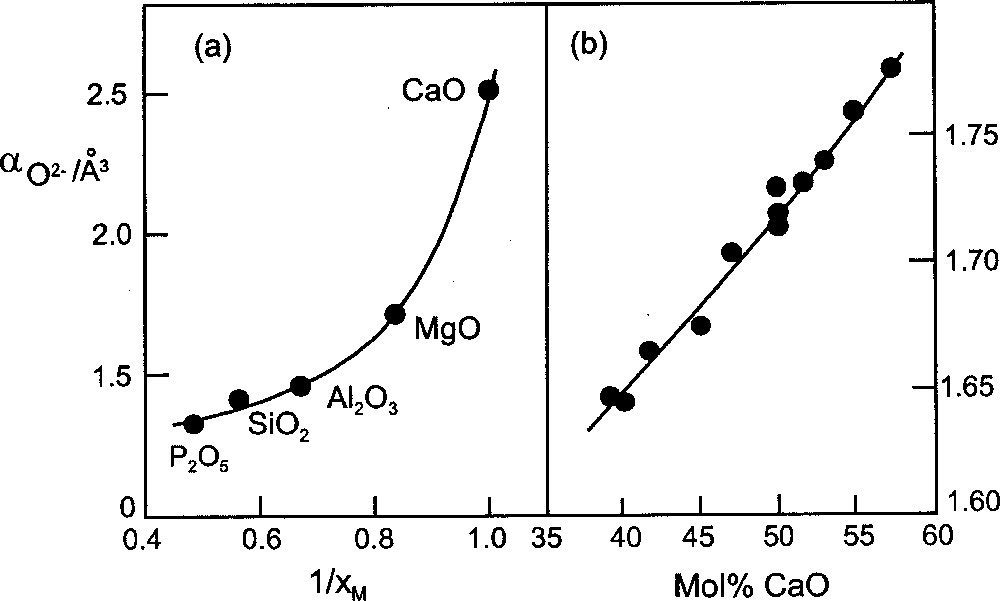
Increasing oxygen polarisability, αO2-, with (a) decreasing electronegativity of the element with which it is combined (plotted as 1/xM), (b) increasing basicity in the CaO–SiO2 glass system.
For a series of glasses, e.g. in the CaO–SiO2 system, the increasing trend in αO2- (Fig. 1b) shows that oxide(–II) becomes more ionic with increasing modifier oxide. This effect can be viewed in terms of the decrease in the silicon:oxygen ratio resulting in less polarisation of the (original) oxide(–II) ions and therefore less electron charge being drawn off the oxide(–II)s. This has the interesting effect of making available a larger quantity of negative charge for drawing off by the Ca2+ ions. As a consequence, increasing the CaO content in the glass system causes the positive charge borne by the Ca2+ ions, Z*, to fall while, simultaneously, the negative charge on the oxide(–II)s undergoes an increase. Although the degree of charge assigned to an ion, under normal chemical conditions, is bound to be arbitrary, it is possible to make calculations from spectroscopic data that serve to indicate trends 〚9, 10〛. Such data are available 〚11〛 for Tl+, Pb2+ and Fe3+ in the Na2O-–P2O5 glass system, and values of Z* are calculated here for these ions (Fig. 2). From the trends it can be seen how, as the basicity of the glass increases, so the charge borne by the metal ion decreases. Simultaneously, the (negative) charge on the oxide(–II) atoms undergoes an increase (–qO in Fig. 2) 〚12〛. The implications of these trends are more readily appreciated from the viewpoint of decreasing basicity, e.g. from the Na2O end for the sodium silicate glass system. As the dipositive charge on oxide(–II) is allowed to spread, by forming the silicate anion/network, so the interaction between the oxygen and cation becomes more electrovalent. This principle also operates for simple salts, for example, in going from Na2O to Na2SO4 the sodium-oxygen bonding in sulphate is more ionic than in Na2O. Another simple example is in the comparison of H2O and H2SO4, where the greater ionicity of the hydrogen–oxygen bonding in H2SO4 accounts for the powerful acidity of sulphuric acid.
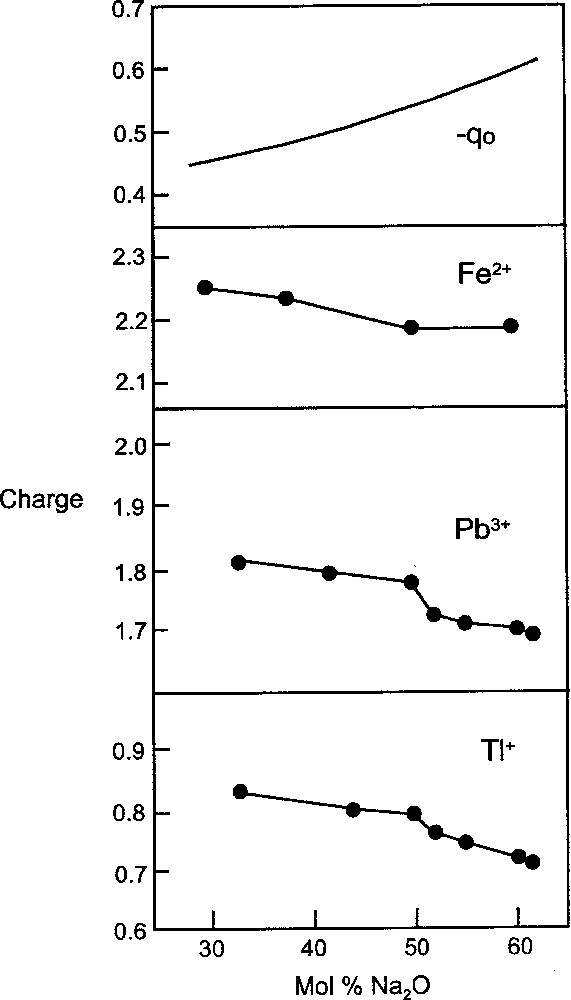
Plot showing how the charge, Z*, borne by Tl+, Pb2+ and Fe3+ in the Na2O–P2O5 glass system decreases with increasing basicity and how the negative charge on oxygen, –qO, increases.
This effect of increasing negative charge on oxide(–II) might be described as an increase in its electron donor power for when it interacts with metal ions. It is important to note that this implies a sharing of oxide(–II) electrons and not a redox electron transfer process 〚13〛. It is this property which makes oxidic materials such as water or a glass such good hosts for metal ions. Dissolution of a metal ion results in its coordination whereby the oxide(–II) atoms surround it and provide a stabilising environment of negative charge.
There is also another important effect, but one that does not normally concern aqueous media. It is, however, very relevant to network materials such as silicate glasses. As the charge on oxide(–II) increases, so there is an increasing tendency for O2– ions to be released in chemical reactions. For example, in ironmaking, the removal of sulphur from the molten iron by the silicate slag is often expressed in the form:
Although, in very simple terms, the position of equilibrium is moved towards the right-hand side by increasing the proportion of CaO, the chemistry is more subtle 〚14, 15〛. This is because the O2– ion itself hardly exists as such. Its electron affinity is negative (at around 7 eV) indicating its strong tendency to dissociate into an electron and the O– ion (usually encountered as the peroxide, , species in certain lower melting systems of oxides). Reactions that involve, superficially, participation of O2– ions are best thought of in terms of oxide(–II) being changed from one state of polarisation to another.
3 Sites for metal ions in glass and aqueous solution
As mentioned above, when metal ions are dissolved in an oxidic medium they become coordinated. Ions such as Cu2+, Ni2+ or Mn2+ form octahedral MO6 units (chromophores) which, in the case of aqueous solutions, exist as discrete aqua complexes, 〚Cu(H2O)6〛2+, 〚Ni(H2O)6〛2+, 〚Mn(H2O)6〛2+ and so on. These aqua complexes are effectively insulated from other charged species, anionic or cationic, owing to the presence of ‘inert’ (and non-coordinating) water molecules of the aqueous medium. The situation for a glass is significantly different. The MO6 units are not present as discrete complexes but are an integral part of the glass structure. Unlike aqua complexes they do not have a distinct identity and there is no boundary between the MO6 chromophore and the oxidic network of the medium. The σπ-bonding that extends throughout the glass network means that the chromophore is not immune to electronic effects resulting from, e.g. changes in acidity or basicity. For example, the pink CoO6 chromophore changes to the blue (tetrahedral) CoO4 when the glass composition changes toward more basic. In contrast, the metal ion in aqueous solution experiences these effects only if one or more coordinating water molecules in the aqua complex is replaced by another species, such as when chloride ions replace water molecules with the formation of 〚Co(H2O)Cl3〛– or 〚CoCl4〛2–. Otherwise, if the aqua ion remains intact, the metal ion is virtually unaffected.
In spite of this major difference, it is commonly observed that glasses containing these metal ions have colours that are at least fairly similar to those of the corresponding aqua ion. Furthermore, their optical spectra are usually broadly similar, with absorption band maxima being at roughly similar frequencies. Usually the degree of absorption is somewhat greater for the metal ion in the glass.
The excited energy levels of a metal ion are affected by coordination in two ways 〚16〛. First of all, they are split into two or more levels, and it is the magnitude of this ‘crystal field’ splitting that determines the frequencies of the band maxima. Second, coordination affects the probability for an electronic transition to take place, and this therefore governs the band absorption intensity. A third effect is a lowering in the energy of a particular level owing to an expansion of the orbitals involved with that level. This is the ‘nephelauxetic’ effect 〚16〛. For transition metal ions, this results in only a small frequency shift compared with the aqueous condition, but in certain other ions, e.g. Tl+ or Pb2+, the effect is much more pronounced.
4 Acidity and basicity
In dilute aqueous solutions of acids, the (solvated) H+ ions are isolated from each other by ‘inert’ water molecules. A similar situation exists for OH– ions in basic solution. This isolation of the H+ or OH– ions allows acidity or basicity to be regarded in terms of their concentration or activity, usually with reference to the pH scale.
Glass is usually thought of in terms of basicity rather than acidity because it is derived from strong bases (CaO, Na2O and so on) and a weak acid (SiO2). Attempts to express the basicity in terms of O2– activity in order, for example, to handle equilibria such as equation (1), are unsuccessful, because O2– ions, unlike solvated H+ ions in water, are not isolated. Instead, they are ‘stored’ in the form of non-bridging oxygen atoms in reactions that can be thought of in terms of the following example:
In effect, increasing the concentration of a basic oxide such as CaO results in such a reaction and, simultaneously, an increase in the average negative charge borne by the oxide(–II) atoms, (–qO in Fig. 2). As discussed above, the electron donor power of the oxide(–II) atoms increases, and this concept lends itself to regarding basicity in terms of the Lewis theory. If an acidic probe, such as a metal ion is introduced into an oxidic network system, then the basicity can be regarded as the extent to which the oxide(–II) atoms can share their electron density with the metal ion. It is this Lewis acid-base interaction that is responsible for the nephelauxetic effect, referred to earlier, and which results in large frequency shifts in the s–p spectra of ions such as Tl+ and Pb2+. Examination of the nephelauxetic effect has shown that it is possible to define a quantity, , called the ‘optical basicity’, in terms of a ratio of frequency shifts 〚17–20〛:
On the basis of accumulated spectroscopic data, it became possible to assign a parameter, γ (the so-called ‘basicity moderating parameter’) to the calcium, sodium, silicon, etc. in the glass 〚18, 19〛. Values for some elements are in Table 1, and they enable the optical basicity of a glass to be calculated from its composition, using the relationship:
Basicity moderating parameters for elements in oxidation states denoted, and values of Λ(oxide) for individual oxides.
| Element | γM | Oxide | Λ (oxide) |
| Caesium (I) | 0.60 | Cs2O | 1.7 |
| Potassium (I) | 0.73 | K2O | 1.4 |
| Sodium (I) | 0.87 | Na2O | 1.15 |
| Lithium (I) | 1.0 | Li2O | 1.0 |
| Barium (II) | 0.87 | BaO | 1.15 |
| Strontium (II) | 0.91 | SrO | 1.1 |
| Calcium (II) | 1.00 | CaO | 1.00 |
| Iron (II) | 1.0 | FeO | 1.0 |
| Manganese (II) | 1.0 | MnO | 1.0 |
| Magnesium (II) | 1.3 | MgO | 0.78 |
| Aluminium (III) | 1.65 | Al2O3 | 0.60 |
| Silicon (IV) | 2.1 | SiO2 | 0.48 |
| Boron (III) | 2.36 | B2O3 | 0.42 |
| Hydrogen (I) | 2.5 | H2O | 0.40 |
| Phosphorus (V) | 3.0 | P2O5 | 0.33 |
Equation (4) indicates that the optical basicity for a single oxide, Λ(AOa/2), is simply 1/γA. As seen from Table 1, optical basicity ranks oxides according to acidity or basicity. It is worth noting that the position of H2O (Λ = 0.40) is between SiO2 and P2O5. Equation (4) can be rewritten in terms of the optical basicity values of the individual oxides, Λ(AOa/2), Λ(BOb/2), …
For example, Λglass for a sodium silicate glass of composition Na2O·SiO2 (1:1) is , i.e. . Similarly, for Li2O–P2O5 (2:3) glass, Λglass is , i.e. , indicating that the sites in this glass are only slightly more basic than those for an aqua metal ion.
The optical basicity method has found much application for handling the chemistry and physics of network oxidic media especially glasses and melts 〚21〛.
5 Redox equilibria
Reactions involving oxidation and reduction are an important aspect of the chemistry of glass melts, and a number of metal ion couples have been studied, such as between Fe2+ and Fe3+, Sn2+ and Sn4+ 〚22–27〛. In most cases, the corresponding redox couple involves atmospheric oxygen in the change oxygen(O)/oxide(–II). Similar redox reactions can occur in aqueous media, dissolved oxygen oxidising many metal ions, e.g. Fe2+, Ti3+. Usually, however, redox reactions in aqueous solution are conducted so as to exclude oxygen, and they form the basis of important analytical methods, for example, in the quantitative oxidation of Fe2+ by MnO-4 or Cr2O2-7 ions. Analogous reactions in melts have received comparatively little study 〚28〛.
It is a feature of melt chemistry that increasing the basicity causes the redox equilibrium to move in favour of the upper oxidation state. This occurs for all metal ion couples that have been studied, apart from the copper(I)/copper(II) reaction 〚25〛. Redox reactions are best written in a form which avoids reference to O2– ions. For example, for the Fe2+/Fe3+ reaction, conversion of Fe3+ to Fe2+ involves the transference of an electron from an oxygen atom (in the oxidation state of –2) to Fe3+, so that in the following equation,·Fe3+ represents Fe2+:
It follows that the overall reaction might be represented by:
The increase in upper oxidation state with increasing melt basicity has been demonstrated by plotting log redox ratio, R (R = 〚lower state〛/〚upper state〛) against the optical basicity of the glass melt 〚29〛. These relationships, which are almost linear (see Fig. 3a and Table 2), are based on redox data obtained for alkali and alkaline earth silicates at 1400 °C and air atmosphere. In these original studies, the effect of basicity on the redox ratio was demonstrated as a trend occurring with increasing alkali oxide content. There were separate trends for different alkali metals, and these also indicated increasing stabilisation of the upper oxidation state on going from e.g. lithium to sodium to potassium. An advantage of using optical basicity is that it unites these separate trends into a single one. For example, the 〚Fe2+〛/〚Fe3+〛 ratio which exists in a 33% Na2O sodium silicate glass is attained in a potassium silicate or lithium silicate glass which have the same optical basicity (by equation (5), Λglass for the 33% Na2O glass is 0.614, corresponding to 25% K2O and 41% Li2O).
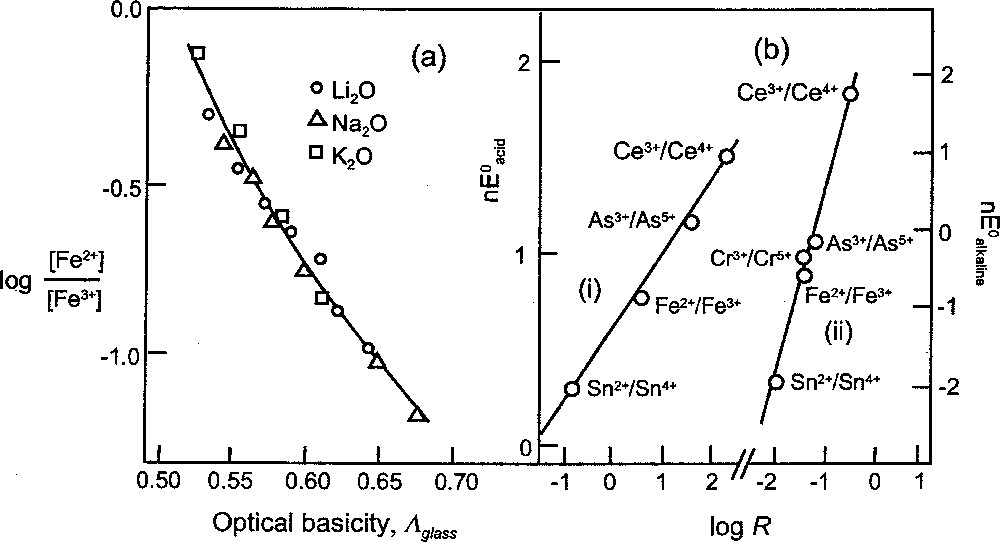
Optical basicity/redox relationships: (a) log 〚Fe2+〛/〚Fe3+〛 versus Λglass for iron in lithium, sodium and potassium silicate glass melts at 1400 °C, (b) n E0 versus log of redox ratio, R, for metal ion couples indicated (E0 in volts for (i) acidic and (ii) alkaline solution, see Table 2).
Relationship between the redox ratio, R (R = lower/upper oxidation state)(a) and the optical basicity, Λglass . E0 aqueous solution data are included.
| Ion–couple | Electrode potential equilibrium | Redox relationship | E0alkaline (volts) | E0acid (volts) |
| Fe3+→Fe2+ | –0.56 | –0.036 | 4 Fe3+ + 2 O2– = 4 Fe2+ + O2 | log {〚Fe2+〛/〚Fe3+〛} = 3.2 – 6.5 Λ |
| Cr6+→Cr3+ | –0.12 | 1.10 | 4 Cr6+ + 6 O2– = 4 Cr3+ + 3 O2 | log {〚Cr3+〛/〚Cr6+〛} = 8.2 – 13.7 Λ |
| Ce4+→Ce3+ | 1.71 | 1.45 | 4 Ce4++ 2 O2– = 4 Ce3+ + O2 | log {〚Ce3+〛/〚Ce4+〛} = 5.4 – 8.3 Λ |
| Sn4+→Sn2+ | –0.96 | 0.15 | 2 Sn4+ + 2 O2– = 2 Sn2+ + O2 | log {〚Sn2+〛/〚Sn4+〛} = 0.6 – 3.6 Λ |
| As5+→As3+ | –0.08 | 0.58 | 2 As5+ + 2 O2– = 2 As3+ + O2 | log {〚As3+〛/〚As5+〛} = 5.2 – 8.9 Λ |
It has been shown that the optical basicity value of an oxidic medium is a measure of the negative charge borne by the oxide(–II) atoms (or ions) 〚12〛. It is implicit, therefore, that different media with the same optical basicity value provide (on average) sites of equivalent electron density for hosted metal ions. The calculations at the end of the previous section show that water has the same optical basicity value as a 2:3 Li2O–P2O5 glass (actually, 37% Li2O), and it follows that a metal ion in the form of an aqua species is provided with a site that has the same electron density as in a 37% Li2O phosphate glass. Since it is the electron density of the site that is largely responsible for the stability of a metal ion, it is possible that there is a straightforward relationship between the redox ratio in this, or any other glass melt, and the corresponding electrode potential in aqueous (acidic) solution. There is a similar expectation for the more basic environment provided in hydroxo complexes (for which Λ has been shown to be 0.70) and glasses of the same basicity. These expectations have been borne out, as indicated in Fig. 3b 〚29〛.
A remarkable feature of the relationships in Fig. 3b is that they connect two very different environments for metal ion couples: (i) for the aqueous conditions at 25 ºC and (ii) for the molten glass environment at 1400 °C. They are expressed as 〚29〛:
These equations allow calculation, from aqueous solution E0 data, of the redox ratio in glass melts having Λglass = 0.40 (equation (8)) and Λglass = 0.70 (equation (9)). From these, expressions analogous to those in Table 2 can then be obtained. The expressions allow rough estimates of redox ratios in glasses for which optical basicity can be calculated from composition. They can also give an indication of what glass composition to employ in order to attain a particular value of the redox ratio. For example, in an investigation of antimony in silicate glass systems it might be necessary to establish a suitable Sb3+/Sb5+ ratio so that sensible concentrations of both oxidation states are present. Using the E0 values of 0.64 and –0.59 V 〚30〛, equations (8) and (9) yield values of log{〚Sb3+〛/〚Sb5+〛} equal to 1.74 for Λ = 0.40 and to –1.60 for Λ = 0.70. Assuming the same linearity that was observed for the metal ion couples in Table 2, these results provide a general equation linking the redox ratio for antimony with the optical basicity of the glass:
6 Metal corrosion
The above strategy can also be applied to the situation where the lower oxidation state is zero and the upper state corresponds to the usual oxidation state of the metal in the glass melt. Such reactions correspond to the precipitation of metals from melts (commonly encountered for silver and lead) 〚31〛 or the converse, that is, the corrosion of metals by melts 〚29〛. If we consider arsenic, for example, the equilibrium in acidic solution can be written as:
The E0 values for these aqueous conditions are 0.234 V and –0.71 V, respectively 〚30〛, and these yield values of 0.255 (equation (8)), and –1.995 (equation (9)) for log 〚As〛/〚As3+〛. The electrode potential for the melt, Emelt, is related to the equilibrium redox ratio by:
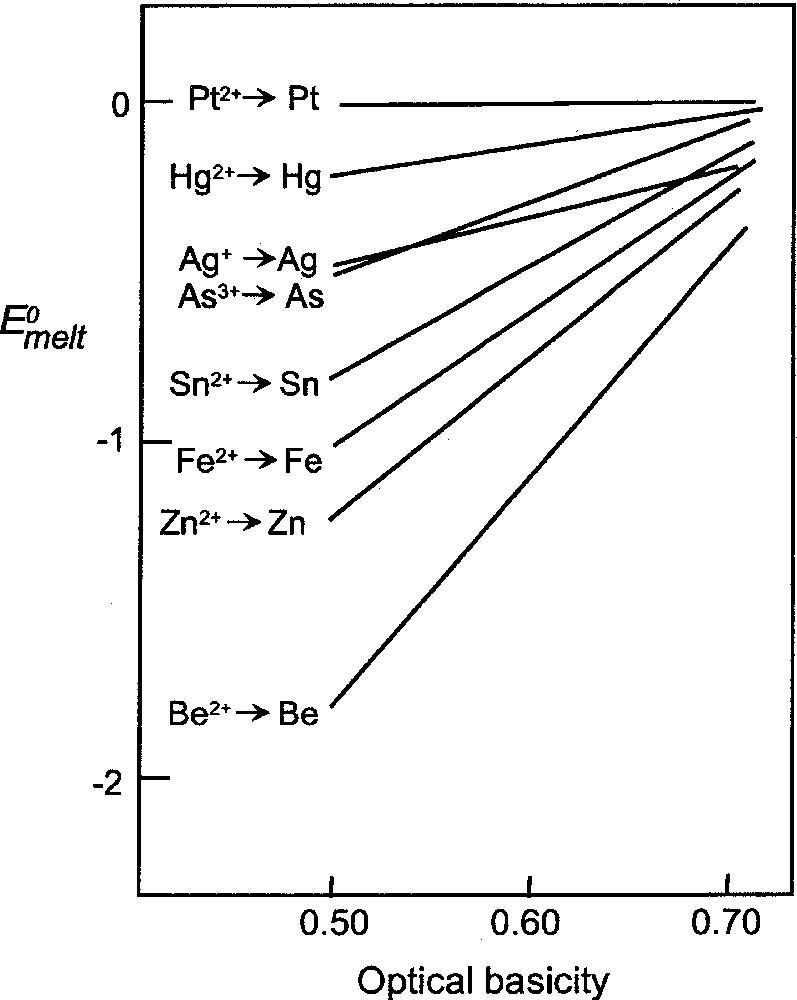
Plot of E0melt (volts), for couples designated, versus melt optical basicity.
Comparison with the series for the aqueous condition (based on E0alkaline values, since the melts are basic), which is:
7 Concluding remarks
Although in several respects there are resemblances between glasses and aqueous media, there are major differences in their solvent behaviour and these are largely accountable in terms of the chemical bonding. In aqueous media, covalent bonding exists within the H2O molecule and it is the much weaker hydrogen bonding that operates between the molecules. This allows the formation of metal aqua ions that are virtually insulated from the medium as a whole. In a glass, covalent bonding exists throughout the network, and discrete metal complexes are not formed. The oxide(–II) atom is the significant feature common to the two media, and it is the power that oxide(–II) has for sharing its negative charge that permits the hosting of dissolved metal ions.
Optical basicity is a measure of this electron donor power and is based on the Lewis concept. However, since optical basicity can also be applied to aqueous media, which are usually dealt with in the context of the Brønsted–Lowry theory, it might be expected that optical basicity should link these two approaches to acids and bases. This possibility was examined several years ago during the early development of optical basicity theory and it was found that there was an approximate correlation of the pK values of acids and the set of Λ values for the conjugate bases 〚32〛. This involved plotting, for example, the pK of H3PO4 against the Λ value of the HPO2-4 ion. Using more up-to-date data, this relationship is shown in Fig. 5 for phosphoric acid and its derivatives HPO2-4 and H2PO-4, and similarly for pyrophosphoric acid. Fig. 5 also includes the data points for the dissociations
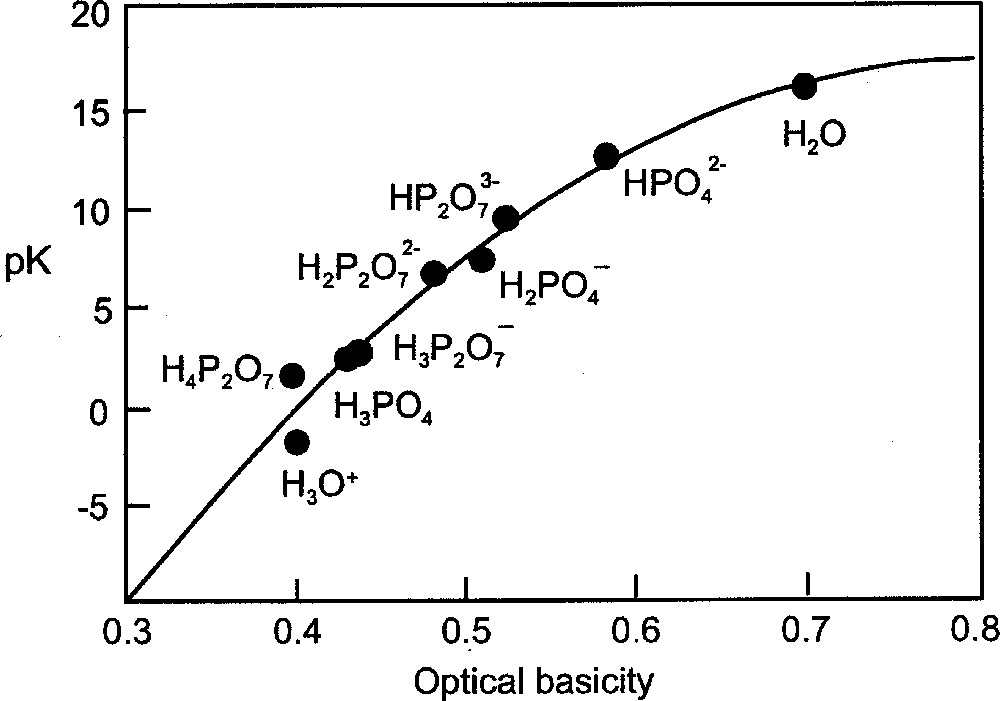
Plot of pK of acidic species denoted versus optical basicity of corresponding anion (conjugate base). Values of pK are taken from reference 〚33〛.
It should be noted that in the calculation of Λ, using equation (4) and the γ values in Table 1, it is necessary to choose a cationic partner for the anionic species. This was arbitrarily selected as one with γ = 1.00


