1 Introduction
Exchange and correlation phenomena describe the effects of electron–electron interactions beyond the one-electron mean-field approximation; they are necessary to build correct electronic configurations based on an orbital description for 3dn ions. A large part of the correlation energy, in the sense of electron–electron interactions, is included in mean-field approaches: for example, most one-electron schemes account for screening phenomena (i.e. Slater screening constant). In the Hartree–Fock framework, correlation energy is defined restrictively as the difference between the exact and the Hartree–Fock ground-state energy.
Exchange phenomena are more complex, including the symmetry of the wave functions and the Fermi hole, both giving rise to Hund’s rules [1]. In the case of partially occupied orbitals, for example 3d orbitals for transition metals, exchange will contribute to differentiate up- and down-spin populations.
In inorganic molecular chemistry, exchange and correlation are discussed on the basis of Racah A, B, C, or Slater parameters, which allow to quantify electron–electron interactions and result in the Tanabe–Sugano diagrams for octahedral complexes. What about solid-state chemistry?
Tight-binding methods as Extended Hückel (EHTB), which emphasise atomic orbital overlaps, do not include exchange and correlation effects. Moreover, in non self-consistent methods as EHTB, crystal or molecular orbital energies do not depend on the electron count.
Methods based on the Density Functional Theory (DFT) use approximate exchange-correlation functionals (so-called LDA, GGA, WDA...), based on the analytical expression for the exchange-correlation energy of an homogenous electron gas. Although closer to the exact energy than single-determinant Hartree–Fock, DFT remains at the mean-field stage. A step beyond correlation effects can be achieved through the LDA+U method, in which on-site electron–electron repulsion terms are added to the exchange-correlation functional [2].
Chemical bonding in transition metal oxides can be described on the basis of two types of atomic orbitals:
- • (i) s and p orbitals, for which ζ Slater exponents take low values (ζ4s ∼ 1–1.5 [3]), corresponding to diffuse orbitals;
- • d orbitals, more localised (ζ3d ∼ 2.5–4.5 [3]), describing strongly interacting electrons, for which exchange and correlation phenomena are often crucial.
As an example, a monoelectronic band description of the three following double oxides with rhombohedral perovskite-related structures would predict a metallic behaviour for LaFeO3 (d5) and LaNiO3 (d7), and an insulating one for LaCoO3 (d6) (Fig. 1). Whereas LaNiO3 indeed is a metal at any temperatures (within its stability range), LaFeO3 actually is always insulating and LaCoO3 undergoes an insulating to metal transition at high temperature. So a simple low-spin band description, neglecting exchange and correlation effects, does not correspond to experimental facts.
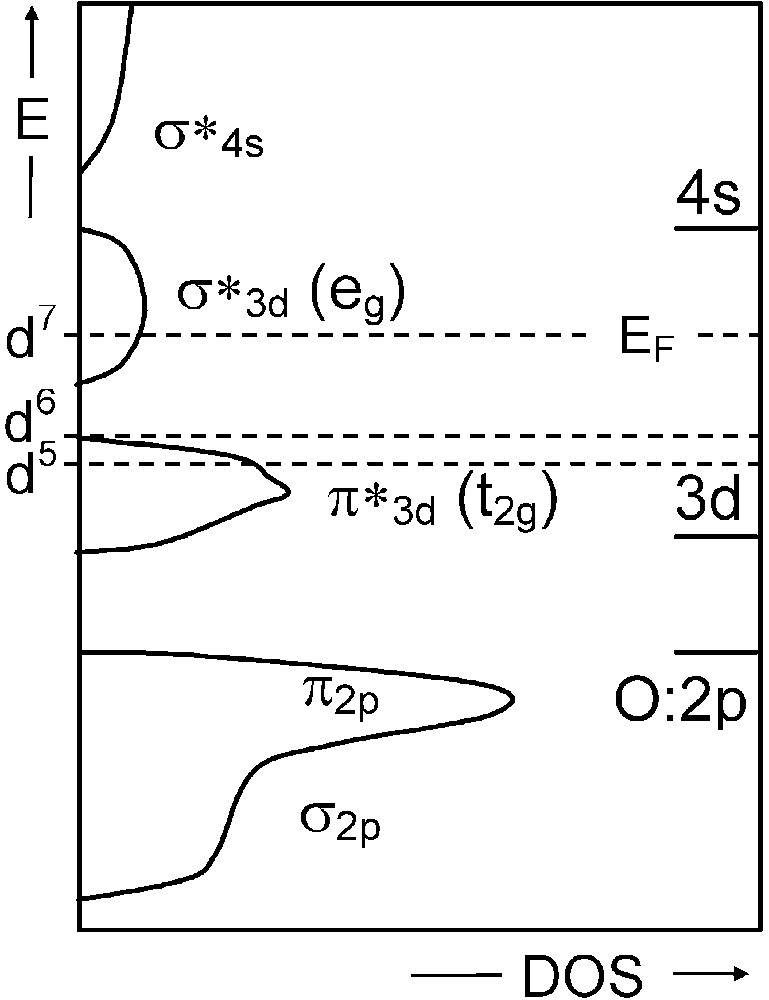
Schematic monoelectronic band structure for a cubic perovskite LaMO3(M = d5, d6, and d7 cation) on the basis of EHTB method.
In LaFeO3, trivalent iron (3d5) is not in the low-spin t2g5eg0 configuration (favoured by the crystal field), but in the high-spin t2g3eg2 configuration (favoured by exchange and correlation). The competition between crystal field (which stabilises some energy levels) and exchange and correlation (which tend to keep electrons apart in space) is at the origin of spin equilibria and spin transition phenomena. At low temperature, the six 3d electrons of cobalt in LaCoO3 lie in the three low-lying t2g orbitals, giving an insulating state; at high temperature, exchange and correlation prevail and spread the six electrons in the five d orbitals. Then LaCoO3 becomes a metal, with the cobalt ion in an intermediate spin state.
In the following, we will describe exchange and correlation effects for transition metal ions in various coordination polyhedra the symmetry of which strongly influences the energy splitting of the five 3d orbitals. We will extend the treatment of most-common octahedral (Oh) and tetrahedral (Td) sites to the square-based pyramidal (C4v), square planar (D4h), dumbbell (D∞h), cubic (Oh) and antiprismatic (D4d) environments (Fig. 2).
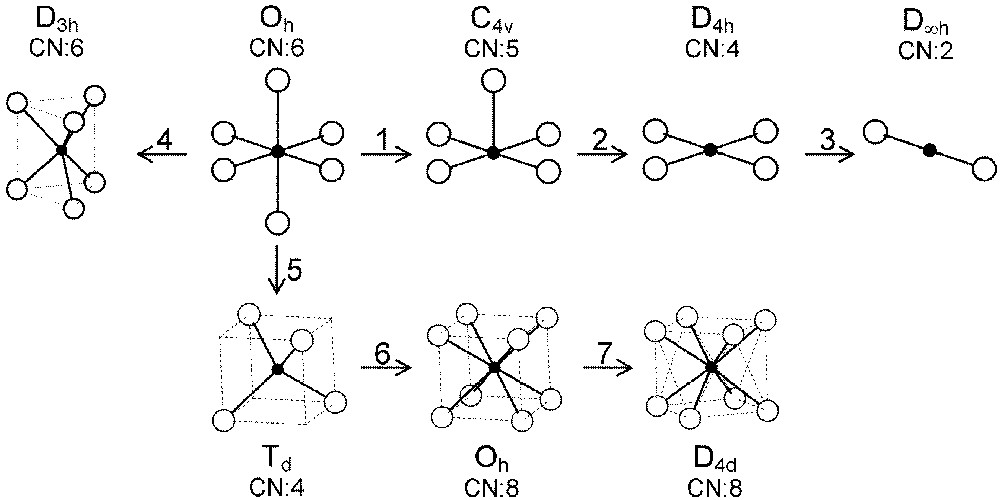
Various coordinations and symmetries of cationic sites in oxides.
We will restrict our discussion to d4, d5 and d6 ions, most interesting because they are to be found in three different spin states: S = 0, 1 and 2 for d4 and d6 ions; S = 1/2, 3/2 and 5/2 for the d5 ion. Our approach can then be applied to metal ions such as, for example, Fe4+ and Mn3+ (3d4), Fe3+ and Co4+ (3d5), Co3+ (3d6). Its extension to the 4d and 5d series should be handled cautiously because of the spin–orbit coupling.
The aim of this work is to guide inorganic chemists in the choice of appropriate crystal structures for stabilising a chosen electronic configuration for these 3d transition ions, and to help in the interpretation of their remarkable physical properties.
2 Expression of the exchange and correlation using U, U′ and JH parameters of Kanamori and Brandow
According to Kanamori [4] and Brandow [5], Coulomb repulsion energy between two electrons belonging to the same atomic orbital (U) or to two different orbitals (U′) is balanced by an exchange energy (JH) that stabilises parallel vs antiparallel spins. These parameters are expressed by the following integrals:
These energies are linked to Racah parameters through the following relationships [5]:
These relationships show that U, U′ and JH are not independent and immediately lead to U – U′ = 2 JH, which will allow us to compare the energy of the various spin states using a single parameter, the Hund’s rule exchange energy, JH. For a 3d4 ion in an octahedral site and a HS configuration (t2g3eg1), the energy of a singly occupied (so) eg orbital can be written as:
Summing the crystal field energy over the four electrons and taking half the sum of exchange and correlation energies (as each contribution is shared by two electrons), the ion overall energy (ET), including nucleus–electron and electron–electron interactions, becomes:
The so-called t2g4(S = 1) low spin (LS) state actually is an intermediate spin (IS) state, but in no case the S = 0 state can be the ground state in an octahedral site of Oh symmetry owing to the Hund’s rule. Depending on whether the site is singly (so) or doubly occupied (do) and whether the spin is a majority (denoted α) or minority (denoted β) one, the electron energies respectively are:
In the same way as above, we obtain for the total energy:
It should be pointed out that in a Td tetrahedral site where the e orbitals are stabilised by –2.67 Dq and t2 orbitals are lifted by 1.78 Dq, the e4 LS (S = 0) configuration reversely becomes stable vs the S = 1 state. The energy of an electron belonging to one of the two doubly occupied degenerate e-orbitals (as there is the same number of spin up and spin down electrons) is:
Making equal the ET energies of the HS (S = 2) and IS (S = 1) states of a d4 ion in Oh symmetry leads to JH/Dq = 2. For high values of JH, the HS state is stable and for high values of Dq the IS state on the contrary becomes the ground state.
In Td symmetry, the condition for passing from S = 2 to S = 0 becomes JH/Dq = 1.1125.
For the d5and d6 cations, the IS state (S = 3/2 or S = 1, respectively) is unstable in Oh symmetry from the following conditions: in the d5 case, the LS→IS transition requires JH/Dq > 5/2, but the IS→HS transition requires only JH/Dq > 5/3. Therefore, one predicts a direct LS→HS transition which is actually expected for JH/Dq > 2. In the d6 case, the LS→IS transition requires JH/Dq > 10/3, the IS→HS transition only JH/Dq > 2. The direct LS→HS transition occurs at JH/Dq > 2.5.
3 Influence of a structural distortion on spin transitions of a d4 ion
Let us first consider the case in which one of the six oxygen atoms moves away from the central ion, the coordination progressively changing from octahedral of Oh symmetry to a (5 + 1) coordination of C4v symmetry until the limiting case of the square based pyramid is reached. In this type of coordination, a simple crystal field approach gives the following energy values in Dq units for the five d orbitals [6]:
In octahedral (Oh) coordination:
We assume that the magnitude of the distortion can be measured by a coefficient k (0 ≤ k ≤ 1) and that the energy of the orbital i is a function of k:
For instance, in the present case, with and , we obtain:
Using these energy values Ei(k,Dq) to take into account the crystal field effect in the computation of the atomic orbital energies including the exchange correlation effects and then in the computation of the overall energy of the ion for each configuration, the following relations are obtained for the three possible spin equilibria:
It is now possible to delimit in a JH/Dq-vs-k diagram the existence domains of each electronic configuration, S = 2, S = 1 and S = 0 (Fig. 3).
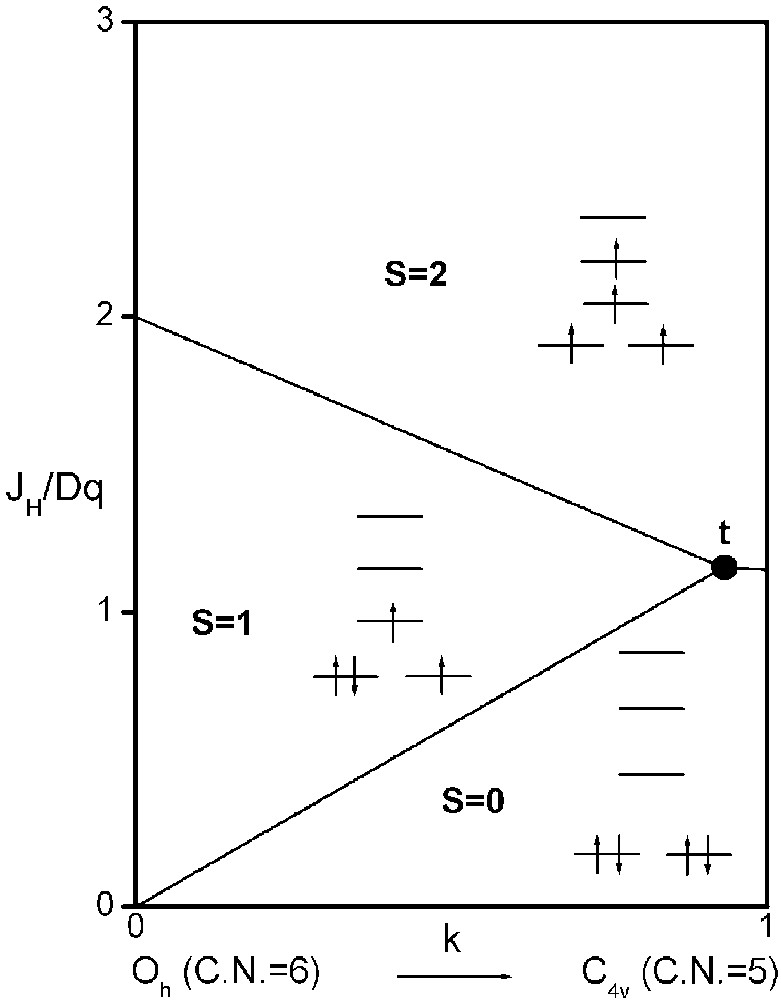
Spin-state phase diagram for a d4 ion in C4v symmetry depending on exchange (JH), crystal field (Dq) and distortion (k) parameters.
The three straight lines intercept at a triple point t of abscissa kt where the three spin states are simultaneously stable (kt = 0.923 and JH/Dq = 1.142). As usual, if we look for the more stable state, only three half-line starting from t correspond to an actual equilibrium. As already pointed out, S = 0 cannot be stable in Oh symmetry. On the other hand, S = 1 cannot exist beyond the k value of 0.923. We can extend the calculations of the crystal field contribution to the five 3d atomic orbitals to the seven types of distortions illustrated in Fig. 2 , which encompasses most of the crystal sites usually observed in transition metal oxides. In cases (4) and (7), k represents a rotation from 0 to 60° and from 0 to 45°, respectively. Case (5) corresponds to a hypothetic case progressively passing from an octahedron (CN = 6) to a tetrahedron (CN = 4). The orbital energies are given in Table 1. The JH/Dq-vs-k diagrams are given for each spin state in Figs. 4–6 , for 3d4, 3d5, and 3d6 ions, respectively. These diagrams show that, whereas in Oh symmetry no value of JH/Dq allows to stabilise the three possible spin states of the d4, d5 and d6 ions – at least for narrow d levels –, most of the distortions (C4v, D4h, D∞ h, D3 h, D4d) allow it, with one triple point t or even two triple points t1 and t2. For a d4 ion in D4h symmetry (i.e. an octahedron distorting into a square) kt1 = 0.465 and kt2 = 0.735, and for a d5 ion in D3 h symmetry (i.e. an octahedron distorting into a triangle based prism), kt1 = 0.175 and kt2 = 0.728. Some diagrams exhibit particular points of abscissa kc generally corresponding to the energy crossover of some atomic orbitals as k varies. Let us finally notice that predicted spin transitions are occurring for JH/Dq values close to 2 (±0.5). As according to literature, depending on the covalence of the bond, JH values are ranging from 0.6 to 0.9, such spin transitions are expected for Dq values ranging from 1.2 to 1.8 eV (i.e. from 2400 to 3600 cm–1 ± 25%).
Energies (in Dq units) of the five d orbitals for the site distortions illustrated in Fig. 2.
| dz2 | dx2 – y2 | dxy | dxz,yz | |
| C4v | 6 – 5.14 k | 6 + 3.14 k | –4 + 3.14 k | –4 – 0.57 k |
| D4h | 6 – 10.28 k | 6 + 6.28 k | –4 + 6.28 k | –4 – 1.14 k |
| D∞h | 6 + 4.28 k | 6 – 12.28 k | –4 – 2.28 k | –4 + 5.14 k |
| D3h | 6 – 5.04 k | 6 – 11.84 k | –4 – 1.84 k | –4 + 9.36 k |
| Td (hyp.) | 6 – 8.67 k | 6 – 8.67 k | –4 + 5.78 k | –4 + 5.78 k |
| Oh (CN8) | –2.67 – 2.67 k | –2.67 – 2.67 k | 1.78 + 1.78 k | 1.78 + 1.78 k |
| D4d | –5.34 | –5.34 + 4.45 k | 3.56 – 4.45 k | 3.56 |
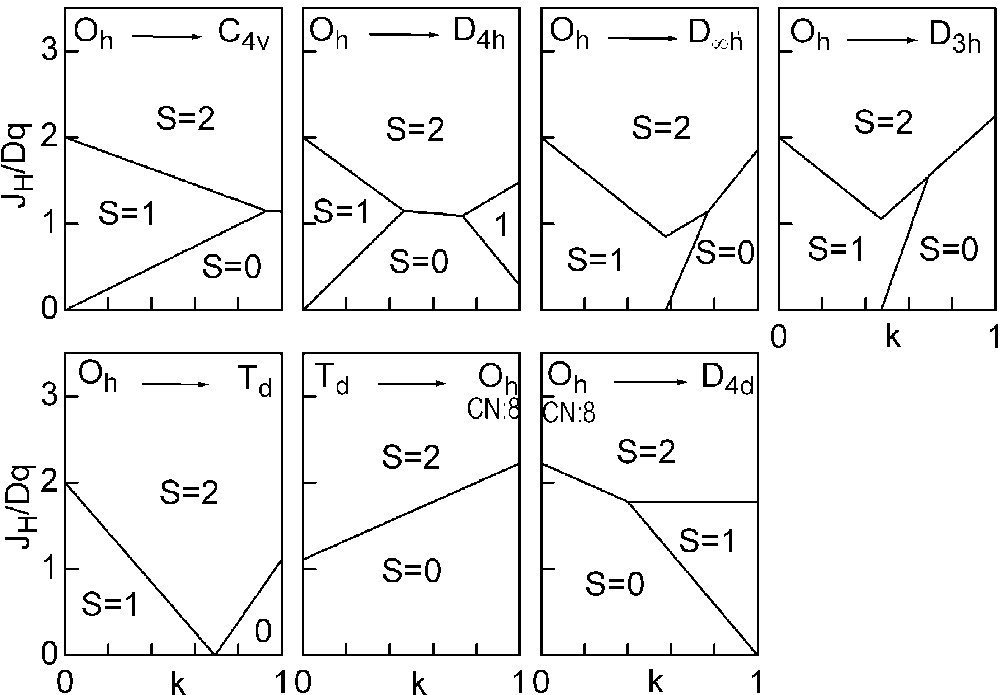
Spin-state phase diagram for a d4 ion in the various symmetry sites shown in Fig. 2.
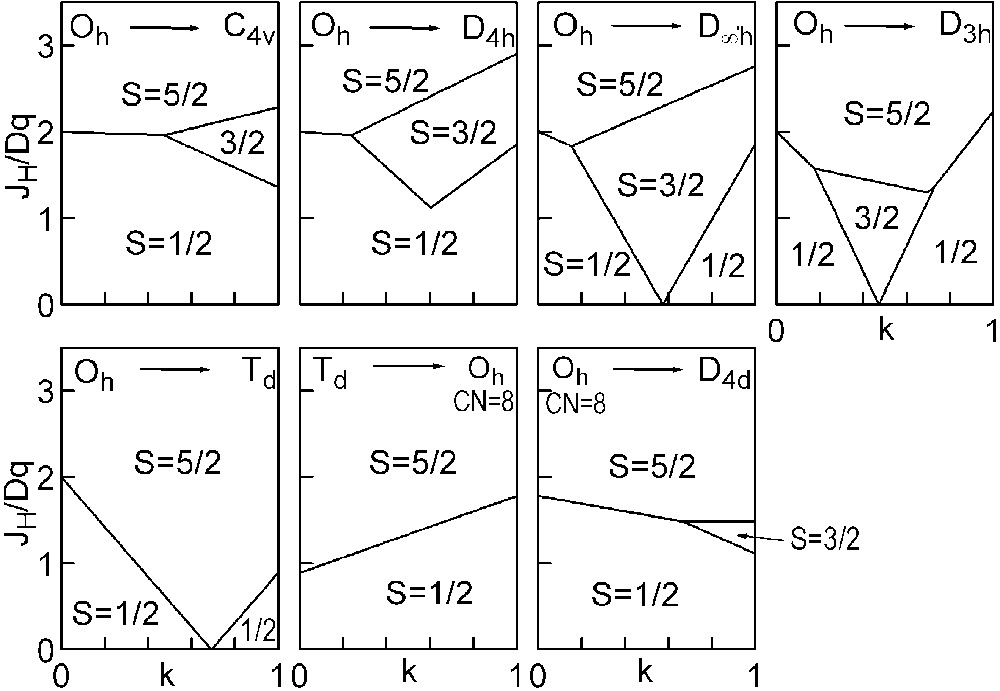
Spin-state phase diagram for a d5 ion in the various symmetry sites shown in Fig. 2.
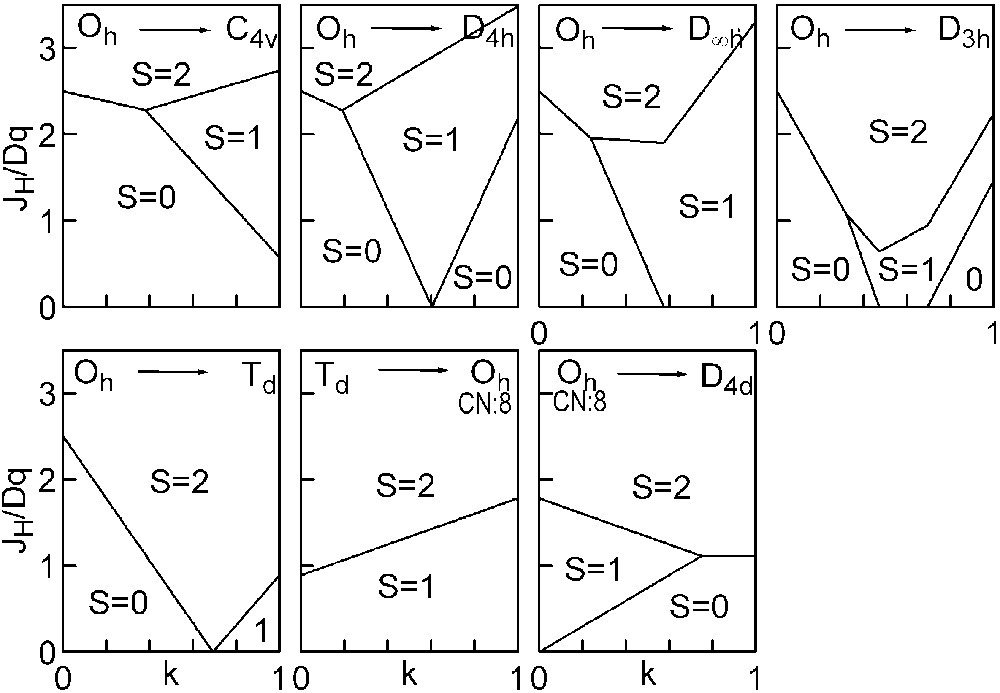
Spin-state phase diagram for a d6ion in the various symmetry sites shown in Fig. 2.
4 Energies of atomic orbitals for dn (n = 4, 5, 6) ions at the triple point taking into account exchange and correlation
In Fig. 7 we give the orbital splitting for dn (n = 4, 5, 6) ions at some triple points (t) of the above diagrams (D4d: d4; C4v: d5 and d6) for each of the three spin states.
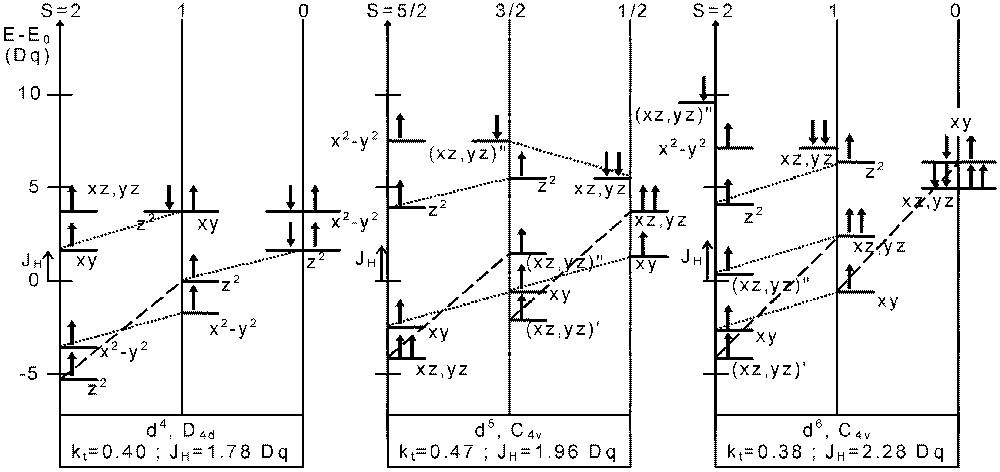
Atomic orbital energies at the triple point determined in Figs. 4–6 for d4 in D4d, d5 and d6 in C4v symmetry. The origin for the energy scale is E0 = 3 U’ – 3 JH, E 0 = 4 U’ – 4 JH, E0 = 5 U’ – 4 JH for d4, d5 and d6, respectively. Dotted lines and dashed lines indicate JH and 3 JH energy differences, respectively. In some cases, (′): singly occupied orbitals, (′′): doubly occupied orbitals.
In each case, we can point out that various orbitals with majority α spin and minority β spin are degenerate. For instance, for a d6 ion in C4v symmetry, the dαdoxy or orbital from S = 0 is degenerate with dαz2 from S = 1. In the same way, from S = 1 is degenerate, with dαx2-y2 from S = 2.
For a band diagram, in the vicinity of the triple point, bands with different symmetry and spin directions will thus overlap.
Hence, starting from S = 1, a spin equilibrium will be described as:
- • (i) the excitation of an electron from into (empty) dαx2-y2 with a spin flip; all the α spin states will be stabilised by –JH and the energy of the remaining electron will increase by + JH; in this way we have got the S = 2 (HS) state of Fig. 7;
- • (ii) the excitation of an electron from dαz2 into dαsoxy with a spin flip; it will increase the stability of the β spin states (by –JH); we shall then obtain the S = 0 (LS) state ofFig. 7.
In the case of the d4 ion, we even observe a degeneracy of the HOMO – including both spin directions – of all the three (S = 0, 1 and 2) spin states simultaneously.
For S = 1, the HOMO itself contain both majority and minority spin states.
5 Discussion
5.1 Structural distortions and stabilisation of unusual electronic configurations
5.1.1 d4 ion
Fig. 4 shows that any distortion of the coordination polyhedron with respect to the Oh (CN = 6) symmetry – with the exception of the prismatic D3h distortion – favours the HS configuration (S = 2). This is the well-known Jahn–Teller effect. On the other hand, a very unusual LS (S = 0) e4 configuration is favoured in cubic (CN = 8) coordination as well as in triangular prismatic (CN = 6) coordination as a result of the strong stabilisation of the dx2-y2 and dxy orbitals.
5.1.2 d5 ion
The usual configurations are HS (S = 5/2) and LS (S = 1/2). An IS (S = 3/2) configuration is possible, especially in C4 v and D4 h symmetry, and for realistic (close to 2) values of JH/Dq. This IS configuration could also be associated with a metallic state.
5.1.3 d6 ion
This is the most favourable number of d electrons for stabilising a LS (S = 0) configuration in an oxygen surrounding as the transition is occurring at JH/Dq = 2.5, corresponding to the lowest Dq value.
Obviously, the square planar D4h symmetry is the most appropriate for the IS (S = 1) state (see, for instance, [7] ) as well as the much more unusual D∞h (CN = 2) one.
5.2 Exchange, correlation and covalence
U, U′ and JH first are atomic parameters measuring the exchange and correlation effects. As for Racah parameters and particularly B parameter, their values decrease with the hybridisation of metal 3d orbitals with oxygen 2p orbitals, i.e. the covalence of the M–O bond. As we have pointed out earlier [7], the energies of the electrons with majority α spin state are lowered by a value that can reach several times (up to 6 times in some cases) that of JH, which therefore favours the covalence of the M–O bond, whereas the contribution of electrons with minority β spins is more ionic – the covalent stabilisation is proportional to where βMO is the resonance integral of the bond and Hii (X) the Coulomb integral of the atom X [8]. This model provides a simple explanation for the high rate of metal-to-ligand hole transfer generally denoted (O–) or even and observed by XAS for ions such as Fe4+, Co4+, Ni3+ or Cu3+.
5.3 Exchange, correlation and insulating vs metallic character
The metallic-vs-insulating character of a transition-metal oxide depends on the relative magnitude of the transfer energy βMO or of the bandwidth W and of the so-called Coulomb intra-atomic repulsion UHubbard, corresponding, in an ionic model, to the charge transfer Mn+ + Mn+ → M(n–1)+ + M(n+1)+. An upper limit of U Hubbard is then given by the difference between the (n + 1)th and nth ionisation energies. Actually UHubbard and W are not independent and UHubbard decreases as W increases. The Mott–Hubbard metal–insulator transition is thus governed by the magnitude of the U Hubbard/W ratio.
For a given dn configuration, it is then important to evaluate the orbital energy of the d n +1 configuration for the various possible spin states as a function of U or U′, and the type of orbital overlap that controls the value of W and thus the stabilisation due to the transfer. For instance, one sees that for a HS (S = 5/2) d5 ion in C4v symmetry only the HS d6 configuration involving the π-type dxz,yz orbitals is concerned (Fig. 7), whereas a IS (S = 3/2) ion can lead to two possible states S = 2 or S = 1 of the d6 configuration. Thus, the insulating-vs-metallic character of a dn transition metal oxide results from the magnitude of the energy gap separating the dn from the dn+1 configurations.
Confining us to the Oh symmetry and to the above d5/d6 case, the following electronic transitions can be considered, in which the type of bonding involved in the charge transfer is given between parentheses:
- • (i) d5HS+ d5HS → d4HS + d6HS (σ, π)
- • (ii) d5IS+ d5IS → d4IS + d6HS (σ)
- • (iii) d5IS+ d5IS → d4HS + d6IS (π)
- • (iv) d5LS+ d5LS → d4IS + d6LS (π)
for each of them we can calculate the energy gaps using the total energies including exchange, correlation and crystal field contributions for all the valence electrons (Table 2).
Exchange and correlation energies for valence electrons of various d4, d5 and d6 configurations.
| HS | IS | LS | |
| d4 | 6 U' – 6 JH – 6 Dq | U + 5 U' – 3 JH – 16 Dq | |
| d5 | 10 U' – 10 JH | U + 9 U' – 6 JH – 10 Dq | 2 U + 8 U' – 4 JH – 20 Dq |
| d6 | U + 14 U' – 10 JH – 4 Dq | 2 U + 13 U' – 7 JH – 14 Dq | 3 U + 12 U' – 6 JH – 24 Dq |
With the exception of (i), all the transfers correspond to a minimal energy of U′ – JH. For the first case, the gap (U′ + JH, assuming JH/Dq = 2) is less favourable to such a transfer.
However, only (ii) involves σ-type bands that are broader than π-type ones. The ratio (U′ – JH)/Wσ is then the most favourable for the formation of a metallic state from an IS state.
In the case of a lower symmetry favouring the HS↔IS spin equilibrium (Fig. 5), it should be noticed that case (i) can be split into two steps:
- • (i′) d5HS + d5HS → d5IS + d5HS
- • (i′′) d5IS + d5HS → d4HS + d6HS (σ)
the gap corresponding to (i′′) is equal to U′.
This HS/IS configuration mixing could also lead to a metallic state, as it implies a σ-type transfer.
This simple ionic-type approach of exchange and correlation explains the insulating behaviour of LaFeO3and of LaCoO3 at low temperature as well as the transition to a metallic behaviour at high temperature for the latter.
Indeed, for Fe3+ in LaFeO3, the JH/Dq ratio, much larger than 2.5, favours the exchange energy gain with respect to the crystal field and leads to a HS state. The upper Hubbard band corresponding to the HS d6 configuration lies at a much higher energy than the lower Hubbard band and is well separated from it, which accounts for the insulating character.
On the other hand, in LaCoO3, Co3+ is in a LS
we have to compare the energy of iron d orbitals (EFe:3d = –16.5 eV) modified by crystal field, exchange and correlation effects (tαso2g of Fe2+ is shifted by 6 JH above ) with that of M5+ ions orbitals (Mo5+: 4d1, W5+: 5d1, Re5+: 5d2), the energies of which depend on the main quantum number n and atomic number Z (EMo:4d = –11.5 eV, EW:5d = –11.0 eV, ERe:5d = –12.3 eV) (Fig. 8).

M5+/Fe3+charge transfer in Sr2FeMO6 (M = Mo, W, Re) perovskites.
We now understand why a partial transfer is possible in the molybdenum and rhenium cases: a band of the Fe–Mo(Re)–O type involving mixed valences FeIII/FeII and MoV/MoVI gives rise to a metallic character and strong ferromagnetic interactions between localised iron moments via the itinerant π*β electrons accounting for a high Tc value.
The highest energy of tungsten 5d orbitals leads to a complete charge transfer, giving single valence Fe2+(3d6) and W6+ (5d0) ions, resulting in an insulating character and weak antiferromagnetic interactions (TN ≈ 20 K) between Fe2+ ions.
6 Conclusions
In order to clarify the competition of exchange and correlation energies vs crystal field stabilisation energy, a simple approach is proposed. The exchange and correlation contributions have been described on the base of Brandow and Kanamori’s U, U′ and JH parameters. The dependence of the crystal field on site distortion has simply been modelled using a linear interpolation between undistorted and fully distorted site. This approach led to establish phase diagrams for d4, d5 and d6 cations, allowing us to predict the spin-state stability range depending on exchange (JH), crystal field (Dq) and distortion (k) parameters. It can be used to complement the Extended Hückel Tight Binding calculations of the electronic structure of materials with a noticeable ionic character such as 3d transition-metal oxides, in order to interpret their electronic behaviour and, particularly, discuss their insulating-vs-metallic character, as we recently did [13] .


