1 Introduction
A renewed interest for CuFeO2 delafossite-type oxides has been observed in the last few years. The reason is that, in addition to previously mentioned applications of these materials such as catalysis [1], new areas seem to be concerned such as transparent p-type conductors [2] and thermoelectric conversion [3]. The delafossite structure also provides triangular lattices appropriate for investigating frustrated magnetic systems [4]. From the point of view of crystal chemistry, we have recently shown that, although CuVO2 does not exist, V+III can be stabilized in the delafossite networks of CuFe1–xVxO2 solid solutions [5]. This shows that a delafossite solid solution can be prepared even when one of the end members does not exist. The case of the CuNi1–xVxO2 compositions is interesting, since CuNiO2 does not have a delafossite-type structure, but exhibits a rocksalt-related structure in which copper is divalent instead of being monovalent, which is actually required for stabilizing the delafossite structure.
2 Sample preparation
Polycrystalline samples of nominal compositions CuNi1–xVxO2 with x = 1/3, 1/2 and 2/3 were prepared by heating stoichiometric mixtures of Cu, CuO (Merck, 99.9%), NiO (Strem Chemicals, 99.99%) and V2O5 (Schüchardt München, 99.8%) in an evacuated silica tube. Experimental conditions and reaction product compositions, determined by XRD analysis, are summarized in Table 1.
Conditions for sample preparation
| x-Value in CuNi1–xVxO2 | Starting mixture | Reaction temperature (K) | Reaction time (h) | Colour of reaction product | Reaction products |
| 1/3 | 3 Cu + 3 CuO + 4 NiO + V2O5 | 870, 970 | 24 | dark green | Ni3V2O8 + Cu2O + NiO |
| 1/2 | CuO + 3 Cu + 2 NiO + V2O5 | 870, 920, 970, 1 070 | 12, 24 | orange–yellow | delafossite phase + Ni3V2O8 + Cu2O + NiO |
| 2/3 | 3 Cu + NiO + V2O5 | 920, 970 | 24 | black | single delafossite phase |
Only for x = 2/3 a single phase was obtained. Its stability in air was studied by TGA. Fig. 1 shows that, at a heating rate of 110 K per hour, weight uptake starts at 450 K and that the oxidation process is complete at 650 K. Assuming that the oxidized material contains divalent copper, divalent nickel and pentavalent vanadium, the theoretical weight gain should be of 10.72%. The experimental value (9.5%) is slightly smaller. At least three effects can account for this discrepancy. First the oxidized products can be oxygen-deficient, as it is well known for V+V oxides. Second oxygen can be intercalated into the starting delafossite network. However, this latter effect should be limited as, first, the synthesis is carried out in an evacuated sealed ampoule and, secondly, the lattice constant a is not large enough to allow large amounts of intercalated oxygen, like, for instance, in rare-earth delafossites [6]. The third effect could be an unexpected very weak deviation of the Cu/Ni/V ratios from 3/1/2, such as, for example, a Ni/V ratio slightly larger than 1/2.
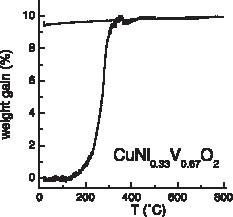
TGA of CuNi1/3V2/3O2 under oxygen. Heating rate: 110 °C h–1.
3 Structural characterization
Powder XRD data of CuNi1/3V2/3O2 were collected using the experimental conditions given in Table 2.
Conditions for powder XRD data collection and Rietveld refinement of CuNi1/3V2/3O2 in
| Diffractometer | Philips X′Pert MPD |
| Radiation | Cu Kα |
| Temperature | RT |
| 2θ range (°) ; step (°) ; counting time (s) | 5–120; 0.02; 19 |
| Rietveld program | Fullprof [7] |
| Profile function | pseudo-Voigt |
| Number of reflections | 41 |
| Number of fitted parameters | 16 |
| Rpa | 0.030 |
| Rwpa | 0.046 |
| Conventional Rpb | 0.18 |
| Conventional Rwpb | 0.14 |
| R-Bragg | 0.057 |
| χ2 | 5.6 |
a R-factors not corrected for background.
b Conventional Rietveld R-factors corrected for background.
Cell and structural parameters were refined using the Rietveld method. Program reference [7] and refinement conditions are also mentioned in Table 2. Crystal system, space group, lattice constants and other crystallographic and structural data are given in Table 3.
Crystallographic data of CuNi1/3V2/3O2
| Crystal system | rhombohedral |
| Space group | |
| Z | 3 |
| a (Å) (hexagonal cell) | 2.9865(2) |
| c (Å) (hexagonal cell) | 17.191(1) |
| Unit cell volume (Å3) (h.c.) | 132.79 |
| Molar mass (g mol–1) | 149.08 |
| Calculated density (g cm–3) | 5.59 |
| Measured density (g cm–3) | 5.57 |
The refinement procedure finally provided the atomic positions and the isotropic thermal parameters reported in Table 4. Experimental and calculated diffractograms are displayed in Fig. 2 .
Atomic position parameters for CuNi1/3V2/3O2
| Atom | Multiplicity and Wyckoff site | x | y | z | B (A2) | Fractional occupancy |
| Cu | 3a | 0 | 0 | 0 | 1.1(2) | 1 |
| Ni | 3b | 0 | 0 | 1/2 | 0.7(2) | 1/3 |
| V | 3b | 0 | 0 | 1/2 | 0.7(2) | 2/3 |
| O | 6c | 0 | 0 | 0.106(1) | 1.5(4) | 1 |
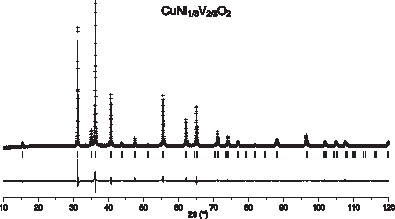
Measured (discrete points) and calculated (solid line) XRD intensities and their difference for CuNi1/3V2/3O2, at room temperature. Peak positions are indicated by vertical lines.
Interatomic distances are given in Table 5.
Main interatomic distances (Å) and bond angles (°) in CuNi1/3V2/3O2
| Cu–O | ×2 | 1.82(2) | O–(Ni,V)ii–Oi | 95.6(4) |
| (Ni,V)ii–O | ×6 | 2.02(1) | O–(Ni,V)ii–Oiv | 84.4(8) |
| O–Oi | ×6 | 2.9865(2) | Cu–O–(Ni,V)ii | 121.2(6) |
| O–Oiv | ×3 | 2.71(2) | (Ni,V)ii–O–(Ni,V)iii | 95.6(4) |
| Symmetry code | none | x | y | z |
| i | x | y – 1 | z | |
| ii | x + 1/3 | y + 2/3 | z – 1/3 | |
| iii | x + 1/3 | y – 1/3 | z – 1/3 | |
| iv | x + 2/3 | y + 2/3 | 1/3 –z |
The Cu–O distance (1.82 Å) is in good agreement with the sum of ionic radii (1.84 Å) assuming CN = 2 for Cu+ (0.46 Å) and CN = 4 for O2– (1.38 Å) [8]. As no superstructure peak was observed, we shall assume, in this preliminary report, that the Ni and V atoms are randomly distributed (neutron diffraction experiments are planned to verify this assumption). In these conditions, the M–O distance (2.02 Å) leads to an average ionic radius of 0.64 Å for M-atoms (taking rO2–IV=1.38Å from the Shannon table as oxygen is fourfold coordinated [8]). This value can be compared to two formal hypotheses concerning the oxidation states of Ni and V either Ni2+ + V4+ + V3+ or Ni3+(LS) + 2 V3+. The possibility of Ni3+(HS) is discarded as the HS state was never found in such a D3d site [9]. In the first case, the average ionic radius would be 0.637 Å and in the second case 0.613 Å. The comparison with the experimental value of 0.64 Å is in favour of the first hypothesis, which is the one expected if we consider that the redox equilibrium:
| (1) |
4 Magnetic and electrical properties
Magnetic measurements were performed between 4 and 300 K with a SQUID equipment.
The sample was first cooled in a zero magnetic field (ZFC); the magnetization was measured upon increasing temperature, under 1 T, and then decreasing it (FC). No difference was observed between the two curves. The temperature dependence of the reciprocal molar susceptibility is given in Fig. 3 . A linear variation is observed between 200 and 300 K. Fitting with a Curie–Weiss law leads to a molar Curie constant CM = 0.86 (emu) and a Weiss parameter θp = –80 K. The theoretical spin-only value expected is 0.792 for the two hypotheses illustrated by each side of equilibrium (1). We note that the hypothesis in which trivalent nickel would be in a high-spin state would lead to a spin only CM value of 1.292 and hence can be ruled out in agreement with previous studies [9]. The negative θp value reveals that dominant magnetic interactions are antiferromagnetic (AF). However, the behaviour of the reciprocal susceptibility appears rather unusual with respect to that of the previously investigated delafossite oxides containing a single trivalent transition element [10]. The 2D character of the structure generally leads to a minimum in the temperature dependence of the reciprocal susceptibility. This more or less broad minimum is due to short-range spin ordering or spin fluctuations. Instead, in CuNi1/3V2/3O2, the reciprocal susceptibility decreases more rapidly than what is predicted by the Curie-Weiss law. Accounting accurately for such a behaviour would require an appropriate modelling of the system in which at least three types of nearest neighbour interactions should be taken into account, provided that trivalent nickel and vanadium would coexist: V–V, Ni–Ni, and V–Ni interactions. In the other hypothesis, six different types of interactions are theoretically possible and the mixed valence V3+/4+ could also give rise to a mechanism of double exchange. Anyway, no long-range ferro- or ferrimagnetic ordering takes place, as the susceptibility does not diverge at a finite temperature. Whether an AF long-range order occurs at low temperature cannot simply be deduced from the present results. We made an attempt to clarify this point using X-band EPR. Unfortunately, the material is EPR silent at room temperature and only an extremely weak signal is detected at 4 K. The absence of signal at room temperature, at first sight, could rule out the presence of LS Ni3+ (and hence V3+), which gives a large broad signal in AgNiO2 [9]. However, we have observed that in CuM1–xVxO2 (M = Cr, Fe), the presence of V3+ kills the signal expected from the other transition element. At the present time, we do not understand well this effect and its explanation will require further studies. One possible reason would originate from either dynamic charge fluctuations or dynamic spin fluctuations.
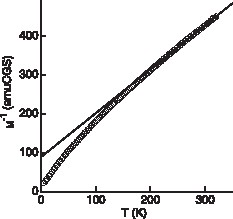
Temperature-dependence of the reciprocal magnetic susceptibility of CuNi1/3V2/3O2.
The electrical conductivity is thermally activated, but does not follow an Arrhenius law. It can be fitted according to σ = σ0 exp(–B/Tn) with n = 0.26. This n value is very close to 1/4, a value that was predicted by Mott for the case where the prevailing conduction mechanism is variable-range hopping (VRH) and electron–electron correlations are not taken into account [11]. The logarithm of the electrical conductivity is plotted as a function of T–1/4 in Fig. 4 , showing the expected linear dependence over the whole temperature range in which the measurements were carried out.
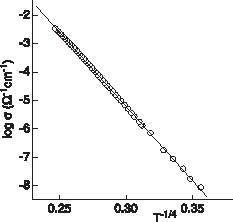
Logarithm of the electrical conductivity of CuNi1/3V2/3O2 vs. T–1/4.
5 Discussion
The only pure sample that could be synthesized in the system CuNi1–xVxO2 is CuNi1/3V2/3O2. On the basis of the bond-length arguments given above, we suggest that nickel is divalent and that vanadium is in a +III/+IV mixed valence state. This assumption is supported by the consideration that Ni3+ is strongly oxidizing with respect to V3+.
The nickel and vanadium atoms occupy a flattened octahedron undergoing a D3d distortion that splits the degenerate t2g orbitals into a more stable orbital singlet, a1, and two degenerate e orbitals at a higher energy. Assuming 1.5 electrons per vanadium atom, the a1 band is half occupied and the e band is one eights occupied. As the electron density of the a1 orbital is rather located out of the M layer, the a1 band should be rather narrow and the corresponding electrons are localized. The opposite holds for the e band. However, two effects should limit its bandwidth We. The first one is the 2D character of the structure and the second one is the dilution effect, as one third of the vanadium atoms is replaced by nickel. As no metallic behaviour is experimentally observed, we may conclude that the bandwidth is not large enough to overcome the correlation effects. The resulting state, especially when one deals with cations of d1 and d2 configurations, is generally unstable with respect to the formation of metal–metal bonds. XRD did not reveal any superstructure that could have accounted for an ordered arrangement of such pairs. However, pairs can be randomly distributed and move via an activated electron hopping process. The picture is strongly supported by the observation of the Mott T–1/4-behaviour for the electrical conductivity as the VRH mechanism is observed when disorder creates a modulation of the potential energy at the available sites [11].
6 Conclusion
Whereas neither delafossite-type CuVO2 nor CuNiO2 exist, we succeeded in preparing CuNi1/3V2/3O2 using classical solid-state reaction. The most probable formal oxidation state for nickel is II, while for vanadium it is a mixed state +III/+IV, as can simply be anticipated from the strong oxidizing character of Ni3+ and the strong reducing character of V3+. Nevertheless, this should be confirmed, and more sophisticated methods than those used up to now are needed. Although it can be clearly stated that the predominant magnetic interactions are antiferromagnetic, an accurate modelling of the magnetic behaviour still requires further investigations. Actually, the edge sharing (MO6) octahedron triangular network leads to weak superexchange interactions as the M–O–M angle is close to 95.6° and favours frustration effects. In addition, a double exchange mechanism associated with electron hopping from V3+ to V4+ cations – more or less randomly distributed – could also play a part in the magnetic behaviour. At this stage of the study, this hopping process is considered to be the main cause of the charge transport observed in the oxide and accounts for the T–1/4-dependence of the electrical conductivity.
Acknowledgements
We acknowledge technical assistance from Joël Villot (density measurements), Philippe Dagault (TGA), Rodolphe Decourt (resistivity measurements). We also thank Dr. J.-M. Bassat for help with EPR measurements, and Profs G. Villeneuve and P. Gravereau for helpful discussions.



Vous devez vous connecter pour continuer.
S'authentifier