Nonlinear dynamics of a magnetization subject to RF feedback field: new experimental evidence

Alain Louis-Joseph; Jean-Yves Lallemand; Daniel Abergel

doi:10.1016/j.crci.2003.10.016

Résumés

Anglais
Français

In a recent study, the dynamics of large magnetization subject to a RF feedback field from the detection circuit of the probe was investigated both theoretically and experimentally. A simple model including non-linear modification of the Bloch equations allowed us to predict the occurrence of repeated bursts of NMR transverse magnetization during evolution (named self-sustained maser pulses). However, the decay of the amplitude of these repeated maser pulses with a characteristic time 4T₁ predicted by this simple model could not be observed and the experiments showed a regime of non-attenuated self-sustained maser pulses. This was interpreted as a direct consequence of B₀ inhomogeneities. In this paper we present new experimental evidence that support this assumption and that further demonstrate the role of B₀ inhomogeneity.

Dans un article récent, nous avons étudié théoriquement et expérimentalement le comportement quelque peu inattendu d'une aimantation intense, comme celle du solvant en RMN biologique, soumise à un champ de contre-réaction issue de la sonde. Sur les bases d'un modèle simple, nous avons montré que l'on pouvait prédire des trains d'impulsions maser au cours de l'évolution du signal de libre précession (FID, Free Induction Decay). Cependant, contrairement à la théorie, les données expérimentales ne montraient aucune décroissance caractéristique en 4T₁ des amplitudes masers au cours du temps. Nous avions alors émis l'hypothèse de l'effet del'inhomogénéité du champ magnétique statique. Dans cette note, nous présentons des observations expérimentales qui confirment cette hypothèse.

1 Introduction

The dynamics of an ensemble of spins that do not exhibit mutual couplings may be described by the Bloch equations [1]. The evolution of the magnetization is the combination of a precession about a magnetic field and of a damping of its longitudinal and transverse components with respective relaxation rates 1/T₁ and 1/T₂. However, in the presence of radiation damping, the Bloch equations must be modified [2]. Indeed, radiation damping [3] results from the interaction between a large magnetization and the radio frequency field that it induces in the detecting coil. A magnetization-dependent RF field is thus generated, which is proportional to the transverse component of the magnetization and perpendicular to it. This is known to have various unfortunate consequences in high-field NMR spectroscopy, which are mainly due to an uncontrolled behaviour of the water magnetization.

Therefore, numerous approaches have been proposed to efficiently suppress radiation damping or its consequences [4,5]. Among these, some more ambitious schemes aimed at compensating radiation damping by means of an electronic feedback from the probe [6,7]. In the methodology developed by the authors, a radiofrequency feedback field is generated, whose intensity and phase with respect to the transverse component of the magnetization may be entirely controlled, which, as discussed elsewhere [7], allows either suppression or amplification of the radiation damping field. This approach has been shown to be quite versatile and has led to several applications, such as enhancement of solvent suppression [8] or the study of water–protein interactions [9] or the introduction of a new concept of selective excitation of the solvent with interesting properties of phase and length self-calibration [10,11].

Recently [12], the non-linear Bloch equations (NLBE) governing the dynamics of a magnetization undergoing the effect of a feedback field of arbitrary amplitude and phase were investigated in details, both theoretically and experimentally.

It was shown that under certain conditions of phase and gain, the feedback field could induce unconventional long-time behaviour in the form of repeated bursts of in-plane magnetization, reminiscent of the so-called maser pulse caused by radiation damping, and therefore designated as self-sustained maser pulses. These were explicitly related to the simultaneous presence of T₁ relaxation and the antagonist RF feedback field from the probe; the former drives the magnetization to its equilibrium direction, whilst the latter rotates the magnetization towards the z direction, for certain values of phase and intensity. However, the characteristic damping of these bursts of in-plane magnetization could not be observed. This was interpreted by assuming a role of inhomogeneous static magnetic field, which was supported by numerical simulations.

The aim of this communication is to present recent experimental evidence supporting this assumption and to further discuss the influence of B₀ inhomogeneity on the amplitude of these repeated masers pulses.

2 Theory

In this section, we briefly recall the framework of this study. Consider the simple model of a magnetization M precessing in the magnetic induction field B₀ in the presence of a constant radiofrequency field B₁ with intensity B₁ = ω₁/γ and frequency ω_rf, which, without loss of generality, is assumed to be aligned along the x-axis in the rotating frame.

In addition, the back action of the probe onto the magnetization is expressed by a magnetization-dependent field B_FB:

𝐁_{FB} = γ G 𝐌_{t} e^{- i ψ}

(1)

with: M_t = M_x + i M_y, where G is the enhancement factor (gain) with respect to the magnitude of the transverse magnetization and ψ is the phase of the feedback field.

The dynamical equations governing the evolution of the magnetization are the following modified non-linear Bloch equations [12,13]:

{\begin{matrix} {\dot{M}}_{x} = δ M_{y} + γ {GM}_{z} (M_{x} \sin ψ - M_{y} \cos ψ) - M_{x} / T_{2}, \\ {\dot{M}}_{y} = - δ M_{x} - ω_{1} M_{z} + γ {GM}_{z} (M_{x} \cos ψ + M_{y} \sin ψ) - M_{y} / T_{2}, \\ {\dot{M}}_{z} = ω_{1} M_{y} - γ Gsin ψ (M_{x}^{2} + M_{y}^{2}) - (M_{z} - M_{0}) / T_{1} \end{matrix}

(2)

where δ = ω_rf – ω₀ is the frequency shift offset and T₁ and T₂ are the longitudinal and transverse relaxation times, respectively.

It is convenient to recast these equations by introducing the reduced dimensionless variables:

t \to ω_{1} t, γ G \to γ {GM}_{0} / ω_{1} = λ, δ \to δ / ω_{1}, T_{1, 2} \to ω_{1} T_{1, 2} = τ_{1, 2}, and M \to M / M_{0} = m

One thus gets:

{\begin{matrix} {\dot{m}}_{x} = δ m_{y} + λ m_{z} (m_{x} \sin ψ - m_{y} \cos ψ) - m_{x} / τ_{2} \\ {\dot{m}}_{y} = - δ m_{x} - m_{z} + λ m_{z} (m_{y} \sin ψ + m_{x} \cos ψ) - m_{y} / τ_{2} \\ {\dot{m}}_{z} = m_{y} - λ \sin ψ (m_{x}^{2} + m_{y}^{2}) - (m_{z} - 1) / τ_{1} \end{matrix}

(3)

Note that radiation damping corresponds to the special case where ψ = – π/2 and G = ηQ μ₀/2 in SI units, where η and Q are, respectively, the filling factor and the quality factor of the probe. In the remainder of this paper, only the simplest situation where no applied constant radiofrequency field B₁ is considered, but for sake of consistency with previous work, the general version of the NLBE is given here.

The dynamics of a large magnetization in radiation damping conditions is fairly well understood, and in fact quite simple in most situations of practical interest [4]. In other cases, and if relaxation is neglected, the motion is still limited to the Bloch sphere and, in the absence of a constant rf field, the north pole of the sphere is a stable equilibrium for sin ψ < 0 (the radiation damping case falls into this category), whereas the south pole is a stable equilibrium for sin ψ > 0.

In the presence of relaxation, however, the problem becomes more complex, and extensive study of the NLBE shows that under certain conditions and provided that sin ψ > 0, the magnetization reaches a state of steady-state precession about a constant field [1]. The approach to this equilibrium has also been studied and exhibits repeated bursts of in-plane magnetization whose intensities are damped, with a time constant 4T₁. This corrects an error in the text of ref. [12], where the time constant was erroneously written as T₁ instead of 4T₁. However, experiments showed the existence of self-sustained maser pulses without any clear attenuation of their magnitude. The interpretation was that B₀ inhomogeneity must be taken into account in the model. Therefore, the system studied should be treated as an ensemble of isochromats, with resonance frequencies spanning the inhomogeneous linewidth of B₀. Each of the isochromats is thus acted upon by a feedback field originating from itself and from all the other isochromats of the ensemble. In Fig. 1, simulations are shown to illustrate this point. It is seen that for relatively large inhomogeneous linewidth the model predicts multiple non-attenuated maser pulses (Fig. 1a). Moreover, simulations show that reducing inhomogeneous broadening progressively in the simulation reintroduces a decay of the pulses magnitude (Fig. 1b) which, in the case of vanishing inhomogeneous contribution to the linewidth reaches the theoretical 4T₁ exponential damping, characteristic of the simple non-linear Bloch equations (Eq. (2)) [1]. In the next section, experimental evidence is presented that further support this assumption.

Fig. 1
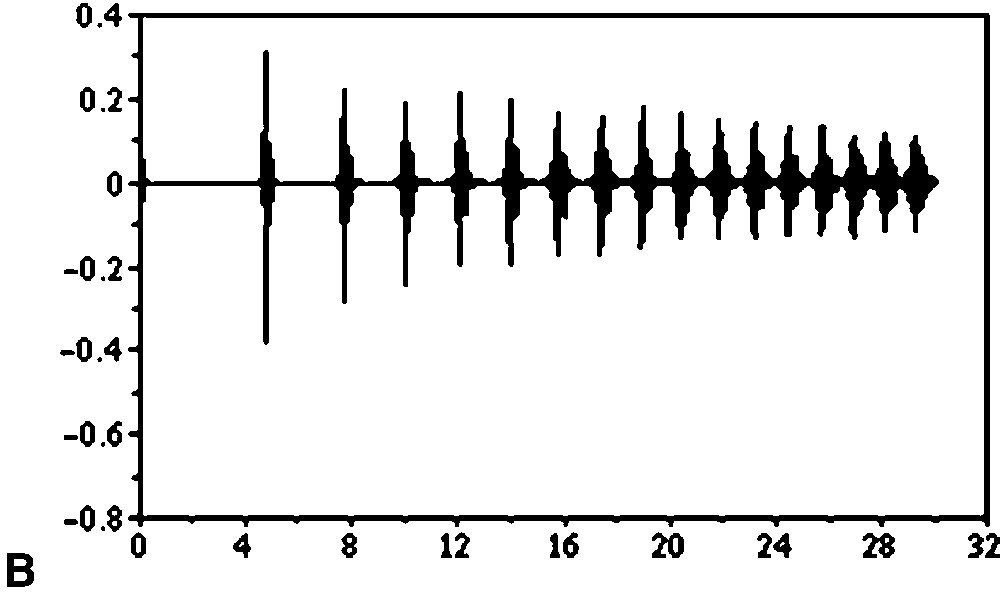
(a) Evolution (simulations) of the transverse component of the magnetization driven by an RF feedback field, in the presence of different inhomogeneous broadening. In both cases, numerical evaluation was performed using T₁ = 3.3 s and T₂ = 2.2 s, ψ = 70°. A Lorentzian-shape function was used for line broadening. In (a), line broadening is simulated with a T₂⁺ = 50 ms. In (b), line broadening is reducing to T₂⁺ = 150 ms.

3 Results. Discussion

Experiment were performed on Bruker DRX600 MHz spectrometer equipped with the Radiation Damping Control Unit (RDCU) hardware based on the authors’ prototype [7] and a high-Q TXI probe with Oz gradient facility. Radiofrequency feedback field, Eq. (1), was achieved by feeding into the probe a fraction of the residual water signal, after appropriate phase and gain adjustment. After optimum tuning and matching of the probe, amplitude and phase of the RDCU were carefully adjusted for cancellation of radiation damping, following a protocol described elsewhere [14], on a sample of 90% H₂O–10% D₂O. The basic experiment started with a hard pulse in order to create in-plane magnetization, then followed by acquisition during which feedback was turned on. The feedback power used for all experiments was 10 dB stronger than that needed for the suppression of radiation damping and the phase was set to values close to that of suppression. Signal was acquired during 32-s-long transients and self-sustained maser pulses were observed as expected. In addition, at this fixed feedback gain, the time interval between bursts increased as the feedback phase approached the phase for exact cancellation of radiation damping (Fig. 2a).

Fig. 2
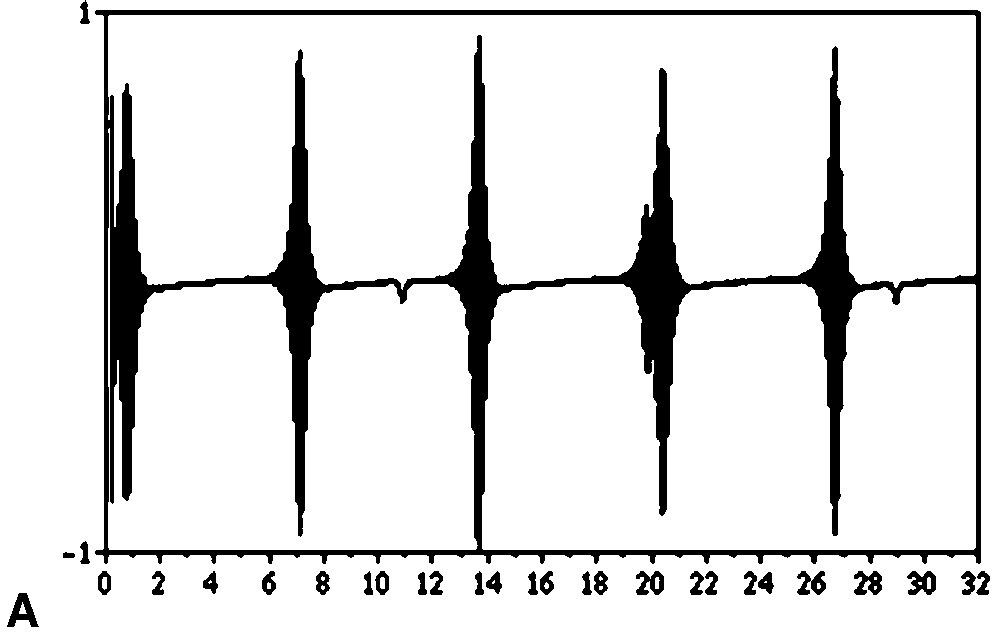
Experimental observation of self-sustained maser pulses. One transient acquired during 32 s, the spectral acquisition width was 250 Hz. The feedback gain used was 10 dB higher the one needed for cancellation of radiation damping, and the feedback phase was the one for cancellation. (a) Degradation of B₀ field homogeneity. Note the absence of the decay of maser pulse amplitude. (b) Similar experiment performed on the same sample, with a careful adjustment of the field homogeneity.

However, interestingly, after yet more careful adjustment of the field homogeneity a decay of the maximum intensity of these maser pulses towards a constant value was observed (4.4s for the FID shown in Fig. 2b). Although the time constant of the decay was substantially smaller than the 4T₁ predicted by the theory, it nevertheless brings new evidence that B₀ inhomogeneity is the cause of the discrepancy between theory and experiments.

Finally, it is noteworthy that the time delay between pulses increases with increasing inhomogeneity, in accordance with results from numerical simulation.

The interest of these observations is twofold. First, as mentioned above, it gives credit to a model proposed to account for the behaviour of the magnetization driven by a radiation-damping-based electronic feedback. Indeed, in a previous article, the assumption of B₀ inhomogeneity was postulated and the relevance of such an assumption was supported by experimental observation. However, the present findings bring further evidence that confirm this assumption by exhibiting a change in the time evolution of the signal (non-attenuated to attenuated) when the homogeneity of B₀ is spoiled. Note in addition that other factors may have an influence on the details of the dynamics of the magnetization, such as the presence of a weak constant RF leakage at the reference frequency of the synchronous detectors of the spectrometer, or the presence of dipolar field effects.

Second, it helps clarify the discussion on the possibility of observing chaotic behaviour in this context. Indeed, recent studies in high-resolution NMR of liquids have shown the existence of unconventional behaviour of the magnetization such as instabilities and possibly chaotic behaviour [15,16]. Here, the dynamics of the magnetization is governed by a set of non-linear differential equations and the discussion relies primarily on the choice of a model for the description of the experiments. Indeed, non-linear dynamical systems may admit chaotic behaviour. This, however, can only be the case for differential systems of dimension larger than 3 [17]. In the case of the NLBE, i.e., a simple set of three differential equations, it could be shown that non regular behaviour can only occur if (at least) an additional RF field is present and Eq. (2) admits chaotic solutions for certain sets of parameters [18]. However, as the experiments presented in this paper suggest, it is likely that in practice one should take into account the existence of a B₀ inhomogeneity. This amounts to describing the system as non-local and gives a discretized version of it as a set of N non-linear coupled differential systems of size 3. Thus the possibility of a kind of spatial-temporal chaos should be considered. This is a quite different situation than the one described by Eq. (2) and the constraint on an additional B₁ RF field is dropped. Therefore, even though dipolar field effects are neglected (which is exactly the case for a spherical sample with uniform magnetization), the system at hand is likely to exhibit chaotic behaviour for some sets of suitable experimental parameters.

Acknowledgements

The authors thank Dr Yves Lassailly for reading the manuscript and both referees for their useful comments and suggestions.