Observation of diffraction-like effects in Multiple Spin Echoe (MSE) experiments in structured samples

Paulo Loureiro de Sousa; Daniel Gounot; Daniel Grucker

doi:10.1016/j.crci.2003.11.006

Observation of diffraction-like effects in Multiple Spin Echoe (MSE) experiments in structured samples

Paulo Loureiro de Sousa ¹ ; Daniel Gounot ¹ ; Daniel Grucker ¹

¹ Institut de physique biologique, université Louis-Pasteur, UMR 7004-ULP/CNRS, 4, rue Kirschléger, 67085 Strasbourg cedex, France

Comptes Rendus. Chimie, Volume 7 (2004) no. 3-4, pp. 311-319.

Résumés

Anglais
Français

A single sequence of two r.f. pulses applied at times 0 and τ is capable of producing a train of echoes (multiple spin echoes, MSE) occurring at multiples of τ. This has been interpreted as a non-linear effect of the ‘dipolar field’' generated by the bulk nuclear magnetization acting on the spins as an additional component of the magnetic field. This effect, originally observed in solid and liquid ³He, has also been observed in ordinary samples such as water, at room temperature. It has been proposed that MSE could be used to investigate structured samples, such as porous media. Bowtell and Robyr (Phys. Rev. Lett. 76 (1996) 4971) have deduced a direct relationship between the sample structure and the echo amplitude in MSE experiments. Simple Fourier transform arguments show that diffraction-like effects in the k-space are expected if the dipolar field is modulated by a sample with a periodic structure. Our theoretical analysis and experimental results show that such effects can be detected as additional anomalous echoes refocusing at times other than multiples of τ. Without careful setting of timings and pulse cycling, these echoes interfere and corrupt MSE measurements. The effects observed agree well with the theoretical predictions.

Une simple séquence de deux impulsions r.f. aux temps 0 et τ est capable de produire un train d’échos (multiples spin écho, MSE) apparaissant aux différents multiples du temps τ. Ceci a été interprété comme un effet non linéaire du champ dipolaire généré par l’aimantation nucléaire volumique, agissant sur les spins comme un champ magnétique additionnel. Cet effet, observé à l’origine dans l’hélium solide et liquide, a aussi été observé dans des échantillons très simples, d’eau par exemple, à température ambiante. Il a été proposé d’utiliser la technique des MSE pour explorer des corps structurés, tels que les milieux poreux. Une relation directe entre la structure de l’échantillon et l’amplitude des échos dans les expériences MSE a été proposée par Bowtell and Robyr (Phys. Rev. Lett. 76 (1996) 4971). Un calcul simple dans l’espace de Fourier (espace-k) montre que si l’échantillon est très régulièrement structuré, la modulation du champ dipolaire est responsable d'échos supplémentaires en MSE, apparaissant à des temps autres que des multiples de τ. Sans un choix judicieux du timing et du cyclage de phase, ces différents échos peuvent interférer entre eux et fausser les mesures. Les effets que nous observons en tenant compte aussi bien de la séquence que de la structure périodique de l’échantillon correspondent bien aux prédictions théoriques.

Métadonnées

Reçu le : 2003-05-14
Accepté le : 2003-11-05
Publié le : 2004-03-01

DOI : 10.1016/j.crci.2003.11.006

Keywords: Multiple Spin Echoes (MSE), Porous media, NMR diffraction, iMQC
Mots clés : Multiple Spin Echoes (MSE), Milieux poreux, diffraction par RMN, iMQC

Affiliations des auteurs :

Paulo Loureiro de Sousa ¹ ; Daniel Gounot ¹ ; Daniel Grucker ¹

¹ Institut de physique biologique, université Louis-Pasteur, UMR 7004-ULP/CNRS, 4, rue Kirschléger, 67085 Strasbourg cedex, France

@article{CRCHIM_2004__7_3-4_311_0,
     author = {Paulo Loureiro de Sousa and Daniel Gounot and Daniel Grucker},
     title = {Observation of diffraction-like effects in {Multiple} {Spin} {Echoe} {(MSE)} experiments in structured samples},
     journal = {Comptes Rendus. Chimie},
     pages = {311--319},
     publisher = {Elsevier},
     volume = {7},
     number = {3-4},
     year = {2004},
     doi = {10.1016/j.crci.2003.11.006},
     language = {en},
}

TY  - JOUR
AU  - Paulo Loureiro de Sousa
AU  - Daniel Gounot
AU  - Daniel Grucker
TI  - Observation of diffraction-like effects in Multiple Spin Echoe (MSE) experiments in structured samples
JO  - Comptes Rendus. Chimie
PY  - 2004
SP  - 311
EP  - 319
VL  - 7
IS  - 3-4
PB  - Elsevier
DO  - 10.1016/j.crci.2003.11.006
LA  - en
ID  - CRCHIM_2004__7_3-4_311_0
ER  -

%0 Journal Article
%A Paulo Loureiro de Sousa
%A Daniel Gounot
%A Daniel Grucker
%T Observation of diffraction-like effects in Multiple Spin Echoe (MSE) experiments in structured samples
%J Comptes Rendus. Chimie
%D 2004
%P 311-319
%V 7
%N 3-4
%I Elsevier
%R 10.1016/j.crci.2003.11.006
%G en
%F CRCHIM_2004__7_3-4_311_0

Paulo Loureiro de Sousa; Daniel Gounot; Daniel Grucker. Observation of diffraction-like effects in Multiple Spin Echoe (MSE) experiments in structured samples. Comptes Rendus. Chimie, Volume 7 (2004) no. 3-4, pp. 311-319. doi : 10.1016/j.crci.2003.11.006. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2003.11.006/

Version originale du texte intégral

1 Introduction

In NMR experiments, a single sequence of two r.f. pulses separated by a time τ is capable of producing a train of echoes (multiple spin echoes, MSE) occurring at multiples of τ (Fig. 1a). This has been interpreted as a non-linear effect due to interaction between spins and the dipolar field generated by the bulk nuclear magnetization. This effect, originally observed in solid and liquid ³He [1,2] has also been observed in liquids, at room temperature [3,4]. Although this ‘classical’ mean-field approach provides a correct explanation of the experimental observations [5], an alternative quantum-mechanical interpretation has been proposed [6–9]. In the ‘quantum’ framework, the signal arises from intermolecular multiple quantum coherences (iMQC) involving the (usually neglected) interaction between distant spins belonging to different molecules. iMQC can be detected as unexpected cross-peaks in 2D-spectroscopy based on the CRAZED (COSY Revamped by Asymmetric Z-gradient Echo Detection) sequence (Fig. 1b). The dipolar interaction distance (so called ‘correlation distance’) can be set by appropriate experimental parameters. Typically, for highly diffusive liquids such as water, the correlation distance ranges between 10 μm and a few millimetres. The equivalence between the ‘classical’ and the ‘quantum-mechanical’ approaches has been demonstrated by different authors [8,10–12]. MSE experiments can be thought of as the superimposition of CRAZED experiments: the nth-order MSE echo corresponds to the signal of intermolecular n-quantum coherence in the CRAZED experiment.

Fig. 1
Pulse sequences used to generate (a) Multiple Spin Echoes (MSE) and (b) intermolecular n-quantum coherences (CRAZED sequence). As discussed in the text, MSE experiments can be thought of as the superimposition of CRAZED experiments. In all the experiments described in this paper the second r.f. pulse (β) = 120°.

NMR based on the distant dipolar-field effects has been proposed as a structure-sensitive method to investigate heterogeneous samples [13–17]. It has been demonstrated that if the nuclear magnetization is spatially modulated, the dipolar-field results mainly from magnetization found within a distance less than half the wavelength of the modulation (which corresponds to the correlation distance in the ‘quantum’ framework) [13,17]. This is a remarkable consequence of the non-locality of the dipolar field. As a result, in MSE-based images, the pixel intensity depends on the magnetization distribution within a volume bounded by the modulation wavelength, even if this volume is larger (or smaller) than a voxel [13,17]. By tuning the modulation wavelength, it might be possible to obtain a contrast dependent on the magnetization distribution within sub-voxel structures.

It has been suggested that signal arising from the long-range dipolar-field effect also depends on magnetic susceptibility variations over the correlation distance [6,18]. This selected distance-sensitive mechanism presents great potentials in medical magnetic resonance imaging (MRI). Recent studies have suggested that the sensitivity of iMQC to the local blood oxygenation level could be advantageous (compared to the traditional MRI techniques) to determine more specifically activation areas in the human brain [19–22]. The localization of micro-tumours and micro-vessels has also been considered [18]. Long-range dipolar-field MRI has been used to enhance diffusion-weighted MRI [23], to map the absolute value of nuclear magnetization at equilibrium [24] and for the characterization of trabecular bone quality [25,26]. It has been ascertained that MSE contrast does not depend on typical experimental parameters (T₁, T₂, T₂*, magnetization density, diffusion coefficient and flow) in the same way as traditional SE (spin-echo) or GE (gradient-echo) contrasts [18,19,27–29]. Despite such stimulating results, no experimental corroboration of a specific length-scale contrast, sensitive to local magnetic field variations at the sub-voxel scale, has been provided.

MSE experiments in porous media, where the inter-pulse delay time varies systematically, have shown discrete drops in signal intensity for certain values of the modulation wavelength [25,30,31]. It has been argued that these ‘dips’ occur when the pitch of modulation matches the size of pores. These ‘dips’ have been interpreted as evidence of a diffraction-like phenomenon [25] associated with sensitivity to local variations in magnetic susceptibility in the solid-liquid porous interface [31].

NMR diffraction in structured liquid samples has been originally demonstrated by Mansfield using a single sequence constituted by a r.f. pulse, followed by a steady field gradient [32]. Robyr and Bowtell have demonstrated theoretically that diffraction-like effects also are expected in MSE and CRAZED experiments involving samples with periodical structures if the modulation wavelength is a multiple of the reciprocal lattice vector [15].

Strongly ordered samples (such as arrays of packed glass beads, for example) have been frequently used to demonstrate the local-field sensitive mechanism acting in the porous interface [24,31]. The fact that a diffraction phenomenon in structured samples can generate additional multiple echoes interfering with dipolar echoes has not always been fully appreciated. MSE measurements can therefore be misevaluated if no adequate pulse sequence is used to discriminate dipolar echoes from diffraction ones.

The aims of this paper are: to determine the conditions allowing diffraction-like effects to be observed in MSE experiments, to explain how diffraction in MSE can modify signal intensities and to discuss the use of phase cycling as a method to eliminate interference from diffraction echoes.

2 Theory

In an isotropic fluid an interspin vector samples all directions during an NMR time scale experiment (typically from milliseconds to seconds), through molecular diffusion, and therefore the dipolar coupling averages to zero. For long-range distances between interacting spins, dipolar averaging through diffusion becomes less effective and the net effect of the dipolar interaction in a spherical sample vanishes by symmetry. It has been demonstrated that the long-range inter-molecular interaction could be reintroduced by applying an external field gradient, which breaks the spherical symmetry [1]. This long-range interaction between spins can be described as the resulting mean ‘distant dipolar field’ (B_d) [1]:

𝐁_{d} (𝐫) = \frac{μ_{0}}{4 π} \int d^{3} 𝐫^{'} \frac{1 - 3 \cos^{2} θ_{{rr}^{'}}}{2 | 𝐫 - 𝐫^{'} |^{3}} [3 M_{z} (r^{'}) \hat{𝐳} - 𝐌 (𝐫^{'})]

(1)

where μ₀ is the magnetic permeability constant and θ_rr' is the angle between the interspin vector

(𝐫 - 𝐫^{'})

and the z-axis.

The non-linear effects of this mean dipolar field can be understood by inspection of the Bloch Equation. If, for the sake of simplicity, relaxation and diffusion are neglected in the rotating frame, the Bloch equation in the presence of a steady field gradient G and of the dipolar field B_d is:

\frac{d 𝐌 (𝐫, t)}{dt} = γ 𝐌 (𝐫, t) \times [𝐁_{d} (𝐫, t) + (𝐆 \cdot 𝐫) \hat{𝐳}]

(2)

Since B_d depends on M, then the cross product M × B_d will generate a non-linear term for the magnetization in Eq. (2). But, because the dipolar field is non-local (Eq. (1)) finding an analytical solution to this non-linear Bloch equation is not an easy task. Numerical methods have been proposed to calculate the evolution of magnetization in heterogeneous materials [13,33,34]. Analytical solutions are possible provided simplifications are made. Deville et al. [1] have shown that if the dimensions of the sample exceed by far the spatial modulation of the magnetization (which can be set by applying a relatively strong gradient field), then Eq. (1) can be approximated to a simple local relation:

𝐁_{d} (𝐫) = μ_{0} Λ [M_{z} (𝐫) \hat{𝐳} - 𝐌 (𝐫) / 3]

(3)

where Λ = [3 cos²θ – 1]/2 and θ is the angle between the main field and the field gradient direction.

Let us consider an MSE sequence (Fig. 1a) applied to a homogeneous sample. Just after the second r.f. pulse, the transverse and longitudinal magnetization are spatially modulated by the steady field gradient G, applied continuously throughout the time interval τ:

M^{+} (𝐫, τ) = M_{0} {\cos (𝐤_{m} \cdot 𝐫) \cos β + isin (𝐤_{m} \cdot 𝐫)}

(4a)

M_{z} (𝐫, τ) = - M_{0} \cos (𝐤_{m} \cdot 𝐫) \sin β

(4b)

where k_m = γ G τ, M₀ is the equilibrium magnetization and M⁺ = M_x + i M_y is the transverse magnetization. Since transverse magnetization is not modulated before the second r.f. pulse, then dipolar-field effects can be neglected throughout the time interval τ. Einzel et al. [2,3] have shown a way of solving the non-linear Bloch equation (Eq. (2)), for any time after the second r.f. pulse, by expanding M(r,t) into a Fourier series. Algebra is simplified if we express the Fourier series in terms of exp(i k_m r):

𝐌^{+} (𝐫, t) = M_{0} e^{- {ik}_{t} \cdot r} \sum_{n = - \infty}^{n = + \infty} a_{n} (t) e^{in 𝐤_{m} \cdot 𝐫}

(5a)

𝐌_{z} (𝐫, t) = M_{0} \sum_{n = - \infty}^{n = + \infty} b_{n} (t) e^{in 𝐤_{m} \cdot 𝐫}

(5b)

where k_t = γ G t. The amplitude of the nth echo is then A_n=M₀|a_n(nτ )|. The coefficients a_n(t)can be found by substituting for M from Eqs. (5a) and (5b) into Eqs. (3) and (2). For the MSE sequence shown in Fig. 1a, the initial conditions impose that immediately after the second pulse, only the coefficients a_–1, a₁, b_–1 and b₁ be nonzero. If relaxation and diffusion are neglected, then a₁(t) = a₁(0) and b₁(t) = b₁(0) for n = 1. For n > 1, the following recurrent expression for a_n may be deduced [3]:

a_{n} (t) = - i μ_{0} γ Λ M_{0} \underset{0}{\int^{t}} \sum_{p = - \infty}^{\infty} a_{p} (t^{'}) b_{n - p} (t^{'}) {dt}^{'}

(6)

It should be noted that for structured samples (i.e. in which M₀ depends on r), Eq. (6) shows that a_n(t) = a_n(r, t), for n > 1.

The relative amplitude of the second-order echo (A₂) compared to the first-order echo (A₁) can be evaluated by assuming that the second r.f. pulse = 90° (the angle value is not critical to observe MSE and diffraction effects, except if the r.f. angle is a multiple of 180°) and that G is parallel to B₀:

\frac{A_{2}}{A_{1}} = | \frac{M^{+} (2 τ)}{M^{+} (τ)} | = γ μ_{0} M_{0} τ

(7)

Eq. (7) was obtained for an ideal experiment. In real experiments, transverse relaxation and diffusion restrict the choice of the delay time τ [3,4]. Relaxation, diffusion and flow modify the dipolar field, and consequently the amplitude of the non-linear echoes. In heterogeneous samples, the signal depends on magnetic susceptibility variations and on the magnetization distribution at the correlation distance scale. Thus, the dependence of MSE signal on the correlation-distance scale suggests that this technique could be used as a method to study structured samples.

In order to understand the effects of magnetization modulation by the lattice in the MSE experiments involving structured samples, let us write the total transverse magnetization M^Σ in the Fourier space (the k-space).

\begin{matrix} M^{Σ} (t) = \int_{- \infty}^{+ \infty} d^{3} 𝐫 M^{+} (𝐫, t) \\ = \sum_{n = - \infty}^{n = + \infty} \int_{- \infty}^{+ \infty} d^{3} 𝐫 \cdot [a_{n} (𝐫, t) M_{0} (𝐫)] e^{i (n 𝐤_{m} - 𝐤_{t}) \cdot 𝐫} \end{matrix}

= \sum_{n = - \infty}^{n = + \infty} a_{n} (𝐤_{n}, t) \otimes M_{0} (𝐤_{n})

(8)

where Σ denotes the integral over the whole sample volume, k_n = n k_m – k_t = γ G (n τ – t), and a_n(k) ⊗ M₀(k) represents the convolution of a_n(k) and M₀(k), the Fourier transforms of a_n(r) and M₀(r), respectively.

Let us examine the case where dipolar-field effects can be neglected (which is the most usual case). In this case the only relevant term in Eq. (8) is n = 1. Then

M_{1}^{Σ} (t) = a_{1} M_{0} (𝐤_{1})

(9)

where the subscript in M_n^Σ denotes the nth term of the series (Eq. (8)). Eq. (9) is a well-known result that evidences the direct relationship between the NMR signal (in the presence of a magnetic field gradient) and a Fourier transform of the magnetization distribution [32].

If the dipolar field is taken in account, for n = 2:

M_{2}^{Σ} (t) = a_{2} (k_{2}) \otimes M_{0} (k_{2}) = - i γ μ_{0} Λ a_{1} b_{1} 2 t {(M_{0} (k_{2}))}^{2}

(10)

where k₂ = γ G (2 τ – t) as defined above. In another context, Talini et al. have shown that the squared modulus of the magnetization in a pulsed-field-gradient NMR experiment can provide information about the sample structure [35]. For MSE experiments, Robyr and Bowtell have discussed the case where k_n = 0 [15], i.e. when k_t = n k_m. They have anticipated that even when this condition is not met, echoes could be produced in ordered samples if k_n is a multiple of the reciprocal lattice vector. In this case, diffraction-like peaks can be expected in MSE experiments.

In order to gain insight into the diffraction effects on the dipolar-field echoes in periodic samples, let us examine an example of MSE in a single regular structure. For the sake of simplicity, we will consider a one-dimensional array of N closed boxes (of size d) containing uniformly distributed spins (magnetization density = 1) equally spaced (lattice constant = Δs) along an arbitrary direction given by the unitary vector $\hat{𝐬}$ (Fig. 2a). For a large number of elements, the (normalized) Fourier transform of the magnetization M₀(k) is:

M_{0} (k) = \frac{\sin (kd / 2)}{kd / 2} \frac{\sin [Nk Δ s / 2]}{Nsin (k Δ s / 2)}

(11)

Fig. 2
One-dimensional model of a structured sample, and corresponding (simulated) MSE experiment results. (a) Magnetization distribution in the one-dimensional lattice constituted from N closed boxes (of size d) containing uniformly distributed spins (magnetization density = 1) equally spaced (lattice constant = Δs) along an arbitrary direction given by the unitary vector $\hat{𝐬}$ . (b) First-order MSE and its respective diffraction peaks. The envelope (dotted line) corresponds to the term |sinφ/φ| where φ=γG(τ −t)d/2. (c) Second-order MSE and its respective diffraction peaks. In (b) and (c), the distance between diffraction peaks is Δt=2π /γGΔs, while the distance between MSE peaks is τ. The diffraction pattern is not the same in (b) and (c), because the amplitude of the peaks depends on |M₀ (k_n)|ⁿ. In real experiments, MSE of different orders can be selected by appropriate phase cycling. Data in (b) and (c) have been normalized by their maximal values.

Inspection of Eq. (11) indicates that (for N >> 1)? only k values multiples of the lattice wave vector (2π/Δs) will produce a nonzero M₀(k). The time evolution of MSE signal can be evaluated by substituting for M₀(k) from Eq. (11) into Eqs. (9) and (10) – terms of order higher than 2 in the Fourier series have been neglected, for the sake of simplicity). Figs. 2b and 2c display a simulation of MSE in the one-dimensional array described above. Multiple diffraction peaks are visible around both the first- and second-order MSE peaks. In real experiments, diffraction peaks originating from the first-order MSE peak can be more intense than the second-order MSE peak.

3 Materials and methods

In order to study diffraction-like effects in echoes generated by the long-range dipolar field, we performed both MSE and CRAZED experiments on a structured sample, constituted from a packed array of parallel hollow cylinders (i.d. ~0.9 mm, o.d. ~1.4 mm, length, 200 mm) filled with doped water (T₂ ~ 100 ms, T₁ ~ 200 ms). All cylinders were sealed and the array was inserted in a 180-mm long glass tube (i.d. ~14.5 mm, o.d. ~18.0 mm). The alignment of the tubes was verified through NMR imaging. Another sample, constituted from packed glass beads (diameter ~ 2.8 mm) surrounded by water, was occasionally used to verify the results obtained with the cylinders.

Experiments were carried out in a 4.7-T SMIS small animal imager, with a 200-mm-diameter horizontal bore magnet (MR Research Systems, UK), using a 10-cm-long, 72-mm-diameter birdcage r.f. coil. A long repetition time (T_R = 5 s) was used in order to ensure complete magnetization recovery.

Two sets of MSE experiments were performed: one with a steady field gradient oriented along the main axis of the tubes (z-axis) and one with a gradient perpendicular to the tubes (x-axis). For both experiments, the gradient amplitude (G) and delay time τ were maintained unchanged. The r.f. pulse β was set to 120° in all experiments in order to maximize the second-order spin echo [2]. Simple phase cycling was used to retain only the desired nth order of a MSE experiment. The phase cycling used to select the first-order echo was (90°)(x,–x) – (β°)(x,x) – ACQ(x,–x), and (90°)(x,–x) – (β°)(x,x) – ACQ(x,x) to select the second-order echo. Another set of MSE experiments was made to study the effect of the delay time duration and of the gradient amplitude over the temporal position of the diffraction peaks.

CRAZED experiments were carried out, by setting the pulsed field gradient along and perpendicular to the main axis of the tubes. In each case, the first pulsed gradient (G₁) was maintained constant, while the second gradient (G₂) was systematically made to vary.

4 Results

Fig. 3 displays the results of MSE experiments in which the field gradient was oriented along and perpendicular to the tubes, respectively. In both experiments, three echoes were observed (at t = 30, 60 and 90 ms), corresponding to the first, second and third orders of MSE. In Fig. 3b, ‘satellite’ peaks are observed corresponding to the diffraction echoes. If it is assumed that the tubes were arranged into a hexagonal array (this was confirmed by imaging), with a lattice parameter (in the direction x) d_x ≈ 1.4 mm (outer diameter of the cylinders), then the (first-order) diffraction peaks are expected at the time Δt = |τ – t| = 2 π/γ G d_x ≈ 6.8 ms relative to the position of the MSE peaks. This agrees with our experimental results.

Fig. 3
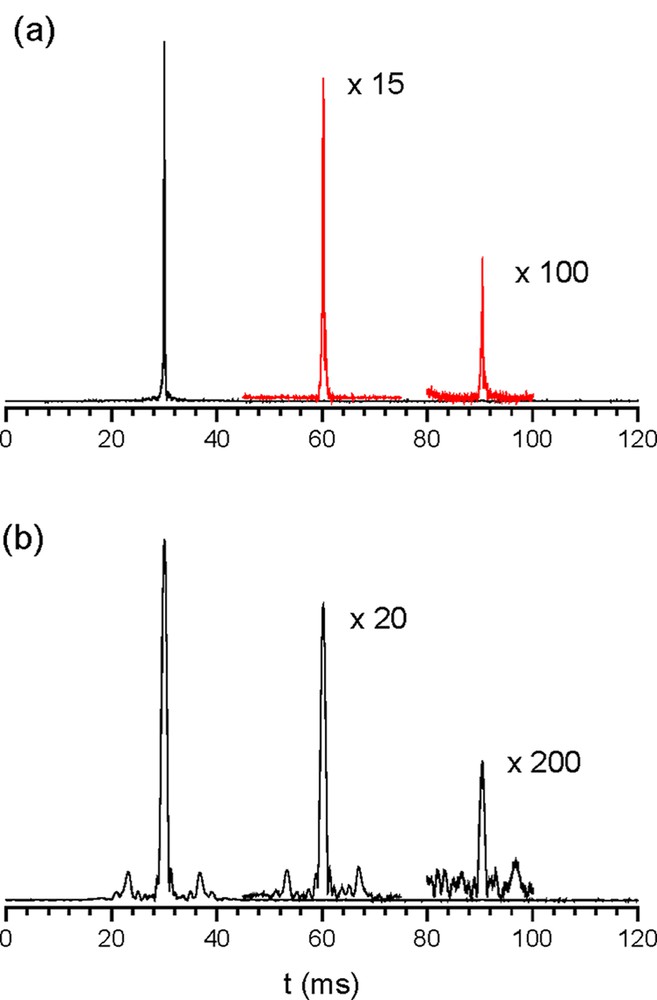
MSE observed in an array of hollow tubes filled with doped water. The steady field gradient was applied (a) along the main axis of the tubes and (b) perpendicular to the tubes. In both experiments, G (amplitude of modulation gradient) was ~2.5 mT m^–1 and τ (delay between the r.f. pulses) was 30 ms. The diffraction peaks are clearly observed in MSE only when the field gradient is perpendicular to the tubes. Magnification relative to the first-order echo has been indicated in (a) and (b).

Figs. 4a–c display the results of the MSE experiment where the delay time τ was made to vary, while the steady gradient was kept constant. When τ is incremented by Δτ, MSE echoes and their respective ‘satellite’ echoes are all shifted by n Δτ, where n is the MSE order. In Figs. 4d and 4f, the gradient amplitude G was made to vary, while the delay time τ was kept constant. If G is changed to α G (where α is an arbitrary positive number), the relative positions of the diffraction echoes changes to Δt/α. An interesting situation happens when a suitable combination of gradient amplitude and delay time are set and a satellite echo is focused at a time t multiple of τ. Fig. 5 displays two MSE experiments in which this condition is met. If no phase cycling is used, a diffraction echo arising from first-order MS echo overlaps the second-order MSE.

Fig. 4
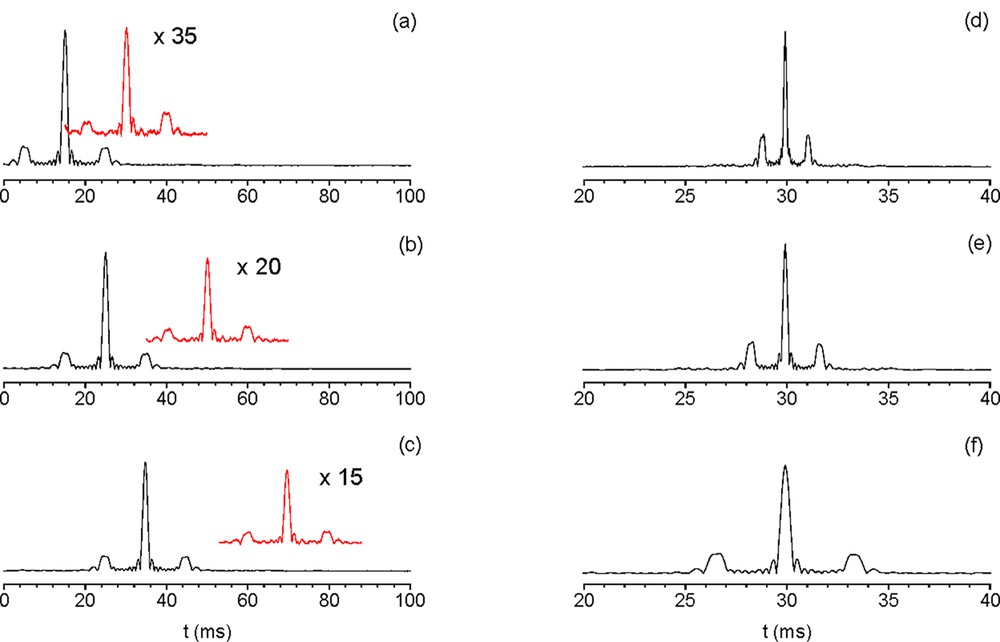
Effect of the delay time duration and of the gradient amplitude over the temporal position of the diffraction peaks. From (a) through (c): the gradient amplitude G was 1.7 mT m^–1 and the delay time τ was (a) 15 ms, (b) 25 ms and (c) 35 ms. Magnification relative to the first-order echo has been indicated in (a) through (c). Phase cycling was used to select only the first-order echo (main line) or the second-order echo (insert). Second-order echoes have been shifted vertically to prevent the two displays from overlapping. Diffraction peaks are visible in both first- and second-order MSE experiments. From (d) through (f): the delay time τ was 30 ms and gradient amplitude G was (d) 14.6 mT m^–1, (e) 9.7 mT m^–1 and (f) 4.9 mT m^–1. First-order echoes have been normalized in all sub-figures.

Fig. 5
Overlapping second-order MSE and diffraction echoes. In (a) and (b), phase cycling was used to select the first-order MSE (line down) or the second-order MSE (line up). (a) Diffraction NMR pattern observed in an array of parallel hollow cylinders. The gradient amplitude G was 1.7 mT m^–1 and the delay time τ was 9.6 ms. Magnification relative to the first-order echo has been indicated. (b) Diffraction NMR pattern observed in a packed glass bead sample (diameter ~ 2.8 ms). G was 1.9 mT m^–1 and the delay time τ was 15 ms. A second-order MSE was refocused at t = 30 ms (inset). Multiple diffraction peaks are visible around the first-order MSE (main line).

Diffraction-like effects can also be observed in pulsed-field-gradient experiments (Fig. 6). In an n-CRAZED sequence (Fig. 1b), an echo is focused at the time t = n τ after the second r.f. pulse, when the ratio between gradient amplitudes (G₂/G₁) is n (where n = 0,1,2, ...); otherwise, no echo is refocused. While in the MSE experiments described here, the k-space was sampled in the time domain (k_n = γ G (n τ – t), where t was made to vary during the acquisition), in CRAZED experiments the k-space was sampled in the gradient amplitude domain (k_n = γ δ (n G₁ – G₂), where δ was maintained constant and G₂ was made to vary). Thus, Fig. 6 is analogous to Fig. 3. As in the MSE experiments, we detected echoes in periodical samples even when the condition k_n = 0 was not met (in pulsed-field-gradient experiments, this condition corresponds to G₂ = n G₁).

Fig. 6
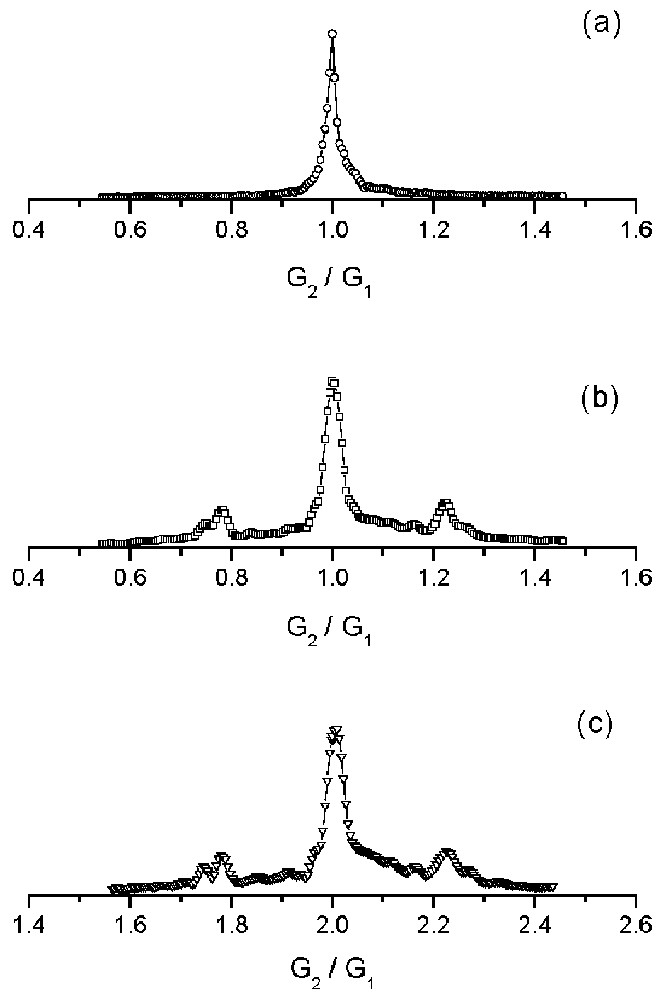
Signal amplitude of CRAZED experiments in an array of hollow tubes filled with doped water: the pulsed field gradient was applied (a) along the main axis of the tubes and (**b–c**) perpendicularly to the tubes. In all experiments, the amplitude of the first pulsed gradient G₁ was 24.7 mT m^–1, the gradient pulse duration δ 3 ms and the delay time τ 30 ms. Figs. 6a and 6b display the signal when G₂/G₁ varies around 1 and Fig. 6c when G₂/G₁ varies around 2. Satellite peaks due to the sample structure are present in both Figs. 6b and c. The symbols correspond to the experimental data (echo amplitude). The solid line is only used as a guide. The data have been normalized.

Figs. 6a and 6b display the echo amplitude at t = τ, in an experiment in which the field gradient pulses were parallel and perpendicular to the tubes, respectively. The maximum intensities in Figs. 6a and 6b correspond to the case n = 1 (Eq. (5)), i.e., when dipolar-field effects are neglected. The two ‘satellite’ peaks visible in Fig. 6b correspond to the diffraction condition for k₁ = γ δ (G₁ – G₂).

In Fig. 6c, pulsed gradients were oriented as in Fig. 6b, but a different amplitude range was used for G₂. The maximum intensity corresponds to the case n = 2 (Eq. (5)), in which dipolar-field effects are taken into consideration. As in Fig. 6b, two ‘satellite’ peaks are visible, corresponding to the diffraction condition for k₂=γ δ|2G₁−G₂|.

5 Discussion

Over the past few years, it was suggested that long-range dipolar-field effects in NMR could be used as a new method to study structured samples, including living systems. It was also suggested that MSE was sensitive to local-field variations in heterogeneous samples. Local-field variations at different length scales could be probed by ‘tuning’ an experimental parameter: the correlation distance. This unique feature of MSE presents potentially important applications in medical imaging. Calibrated porous samples have frequently been used to demonstrate this mechanism. Simple Fourier transform arguments show that diffraction-like effects are expected in samples with a strong periodicity. In such samples, without careful setting of timings and pulse cycling, multiple echoes originating from NMR diffraction could interfere with the (commonly weak) second-order MSE signal. Indiscriminate choice of the acquisition window can result in the detection of pseudo-modulations of the MSE signal in the k-space, arising from the periodical pattern of diffraction peaks.

Bibliographie

[1] G. Deville; M. Bernier; J.-M. Delrieux Phys. Rev. B, 19 (1979), p. 5666

[2] D. Einzel; G. Eska; Y. Hirayoshi; T. Kopp; P. Wölfle Phys. Rev. Lett., 53 (1984), p. 2312

[3] R. Bowtell; R.M. Bowley; P. Glover J. Magn. Reson., 88 (1990), p. 643

[4] R.P. Jones; G.A. Morris J. Magn. Reson., 98 (1992), p. 115

[5] M.H. Levitt Concepts Magn. Reson., 8 (1996), p. 77

[6] Q. He; W. Richter; S. Vathyam; W.S. Warren J. Chem. Phys., 98 (1993), p. 6779

[7] W.S. Warren; W. Richter; A.H. Andreotti; B.T. Farmer Science, 262 (1993), p. 2005

[8] S. Lee; W. Richter; S. Vathyam; W.S. Warren J. Chem. Phys., 105 (1996), p. 874

[9] W. Richter; W.S. Warren Concepts Magn. Reson., 12 (2000), p. 396

[10] E.D. Minot; P.T. Callaghan; N. Kaplan J. Magn. Reson., 140 (1999), p. 200

[11] J. Jeener J. Chem. Phys., 112 (2000), p. 5091

[12] J. Jeener Collective Effects in Liquid NMR: Dipolar Field and Radiation Damping (D.M. Grant; R.K. Harris, eds.), Supplement of the Encyclopedia of Nuclear Magnetic Resonance, Wiley, New York, 2002, p. 642

[13] L.-S. Bouchard; R.R. Rizzi; W.S. Warren Magn. Reson. Med., 48 (2002), p. 973

[14] R. Bowtell; P. Robyr Phys. Rev. Lett., 76 (1996), p. 4971

[15] P. Robyr; R. Bowtell J. Chem. Phys., 106 (1997), p. 467

[16] P. Robyr; R. Bowtell J. Chem. Phys., 107 (1997), p. 702

[17] R. Bowtell; S. Gutteridge; C. Ramanathan J. Magn. Reson., 150 (2001), p. 147

[18] W.S. Warren; S. Ahn; M. Mescher; M. Garwood; K. Ugurbil; W. Richter; R.R. Rizi; J. Hopkins; J.S. Leigh Science, 281 (1998), p. 247

[19] R.R. Rizi; S. Ahn; D.C. Alsop; S. Garrett-Roe; M. Mescher; W. Richter; M.D. Schnall; J.S. Leigh; W.S. Warren Magn. Reson. Med., 43 (2000), p. 627

[20] W. Richter; M. Richter; W.S. Warren; H. Merkle; P. Andersen; G. Adriany; K. Ugurbil Magn. Reson. Imag., 18 (2000), p. 489

[21] J. Zhong; E. Kwok; Z. Chen Magn. Reson. Med., 43 (2001), p. 356

[22] J. Zhong; Z. Chn; W.E. Kwok; S. Kennedy; Z. You J. Magn. Reson. Imag., 16 (2002), p. 733

[23] J. Zhong; Z. Chen; E. Kwok; S. Kennedy Magn. Reson. Imag., 19 (2001), p. 33

[24] S. Gutteridge; C. Ramanathan; R. Bowtell Magn. Reson. Med., 47 (2002), p. 871

[25] S. Capuani; F. Curzi; F.M. Alessandri; B. Maraviglia; A. Bifone Magn. Reson. Med., 46 (2001), p. 683

[26] S. Capuani; F.M. Alessandri; A. Bifone; B. Maraviglia MAGMA, 14 (2002), p. 3

[27] J. Zhong; Z. Chen; E. Kwok J. Magn. Reson. Imag., 12 (2000), p. 311

[28] J. Zhong; Z. Chen; E. Kwok Magn. Reson. Med., 43 (2000), p. 335

[29] P.L. de Sousa; D. Gounot; D. Grucker J. Magn. Res., 162 (2003), p. 356

[30] S. Capuani; M. Alesiani; F.M. Alessandri; B. Maraviglia Magn. Reson. Imag., 19 (2001), p. 319

[31] F.M. Alessandri; S. Capuani; B. Maraviglia J. Magn. Reson., 156 (2002), p. 72

[32] P. Mansfield; P.K. Grannell Phys. Rev. B, 12 (1975), p. 3618

[33] T. Enss; S. Ahn; W.S. Warren Chem. Phys. Lett., 305 (1999), p. 101

[34] S. Garrett-Roe; W.S. Warren J. Magn. Reson., 146 (2000), p. 1

[35] L. Talini; J. Leblond; F. Feuillebois J. Magn. Reson., 132 (1998), p. 287

Commentaires - Politique

Ces articles pourraient vous intéresser

Geometrical description of echoes and macroscopic reorientation of samples in solid-state NMR

Christian Bonhomme; Thierry Azaïs

C. R. Chim (2004)

SPROM – an efficient program for NMR/MRI simulations of inter- and intra-molecular multiple quantum coherences

Congbo Cai; Meijin Lin; Zhong Chen; ...

C. R. Phys (2008)

Nonlinear NMR dynamics in hyperpolarized liquid ³He

Emmanuel Baudin; Michael E. Hayden; Geneviève Tastevin; ...

C. R. Chim (2008)