Plan
Comptes Rendus
no. 5

Small-angle X-ray scattering investigation of the cluster distribution in inorganic–organic hybrid polymers prepared from organically substituted metal oxide clusters
Viktoria Torma1  ; Nicola Hüsing1  ; Herwig Peterlik2  ; Ulrich Schubert1
1 Institute of Materials Chemistry, Vienna University of Technology, Getreidemarkt 9, A-1060 Wien, Austria
2 Institute of Materials Physics, University of Vienna, Boltzmanngasse 5, A-1090 Wien, Austria
Comptes Rendus. Chimie, Volume 7 (2004) no. 5, pp. 495-502.

Résumés

Hybrid polymers prepared by radical polymerisation of the tetranuclear metal oxide clusters Ta4O4(OEt)8(OMc)4 (OMc = methacrylate) with styrene, or of Ta4O4(OEt)8(OMc)4, Ti4O2(OEt)6(OMc)6 and Hf4O4(OMc)12 with methyl methacrylate were investigated by small-angle X-ray scattering (SAXS) to elucidate the distribution of the clusters in the polymer. Besides the random distribution of the clusters, three different types of aggregation behaviour were observed with two different inter-cluster distances each: the shorter distance being constant when the cluster portion in the polymer was varied, the longer distance being constant or both distances being constant. .

La préparation de polymères hybrides par polymérisation radicalaire de clusters d'oxydes métalliques tétranucléaires Ta4O4(OEt)8(OMe)4 (OMe = métacrylate) avec le styrène ou de Ta4O4(OEt)8(OMe)4, Ti4O2(OEt)6(OMe)6 et Hf4O4(OMe)12 avec le métacrylate de méthyle a été étudiée par diffusion des rayons X aux petits angles (SAXS) pour déterminer la distribution des clusters dans le polymère. Hormis la distribution aléatoire des clusters, trois types d'agrégats différents ont été observés avec, pour chacun, deux distances « inter-clusters » différentes. Dans l'un des agrégats, la plus petite distance étant constante pour une quantité variable de clusters dans le polymère. Dans le second type d'agrégats, la distance la plus longue reste constante et, dans le troisième type, les deux distances sont constantes. .

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2004.01.006
Keywords: Tantalum oxide cluster, Titanium oxide cluster, Hafnium oxide cluster, Inorganic–organic hybrid materials, Crosslinked polymers, Cluster aggregation
Mots clés : Cluster d'oxyde de tantale, Cluster d'oxyde de titane, Cluster d'oxyde d'hafnium, Matériaux hybrides inorganiques–organiques, Polymères réticulés, Agrégat de clusters
Viktoria Torma 1 ; Nicola Hüsing 1 ; Herwig Peterlik 2 ; Ulrich Schubert 1

1 Institute of Materials Chemistry, Vienna University of Technology, Getreidemarkt 9, A-1060 Wien, Austria
2 Institute of Materials Physics, University of Vienna, Boltzmanngasse 5, A-1090 Wien, Austria 
@article{CRCHIM_2004__7_5_495_0,
     author = {Viktoria Torma and Nicola H\"using and Herwig Peterlik and Ulrich Schubert},
     title = {Small-angle {X-ray} scattering investigation of the cluster distribution in inorganic{\textendash}organic hybrid polymers prepared from organically substituted metal oxide clusters},
     journal = {Comptes Rendus. Chimie},
     pages = {495--502},
     publisher = {Elsevier},
     volume = {7},
     number = {5},
     year = {2004},
     doi = {10.1016/j.crci.2004.01.006},
     language = {en},
}
TY  - JOUR
AU  - Viktoria Torma
AU  - Nicola Hüsing
AU  - Herwig Peterlik
AU  - Ulrich Schubert
TI  - Small-angle X-ray scattering investigation of the cluster distribution in inorganic–organic hybrid polymers prepared from organically substituted metal oxide clusters
JO  - Comptes Rendus. Chimie
PY  - 2004
SP  - 495
EP  - 502
VL  - 7
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crci.2004.01.006
LA  - en
ID  - CRCHIM_2004__7_5_495_0
ER  - 
%0 Journal Article
%A Viktoria Torma
%A Nicola Hüsing
%A Herwig Peterlik
%A Ulrich Schubert
%T Small-angle X-ray scattering investigation of the cluster distribution in inorganic–organic hybrid polymers prepared from organically substituted metal oxide clusters
%J Comptes Rendus. Chimie
%D 2004
%P 495-502
%V 7
%N 5
%I Elsevier
%R 10.1016/j.crci.2004.01.006
%G en
%F CRCHIM_2004__7_5_495_0
Viktoria Torma; Nicola Hüsing; Herwig Peterlik; Ulrich Schubert. Small-angle X-ray scattering investigation of the cluster distribution in inorganic–organic hybrid polymers prepared from organically substituted metal oxide clusters. Comptes Rendus. Chimie, Volume 7 (2004) no. 5, pp. 495-502. doi : 10.1016/j.crci.2004.01.006. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2004.01.006/

Version originale du texte intégral

1 Introduction

Inorganic–organic hybrid materials [1] are characterized by the combination of organic and inorganic building blocks on a molecular or nanometre scale. One of the most versatile methods to prepare such materials is sol–gel processing, which allows the molecular, oligomeric or polymeric organic species to be either physically entrapped in an inorganic host matrix or covalently bonded to it. A typical procedure for the preparation of the latter type of hybrid materials is the processing of mixtures of unsubstituted and organically substituted metal or semi-metal alkoxides. The macroscopic homogeneity of materials prepared by this approach is sufficient for most applications, but their homogeneity on a molecular or nanometre scale is mostly unknown. Because substituted and unsubstituted alkoxides have different reactivities and because the structure of sol–gel materials is kinetically controlled, some microphase separation must be expected. The influence of such microphase separation on the macroscopic materials properties is not known.

A better correlation between the nanoscale structural features of hybrid materials and their macroscopic properties can be expected if the different precursors are not processed in parallel (i.e., by processing precursor mixtures) but sequentially instead. In this article we are dealing with an example for the latter approach, viz. the polymerisation of organic compounds in the presence of pre-formed metal oxide clusters. Metal oxide clusters capped by polymerisable ligands can be easily prepared by controlled hydrolysis of metal alkoxides in the presence of acrylic or methacrylic acid. The organically modified transition metal oxide clusters (OMTOC) can then be polymerised with organic co-monomers to result in inorganic–organic hybrid materials in which the organic and inorganic building blocks are connected by strong covalent bonds [2,3,4]. Since the clusters are incorporated unchanged in the polymer [5], this approach allows a much better structural control on the nanometre scale than the more common co-processing of metal alkoxides, (meth)acrylic acid and additional organic monomers.

Our first results on this class of hybrid materials, viz. the cluster-crosslinked polymers, showed that their properties not only depend on the cluster/organic monomer ratio, as expected, but also on the kind of the employed cluster [6]. However, there is no obvious correlation between the cluster size, structure or composition and the materials properties. One of the possible reasons for this phenomenon is that the clusters are not statistically distributed in the polymers, although the hybrid materials appear homogeneous to the naked eye.

The employed clusters are structurally well-defined (monodisperse) inorganic objects with a typical diameter of the inorganic core of about 0.7–1.2 nm. A very suitable method for studying the distribution of such objects in a polymeric organic matrix is small-angle X-ray scattering (SAXS), because the inter-cluster distance is 1–5 nm and the electron density difference between the organic and inorganic entities is large.

In this article, we restrict ourselves to the tetra-nuclear clusters Ta4O4(OEt)8(OMc)4 (OMc = methacrylate) (1) [6], Ti4O2(OEt)6(OMc)6 (2) [7], and Hf4O4(OMc)12 (3) [8] (to exclude effects of the nuclearity of the clusters), and to poly(methyl methacrylate) (PMMA) and polystyrene as the organic polymers. We will show (together with results from some previously characterized polymers) that the dispersion of the clusters in the polymer can be described by four different models.

2 Results and discussion

The structures of the organically modified transition metal oxide clusters used for the preparation of the polymers are shown in Fig. 1. The tetranuclear clusters have different shapes and a different number of polymerisable methacrylate ligands covering their surface. This allows polymerisation of the clusters with methyl methacrylate or styrene as co-monomers by free radical polymerisations as previously described, [6,7,9] with a typical cluster portion of 0.5–2 mol%. The obtained hybrid polymers are transparent glassy materials with materials properties typical of highly crosslinked polymers.[4] The reason why different clusters were used is that their individual structure and the number of polymerisable ligands might influence their aggregation behaviour and thus the properties of the resulting materials.

Fig. 1

Structures of the clusters Ta4O4(OEt)8(OMc)4 (1) (top) [6], Ti4O2(OEt)6(OMc)6 (2) (centre) [7], and Hf4O4(OMc)12 (3) (bottom) [8]. (Reproduction with friendly permission of the Materials Research Society, from [6]).

In the remainder of this article, the samples are labelled as follows: the number of the cluster (1–3) is followed by STY (for styrene) or MMA (for methyl methacrylate) and the mol% of the cluster used in the preparation. For example, 1STY0.5 is a hybrid polymer, where 0.5 mol% of cluster 1 and 99.5 mol% of styrene was copolymerised. Labels without the second number refer to the particular hybrid polymer in general.

The SAXS data were recorded in transmission geometry and were first normalized to I = 100 at q = 9 nm–1 (where q is the scattering vector, and I is the intensity). Then, the scattering curve from undoped polymer, also normalized to I = 100 at q = 9 nm–1, was subtracted from each of the data sets to yield the scattering from the clusters alone. The underlying assumption is that the scattering from the organic polymer matrix is the same in the cluster-doped and undoped materials. Therefore, the signal is dominated by the organic part of the material at higher q.

The existence of a maximum in the SAXS function indicates some kind of short-range order in the arrangement of the cluster units. The position of the maximum corresponds to the inter-cluster distance in reciprocal space, which can be converted in good approximation to a mean distance (D) in the real space by the formula D = 2 π/q. The position of the maximum is only slightly affected by the particle form factor, because the particle size is much smaller than the inter-cluster distance. Every maximum of the scattering curve was fitted with a Gaussian function with the following parameters: QC is the q value at maximum, w is the half-width and A is the intensity at the maximum.

The SAXS curves of Ta4O4(OEt)8(OMc)4 (1) polymerised with styrene as comonomer (1STY) are shown in Fig. 2 and Table 1.

Fig. 2

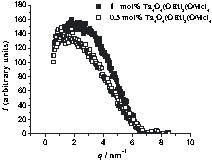
SAXS curves of 1STY polymers with 0.5 or 1 mol% cluster portion. The x-axis corresponds to the scattering vector, q, and the y-axis to I(q). I(q) is the scattering intensity after normalization and subtraction of the curve of cluster-free polymer.

Table 1

Fitted parameters to the scattering curves of the hybrid polymers. QC = q value at maximum, w = half-width of the curve, A = amplitude

1STY11STY0.52MMA22MMA12MMA0.51MMA41MMA21MMA11MMA0.53MMA23MMA13MMA0.5
QC1 [nm–1]2.221.612.592.191.841.941.911.992.132.980.3.061.95
w1 [nm–1]2.242.382.082.261.090.9510.9911.070.7171.971.931.30
A1 (a. u.)1681440.610.340.1445.742.8754.119.5318014737.0
QC2 [nm–1]5.635.625.425.054.184.065.315.324.94
w2 [nm–1]1.241.011.402.041.741.710.4910.4330.473
A2 (a. u.)0.150.160.1529.333.629.539.11168.51

Only one maximum was observed for these polymers. As the cluster portion in the polymer decreases from 1 mol% to 0.5 mol%, the half-width of the peak increases and its maximum is shifted to a smaller scattering vector (q). This implies that the average cluster-cluster distance increases from 2.83 to 3.90 nm as the cluster portion decreases. This observation can be interpreted as a random distribution of the clusters in the polymer. From the increase of the half-width one can conclude that the distribution of the interparticle distances gets broader when a smaller cluster portion is incorporated in the polymer.

A random distribution of the clusters was already found in cluster-crosslinked polymers prepared by this approach, such as PMMA crosslinked by Zr6(OH)4O4(OMc)12 [9,10], Zr4O2(OMc)12 [10] or Ti6O4(OPr)8(acrylate)8,[7] or poly(methacrylic acid) (PMA) crosslinked by Ti6O4(OPr)8(acrylate)8 [7].

We also observed SAXS curves with two maxima instead of one. This indicates a different distribution of the clusters with two different inter-cluster distances. One possible explanation of the double-maximum is that the anisotropic shape of some cluster types may result in a kind of stacking. The shorter distance (D1) would then correspond to the inter-cluster distances within a pile of disks, and the longer distance (D2) to the distance between clusters of neighbouring piles (Fig. 3).

Fig. 3

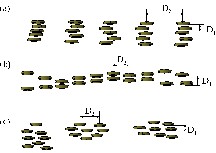
Models for the distribution of flat clusters in the hybrid polymers (see text for an explanation).

We so far observed three sub-classes for this arrangement, which will be discussed in the following:

  • • (i) D1 is independent of the portion of the inorganic building blocks, but the distance between the stacks (D2) varies (Fig. 3a);
  • • (ii) D2 is independent of the portion of the inorganic building blocks, but the distance within the stacks (D1) varies (Fig. 3b);
  • • (iii) both D1 and D2 are independent of the cluster portion in the polymer (Fig. 3c).

The first case is represented by the SAXS data of Ti4O2(OEt)6(OMc)6 (2) polymerised with methyl methacrylate (2MMA, Fig. 4). The SAXS measurements on this polymer system were already reported earlier.[7] The data were re-fitted and are discussed here in comparison with the other aggregation models.

Fig. 4

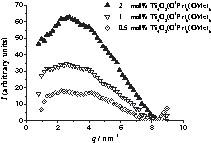
SAXS curves of 2MMA polymers with cluster concentrations ranging from 0.5–2 mol%. The x-axis corresponds to the scattering vector, q, and the y-axis to I(q). I(q) is the scattering intensity after normalization and subtraction of the curve of cluster-free polymer.

The half-width, the amplitude and the position of the peak at higher q values (smaller inter-cluster distances) are independent from the cluster portion in the polymer (D1 ≈ 1.5 nm). Contrary to this, the peak at smaller q (larger inter-cluster distances) is shifted to smaller values (larger distances) as the cluster portion is decreased (D2 ≈ 2.3 nm for 2 mol% of cluster and ≈ 3.1 nm for 0.5 mol% of cluster), whereas the half-width does not change. This indicates that the inter-cluster distances within a pile of disks remains constant and additional organic monomer is incorporated between the cluster piles. D1 (the distance between the clusters inside one stack) is thus independent from the portion of the inorganic building blocks, but the distance between the stacks (D2) becomes larger when a smaller cluster portion is employed. The amplitude of the second maximum becomes smaller when the cluster portion is decreased, which shows that the number of the scattering objects decreased. A possible arrangement of the inorganic building blocks in this polymer is presented in Fig. 3a. The same microstructure was observed for Ti6O4(OPr)8(acrylate)8 in PMMA (D1 ≈ 1.3 nm; D2 ≈ 2.5 nm for 2 mol% of cluster and ≈ 3.0 nm for 1 mol% of cluster) [7].

The second case of a cluster distribution in the polymer with two maxima in the SAXS curves is Ta4O4(OEt)8(OMc)4 (1) polymerised with methyl methacrylate (1MMA). The SAXS data are shown in Fig. 5 and Table 1.

Fig. 5

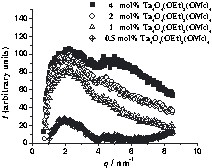
SAXS curves of 1MMA with cluster portions ranging from 0.5–4 mol%. The curves are shifted relative to each other for a better overview. The x-axis corresponds to the scattering vector, q, and the y-axis to I(q). I(q) is the scattering intensity after normalization and subtraction of the curve of cluster-free polymer. The curves are shifted by 20 units relative to each other for clarity.

There are again two maxima of the curve, corresponding to two characteristic distances between the clusters. In this case the half-width, amplitude and position of the maximum at smaller q values (larger inter-cluster distance, D2 ≈ 3.2 nm) are independent of the cluster portion in the polymer. However, the second peak at higher q (smaller inter-cluster distance) is shifted to smaller values as the cluster portion is decreased (D1 ≈ 1.2 nm for 4 mol% of cluster and ≈1.6 nm for 1 mol% of cluster), but the half-width and the amplitude do not change. This indicates that the inter-cluster distances between the piles of disks remain constant and additional organic monomer is incorporated between the clusters of the same pile, i.e. a chain-like arrangement of the clusters may be formed where the distance between the chains becomes larger when a smaller cluster portion is employed. A model for the distribution of the inorganic clusters in 1MMA is shown in Fig. 3b.

The third case is represented by the SAXS curves of Hf4O4(OMc)12 (3) polymerised with methyl methacrylate (3MMA), as shown in Fig. 6 and Table 1.

Fig. 6

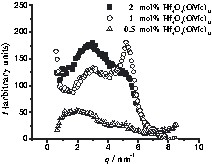
SAXS curves of 3MMA with cluster concentrations ranging from 0.5–2 mol%. The x-axis corresponds to the scattering vector, q, and the y-axis to I(q). I(q) is the scattering intensity after normalization and subtraction of the curve of cluster-free polymer.

The half-width and the position of both maxima are independent of the cluster portion in the polymer (D1 ≈ 1.3 nm and D2 ≈ 2.1 nm). A possible explanation is that the clusters in the polymer matrix are arranged in islands (clusters of clusters) (Fig. 3c). When a higher proportion of MMA co-monomer is employed in the polymerisation reactions, the inter-cluster distance is not increased, but instead the additional organic monomer is apparently incorporated between the cluster aggregates, and therefore the average inter-cluster distance determined by SAXS is independent of the cluster concentration. The same behaviour (although less pronounced) was already observed for PMA crosslinked by Ti4O2(OEt)6(OMc)6 (2) (D1 ≈ 1.6 nm and D2 ≈ 2.5 nm) [7].

3 Conclusions

The systematic SAXS study reported in this article, as well as previous SAXS investigations on related systems, have revealed four different types of microstructures.

  • • (1) Only one average inter-cluster distance that changes when the cluster portion in the polymer is varied. This behaviour was found for PMMA crosslinked by Zr6(OH)4O4(OMc)12), Zr4O2(OMc)12 or Ti6O4(OPr)8(acrylate)8, PMA crosslinked by Ti6O4(OPr)8(acrylate)8 or polystyrene crosslinked by Ta4O4(OEt)8(OMc)4.
  • • (2) Two inter-cluster distances, the shorter being constant when the cluster portion in the polymer is varied. This behaviour was found for PMMA crosslinked by Ti6O4(OPr)8(acrylate)8 or Ti4O2(OEt)6(OMc)6.
  • • (3) Two inter-cluster distances, the longer being constant when the cluster portion in the polymer is varied. This behaviour was found for PMMA crosslinked by Ta4O4(OEt)8(OMc)4.
  • • (4) Two inter-cluster distances, both being constant when the cluster portion in the polymer is varied. This behaviour was found for PMMA crosslinked by Hf4O4(OMc)12 or PMA crosslinked by Ti4O2(OEt)6(OMc)6.

Cases 2–4 reflect different aggregation behaviour of the clusters crosslinking the organic polymers. It must be emphasized, however, that the aggregates cannot be large, because the polymers are transparent at the investigated cluster concentrations. In addition, there is no long-range ordering of the clusters, because no X-ray diffraction pattern was observed.

The reasons for the different aggregation behaviour of the clusters are currently unknown. We do not see an obvious correlation with any structural or kinetic property of the clusters or the organic monomers. The same reaction conditions were applied for the preparation of each hybrid polymer. It can be speculated that aggregation might be caused by the different geometrical arrangement of the methacrylate ligands at the cluster surface, reactivity differences of the cluster-bonded methacrylate ligands, or still unknown inorganic reactions connecting the clusters with each other.

The magnitude of the smaller inter-cluster distance of about 1.2–1.5 nm observed in several cases can possibly provide the onset for an explanation. This distance corresponds quite well to the shortest inter-cluster distance given by the diameter of the cluster core and the organic shell. A direct contact of two clusters can result from two different processes.

  • • (1) When the reactivity of the cluster-bonded methacrylate ligands is higher than that of the organic monomers, the clusters may aggregate by preferred reaction of the ligands with each other rather than undergo reaction with the organic monomers.
  • • (2) Oligomers of clusters may be formed by converting intra-cluster carboxylate ligands into inter-cluster carboxylate bridges. For example, we have previously found that Zr6(OH)4O4(OMc)12 is monomeric in the solid state [11], while the derivatives Zr6(OH)4O4(acrylate)12, [12] and Zr6O4(OH)4(vinylacetate)12–x(OOCMe)x]2 (x = 4, 5.5 or 6) [13] are dimeric with cluster-bridging (meth)-acrylate ligands.

An alternative explanation, however, could be that the cluster aggregation is associated with the crystallization of the inorganic clusters in the polymer. Such phenomena are well known for the related POSS (polyhedral silsesquioxane) reinforced polymers [14]. It was postulated that the formation of POSS domains and, as a consequence, the nanoscale structuring of the copolymer, has significant consequences on the materials properties.

4 Experimental

The cluster-crosslinked polymers were prepared as previously described, [6,7,9] by radical polymerisation of the methacrylate-substituted clusters with methyl methacrylate or styrene as co-monomers. For the SAXS measurements, a piece of polymer of about 8 mm3 was placed in the sample holder.

4.1 Small angle scattering (SAXS)

The measurements were performed in transmission geometry using a pinhole camera with a rotating anode generator (Ni-monochromated Cu Kα radiation) and an area detector (Bruker AXS, Karlsruhe). Transmission geometry was used because the evaluation is simpler than, for example, for grazing incidence, where particle reflection and attenuation corrections are needed [15]. From each sample of the glassy material, SAXS measurements were carried out at three different positions within each specimen. Scattering curves were obtained in the q range 0.65–9 nm–1 with a detector distance of about 20 cm.

All SAXS patterns were first radially averaged to obtain the function I(q), where q = (4 π/λ) sinθ is the scattering vector (2θ = diffraction angle; λ = 0.154 nm the X-ray wavelength), and then corrected for background scattering from the experimental set-up. Then the data were normalized to I = 100 at q = 9 nm–1. Since the SAXS data at the three different positions within each specimen were the same within the experimental error limits, the data were averaged by averaging the normalized intensities at each q value. Finally, the normalized curve of the corresponding cluster-free polymer was subtracted.

The inter-cluster distance (D) was calculated by fitting the SAXS curves by a Gaussian function and converting the maximum into D by the equation D = 2 π/q.

Acknowledgments

This work was supported by the ‘Fonds zur Förderung der wissenschaftlichen Forschung’ (FWF). We thank Dr Silvia Gross and Dr Bogdan Moraru for the preparation of the polymer samples.

Bibliographie

[1] A.D. Pomogailo Russ. Chem. Rev., 69 (2000), p. 53

[2] F. Ribot; C. Sanchez Comments Inorg. Chem., 20 (1999), p. 327

[3] G. Kickelbick; U. Schubert Monatsh. Chem., 132 (2001), p. 13

[4] U. Schubert Chem. Mater., 13 (2001), p. 3487

[5] G. Kickelbick; M.P. Feth; H. Bertagnolli; B. Moraru; G. Trimmel; U. Schubert Monatsh. Chem., 133 (2002), p. 919

[6] S. Gross; V. Di Noto; G. Kickelbick; U. Schubert Mat. Res. Soc. Symp. Proc., 726 (2002), p. 47

[7] B. Moraru; N. Hüsing; G. Kickelbick; U. Schubert; P. Fratzl; H. Peterlik Chem. Mater., 14 (2002), p. 2732

[8] S. Gross; G. Kickelbick; M. Puchberger; U. Schubert Monatsh. Chem., 134 (2003), p. 1053

[9] G. Trimmel; P. Fratzl; U. Schubert Chem. Mater., 12 (2000), p. 602

[10] U. Schubert; G. Trimmel; B. Moraru; W. Tesch; P. Fratzl; S. Gross; G. Kickelbick; N. Hüsing Mat. Res. Soc. Symp. Proc., 628 (2001), p. CC2.3.1

[11] G. Kickelbick; U. Schubert Chem. Ber., 130 (1997), p. 473

[12] G. Kickelbick; P. Wiede; U. Schubert Inorg. Chim. Acta, 284 (1999), p. 1

[13] F. Kogler, G. Kickelbick, U. Schubert, unpublished.

[14] A.J. Waddon; L. Zhen; R.J. Farris; E.B. Coughlin Nano Lett., 2 (2002), p. 1149 (and references cited therein)

[15] B. Kutsch; O. Lyon; M. Schmitt; M. Mennig; H. Schmidt J. Appl. Crystallogr., 30 (1997), p. 948

Commentaires - Politique

Ces articles pourraient vous intéresser

Design of functional nano-structured materials through the use of controlled hybrid organic–inorganic interfaces

Clément Sanchez; Galo J.De A.A. Soler-Illia; François Ribot; ...

C. R. Chim (2003)

“Chimie douce”: A land of opportunities for the designed construction of functional inorganic and hybrid organic-inorganic nanomaterials

C. Sanchez; L. Rozes; F. Ribot; ...

C. R. Chim (2010)

Hybrid copolymer latexes cross-linked with methacryloxy propyl trimethoxy silane. Film formation and mechanical properties

Solweig Vitry; Audrey Mezzino; Catherine Gauthier; ...

C. R. Chim (2003)