facteur pré-exponentiel (s–1)
A1facteur pré-exponentiel (mole/m2s)
Csoconcentration molaire initiale du carbonate de calcium dans la particule (mol m–3)
Dediffusivité effective du gaz carbonique dans la couche d'oxyde de calcium (m2 s–1)
Eénergie d'activation (kJ/mol)
kgcoefficient de transfert du gaz carbonique à travers le film gazeux entourant la particule (m s–1)
ksconstante de vitesse de la réaction de décomposition du carbonate de calcium (mol m–2s–1)
k1constante de vitesse de la réaction de décomposition du carbonate de calcium (mol m–2s–1)
k2constante de vitesse de la réaction de carbonatation de la chaux (mol m–2 s–1 Pa–1)
nordre de réaction par rapport au réactif solide
PCO2pression partielle du gaz carbonique (Pa)
pression partielle du gaz carbonique dans le courant gazeux (Pa)
pression partielle du gaz carbonique à la surface du noyau réactif (Pa)
pression partielle du gaz carbonique à l'équilibre (Pa)
pression partielle du gaz carbonique à la surface de la particule (Pa)
rsvitesse de la réaction de décomposition de la pierre à chaux par unité de surface du noyau réactif (mol m–2s–1)
Rconstante des gaz parfaits (m3 atm mol–1 K–1)
R0rayon initial de la particule (m)
Rcrayon du noyau réactif (m)
Sgsurface spécifique (m2 mol–1)
ttemps (s)
Ttempérature (K)
Xtaux de conversion
Lettres grecquesεporosité de la couche d'oxyde de calcium
1 Introduction
Dans les procédés de fabrication du sucre à partir de la betterave, la chaux et le gaz carbonique, représentent deux réactifs indispensables à la réalisation de l'étape d'épuration du jus extrait de cette matière première.
Ces deux composés sont produits au sein de la sucrerie, dans un réacteur gaz–solides consommables appelé four à chaux.
Ce dernier est un réacteur à lit mouvant où se déroulent deux réactions principales : la combustion du coke et la décomposition de la pierre à chaux. Cette dernière est une réaction endothermique, qui consomme l'énergie produite par la première pour produire la chaux et le gaz carbonique. La non-régularité des caractéristiques de la pierre à chaux et du coke alimentant le four, ainsi que l'aspect des transferts au sein de ce dernier, rendent la tâche de la conduite du four très difficile.
Dans le but de résoudre ces problèmes, notre laboratoire (LASPI) et la Sucrerie nationale de betterave du Loukkos (Sunabel, Ksar El Kebir, Maroc) ont lancé des travaux de recherche en vue de développer un modèle mathématique susceptible d'être utilisé pour une conduite optimisée du four à chaux de cette sucrerie. Le modèle mathématique projeté est basé sur une analyse assez détaillée des phénomènes physico-chimiques qui interviennent dans le four en question.
La décomposition de la pierre à chaux est une réaction équilibrée. Sous l'effet de la chaleur, le carbonate de calcium (CaCO3) se décompose en oxyde de calcium (CaO) et en gaz carbonique (CO2) selon la réaction suivante : CaCO3 ⇆ CO2 + CaO.
Langmuir [16] suppose que la réaction se produit sur une surface de séparation entre les phases solides CaCO3 et CaO appelée interface. Cette dernière se déplace à une vitesse constante vers le centre de la particule.
L'analyse des travaux de recherche réalisés sur la cinétique de décomposition de la pierre à chaux publiés dans la littérature a montré une dispersion des résultats obtenus et l'existence de différents modèles décrivant la cinétique intrinsèque.
En fonction de la composition de la pierre à chaux et des conditions expérimentales du déroulement de la réaction, la vitesse du processus globale de décomposition de la pierre à chaux peut être contrôlée par l'une ou une combinaison des étapes suivantes :
- • transfert de chaleur extragranulaire ;
- • transfert de chaleur intragranulaire de la surface des grains vers la zone de réaction ;
- • réaction chimique à l'interface de séparation entre la chaux formée et le carbonate de calcium ;
- • transfert du gaz carbonique produit de la zone de réaction vers la surface des particules à travers la couche de CaO formé ;
- • transfert extragranulaire de CO2 à travers le film gazeux entourant les particules de la pierre à chaux.
Ainsi, Satterfield et Feakes [1], Gallagher et Johnson [2] et Caldwell et al. [3] ont montré que la vitesse de décomposition du carbonate de calcium est limitée par le transfert de chaleur. Ces études ont été réalisées respectivement dans les intervalles de température suivants : 998–1043,3 °C ; 900–950 °C ; 550–680 °C.
Hills [4] et Narsimhan [5] rapportent, au terme d'une étude cinétique portant sur la vitesse de décomposition du carbonate de calcium, un contrôle par les effets combinés des transferts de chaleur et de matière.
Asaki et al. [6] et Koloberdin et al. [7] ont montré que la vitesse de décomposition de petites particules de CaCO3 se déroule en régime mixte régi par le transfert de chaleur et la réaction chimique.
Khraisha et Dugwell [8] ont abouti à la même conclusion après une étude cinétique réalisée sur des échantillons de pierre à chaux dans l'intervalle de température 803–883 °C.
Borgwardt [9] et Dennis et Hayhurst [10] ont étudié la cinétique de décomposition de la pierre à chaux dans les intervalles de température respectifs suivants : 516–1000 °C et 800–975 °C. Ils ont montré que le processus global de décomposition de la pierre à chaux est limité par l'étape de réaction chimique.
Rao [11] a obtenu le même résultat en réalisant une étude cinétique sur des pastilles minces de carbonate de calcium dans l'intervalle de température 670–740 °C.
Les paramètres de la cinétique intrinsèque cités dans la littérature diffèrent d'une étude à l'autre. Ils dépendent du modèle cinétique intrinsèque choisi pour traiter les résultats expérimentaux et du matériau utilisé pour mener l'étude expérimentale.
Ainsi, Borgwardt [9] a obtenu une valeur d'énergie d'activation égale à 200,83 kJ mol–1 en utilisant le modèle suivant: ln (1 – X) = –ks Sg t. Dennis et Hayhurst [10] ont traité les résultats expérimentaux à l'aide du modèle cinétique intrinsèque suivant: rs=k1−k2PCO2c. Ils ont trouvé la valeur de 169,16 kJ mol–1 pour l'énergie d'activation. En utilisant la même expression que Dennis et Hayhurst, Rao [11] a trouvé pour ce paramètre la valeur de 192,17 kJ mol–1.
L'embarras du choix relevé dans la littérature des paramètres intrinsèques de la vitesse de la réaction de décomposition de la pierre à chaux et du modèle cinétique intrinsèque nous ont poussé à mener une étude appropriée de la vitesse de cette réaction.
Le présent travail consiste à développer un modèle mathématique de la cinétique intrinsèque de la réaction de décomposition de la pierre à chaux utilisée dans le four à chaux de la Sucrerie nationale de betterave du Loukkos (Sunabel, Ksar El Kebir, Maroc) et à déterminer les paramètres intrinsèques de cette réaction. Ce modèle et les valeurs de ces paramètres seront utilisés ultérieurement pour la simulation du four en question.
2 Aspect thermodynamique de la réaction
La réaction étudiée fait intervenir deux phases solides indépendantes : le carbonate de calcium et l'oxyde de calcium. Si on prend l'état pur comme état de référence pour ces deux composés solides, chacun d'eux aura une activité unité. Par conséquent, la constante d'équilibre de la réaction Kp est donnée par la relation (1) suivante [15] :
| (1) |
L'enthalpie libre de la réaction est donnée par l'expression (2) :
| (2) |
Selon la valeur de ΔG, trois cas peuvent se présenter :
- • si PCO2=PCO2e, ΔG = 0 ; le système est en équilibre ;
- • si PCO2<PCO2e, ΔG < 0 ; le carbonate de calcium se décompose pour donner de la chaux et du dioxyde de carbone ;
- • si PCO2>PCO2e, ΔG > 0 ; la réaction de décomposition ne peut pas avoir lieu.
3 Matériel et méthodes
3.1 Caractérisation de la pierre à chaux
La pierre à chaux avec laquelle les essais expérimentaux ont été réalisés est une pierre d'origine marocaine. Elle est utilisée comme matière première dans le four à chaux de la Sucrerie nationale de betterave de Loukkos (Sunabel Ksar El Kebir Maroc). Sa composition chimique, obtenue par analyse volumétrique et gravimétrique est donnée dans le Tableau 1.
Résultats d'analyse de la pierre à chaux étudiée (pourcentage massique)
| Composé | % massique |
| SiO2 | 0,9 ± 0,2 |
| Al2O3 | 0,37 ± 0,04 |
| Fe2O3 | 0,36 ± 0,04 |
| CaO | 53,2 ± 0,5 |
| MgO | 0,48 ± 0,03 |
La densité de la pierre à chaux étudiée a été déterminée en utilisant l'autopycnomètre Micromeritics Autopycnometer 1320. Le volume et la surface spécifique des pores ont été mesurés par un porosimètre à mercure Micromeritics Autopor II 9220. Les résultats sont regroupés dans le Tableau 2.
Valeurs de la densité, volume spécifique, surface spécifique et porosité de la pierre à chaux étudiée
| Densité (kg m–3) | 2739,33 ± 12,08 |
| Surface spécifique (m2 g–1) | 1,06 ± 0,03 |
| Volume spécifique (m3 kg–1) | 0,148 × 10–4 ± 0,004 × 2 10–4 |
| Porosité (%) | 4,05 ± 0,12 |
3.2 Essais cinétiques
3.2.1 Montage expérimental
L'étude expérimentale de la cinétique de décomposition de la pierre à chaux a été réalisée à l'aide de l'ensemble thermogravimétrique Setaram TGA 92 (Fig. 1).
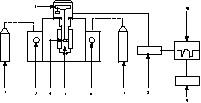
Représentation schématique de l'ensemble thermogravimétrique TGA92 : 1, bouteille de gaz carbonique ; 2, manomètre indiquant la pression d'entrée du gaz carbonique ; 3, microbalance ; 4, creuset ; 5, four ; 6, manomètre indiquant la pression d'entrée d'air ; 7, bouteille d'air ; 8, contrôleur CS 92 ; 9, imprimante ; 10, micro-ordinateur PC 92.
Cet appareillage se compose de la thermobalance proprement dite, du contrôleur CS 92, d'un micro-ordinateur et d'une imprimante.
La thermobalance se compose d'une microbalance électronique, d'un four à résistance en graphite et d'un circuit gazeux pour l'utilisation de gaz inerte et de gaz réactif. La température du four peut varier de la température ambiante jusqu'à 1750 °C. Le contrôleur CS 92 a pour fonction de gérer la programmation et la régulation de la température du four, les circuits de gaz et de vide, l'imprimante, l'acquisition et la numérisation des différents signaux (T, TG, ATD) et le calcul de la dérivée DTG, du signal thermogravimétrique. Le micro-ordinateur permet de piloter le thermoanalyseur à travers le contrôleur CS 92, selon des séquences définies par l'opérateur.
3.2.2 Mode opératoire
L'étude expérimentale de la cinétique de décomposition de la pierre à chaux a été réalisée à l'aide de la technique d'analyse thermogravimétrique (ATG) isotherme.
Les expériences ont été menées à température et pression constantes, en présence d'un courant gazeux d'air et de gaz carbonique.
Chaque essai expérimental est programmé sur un tableau de séquences permettant de fournir les paramètres nécessaires à la programmation du tarage de la balance, de la température du four, de la vitesse de chauffe et de l'ouverture–fermeture des électrovannes relatives aux circuits de gaz.
Pour mener à bien les essais expérimentaux, le mode opératoire composé des étapes suivantes a été adopté :
- • chauffage du four à la vitesse de chauffe 10 °C min–1, de sa température initiale à la température prévue pour le déroulement de l'essai expérimental ; ouverture des électrovannes correspondant à l'air et au gaz carbonique (la pression partielle de CO2 (PCO2) dans ce courant gazeux est maintenue supérieure à celle d'équilibre (PCO2e) pour éviter la décomposition d'échantillons à une température autre que celle désignée pour la réalisation de l'essai expérimental) ;
- • changement de la pression partielle de CO2 dans le courant gazeux (PCO2<PCO2e) et tarage de la balance, le débit gazeux étant maintenu constant ;
- • refroidissement du four de la température de réaction à la température ambiante et fermeture des électrovannes d'air et de gaz carbonique.
4 Résultats et discussion
4.1 Présentation des essais cinétiques
Des essais préliminaires ont permis de choisir les conditions opératoires susceptibles de réduire les effets de transfert.
Ainsi, un débit gazeux de 2 l h–1 et des échantillons de masse 5 mg et de granulométrie comprise entre 50 et 125 μm ont été adoptés.
Deux séries d'essais ont été réalisées pour étudier la cinétique de décomposition de la pierre à chaux. La première série examine l'influence de la température, tandis que la deuxième traite l'effet de la pression partielle de gaz carbonique.
Dans la première série, les essais ont été réalisés aux températures suivantes : 820, 850, 860, 890 et 900 °C, dans un courant d'air et de gaz carbonique de pression partielle en CO2 égale à 16,71 kPa. Les résultats expérimentaux obtenus sont représentés sur la Fig. 2. Les courbes de la Fig. 2 sont de même allure, et montrent que la vitesse de décomposition de la pierre à chaux augmente avec la température. Dans la deuxième série d'essais, l'influence de la pression partielle de CO2 a été examinée avec des mélanges gazeux d'air et de gaz carbonique. Les essais expérimentaux ont été réalisés à la température de 890 °C, avec une pression partielle de CO2 variant entre 16,71 et 42,54 kPa. Les résultats expérimentaux correspondants sont représentés sur la Fig. 3. On constate sur cette figure que la vitesse de décomposition de la pierre à chaux diminue avec la pression partielle de CO2. Ce résultat peut être expliqué par le fait que lorsque la pression partielle de CO2 augmente, l'effet de la vitesse de la réaction inverse (CaO + CO2 → CaCO3) devient plus important et se traduit par une diminution de la vitesse globale de la réaction. Cette vitesse est égale à la différence entre les vitesses de la réaction directe (CaCO3 → CaO + CO2) et de la réaction inverse.
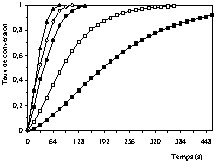
Influence de la température sur la vitesse de décomposition de la pierre à chaux à pression partielle de CO2 de 16,71 kPa et à différentes températures : 820 °C (■), 850 °C (□), 860 °C (•), 890 °C (○), 900 °C (▴).

Influence de la pression partielle de CO2 sur la vitesse de décomposition de la pierre à chaux à 890 °C et à différentes pressions partielles de CO2 : 16,71 kPa (○), 27,35 kPa (•), 36,47 kPa (□), 46,59 kPa (■).
4.2 Modélisation de la cinétique de décomposition de la pierre à chaux
4.2.1 Modèles testés
Pour établir le modèle mathématique permettant de décrire les résultats expérimentaux de la cinétique de décomposition de la pierre à chaux, deux modèles ont été testés :
4.2.1.1 Modèle à cœur rétrécissant
Ce modèle décrit le processus de déroulement de la réaction comme suit : au début, la réaction prend place à la surface extérieure de la particule. Au fur et à mesure que la réaction avance, il y a formation d'une couche d'oxyde de calcium et la réaction a lieu à l'interface entre le carbonate de calcium non décomposé et la couche de CaO produite.
Ainsi, le réactif solide se présente sous forme d'un noyau, qui se rétrécit au cours du déroulement de la réaction, et le gaz carbonique produit doit diffuser vers l'extérieur de la particule à travers la couche poreuse de CaO produite.
Le modèle est représenté par l'équation de bilan de matière relative au gaz carbonique:
| (3) |
avec les conditions aux limites suivantes :
- • à la surface de la particule, r = R0 :
(4) - • à la surface du noyau réactif, r = Rc :
(5)
| (6) |
À l'équilibre, rs = 0 ; par conséquent :
| (7) |
Baker [17] a étudié l'équilibre de la réaction de décomposition du carbonate de calcium. Il a proposé une expression pouvant prédire la pression partielle de CO2 à l'équilibre en fonction de la température. Cette expression est donnée par la relation suivante :
| (8) |
L'expression de la vitesse rs devient :
| (9) |
En supposant que les particules solides sont sphériques, que la température est uniforme à l'intérieur des particules et que le régime est quasi stationnaire, l'expression du modèle s'écrit comme suit :
| (10) |
Après intégration, l'équation représentant ce modèle devient :
| (11) |
La constante de vitesse intrinsèque est supposée suivre la loi d'Arrhenius :
| (12) |
En régime contrôlé par la cinétique chimique, le modèle est représenté par l'équation suivante :
| (13) |
4.2.1.2 Modèle empirique proposé par Coats et Redfern
Ce modèle est basé sur l'expression de la vitesse décrivant la cinétique de la réaction, où k et f(X) représentent, respectivement, la constante de vitesse de la réaction et une fonction du taux de conversion, dont l'expression dépend de la nature de la réaction.
En adoptant l'expression (1 – X)n pour f(X), Coats et Redfern expriment leur modèle à l'aide de l'équation suivante :
| (14) |
Après développement des calculs, l'expression du modèle s'écrit comme suit :
| (15) |
4.2.2 Estimation des paramètres des modèles testés
La qualité des deux modèles testés a été examinée par confrontation des données expérimentales et les résultats obtenus par calcul à partir des modèles décrit précédemment.
Cette confrontation a été menée à l'aide de la méthode d'ajustement basée sur le critère des moindres carrés non linéaires utilisant la méthode d'optimisation de Marquardt [14]. Les Figs. 4–10 présentent les résultats de cette confrontation. Le Tableau 3 fournit, pour chaque modèle testé et pour chaque essai expérimental, la moyenne des valeurs absolues des erreurs et l'erreur maximale.

Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 820 °C et PCO2 = 16,71 kPa : (•) valeurs expérimentales, (■) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (□) valeurs calculées à l'aide du modèle de Coats et Redfen.
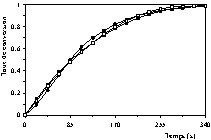
Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 850 °C et PCO2 = 16,71 kPa : (•) valeurs expérimentales, (■) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (□) valeurs calculées à l'aide du modèle de Coats et Redfern.
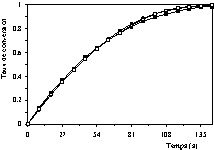
Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 860 °C et PCO2 = 16,71 kPa : (•) valeurs expérimentales, (■) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (□) valeurs calculées à l'aide du modèle de Coats et Redfern.

Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 890 °C et PCO2 = 16,71 kPa : (■) valeurs expérimentales, (□) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (•) valeurs calculées à l'aide du modèle de Coats et Redfern.
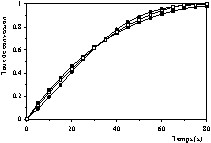
Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 900 °C et PCO2 = 16,71 kPa, (•) valeurs expérimentales, (■) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (□) valeurs calculées à l'aide du modèle de Coats et Redfern.

Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 890 °C et PCO2 = 36,47 kPa, (•) valeurs expérimentales, (■) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (□) valeurs calculées à l'aide du modèle de Coats et Redfern.

Courbes cinétique de décomposition de la pierre à chaux (taux de conversion en fonction du temps) à T = 890 °C et PCO2 = 46,59 kPa, (•) valeurs expérimentales, (□) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (■) valeurs calculées à l'aide du modèle de Coats et Redfern.
Moyenne des valeurs absolues des erreurs et erreur maximale des deux modèles testés, pour chaque essai expérimental réalisé en isotherme
| Modèle | Température (°C) | Pression partielle de CO2 (kPa) | Moyenne des valeurs absolues des erreurs (%) | Erreur maximale (%) |
| Modèle à cœur rétrécissant en régime chimique | 820 | 16,71 | 7,16 | 20,68 |
| 850 | 16,71 | 4,98 | 19,11 | |
| 860 | 16,71 | 4,73 | 11,41 | |
| 890 | 16,71 | 4,58 | 14,85 | |
| 900 | 16,71 | 7,19 | 19,87 | |
| 890 | 27,35 | 8,43 | 23,06 | |
| 890 | 36,47 | 5,32 | 20,62 | |
| 890 | 46,59 | 5,80 | 20,39 | |
| Modèle empirique proposé par Coats et Redfern | 820 | 16,71 | 5,50 | 19,60 |
| 850 | 16,71 | 4,33 | 15,60 | |
| 860 | 16,71 | 1,34 | 4,16 | |
| 890 | 16,71 | 2,28 | 8,18 | |
| 900 | 16,71 | 4,54 | 17,53 | |
| 890 | 27,35 | 6,07 | 23,06 | |
| 890 | 36,47 | 4,49 | 13,73 | |
| 890 | 46,59 | 5,19 | 20,64 |
L'analyse des Figs. 4–10 et des valeurs du Tableau 3 permet de constater que les données expérimentales relatives à l'intervalle de température compris entre 820 et 900 °C sont bien reproduites à l'aide du modèle de Coats et Redfern et du modèle à cœur rétrécissant en régime contrôlé par la cinétique chimique. Ce dernier résultat permet de dire que, dans l'intervalle de température compris entre 820 et 900 °C, la cinétique observée est bien une cinétique intrinsèque.
Les valeurs des paramètres cinétiques ajustés pour le modèle à cœur rétrécissant en régime contrôlé par la cinétique chimique et le modèle de Coats et Redfern sont données respectivement dans les Tableaux 4 et 5.
Valeurs des paramètres cinétiques du modèle à cœur rétrécissant en régime chimique dans l'intervalle de température compris entre 820 et 900 °C.
| Paramètres | Écarts types | ||
| A1 (mole m–2s–1) | E (kJ mol–1) | A1 (mole m–2s–1) | E (kJ mol–1) |
| 1,66 × 107 | 205,41 | 0,19 × 107 | 42,59 |
Valeurs des paramètres cinétiques du modèle empirique de Coats et Redfern dans l'intervalle de température compris entre 820 et 900 °C.
| Paramètres | Écarts types | ||||
| A (s–1) | n | E (kJ mol–1) | A (s–1) | n | E (kJ mol–1) |
| 5,22 × 108 | 0,5 | 233,15 | 0,66 × 108 | — | 46,76 |
Les valeurs d'énergie d'activation de la cinétique intrinsèque de la réaction de décomposition du carbonate de calcium rencontrées dans la littérature sont reportées dans le Tableau 6. L'examen de ce tableau permet de constater que la valeur d'énergie d'activation obtenue dans le présent travail diffère plus ou moins de celles publiées dans la littérature. Cette différence peut être attribuée à la nature de la pierre à chaux utilisée dans l'étude expérimentale et à l'expression du modèle cinétique intrinsèque adoptée pour le traitement des résultats expérimentaux. Ainsi, Dennis et Hayhurst [10] ont trouvé une valeur d'énergie d'activation égale à 169,16 kJ mol–1 en utilisant l'expression du modèle suivante : rs=k1−k2PCO2c. En utilisant la même expression du modèle cinétique intrinsèque que Dennis et al., Rao [11] a obtenu une valeur d'énergie d'activation égale à 192,17 kJ mol–1. Borgwardt [9] a trouvé pour ce paramètre la valeur de 200,83 kJ mol–1 en adoptant l'expression du modèle suivante: ln (1 – X) = –ks Sg t.
Valeurs d'énergie d'activation de la cinétique intrinsèque rencontrées dans la littérature pour la réaction de décomposition de la pierre à chaux et celle obtenue dans ce travail
| Auteur | Nature du réactif solide | Appareillage | Atmosphère gazeuse | Intervalle de température (°C) | Énergie d'activation E (kJ mol–1) |
| Borgwardt [9] | pierre à chaux | réacteur à lit entraîné | N2 | 516–1000 | 200,83 |
| Dennis et Hayhurst [10] | pierre à chaux | réacteur à lit fluidisé | air + CO2 | 800–975 | 169,16 |
| Rao [11] | pastilles minces de CaCO3 | thermobalance | N2 | 670–740 | 192,17 |
| Présent travail | pierre à chaux | thermobalance | air + CO2 | 820–900 | 205,41 |
5 Conclusion
La diversité des résultats publiés dans la littérature quant à la vitesse de décomposition de la pierre à chaux et la difficulté qu'il y a à choisir entre ces résultats pour les appliquer à la simulation d'un four à chaux de sucrerie ont été les causes principales qui nous ont poussé à mener une étude appropriée sur la cinétique de cette réaction.
L'étude expérimentale de la cinétique de décomposition de la pierre à chaux a été réalisée par analyse thermogravimétrique isotherme dans l'intervalle de température compris entre 820 et 900 °C. Il a été montré que la réaction se déroule en régime contrôlé par la cinétique chimique. Le modèle à cœur rétrécissant en régime contrôlé par la cinétique chimique et le modèle empirique de Coats et Redfern décrivent convenablement les résultats expérimentaux. Les valeurs d'énergie d'activation ajustées à l'aide des deux modèles testés ne sont pas significativement différentes. Elles sont égales à 205,41 et 233,15 kJ mol–1, respectivement, pour le modèle à cœur rétrécissant en régime chimique et le modèle de Coats et Redfern. Ces valeurs diffèrent plus ou moins de celles publiées dans la littérature. Cette différence est due à la nature de la pierre à chaux utilisée dans l'étude expérimentale et à l'expression du modèle cinétique intrinsèque adopté pour le traitement des résultats expérimentaux.
Remerciements
Ce travail a été réalisé grâce à l'aide de l'ENSIGC de Toulouse France (équipe du regretté Prof. Laguérie) et de la Sucrerie nationale de betterave du Loukkos, Ksar El Kebir (Maroc).


