facteur pré-exponentiel (mol m–2 s–1 atm–n)
CS0concentration molaire initiale de carbone dans la particule (mol m–3)
Csconcentration molaire instantanée du carbone dans la particule (mol m–3)
Dediffusivité effective d'oxygène dans la couche de cendres (m2 s–1)
Eénergie d'activation (kJ/mol)
knombre d'observations
kgcoefficient de transfert d'oxygène à travers le film gazeux entourant la particule (m s–1)
KSconstante de vitesse de réaction basée sur la surface du noyau réactif (mole m–2 s–1 atm–n)
mordre de réaction par rapport au carbone
nordre de réaction par rapport à l'oxygène
pnombre de paramètres
Po2pression partielle d'oxygène (Pa)
rsvitesse de consommation du coke par unité de surface du noyau réactif (mol m–2 s–1)
Rconstante des gaz parfaits (m3 atm mol–1 K–1)
R0rayon initial de la particule (m)
Rcrayon du noyau réactif (m)
ttemps (s)
Ttempérature (K)
T'température (°C)
Xtaux de conversion
Lettres grecquesβparamètre empirique utilisé dans le modèle d'Ocampo
εporosité de la couche de cendres
1 Introduction
Dans les procédés de fabrication du sucre à partir de la betterave, l'étape d'épuration du jus brut extrait de cette matière nécessite la disponibilité de la chaux et du gaz carbonique. Ces deux composés sont produits au sein de la sucrerie dans un réacteur gaz–solides consommables appelé four à chaux.
Ce dernier est un réacteur à lit mouvant, où se déroulent deux réactions principales : la combustion du coke et la décomposition de la pierre à chaux. La première est une réaction exothermique permettant de fournir la chaleur nécessaire au déroulement de la seconde. Cette dernière permet de produire de la chaux, en plus du gaz carbonique qui résulte aussi de la combustion du coke. L'antagonisme thermique de ces deux réactions rend la conduite du four très délicate. Cette difficulté est accentuée par la non-régularité des caractéristiques de la pierre à chaux et du coke alimentant le four.
Dans le cadre d'une collaboration entre notre laboratoire (LASPI) et la Sucrerie nationale de betterave du Loukkos (Sunabel Ksar El Kebir), des travaux de recherche sont menés en vue de développer un modèle mathématique susceptible d'être utilisé pour une conduite optimisée du four à chaux de cette sucrerie. Le modèle mathématique projeté est basé sur une analyse assez détaillée des phénomènes physico-chimiques qui se déroulent dans le four en question.
La cinétique de combustion du coke a fait l'objet de plusieurs travaux de recherche publiés dans la littérature scientifique. La diversité des résultats obtenus par ces études a montré que la vitesse de cette réaction peut être contrôlée par l'une ou une combinaison des étapes suivantes :
- • transfert de matière extragranulaire à travers la couche de gaz entourant la particule de coke ;
- • transfert de matière intragranulaire à travers les pores du solide ;
- • réaction chimique entre le réactif solide (carbone) et le gaz réactif (oxygène).
En général, le processus de combustion est limité par l'étape de réaction chimique pour les températures situées entre 350 et 750 °C [1–6], alors qu'il dépend des phénomènes de transfert dans l'intervalle 800–1390 °C [1,3,6–8].
Les études théoriques développées sur les réactions gaz–solides ont montré que l'énergie d'activation intrinsèque (contrôle par la cinétique chimique, régime I) vaut à peu près le double de celle obtenue dans le cas où le processus de réaction est limité par la réaction chimique et la diffusion intragranulaire (régime II) [9,10].
Ainsi, TIA et al. [11] ont obtenu dans leur étude cinétique sur la combustion d'un coke ligniteux une énergie d'activation égale à 103,24 kJ mol–1 en régime I et 56,59 kJ mol–1 en régime II. Les valeurs de ce même paramètre en régime I et II calculées par SMITH et al. [6] sont égales respectivement à 180 et 90 kJ mol–1.
Certains travaux se sont intéressés à l'étude du mécanisme de combustion du coke [17,18]. Basu et al. [17] rapportent dans leur étude sur la combustion des particules de coke à basses températures (température inférieure à 800 °C) que le carbone brûle selon un mécanisme basé sur un modèle à un seul film : le carbone réagit directement avec l'oxygène pour produire le monoxyde de carbone (CO) et le dioxyde de carbone (CO2) selon les deux réactions suivantes : 2 C + O2 → 2CO et C + O2 → CO2. Le monoxyde de carbone formé est ensuite oxydé dans le film gazeux entourant la particule selon la réaction :
A plus haute température (au-delà de 1000 °C), Avedesian et Davidson [18] ont proposé un autre mécanisme, appelé modèle à double film. Dans ce modèle, l'oxygène qui diffuse vers la surface de la particule du coke se consomme en totalité dans le premier film, avant d'atteindre la surface de la particule selon la réaction suivante : 2 CO + O2 → 2 CO2.
Une partie de CO2 produit lors de cette réaction diffuse vers la surface de la particule à travers le deuxième film et réagit selon la réaction suivante : C + O2 → 2 CO.
Les paramètres intrinsèques de la vitesse de combustion du coke, cités dans la littérature, ont été estimés en utilisant différents modèles proposés pour décrire la cinétique intrinsèque de cette réaction. Lin et al. [2] ont traité leurs résultats expérimentaux à l'aide du modèle suivant: . Tia et al. [11] et Dutta et Wen [4] ont utilisé la même expression du modèle de Lin et al., avec n = m = 1. Tandis que Hamor et al. [1], Smith et al. [6] et Boumahmaza [5] ont proposé l'expression du modèle de la cinétique intrinsèque suivante: rs=KPno2.
Les paramètres de la cinétique intrinsèque fournis dans la littérature diffèrent d'une étude à l'autre. Ils dépendent de la matière première utilisée et de l'expression du modèle cinétique intrinsèque choisi pour traiter les résultats expérimentaux. Hamor et al. [1] et Tia et al. [11] ont trouvé respectivement pour un coke ligniteux les valeurs d'énergie d'activation suivantes: 133,9 et 103,24 kJ mol–1. Smith et al. [6] ont obtenu la valeur de 180 kJ mol–1 pour un coke de charbon de faible volatilité. Boumahmaza [5] rapporte dans son étude cinétique sur un anthracite une énergie d'activation égale à 61.95 kJ mol–1.
Étant donné la dispersion des valeurs des paramètres cinétiques et des expressions des modèles mathématiques de la cinétique intrinsèque observée dans la littérature, il a été jugé indispensable de mener une étude appropriée pour la modélisation de la cinétique de combustion du coke dans les conditions opératoires du four à chaux industriel tel qu'il est exploité à Sunabel Ksar El-Kebir.
Le présent travail est consacré au développement d'un modèle mathématique décrivant la cinétique de la réaction de combustion du coke utilisé dans le four à chaux de la sucrerie Sunabel Ksar El-Kebir, dans l'intervalle de température compris entre 550 et 1100 °C. Ce modèle sera exploité ultérieurement pour la simulation du four à chaux.
2 Matériel et méthodes
2.1 Caractérisation du coke
Le coke utilisé dans ce travail est un coke obtenu par pyrolyse d'un charbon d'origine anglaise. Les résultats de son analyse immédiate sont donnés dans le Tableau 1.
Résultats de l'analyse immédiate du coke étudié
| Composé | % Massique |
| Humidité | 1,69 ± 0,03 |
| Matières volatiles | 2,50 ± 0,2 |
| Cendres | 6,6 ± 0,6 |
| Carbone fixe | 89,2 ± 0,6 |
Cette analyse permet l'évaluation de la teneur en humidité, en matières volatiles, en carbone fixe et en cendres. L'humidité a été déterminée en mesurant la perte de poids d'un échantillon séché dans une étuve pendant 1 h à 105 °C (norme Afnor M03-002). La teneur en cendres a été évaluée à partir du résidu de la combustion d'un échantillon de coke, à une température de 800 °C (norme Afnor M03-003). La matière volatile a été déterminée par la perte de poids d'un échantillon de coke maintenu à une température de 900 °C, à l'abri de l'air pendant 7 min (norme Afnor M03-004). Le carbone fixe est obtenu par différence.
La densité du coke étudié a été déterminée en utilisant l'autopycnomètre Micromeritics Autopycnometer 1320. Le volume et la surface spécifique des pores ont été mesurés à l'aide d'un porosimètre à mercure Micromeritics Autopor II 9220. Les résultats sont regroupés dans le Tableau 2.
Valeurs de la densité, du volume spécifique, de la surface spécifique et de la porosité du coke étudié
| Densité (kg m–3) | 1793,7 ± 13,5 |
| Surface spécifique (m2 g–1) | 4,09 ± 0,04 |
| Volume spécifique (m3 kg–1) | 0,82 × 10–4 ± 0,01 × 10-4 |
| Porosité (%) | 14,7 ± 0,1 |
2.2 Essais cinétiques
2.2.1 Montage expérimental
L'étude expérimentale de la cinétique de combustion du coke a été réalisée à l'aide de l'ensemble thermogravimétrique Setaram TGA 92 (Fig. 1).
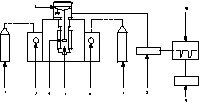
Représentation schématique de l'ensemble thermogravimétrique TGA92 : 1, bouteille de gaz réactif ; 2, manomètre indiquant la pression d'entrée du gaz réactif ; 3, microbalance ; 4, creuset ; 5, four ; 6, manomètre indiquant la pression d'entrée du gaz inerte ; 7, bouteille de gaz inerte ; 8, contrôleur CS 92 ; 9, imprimante ; 10, micro-ordinateur PC 92.
Cet appareillage se compose de la thermobalance proprement dite, du contrôleur CS 92, d'un micro-ordinateur et d'une imprimante. La thermobalance se compose d'une microbalance électronique, d'un four à résistance en graphite et d'un circuit gazeux pour l'utilisation de gaz inerte et de gaz réactif, la circulation des gaz à l'intérieur du dispositif expérimental se réalise parallèlement à l'axe de fixation du creuset porte-échantillon. Ce dernier est de nature compacte. La température du four peut varier de la température ambiante jusqu'à 1750 °C. Le contrôleur CS 92 a pour fonction de gérer la programmation et la régulation de la température du four, les circuits de gaz et de vide, l'imprimante, l'acquisition et la numérisation des différents signaux (T, TG, ATD) et le calcul de la dérivée DTG du signal thermogravimétrique. Le micro-ordinateur permet de piloter le thermoanalyseur à travers le contrôleur CS 92, selon des séquences définies par l'opérateur.
2.2.2 Mode opératoire
La technique expérimentale adoptée pour étudier la cinétique de combustion du coke est l'analyse thermogravimétrique (ATG).
Les expériences ont été réalisées en isotherme, à pression atmosphérique. Chaque essai expérimental est programmé sur un tableau de séquences permettant de fournir les paramètres nécessaires à la programmation du tarage de la balance, de la température du four et de l'ouverture et fermeture des électrovannes relatives aux circuits de gaz et du vide.
Pour réaliser les essais expérimentaux, le mode opératoire composé des étapes suivantes a été adopté :
- • évacuation de l'air contenu dans le four par ouverture de l'électrovanne relative au vide ; au cours de cette étape, la température du four reste constante et garde sa valeur initiale ;
- • fermeture de l'électrovanne relative au vide et ouverture de celle correspondant au remplissage du four par le gaz inerte, le four étant maintenu à sa température initiale ;
- • tarage de la balance et chauffage du four de sa température initiale à la température de réaction, selon une vitesse de chauffe de 5 °C min–1, l'électrovanne du gaz inerte étant maintenue ouverte ;
- • fermeture de l'électrovanne du gaz inerte et ouverture de celle du gaz réactif pour réaliser la réaction de combustion du coke à la température atteinte par chauffage lors de l'étape précédente ;
- • fermeture de l'électrovanne du gaz réactif et refroidissement du four de la température de réaction à la température ambiante.
3 Résultats et discussion
3.1 Présentation des essais cinétiques
L'intervalle de température 550–1100 °C a été choisi pour les essais expérimentaux de manière à couvrir la gamme de température qui règne dans la zone de combustion du four à chaux.
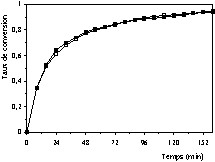
Des essais préliminaires ont été effectués à différentes températures pour choisir les conditions opératoires appropriées à l'étude cinétique. Les courbes (Figs. 2 et 3) permettent de constater qu'à 600 °C (Fig. 2) une valeur double du débit du gaz vecteur a un effet négligeable sur la cinétique, alors qu'à 1000 °C (Fig. 3), un effet très significatif est obtenu pour la même variation de ce débit. Ce résultat permet de mettre en évidence l'effet important des transferts de matière et de chaleur sur la vitesse de réaction pour les essais réalisés à haute température. Ces essais ont été réalisés avec une masse d'échantillon de 5 mg et une granulométrie inférieure à 200 μm. Afin de réduire cet effet, des essais ont été effectués en réduisant la granulométrie des particules. La Fig. 4 montre que cette réduction ne permet pas d'éliminer l'effet en question. De ces essais préliminaires on peut déduire, qu'a priori, la cinétique intrinsèque de combustion du coke étudié ne pourra pas être obtenue à l'aide d'essais effectués à des températures supérieures à 1100 °C. Cependant, pour déterminer avec assez de précision le seuil de température au-delà duquel l'effet des transferts devient non négligeable, l'intervalle de température adopté pour les essais cinétiques est compris entre 550 et 1100 °C.
Influence du débit de gaz réactif sur la vitesse de combustion du coke à 600 °C, à pression partielle d'oxygène de 20,26 kPa et à différents débits d'air : 1,06 (□) et 1,9 l h–1 (■).
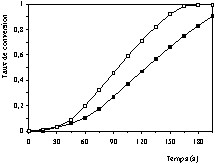
Influence du débit de gaz réactif sur la vitesse de combustion du coke à 1000°C, à pression partielle d'oxygène de 20,26 kPa et à différents débits d'air : 1,06 (□) et 1,9 l h–1 (■).
Influence de la granulométrie sur la vitesse de combustion du coke à 800 °C, à pression partielle d'oxygène de 20,26 kPa et à différentes granulométries : < 0,2 mm (•), entre 0,2 et 0,4 mm (■), entre 0,4 et 0,6 mm (□).
Deux séries d'essais ont été réalisées pour étudier la cinétique de combustion du coke. Pour ces deux séries d'essais, la masse de l'échantillon et le débit du gaz vecteur ont été fixés respectivement à 5 mg et 1,9 l h–1, la granulométrie étant inférieure à 200 μm. La première série examine l'influence de la température, tandis que la deuxième traite l'effet de la pression partielle d'oxygène.
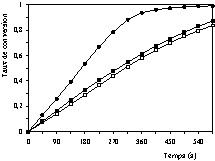
Dans la première série d'essais la température a été fixée à plusieurs valeurs dans l'intervalle 550–1100 °C, en utilisant l'air. Les résultats expérimentaux obtenus sont représentés sur les Figs. 5 et 6. Les courbes de la Fig. 5 sont de même allure et montrent l'effet évident de la température sur la vitesse de combustion du coke. En revanche, les courbes de la Fig. 6 sont d'une allure différente de celles de la Fig. 5, notamment par la présence d'un point d'inflexion. Celui-ci peut être interprété par le déroulement simultané de deux phénomènes différents ayant un effet significatif sur la vitesse de combustion observée : la réaction de combustion proprement dite et les phénomènes de transfert.
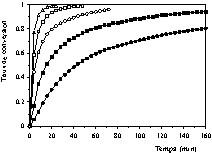
Influence de la température sur la vitesse de combustion du coke à pression partielle d' oxygène de 20,26 kPa et à différentes températures: 550 °C (•), 600 °C (■), 650 °C (○), 700 °C (□), 750 °C (▵).
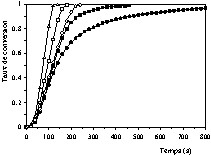
Influence de la température sur la vitesse de combustion du coke à pression partielle d'oxygène de 20,26 kPa et à différentes températures : 750 °C (•), 800 °C (■), 900 °C (○), 1000 °C (□), 1100 °C (▵).
Dans la deuxième série d'essais, l'influence de la pression partielle d'oxygène a été examinée en utilisant des mélanges gazeux d'oxygène et d'argon, avec une pression partielle d'oxygène variant entre 15,198 et 60,795 kPa. Les résultats expérimentaux correspondant sont représentés sur les Figs. 7 et 8. Les figures mettent bien en évidence l'influence de la pression partielle d'oxygène sur la vitesse de combustion observée. La comparaison de ces deux figures confirme la même différence dans les allures des courbes que pour les Figs. 5 et 6, cette différence pouvant être interprétée de la même manière.
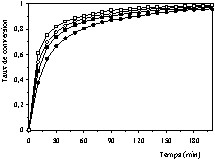
Influence de la pression partielle d' oxygène sur la vitesse de combustion du coke à 600 °C et à différentes pressions partielles d'oxygène : 20,26 kPa (•), 33,94 kPa (■), 43,36 kPa (○), 58,76 kPa (□).
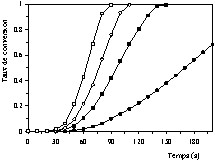
Influence de la pression partielle d'oxygène sur la vitesse de combustion du coke à 1000 °C et à différentes pressions partielles d'oxygène : 18,54 kPa (•), 33,94 kPa (■), 43,36 kPa (○), 58,76 kPa (□).
3.2 Modélisation de la cinétique de combustion du coke
3.2.1 Modèles testés
Pour établir le modèle mathématique permettant de décrire de manière fiable la vitesse de combustion, dans l'intervalle de température choisi, deux modèles ont été testés :
- • le modèle à cœur rétrécissant Wen [12], Ishida et Wen [13] ;
- • le modèle empirique proposé par Ocampo [14].
3.2.1.1 Modèle à cœur rétrécissant [12,13]
Ce modèle décrit le processus de déroulement de la réaction comme suit : au début, la porosité du solide est très faible, la réaction prend place à la surface extérieure de la particule. Au fur et à mesure que la réaction avance, il y a formation d'une couche poreuse de produits solides (cendres), qui laisse diffuser le réactif fluide à l'intérieur de la particule, et la réaction a lieu à l'interface située entre le solide réactif et la couche de cendres produite.
Ainsi, le réactif solide se présente sous forme d'un noyau, qui se rétrécit au cours du déroulement de la réaction. Quant au réactif gazeux, il doit vaincre deux résistances pour atteindre la surface du noyau réactif : la résistance au transfert d'oxygène à travers le film gazeux entourant la surface extérieure de la particule et la résistance à la diffusion de cette même substance dans la couche poreuse de cendres. Le modèle est représenté par l'équation de bilan de matière relatif à l'oxygène :
| (1) |
- • à la surface de la particule, r = R0
(2) - • à la surface du noyau réactif, r = Rc
(3)
(Po2)0, (Po2)s et (Po2)c représentent, respectivement, la pression partielle d'oxygène à la surface extérieure du film gazeux entourant la particule, à la surface de la particule et à la surface du noyau réactif, De est le coefficient de diffusion effectif de l'oxygène dans la couche de cendres, et kg le coefficient de transfert d'oxygène à travers le film gazeux entourant la particule.
Lin et al. [2] proposent l'expression suivante pour la vitesse intrinsèque de la combustion du coke:
| (4) |
En supposant que les particules solides sont sphériques, que la température est uniforme à l'intérieur des particules et que le régime est quasi stationnaire, l'expression du modèle en régime contrôlé par la cinétique chimique, pour n quelconque, peut s'écrire comme suit :
| (5) |
La constante de vitesse intrinsèque, Ks, est supposée suivre la loi d'Arrhenius :
| (6) |
3.2.1.2 Modèle empirique proposé par Ocampo [14]
OCAMPO [14] a proposé un modèle empirique pour décrire la cinétique de gazéification d'un anthracite en thermobalance. Ce modèle se base sur l'expression du modèle à cœur rétrécissant en régime contrôlé par la cinétique chimique, en faisant intervenir un paramètre empirique β. Il est représenté par l'expression suivante :
| (7) |
3.2.2 Estimation des paramètres des deux modèles
Le test des deux modèles présentés ci-dessus a été réalisé par confrontation avec les données expérimentales décrites précédemment. Cette confrontation a été menée à l'aide de la méthode d'ajustement basée sur le critère des moindres carrés non linéaires utilisant la méthode d'optimisation de Marquardt [15]. Les Figs. 9 à 13 présentent les résultats de cette confrontation. Le Tableau 3 regroupe, pour chaque modèle, la moyenne des valeurs absolues des erreurs, l'erreur maximale et la variance du modèle. Cette dernière est calculée à l'aide de l'expression suivante :
| (8) |
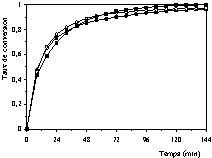
Courbes cinétiques de combustion du coke (taux de conversion en fonction du temps) à T = 600 °C et PO2 = 43,36 kPa : (•) valeurs expérimentales, (○) valeurs calculées à l'aide du modèle à coeur rétrécissant en régime chimique, (■) valeurs calculées à l'aide du modèle empirique.
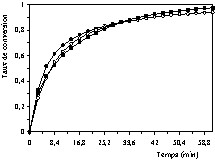
Courbes cinétiques de combustion du coke (taux de conversion en fonction du temps) à T = 650 °C et PO2 = 20,26 kPa : (•) valeurs expérimentales, (○) valeurs calculées à l'aide du modèle à coeur rétrécissant en régime chimique, (■) valeurs calculées à l'aide du modèle empirique.
Courbes cinétiques de combustion du coke (taux de conversion en fonction du temps) à T = 700 °C et PO2 = 20,26 kPa : (□) valeurs expérimentales, (○) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (■) valeurs calculées à l'aide du modèle empirique.
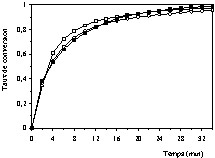
Courbes cinétiques de combustion du coke (taux de conversion en fonction du temps) à T = 900 °C et PO2 = 20,26 kPa : (•) valeurs expérimentales, (■) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (□) valeurs calculées à l'aide du modèle empirique.
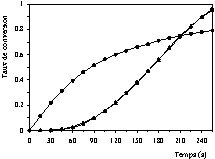
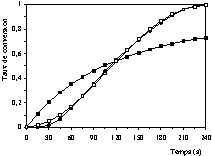
Courbes cinétiques de combustion du coke (taux de conversion en fonction du temps) à T = 1000 °C et PO2 = 18,54 kPa, (○) valeurs expérimentales, (•) valeurs calculées à l'aide du modèle à cœur rétrécissant en régime chimique, (▴) valeurs calculées à l'aide du modèle empirique.
Moyenne des valeurs absolues des erreurs, variance et erreur maximale des modèles testés
| Modèle | Intervalle de température | Moyenne des valeurs absolues des erreurs (%) | Erreur maximale (%) | Variance du modèle |
| Modèle à cœur | 550 ≤ T ≤ 750 °C | 4,71 | 21,3 | 0,00195 |
| rétrécissant | 800 ≤ T ≤ 1100 °C | 23,31 | 60,1 | 0,04339 |
| Modèle empirique | 550 ≤ T ≤ 750 °C | 5,79 | 17,54 | 0,0038 |
| 800 ≤ T ≤ 1100 °C | 2,29 | 8,51 | 0,00089 |
L'analyse des Figs. 9–13 et des valeurs du Tableau 3 permet de constater que le modèle empirique décrit la cinétique de combustion dans l'intervalle de température étudié (500 ≤ T′ ≤ 1100 °C). En plus, on remarque que les paramètres cinétiques ajustés à l'aide de ce modèle changent lorsqu'on passe de l'intervalle de température 550–750 °C à l'intervalle 800–1100 °C. La valeur de l'énergie d'activation obtenue dans le premier intervalle (113,94 kJ mol–1) vaut à peu près le double de celle correspondant au deuxième intervalle (43,39 kJ mol–1). Ce résultat permet de conclure que dans le deuxième intervalle de température, la cinétique de combustion est influencée par les phénomènes de transfert [6,9–11].
D'un autre côté, les données expérimentales relatives au premier intervalle sont bien reproduites à l'aide du modèle à cœur rétrécissant en régime contrôlé par la cinétique chimique (Figs. 9–11). Par ailleurs, ce modèle ne convient pas à la description des données expérimentales du deuxième intervalle, dans lequel la cinétique est influencée par l'effet des phénomènes de transfert (Figs. 12 et 13). Ainsi, on peut dire que dans l'intervalle de température compris entre 550 et 750 °C, la cinétique observée est bien une cinétique intrinsèque.
Ces résultats peuvent être justifiés par les mécanismes proposés par Basu et al. [17] et Avedesian et Davidson [18]. Cependant, la méthode expérimentale utilisée dans le présent travail et qui est basée sur la technique ATG ne permet pas de tester la validité de tels mécanismes.
Les valeurs des paramètres cinétiques ajustés pour les deux modèles testés sont données dans les Tableaux 4 et 5. Les résultats d'ajustement pour le modèle empirique ont montré que, pour l'intervalle de température compris entre 550 et 750 °C, les valeurs de β ajustées pour différentes températures ne sont pas significativement différentes. En revanche, dans l'intervalle de température compris entre 800 et 1100 °C, la valeur de β dépend de la température et de la pression partielle d'oxygène (Tableau 6).
Valeurs des paramètres cinétiques du modèle à cœur rétrécissant en régime chimique dans l'intervalle de température compris entre 550 et 750 °C.
| Paramètres | Écarts types | ||||||
| n | As (mol m–2 s–1 atm–n) | m | E (kJ mol–1) | n | As (mol m–2 s–1 atm–n) | m | E (kJ mol–1) |
| 0,8 | 981,347 | 0,933 | 113,53 | 0,05 | 63,787 | — | 2,04 |
Valeurs des paramètres cinétiques du modèle empirique dans les intervalles de températures 550–750 °C et 800–1100 °C.
| Intervalle de température | Paramètres | Écarts types | ||||||
| n | As (mole m–2 s–1 atm–n) | β | E (kJ mol–1) | n | As (mole m–2 s–1 atm–n) | β | E (kJ mol–1) | |
| 550 ≤ T ≤ 750 °C | 0,62 | 6770,49 | 1,69 | 113,94 | 0,06 | 592,41 | 0,03 | 2,98 |
| 800 ≤ T ≤ 1100 °C | 0,99 | 7,3 | — | 43,39 | 0,08 | 0,1 | — | 1,99 |
Valeurs du paramètre β dans l'intervalle de température compris entre 800 et 1100 °C pour différentes valeurs de la pression partielle d'oxygène
| T (°C) | PO2 (atm) | β |
| 800 | 0,21 | 0,750 |
| 900 | 0,21 | 0,527 |
| 1000 | 0,21 | 0,449 |
| 1100 | 0,21 | 0,392 |
| 1000 | 0,183 | 0,361 |
| 1000 | 0,335 | 0,296 |
| 1000 | 0,428 | 0,250 |
| 1000 | 0,58 | 0,233 |
Le paramètre β a été corrélé à la température et à la pression partielle d'oxygène, en utilisant la technique de régression non linéaire basée sur le même critère d'ajustement que celui utilisé précédemment :
| (9) |
Les valeurs de l'erreur maximale et de la moyenne des valeurs absolues des erreurs sont de 9 et 4%, respectivement.
Les valeurs des paramètres de la cinétique intrinsèque rencontrées dans la littérature pour la réaction de combustion du coke et celles obtenues dans ce travail sont regroupées dans le Tableau 7. Comme on peut le constater, les résultats montrent une dispersion assez importante. Cette dispersion peut être attribuée à la nature de la matière première (coke) et de l'expression du modèle mathématique de cinétique intrinsèque choisi pour traiter les résultats expérimentaux. Ainsi, Tia et al. [11] ont estimé les valeurs des paramètres de la cinétique intrinsèque en utilisant l'expression du modèle suivant :
Valeurs des paramètres de la cinétique intrinsèque (ordre de réaction par rapport à l'oxygène, énergie d'activation) et modèle de la cinétique intrinsèque rencontrées dans la littérature pour la réaction de combustion du coke et celles obtenues dans le présent travail
| Auteurs | Type de coke | Intervalle de température (°C) | modèle de la cinétique intrinsèque (mol m–2s–1) | Ordre par rapport à l'oxygène | Énergie d'activation E (kJ mol–1) |
| Lin et al. [2] | coke du sable goudronné d'Utah (États-Unis) | 370–500 | Ks PO2n (1 – X)m | Pour PO2 > 5 kPa 0,75 | 175,14 |
| Pour PO2 < 5 kPa 0,5 | 127,00 | ||||
| Boumahmaza [5] | coke d'anthracite (Jerada, Maroc) | 550–750 | Ks PO2n | 0,66 | 61,94 |
| Smith et Harris ;Valix et Trimm [6] | coke d'un charbon australien de faible volatilité | 350–450 | Ks PO2n | 0,6 | 180,00 |
| Tia et al. [11] | coke de lignite thaïlandais | 250–450 | Ks PO2n(1 – X) | 1 | 89,12 |
| Tyler [16] | coke de pétrole | 390–560 | Ks PO2n | 0,6 | 159,16 |
| Le présent travail | coke étudié | 550–750 | Ks PO2n(1 – X)m | 0,8 | 113,53 |
Boumahmaza [5] a adopté dans son travail l'expression du modèle suivant : rs=KsPO2n. La même expression du modèle a été utilisée pour l'étude de la cinétique de combustion d'un coke de charbon de faible volatilité, réalisée par Smith et al. [6]. En utilisant le modèle suivant :
Lin et al. [2] ont trouvé, pour un coke de sable goudronné, et pour des pressions partielles d'oxygène inférieures à 5 kPa, les valeurs suivantes pour les paramètres cinétiques : E = 127 kJ mol–1, n = 1 et m = 0,5.
4 Conclusion
La dispersion des paramètres intrinsèques de la cinétique de combustion du coke qui existe dans la littérature et la difficulté qu'il y a à choisir entre ces paramètres pour la simulation d'un four à chaux de sucrerie ont été les causes principales qui nous ont poussé à mener une étude appropriée sur la cinétique de cette réaction.
L'étude expérimentale de la cinétique de combustion du coke a été réalisée par analyse thermogravimétrique isotherme dans l'intervalle de température compris entre 550 et 1100 °C, choisi pour couvrir la gamme de température qui règne dans la zone de combustion du four à chaux.
Pour les valeurs de température comprises entre 550 et 750 °C, il a été montré que cette réaction se déroule en régime contrôlé par la cinétique chimique et que les modèles à cœur rétrécissant en régime chimique et empirique décrivent d'une manière satisfaisante les résultats expérimentaux.
Par ailleurs, dans le domaine de température compris entre 800 et 1100 °C, la cinétique de réaction s'est avérée influencée par les phénomènes de transfert, le modèle empirique permettant un très bon ajustement des données expérimentales dans cet intervalle.
Les valeurs de l'énergie d'activation et de l'ordre de réaction par rapport à l'oxygène obtenues pour le modèle à cœur rétrécissant en régime contrôlé par la cinétique chimique sont respectivement de 113,52 kJ mol–1 et de 0,8, alors qu'elles sont respectivement de 113,94 kJ mol–1 et de 0,62 pour le modèle empirique. Ces valeurs sont parfois significativement différentes de celles de la littérature. Cette différence est due à la nature de la matière première (coke) utilisée dans l'étude expérimentale et de l'expression du modèle mathématique de la cinétique intrinsèque adoptée pour le traitement des résultats expérimentaux.
Remerciements
Ce travail a été réalisé grâce à l'aide de l'ENSIGC de Toulouse France (équipe du regretté Prof. Laguérie) et de la Sucrerie nationale de betterave du Loukkos Ksar El Kebir (Maroc).


