Les fluorures inorganiques, des matériaux modèles pour tester les méthodes de calcul de paramètres RMN (déplacement chimique et paramètres quadripolaires)

Gilles Silly; Monique Body; Jean-Yves Buzaré; Christophe Legein; Bruno Bureau

doi:10.1016/j.crci.2004.02.006

Les fluorures inorganiques, des matériaux modèles pour tester les méthodes de calcul de paramètres RMN (déplacement chimique et paramètres quadripolaires)

Gilles Silly ¹ ; Monique Body ² ; Jean-Yves Buzaré ¹ ; Christophe Legein ² ; Bruno Bureau ³

¹ Laboratoire de physique de l'état condensé, CNRS UMR 6087, France
² Laboratoire des oxydes et fluorures, CNRS UMR 6010, Institut de recherche en ingénierie moléculaire et matériaux fonctionnels, CNRS FR 2575, université du Maine, av. Olivier-Messiaen, 72085 Le Mans cedex 9, France
³ Laboratoire des verres et céramiques CNRS UMR 6512, université de Rennes-1, campus de Beaulieu, 35042 Rennes cedex, France

Comptes Rendus. Chimie, Volume 7 (2004) no. 3-4, pp. 403-416.

Résumés

Français
Anglais

Cet article présente des méthodes de modélisation des paramètres RMN appliquées à des fluorures inorganiques cristallisés et/ou désordonnés : déplacement chimique isotrope de ¹⁹F, paramètres quadripolaires de ²³Na, ²⁷Al, ^69,71Ga. Ces grandeurs ont été obtenues en utilisant des calculs semi-empiriques ou ab initio dont les principes sont présentés. Les résultats obtenus sont en général en bon accord avec les valeurs mesurées.

Inorganic fluorides: model materials to investigate NMR parameters calculation methods (chemical shift and quadrupolar parameters). In this paper, NMR parameters calculation methods applied to crystallized and/or disordered inorganic fluorides are presented: ¹⁹F isotropic chemical shift, and ²³Na, ²⁷Al, ^69,71Ga quadrupolar parameters. These values were obtained using semi-empirical or ab initio calculations, whose principles are presented. The results are generally in good agreement with the experimental values.

Métadonnées

Reçu le : 2003-06-10
Accepté le : 2004-02-18
Publié le : 2004-03-01

DOI : 10.1016/j.crci.2004.02.006

Mot clés : RMN, Déplacement chimique, Noyaux quadripolaires, Fluorures inorganiques, Semi-empirique, Ab initio, Chimie quantique
Mots clés : NMR, Chemical shift, Quadrupolar nuclei, Inorganic fluorides, Semi-empirical, Ab initio, Quantum chemistry

Affiliations des auteurs :

Gilles Silly ¹ ; Monique Body ² ; Jean-Yves Buzaré ¹ ; Christophe Legein ² ; Bruno Bureau ³

¹ Laboratoire de physique de l'état condensé, CNRS UMR 6087, France
² Laboratoire des oxydes et fluorures, CNRS UMR 6010, Institut de recherche en ingénierie moléculaire et matériaux fonctionnels, CNRS FR 2575, université du Maine, av. Olivier-Messiaen, 72085 Le Mans cedex 9, France
³ Laboratoire des verres et céramiques CNRS UMR 6512, université de Rennes-1, campus de Beaulieu, 35042 Rennes cedex, France

@article{CRCHIM_2004__7_3-4_403_0,
     author = {Gilles Silly and Monique Body and Jean-Yves Buzar\'e and Christophe Legein and Bruno Bureau},
     title = {Les fluorures inorganiques, des mat\'eriaux mod\`eles pour tester les m\'ethodes de calcul de param\`etres {RMN} (d\'eplacement chimique et param\`etres quadripolaires)},
     journal = {Comptes Rendus. Chimie},
     pages = {403--416},
     publisher = {Elsevier},
     volume = {7},
     number = {3-4},
     year = {2004},
     doi = {10.1016/j.crci.2004.02.006},
     language = {fr},
}

TY  - JOUR
AU  - Gilles Silly
AU  - Monique Body
AU  - Jean-Yves Buzaré
AU  - Christophe Legein
AU  - Bruno Bureau
TI  - Les fluorures inorganiques, des matériaux modèles pour tester les méthodes de calcul de paramètres RMN (déplacement chimique et paramètres quadripolaires)
JO  - Comptes Rendus. Chimie
PY  - 2004
SP  - 403
EP  - 416
VL  - 7
IS  - 3-4
PB  - Elsevier
DO  - 10.1016/j.crci.2004.02.006
LA  - fr
ID  - CRCHIM_2004__7_3-4_403_0
ER  -

%0 Journal Article
%A Gilles Silly
%A Monique Body
%A Jean-Yves Buzaré
%A Christophe Legein
%A Bruno Bureau
%T Les fluorures inorganiques, des matériaux modèles pour tester les méthodes de calcul de paramètres RMN (déplacement chimique et paramètres quadripolaires)
%J Comptes Rendus. Chimie
%D 2004
%P 403-416
%V 7
%N 3-4
%I Elsevier
%R 10.1016/j.crci.2004.02.006
%G fr
%F CRCHIM_2004__7_3-4_403_0

Gilles Silly; Monique Body; Jean-Yves Buzaré; Christophe Legein; Bruno Bureau. Les fluorures inorganiques, des matériaux modèles pour tester les méthodes de calcul de paramètres RMN (déplacement chimique et paramètres quadripolaires). Comptes Rendus. Chimie, Volume 7 (2004) no. 3-4, pp. 403-416. doi : 10.1016/j.crci.2004.02.006. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2004.02.006/

Version originale du texte intégral

1 Introduction

Notre groupe s'intéresse depuis plusieurs années à la description de l'ordre local dans les matériaux fluorés désordonnés obtenus par trempe, dépôt en phase vapeur ou broyage haute énergie. L'utilisation des méthodes RMN haute résolution appliquées à ¹⁹F et aux noyaux quadripolaires ^69,71Ga, ²⁷Al, etc., s'est avérée particulièrement fructueuse. Dans le cas du fluor, les résultats obtenus permettent de caractériser la connectivité du réseau d'octaèdres qui constitue la charpente structurale de ces matériaux [1,2] et, dans le cas des noyaux quadripolaires, ils donnent accès aux distributions radiales et angulaires des distances métal–fluor [3,4].

Nous nous appuyons sur les résultats expérimentaux obtenus dans de nombreuses phases cristallisées, dont la structure est connue, pour élaborer des méthodes de calcul prédictives des paramètres RMN.

Deux approches sont présentées pour chaque interaction ; dans un premier temps, des méthodes semi-empiriques de calcul des paramètres RMN ont été développées. Pour ¹⁹F, un modèle de superposition [5] permet de relier le déplacement chimique isotrope mesuré en MAS au nombre, à la nature et à la distance des cations premiers voisins. De nombreuses phases cristallisées ont été examinées, dans lesquelles le fluor occupe plus de 40 sites cristallographiques différents.

Dans le cas des noyaux quadripolaires ^69,71Ga, des calculs auto cohérents de gradients de champs électriques utilisant un modèle de charges ponctuelles polarisables permettent d'établir une relation entre les paramètres quadripolaires et les distributions radiales et angulaires des liaisons métal fluor.

La seconde approche concerne la mise en œuvre de calculs ab initio utilisant des logiciels commercialisés : GAUSSIAN [6] et WIEN97 [7]. Les principes du calcul spécifiques à chaque interaction sont présentés et les principes de base sont rappelés en appendice. Pour ¹⁹F, la méthode utilisée s'appuie sur la construction de clusters centrés sur le noyau étudié et dont l'environnement est reconstruit à partir des données cristallographiques (GAUSSIAN). Pour les noyaux quadripolaires, les calculs sont menés en exploitant les conditions aux limites périodiques avec la méthode LAPW (WIEN97).

Les conclusions porteront sur l'intérêt de la mise en oeuvre de l'une ou de l'autre des approches en fonction des moyens de calcul et de l'objectif à atteindre.

2 Mesures RMN : notations et conventions

2.1 Interaction de déplacement chimique

Le hamiltonien représentant l'énergie d'un noyau soumis à un champ magnétique extérieur statique ${\vec{B}}_{0}$ s'écrit :

H = - γ \vec{I} (1 - \overset{\tilde{}}{σ}) {\vec{B}}_{0}

où

\vec{I}

est le moment cinétique nucléaire du noyau, γ son facteur gyromagnétique et

\overset{\tilde{}}{σ}

le tenseur rendant compte de l'écrantage de

{\vec{B}}_{0}

par le nuage électronique. Dans son système d'axes propres (x, y, z), ce tenseur aura trois composantes, notées σ_xx, σ_yy et σ_zz. On notera alors :

σ_{iso} = \frac{1}{3} (σ_{xx} + σ_{yy} + σ_{zz})

la composante isotrope du tenseur d'écrantage. On utilisera la convention :

| σ_{zz} - σ_{iso} | > | σ_{yy} - σ_{iso} | > | σ_{xx} - σ_{iso} |

La condition de résonance s'écrit :

h ν = ℏ γ (1 - σ) B_{0}

et pour le composé de référence :

h ν_{ref} = ℏ γ (1 - σ_{ref}) B_{0}

δ le déplacement chimique est alors défini par :

δ = \frac{ν - ν_{ref}}{ν_{ref}}

Le coefficient d'écran isotrope et la composante isotrope du tenseur de déplacement chimique sont reliés l'un à l'autre par la formule :

δ_{iso} \approx (σ_{ref} - σ_{iso})

2.2 Interaction quadripolaire

Les quantités mesurées par RMN sur des poudres cristallisées contenant des noyaux quadripolaires (I > 1/2), de moment quadripolaire Q, sont :

• la constante de couplage quadripolaire :
$C_{Q} = \frac{e V_{ZZ} Q}{h}$
ou la fréquence quadripolaire :
$ν_{Q} = 3 {eQV}_{ZZ} / 2 I (2 I - 1) h$
• le paramètre d'asymétrie :
$η_{Q} = \frac{V_{XX} - V_{YY}}{V_{ZZ}}$
qui sont proportionnels aux composantes du gradient de champ électrique (GCE) exprimé dans son système d'axes principaux (X, Y, Z), avec la condition :
$| V_{ZZ} | \geq | V_{YY} | \geq | V_{XX} |$

3 Modélisation semi-empirique du déplacement chimique de ¹⁹F

Les fluorures de métaux de transition sont constitués d'un réseau d'octaèdres centrés sur les métaux et interconnectés par sommet. On distingue donc les fluors pontants deux octaèdres, des fluors non pontants n'appartenant qu'à un seul octaèdre et des fluors « libres », en position interstitielle, qui ne sont impliqués dans aucun octaèdre.

La décomposition des spectres obtenus dans les verres fluorés de métaux de transition révèle trois raies qu'il a été possible d'affecter aux trois types d'ion F^– précédents grâce à une étude en composition [1]. Pour ne pas avoir à recourir systématiquement à cette méthode laborieuse, nous avons élaboré un modèle très simple à mettre en œuvre [5], ne faisant intervenir, en plus des distances, que la connaissance de trois paramètres phénoménologiques par type d'ion présent dans l'environnement du fluor considéré.

Cette construction repose sur la théorie de Ramsey du déplacement chimique [8] et fait usage de la méthode d'orthogonalisation de Lowdin [9], qui est bien adaptée au cas des matériaux ioniques. Elle conduit à :

δ_{iso / C_{6} F_{6}} = - 127, 1 - \sum_{l} σ_{l}^{p}

où le premier terme est la contribution diamagnétique au déplacement chimique, constante, et le second une somme de contributions paramagnétiques dues aux plus proches cations. Ces dernières peuvent se mettre sous la forme :

σ_{l}^{p} = σ_{l 0} \exp [- α_{l} (d - d_{0})]

où :

• d₀ est la distance fluor–cation dans le fluorure le plus simple (MF, MF₂ ou MF₃, etc.) qui puisse être formé ;
• σ_l₀ est déduit de la mesure dans le même fluorure simple ;
• α_l est déduit d'une relation empirique obtenue à partir de calculs d'intégrales de recouvrement, qui montre qu'en première approximation :
$α_{l} = - 0, 806 r_{l} + 4, 048$

où r_l est le rayon ionique du ligand l exprimé en angströms.

La Fig. 1 montre l'application de ce modèle dans des fluorures simples. Par construction, les valeurs calculées coïncident avec les valeurs expérimentales dans les fluorures simples (MF, MF₂,MF₃). Il a été ensuite validé sur des fluoroperovskites AMF₃ (A = K, Rb, Cs, Ba et M = Li, Mg, Zn, Ca,), dans des fluoroaluminates en couches AAlF₄ (A = K, Rb) présentant deux fluors cristallographiquement inéquivalents (pontant et non pontant), dans BaZnF₄ et Ba₂ZnF₆ qui comportent des fluors libres, pontants et non pontants, ainsi que dans BaMgF₄.

Fig. 1
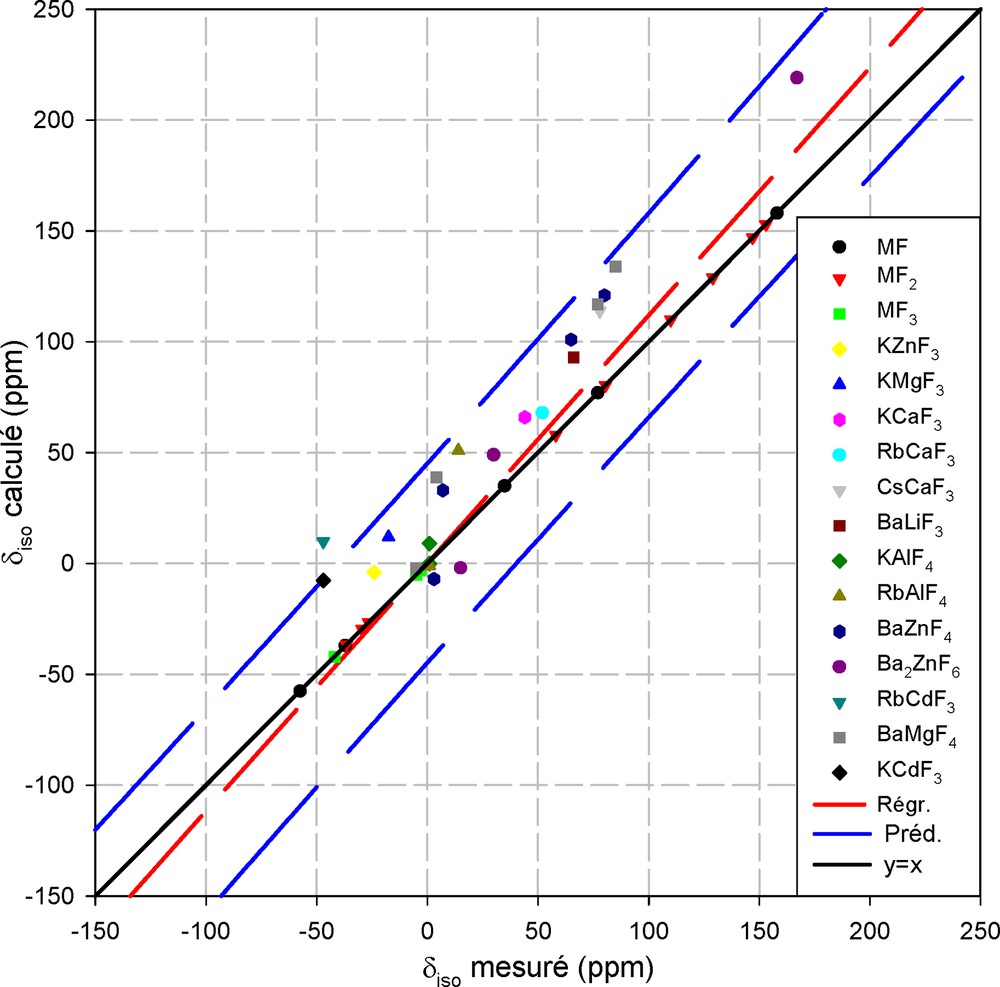
Représentation du déplacement chimique isotrope de ¹⁹F, calculé avec le modèle semi-empirique en fonction de la valeur mesurée. Les intervalles de confiance à 95% (en pointillés) encadrent la droite de régression et la diagonale principale.

La droite de régression linéaire a une pente de 1,129 avec un coefficient de corrélation R² = 0,897 ; ce résultat est satisfaisant eu égard aux moyens de calculs élémentaires mis en jeu, même s'ils conduisent globalement à surévaluer la valeur calculée. De plus, pour chaque cation, les valeurs numériques des trois paramètres phénoménologiques (d₀, σ_l₀, α_l) incluses dans [5] doivent être considérées comme des jeux de paramètres initiaux, qu'il est possible d'affiner en s'appuyant sur de nouvelles mesures dans de nombreux composés de structure connue.

4 Modélisation ab initio du déplacement chimique de ¹⁹F

Pour pallier l'introduction des paramètres phénoménologiques, nous avons mis en œuvre des calculs ab initio qui permettent de déterminer le déplacement chimique isotrope de ¹⁹F à l'aide des premiers principes et des méthodes de calculs propres à la chimie quantique.

4.1 Calcul ab initio du tenseur d'écrantage

Par rapport aux principes généraux des méthodes de calcul ab initio rappelées en appendice, quelques considérations supplémentaires sont à prendre en compte dans le calcul du tenseur $\overset{\tilde{}}{σ}$ . Elles sont liées à la présence du champ magnétique extérieur ${\vec{B}}_{0}$ et au potentiel vecteur $\vec{A} (\vec{r}) = \frac{1}{2 μ_{0}} {\vec{B}}_{0} ⋀ \vec{r}$ (dans la jauge de Coulomb) [10] qui lui est associé. Le hamiltonien du système doit faire intervenir explicitement les moments magnétiques nucléaires ${\vec{μ}}_{ν}$ , puisque le tenseur d'écrantage est calculé à leur niveau :

H = \frac{1}{2 m_{e}} \sum_{i} {[- i ℏ {\vec{\nabla}}_{{\vec{r}}_{i}} - \frac{e}{c} \vec{A}' ({\vec{r}}_{i})]}^{2} - \frac{1}{4 π ϵ_{0}} \sum_{i, j} \frac{e^{2} Z_{i}}{| {\vec{R}}_{i} - {\vec{r}}_{j} |} + \frac{1}{8 π ϵ_{0}} \sum_{\begin{matrix} i, j \\ i \neq j \end{matrix}} \frac{e^{2}}{| {\vec{r}}_{i} - {\vec{r}}_{j} |}

où

\vec{A}' ({\vec{r}}_{i}) = \vec{A} ({\vec{r}}_{i}) + \sum_{ν} ({\vec{μ}}_{ν} ⋀ {\vec{r}}_{i ν}) / r_{i ν}^{- 3}

est le potentiel vecteur à la position de l'électron i, somme du potentiel vecteur dû au champ extérieur et du potentiel vecteur dû aux moments magnétiques nucléaires.

La base des fonctions d'onde doit être adaptée, car la solution finale ne doit pas dépendre du choix de jauge [11]. Si ${\vec{R}}_{ν}$ repère la position du noyau ν et φ_ν est une fonction électronique de base centrée sur ce noyau, cette condition est satisfaite en utilisant la méthode GIAO [10], où les fonctions atomiques de la base {φ_ν} subissent la transformation :

ζ_{ν} = \exp (- \frac{i}{c} {\vec{A}}_{ν} \cdot \vec{r}) ϕ_{ν}

avec

{\vec{A}}_{ν} = \frac{1}{2 μ_{0}} {\vec{B}}_{0} ⋀ {\vec{R}}_{ν}

Après avoir obtenu une solution auto-cohérente, la fonction d'onde ψ obtenue pour chaque niveau d'énergie ε dépendra explicitement de ${\vec{B}}_{0}$ et de ${\vec{μ}}_{ν}$ . Pour les faibles valeurs de ces deux paramètres, un développement en perturbation montre que le tenseur d'écrantage s'obtiendra finalement grâce à la relation [12] :

σ_{ij}^{ν} = \frac{\partial^{2} 〈 ϵ 〉}{\partial {\vec{B}}_{0 i} \partial {\vec{μ}}_{ν i}}

Ainsi, toutes les composantes de ce tenseur peuvent être déterminées.

La version du programme GAUSSIAN98 pour Windows [6] a été employée pour réaliser les calculs que nous présentons. Les valeurs de déplacement chimique sont référencées par rapport à C₆F₆ en prenant σ_C₆F₆ = 352,9 ppm [5].

4.2 Application aux fluorures inorganiques

Les premiers calculs ab initio dans les fluorures inorganiques ont été publiés par S.H. Cai et al. Tout d'abord, dans les fluorures alcalins MF [13] le cluster [FM₆]⁵⁺ construit avec les distances MF issues des données cristallographiques a été utilisé avec les bases 3-21 + G pour M et 6-311 + G(d) pour F.

La séquence RbF, KF, LiF, NaF permet de classer les valeurs expérimentales de δ_iso par ordre croissant. Ce comportement est bien reproduit avec les trois méthodes HF, BLYP et B3LYP qui ont été employées, cette dernière conduisant à une convergence plus rapide. Les valeurs calculées les plus proches des valeurs expérimentales sont obtenues avec les méthodes de la fonctionnelle densité BLYP et B3LYP, avec néanmoins des écarts systématiques de l'ordre de 30 à 40 ppm.

Dans la série MF₂ [14], cinq types de base ont été testés avec la méthode B3LYP pour examiner leur influence. Les clusters utilisés sont [FBe₂F₆]^3– pour BeF₂, [FMg₃F₉]^4– pour MgF₂ et [FM₄F₆]⁺ pour M = Ca, Sr, Ba. De la confrontation aux valeurs expérimentales, il ressort que les meilleurs résultats sont obtenus lorsque la base 6-311+G(d) est utilisée pour l'atome de fluor situé au centre du cluster (pour lequel on cherche à calculer σ_iso), la base LanL2DZ étant utilisée pour les autres. La base CRENBL (utilisant des ECP) complétée de deux fonctions de polarisation d (quand elles sont disponibles, ce qui n'est pas le cas pour Ba, par exemple) est utilisée pour les métaux. Il faut noter que, dans cette étude, les ECP ont été retirés pour Li et Be, ce qui nous paraît en contradiction avec la conception de la base. Dans ces conditions, la séquence des valeurs expérimentales croissantes BaF₂, SrF₂, CaF₂, MgF₂ est encore bien reproduite avec des écarts compris entre 8 et 27 ppm. Les calculs repris dans les mêmes conditions sur les composés MF conduisent à des écarts compris entre 1 et 27 ppm notablement meilleurs que les précédents.

La série des MF₂ a été complétée pour M = Zn et Pb, puis étendue aux MF₃ dans [15]. Les clusters utilisés sont [FM₂F₈]^3– dans la série MF₃. Pour les composés MF₂, plusieurs autres clusters ont été mis en œuvre, car ces composés ne sont pas tous iso-structuraux. Ils comportent au centre l'atome de fluor pour lequel on veut déterminer $\overset{\tilde{}}{σ}$ entouré des métaux premiers voisins, avec ensuite un nombre variable de fluors. L'effet de la taille du cluster a ainsi été examiné dans MgF₂ et ZnF₂.

Les bases utilisées sont l'aug-cc-pVTZ pour le fluor central, LanL2DZ pour les autres, la base CRENBL et deux fonctions de polarisation d pour les métaux, excepté pour Al pour lequel la base 3-21G(2d) a été sélectionnée. Une nouvelle fois, pour l'atome Mg, la base a été curieusement utilisée sans l'ECP correspondant. Pour Zn et Cd, des résultats plus satisfaisants ont été obtenus avec la base DZVP.

Le choix des clusters et des bases les plus favorables conduit à des écarts entre valeurs calculées et valeurs expérimentales compris entre 0 et 31 ppm pour une plage de valeur de σ_iso comprise entre 200 et 400 ppm. En ce sens, les résultats sont, là encore, satisfaisants. Cependant, pour ZnF₂, il ressort que le cluster contenant le plus grand nombre d'atomes donne le meilleur résultat, lequel est obtenu avec la base DZVP qui semble avoir été utilisée spécifiquement. En revanche, pour MgF₂, la situation est différente et c'est le cluster de taille intermédiaire qui est retenu.

Considérant que l'utilisation de ces moyens de calculs n'est viable que si une systématique claire et simple de choix des bases de fonction d'onde est adoptée, nous avons tout d'abord examiné comment procéder à ce choix.

Pour le fluor, il ressort des calculs que nous avons effectués que, concernant le F central, la base aug-cc-pVTZ augmente les temps de calcul de façon importante, sans apporter d'améliorations significatives par rapport à la base 6-311+G(d), qui est donc retenue. La base LanL2DZ est conservée pour les autres atomes de fluor du cluster. Pour les cations, il ressort des travaux précédents que la base CRENBL (base I) et la base 3-21G(2d) (base II) sont des candidates privilégiées.

Le Tableau 1 regroupe les résultats précédemment publiés et les calculs que nous avons réalisés sur les séries MF, MF₂ et MF₃. Avec la base I, les écarts que nous obtenons avec les résultats antérieurs s'expliquent par la ré-introduction des ECP pour LiF, BeF₂ et MgF₂ ; pour BaF₂, nous n'avons pas retrouvé les données cristallographiques citées en référence et, pour les valeurs en italique, le choix de la base du fluor central peut être incriminé. Pour CaF₂ et SrF₂, ils ne se justifient pas. Avec cette base, nous obtenons un écart moyen entre valeurs calculées et valeurs expérimentales de 20 ppm. En utilisant la base II, nous obtenons un écart moyen avec les valeurs expérimentales de 13 ppm pour des temps de calcul systématiquement inférieurs. Notre choix s'est donc porté sur la base II ; cependant, celle-ci n'inclut pas les atomes Ba et Pb, pour lesquels nous utiliserons la base CRENBL.

Composé	Groupe d'espace	cluster	ref [14,15]	base I	base II	δ_iso^exp
LiF	$Fm \overset{\bar{}}{3} m$	[FLi₆]⁵⁺	–52	–115	*	–37
NaF	$Fm \overset{\bar{}}{3} m$	[FNa₆]⁵⁺	–84	–83	–89	–58
KF	$Fm \overset{\bar{}}{3} m$	[FK₆]⁵⁺	26	26	25	35
RbF	$Fm \overset{\bar{}}{3} m$	[FRb₆]⁵⁺	69	65	81	77
CsF	$Fm \overset{\bar{}}{3} m$	[FCs₆]⁵⁺	157	157	182	158
BeF₂	P3₂2	[FBe₂F₆]^3–	–27	–35	–27	/
BaF₂	$Fm \overset{\bar{}}{3} m$	[FBa₄F₆]⁺	132	143	/	153
CaF₂	$Fm \overset{\bar{}}{3} m$	[FCa₄F₆]⁺	50/46	53	55	58
CdF₂	$Fm \overset{\bar{}}{3} m$	[FCd₄F₆]⁺	24	34	3	–26
β–PbF₂	$Fm \overset{\bar{}}{3} m$	[FPb₄F₆]⁺	149	148	/	129
SrF₂	$Fm \overset{\bar{}}{3} m$	[FSr₄F₆]⁺	54	63	70	81
AlF₃	$R \overset{\bar{}}{3} c$	[FAl₂F₈]^3–	–12	–21	–8	–5
GaF₃	$R \overset{\bar{}}{3} c$	[FGa₂F₈]^3–	–3	15	11	–3
InF₃	$R \overset{\bar{}}{3} c$	[FIn₂F₈]^3–	–33	–33	–46	–42
α–PbF₂	Pnma	[FPb₄F₅]²⁺	177	182	/	147
[FPb₅F₅]⁴⁺	85	92	/	110
MgF₂	P4₂/mmm	[FMg₂F₉]^6–	–39/–33	–28	–30	–29
ZnF₂	P4₂/mmm	[FZn₂F₁₁]^8–	19	–40	–28	–36

^* pas de convergence

Le Tableau 2 regroupe les résultats de nos calculs ab initio dans les autres fluorures, pour lesquels le modèle semi-empirique avait été utilisé. Les clusters retenus sont ceux qui donnent le résultat le plus proche des valeurs expérimentales. Dans les structures pérovskites, cela revient à prendre les deux premières sphères de coordination du fluor, sauf dans KCaF₃,qui est une pérovskite distordue à température ambiante, pour laquelle des clusters plus petits donnent de meilleurs résultats. BaZnF₄, BaMgF₄ et Ba₂ZnF₆ sont des composés modèles, pour lesquels des clusters associés à des fluors libres pontants et non pontants sont obtenus sans qu'aucune systématique ne se dégage. Dans KAlF₄ et RbAlF₄ à structure en couches, on est en présence de fluors pontants et non pontants, reconnaissables au nombre d'atomes d'aluminium premiers voisins. Le cluster [FAl₂F₈]^3– est utilisé pour les premiers, comme dans AlF₃, et le cluster [FAlF₅A₄]⁺ pour les autres.

Composé	Groupe d'espace	Cluster	Base II	δ_iso^exp
KMgF₃	$Pm \overset{\bar{}}{3} m$	[FMg₂K₄F₈]^–	–18	–17
KCdF₃	$Pm \overset{\bar{}}{3} m$	[FCd₂K₄F₈]^–	–43	–47
BaLiF₃	$Pm \overset{\bar{}}{3} m$	[FLi₂Ba₄F₈]⁺	85	66
RbCaF₃	$Pm \overset{\bar{}}{3} m$	[FCa₂Rb₄F₈]^–	23	52
KZnF₃	$Pm \overset{\bar{}}{3} m$	[FZn₂K₄F₈]^–	–19	–24
RbCdF₃	$Pm \overset{\bar{}}{3} m$	[FCd₂Rb₄F₈]^–	–33	–37
CsCaF₃	$Pm \overset{\bar{}}{3} m$	[FCa₂Cs₄F₈]^–	60	78
KCaF₃	B2₁/m	[FCa₂K₂F₄]⁺	51	44
[FCa₂KF₂KF₂]⁺	45	44
[FCa₂F₂K₂F]²⁺	68	44
[FCa₂KF₂KF]²⁺	59	44
BaZnF₄	Cmc2₁	[FZnFBa₃]⁶⁺	115	80
[FZnBa₂]⁵⁺	34	65
[FZn₂F₃Ba₂]⁴⁺	44	7
[FZn₂F₂BaF₄]^–	26	3
BaMgF₄	Cmc2₁	[FMg₂F₆]^3–	–39	4
[FMgBa₂]⁵⁺	56	77
[FMgFBa₃]⁶⁺	106	85
[FMg₂F₄]^–	–2	–5
KAlF₄	P4/mbm	[FAl₂F₉K₂]^2–	0	1
[FAlF₄]^2–	17	1
RbAlF₄	P4/mmm	[FAl₂F₉Rb₂]^2–	9	1
[FAlF₄]^2–	24	14
Ba₂ZnF₆	I4/mmm	[FBa₄F₄]³⁺	188	167
[FZn₂F₄]^–	–21	15
[FZnF₈Ba₄]⁺	67	30

Dans ces conditions, le graphique de la Fig. 2 représente les valeurs des déplacements chimiques calculées en fonction des valeurs expérimentales pour les 42 environnements différents étudiés. La droite de régression linéaire a une pente de 1,072 et un coefficient de corrélation de 0,885. L'écart moyen entre calcul et expérience est de 18 ppm pour une plage de déplacement chimique de 225 ppm, ce qui donne un résultat globalement très satisfaisant. Il ne faut néanmoins pas perdre de vue que, dans cette approche, hormis le fait que les temps de calculs sont très longs comparativement à l'utilisation du modèle semi-empirique, le plus gros obstacle à son utilisation est l'absence de moyen de définir a priori le cluster à utiliser.

Fig. 2
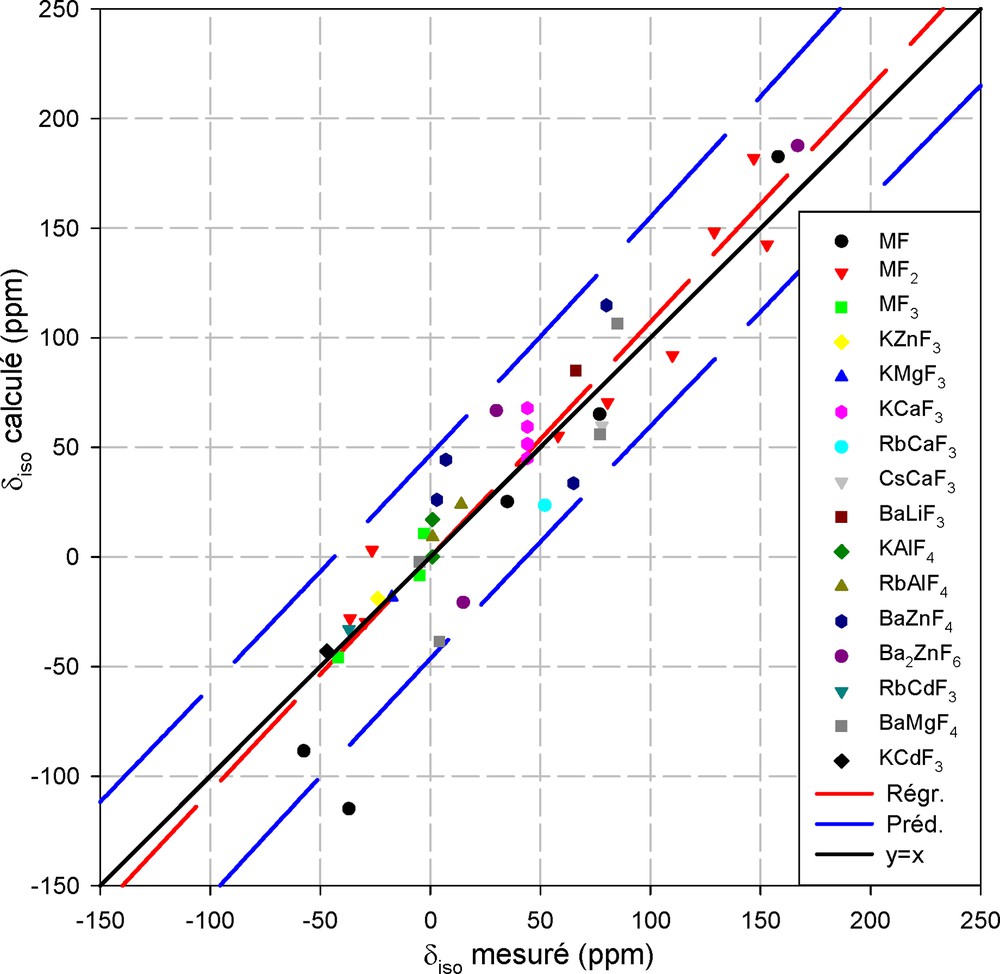
Représentation du déplacement chimique isotrope ab initio de ¹⁹F en fonction de la valeur mesurée. Les intervalles de confiance à 95% (en pointillés) encadrent la droite de régression et la diagonale principale.

5 Modélisation semi-empirique des paramètres quadripolaires

5.1 Modèle semi-empirique de calcul des GCE

Le système est assimilé à un ensemble de charges ponctuelles polarisables, le champ électrique et V_ij au site de chaque ion sont obtenus de façon auto-cohérente [3] :

E_{i} (μ) = \frac{1}{4 π ϵ_{0}} \sum_{λ} [q (λ) X_{i} ({\vec{R}}_{μ, λ}) + \sum_{k} α_{e} (λ) E_{k} (λ) X_{ik} ({\vec{R}}_{μ, λ}) + . . .]

V_{ij} (μ) = \frac{1}{4 π ϵ_{0}} \sum_{λ} [q (λ) X_{ij} ({\vec{R}}_{μ, λ}) + \sum_{k} α_{e} (λ) E_{k} (λ) X_{ijk} ({\vec{R}}_{μ, λ}) + . . .]

Les expressions ci-dessus indiquent que ce calcul nécessite la connaissance des polarisabilités des ions présents dans le système.

La diagonalisation du tenseur correspondant à l'ion auquel appartient le noyau étudié conduit à la valeur de V_zz au niveau de l'ion. La fréquence quadripolaire est obtenue en tenant compte de la déformation du nuage électronique grâce à la constante de Sternheimer γ_∞ :

ν_{Q} = (1 - γ_{\infty}) \frac{3 {eQV}_{zz}}{2 I (2 I - 1) h}

5.2 Applications aux phases désordonnées de GaF₃

Dans les fluorures de métaux de transition, les noyaux quadripolaires présents dans le réseau appartiennent systématiquement aux ions métalliques et sont donc localisés au centre des octaèdres de fluor. La Fig. 3 représente les transitions centrales des spectres de ⁷¹Ga obtenus dans les fluorogallates GaF₃ cristallisé, GaF₃ amorphe et un verre PZG [4]. Dans la phase cristallisée la largeur de raie est faible, la fréquence quadripolaire mesurée est de 460 kHz et le paramètre d'asymétrie est nul, en accord avec la structure cristalline. Les spectres de verre et du composé amorphe sont identiques, ce qui signifie que la présence des ions Pb²⁺ n'intervient pas dans cette situation. La forme dissymétrique du spectre est caractéristique d'une distribution des paramètres ν_Q et η_Q.

Fig. 3
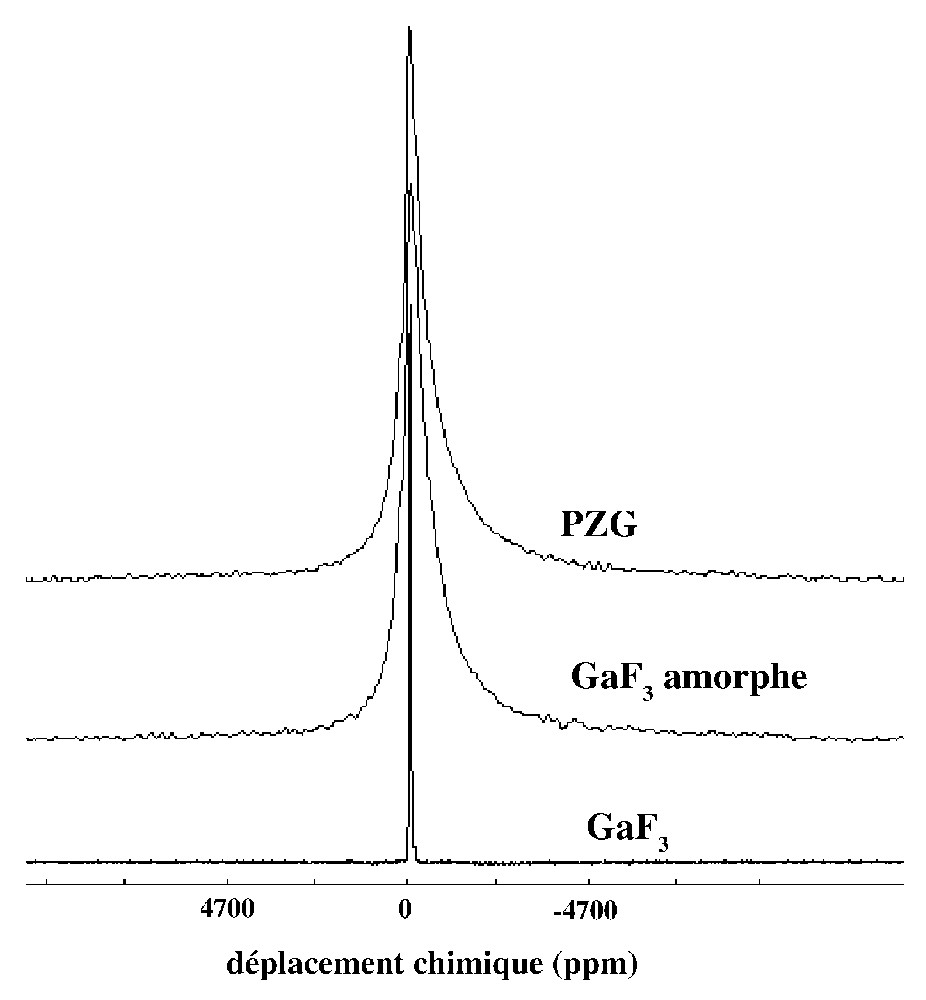
Transition centrale du spectre RMN de ⁷¹Ga dans un verre PZG, dans GaF₃ obtenu par dépôt en phase vapeur et dans la phase cristallisée.

5.3 Forme de la distribution des paramètres RMN

La distribution des paramètres quadripolaires que nous avons employée a initialement été introduite par Czjzek [16,17] pour des composés métalliques. Elle repose sur l'invariance par rotation du système avec une distribution gaussienne des cinq composantes indépendantes du gradient de champ électrique (GCE). Elle peut se mettre sous la forme :

P (ν_{Q}, η_{Q}) = \frac{1}{\sqrt{2 π} σ^{d}} ν_{Q}^{d - 1} η_{Q} (1 - η_{Q}^{2} / 9) \times \exp {- \frac{ν_{Q}^{2} (1 + η_{Q}^{2} / 3)}{2 σ^{2}}}

Elle est définie par deux paramètres ajustables : d, qui vaut 5 si toutes les composantes du GCE sont indépendantes et dont une valeur inférieure reflète l'existence de corrélations entre ces composantes à cause de l'ordre à courte distance, et σ, qui est la force de l'interaction. La valeur de σ détermine l'ordre de grandeur de la valeur de la fréquence quadripolaire de plus forte probabilité. La Fig. 4 représente une telle distribution. On notera les probabilités nulles pour ν_Q = 0 et η_Q = 0.

Fig. 4
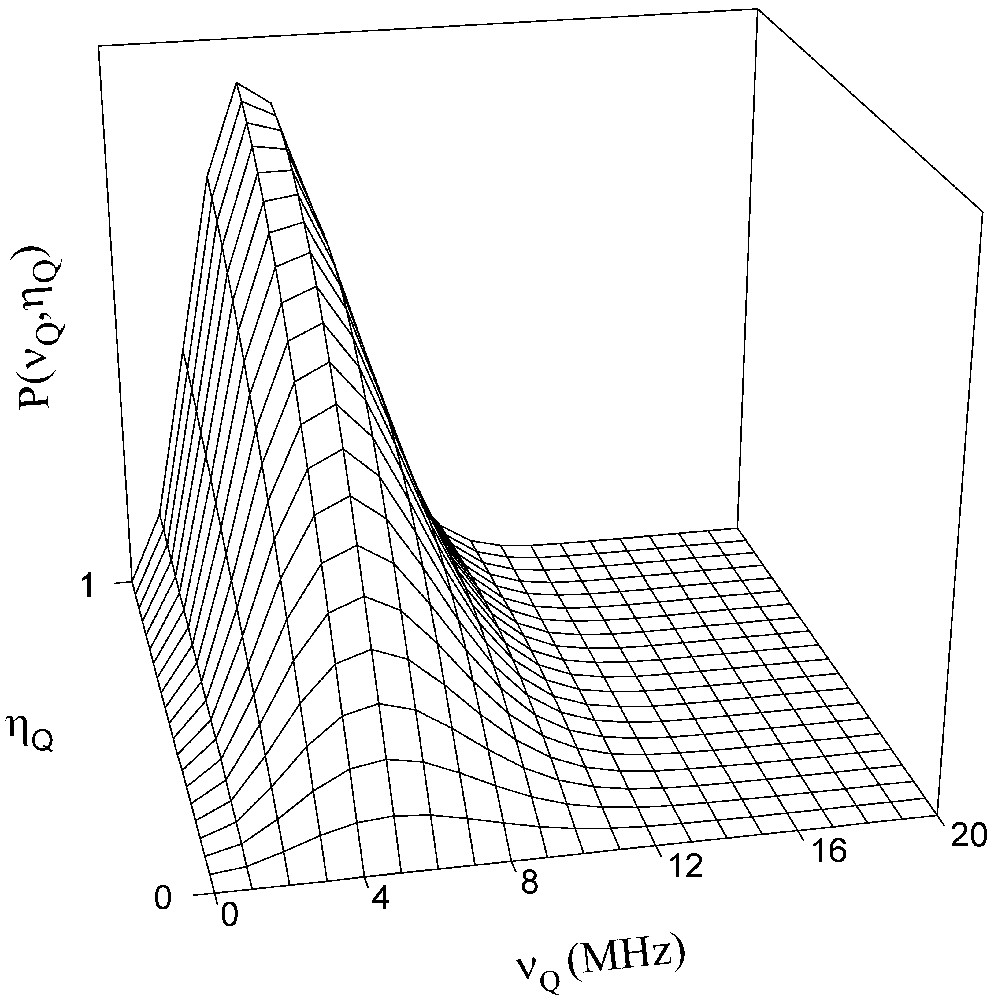
Représentation de la distribution de Czjzek obtenue pour d = 3 et σ = 3500 kHz.

Dans le fluorure de gallium amorphe on ne peut avoir que d = 3 et σ = 3500 kHz ou d = 2 et σ = 4500 kHz [3,18].

Le modèle semi-empirique de calcul des GCE permet de relier ces paramètres aux distributions radiales et angulaires [3]. Les distributions de positions atomiques sont obtenues à l'aide de la dynamique moléculaire en partant de la phase rhomboédrique de GaF₃ portée à la « température » T, qui n'est qu'une mesure du désordre.

5.3.1 GaF₃ amorphe

C'est pour la température T = 120 K que l'on obtient la meilleure reproduction du spectre expérimental de la phase amorphe de GaF₃ [3]. La Fig. 5 montre le spectre calculé comparé au spectre expérimental, la distribution des paramètres associée à la distribution de positions atomiques et les distributions radiales et angulaires des liaisons Ga–F. On notera la grande similitude de l'enveloppe de la distribution des paramètres RMN avec la distribution de Czjzek de la Fig. 4.

Fig. 5
(a) transition centrale du spectre RMN expérimental (en haut) et calculé (en bas) de ⁷¹Ga dans GaF₃ amorphe ; (b) distribution des paramètres RMN obtenue pour T = 120 K ; (c) histogramme de la distribution angulaire ; (d) histogramme de la distribution radiale.

Les valeurs des paramètres phénoménologiques utilisés sont : α_F⁻ = 1,75Å³, γ_∞ = –9,5 et Q = 0,11 × 10^–28 m². Les largeurs des distributions radiales et angulaires sont respectivement Δr = 0,026 Å et Δθ = 3°.

5.3.2 GaF₃ nanostructuré

Dans le cas d'une phase obtenue par broyage haute énergie, le spectre comporte deux contributions. La plus étroite peut être associée aux grains et l'autre aux joints de grains [4,19]. On remarque sur la Fig. 6 que les distributions radiales et angulaires sont plus larges dans les joints de grains que dans la phase amorphe.

Fig. 6
Image schématisant grains nanostructurés et joints de grain avec les distributions des paramètres RMN de ⁷¹Ga et les distributions radiales et angulaires qui leurs sont associées dans GaF₃ obtenu par broyage haute énergie.

Trois types de paramètres phénoménologiques ont donc été nécessaires pour mettre en œuvre ce modèle :

• la polarisabilité des ions α_e,
• la constante de Sternheimer γ_∞,
• le moment quadripolaire Q.

Les valeurs de ces paramètres ne sont pas toujours clairement établies ; c'est pourquoi nous nous sommes, là encore, intéressés à l'approche ab initio.

6 Modélisation ab initio des GCE

6.1 La méthode LAPW

La méthode que nous avons employée pour mener à bien les calculs des trois composantes du gradient de champ électrique est la méthode LAPW, qui relève de la théorie de la fonctionnelle densité [20]. Elle est parfaitement adaptée aux matériaux cristallisés, puisqu'elle utilise les conditions aux limites périodiques du système. Le volume de la maille cristallographique est divisé en deux régions : la première est constituée de sphères non jointives, centrées sur les positions atomiques, et la seconde correspond au volume interstitiel. On note R_MT le plus petit rayon des sphères. La base des fonctions d'onde est formée de combinaisons linéaires d'harmoniques sphériques dans les sphères :

ϕ_{k_{n}} = \sum_{l, m} [A_{lm} u_{l} (r, E_{l}) + B_{lm} \overset{\dot{}}{u} (r, E_{l})] Y_{lm} (\vec{r})

et d'ondes planes en dehors :

ϕ_{k_{n}} = \frac{1}{\sqrt{ω}} e^{i {\vec{k}}_{n} \cdot \vec{r}}

avec

{\vec{k}}_{n} = \vec{k} + {\vec{K}}_{n},

où

\vec{k}

appartient à la première zone de Brillouin et

{\vec{K}}_{n}

est un vecteur du réseau réciproque.

Les calculs sont menés en utilisant un développement multipolaire du potentiel et de la densité de charge :

{\begin{matrix} \sum_{LM} V_{LM} Y_{LM} (\vec{r}) \\ \sum_{\vec{K}} V (\vec{K}) e^{i \vec{K} \vec{r}} \end{matrix}

Les composantes des gradients de champs électriques correspondent aux termes associés à L = 2.

Les paramètres qui influent sur la qualité du calcul sont le nombre de k-points et la valeur du produit R_MT × K_MAX, qui définit le nombre d'ondes planes utilisées.

6.2 Application à des fluoroaluminates simples

Les calculs ont été réalisés sur les composés modèles AlF₃, la cryolite Na₃AlF₆ et la chiolite Na₅Al₃F₁₄ [21]. Le code de calcul WIEN97 [7] a été employé sur un calculateur parallèle de type béowulf ; il est constitué d'une grappe de six ordinateurs équipé de cartes mères bi-processeurs P650, avec 1 Go de mémoire vive chacune. Pour la maille contenant le plus d'atomes, à savoir la chiolite, le calcul demandant l'effort le plus important a été réalisé sur les 12 processeurs, pour R_MT × K_MAX = 8 et 1000 k-points. Chaque cycle durait environ 28 h et la convergence a été atteinte en une douzaine de cycles.

Pour le noyau ²³Na, Na₃AlF₆ et Na₅Al₃F₁₄ comportent chacun deux sites non équivalents, dont l'un est de symétrie axiale dans la chiolite. Pour le noyau ²⁷Al, AlF₃ et Na₃AlF₆ comportent chacun un site cristallographique, de symétrie axiale pour le premier. Na₅Al₃F₁₄ comporte deux sites, dont un de symétrie axiale. Nous disposons donc de quatre jeux de paramètres pour chaque noyau. La Fig. 7 représente la fréquence quadripolaire mesurée en fonction du paramètre V_zz calculé.

Fig. 7
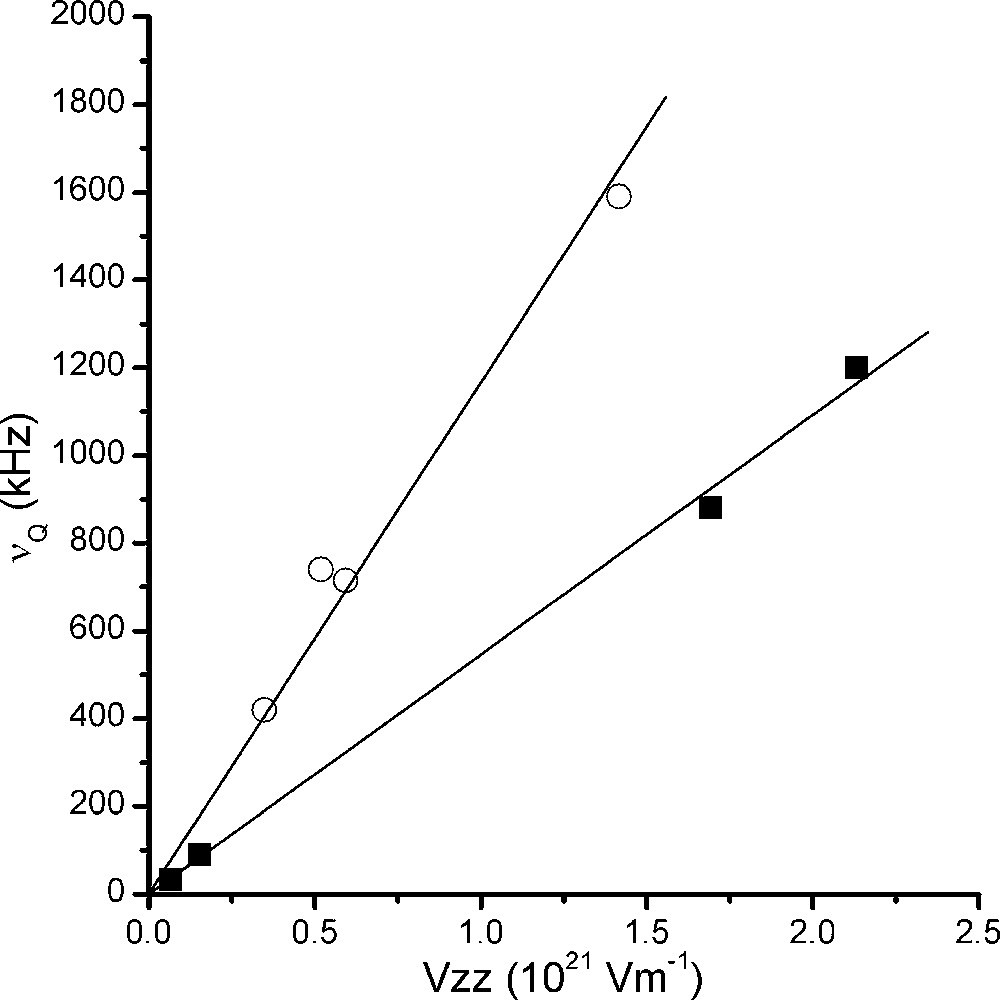
Représentation de la fréquence quadripolaire mesurée en fonction du paramètre V_zz calculé par la méthode LAPW dans AlF₃, Na₃AlF₆ et Na₅Al₃F₁₄. Les points sont représentés par des cercles pour ²³Na et par des carrés pour ²⁷Al.

Les valeurs des moments quadripolaires calculées à partir des pentes des droites de régression linéaire sont respectivement Q_Al = 1,506 × 10^–29 em² et Q_Na = 0,965 × 10^–29 em², et sont en bon accord avec les valeurs que l'on peut trouver dans les tables, à savoir Q_Al = 1,466 × 10^–29 em² et Q_Na = 1,04 × 10^–29 em² [22,23]. Ainsi, les différences entre les fréquences quadripolaires calculées et mesurées correspondent à des écarts relatifs inférieurs à 10%.

La Fig. 8 représente la valeur du paramètre d'asymétrie calculé en fonction de la valeur mesurée. Les valeurs expérimentales sont très bien reproduites, puisque la pente de la droite de régression linéaire vaut 1,055 et le coefficient de corrélation 0,997.

Fig. 8
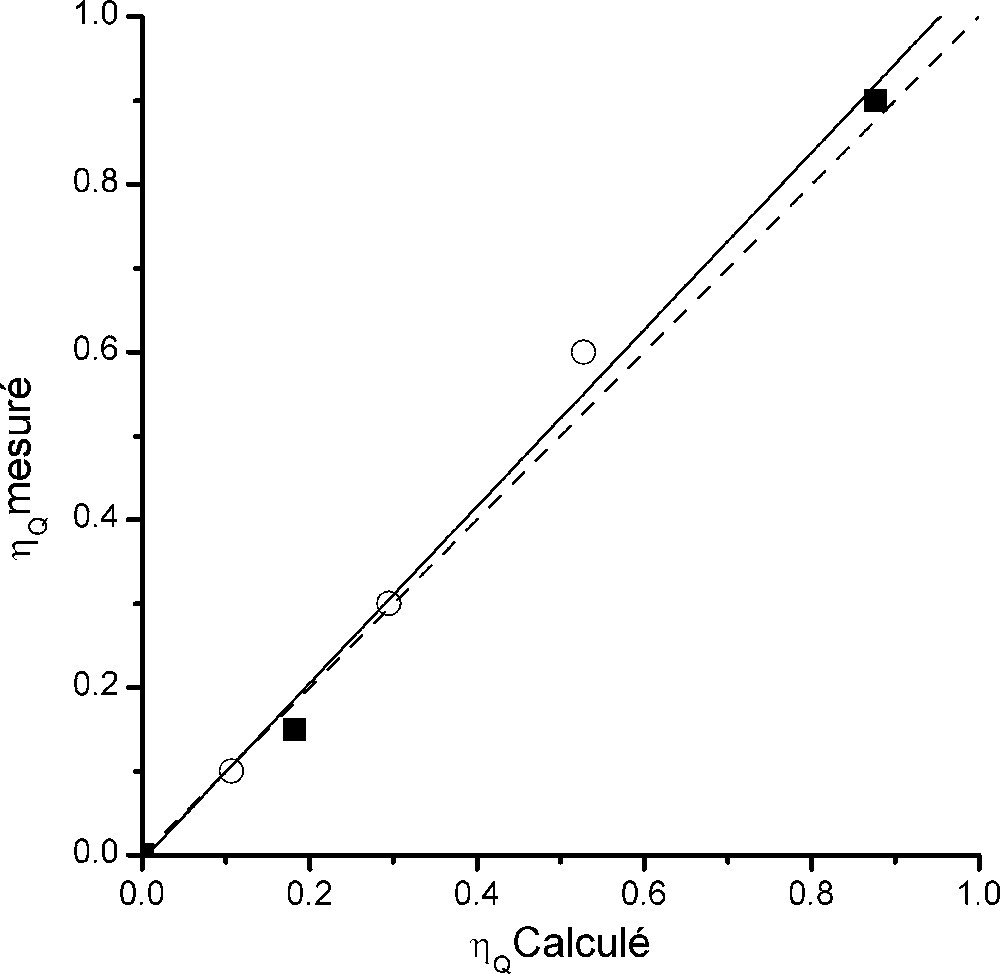
Représentation du paramètre d'asymétrie mesuré en fonction de la valeur calculée par la méthode LAPW dans AlF₃, Na₃AlF₆ et Na₅Al₃F₁₄. Les points sont représentés par des cercles pour ²³Na et par des carrés pour ²⁷Al.

Cette méthode de calcul des paramètres quadripolaires est donc particulièrement performante ; c'est la première fois qu'elle est utilisée pour calculer les composante des gradients de champs électriques de ²³Na et ²⁷Al dans des fluorures inorganiques.

7 Conclusion

Nous avons montré que les fluorures inorganiques forment une famille de composés particulièrement intéressante pour la mise en œuvre et le développement de méthodes de calcul des paramètres RMN. Le modèle semi-empirique de calcul du déplacement chimique s'avère très efficace, puisqu'il est facile à mettre en œuvre, qu'il permet de réaliser une attribution des raies avec une bonne fiabilité et qu'il est très peu demandeur en termes de moyens de calcul. Son utilisation dans les verres fluorés de métaux de transition a permis en particulier d'atteindre le degré de connectivité du réseau d'octaèdres [5]. Même si les méthodes ab initio, conceptuellement plus satisfaisantes, semblent pouvoir atteindre les mêmes objectifs, elles ne seront vraiment utilisables que lorsque l'on saura construire le cluster autour de l'atome étudié sans avoir connaissance au préalable du résultat de la mesure. En ce qui concerne les paramètres quadripolaires, le modèle semi-empirique nécessite la connaissance de paramètres phénoménologiques, comme la polarisabilité des ions, la constante de Sternheimer ou le moment quadripolaire des noyaux utilisés. Cependant, il a permis d'établir une relation entre les fréquences quadripolaires mesurées en RMN et les distributions radiales et angulaires des liaisons métal–fluor dans les composés désordonnés [3]. Dans les composés cristallisés, la méthode LAPW est très performante [21] ; elle devrait également permettre de remonter aux valeurs des paramètres phénoménologiques, comme la polarisabilité des ions, grâce au développement multipolaire utilisé pour le calcul du potentiel. Cette approche ab initio sera très difficilement transposable aux matériaux désordonnés, mais devrait néanmoins permettre de conforter le modèle de charges ponctuelles polarisables.

Appendice Rappels sur les méthodes ab initio

1 Le problème à N corps

Une assemblée d'atomes, que ce soit une molécule ou un solide composé d'un grand nombre d'atomes est constituée de N noyaux de charge +N Z_i e, de masse M_i et de vecteur position ${\vec{R}}_{i}$ , ainsi que de N Z_i électrons de charge –e, de masse m_e et de vecteur position ${\vec{r}}_{i}$ . Le hamiltonien d'un tel système, en l'absence de champ magnétique, peut se mettre sous la forme :

H = - \frac{ℏ^{2}}{2} \sum_{i} \frac{\nabla_{{\vec{R}}_{i}}^{2}}{M_{i}} - \frac{ℏ^{2}}{2} \sum_{i} \frac{\nabla_{{\vec{r}}_{i}}^{2}}{m_{e}} + \frac{1}{8 π ϵ_{0}} \sum_{i \neq j} \frac{e^{2}}{| {\vec{r}}_{i} - {\vec{r}}_{j} |} - \frac{1}{4 π ϵ_{0}} \sum_{i, j} \frac{e^{2} Z_{i}}{| {\vec{R}}_{i} - {\vec{r}}_{j} |} + \frac{1}{8 π ϵ_{0}} \sum_{i \neq j} \frac{e^{2} Z_{i} Z_{j}}{| {\vec{R}}_{i} - {\vec{R}}_{j} |}

Ces opérateurs sont associés, dans l'ordre, à l'énergie cinétique des noyaux, à celle des électrons T, puis aux énergies de l'interaction de Coulomb entre électrons V_e, entre électrons et noyaux et enfin entre noyaux, ces deux derniers termes étant regroupés dans V_ext.

Pour résoudre un problème aussi complexe, un certain nombre de simplifications sont nécessaires. La première, connue sous le nom d'approximation de Born–Oppenheimer, consiste à considérer que, les noyaux étant beaucoup plus lourds que les électrons, ils sont immobiles aux échelles de temps caractéristiques des électrons. Le premier terme du hamiltonien disparaît et le dernier est constant. On est amené à résoudre l'équation de Schrödinger, où seules les variables spatiales électroniques interviennent :

H ψ (\vec{r}) = E ψ (\vec{r})

avec

H = T + V_{e} + V_{ext}

V_e correspond au potentiel d'échange et V_ext à un potentiel qui s'exerce sur les électrons sous l'action d'un système extérieur.

2 Développement sur une base de fonctions d'ondes

Si $ψ_{i} (\vec{r})$ est la fonction d'onde orbitale d'un électron i, elle appartient à un espace de Hilbert de dimension n (supposée finie), auquel on peut associer une base {ϕ_μ} et $ψ_{i} = \sum_{μ = 1}^{n} c_{μ i} ϕ_{μ}$ .

Déterminer la fonction d'onde équivaut donc à déterminer les coefficients c_μi.

3 Construction des fonctions d'onde atomiques

Si $ψ_{i} (\vec{r})$ est la fonction d'onde orbitale d'un électron i d'un atome, alors la prise en compte des deux valeurs possibles du spin de l'électron ξ = α ou ξ = β conduit à la création de deux fonctions d'onde spin–orbite $χ_{i} (\vec{r}, ξ) = ψ (\vec{r}) α$ et $χ_{i} (\vec{r}, ξ) = ψ (\vec{r}) β$ .

Pour les N électrons du système atomique, particules indiscernables, la fonction d'onde doit appartenir à l'espace tensoriel des fonctions d'ondes mono-électroniques et être antisymétrique ; elle se met donc sous la forme d'un déterminant de Slater :

Ψ = \frac{1}{\sqrt{n!}} | \begin{matrix} χ_{1} (1) & χ_{2} (1) & \dots & χ_{N} (1) \\ χ_{1} (2) & χ_{2} (2) & \dots & χ_{N} (2) \\ ⋮ & ⋮ & ⋮ \\ χ_{1} (N) & χ_{2} (N) & \dots & χ_{N} (N) \end{matrix} |

4 Choix de la base des fonctions d'onde atomiques

Le choix idéal consisterait à prendre des fonctions d'onde du type de celles obtenues pour l'ion hydrogénoïde :

ϕ_{nl} = R_{nl} (r) \exp (- Z_{n} r) Y_{lm} (θ, ϕ)

où (r, θ, ϕ) sont les coordonnées sphériques repérant la position de l'électron, R_nl la partie radiale de la fonction d'onde et les fonctions Y_lm les harmoniques sphériques.

Ce type de fonction peut être mis sous une forme équivalente :

ϕ = r^{n} x^{p} y^{q} z^{s} \exp (- Z_{n} r)

(x, y, z) étant les coordonnées cartésiennes repérant l'électron.

Pour des raisons d'efficacité de calcul, nombre de codes de chimie quantique utilisent à la place des fonctions gaussiennes, qui sont de la forme :

ϕ = x^{p} y^{q} z^{s} \exp (- {ar}^{2})

La partie angulaire est la même que dans les déterminants de Slater, mais la partie radiale est différente. En particulier, le terme quadratique en r dans les fonctions gaussiennes fait qu'elles se comporteront de façons très différentes aux grandes et aux faibles valeurs de r.

Pour chaque atome, il existe une grande variété de bases de fonctions construites comme combinaisons linéaires de une à six fonctions de type gaussienne ; la plupart sont disponibles sur le site de l'Environmental Molecular Sciences Laboratory. Le choix de la base de calcul est à examiner de près, car il aura une influence importante sur le résultat.

5 Construction des orbitales moléculaires

Une fois le choix de la base des fonctions d'onde atomiques effectué, les fonctions d'onde moléculaires sont construites sous la forme de combinaisons linéaires des orbitales atomiques (LCAO).

6 Les potentiels de cœur effectifs ou ECP

L'utilisation des ECP consiste à substituer un potentiel effectif aux électrons des couches profondes d'un atome, puisqu'ils ne participent peu ou pas à la liaison chimique. De ce fait, il faut utiliser, pour cet atome, une base de fonction d'ondes spécifique construite pour être utilisée conjointement à ce potentiel.

7 Méthode de Hartree–Fock (HF) et théorie de la fonctionnelle densité (DFT)

Toutes les solutions obtenues par les méthodes ab initio (Hartree–Fock, fonctionnelle de la densité, les méthodes hybrides comme B3LYP ou d'autres) proviennent d'un calcul auto-cohérent : une hypothèse est formulée initialement sur la forme de la solution qui permet de construire le hamiltonien H_HF ou H_KS, lequel est diagonalisé et conduit à une nouvelle solution, que l'on réutilise comme nouveau point de départ. La convergence vers une solution auto-cohérente donne la solution finale : c'est la boucle Self Consistent Field.

Ne sont mentionnées ici que les deux méthodes fondamentales, bien qu'il en existe de nombreuses autres, qui en dérivent.

Dans la méthode de Hartree–Fock le hamiltonien du système se met sous la forme d'une somme de hamiltoniens mono-électroniques :

H_{HF} = H_{1} + H_{2}

H_{1} = \sum_{i} {- \frac{ℏ^{2}}{2} \frac{\nabla_{{\vec{r}}_{i}}^{2}}{m_{e}} - \sum_{j} \frac{1}{4 π ϵ_{0}} \frac{e^{2} Z_{i}}{| {\vec{R}}_{i} - {\vec{r}}_{j} |}} = \sum_{i} h_{i}

H_{2} = \sum_{i < j} V_{ij} = V_{e}

où h_i représente l'énergie d'un électron dans le potentiel créé par les noyaux et V_ij est le potentiel d'interaction entre le i^e et le j^e électron ou potentiel d'échange.

Dans la méthode de la fonctionnelle densité, la notion de fonction d'onde perd de son importance au bénéfice de la densité de charge électronique $ρ (\vec{r})$ . Néanmoins, les principes de recherche des solutions numériques sont semblables. La mise en équation repose sur le Théorème de Kohn–Sham.

La densité électronique exacte de l'état fondamental d'un système à N électrons est $ρ (\vec{r}) = \overset{N}{\sum^{i = 1}} ϕ_{i} * (\vec{r}) ϕ_{i} (\vec{r})$ , où les fonctions d'onde $ϕ_{i} (\vec{r})$ sont les N solutions de plus basse énergie des équations de Kohn–Sham :

H_{KS} ϕ_{i} = E_{i} ϕ_{i}

avec

H_{KS} = - \frac{ℏ^{2}}{2} \sum_{i} \frac{\nabla_{{\vec{r}}_{i}}^{2}}{m_{e}} + \frac{e^{2}}{4 π ϵ_{0}} \int \frac{ρ (\vec{r}')}{| \vec{r} - \vec{r}' |} d \vec{r}' + V_{xc} + \frac{1}{8 π ϵ_{0}} \sum_{i \neq j} \frac{e^{2} Z_{i} Z_{j}}{| {\vec{R}}_{i} - {\vec{R}}_{j} |}

où V_xc est le potentiel d'échange corrélation, qui n'existe pas dans H_HF. Il n'est pas connu formellement, sauf dans le cas du gaz d'électrons libres. L'approximation la plus courante est celle de la densité locale LDA, tandis qu'une forme plus élaborée est celle de l'approximation des gradients généralisés GGA. Dans le premier cas, l'énergie d'échange corrélation dans un volume élémentaire entourant le point

\vec{r}

est obtenue en supposant qu'elle est identifiable localement à celle obtenue pour le gaz d'électrons libres avec la densité constante

ρ (\vec{r})

. Dans le second cas, l'énergie d'échange corrélation est en plus pondérée par la valeur que prend la densité dans les volumes élémentaires voisins (il existe plusieurs versions de gradients).

Bibliographie

[1] B. Bureau; G. Silly; J.-Y. Buzaré; J. Emery; C. Legein; C. Jacoboni J. Phys. : Condens. Matter, 9 (1997), p. 6719

[2] B. Bureau; G. Silly; J.-Y. Buzaré; C. Jacoboni J. Non-Cryst. Solids, 258 (1999), p. 110

[3] B. Bureau; G. Silly; J.Y. Buzaré; B. Boulard; C. Legein J. Phys.: Condens. Matter, 12 (2000), p. 5775

[4] B. Bureau; H. Guérault; G. Silly; J.-Y. Buzaré; J.-M. Grenèche J. Phys.: Condens. Matter, 11 (1999), p. L423

[5] B. Bureau; G. Silly; J.-Y. Buzaré; J. Emery Chem. Phys, 249 (1999), p. 89

[6] M.J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; V.G. Zakrzewski; J.A. Montgomery; R.E. Stratmann; J.C. Burant; S. Dapprich; J.M. Millam; A.D. Daniels; K.N. Kudin; M.C. Strain; O. Farkas; J. Tomasi; V. Barone; M. Cossi; R. Cammi; B. Mennucci; C. Pomelli; C. Adamo; S. Clifford; J. Ochterski; G.A. Petersson; P.Y. Ayala; Q. Cui; K. Morokuma; D.K. Malick; A.D. Rabuck; K. Raghavachari; J.B. Foresman; J. Cioslowski; J.V. Ortiz; A.G. Baboul; B.B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R. Gomperts; R.L. Martin; D.J. Fox; T. Keith; M.A. Al-Laham; C.Y. Peng; A. Nanayakkara; M. Challacombe; P.M.W. Gill; B. Johnson; W. Chen; M.W. Wong; J.L. Andres; C. Gonzalez; M. Head-Gordon; E.S. Replogle; J.A. Pople, Gaussian 98, Revision A.9. Gaussian Inc, Pittsburgh, PA, USA, 1998

[7] P. Blaha; K. Schwarz; J. Luitz WIEN97, A Full Potential Linearized Augmented Plane Wave Package for Calculating Crystal Properties, Karlheinz Schwarz, Technische Universität Wien, Austria, 1999, ISBN 3-9501031-0-4

[8] N.F. Ramsey Phys. Rev, 78 (1950), p. 699

[9] P.Ö Löwdin Adv. Phys, 5 (1956), p. 1

[10] R. Ditchfield Mol. Phys, 27 (1974), p. 789

[11] F. London J. Phys. Radium, 8 (1958), p. 397

[12] J. R. Cheeseman; G. Gary; W. Trucks; T. A. Keith; M.J. Frisch J. Chem. Phys, 104 (1996) no. 14, p. 5497

[13] S.H. Cai; Z. Chen; X. Xu; H.L. Wan Chem. Phys. Lett, 302 (1999), p. 73

[14] S.H. Cai; Z. Chen; H.L. Wan J. Phys. Chem. A, 106 (2002), p. 1060

[15] S.H. Cai; Z. Chen; Z.W. Chen; H.L. Wan Chem. Phys. Lett, 362 (2002), p. 13

[16] G. Czjzek; J. Fink; F. Gotz; H. Schmidt; J.M.D. Coey; J.P. Rebouillat; A. Liénard Phys. Rev. B, 23 (1981), p. 2513

[17] G. Czjzek Phys. Rev. B, 23 (1982), p. 4908

[18] B. Bureau; G. Silly; J.-Y. Buzaré; C. Legein; D. Massiot Solid-State NMR, 15 (1999), p. 129

[19] H. Guerault; B. Bureau; G. Silly; J.-Y. Buzaré; J.-M. Grenèche J. Non-Cryst. Solids, 287 (2001), p. 65

[20] S. Cottenier Density Functional Theory and the family of (L)APW-methods: a step-by-step introduction, Instituut voor Kern- en Stralingsfysica, K.U. Leuven, Belgium, 2002 (ISBN 90-807215-1-4)

[21] G. Silly; C. Legein; J.-Y. Buzaré; F. Calvayrac Solid-State NMR (2004) (sous presse)

[22] V. Kellö; A. J. Sadlej; P. Pyykkö; D. Sundholm; M. Tokman Chem. Phys. Lett, 304 (1999), p. 414

[23] P. Pyykkö; A.J. Sadlej Chem. Phys. Lett, 227 (1994), p. 221

Commentaires - Politique

1 Introduction

2 Mesures RMN : notations et conventions

2.1 Interaction de déplacement chimique

2.2 Interaction quadripolaire

3 Modélisation semi-empirique du déplacement chimique de 19F

4 Modélisation ab initio du déplacement chimique de 19F

4.1 Calcul ab initio du tenseur d'écrantage

4.2 Application aux fluorures inorganiques

5 Modélisation semi-empirique des paramètres quadripolaires

5.1 Modèle semi-empirique de calcul des GCE

5.2 Applications aux phases désordonnées de GaF3

5.3 Forme de la distribution des paramètres RMN

5.3.1 GaF3 amorphe

5.3.2 GaF3 nanostructuré

6 Modélisation ab initio des GCE

6.1 La méthode LAPW

6.2 Application à des fluoroaluminates simples

7 Conclusion

Appendice Rappels sur les méthodes ab initio

1 Le problème à N corps

2 Développement sur une base de fonctions d'ondes

3 Construction des fonctions d'onde atomiques

4 Choix de la base des fonctions d'onde atomiques

5 Construction des orbitales moléculaires

6 Les potentiels de cœur effectifs ou ECP

7 Méthode de Hartree–Fock (HF) et théorie de la fonctionnelle densité (DFT)

3 Modélisation semi-empirique du déplacement chimique de ¹⁹F

4 Modélisation ab initio du déplacement chimique de ¹⁹F

5.2 Applications aux phases désordonnées de GaF₃

5.3.1 GaF₃ amorphe

5.3.2 GaF₃ nanostructuré