1 Introduction
Les apatites, isomorphes de la fluoroapatite Ca10(PO4)6F2, offrent de nombreuses possibilités de substitution des groupements cationiques et/ou anioniques, en raison de la stabilité et de la flexibilité particulière de leur structure [1–3]. La structure apatitique cristallisant dans le système hexagonal, groupe d'espace P63/m [4], est construite sur un squelette formé de couches parallèles d'ions PO43–, disposés en arrangement hexagonal et donnant naissance à deux types de tunnels, où sont localisés les ions calcium Ca2+ (Fig. 1). Ainsi, deux types de cations peuvent être définis : les calciums, dans les sites S(I), au nombre de quatre par maille, s'alignant en colonnes le long de l'axe c et les calciums, dans les sites S(II), au nombre de six par maille, s'organisant en triangles équilatéraux autour de l'axe sénaire hélicoïdal (Fig. 2). Le calcium peut être substitué par de nombreux ions, mono-, di- ou trivalents. Ces substitutions se font suivant les règles classiques de la cristallochimie, qui font intervenir les rayons, la charge et la polarisabilité des ions [5].
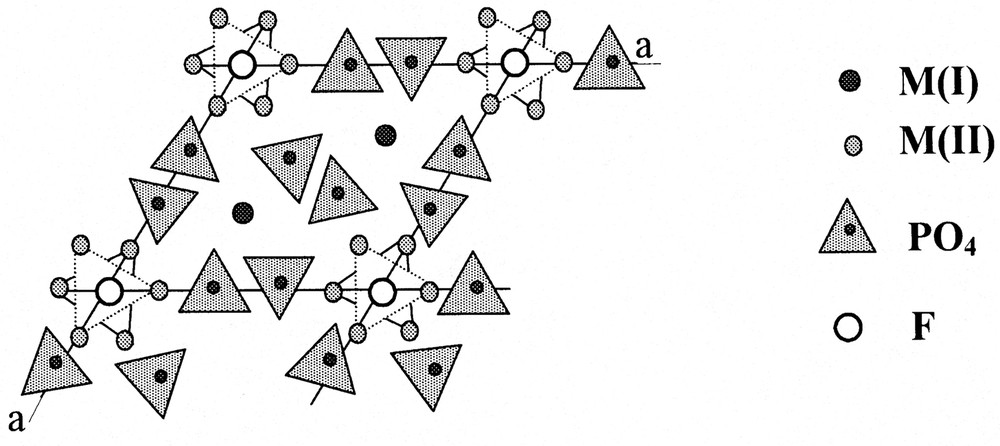
Projection de la structure de la fluoroapatite selon la direction (001).

Polyèdres de coordination de S(I) : (a) et S(II) (b) [17].
Par ailleurs, des observations réalisées lors des travaux antérieurs [6–9] laissent à penser que l'effet stérique influe notablement sur la limite de substitution du calcium par d'autres atomes. Ainsi, la substitution de ce dernier par Ba, Sr ou Cd, par exemple, conduit à des solutions solides continues [10–13], alors que d'autres atomes, tels que Mg ou Mn ne peuvent s'incorporer qu'à des taux limités [14–17]. Toutefois, la limite de substitution reste, dans la plupart des cas, mal définie.
Le présent travail s'inscrit dans le cadre de la détermination de la limite de substitution du calcium par le magnésium en mettant à profit la méthode de Rietveld.
2 Partie expérimentale
2.1 Synthèse
Les fluoroapatites substituées au magnésium ont été synthétisées par précipitation à partir de nitrate de calcium tétrahydraté [Ca(NO3)24 H2O], de nitrate de magnésium hexahydraté [Mg(NO3)26 H2O], d'hydrogénophosphate de diammonium [(NH4)2HPO4] et de fluorure d'ammonium (NH4F). Une solution contenant Ca2+ et Mg2+, en concentration globale 0,40 mol l–1 afin d'obtenir des apatites stœchiométriques, a été ajoutée au moyen d'une pompe péristaltique à une solution, bouillante et maintenue sous agitation, contenant 0,33 mol l–1 (NH4)2HPO4 et 0,16 mol l–1 NH4F. Le pH du mélange est ajusté à 9 par addition d'une solution d'ammoniaque. Le précipité a été filtré, lavé à chaud puis séché à 70 °C pendant 12 h.
Le nitrate de magnésium a été introduit dans les solutions pour obtenir des rapports molaires Mg/(Ca + Mg) de 0,025, 0,05, 0,10, 0,15, 0,20 et 0,30, respectivement. Les échantillons seront nommés, dans la suite du texte Ca10–xMgx(PO4)6F2, où x désigne le nombre d'atomes de magnésium introduit dans la solution de départ.
2.2 Techniques de caractérisation
Les teneurs des ions métalliques Ca2+ et Mg2+ ont été déterminées par spectrophotométrie d'absorption atomique à l'aide d'un spectrophotomètre Perkin Elmer modèle 3110. Les ions phosphate ont été dosés par colorimétrie selon la méthode de Gee et Deitz [18]. Le dosage des ions fluorures a été effectué par ionométrie, en utilisant une électrode spécifique au fluor Ingold [19], à pH 5,5, en présence d'une solution « TISAB » (Total Ionic Strength Adjustment Buffer).
Les spectres d'absorption infrarouge ont été réalisés à l'aide d'un spectromètre Jasco FT/IR-420. Les échantillons sont dispersés dans du bromure de potassium (KBr), pur et sec. Le mélange a été comprimé sous forme de pastille. Le domaine spectral s'étend entre 4000 et 500 cm–1.
Les diagrammes de diffraction des rayons X ont été acquis à la température ambiante, à l'aide d'un diffractomètre Philips PW 1800. Le rayonnement utilisé est produit par une anticathode de cuivre dont la longueur d'onde est celle de la raie Kα du cuivre (λ = 1,5406 Å). La gamme angulaire de diffraction varie en 2θ entre 10 et 90°, avec un pas de 0,02° et un temps de comptage de 10 s par pas. Les phases cristallines ont été identifiées par référence aux fichiers ICDD.
2.3 Analyse structurale
Pour les fluoroapatites mixtes de formule générale Ca(10–x)Mgx(PO)4F2, l'affinement a été réalisé par affinement au moyen de la méthode de Rietveld à l'aide du programme DBWS 9411 [20–21]. Ainsi, le groupe d'espace P63/m, les valeurs Z = 2 et M = 1008 (no 176) [4], les paramètres de maille (a = b = 9,391(2) ; c = 6,890(3); V = 525,7(4)), les positions atomiques et les facteurs de Debye–Waller des atomes constitutifs de la fluoroapatite Ca10(PO4)6F2 ont été introduits comme modèle structural initial pour l'apatite de plus faible teneur en Mg. Ensuite, ces paramètres affinés ont été utilisés comme modèle initial pour l'apatite de teneur en Mg immédiatement supérieure, et ainsi de suite.
Le bruit de fond a été traité par un polynôme de troisième degré, alors que les pics ont été ajustés par une fonction pseudo-voigt. La distance à mi-hauteur H (fonction de 2θ) des pics de diffraction a été évaluée par la fonction Caglioti [22].
| (1) |
L'affinement des facteurs d'occupation s'est limité aux cations métalliques Ca2+ et Mg2+, tout en supposant que ces deux cations sont initialement équitablement répartis entre les deux sites S(I) et S(II). Dans le dernier cycle d'affinement, 28 paramètres structuraux et non structuraux ont été optimisés. La fiabilité des affinements a été évaluée par les facteurs R définis dans le programme DBWS 9411 [20–21].
La distorsion de la structure peut être calculée à partir du tétraèdre PO43– selon l'équation (2) :
| (2) |
3 Résultats et discussion
3.1 Analyse chimique
Les résultats des analyses chimiques des éléments de la série des apatites mixtes Ca–MgFap sont rapportés dans le Tableau 1. Le rapport [(Ca+Mg)/P] dans les solides est voisin du rapport théorique (1,667). Ceci laisse à penser que les apatites synthétisées sont sensiblement stœchiométriques. Ce tableau montre aussi que le taux de magnésium est très voisin de celui introduit dans les solutions de départ, ce qui indique que la majeure partie du magnésium utilisé a été incorporée dans les solides.
Résultats des dosages chimiques des fluoroapatites mixtes Ca–Mg
| Produits | Mg2+ | Ca2+ | PO43– | (Ca + Mg)/P | F– |
| Ca10FAp | 0,00 | 9,84(2) | 5,94(4) | 1,656(5) | 1,96(2) |
| Ca9,75Mg0,25FAp | 0,23(1) | 9,72(3) | 5,94(4) | 1,675(4) | 1,98(2) |
| Ca9,75Mg0,25FAp | 0,47(2) | 9,44(3) | 5,93(4) | 1,671(4) | 2,03(1) |
| Ca9Mg1FAp | 0,96(1) | 8,94(2) | 5,95(4) | 1,663(3) | 1,98(2) |
| Ca8,5Mg1,5FAp | 1,44(2) | 8,39(4) | 5,91(4) | 1,665(4) | 1,92(4) |
| Ca8Mg2FAp | 1,85(3) | 8,08(2) | 5,94(4) | 1,670(2) | 2,01(1) |
3.2 Spectroscopie infrarouge
Les spectres infrarouges types des solutions solides étudiées sont regroupés dans la Fig. 3. Ils montrent les bandes caractéristiques de la fluoroapatite. Les pics d'absorption observés vers 3433 et 1646 cm–1 sont attribués à l'eau incluse dans la poudre et/ou dans celle de KBr. Les bandes d'absorption observées vers 870 cm–1 et 1380 cm–1 sont relatives aux ions HPO42– et NO3–. Ces deux bandes disparaissent après calcination à 500 °C.
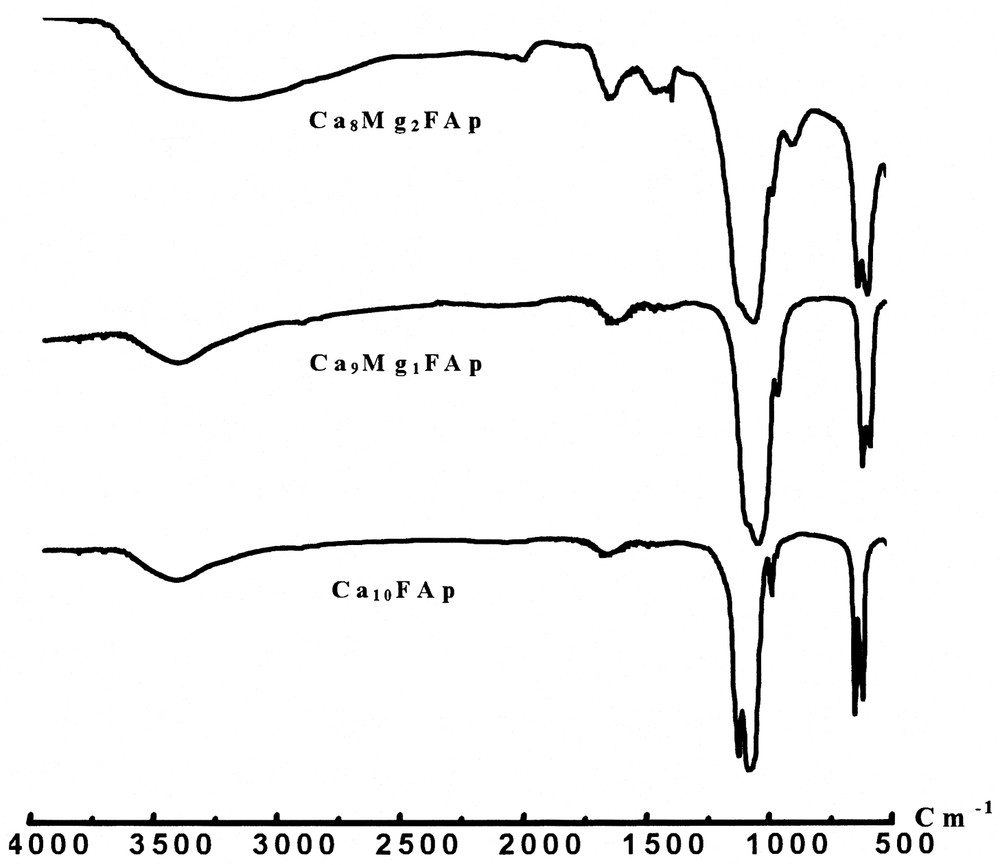
Spectres d'absorption infrarouge des fluoroapatites mixtes Ca–Mg.
Le Tableau 2, dans lequel sont consignées les bandes d'absorption relatives au groupement PO43–, montre une légère augmentation des fréquences de vibration de celui-ci lorsque le taux de magnésium utilisé augmente. Cette augmentation est à relier à la taille plus faible de l'atome de magnésium par rapport à celle du calcium.
Positions des bandes relatives au groupement PO43– dans les fluoroapatites mixtes Ca(10–x)MgxFAp
| x | v1 (cm–1) | v3 (cm–1) | v4 (cm–1) |
| 0,00 | 966 | 1100–1045 | 606–565 |
| 0,25 | 966 | 1103–1046 | 606–566 |
| 0,50 | 968 | 1103–1047 | 608–568 |
| 1,00 | 967 | 1105–1039 | 610–568 |
| 1,50 | 969 | 1107–1042 | 609–567 |
| 2,00 | 969 | 1107–1048 | 614–571 |
3.3 Analyse des diffractogrammes
Les diffractogrammes acquis sont présentés sur la Fig. 4. Pour x ≤ 2, ils sont en accord avec celui de la fluoroapatite. Toutefois, il n'est pas exclu que la poudre renferme des impuretés en trop faible quantité pour être détectées, ou d'autres phases à l'état amorphe. En effet, il a été mis en évidence, au cours du traitement thermique de la poudre de composition Ca9Mg(PO4)6 F2, la cristallisation à 650 °C de la phase Mg2F(PO4)6 [23] ; cette même phase a aussi été observée pour des teneurs en magnésium supérieures à 2,5 atom%. Par ailleurs, ces diffractogrammes montrent un élargissement des pics, indiquant une diminution du degré de cristallinité des poudres. Le même effet a été observé pour les poudres d'hydroxyapatite substituée au magnésium [24–25]. Toutefois, son effet sur la fluoroapatite est moins prononcé. Un tel résultat est à relier à la présence des ions F– [26–28]. Pour x > 2, les poudres sont caractéristiques de phases amorphes. Contrairement à d'autres auteurs [15], nous n'avons pas observé la formation de la phase Mg(NH4)PO4H2O.
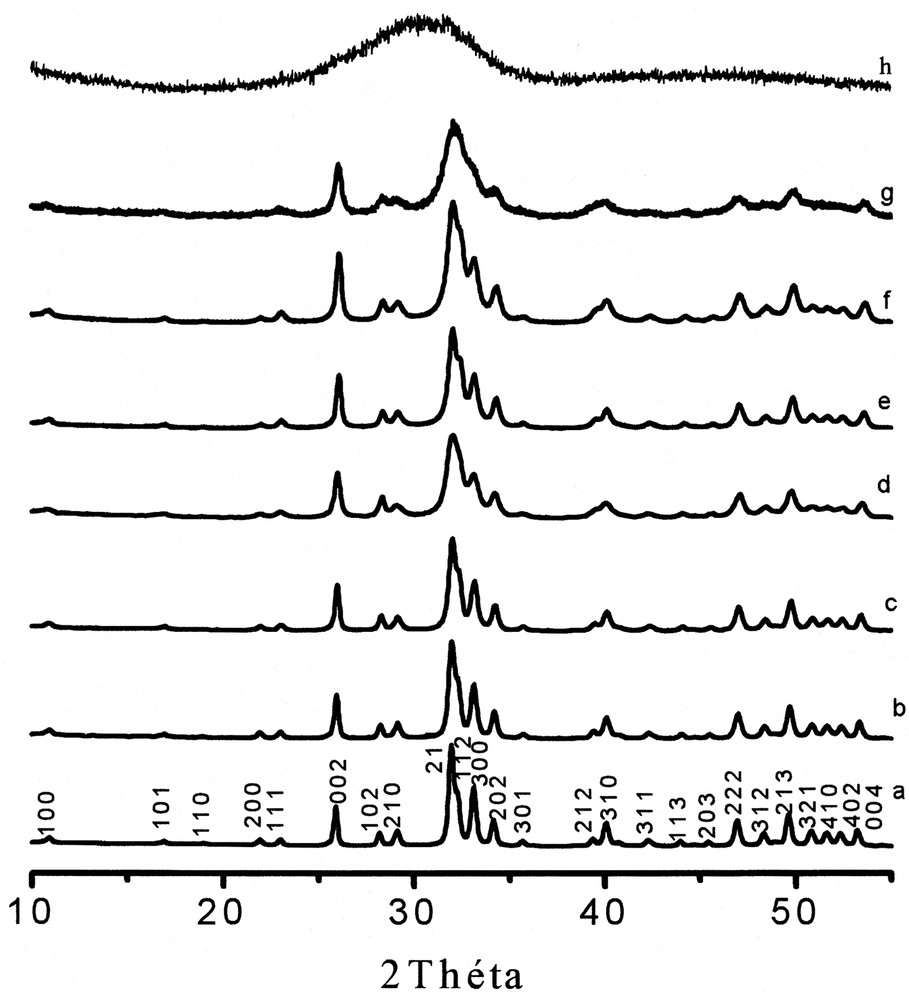
Diffractogrammes des fluoroapatites mixtes Ca–Mg. (a) Ca10Fap ; (b) Ca9,75Mg0,25Fap ; (c) Ca9,5Mg0,5Fap ; (d) Ca9Mg1Fap ; (e) Ca8,75Mg1,25Fap ; (f) Ca8,5Mg1,5Fap ; (g) Ca8Mg2Fap ; (h) Ca7Mg3Fap.
L'influence du magnésium sur la taille des cristallites (D) a été contrôlée à partir des réflexions de diffraction des rayons X (300), (002) et (022) à l'aide de l'équation de Sherrer [29]:
| (3) |
Évolution de la taille des cristallites en fonction de la teneur en magnésium
| Produits | β1/2(300) | D(300) | β1/2(002) | D(002) | β1/2(022) | D(022) | Dint (%) |
| Ca10Fap | 0,26 | 319,21(3) | 0,18 | 435,51(4) | 0,22 | 378,43(3) | 1,71 |
| Ca9,75Mg0,25Fap | 0,30 | 276,65(4) | 0,24 | 340,13(4) | 0,28 | 297,34(3) | 1,13 |
| Ca9,5Mg0,5Fap | 0,30 | 276,65(4) | 0,24 | 340,13(4) | 0,28 | 297,34(3) | 1,66 |
| Ca9Mg1Fap | 0,38 | 218,41(2) | 0,30 | 272,10(3) | 0,36 | 231,26(3) | 0,48 |
| Ca8,5Mg1,5Fap | 0,36 | 230,21(2) | 0,41 | 198,9(2) | 0,36 | 230,98(3) | 3,99 |
| Ca8Mg2Fap | 0,37 | 223,94(3) | 0,38 | 214,54(3) | 0,36 | 230,84(3) | 7,97 |
3.4 Affinement Rietveld
La comparaison des diffractogrammes calculés et théoriques, représentés sur la Fig. 5, confirme le déplacement des pics de diffraction vers les grands angles, ce qui se traduit par la réduction des paramètres cristallins ainsi que le volume de la maille, comme indiqué sur la Fig. 6. Pour une concentration inférieure à 15 atom% de Mg, l'évolution de ces paramètres suit la loi de Végard [30], selon les équations (4) :
| (4) |
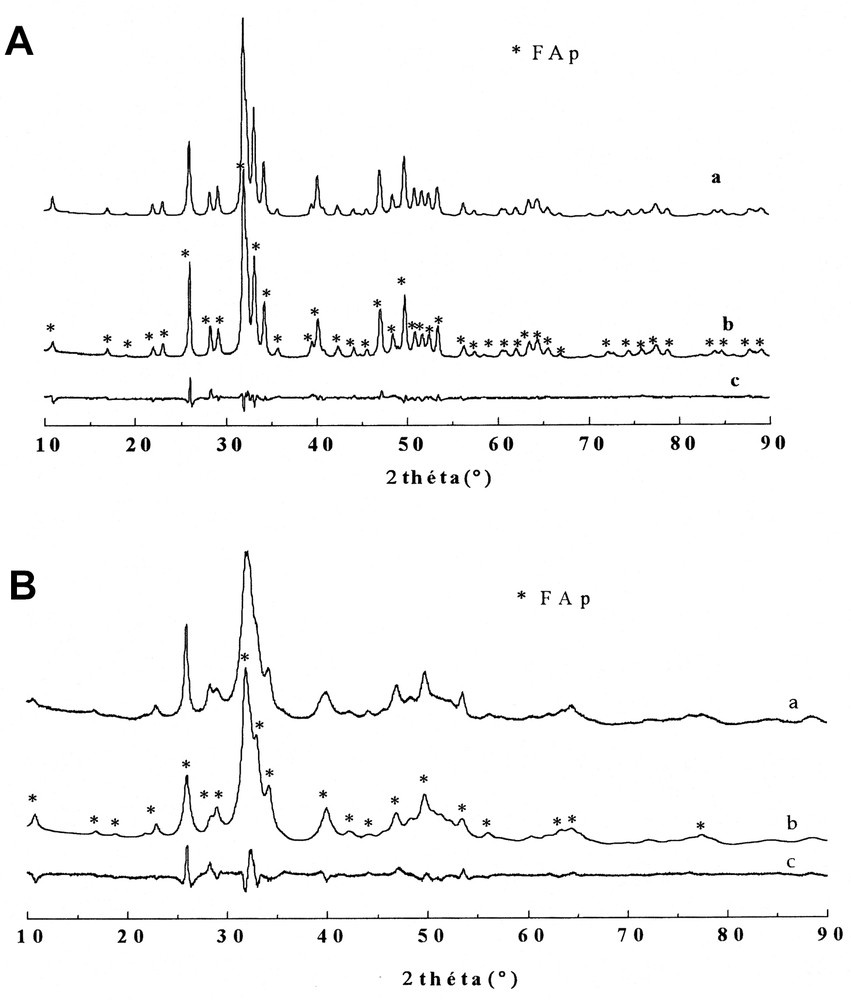
Diffractogrammes observé (a), calculé (b) et leur différence (c) de deux fluoroapatites mixtes Ca2+–Mg2+. (A) Ca9,5Mg0,5Fap ; (B) Ca8Mg2Fap.
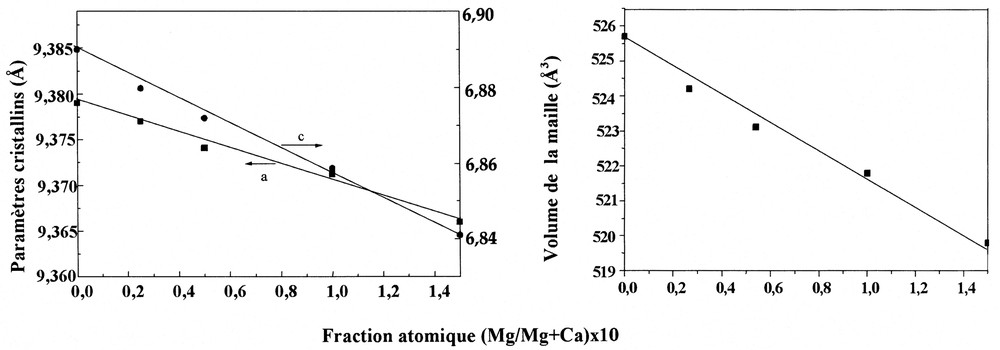
Paramètres cristallins et volume de la maille en fonction du rapport atomique (Mg/Mg + Ca) × 10.
L'augmentation des valeurs des paramètres cristallins de la composition Ca8Mg2FAp (a = 9,383 Å et c = 6,841 Å) est due à la diminution de la cristallinité de la poudre, qui est observée sur le diffractogramme RX par élargissement des pics. Ceci devrait sans doute avoir une influence sur la procédure d'affinement, et on aboutit par conséquent à des valeurs sous-estimées.
Le Tableau 4, dans lequel sont consignées les répartitions cationiques entre les deux sites cristallographiques, reproduites sur la Fig. 7, montre que la substitution du calcium par le magnésium est limitée à un taux de 16,8 atom%. Cette limite s'explique par la différence des tailles des deux cations (rCa2+ = 0,99 Å, rMg2+ = 0,86 Å) [31], qui induit une augmentation des indices de distorsion des tétraèdres PO43– (Tableau 3). En comparant les limites de substitution des solutions solides fluorées (16,8%) et celles de leurs homologues hydroxylées (12%) [32], on peut déduire qu'elles sont influencées par la nature de l'anion. En effet, la substitution de Ca2+ par Mg2+ dans l'hydroxyapatite entraîne au sein de la structure des contraintes plus importantes que celles engendrées par la même substitution dans la structure de la fluoroapatite, et ceci en raison de la taille de l'ion OH–, plus importante que celle de F–. La limite plus élevée, déterminée par analyse chimique, est à relier probablement à la présence d'une phase amorphe [23].
Distribution des ions magnésium entre les deux sites S(I) et S(II) dans les fluoroapatites mixtes Ca–Mg
| Produits | x (affinement) | x (analyse chimique) | Distribution par affinement (A) | Distribution statistique (B) | (A–B/B) | |||
| S(I) | S(II) | S(I) | S(II) | S(I) | S(II) | |||
| Ca9,75Mg0,25FAp | 0,22 | 0,23 | 0,02 | 0,20 | 0,09 | 0,13 | –0,78 | 0,54 |
| Ca9,5Mg0,5FAp | 0,45 | 0,47 | 0,07 | 0,38 | 0,18 | 0,27 | –0,61 | 0,41 |
| Ca9Mg1FAp | 0,92 | 0,96 | 0,39 | 0,53 | 0,37 | 0,55 | 0,05 | –0,04 |
| Ca8,5Mg1,5FAp | 1,42 | 1,46 | 0,59 | 0,82 | 0,57 | 0,85 | 0,03 | –0,04 |
| Ca8Mg2FAp | 1,68 | 1,86 | 0,74 | 0,94 | 0,67 | 1,01 | 0,10 | –0,07 |

Écart à la répartition statistique de Mg2+ en fonction de la fraction molaire (Mg/Ca + Mg) × 10.
La localisation des cations substituants dans la structure apatitique est généralement corrélée au rayon ionique. En raison de sa taille plus faible que celle du calcium, le magnésium devrait se placer dans le site S(I) puisque le volume de cette dernière est plus faible que celui du site S(II) [33]. Or, d'après les facteurs d'occupation des sites métalliques, il apparaît que la répartition du magnésium entre les deux sites cristallographiques est en étroite relation avec la teneur introduite. En effet, pour des faibles concentrations (< 10%), il a tendance à occuper préférentiellement le site II, alors que pour des concentrations plus élevées, la répartition devient proche de la statistique (Fig. 7). La préférence relative des cations Mg2+ à occuper le site S(II) ne peut pas s'expliquer par la différence de tailles respectives des deux cations, mais d'autres paramètres doivent certainement intervenir, tels que la faible polarisabilité et l'affinité particulière du magnésium (acide dur) vis-à-vis de l'ion fluorure (base dure). Ceci montre que les substitutions dans les apatites ne sont pas gouvernées uniquement par les facteurs géométriques, mais aussi par des effets chimiques.
La diminution des paramètres cristallins est à relier à la diminution des distances interatomiques M–O, M–M et M–F, lorsque le taux de magnésium incorporé dans la structure apatitique augmente. Ces distances diminuent effectivement, bien que cette diminution reste faible, mais ceci est dû aux faibles taux de Mg incorporé.
4 Conclusion
Dans le but de préciser la limite de substitution du calcium par le magnésium dans la fluoroapatite, une série de solutions solides, de formule générale Ca10–xMgx(PO4)6F2 (0 ≤ x ≤ 3) a été préparée par voie humide. La cristallinité des poudres, déterminée à partir de la taille des cristallites, diminue lorsque le taux de Mg augmente. Pour x supérieur à 2, la poudre devient amorphe. L'affinement par la méthode Rietveld à permis de préciser la limite de substitution du calcium par le magnésium, le taux introduit dans la structure de la fluoroapatite étant de l'ordre de 16,8 atom%. Pour les faibles teneurs (< 10 atom%) le magnésium occupe préférentiellement le site S(II), cette préférence étant attribuée à des effets chimiques. Pour des teneurs supérieures, la répartition devient proche de la statistique.
Matériel supplémentaire
Les positions atomiques, les facteurs d'occupation, le paramètre d'agitation thermique isotrope, les paramètres cristallins, les facteurs de fiabilités et d'autres paramètres non structuraux ont été déposés et peuvent être obtenus sur demande auprès du Fachinformationzentrum Karlsruhe, Abt. PROKA, 76344 Eggenstein-Leopoldshafen, Allemagne, en tant que matériel supplémentaire.


