1 Molecule based magnetic materials
Magnetic materials are useful for devices in high-tech products of the 21st century but have also been intriguing objects for scientific scrutiny ever since ancient times [1]. The last 20 years has seen a rapid growth in the quest for non-metallic magnets, based on molecular compounds with or without metal ions [2,3]. These compounds are not ‘glamorous’ in the same way as high temperature superconducting ceramics, but may nevertheless hold great promises for future materials [4,5]. These areas are somewhat related as also in the magnetic case the race is for useful materials with Tc above room temperature. Presently there are only a few such compounds, the vanadium(tetracyanoethyleneradical)n·x CH2Cl2 probably being the most well known of these [5]. Recently the highest Tc for a purely organic material (an organic π-conjugated polymer) 10 K, was reported [6,7].
A critical question in the search for molecule based magnets is why open shell molecules (radicals or paramagnetic metal complexes) sometimes assemble to form materials where the spins interact to give magnetism (ferromagnetic coupling) but more often not (antiferromagnetic coupling).
Currently two mechanisms are used to predict and interpret such magnetic behavior. In the McConnell I mechanism [8] close contacts of spin densities in the interacting molecules are considered and ferro- or antiferromagnetic couplings are often easily interpreted by this model [3].
Essentially, this theory predicts that, whenever possible, a weak chemical bond will be formed containing electrons of opposite spins on the interacting molecules, thus an antiferromagnetic coupling. The only situation where this is impossible is if the spins are situated in orthogonal orbitals (zero overlap), and then the coupling is ferromagnetic.
Only occasionally is the McConnell II mechanism [9,10] found in which charge transfers (or configuration interaction) between the interacting units are taken into account [4].
Such ferro- and antiferromagnetic couplings are routinely extracted from SQUID measurements of the temperature dependence of the magnetic susceptibility. There are also quantum chemical methods that can, in many cases, be used to reproduce the measured interactions fairly well. Owing to the nature of the problem, that is to consider all magnetic interactions in a molecular crystal and the often very small energy differences between high- and low-spin states, these calculations are large. Moreover, density functional theory (DFT) (that scale well with an increasing size of a problem therefore the method of choice) often requires calculation of the so-called broken-symmetry (BS) solutions, a feature not available in all quantum chemical program systems.
While this is a great success for theoretical chemistry, and much insight can be gained from these calculations, the mere reproduction of experimental data will never be satisfying for the practical chemist unless they come with a great deal of improved understanding. As a scientist playing this kind of tinker-toy game with molecules, one would want an easier way to get some idea of the possibilities of ferro- or antiferromagnetic interactions. Preferably before the synthetic work!
1.1 The importance of spin densities
As spin density features are the most common way to interpret the magnetic measurements (the McConnell I mechanism, see above and below), the spin density of the interacting radical (or paramagnetic) molecules could be such a parameter. This article deals with the use of DFT calculations on small molecular building blocks with two goals in mind. First, just as with larger more elaborate calculations, we wanted to gain insight into the spin interactions of particular cases with known geometries and magnetic couplings. We also wanted to understand the spin distribution, especially the mechanisms of spin polarization (the appearance of spin densities, positive or negative, outside the singly occupied molecular orbital (SOMO)) in the building blocks in order to: (a) Get a general understanding of the magnetic properties of related compounds without making more calculations. (b) More efficiently use these compounds in further preparations.
Another point that makes spin densities an interesting goal for calculations is that they are not easily measurable. The most important methods are ESR and polarized neutron diffraction (PND). However, these methods do not measure the same spin density. Briefly; from ESR we can use the hyperfine coupling constant to extract the spin density that reaches all the way to the nucleus, the Fermi contact density. Moreover, the hyperfine coupling constant for C–H hydrogens in π systems gives a measure of the π spin density on the carbon. PND on the other hand gives us a total spin density map of the whole molecule. However, some arbitrariness is involved when assigning the measured spin to individual atoms.
Since all these methods suffer from certain restrictions such as magnetic nuclei in the molecule, time or expensive instrumentation, quantum chemical calculations is an important complementary tool. Furthermore, we may get insight into the underlying mechanism of the spin distribution.
1.2 Spin delocalization and spin polarization
Spins are spread out in the molecule in two ways. The first is obvious, the single α-spin electron resides alone in a molecular orbital, and the more this orbital is delocalized, the more will the spin density be spread out.
The second effect is spin polarization, and the allyl radical is the classic example of this [11]. In this molecule large positive spin density is found on to the two end carbons and a smaller negative spin density at the central carbon, see Fig. 1. This is an effect of polarization of the underlying orbitals in order to minimize electron-electron repulsion [12]. In the extreme case of 100% polarization of the β-electron to the central carbon we get three independent spin-MO:s with one electron on each carbon, and thus no π-bonding. What we observe in reality is thus a balance between bonding and electron-electron repulsion. The spin polarization is due to the fact that electron-electron repulsion is minimized when two electrons, that share the same space, have the same (parallel) spins since they will then automatically avoid each other because of the Pauli principle.
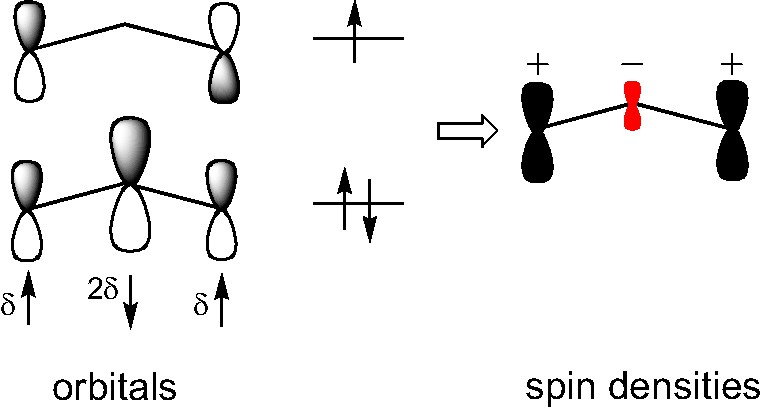
The highest SOMO and the second highest occupied orbital for the allyl radical (CH2CHCH2) in a spin restricted molecular orbital calculation (number of singly occupied orbitals equal to the number of unpaired electrons). In an unrestricted calculation all orbitals are singly occupied which allows spin polarization of underlying ‘doubly occupied’ orbitals, indicated by the δ-arrows. The net effect is negative spin populations on the nodes of the highest SOMO, and a spin density as shown to the right.
Consequently, we may expect induced negative spin density on the SOMO's nodal carbon atoms if there is an underlying π-orbital to polarize and if this π-orbital coincides to a large extent with the magnetic orbital.
1.3 Magnetic couplings
We begin with a recapitulation of the four cases arising from interacting spin densities as proposed by McConnell (Fig. 2). Of these, case I is the most common. Normally, open shell molecules interact to give antiferromagnetic coupling and no spontaneous magnetism. Ferromagnetic interactions are often found when the interacting spins are found in orthogonal orbitals, either by design or accidentally: this is case II.
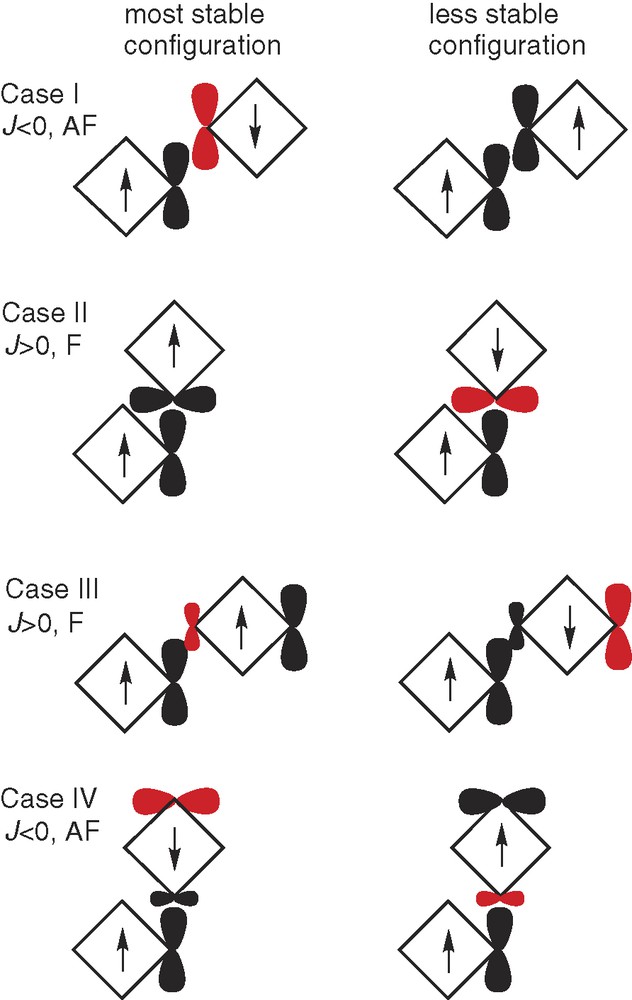
Schematic picture of magnetic couplings according to the McConnell spin density mechanism. Arrows indicate the total spin of each molecular subunit (symbolized by a square), dark ‘orbitals’ positive spin density, red ‘orbitals’ negative spin density, smaller ‘orbitals’ spin polarization. Adapted from Ref. [13].
Case III invokes spin polarization. Ferromagnetic coupling should be the result when: “atoms of positive spin density are exchange coupled most strongly to atoms of negative spin density in neighboring molecules” [8]. No such systems existed at the time of McConnell's prediction (1963), but this mechanism has since been confirmed experimentally several times [3].
Case IV is case II but with reversed signs on one of the interacting centers, thus also reversing the sign of the magnetic interaction giving antiferromagnetic coupling.
McConnell also suggested the charge transfer mechanism. An example leading to ferromagnetic coupling (depending on the orbitals involved the coupling can also be antiferromagnetic) is given in Fig. 3. This could be thought of as cases when the ground state of the system cannot be described by a single configuration (left part of Fig. 3) but is a mixture of this configuration and another one (right part of Fig. 3).
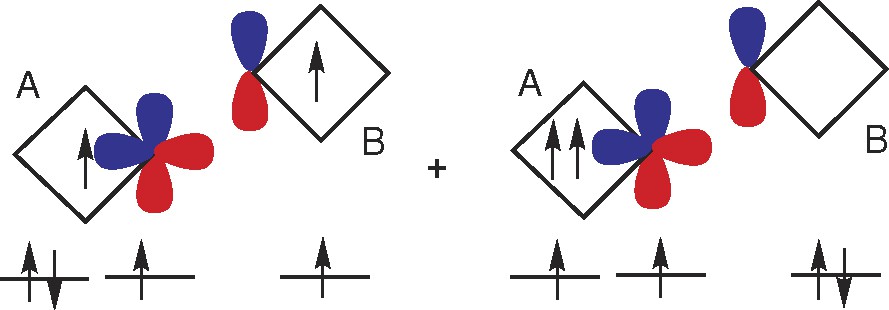
Schematic picture of a ferromagnetic coupling according to the McConnell's charge transfer mechanism (McConnell II). The ground state of the system (A + B) cannot be described by a single configuration (left) but is a mixture of this configuration and another one (right). In the right side configuration two electrons are placed in degenerate and orthogonal orbitals in A and must therefore have the same spin (Hund's rule). Note that antiferromagnetic coupling in the right side (not shown) would then lead to a violation of Hund's rule in the left configuration, thus the stabilization of the ferromagnetic state.
1.4 The scope and limitations of this article
The bottom line of this article is that scientific work in chemistry can be greatly enhanced if theory, in this case quantum chemistry, and experimental work are combined. I will present examples from my own work during the last 10 years. The emphasis is not on the theoretical methods, but on how the experimental work benefited (or, in some cases could have benefited) from the additional calculations. For, and I want to be frank about this, the calculations presented here could never, item by item, have stood on their own legs. They become scientifically meaningful only when presented together with the experimental data.
2 Direct coupling between delocalized or polarized spin densities
The radicals 1–3 in Fig. 4 (top) can all be used as ligands to paramagnetic metal ions, thus coupling the unpaired spin(s) on the metal with the unpaired spin on the organic molecule. Graphical representations of the spin populations from DFT calculations of these radicals are shown at the bottom of the picture [14,15].
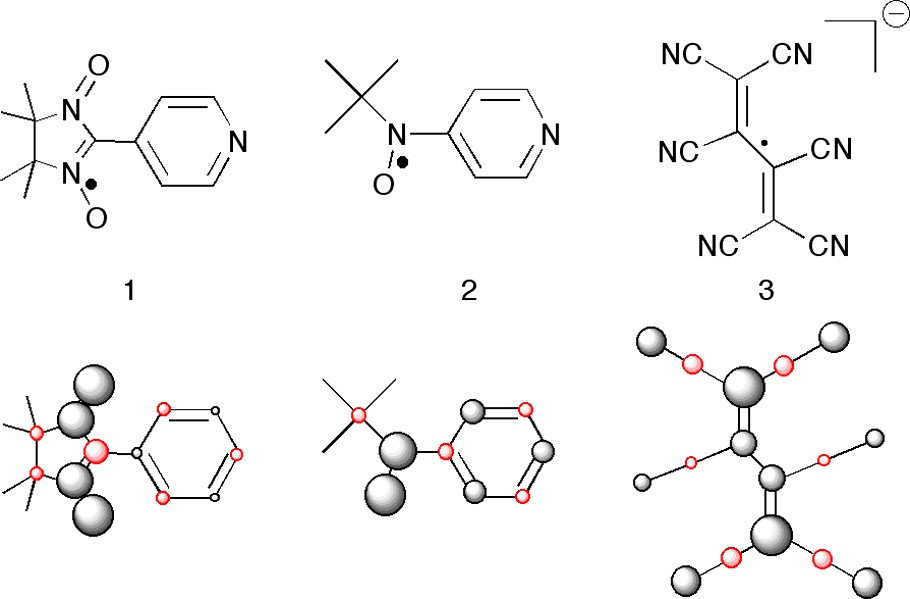
The radicals 1–3 and their calculated spin populations(+ black, – red) represented as spheres (the volumes of the spheres are proportional to the spin populations).
The two nitroxides, 1 and 2, have large positive spin densities on the NO units, where one metal can be attached (although the basicity of these sites are low). Here, the coupling can be ferromagnetic or antiferromagnetic, depending on the orientation of the half occupied metal orbitals. The interesting point is the pyridyl site. Here, the spin densities of the two compounds have different signs! Thus there is a coupling [↓↑]↓ or [↓↓]↑ provided that the interacting orbitals are not orthogonal [14].
This change in coupling is also what was found experimentally for the two similar compounds whose structures are shown in Fig. 5. The large difference in magnitude and sign of 1 and 2 coupled to Mn(II) in these complexes was noted by Iwamura et al. [16,17]. The structures of these two similar compounds are shown in Fig. 5. In the case of Mn(hexafluoroacetylacetonate)2(2)2 there is an antiferromagnetic coupling of (–)8.6 cm–1 and in Mn(hexafluoroacetylacetonate)2(1)2 the spin polarization reverses the sign so that we now have a ferromagnetic interaction of (+)0.5 cm–1. We also noted that the ratio of the absolute couplings, 17, corresponded well to the ratio of the two spin populations, 12.

The X-ray structures of Mn(hexafluoroacetylacetonate)2(1)2 (above) and Mn(hexafluoroacetylacetonate)2(2)2 (below) [16,17].
At the time of this experimental work DFT methods were not yet widespread, and it is therefore not surprising that these calculations appeared later. However, the third example illustrates well the theme of this article.
Coordination polymers with Mn(III) porphyrine complexes and the hexacyanobutadiene radical 3 had been shown to give ferromagnetic couplings through the terminal nitrogens, but with a new porphyrine derivative this effect was dramatically changed, and instead antiferromagnetic inter-chain interactions prevailed. Now, the question arose, could this be explained by the fact that in the latter compound the Mn(III)ions were connected via the internal nitrogens instead? Earlier EPR measurements were inconclusive or possibly in error as to the spin densities of this radical, but a DFT calculation on the hexacyanobutadiene radical 3 gave the spin populations shown in Fig. 4 (bottom right). As the spin densities on the coordinating middle nitrogens is only 18% of the terminal nitrogens a substantial reduction in coupling is expected, and it is reasonable that the antiferromagnetic inter-chain interactions dominate [15].
Compared to the experimental work of this article, i.e. synthesis, X-ray diffraction and magnetic susceptibility measurements, this calculation represented only a small part, both in terms of money and time. It had no merit on its own, but made a valuable contribution to the final scientific work. A related modus operandi was later reported for a vinylnitroxide radical [18].
When there is not clear-cut pathway, as in the examples above with bonding interactions giving short distances between spin carrying atoms, an analysis based only on the shortest intermolecular distance between spin-carrying atoms only may become less convincing [19]. However, as the exchange coupling J is proportional to r–n (n ≥ 6 for superexchange pathways) [20] changes in r have dramatic effects on the coupling. Supposing that J is also proportional to the product of the spin densities, a simple calculations with n = 6 tells us that if the shortest distance is 2.45 Å, and the alternative pathway is 2.70 Å (a 10% increase) the atom interacting at the longer distance has to have a 80% higher spin density to reach the same magnitude of interaction.
Cases like this are often encountered in organic crystals and we will look at two examples, the cyano-nitroxide radical 4 and the tetraphenyl-verdazyl radical 5 in Fig. 6.
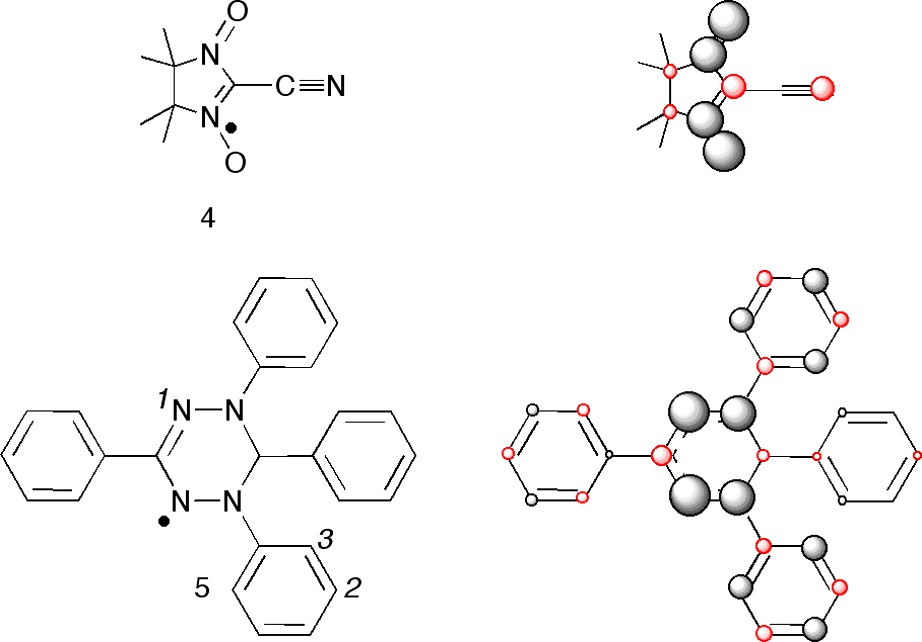
The radicals 4 and 5 and their calculated spin populations represented as spheres (the volumes of the spheres are proportional to the spin populations).
The nitronylnitroxide has the closest spin–spin interaction between the central carbon atom, having a substantial negative spin density, and the oxygen in a neighboring molecule (O–C = 2.953(2) Å). However, somewhat surprisingly, the spins are antiferromagnetically coupled with J = –10 cm–1. The explanation is that the molecules are oriented perpendicularly in such a way that the crystallographic symmetry makes the pz-orbitals (the xy-plane is the molecular plane) on the two atoms orthogonal in the quantum chemical sense (overlap = 0). In terms of Fig. 2, the cyano-nitroxide radical 4 is a highly unusual example of a case IV antiferromagnetic coupling [13].
For the tetraphenyl-verdazyl radical 5 whose calculated spin density is reported in Ref. [14] the situation is more complicated. The shortest spin–spin interaction, 3.52 Å is between the nitrogen(1) (spin pop. +0.42) and the meta-carbon(2)(spin pop. –0.011) on the N-phenyl group, and the next shortest between the same nitrogen and the ortho-carbon(3)(spin pop. +0.048), 3.60 Å [21]. As this distance difference is only just significant (possibly), judging from the X-ray data, and the ortho/meta spin density ration is 0.048/(–)0.011 = –4.4, the antiferromagnetic coupling in this compound can still be attributed to this N(1)–C(3) interaction. Thus, in this case we believe that the closest interaction involve too small spin densities to be decisive, and instead the second shortest interaction take over and determines the sign of the coupling.
These successful examples may give the impression that a spin density calculation will answer all questions about the magnetism of your compound. This may not be the case, as the following discussion of the meta-nitrophenyl-iminonitroxide, 6 (Fig. 7), and the [Cu(hfacac)4(N-meta-pyridyl-iminonitroxide)2], 7 (Figs. 8 and 9 next section) will show.
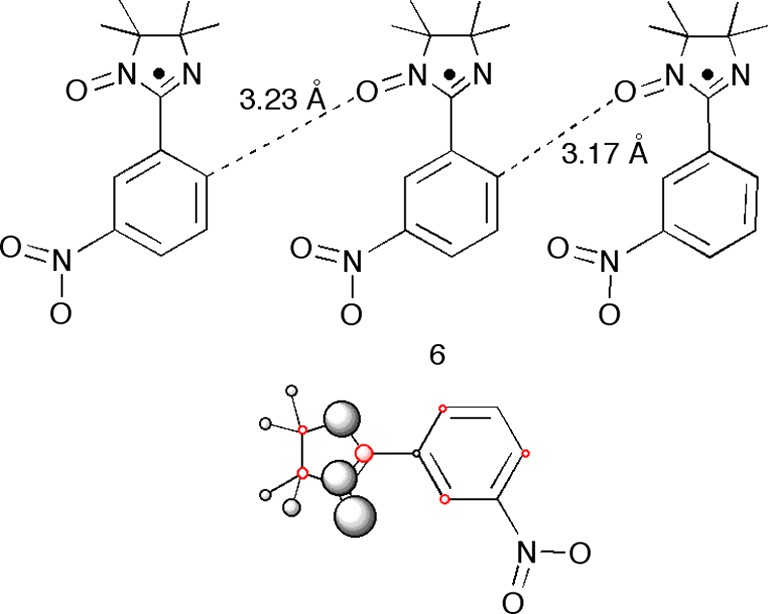
The radical 6 with its nearest neighbors and the closest intermolecular distances indicated. Below the corresponding calculated spin populations represented as spheres (the volumes of the spheres are proportional to the spin populations).
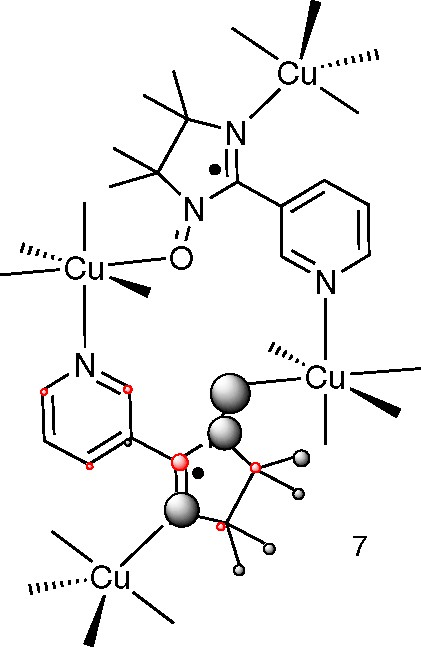
The complex α-[Cu4(hexafluoroacetylacetonate)8(N-meta-pyridyl-iminonitroxide)2] (α-[Cu4(hfac)8(IM-3Py)2]), 7, with the corresponding spin populations represented as spheres. The hexafluoroacetylacetonate ligands have been omitted and the spin density is shown for the bottom radical only and not for copper (the volumes of the spheres are proportional to the spin populations).
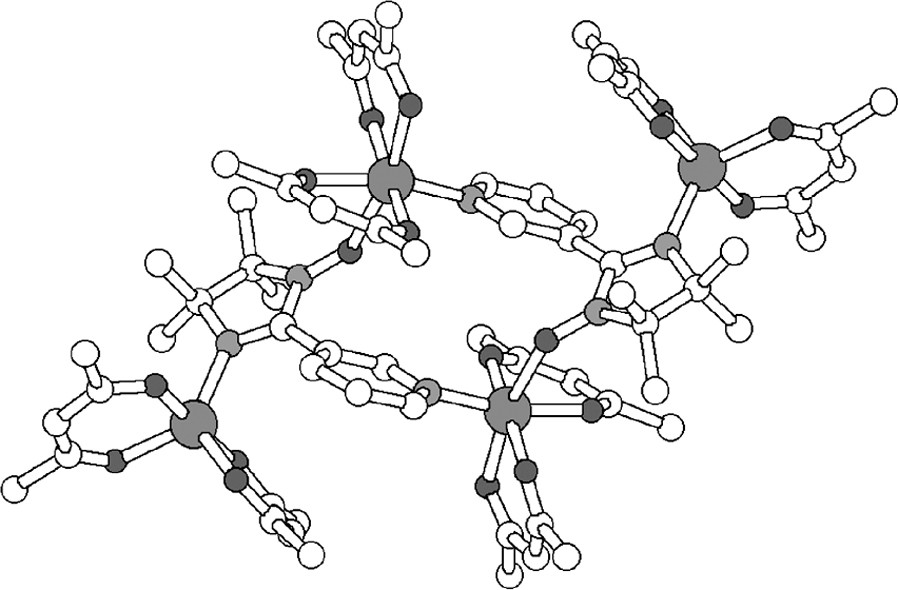
The X-ray structure of the tetranuclear complex 7, which has a has a S = 3 ground spin state [25].
The para-nitrophenylnitronylnitroxide radical, para-PNNO, is famous as the first organic magnet [22], and many different phases and derivatives are known. Many analogous materials have been prepared, and in different polymorphs. A key question was of course the spin density distribution in these compounds, and scientist spent a lot of time and effort in growing large enough crystals of ‘well-behaved’ compounds to be used in PND studies. One of these of was compound 6.
In the case of 6, PND showed a tiny, barely significant, spin density on the nitro group. However, the model calculations of a single molecule carried out on the two different conformations of 6 found in the solid-state gave the pattern presented in Fig. 7 with zero-spin density on the nitro group. As if this were not enough, the closest interaction is between the ‘radical’ oxygen and the ortho-carbons (two ortho-carbons and therefore two O···C distances: 3.32 and 3.17 Å) indicating ferromagnetic coupling (case II) when in reality a weak antiferromagnetism (θ = 1.2 K) was found [23]. Clearly, in this case the ‘brick-only’ model is not good enough.
Using various methods, Yamaguchi and co-workers have successfully made calculations on para-PNNO and related compounds using clusters of molecules [24], so it should be possible to make a good theoretical analysis also of 6, but this is beyond the scope of this article.
3 Electron-transfer mechanisms
Another difficult case was the tetranuclear Cu(II) complex 7 with the iminonitroxide ligand “IM-3Py” whose magnetic properties was explained by the ferromagnetic coupling scheme shown in Fig. 10. Here there are ferromagnetic interactions between the radical part and Cu(II) readily explained by orthogonal orbitals (more or less without any calculations at all). However, surprisingly, a third and likewise ferromagnetic interaction is also present between the octahedral Cu(II) and the unpaired radical electron on the ligand bonded via the pyridyl group.
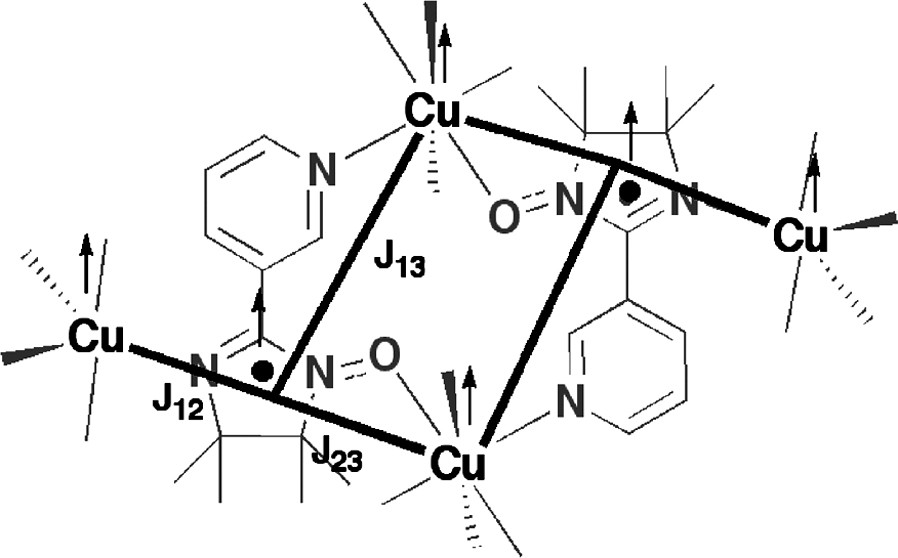
Spin coupling scheme of 7. Numerical diagonalization of the isotropic spin Hamiltonian (H = –2 JijSiSj) gave the following best fit values that were attributed to the three coupling constants as follows: J12 = 213(12), J13 = 93(4), and J23 = 5.5(9) cm–1.
A first theory was that the bonding of three Cu(II) ions to the iminonitroxide radicals would induce a large spin density on the pyridyl nitrogen. This was not found, as is evident from Fig. 8. Instead the calculations indicated a very significant stabilization of the empty β-spin π* orbital. While in no way conclusive, this led us to a tentative explanation involving charge transfer from Cu(II) to the iminonitroxides, that is from orbital G to orbital F in Fig. 11 (McConnell's second mechanism, see introduction and Fig. 3) to give a small but significant contribution of a Cu(III)-species. This would then leave us with the two unpaired electrons now residing on an octahedral copper(III) ion with a d8 electron configuration. Although square planar d8 metals are without exception diamagnetic, a corresponding octahedral species would be expected to be high-spin (two electrons in the eg orbitals) and thus these two spins should be very strongly ferromagnetically coupled (several thousands of reciprocal centimeters) [25].
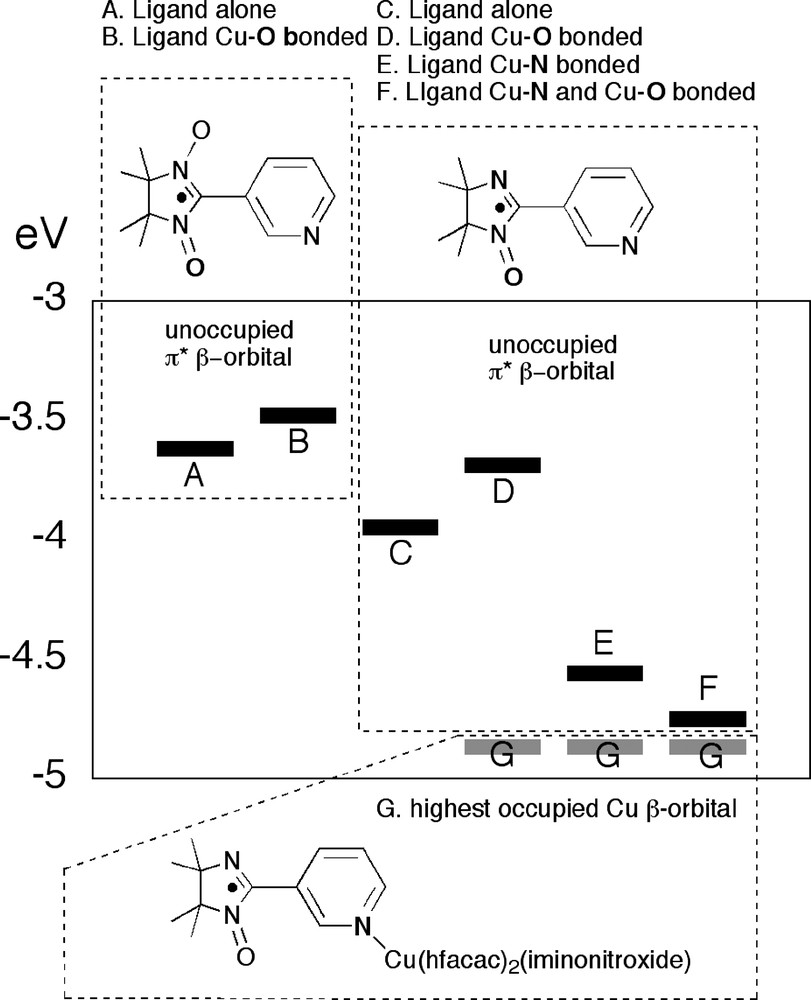
Calculated unrestricted orbital energies for selected model compounds (for 7, F and G additional unpublished material). Only the β-spin orbitals are shown (‘spin down’). Upon coordination the level of the nitronyl-nitroxide π*-orbtial (containing an electron with α-spin, but the β-level is unoccupied) is raised somewhat (A–B). The same effect is mirrored by the iminonitroxide when this radical is coordinated using the oxygen (from C to D). However, when the iminonitroxide is coordinated via the nitrogen atom instead, a substantial stabilization of the π*-orbital is evident (C–E). This is even more pronounced when a Cu(II) ion is also bound to the oxygen atom (F). The reference level G is the highest occupied d-orbital of the Cu(II) ion bound to the pyridyl nitrogen.
While this was a tentative explanation only, the π*-orbital stabilization was the only significant difference when we compared calculations on models for the corresponding nitronylnitroxide complex [Cu4(hfac)8(NIT-3Py)2] having no similar interactions (six independent spins at high temperature) and [Cu4(hfac)8(IM-3Py)2] [25].
A somewhat similar case to 7 was encountered in the verdazyl-hydroquinone molecular crystals 8, where π-stacks of radicals 8a, are hydrogen bonded to hydroquinones (Fig. 12). The radicals are packed head-to-tail, the closest intermolecular distance between the principal spin carrying nitrogen atoms being 4.5 Å, and yet the magnetic coupling (fitting of the susceptibility data to a regular 1D chain model) is strongly antiferromagnetic with J = –58 cm–1 [26].
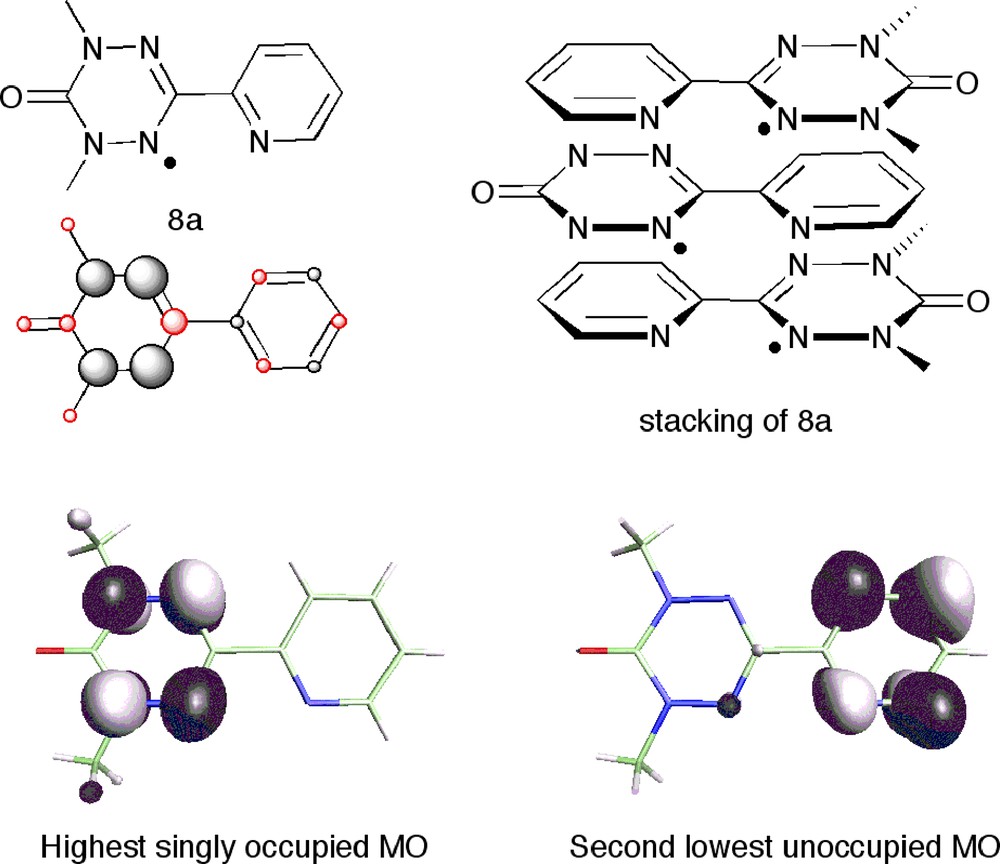
Top: The radical 8a, its spin populations and its stacking in the molecular crystals 8a + hydroquinone. Bottom: MO analysis of the DFT results reveals a low-lying (2:nd LUMO) empty orbital (right) with the same symmetry on the pyridyl ring as the SOMO on the verdazyl ring (left). The head-to-tail stacking (top, right) makes it possible for these two orbitals to interact.
As can be seen in Fig. 12 the calculated spin density of the 8a molecule cannot explain this, and a small ferromagnetic coupling (case II) would have fitted better with this picture. However, further inspection of the orbitals of 8a reveals a low-lying (2:nd LUMO) empty orbital with the same symmetry on the pyridyl ring as the SOMO on the verdazyl ring (Fig. 6, bottom) [26].
With the flat, more or less ideal, head-to-tail stacking of the 8a molecules, these two orbitals match well and, again, a tentative explanation was put forward, based on the transfer of the unpaired electron to the 2nd LUMO of a neighboring molecule. This configuration would give a biradical resembling the 1,1′-tetramethyl-6,6′-dioxo-3,3′-biverdazyl. This latter biradical has an large internal antiferromagnetic coupling of J = –887 cm–1 [27].
The pyridyl rings part in mediating the magnetic coupling was further supported by direct calculations of the high-spin – low-spin energy difference by the broken-symmetry (BS) formalism. For a three-radical model, this calculation gave J = –121 cm–1, an overestimation compared to the real value by 63 cm–1 [26]. Cutting away the middle pyridyl group (replacing with H) gives J = –58 cm–1, and assuming a constant systematic error, this reduces to J = +5 cm–1. To sum up, without the middle pyridyl group the strong antiferromagnetic coupling disappears! [28]
4 Spin density, ESR and unknown geometries
All calculations presented in the preceding parts have been performed using known X-ray geometries, thus even large systems, as the models used for 7 (that once required a CRAY supercomputer), are now achievable on a PC or Mac, and there are relatively few complications for such a calculation (if no transition metals are involved). When the geometry of the compound is unknown, this does not only require much more computer time (or power) but also more skills from the user.
While finding the structures for small molecules through X-ray diffraction is now more or less routine, this problem is of special significance in radical chemistry where we frequently encounter more or less instable species (although for molecular magnetic materials the aim is of course stable radicals!) and the growing of good crystals may consequently be difficult. Then calculation of the geometry using DFT may be a good (or the only) alternative.
This was the case for the phosphaverdazyls 9 and 10 shown in Fig. 13 and prepared by Hicks et al. The structures were unknown, but the ESR spectra gave valuable clues as to their actual geometries in solution. In 9 there is a significant hyperfine coupling of the unpaired electron to the nuclear spin of P [29] whereas in 10 there is no such coupling to phosphorus, but instead an interaction with the amine nitrogen via the N nuclear spin (well reproduced by a simulation of the spectrum) [30]. The question was; exactly what does this mean?
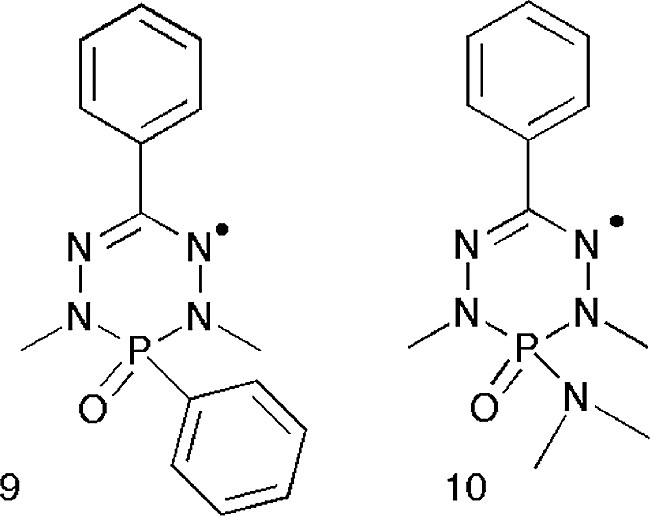
The phosphaverdazyl radicals 9 and 10.
For both 9 and 10 three different stable geometries were found (by ‘stable’ we mean that the geometry optimization has converged to a minimum in energy, and that no imaginary frequencies were found in the subsequent vibrational analysis). For 9, these were all very close in energy (relative energies 0, +1.2 and +3.2 kcal) with a minimum for a planar phosphaverdazyl-ring, and they all have significant spin populations on phosphorus, although somewhat higher for the bent conformers.
The stable conformers found for 10 are displayed in Fig. 14 together with the calculated positive spin density. The first conformer (lowest in energy) is the obvious choice also from experimental data, this geometry has maximal spin density on N and minimal on P agreeing with the coupling to N and no coupling to P [30].
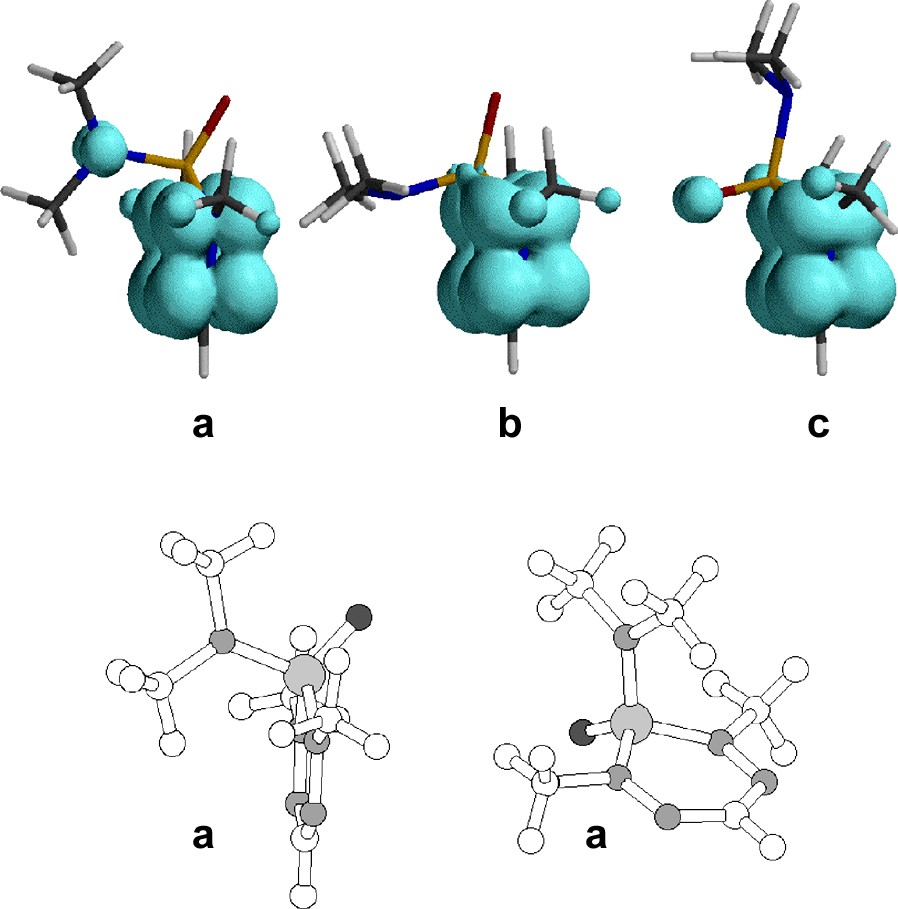
Top: Stable conformers a–c found for phosphaverdazyl 10 and the calculated positive spin density (boundary 0.002). Relative energies are: 0, +2.4 and +19.4 kcal mol–1. Adapted from [30]. Bottom: Two views of conformer a.
It should be stressed that the agreement is qualitative only. We made no attempts to actually calculate these isotropic hyperfine coupling constants since this requires not only a very good description of the valence shell, but also of the core electrons, and possibly averaging over vibrations and conformers (thus a good agreement with bonding and geometries is not a sufficient criterion to say that calculated hyperfine coupling constants should be close to experimental ones) and it seems that even higher levels of theory are needed to reproduce the experimental values correctly [31–33].
5 Comparisons of DFT spin populations with PND
For the bench chemist, theoretical results are useful if they can tell anything new about the compound of interest, or make you think about them in a different way. The mere reproduction of experimental data are not valuable as such, but of course offer a quality validation of the methods used. However, one must keep in mind that, for example, a good agreement with the calculated geometry does not necessary imply that other properties are equally well described and vice-versa.
For the cases discussed here, the spin density is critical. For the iminonitroxide 6 PND was used to determine the experimental spin density [23]. Experiment and DFT are compared in detail in this reference, and in general the agreement is good. However, a small spin population on the nitro groups found by PND was not reproduced by the DFT calculations. From several related studies the conclusion can be drawn that spin polarization is in general underestimated in organic radicals by DFT calculations [34–36]. In contrast, for the tetraphenyl-verdazyl 5 the calculated spin populations agree well with data extracted from NMR measurements [14]. Quantum chemical calculations versus PND for organic radicals have also recently been reviewed by Ressouche and Schweizer [37].
Metal complexes on the other hand, are a different problem. For example, controversy surrounded the mechanism of magnetic interactions in Cu-azide-end-on dimers for a long time, and a PND study of [Cu2(t-Bupy)4(N3)2](ClO4)2 was published in 1998 [38]. This did not completely resolve the question of the coupling mode between the two Cu ions, but gave a detailed spin density map that could be compared to a corresponding DFT map, see Fig. 15.
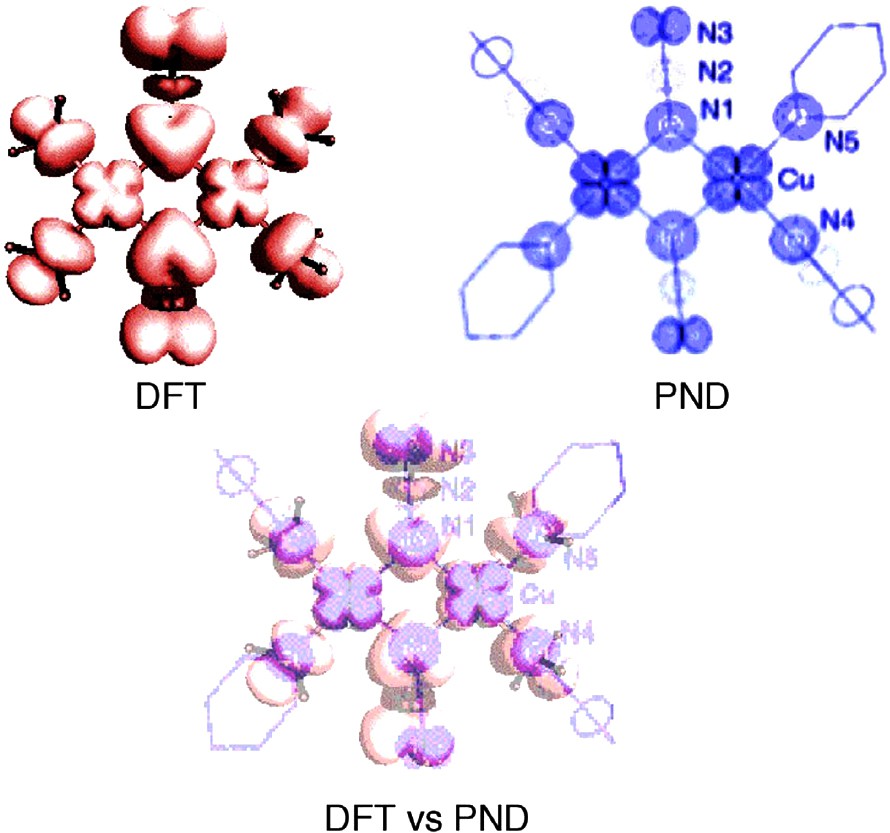
Calculated (DFT red) spin density map in [Cu2(NH3)4(N3)2]2+ and experimental (PND blue) spin density map for [Cu2(t-Bupy)4(N3)2](ClO4)2. Note that the spin density on the azide central nitrogen is negative for both theory and experiment. Below the two pictures are shown superimposed, the deviation of coordinates originates from the slightly different views. Adapted from [38].
Given that the quantum chemical model is somewhat simplified, in that the t-Bupy ligands have been changed for ammonia, DFT reproduces most features of the PND measurements. However, when spin populations are compared there is a large difference on copper. DFT only gives 0.425 (no substantial change with pyridine ligands) while the PND estimate is 0.783(7). The conclusion from this, and from related studies, [39,40] was that DFT overestimates the amount of metal-to-ligand delocalization.
More detailed DFT studies take this argument further and discuss both large basis set effects [41] and the overestimated delocalization [42] and the hybrid DFT functional B3LYP has been advocated as best solution [43]. In the case of [Cu2(NH3)4(N3)2]2+ the B3LYP functional increases the spin population on copper to 0.554 [41] although for a Ti(IV) complex with Schiff-base diquinone radicals the B3LYP functional and the WVN-Stoll functional gave identical populations on Ti [44].
6 Conclusions
Small molecule fixed geometry DFT calculations on ‘bricks’ used in molecular-based magnetic materials can often help in the analysis of spin interactions in these materials. They can give direct indications of the McConnell I type of exchange interaction or they can give hints about possible pathways for the McConnell II electron transfer mechanism.
Moreover, if one relies on the McConnell I mechanism, possible new radicals can be screened for their spin density before preparation and a more educated choice of synthetic targets can be made.
So, yes I would answer the question in the title affirmatively. However, care should be taken not to over-interpret the results and one should be aware of the limitations of the method. Also, the magnetic properties of a compound can sometimes be the result of many complex interactions, and reducing this to one factor only may be misleading. As a word of warning I like to quote American author and critic H.L. Mencken (1880–1956): “For every complex problem, there is a solution that is simple, neat, and wrong.”
Acknowledgements
Thanks to my mentors and collaborators in these projects: André Grand, Béatrice Gillon, Robin Hicks, Dominique Luneau, Joel Miller, Paul Rey, Jacques Schweizer and the late Olivier Kahn. Financial support from the Swedish Research Council is gratefully acknowledged.


