The experimental charge density in transition metal compounds

Riccardo Bianchi; Giuliana Gervasio; Domenica Marabello

doi:10.1016/j.crci.2004.12.015

Account / Revue

The experimental charge density in transition metal compounds

Riccardo Bianchi ¹ ; Giuliana Gervasio ² ; Domenica Marabello ²

¹ CNR-Istituto di Scienze e Tecnologie Molecolari, via Golgi 19, 20133 Milan, Italy
² Dipartimento di Chimica I.F.M., Via P. Giuria 7, 10125 Turin, Italy

Comptes Rendus. Chimie, Volume 8 (2005) no. 9-10, pp. 1392-1399.

Résumés

Anglais
Français

Today, the experimental charge density of transition metal compounds can be determined with a good degree of reliability and analyzed with the quantum theory of atoms in molecules in order to better characterize the atomic interaction. Here, we present a short summary of the main topological results obtained with this technique on Mn₂(CO)₁₀, Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂), KMnO₄ and KClO₄ compounds. .

De nos jours, la densité de charge des composés de métaux de transition peut être déterminée expérimentalement, avec un bon degré de fiabilité, et analysée à l'aide de la théorie quantique des atomes dans la molécule, afin de mieux caractériser l'interaction atomique. Nous présentons ici un court résumé des principaux résultats topologiques obtenus avec cette technique sur les composés Mn₂(CO)₁₀, Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂), KMnO₄ et KClO₄. .

Métadonnées

Reçu le : 2004-03-31
Accepté le : 2004-12-16
Publié le : 2005-05-25

DOI : 10.1016/j.crci.2004.12.015

Keywords: Charge density, Transition metal, Multipole analysis, Topology, QTAIM
Mots clés : Densité de charge, Métaux de transition, Analyse multipole, Topologie, QTAIM

Affiliations des auteurs :

Riccardo Bianchi ¹ ; Giuliana Gervasio ² ; Domenica Marabello ²

¹ CNR-Istituto di Scienze e Tecnologie Molecolari, via Golgi 19, 20133 Milan, Italy
² Dipartimento di Chimica I.F.M., Via P. Giuria 7, 10125 Turin, Italy

@article{CRCHIM_2005__8_9-10_1392_0,
     author = {Riccardo Bianchi and Giuliana Gervasio and Domenica Marabello},
     title = {The experimental charge density in transition metal compounds},
     journal = {Comptes Rendus. Chimie},
     pages = {1392--1399},
     publisher = {Elsevier},
     volume = {8},
     number = {9-10},
     year = {2005},
     doi = {10.1016/j.crci.2004.12.015},
     language = {en},
}

TY  - JOUR
AU  - Riccardo Bianchi
AU  - Giuliana Gervasio
AU  - Domenica Marabello
TI  - The experimental charge density in transition metal compounds
JO  - Comptes Rendus. Chimie
PY  - 2005
SP  - 1392
EP  - 1399
VL  - 8
IS  - 9-10
PB  - Elsevier
DO  - 10.1016/j.crci.2004.12.015
LA  - en
ID  - CRCHIM_2005__8_9-10_1392_0
ER  -

%0 Journal Article
%A Riccardo Bianchi
%A Giuliana Gervasio
%A Domenica Marabello
%T The experimental charge density in transition metal compounds
%J Comptes Rendus. Chimie
%D 2005
%P 1392-1399
%V 8
%N 9-10
%I Elsevier
%R 10.1016/j.crci.2004.12.015
%G en
%F CRCHIM_2005__8_9-10_1392_0

Riccardo Bianchi; Giuliana Gervasio; Domenica Marabello. The experimental charge density in transition metal compounds. Comptes Rendus. Chimie, Volume 8 (2005) no. 9-10, pp. 1392-1399. doi : 10.1016/j.crci.2004.12.015. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2004.12.015/

Version originale du texte intégral

1 Introduction

The charge density in transition metal compounds is of great interest owing to the importance of these systems in catalysis, in solid-state chemistry, and in a large number of key biological processes. Today, the charge density of such compounds can be determined with a good degree of accuracy both theoretically and experimentally from single crystal X-ray diffraction. Recently [1], an exhaustive review has been published on charge density analysis.

However, the calculation of theoretical charge densities on systems with a large number of electrons shows often problems that are mainly connected to the large number of two-electron integrals and relativistic effects.

On the experimental side, the technical improvement of diffractometers and of new devices for data collection at low temperature, and the development of powerful programs based on the use of the aspherical atoms formalism, allow to obtain experimental charge densities with a good degree of reliability. Furthermore, the quantum theory of atoms in molecules (QTAIM) [2] applied to experimental and theoretical charge densities permits a quantitative characterization of the chemical bond for many transition metal compounds appeared in the literature.

2 Determination and topological analysis of the experimental charge density

In the X-ray analysis of crystal structure, the independent atom model (IAM), where the atom is considered isolated with spherical symmetry, is a rule used. The superposition of spherical free-atom densities, each centered at atomic positions, is called the pro-density. The pro-density describes the major part of the charge density of a molecule (or crystal) and only a relatively small part of the electron density of an atom, located in the valence shell, is involved in chemical interactions. When atoms form chemical bonds, the valence shell expands or contracts with variation of atomic charge and valence density is aspherically deformed. In this case, the spherical core and the valence deformation density of each pseudo (or aspherical) atom p is expressed by a sum of terms defined by C_plm R_p(r) Y_lm(θ, φ) (multipole expansion), where C_nlm is a population parameter, R_p(r) is a radial function of Slater type or a fixed linear combination of exponentials and Y_lm(θ, φ) is a surface spherical harmonic [3,4].

The VALRAY [5] and XD [6] are two programs that apply flexible, nucleus centered, pseudo-atom multipole expansions of charge densities in crystals, as described above. The C_nlm population parameters are adjustable parameters that can be refined by the least-squares method on the basis of observed structure amplitudes. Thus at the end of refinement, the multipole charge density can be analyzed using topological methods. The last versions of the VALRAY and XD program packages include also the calculation of an extensive set of electrostatic properties from X-ray data: electrostatic potentials, electric fields, charge densities and electric field gradients etc. Moreover, they include a procedure for a complete topological analysis of the experimental charge density [7]. In this work all the multipole refinements on F² were performed using the atom-centered multipole model by Stewart [3].

The topology of the charge density, ρ(r), and its Laplacian, ∇²ρ(r), is related to chemical concepts by the QTAIM. [2] The definition of the chemical bond is based on the existence of a bond critical point (BCP) along a line of maximum density (bond path), linking the nuclei of neighboring atoms. At the BCP, the gradient of density vanishes and the sign of the Laplacian is determined by the relationship, ∇²ρ_BCP = λ₁ + λ₂ + λ₃ (λ₁ < 0, λ₂ < 0 and λ₃ > 0 are the three non-zero eigenvalues of the Hessian matrix). The values of λ₁ and λ₂ measure the degree of the ρ(r) contraction towards the BCP, while λ₃ gives the ρ(r) contraction towards each of the bonded nuclei. Extremes in ρ(r) and in ∇²ρ(r) are labeled by giving the pair of values (ω, σ): ω denotes the rank that is equal to the number of non-zero eigenvalues and σ denotes the number of positive eigenvalues minus the number of the negative ones. On the basis of the Laplacian sign, the bonding interactions have been divided into two great categories [2]: when ∇²ρ_BCP < 0 the interaction is denoted as ‘shared’ while when ∇²ρ_BCP > 0 the interactions are ‘closed shell’¹. In the first category fall the typical covalent and polar-covalent bonds, in the second the ionic and the van der Waals bonds.

An additional straightforward criterion for the characterization of chemical bond is provided by the local charge energy density, H_BCP = G_BCP + V_BCP , where G_BCP and V_BCP indicate, respectively, the values of the kinetic and potential energy density at the BCP, and they can be estimated from the experimental ρ(r) using the approximate functionals proposed by Kirzhnits [8], Abramov [9] and Espinosa et al. [10]. A negative H_BCP value is indicative of a prevalent potential energy density on kinetic energy density and thus of a covalent character of the interaction. On the contrary, a positive H_BCP value reveals a prevalence of the kinetic energy density, typical behavior of the ionic and van der Waals interactions [11,12].

Recently, Espinosa et al. [13] proposed a classification of the atomic interactions dividing them into three characteristic regions: pure closed shell (region I, ∇²ρ_BCP > 0, H_BCP > 0), transit closed shell (region II, ∇²ρ_BCP > 0, H_BCP < 0) and pure shared shell (region III, ∇²ρ_BCP < 0, H_BCP < 0). The boundaries among regions I, II, and III are defined by H_BCP = 0 (i.e. ∣V_BCP∣/G_BCP = 1) and by ∇²ρ_BCP = 0 (i.e. ∣V_BCP∣/G_BCP = 2). Inside the region I the bond degree parameter (BD = H_BCP/ρ_BCP) is an index of non-covalent interaction and it is indicated as softening degree (SD) per charge density unit at BCP; the weaker the interaction, the greater the SD magnitude. In the regions II and III the BD parameter measures the covalence degree (CD) of any pair-wise interaction; the stronger the interaction, the greater the CD magnitude. For example, a typical covalent bond lies inside the region III (pure shared shell), while an ionic bond in the region I (pure closed shell).

Further information on the bond properties can be obtained from the number and properties of the local ∇²ρ(r) maxima and minima in the valence shell charge concentration (VSCC) of the bonded atoms: these features depend on the chemical environment of each atom.

3 Charge-density studies of transition-metal compounds

The work of our group in this field began in the late 1990s with a paper on the experimental charge density of an organic mesoionic compound (4-cyanoimidazolium-5-olate) [14], joining different experiences in the crystallographic field [15–22]. For the 4-cyanoimidazolium-5-olate a comparison was made of the electrostatic potential between experiment and theory for the isolated molecule. A good agreement between experiment and theory was obtained for the atomic charges and molecular dipole moment (μ_exp = 2.3(3) e Å, μ_HF/6–31G** = 2.40 e Å). Fig. 1a, b show the Laplacian and the electrostatic potential maps, respectively, in the molecular plane.

Fig. 1
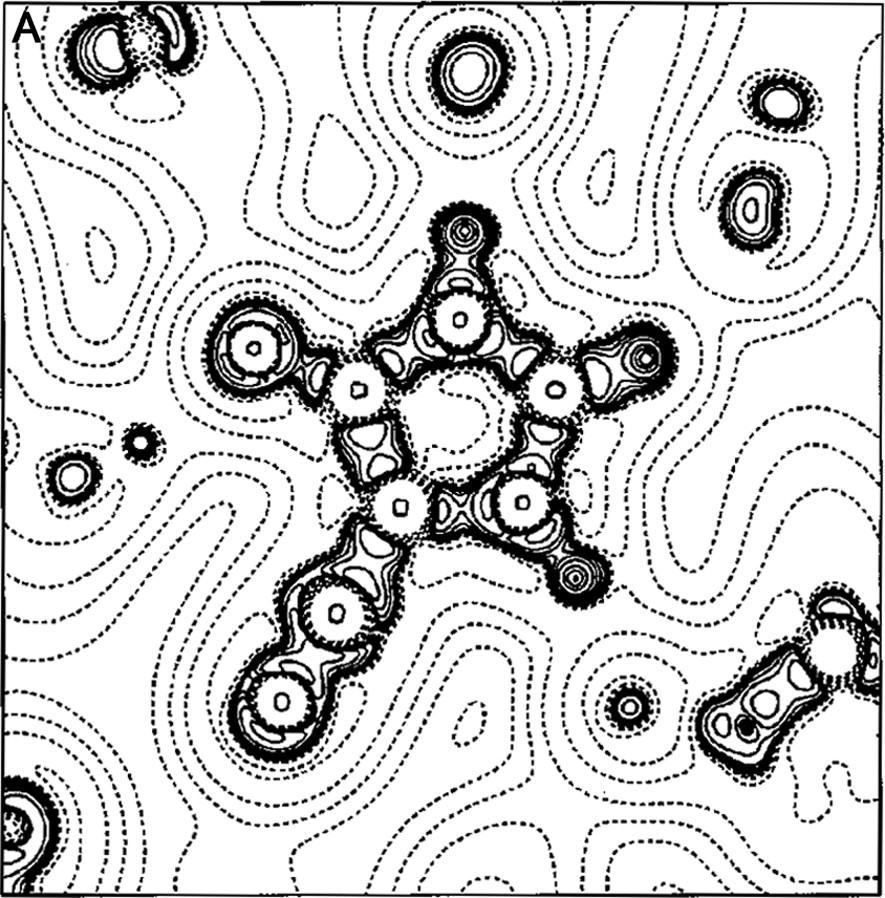
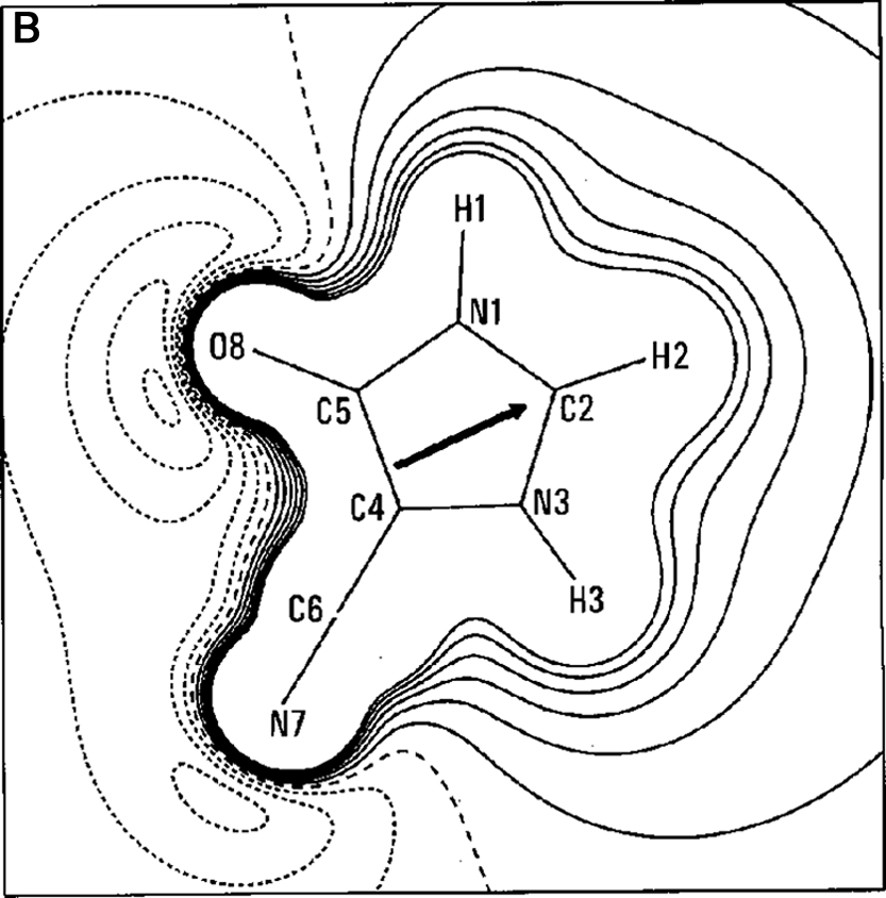
(A) Laplacian of the charge density in the plane of 4-cyanoimidazolium-5-olate molecule. The absolute values of contours (in a. u.) increase from the outermost one inwards in steps of 2 × 10ⁿ, 4 × 10ⁿ and 8 × 10ⁿ, with n beginning at –3 and in steps of 1. Positive values of ∇²ρ are denoted by dashed lines, negative values by solid lines. (B) Multipole electrostatic potential map for molecule. The contours are at intervals of 0.05 e Å^–1; solid lines positive, short dashed lines negative, large dashed line zero contour. The arrow originates at the molecular center of mass and indicates the direction of the molecular dipole moment.

The results obtained for the mesoionic compound stimulated us to direct our research towards the study of the charge density in organometallic compounds. The complex Mn₂(CO)₁₀ was the first system studied [23,24]. The three bonding structures, proposed at that time, are shown in Scheme 1.

Scheme 1
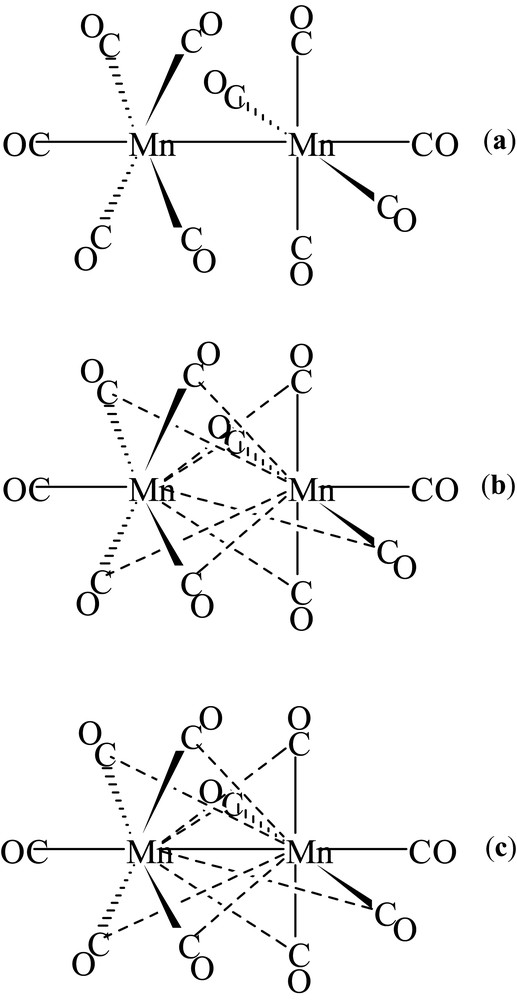
Bonding structures proposed for Mn₂(CO)₁₀.

Other researchers analyzed the charge density and chemical bonding of this compound from the theoretical and experimental point of view [25]. No clear probe, however, of the existence of a direct Mn–Mn bond was achieved and also crossed bonds between Mn and the CO molecules linked to the other manganese atom have not been excluded (Scheme 1b, c). We collected accurate X-ray data at low temperature (120 K) from a single Mn₂(CO)₁₀ crystal, carried out the multipole refinement with VALRAY program and interpreted the experimental ρ(r) with the QTAIM. The topological analysis showed the presence of a bond between the two manganese atoms and none of the hypothesized crossed bonds were found, confirming the bonding Scheme 1a.

The charge density (with bond paths and BCP superimposed) and Laplacian maps, nearly in the plane containing the two Mn atoms, one axial and two equatorial COs, are shown in Fig. 2.

Fig. 2
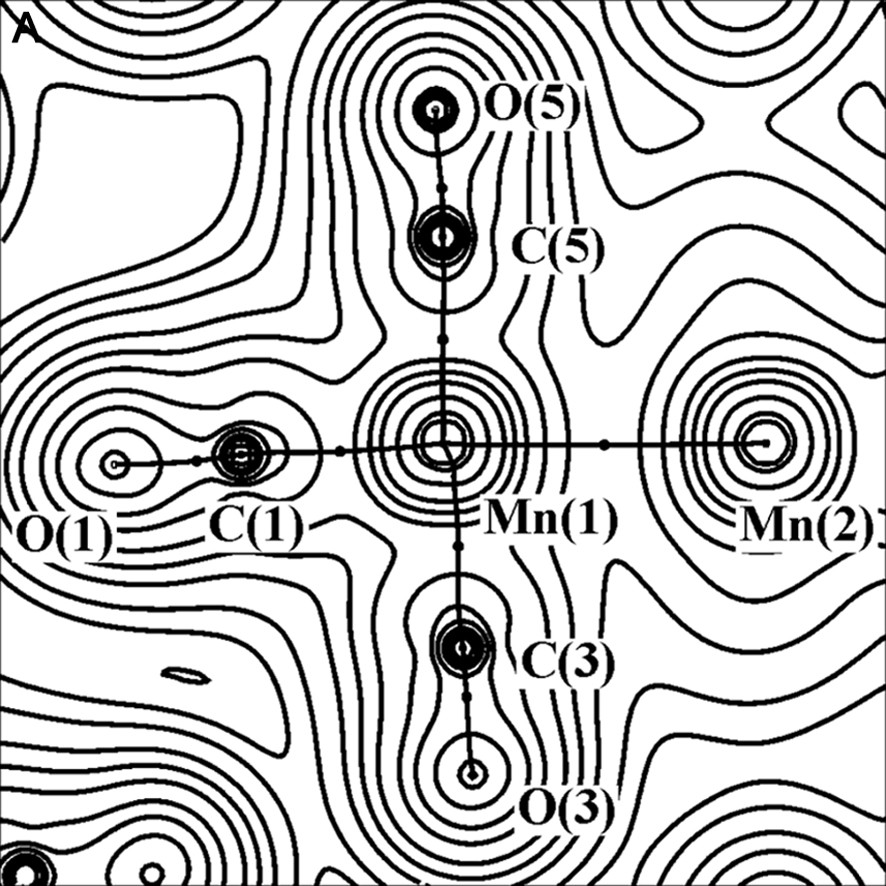
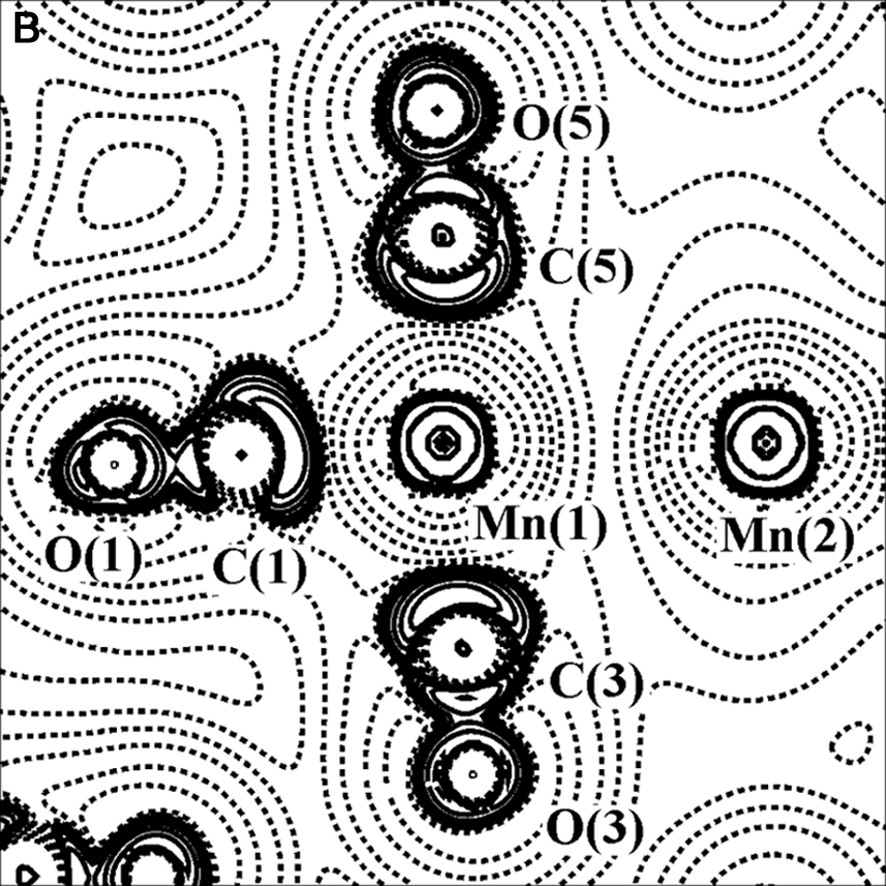
Experimental charge density (A) and its Laplacian (B) of Mn₂(CO)₁₀ molecule, in the plane defined by Mn(1), Mn(1A) and C(3) atoms. The contours are as in Fig. 1a.

As it is shown in Fig. 2b, the C–O bonds have large negative ∇²ρ_BCP (–40 e Å^–5 av.), while the Mn–Mn and Mn–C bonds have positive ∇²ρ_BCP (0.815 and 14.0 e Å^–5 av., respectively). Therefore, the C–O bonds are classified as ‘shared’ interactions, while the metal–metal and metal–ligand bonds belong to the ‘closed-shell’ type and exhibit different topological features with respect to the typical covalent bonds. The low negative H_BCP values of Mn–Mn (–0.031 hartree Å^–3) and Mn–C (–0.28 hartree Å^–3 av.) bonds is also indicative of their little covalent character. A preliminary scheme was proposed for classification of the bonds present in organometallic complexes, utilizing the few data at disposal at that time [26–28] (see Fig. 3).

Fig. 3
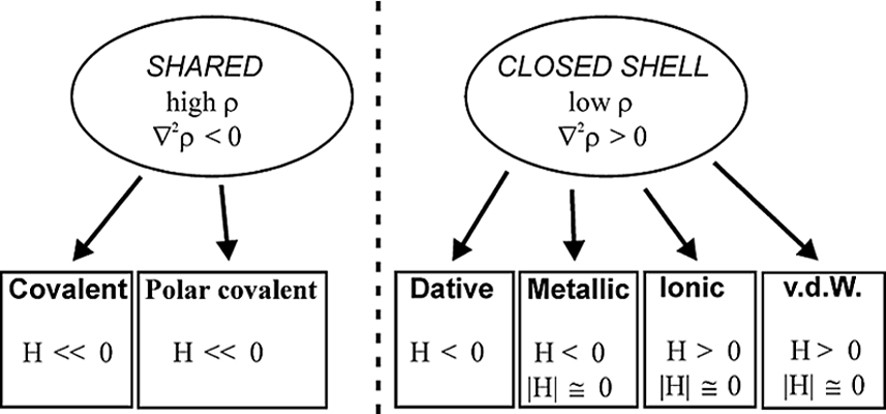
Classification of bonds on the basis of topological parameters ρ_BCP, ∇²ρ_BCP and H_BCP.

On the basis of the topological and energetic parameters, this scheme places the metal–metal bonds between ionic and covalent bonds, attributing to them a peculiar ‘metallic’ feature. The Mn–C bonds can be better described analyzing the Laplacian maxima and minima of the Mn and C atoms: a ∇²ρ_BCP maximum was found on each C-atom pointing toward an hole in the Mn atom, showing the ‘dative’ nature of this bond type [24,29].

The existence of the metal–metal bond in complexes with bridging ligands is another debated problem. For example, three bonding schemes have been proposed for Co₂(CO)₈ with a straight or curved Co–Co bond or with the lacking of a direct Co–Co bond [30]. For this reason we have taken into account a similar dicobalt carbonyl complex containing one bridging CO and one bridging γ-lactonic ring, of formula Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) [28,31–33] (see Fig. 4a).

Fig. 4
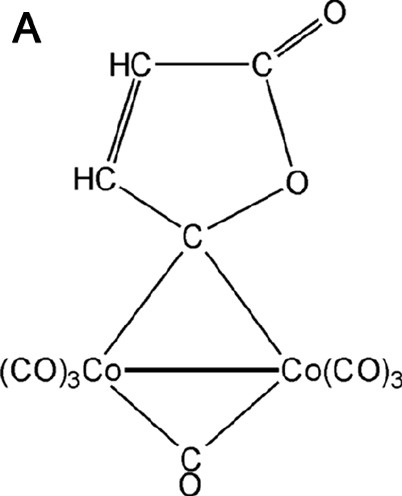
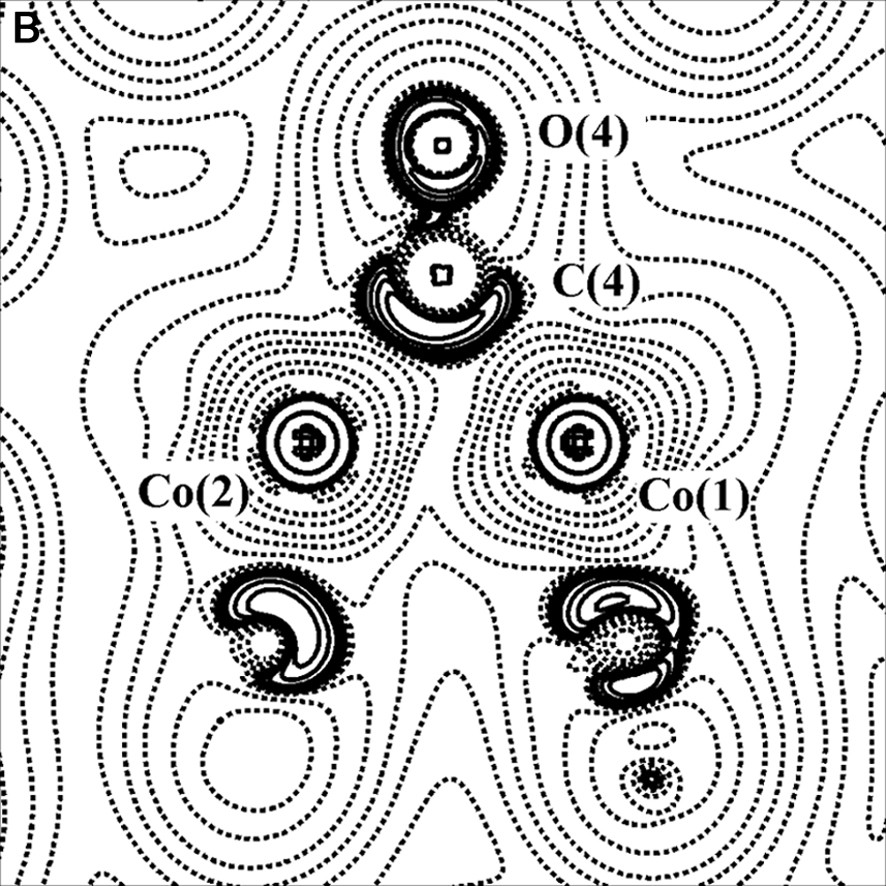
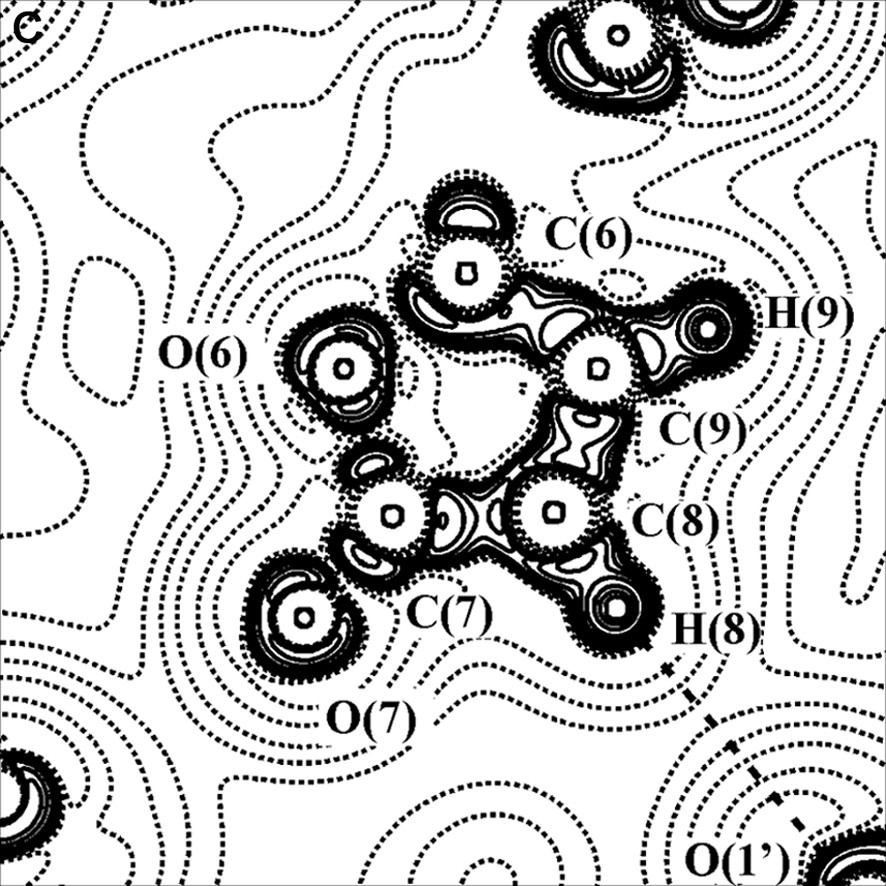
(A) Scheme of the Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) molecule. (B) Laplacian of the experimental charge density in the Co₂(μ-CO) plane and (C) in the γ-lactonic plane (an H···O interaction is evidenced for the triclinic phase). The contours are as in Fig. 1a.

Two polymorphs, one orthorhombic and the other triclinic, of this compound have been topologically analyzed, starting from the multipole-refined charge density. In both cases a direct Co–Co bond path have been found. On the contrary, other authors [34,35] have not found a direct metal–metal bond in their charge density studies of transition metal clusters with supported metal–metal interactions. Furthermore, theoretical calculations on Co₂(CO)₈ and Co₄(CO)₁₂ [36] agree with our experimental results.

For the two crystal phases of the Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) complex, the topological properties of metal–metal, metal–ligand and C–O bonds have been found similar to those obtained in previous studies, thus supporting the bond classification of organometallic compounds above illustrated. The topological data derived for the Co–Co bond are collected in Table 1; it shows that ρ_BCP is inversely proportional to the Co–Co bond distance. Furthermore, it was evidenced a flat charge density distribution around the BCP of the metal–metal bond (see Figs. 2b and 4b) and a small prevalence of potential energy density (V_BCP) over the kinetic energy density (G_BCP) (H_BCP < 0, but near to 0).

Compound	Co–Co (Å)	ρ_BCP (e Å^–3)	References
Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) orthorhombic	2.4222(3)	0.76(6)	[32]
Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) triclinic	2.4402(2)	0.46(2)	[33]
Co₄(CO)₁₁As(Ph)₃	2.528(8)	0.252(3)	[34]
Co₂(CO)₆(AsPh₃)₂	2.6430(2)	0.204(11)	[26]

The study of the two polymorphs of Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) has allowed to detect, even in presence of heavy atoms, the weak intermolecular interactions (O···O, H···O) responsible for the two crystal packings (see for example Fig. 4c); in the orthorhombic form, the hydrogen bonds involving the lactone ligand are the driving forces for the crystal packing, while in the triclinic form the O···O van der Waals interactions are predominant.

The compounds so far examined have the metal atoms in a formal zero oxidation state. It is known that the behavior of transition metals in a high oxidation state differs from that at zero oxidation state. For this reason the charge density study of KMnO₄ has been undertaken and compared with that of the isomorphous KClO₄ [37], containing the non-metal Cl atom in the same chemical environment of the Mn atom. The topological results were also rationalized using the classification recently proposed by Espinosa et al. [13]. According to this classification the K–O and Cl–O bonds have a pure ionic and covalent character, respectively. The Mn–O bonds show an intermediate behavior and fall in the transit CS region (Fig. 5). These results are also in good agreement (even on a quantitative level) with those obtained from fully periodic Hartree–Fock and density functional calculations.

Fig. 5
BD of KMnO₄ and KClO₄ salts (BD = H_BCP/ρ_BCP where the units of H are kJ mol^–1 per atomic unit volume and units of ρ are e Å^–3) as a function of ∣V_BCP∣/G_BCP. Triangles and squares refer to experimental and theoretical data, respectively.

For these salts the atomic charges have been estimated by performing an integration over the topological atomic basins. The charge of about +2 e has been found both for Mn and Cl atoms and the ionic radius, estimated with the distance of the BCP from the nucleus (0.85 Å for Mn) agrees with the Mn²⁺ ionic radius of literature (0.80 Å) [38]. The charge of + 2 e on manganese is also in agreement with the corresponding result from the electron spectroscopy experiment on potassium permanganate [39]. A lower charge (nearly + 1 e) has been found in a theoretical study on MnO₄^– anion [40]. Furthermore, the experimental average VSCC radii are 0.75 Å for Cl, 0.42 Å for Mn, 0.65 Å for K and 0.48 Å for O atoms. A similar VSCC radius value has been obtained for the manganese atom in the Mn₂(CO)₁₀ complex, despite its different formal oxidation state.

We have also taken into account the debated topological characterization of the metal–metal bond. Our experimental and theoretical topological results on metal–metal bonds, together with those reported in the literature, are summarized in [41] and in Fig. 6. For comparison the topological indicators of the ionic NaF and of the covalent C₂H₆ are also reported. In the same Figure the theoretical topological parameters of bulk metals are illustrated [42,43].

Fig. 6
Bond Degree (BD = H_BCP/ρ_BCP where the units of H are kJ mol^–1 per atomic unit volume and units of ρ are e Å^–3) as a function of ∣V_BCP∣/G_BCP. Dots in transit CS zone refers to theoretical values in bulk metals; triangles represent both theoretical and experimental values for metal–metal bonds in organometallic complexes [41].

The metal–metal bonds lie in the transit CS region, with topological features intermediate between typical covalent and ionic bonds for both polynuclear complexes and bulk metals. They have positive ∇²ρ_BCP, low ρ_BCP, a little CD and a flat charge density in the valence region. The index of flatness f is defined as

f = ρ^{\min} / ρ_{BCP}^{\max}

where ρ^min is the absolute minimum of ρ(r) and ρ^max is the maximum ρ(r) found among BCPs [44]. f Approaches unity for metals and goes to zero for non-metals (e.g., for alkaline metals f = 0.89–0.95 and for alkaline earth metals f = 0.64–0.75). For the Co–Co–C rings in the two Co₂(CO)₆(μ-CO)(μ-C₄O₂H₂) polymorphs, the ratio f between the ρ^min of the ring CP and the

ρ_{BCP}^{\max}

of the Co–Co bond is 0.97 av., while for the lactone ring (all covalent bonds) it is 0.21 av. Unfortunately, no data are available at the present for ring or cage critical points of other organometallic complexes.

Thus, using the topological parameters now at our disposal, we can conclude that the metal–metal bond in the polynuclear complexes has the same nature as in the bulk metals. Differently, other authors, on the basis of some topological parameters at the BCP (in particular H_BCP < 0) and of ‘common chemical sense’, classify the metal–metal bond as a ‘genuine covalent bond’ [29,45]. We think instead that the metal–metal bond in complexes has its own unique features, similar to those of bonds in bulk metals.

4 Conclusions

The multipolar refinement, based on low temperature diffraction data, supplies accurate charge density distributions. The QTAIM is a useful tool to analyze the multipolar charge density and to well characterize the intra and inter-molecular bonds even in presence of first-row transition metals. In particular, for some organometallic compounds it has contributed to the long-debated discussion on the existence of a direct metal–metal bond and to the nature of this bond.

We have applied tentatively the classification proposed by Espinosa et al. to several interatomic bond types and it seems a powerful mean for evidencing the charge density features of bonds. In particular this classification together with the topological parameters of metal–metal bonds has allowed to recognize the unique features of these bonds.

Another tool at our disposal is the analysis of VSCC maxima and minima of bonded atoms. For example, it has allowed to associate the metal–ligand bond to a ‘dative’ bond. However, the analysis of this bond is still is in progress.

Note added in proof

A QTAIM analysis of Ru₃(CO)₁₂ was published in the meantime (G. Gervario, R. Bianchi, D. Marabello, Chem. Phys. Lett. 407 (2005) 18.

¹ The ‘shared’ and ‘closed-shell’ terminology are referred exclusively to the shared or not-shared valence shells of the two interacting atoms.

Bibliographie

[1] T.S. Koritsanszky; P. Coppens Chem. Rev., 101 (2001), pp. 1583-1627

[2] R.F.W. Bader Atoms in Molecules – A Quantum Theory, Oxford University Press, Oxford, UK, 1984

[3] R.F. Stewart Acta Crystallogr., A 32 (1976), p. 565

[4] N.K. Hansen; P. Coppens Acta Crystallogr., A 34 (1978), p. 909

[5] R.F. Stewart; M.A. Spackman; C. Flensburg VALRAY, versions, 1995–2000

[6] T. Koritsanszky; S.T. Howard; T. Richter; P. Macchi; A. Volkov; C. Gatti; P.R. Mallinson; L.J. Farrugia; Z. Su; N.K. Hansen XD—A Computer Program Package for Multipole Refinement and Topological Analysis of Charge Densities from Diffraction Data, 2003

[7] C. Gatti TOPOND-96,98: an electron density topological program for systems periodic in N (N = 0–3) dimensions, User’s Manual; CNR-ISTM, Milano, Italy, 1999

[8] D.A. Kirzhnits Sov. Phys. JETP, 5 (1957), p. 64

[9] Y.A. Abramov Acta Crystallogr., A 53 (1997), p. 264

[10] E. Espinosa; E. Molins; C. Lecomte Chem. Phys. Lett., 285 (1998), p. 170

[11] D. Cremer; E. Kraka Croat. Chem. Acta, 57 (1984), p. 1259

[12] D. Cremer; E. Kraka Angew. Chem. Int. Ed. Engl., 23 (1984), p. 67

[13] E. Espinosa; I. Alkorta; J. Elguero; E. Molins J. Chem. Phys., 117 (2002), p. 5529

[14] R. Bianchi; G. Gervasio; G. Viscardi Acta Crystallogr., B 54 (1998), p. 66

[15] R. Destro; R.E. Marsh; R. Bianchi J. Phys. Chem., 92 (1988), p. 966

[16] R. Destro; R. Bianchi; G. Morosi J. Phys. Chem., 93 (1989), p. 4447

[17] R. Bianchi; C. Gatti; V. Adovasio; M. Nardelli Acta Crystallogr., B 52 (1996), p. 471

[18] M. Catti; G. Gervasio; S.A. Mason J. Chem. Soc., Dalton Trans. (1977), p. 2260

[19] G. Gervasio; S.A. Mason; L. Maresca; G. Natile, Inorg Chem., 25 (1986), p. 2207

[20] E. Gatto; G. Gervasio; D. Marabello; E. Sappa J. Chem. Soc., Dalton Trans., 10 (2002), p. 1448

[21] G. Gervasio; R. Rossetti; P.L. Stanghellini; G. Bor Inorg. Chem., 21 (1982), p. 3781

[22] S. Vastag; G. Gervasio; D. Marabello; G. Szalontai; L. Markó Organometallics, 17 (1998), p. 4218

[23] R. Bianchi; G. Gervasio; D. Marabello Chem. Commun. (1998), p. 1535

[24] R. Bianchi; G. Gervasio; D. Marabello Inorg. Chem., 39 (2000), p. 2360

[25] M. Martin; B. Rees; A. Mitschler Acta Crystallogr., B 38 (1982), p. 6

[26] P. Macchi; D.M. Proserpio; A. Sironi J. Am. Chem. Soc., 120 (1998), p. 120

[27] G. Jansen; M. Schubart; B. Findeis; L.H. Gade; I. Scowen; M. McPartlin J. Am. Chem. Soc., 120 (1998), p. 7239

[28] R. Bianchi; G. Gervasio; D. Marabello XXVIth Congresso Nazionale AIC, 1–4 September 1996

[29] L.J. Farrugia; P.R. Mallinson; B. Stewart Acta Crystallogr., B 59 (2003), p. 234

[30] A.A. Low; K.L. Kunze; P.J. MacDougall; M.B. Hall Inorg. Chem., 30 (1991), p. 1079 (and references therein)

[31] R. Bianchi; G. Gervasio; D. Marabello XVIIIth ECM, Praha, 15–20 August 1998

[32] R. Bianchi; G. Gervasio; D. Marabello Helv. Chim. Acta, 84 (2001), p. 722

[33] R. Bianchi; G. Gervasio; D. Marabello Acta Crystallogr., B 57 (2001), p. 638

[34] P. Macchi; L. Garlaschelli; S. Martinengo; A. Sironi J. Am. Chem. Soc., 121 (1999), p. 10428

[35] P. Macchi; L. Garlaschelli; A. Sironi J. Am. Chem. Soc., 124 (2002), p. 14173

[36] M. Finger; J. Reinhold Inorg. Chem., 42 (2003), p. 8128

[37] D. Marabello; R. Bianchi; G. Gervasio; F. Cargnoni Acta Crystallogr., A 60 (2004), p. 494

[38] R.D. Shannon Acta Crystallogr., A 32 (1976), p. 751

[39] F. Reinert; P. Steiner; S. Hüfner J. Magn. Mater., 140–144 (1995), p. 177

[40] H. Nakai; Y. Ohmori; H. Nakatsuji J. Chem. Phys., 95 (1991), p. 8287

[41] G. Gervasio; R. Bianchi; D. Marabello Chem. Phys. Lett., 387 (2004), p. 481

[42] Y. Aray; J. Rodriguez; D. Vega J. Phys. Chem. B, 104 (2000), p. 4608

[43] W. Uhl; S. Melle; G. Frenking; M. Hartmann Inorg. Chem., 40 (2001), p. 750

[44] P. Mori-Sanchez; A.M. Pendás; V. Luaña J. Am. Chem. Soc., 124 (2002), p. 14721

[45] P. Macchi; A. Sironi Coord. Chem. Rev., 238–239 (2003), p. 383

Commentaires - Politique