Protonation behaviour of <i>N</i>,<i>N</i>′-piperazine-dipropionic acid

Constantin Mateescu; Cornelia Wikete; Otilia Costisor; Gilles Bouet; Mustayeen A. Khan

doi:10.1016/j.crci.2005.03.007

Résumés

Anglais
Français

The overall protonation constants of N,N′-piperazine-dipropionic acid (PDPA) were calculated with SUPERQUAD and PSEQUAD computer programs, at 25 and 37 °C and an ionic strength of 0.1 mol dm^–3 (KCl). There is a good agreement between the values calculated with the two programs. The obtained values were checked by a simulation titration curve and by the protonation (observed and calculated) curves for C_L = 2.0716 mmol dm^–3 at 25 °C. A two-step deprotonation mechanism is proposed. In the first step the deprotonation occurs to the carboxyl group and in the second step it is the nitrogen atom of the piperazine ring which undergoes deprotonation. .

Les constantes globales de protonation du N,N′-pipérazine-dipropionic acide (PDPA) ont été calculées à l'aide des programmes SUPERQUAD et PSEQUAD, à 25 et à 37 °C, avec une force ionique constante de 0.1 mol dm^–3 (KCl). Les valeurs calculées avec les deux programmes sont concordantes. Ces valeurs ont été vérifiées par une courbe de titration simulée et par des courbes de protonation (expérimentales et calculées) pour C_L = 2.0716 mmol dm^–3 à 25 °C. Un mécanisme de déprotonation en deux étapes est proposé. Dans la première étape, la déprotonation se produit sur le groupement carboxyle, suivie de la deuxième étape lorsque l'atome d'azote du noyaux pipérazine subit la déprotonation. .

1 Introduction

β-Amino acids are known as intermediates in different biological transformations involving oligometals [1,2]. However, not many results have been reported which refer to the complexes containing these acids as ligands.

By the Mannich reaction, namely the condensation of a primary or secondary amine with formaldehyde and compounds with acidic hydrogen (such as aldehydes, ketones, alcohols, esters and acids), compounds with interesting ligand properties can be obtained. An interesting condensing amine is piperazine with its reinforcing effect shown by coordination in boat conformation [3–6]. In 1922 Mannich and Ganz [7] reported the alkylation of piperazine with malonic acid and formaldehyde and obtained a β-aminoacid, namely N,N′-piperazine-dipropionic acid (PDPA). Their properties had never been extensively investigated, and it was only very recently that the ligand properties of PDPA were studied [8]. This investigation was conducted by using the MM+ force field and AM1 MO semi empirical method. Conformational analysis showed a large number of PDPA low energy conformers. The barriers to rotation of the flexible bonds from side chains also indicate the capability of PDPA to adapt itself easily to conformations which are suited for the coordination at different metal centres. It has also been reported that there is a pronounced medium effect on the protonation of PDPA in aqueous solution [9], which confirms the theoretical prediction described in our earlier publication [8].

The complexes of PDPA are important from analytical and pharmacological point of view, as well as for their optical and magnetic properties. They can also be utilised as models for biological systems [2]. On the basis of overall protonation constants of PDPA, this work proposes a deprotonation mechanism in two steps.

2 Experimental

Potentiometric titrations were performed with a CG 841 Schott pH-meter, equipped with a glass electrode N 6280, which was calibrated for hydrogen ion concentration according to Irving et al. [10].

All calibrations and titrations were carried out in a glass vessel (25 cm³) under a CO₂-free nitrogen atmosphere to avoid any contact with carbon dioxide. The temperature was regulated at 25.0 ± 0.1 and 37.0 ± 0.1 °C, respectively, and the ionic strength was maintained at 0.1 mol dm^–3 (KCl). As titrant, a CO₂-free solution was used, which consisted of 0.078 mol dm^–3 KOH and 0.022 mol dm^–3 KCl, to minimise ionic strength change during titration.

The potentiometric equilibrium studies were carried out with solutions of ligand at three different concentrations. The pH data were obtained after addition of 0.100 cm³ increments of standardised KOH solution. The titrant solution was prepared from KOH and it was standardised with potassium hydrogen iodide. The ligand was synthesised in our laboratory [8]. The purity of the ligand and the exact concentrations of their solutions were checked and measured by the Gran [11] method. The pK_w values for the aqueous system at the ionic strength employed, defined as-log [H⁺]·[OH^–], were taken from the data of Harned and Owen [12].

The global protonation constants of the ligand in aqueous solution were separately determined from the titration data with the Fortran computer programs SUPERQUAD [13] and PSEQUAD [14]. It may be pointed out here that PSEQUAD uses implicit differentiation to minimise the objective function: pH or absorbance. SUPERQUAD also uses the same procedure but develops independently [13]. Species distribution diagrams were computed from the overall protonation constants with HySS computer program [15].

3 Results and discussions

All the reactant concentrations (in mmol dm^–3) used in these studies, along with the pH ranges on which the calculations are based, are reported in Table 1.

System	Ionic strength	C_L	C_H	pH range used	n^a
Proton–PDPA (25 °C)	0.1 M, pK_w = 13.78	1.1780	4.0248	2.660–11.270	23
1.6356	5.5000	2.564–11.264	27
2.0716	7.1004	2.485–11.302	33
Proton–PDPA (37 °C)	0.1 M, pK_w = 13.40	1.1192	4.0124	2.613–10.928	22
1.5440	5.3660	2.525–10.965	27
1.9760	6.7492	2.445–11.020	33

^a n represents the number of experimental observations in each titration.

Analysis of the potentiometric titration curves both by the SUPERQUAD and by PSEQUAD programs yielded the values of the overall protonation constants, β_n defined by Eqs. (1) and (2) (ion charges omitted for clarity in Eq. (2)) and reported in Table 2.(1)

L^{2 -} + n H^{+} ⇌ {LH}_{n}^{n - 2}

(2)

β_{n} = [H_{n} L] \cdot {[L]}^{- 1} \cdot {[H]}^{- n}

The mean number of protons bound to the ligand (

\bar{n}

) is obtained from Eq. (3):(3)

\bar{n} = \frac{C_{H} - C_{O H} - [H^{+}] + [{OH}^{-}]}{C_{L}}

where C_H, C_L and C_OH are, respectively, the total concentrations of ligand, hydrogen and KOH titrated. C_H and C_L are given in Table 1. The addition of titrant (KOH solution) is taken into consideration because of variation of the total volume during the course of titration.

Program	25 °C	37 °C
logβ₁	logβ₂	logβ₁	logβ₂
SUPERQUAD	8.61 (3)	13.09 (4)	8.48 (4)	12.94 (4)
PSEQUAD	8.62 (2)	13.12 (3)	8.49 (2)	12.97 (3)

The calculated values of the mean number of protons bound to the ligand (n_calc) are given by Eq. (4) using the overall protonation constants of the ligand:(4)

{\bar{n}}_{calc} = \frac{\sum n \cdot [H_{n} L]}{C_{L}} = \frac{\sum n \cdot β_{n} \cdot {[H^{+}]}^{n}}{1 + \sum β_{n} \cdot {[H^{+}]}^{n}}

From the data shown in Table 2, it can be noted that the values of the global protonation constants, calculated with the two programs, are almost identical.

On the basis of the overall protonation constants a titration curve was simulated (solid line in Fig. 2) for C_L = 2.0716 mmol dm^–3 at 25 °C and I = 0.1 mol dm^–3 (KCl). The values used for this simulation were obtained with HySS program [15] on the basis of the overall protonation constants calculated in SUPERQUAD or PSEQUAD program. The identity of the two curves (real and simulated) observed in Fig. 1 confirms the model used in these calculations.

Fig. 2
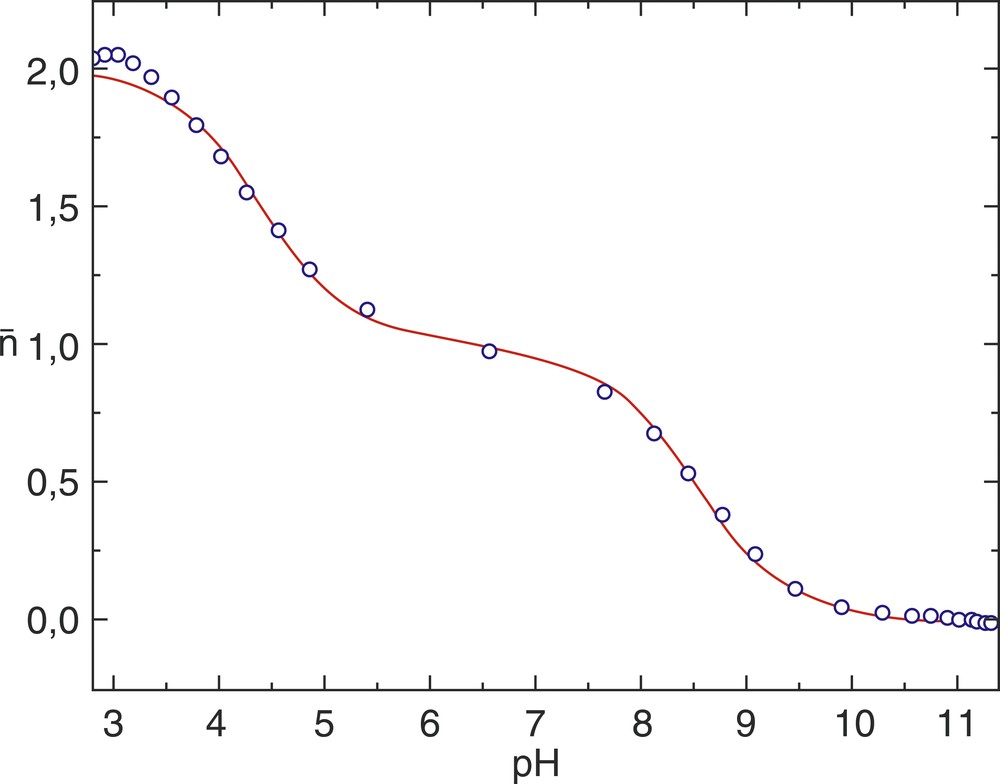
Protonation curves for ligand; solid line represents calculated function from potentiometric data, circles represent experimental protonation curve. Both curves were obtained for C_L = 2.0716 mmol dm^–3 at 25 °C and I = 0.1 mol dm^–3 (KCl).

Fig. 1
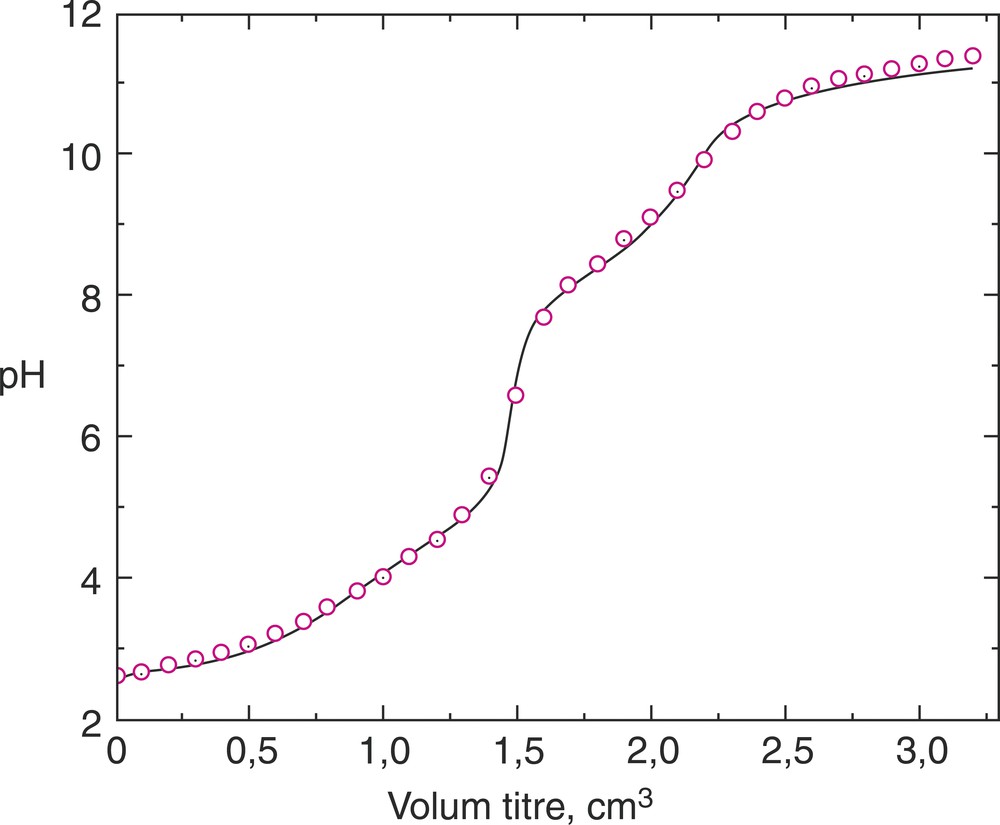
Experimental titration curve (circle) and simulation titration curve (solid line) for C_L = 2.0716 mmol dm^–3 at 25 °C and I = 0.1 mol dm^–3 (KCl).

To examine the experimental data, the protonation curves of the ligand were calculated. All these curves (Fig. 2) represent variations of the average ligand protonation number ( $\bar{n}$ ) as a function of pH. Experimental curve was drawn using Eq. (3), whereas Eq. (4) was the basis of drawing the calculated curve.

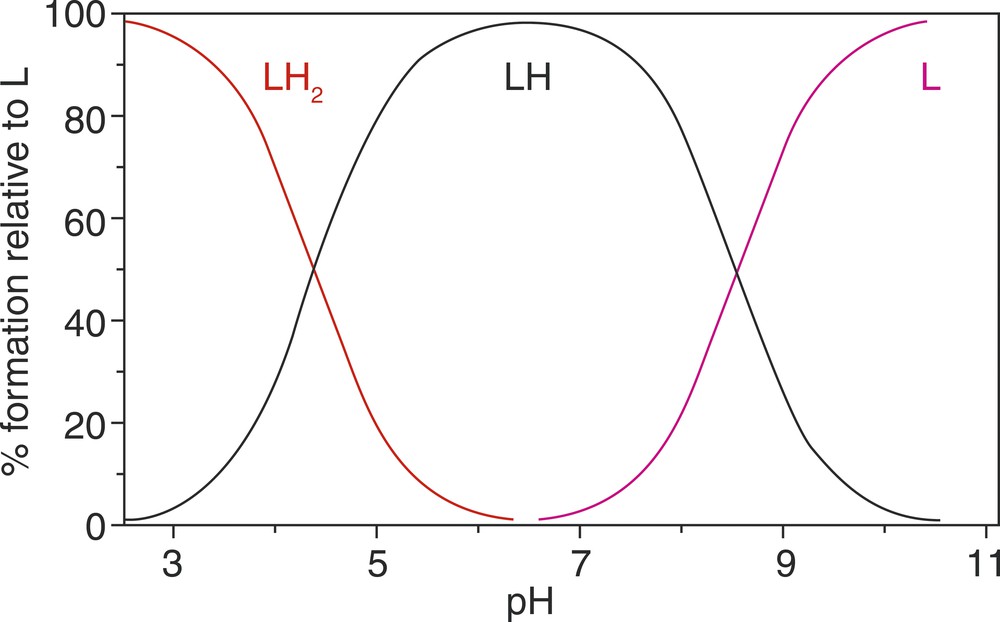
For the ligand (PDPA) at high values of pH (> 9.5), the curve levels off at about zero and this indicates that the last proton can be lost at this pH. Below pH 3.5 the curve levels off at about 2, indicating that two protons have been added to the ligand. These two-protonation constants have been determined in this study. The plateau at $\bar{n}$ = 1 and the pH is between 5.5 and 7.5 which strongly implies that the mono-protonated anion of PDPA (LH^–) is the dominating species. The agreement between calculated function (represented by a solid line in Fig. 2) and experimental data is good and tends to confirm the proposed model. The speciation diagrams of the ligand (Fig. 3), calculated and drawn with HySS program [15] confirm that LH^– dominates at pH values between 5.5 and 7.5.

Fig. 3
Speciation diagrams of the PDPA, calculated for C_L = 2.0716 mmol dm^–3, at 25 °C and I = 0.1 mol dm^–3 (KCl).

The crystallisation of PDPA in aqueous solution in presence of hydrochloric acid, allows the separation of a solid hydrochlorhydrate with molecular formula: C₁₀H₁₈N₂O₄·2HCl. In aqueous solution the hydrochloric acid is totally dissociated and for PDPA the following molecular structure can be assigned:

Being zwitterions, which derives from an amino acid, PDPA can possess buffer capacity which can be utilised in biochemistry and physiological studies. In comparison with the titration curves of other zwitterionic buffers based on piperazine, like piperazine-N,N′-bis[2-hydroxypropanesulfonic] acid (POPSO), N-[2-hydroxyethyl]piperazine-N′-3-propanesulfonic acid (HEPPS) [16] and N-[2-hydroxyethyl]piperazine-N′-(2-hydroxypropanesulfonic acid) (HEPPSO) [17], the titration curves of PDPA show a little plateau at a pH value about 8.5 and a ratio of mol base added per mol ligand of 2.5–2.7.

At 25 °C, the protonation constant of PDPA for the first protonation, pK₁, has a value between 8.60 and 8.61 and for the second protonation step, pK₂, it is between 4.48 and 4.50 (Table 2). The values of pK₂ can be obtained from the values of pβ₂ taking into account that pβ₂ = pK₁ + pK₂. During titration, the first deprotonation of PDPA occurs at a pH range of 4–5 to the carboxylic group (pK₂). At higher values of pH (8–9) the last deprotonation occurs at the aminic nitrogen of the piperazine ring.

The protonation constants of some mono-carboxylic acids are of the same magnitude as those of the pK₂ value for PDPA. Thus, the values of pK = 4.68 for the acetic acid, 4.87 for the propionic acid and 4.82 for the n-butyric acid [18], suggest that in aqueous solution, the carboxylic group is slightly deprotonated. The presence of aminic group, a group with basic character, leads to increase of the protonation constant to pK = 9.78 for amino acetic acid, 9.87 for α-amino propionic acid and 10.36 for β-amino propionic acid [18]. This supposes a protonation of amino group for these amino acids – the deprotonation occurring at high pH values. The aminic nitrogen from the piperazine ring has a weaker basic character than the amino group of mono-carboxylic amino acid. The presence of two electron-releasing carboxylate substituents could confer a more basic character to the piperazine N [19]. Therefore, the pK₁ values for amino acids with piperazinic ring are lower than the values for mono-carboxylic amino acids. Thus, at 25 °C and I = 0.1 mol dm^–3 (KNO₃), for pK₁ for POPSO is 7.60, for HEPPS it is 8.04 [16] and for HEPPSO the value of pK₁ is 7.79 [17]. It is observed that our values obtained for PDPA are comparable with those of other amino acids with piperazinic ring.

Consequently, it is proposed that the deprotonation of PDPA occurs in steps, as shown in the following mechanism:

The first deprotonation concerns the carboxyl group and the second one involves the deprotonation of the cationic group –N⁺H of the piperazine ring.

4 Conclusion

Using Superquad and Psequad computer programs, the overall protonation constants of PDPA were calculated at an ionic strength of 0.1 mol dm^–3 (KCl), and two temperatures, viz. 25 and 37 °C. The values calculated with the two programs are in good harmony. This is further verified by a simulation titration curve and the observed and calculated protonation curves for C_L = 2.0716 mmol dm^–3 at 25 °C and I = 0.1 mol dm^–3 (KCl). A deprotonation mechanism in two steps is proposed.