The binary diagram water + barium chloride

Jo Fenstad; Derek J. Fray

doi:10.1016/j.crci.2006.02.004

Résumé

As part of a larger work on the production of solid metal by FFC electro-deoxidation in liquid salts, some candidate raw materials (i.e. hydrated salts) were studied with respect to thermal equilibria, in particular de-hydration. This paper presents the first complete review and critical assessment of the thermal equilibria of the hydrates of BaCl₂. A consistent set of optimised equations is presented for the water pressure within the bi-phase regions of the binary system H₂O–BaCl₂, along with a complete update of the corresponding T–X phase diagram. Finally, it is suggested that the hemi-hydrate (BaCl₂·1/2 H₂O) is only barely stable, and that the formation of hemi-hydrate (from BaCl₂·H₂O + BaCl₂) is driven by entropy only. An important correction to Holmes (J. Chem. Thermodynamics 28 (1996) 1325; J. Chem. Thermodynamics 29 (1997) 1363) is pointed out. .

1 Introduction

As part of a larger work on producing solid metal by salt electro-deoxidation [1,2], a study was undertaken to map the properties of candidate raw materials, both for the main constituent of the salt electrolyte [3] and for salt additives. One potential additive is BaCl₂, an end member of the binary system reported here. This additive is commercially available as the hydrated chloride, and needs to be de-hydrated prior to use in the high temperature electrolytic process. The end member BaCl₂ stands out (amongst the alkali earth chlorides) due to its relatively low molar solubility in water. In this respect it is more similar to NaF than to either CaCl₂ or SrCl₂. The low solubility is readily linked to the relative ease with which BaCl₂ looses its crystal water, i.e. the barium chloride hydrates are relatively unstable [4–7] at atmospheric pressure (and below). However, when pressurised, the hemi-hydrate is reported to persist as high as 270 °C [8,9], thus ordinary T–X diagrams do not reveal the hemi-hydrate's instability at normal pressures. The most complete and recent T–X diagram for this system is from Kessis and Pascal [9], who combined the liquidus from Benrath and Lechner [8] with their own data for decomposition temperatures of the hydrates. Many key papers for this system are of early date, but they are quite consistent with recent papers, suggesting that the experimental methods were fairly ‘mature’ already in 1940. Some disagreements can be attributed to the particulars of each method, while others are attributable to differing levels of salt purity. This paper aims to present the first complete review and critical assessment of the stable phase equilibria of the H₂O–BaCl₂ binary, and to provide vapour isobars and phase boundaries in a compact graphical form, and as a consistent set of optimised and versatile equations.

2 Peritectic decomposition temperatures

Benrath and Lechner [8] and Eddy and Menzies [10] are the two most extensive and accurate investigations of the H₂O-rich liquidus. Since these two are indistinguishable below 120 °C, we accept their temperature for BaCl₂·2 H₂O decomposition (102 °C) over the recommendations from Kessis and Pascal [9] and Tenu and Counioux [11], which are 3 K higher and coincides closely with another thermal arrest (water boiling). Kessis and Pascal [9] also reported BaCl₂·1/2 H₂O decomposition at a temperature of 2 K higher than Benrath and Lechner's [8], with an error of ± 3 K. Arbitrarily, 2 K was subtracted from the reported temperature [9] for decomposition of the monohydrate, to harmonise with the other investigations. Thus, 207 and 270 °C were selected for the decomposition temperature of mono- and hemi-hydrate, respectively.

3 Liquidi

The extensive liquidus data of Benrath and Lechner [8] and Eddy and Menzies [10], and from several other sources was summarised by Tenu and Counioux [11,12], who modelled these liquidi (up to 200 °C). Tenu's fairly original mathematical approach provided a consistent set of equations, which main weakness is they cannot be re-arranged to an explicit form, i.e. neither T(X) nor X(T). Thus, numeric approximation is needed to utilise Tenu's optimisation.

3.1 Liquidus equations

All liquidi of this system up to 270 °C could be reproduced accurately by second order polynomials with respect to composition, i.e. explicit T(X²) functions.

3.2 Optimised liquidi

Up to 102 °C, the original sources for experimental T–X pairs are abundant, thus explicit T(X) functions were generated directly from these, yielding the following liquidus:

T / ° C = - 166.9 + 7500 X_{{BaCl}_{2}} - 41 500 X_{{BaCl}_{2}}^{2}

For the range 102–207 °C (monohydrate saturation), less experimental solubility data are available. Thus, the present optimisation was based on smoothing functions from Tenu and Counioux [11] and Monnin [13] that were thermodynamically consistent. Unfortunately, the solubility product (K_sp) from Monnin [13] was not based on solubility data alone, but was defined (and optimised) in terms of a particular model for the dilute liquid. Thus, this K_sp was made redundant by Holmes and Mesmer [14] who provided new data (and a different model) for the dilute liquid. Equations from Tenu and Counioux [11] related to solubilities only, and numeric T–X data could be extracted, to optimise an explicit T(X) function:

T / ° C = - 610 + 19 670 X_{{BaCl}_{2}} - 106 050 X_{{BaCl}_{2}}^{2}

which may be combined with vapour pressure data [15] to confirm (independently) the liquid phase model of Holmes and Mesmer [14]. One solubility datum from Holmes and Mesmer [14] allowed a tentative liquidus function between 207 and 270 °C:

T / ° C = - 868 + 26 100 X_{{BaCl}_{2}} - 143 000 X_{{BaCl}_{2}}^{2}

Beyond 270 °C, reasonable estimates could not be made for the liquidus compositions (Fig. 1).

Fig. 1
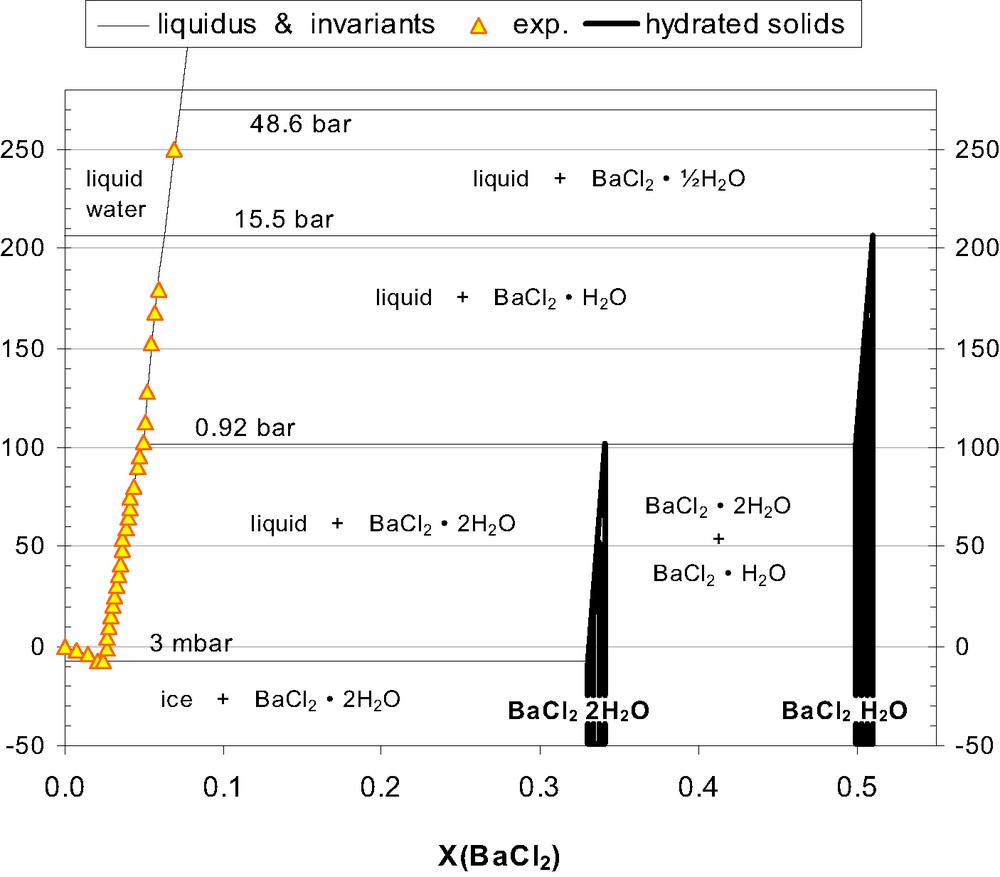
The assessed H₂O–BaCl₂ diagram, shown with emphasis on liquidus equilibria. See Section 4 for H₂O pressures at the invariant equilibria.

4 Equilibrium vapour pressures

4.1 Vapour-pressure equations

With respect to vaporisation equilibria for H₂O + BaCl₂, there has been a steady trickle of relevant papers over the last 100 years. Holmes and Mesmer [19] provided smoothed (refined) data for the osmotic coefficients for aqueous salts over a wide temperature range. Osmotic data may be used with present T(X) functions for the liquidi, to generate explicit equations for the vapour pressure over the liquid solutions in equilibrium with solid hydrates. No attempts were made to estimate the equilibria involving liquid + anhydrous BaCl₂, because of the lack of experimental data. Even if relevant data were available, such a vapour equation would be valid only in a limited temperature range, since these high temperatures causes the simple binary H₂O–BaCl₂ to gradually degenerate into a complex reciprocal system [16] involving molecules and ions formed by combination of H₂O, HCl, BaCl₂ and BaO. We noted, however, that extrapolation of vapour pressure data for dilute solutions (Azizov and Akhundov [17] and Matuzenko et al. [18]) indicate that Holmes' model predict ~ 10% too high vapour pressures (near the liquidus) at 350 °C, i.e. the extrapolative ability [14] may possibly drop off rapidly above 270 °C.

Moreover, this liquid model [14,19] is strikingly complex. This allows small typing errors to remain undetected and create havoc during (re-)calculations. The authors themselves found such errors within their computer implementation, but their erratum [19] failed to identify a printing error in Holmes and Mesmer's [14] paper, i.e. their Eq. (30). The correct version of their Eq. (30) is given here:

F_{0} = p_{1} + (1 / 2) p_{2} (T / T_{0}) + (1 / 6) p_{3} {(T / T_{0})}^{2} + (1 / 12) p_{4} {(T / T_{0})}^{3} + (1 / 6) p_{5} {(T / T_{0})}^{2} {\ln (T / T_{0}) - 5 / 6} + p_{6} {(T / 2 T_{0}) + (3 T_{2}^{2} / 2 T T_{0}) + (T_{2} T_{x} / T) \ln (T_{x})} + p_{7} {2 (T_{y} T_{0} / T) + 1} \ln (T_{y})

For the vapour equilibria over salt di-hydrate plus liquid, Apelblat [20] employed a three-parameter formula equivalent to the following:

\log (P_{H_{2} O} / bar) = A + B / (T / K) + C \ln (T / K)

which requires that the ΔH_rx varies linearly with temperature. An alternative is an Antoine type equation

\log (P_{H_{2} O} / bar) = A + B / (T + C)

The adjustable parameters B and C are given in Kelvin units, while A is dimensionless. The corresponding equation for the enthalpy of reaction is given by

- Δ H_{rx} = B R \ln (10) {(\frac{T}{T + C})}^{2}

with R being the gas constant R = 8.3144 J mol⁻¹ K⁻¹. This review found the first formula [20] less suitable for a number of reasons. Firstly, the implied assumption of ΔH_rx varying linearly with temperature is dubious for vaporisation reactions involving saturated water of varying composition. Secondly, it would be of little value even if correct, because the enthalpy of reaction does not correspond to ΔH_vap, but is a sum of enthalpies of vaporisation, melting and dilution. Thirdly, only the Antoine T(P) equation can easily be transformed to an explicit P(T) form. Finally, while both formulae achieved a very good fit to all available data for saturated liquids, the Antoine equation extrapolated better, so that predictions for the metastable equilibria were more sensible.

For the equilibria involving no liquid (i.e. only vapour plus solid hydrates), a general Arrhenius-type equation (i.e. Antoine with parameter C = 0) was found to provide the proper level of accuracy.

4.2 The water + dihydrate equilibrium

For the lowest aqueous equilibrium, the parametric optimisation of osmotic coefficients [19], combined with the optimal liquidus (Section 3.2) produces H₂O pressures in excellent agreement with experimental vapour pressure data of Collins and Menzies [15] and Speranski [21]. The agreement with pressure data from Apelblat [20] is also very good, except for the lowest temperature (10 °C). However, the optimised equation of Apelblat [20] does not perform well above 50 °C, straying off towards far too low pressures. Notably, Holmes and Mesmer [14,19] did not cite these three earlier papers. The optimised Antoine parameters are A = 4.947, B = –1651 K, C = –43.73 K, which leads to a prediction of nearly atmospheric H₂O pressure (i.e. 0.923 bar) at the decomposition temperature of the di-hydrate.

4.3 The water + monohydrate equilibrium

From 102 to 207 °C (the aqueous equilibrium with monohydrate), the osmotic data [19] were again combined with the optimised solubility data (Section 3.2), yielding vapour pressures that agree very well with direct measurements [15]. The optimised Antoine coefficients were A = 5.174, B = –1776 K, C = –34.18 K.

Thus, 1 bar pressure occurs at 104.3 °C (or 104.7 °C for 1 atm). This implies that investigators reporting peritectic decomposition of di-hydrate around 105 °C [9,11] probably had encountered a thermal pause caused by water boiling.

4.4 The water + hemi-hydrate equilibrium

From 207 to 270 °C (the aqueous equilibrium with hemi-hydrate), no direct experimental data exists for vapour pressures along the liquidus. But vapour data for more dilute solutions [17,18] agrees very well with the osmotic model of Holmes and Mesmer [19]. Thus, these osmotic data were combined with the present liquidus (also from Holmes, see Section 3.2) to generate a tentative vapour equation, described by the Antoine coefficients A = 5.212, B = –1798 K, C = –33.37 K.

4.5 The water –vapour equilibria over solid mixtures

Schottky [22], Tanner [23], Huttig and Slonim [24], Collins and Menzies [15], Rigaud and Ingraham [5] and Shimizu and Taniguchi [25] measured the equilibrium vapour pressure of water over the solid mixtures BaCl₂·2 H₂O + BaCl₂·H₂O and ‘BaCl₂·1 H₂O + BaCl₂·0 H₂O’. That means none of them recognised the existence of the hemi-hydrate (BaCl₂·½ H₂O), which is now established [4,26] and is known to decompose peritectically around 270 °C [9].

For the dihydrate + monohydrate equilibrium, all these papers agree around 100 °C, but disagree at lower temperatures, where Rigaud and Ingraham [5] and Shimizu and Taniguchi [25] reported the lowest vapour pressures. They both used a transpiration method. Schottky [22] and Tanner [23] both employed a static (non-isopiestic) method, reporting higher pressures. The highest pressures were reported by Collins and Menzies [15], using an isopiestic method. In conclusion, results appear to depend significantly on which method was employed, and no method is proven to be superior (Fig. 2).

Fig. 2
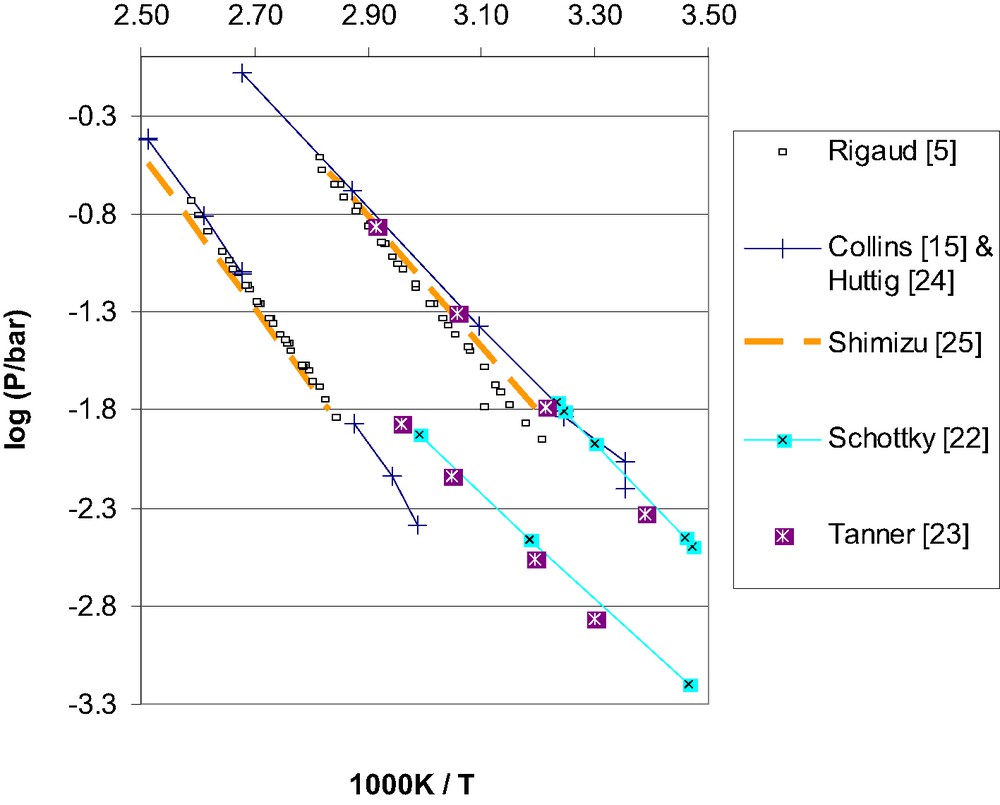
The literature data employed for assessing the vapour pressures over solid hydrates of barium chloride. Each paper reported data for both equilibria: dihydrate + monohydrate (uppermost data group) and monohydrate + hemi-hydrate (lower data groups).

At low temperatures, the thermodynamics of H₂O vapour over the hydrates of any salt is quite difficult to study by experimental means, and Collins and Menzies [15] explicitly identified barium and strontium chloride hydrates as the most troublesome hydrates. Collins and Menzies [15] discussed in impressive detail the errors that are characteristic for vapour measurements at low temperatures, but failed to point out the prime issue; that any measurement of the true equilibrium pressures requires an intimate mixture of finely divided (yet well defined) crystals of the two solids to be equilibrated. Results from Assarsson [4] imply that ~ 100 °C annealing temperature for several days gives well defined crystallites of anhydrous BaCl₂. Even longer annealing time would be required at lower temperatures; at room temperature Haase and Brauer [27] observed three different crystalline modifications for anhydrous BaCl₂. Most papers on the low temperature vapour equilibria of lower hydrates have consistently failed the above criteria, i.e. annealing was never completed during these experiments, and intimate bi-phase mixtures were not made from pre-annealed powders.

By contrast, the higher hydrates readily grow crystals at room temperature, thus problems of the opposite kind may occur. Excessive grain coarsening may cause contact surfaces to become insufficient, explaining the reported ability of some higher hydrates to ‘skip’ certain decomposition stages. Thus, Bergthorsson [28] reported that a closely related substance (SrCl₂ hexahydrate) would consistently decompose to dihydrate after annealing below 50 °C, but transforms directly to monohydrate (upon heating) after annealing around 60 °C.

Even when the above criteria for annealing and pre-mixing have been met, there might be secondary requirements such as long equilibration time and a high volume ratio (solids volume to gas volume).

4.5.1 The water vapour equilibrium for the dihydrate + monohydrate salt

The transpiration experiments of Rigaud and Ingraham [5] involved a packed bed of the pure dihydrate, which was subjected to an in-flux of near-saturated carrier gas. Unfortunately, that is an effective way to prevent nucleation of monohydrate, thereby incurring super-/sub-saturation within the packed bed. For the dihydrate, the expected deviation is a sub-saturation, and an observed water pressure below the true equilibrium. And indeed, Rigaud and Ingraham [5] reported the lowest pressures. Shimizu and Taniguchi [25] employed similar equipment but used mixtures made from annealed near-stoichiometric hydrates, thus circumventing the potential problem of sub-saturation. Predictably, Shimizu and Taniguchi [25] reported significantly higher pressures. In fact, Shimizu is very close to Tanner [23] and only slightly below Collins and Menzies [15], Schottky [22] and Huttig and Slonim [24], all of them employing different methods. Thus, for the dihydrate–monohydrate equilibrium, the recommended vapour equation is optimised from the combined data set [25,23], with the restriction that the pressure must agree with Holmes' data (Holmes and Mesmer [19]) at the three-phase equilibrium (102 °C).

4.5.2 The water vapour equilibrium for the monohydrate + hemi-hydrate salt

The known papers on the evaporation of monohydrate and hemi-hydrate fall into three separate groups. The first group is papers on DTA determinations [4–7], who usually establish a rank of successive decompositions, but are limited to a single pressure, and thus of limited value here. Only Assarsson [4], Wiederholt and Plempel [7], and Kessis and Pascal [9] acknowledged the hemi-hydrate. The second group is Schottky [22] and Tanner [23], who were the only ones to obtain their P–T data for mono + hemi-hydrate by a static (non-isopiestic) method. The third group [5,15,24,25] also provided P–T data, using various experimental methods. These latter four investigations all agree quantitatively on the BaCl₂·1 H₂O dehydration, despite disagreeing about the BaCl₂·2 H₂O dehydration. The implication is that the former reaction (hemi-hydrate formation) is less sensitive to nucleation kinetics than the latter (monohydrate formation). A low sensitivity to phase nucleation is characteristic for transformations from highly ordered structures (monohydrate) to more disordered structures (hemi-hydrate). The implication is that hemi-hydrate is less ordered than monohydrate, which indicates how these phases should be modelled (Section 4.5.3).

However, the very consistent results of this third group of papers are in significant discord with what Schottky [22] and Tanner [23] found. To clarify this, we have employed the data from Holmes and Mesmer [19], which predicts an equilibrium pressure of 15.5 bar over monohydrate + hemi-hydrate at 207 °C. Extrapolations of equations from both Shimizu and Taniguchi [25] and Rigaud and Ingraham [5] yield values very close to this, and for lower temperatures these equations coincide with data from Collins and Menzies [15] and Huttig and Slonim [24]. Thus, these results [5,15,24,25] were erroneously assigned to monohydrate + ‘anhydrous’, and can reliably be taken to represent the stable equilibrium monohydrate + hemi-hydrate. The recommended equation for this vaporisation equilibrium is a standard two-term Arrhenius equation (i.e. Antoine with C = 0), which ensured a very good fit in the full temperature range (60–207 °C):

\log (P_{H_{2} O} / bar) = 9.335 - 3910 K / T

Rigaud and Ingraham [5] derived a more complex four-term free energy function by incorporating specific heat data (Cp) for the solid phases. Since they applied Cp data for anhydrous BaCl₂ to a reaction that (in retrospect) does not involve anhydrous BaCl₂, this four-term function must be considered obsolete.

Extrapolating the data from Tanner [23] and Schottky [22] to 207 °C yields pressures well below the monohydrate + hemi-hydrate equilibrium. Their use of a particular static pressure method may explain this deviation. The accuracy of this method was confirmed [23] for dihydrate decomposition (Section 4.5.1), but the subsequent study of monohydrate decomposition was implemented in a slightly different fashion, thus, a methodic error could be responsible for their anomalous (but reproducible) data for monohydrate. Alternatively, their results could represent a metastable equilibrium, e.g. between the hemi-hydrate and a “disordered” (semi-amorphous) monohydrate phase. Indeed, Lutz et al. [26] identified and characterised a disordered monohydrate phase. It was slightly deficient in water (relative to stable monohydrate), and transformed to the ordered stable monohydrate (plus stable hemi-hydrate) only after holding around 100 °C. The experiments of Schottly [22] and Tanner [23] never exceeded 66 °C, for this particular equilibrium.

4.5.3 The water vapour equilibrium for the hemi-hydrate + anhydrous salt

This is the last bi-phase region to be studied here, and it requires a careful discussion, because available data are scarce. At high temperature, we may rely on osmotic data (for the liquid) from Holmes and Mesmer [19] at the hemi-hydrate decomposition (270 °C).

At lower temperatures, a number of investigators (using DTA techniques) have noticed that release of water vapour from monohydrate and from hemi-hydrate occurs at nearly the same temperature. Some even failed to notice any distinction. Furthermore, Assarsson [4] showed that direct transition from BaCl₂·H₂O to anhydrous BaCl₂ takes place in the presence of small amounts of contaminants such as MgCl₂ and CaCl₂. From the above, it may be deduced that the reaction

{BaCl}_{2} ⋅ H_{2} O + {BaCl}_{2} \to {2BaCl}_{2} ⋅ \frac{1}{2} H_{2} O

is favoured by a fairly small free energy. One consequence is that the vapour equation for monohydrate → hemi-hydrate will not be much different from the equation for hemi-hydrate → anhydrous. In the continuing, it will be argued that these two vapour equations differ only with respect to entropy, i.e. they have the same enthalpy term.

If the above reaction was favoured (mainly) by an enthalpic contribution, then the difference between monohydrate decomposition and hemi-hydrate decomposition would also be (mainly) enthalpic, and would diminish with higher temperatures. But the opposite seems to happen; the difference in decomposition temperature (for these two hydrates) is quite substantial (270 vs. 207 °C). Such a temperature dependence is adequately accounted for by modelling the above reaction with an enthalpy of reaction near zero, so that the formation of hemi-hydrate (from anhydrous + monohydrate) runs spontaneously only due to a slight entropy contribution.

Thus, the vapour pressure equation for hemi-hydrate decomposition will have the same enthalpy term as the equation for monohydrate decomposition, but a different entropy term. Therefore, only the entropy parameter of the 4.5.2 equation need to be re-fitted. Employing the one datum available [19], i.e. the pressure at 270 °C, the estimated equation for the vapour pressure over hemi-hydrate plus anhydrous BaCl₂ becomes

\log (P_{H_{2} O} / bar) = 8.887 - 3910 K / T

In order to compare this estimate with published DTA data for lower temperatures, we are faced with the general problem that DTA curves, which register the heat effects within a specimen, are subject to issues like nucleation, specimen size and specimen grain size and porosity, especially for endothermal reactions (heat absorbing). Small samples subjected to a very dry carrier gas may loose all its water contents far below the boiling/sublimation temperature. However, DTA curves are often very reproducible with respect to the temperature difference between two successive reactions, a phenomenon that forms the basis for all temperature calibration of DTA systems. Thus, since only Assarsson [4] unambiguously separated these successive reactions, we compare the temperature difference he obtained (13 °C at ~80 °C) with what is predicted from our two optimised equations (14 °C). The agreement could hardly have been better.

Finally, we have calculated the entropy difference between the two latter evaporation reactions:

Δ S = 8.5 J {mol}^{- 1} = R \times ln (10) \times (9.335 - 8.887)

The stable monohydrate and anhydrous salt are both highly ordered and well-crystallised (Section 4.5.2), whereas for the hemi-hydrate a simplistic model is considered, involving random distribution of H₂O molecules among available cation sites, and one site per cation. The predicted difference between configurational entropies of hemihydrate and monohydrate is:

Δ S = - R \times (1 \times \ln (0.5) + 1 \times \ln (0.5)) = 11.5 J {mol}^{- 1}

The agreement is fairly close, suggesting that water distribution within the hemihydrate is predominantly random.

5 Conclusions

An updated phase diagram is presented for H₂O–BaCl₂ (Fig. 3), based on the first complete review and assessment of the thermal equilibria of the hydrates of BaCl₂.

Fig. 3
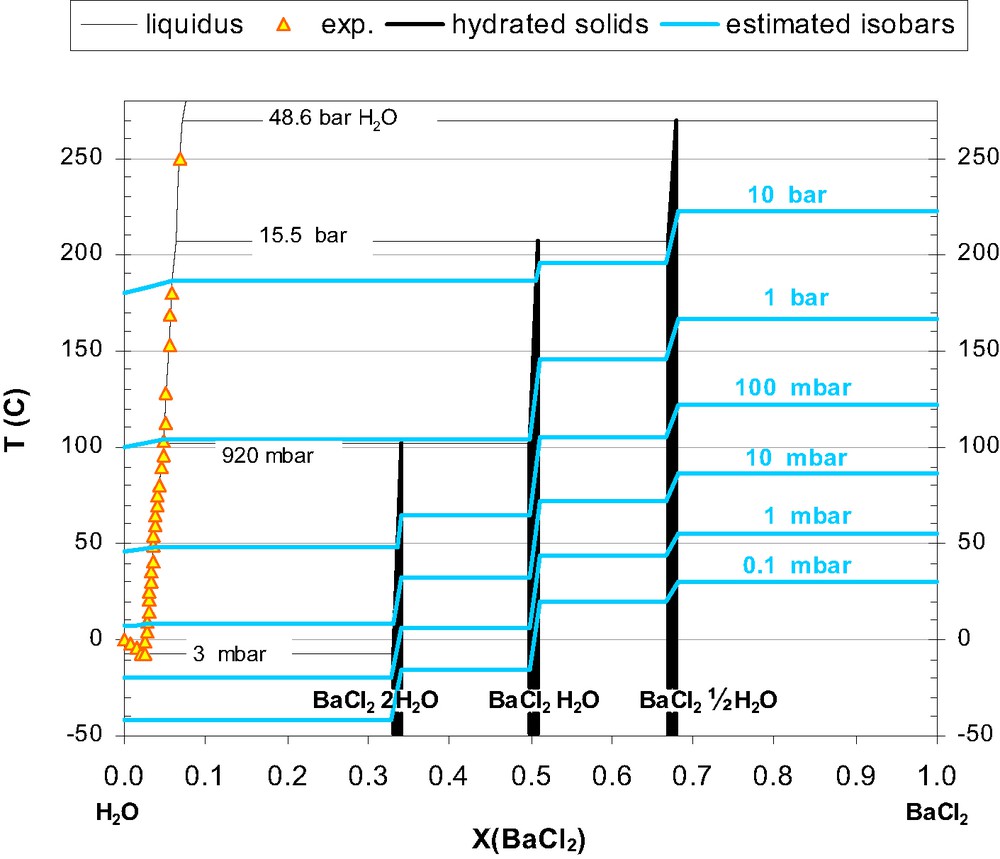
The complete H₂O–BaCl₂ diagram with added isobars for the equilibrium pressures of water vapour. Equilibrium isobars are shown as light blue lines.

Critically assessed and self-consistent H₂O isobars have been included in the diagram so it can be used to find optimal conditions for drying of the respective hydrates. These isobars are based on the following optimised equations for the H₂O vapour equilibria over various bi-phase mixtures:

● BaCl₂·2 H₂O + saturated water:

\log (P_{H_{2} O} / bar) = 4.947 - 1651 K / (T - 43.73 K)

● BaCl₂·H₂O + saturated water:

\log (P_{H_{2} O} / bar) = 5.174 - 1776 K / (T - 34.18 K)

● BaCl₂·½ H₂O + saturated water:

\log (P_{H_{2} O} / bar) = 5.216 - 1798 K / (T - 33.37 K)

● BaCl₂·2 H₂O + BaCl₂·H₂O:

\log (P_{H_{2} O} / bar) = 8.591 - 3236 K / T

● BaCl₂·H₂O + BaCl₂·½ H₂O:

\log (P_{H_{2} O} / bar) = 9.335 - 3910 K / T

● BaCl₂·½ H₂O + anhydrous BaCl₂:

\log (P_{H_{2} O} / bar) = 8.887 - 3910 K / T

Optimised equations were also made for the liquidi of this system, based on a critical assessment of relevant literature. An important correction to Holmes and Mesmer [14,19] is pointed out. The commonly reported DTA peak at 102–105 °C is identified as two separate thermal effects; the di-hydrate peritectic (102.0 °C) and saline water boiling (104.7 °C).

The formation of hemi-hydrate (from BaCl₂·H₂O + BaCl₂) is caused mainly by entropy, thus the water distribution within the hemi-hydrate is predicted to be predominantly random. This explains the large difference between peritectic temperatures for monohydrate and hemi-hydrate.

Further research efforts should involve the use of ultrapure BaCl₂, and proper procedures for powder annealing and mixing, to confirm/quantify the low temperature equilibria for the hemi-hydrate, and independently establish the proposed invariant points 15.5 bar/207 °C and 48.8 bar/270 °C.

Acknowledgements

The authors want to thank Dr Lilia Centeno and Dr Clifford Mc Aleese for help with the literature translation.