Hierarchy of the density-wave states and superconductivity in the organic conductor α-(BEDT-TTF)<sub>2</sub>KHg(SCN)<sub>4</sub>

Mark V. Kartsovnik; Dieter Andres; Werner Biberacher

doi:10.1016/j.crci.2006.06.009

Account / Revue

Hierarchy of the density-wave states and superconductivity in the organic conductor α-(BEDT-TTF)₂KHg(SCN)₄

Mark V. Kartsovnik ¹ ; Dieter Andres ¹ ; Werner Biberacher ¹

¹ Walther-Meissner-Institut, Bayerische Akademie der Wissenschaften, Walther-Meissner-Strasse 8, 85748 Garching, Germany

Comptes Rendus. Chimie, Volume 10 (2007) no. 1-2, pp. 6-14.

Résumé

The layered organic conductor α-(BEDT-TTF)₂KHg(SCN)₄ exhibits a phase transition into the charge-density-wave (CDW) state at an unusually low temperature. This leads to a very high sensitivity of the ground state to magnetic field and pressure. We present a number of novel field-induced CDW states originating from the superposition of the strong paramagnetic and quantized orbital effects of the magnetic field. At temperatures below 0.3 K the CDW phase coexists with a superconducting phase. Surprisingly, the CDW formation is found to remarkably increase the superconducting onset temperature.

Métadonnées

Reçu le : 2006-03-02
Accepté le : 2006-06-14
Publié le : 2006-12-05

DOI : 10.1016/j.crci.2006.06.009

Mots clés : Organic conductors, Charge-density-wave, Superconductivity, Electronic phase transitions, Magnetic field effects

Affiliations des auteurs :

Mark V. Kartsovnik ¹ ; Dieter Andres ¹ ; Werner Biberacher ¹

¹ Walther-Meissner-Institut, Bayerische Akademie der Wissenschaften, Walther-Meissner-Strasse 8, 85748 Garching, Germany

@article{CRCHIM_2007__10_1-2_6_0,
     author = {Mark V. Kartsovnik and Dieter Andres and Werner Biberacher},
     title = {Hierarchy of the density-wave states and superconductivity in the organic conductor {\ensuremath{\alpha}-(BEDT-TTF)\protect\textsubscript{2}KHg(SCN)\protect\textsubscript{4}}},
     journal = {Comptes Rendus. Chimie},
     pages = {6--14},
     publisher = {Elsevier},
     volume = {10},
     number = {1-2},
     year = {2007},
     doi = {10.1016/j.crci.2006.06.009},
     language = {en},
}

TY  - JOUR
AU  - Mark V. Kartsovnik
AU  - Dieter Andres
AU  - Werner Biberacher
TI  - Hierarchy of the density-wave states and superconductivity in the organic conductor α-(BEDT-TTF)2KHg(SCN)4
JO  - Comptes Rendus. Chimie
PY  - 2007
SP  - 6
EP  - 14
VL  - 10
IS  - 1-2
PB  - Elsevier
DO  - 10.1016/j.crci.2006.06.009
LA  - en
ID  - CRCHIM_2007__10_1-2_6_0
ER  -

%0 Journal Article
%A Mark V. Kartsovnik
%A Dieter Andres
%A Werner Biberacher
%T Hierarchy of the density-wave states and superconductivity in the organic conductor α-(BEDT-TTF)2KHg(SCN)4
%J Comptes Rendus. Chimie
%D 2007
%P 6-14
%V 10
%N 1-2
%I Elsevier
%R 10.1016/j.crci.2006.06.009
%G en
%F CRCHIM_2007__10_1-2_6_0

Mark V. Kartsovnik; Dieter Andres; Werner Biberacher. Hierarchy of the density-wave states and superconductivity in the organic conductor α-(BEDT-TTF)₂KHg(SCN)₄. Comptes Rendus. Chimie, Volume 10 (2007) no. 1-2, pp. 6-14. doi : 10.1016/j.crci.2006.06.009. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2006.06.009/

Version originale du texte intégral

1 Introduction

The layered organic conductors, α-(BEDT-TTF)₂MHg(SCN)₄ where M = K, Tl or Rb, have been of high interest since the early 1990s due to their anomalous electronic properties at low temperatures (see e.g. [1–3] and references therein). While the exact nature of some anomalies is still a matter of debate, most of the features are associated with a density-wave instability of the quasi-one-dimensional (Q1D) part of the electronic system and its interaction with the quasi-two-dimensional (Q2D) conducting band. The 2k_F-superstructure, observed originally in the angle-dependent magnetoresistance experiments [4], was recently confirmed by X-ray studies [5], thus suggesting a charge-density-wave (CDW) formation in these compounds. Current–voltage characteristics taken on the M = K salt below the transition temperature [6,7] reveal the existence of a threshold electric field whose behaviour can be interpreted in terms of a CDW with a d-wave order parameter [8,9].

The critical temperature of the CDW transition in these compounds, T_CDW ≈ 8–10 K, and, therefore, the relevant energy gap are much smaller than it is usually met in CDW systems. One of the important consequences of this fact is a strong influence of a magnetic field on electronic properties. On the other hand, the ground state of these materials turns out to be very sensitive to the hydrostatic [10,11] or uniaxial [12,13] pressure. This gives rise to a rich phase diagram including a number of new field-induced CDW (FICDW) subphases and a superconducting phase coexisting with the CDW. This paper is aimed to overview recent results obtained on the best-studied M = K salt. In the next section we will briefly introduce two basic mechanisms of the magnetic field effect on a CDW system and illustrate how they are manifested in α-(BEDT-TTF)₂KHg(SCN)₄. In Section 3 two different types of FICDW transitions will be presented. Finally, in Section 4 the superconducting state and its coexistence with the CDW state under quasi-hydrostatic pressure will be considered.

2 Pauli and orbital effects of a magnetic field on the CDW state

Generally, the magnetic field affects the CDW system via coupling to the spins and to the orbits of charge carriers.

Since the CDW interaction involves electron–hole pairs from the same spin subband [14,15], an external field B, lifting the spin degeneracy, leads to different values of the optimal nesting vector for the subbands with spins parallel and antiparallel to the field:

Q_{opt, x} (B) = Q_{x 0} \pm 2 μ_{B} B / ħ v_{F}

(1)

where x axis is supposed to be along the best conducting direction of the Q1D system, Q_x₀ ≈ 2k_F is the nesting vector in the absence of the field, μ_B is the Bohr magneton, v_F is the Fermi velocity, and the sign +(−) stands for the spins parallel (antiparallel) to the applied field. Thus, the CDW nesting conditions become worse in the magnetic field.

This so-called Pauli effect causes a gradual suppression of the CDW state with increasing field [16–19]. The relevant ‘magnetic field–temperature’ (B–T) phase diagram [17–19] is largely similar to that of a spin-Peierls system or a clean superconductor in the absence of the orbital pair-breaking. In particular, it includes the high-field, low-temperature phase CDW_x corresponding, respectively, to the soliton lattice [20,21] or spatially modulated Larkin–Ovchinnikov–Fulde–Ferrel [22,23] phases in the latter two cases. It is mainly the Pauli effect which determines the shape of the B–T phase diagram of α-(BEDT-TTF)₂MHg(SCN)₄ at ambient pressure, in magnetic field perpendicular or almost perpendicular to the highly conducting ac-plane [24–26]. An example of the phase diagram of the M = K salt obtained from magnetization measurements [26] is presented in Fig. 1. The experimental data show a good agreement with the theoretically predicted phase lines [18] (lines in Fig. 1). The steeper, in comparison with the theory, slope of the experimentally determined border between the low-field CDW₀ state and metallic state is caused by the second, orbital effect of the magnetic field.

Fig. 1
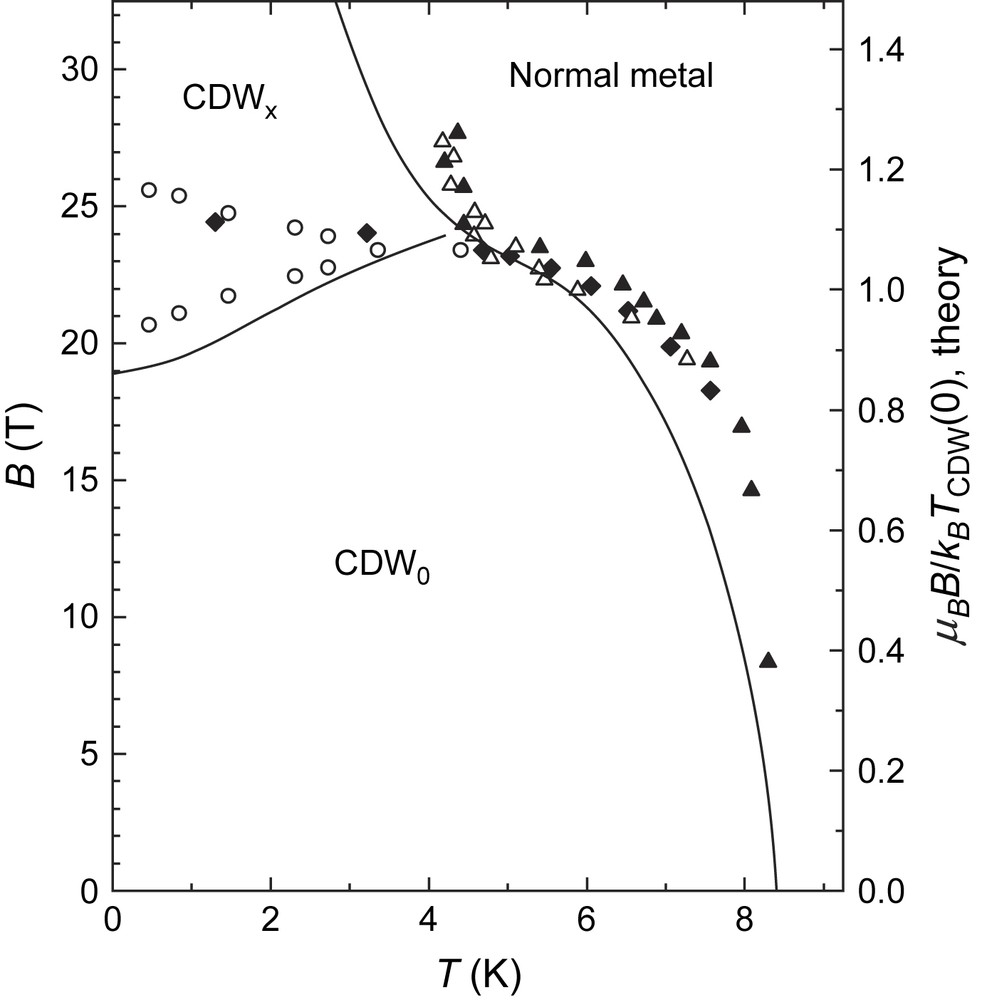
B–T phase diagram of α-(BEDT-TTF)₂KHg(SCN)₄ obtained from the magnetization measurements [26]; different symbols represent data from different samples. Lines (right scale) show the theoretically predicted phase diagram for a perfectly nested CDW system [18].

While the Pauli effect is operative in any CDW system, provided the field is strong enough, the orbital effect becomes important when the Fermi surface nesting is sufficiently imperfect. In the layered conductors, the imperfectness of nesting can be described by a finite second-order transfer integral t_y′, corresponding to the effective next-nearest-chain transfer in the plane of conducting layers, in the dispersion law for the charge carriers near the Fermi level [27]:

ɛ (k) = ħ v_{F} (| k_{x} | - k_{F}) - 2 t_{y} \cos (k_{y} a_{y}) - 2 t_{y}^{'} \cos (2 k_{y} a_{y}),

(2)

where y axis is perpendicular to the most conducting direction in the planes of the layers, ɛ_F = ħv_Fk_F is the Fermi energy of the Q1D electrons, and a_y is the interchain period. In Eq. (2) the dispersion in the least conducting z direction is assumed to be negligibly small which is usually well justified for layered organic conductors [27].

If t_y′ is comparable to the characteristic CDW energy t′^∗ = Δ₀/2 (Δ₀ is the CDW gap at t_y′ = 0), the zero-field transition temperature T_CDW(0) becomes considerably lower than for a perfectly nested Fermi surface. In this case, a magnetic field applied perpendicular to the layers restricts electron orbits to the chain direction, i.e. enhances their one-dimensionality, and restores the density-wave state [18,28].

In the experiment, the usual parameter for controlling the antinesting term t_⊥′ is the external pressure. For α-(BEDT-TTF)₂KHg(SCN)₄ the transition temperature is strongly reduced by applying the quasi-hydrostatic pressure of ∼2 kbar [29,30]. Under this pressure the magnetic field of ∼5–10 T perpendicular to the layers considerably increases T_CDW [30], as can be seen from Fig. 2 in which the lines separating the metallic and CDW states are shown for different pressures. This is a direct manifestation of the orbital effect. At ambient pressure T_CDW monotonically decreases in the field. However, as mentioned above the corresponding phase line is steeper than predicted for a perfectly nested CDW system. This steeper slope is obviously due to the orbital effect, indicating that the nesting is considerably imperfect already at P = 0.

Fig. 2
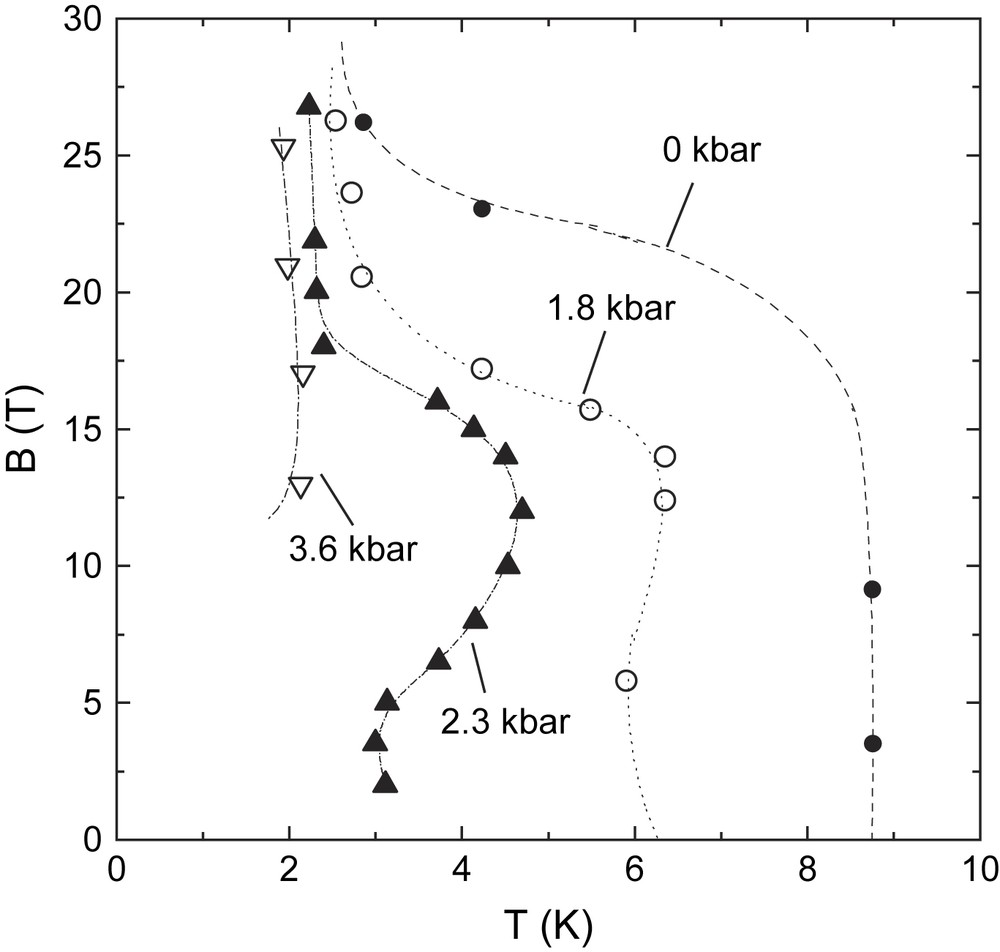
Phase lines between the normal metallic and CDW states determined from resistive measurements at different pressures [30]. The orbital effect is directly seen at P = 1.8 and 2.3 kbar as an increase of T_CDW in the fields between 5 and 12 T.

Obviously, the increase of T_CDW due to the orbital effect is limited: in any case the critical temperature value cannot exceed that of the perfectly nested system. Moreover, the orbital effect competes with the suppressing Pauli effect that further reduces T_CDW. Indeed, as seen from Fig. 2, the field-induced increase of T_CDW at 1.8 and 2.3 kbar saturates by ∼15 T and is followed by a decrease at higher fields.

3 Field-induced charge-density-wave (FICDW) transitions

3.1 Re-entrant CDW state under high pressure

If the antinesting parameter t_y′ exceeds the critical value t′^∗, the CDW state is completely suppressed in the absence of a magnetic field. In this case, a series of first-order phase transitions to FICDW subphases are expected at low temperatures [18,31,32]. These FICDW subphases are characterized by quantized (at a fixed field strength) values of the Q_x component of the nesting vector [32]:

Q_{x}^{N} = Q_{x 0} \pm \frac{2 μ_{B} B}{ħ v_{F}} + N \frac{2 π}{λ_{x}}, N = 0, \pm 1, \pm 2, …

(3)

where λ_x is the magnetic length along the x axis:

λ_{x} = \frac{π ħ}{e a_{y} B_{z}},

(4)

e is the electron charge, and B_z is the magnetic field component perpendicular to the layers. The last term in Eq. (3) originates from the quantization of the orbital motion of the charge carriers under a strong magnetic field. Different subphases are characterized by different quantum numbers N. This is similar to the well known field-induced spin-density wave (FISDW) phenomenon observed on the Bechgaard salts (TMTSF)₂X (see Refs. [27,33] for a review). However, unlike the latter case, the FICDW is influenced by the paramagnetic Pauli effect that is expressed by the second term in the right side of Eq. (3). In particular, this effect leads to a considerably lower coupling constant for the FICDW formation as compared to that of FISDW [32]. Nevertheless, recent experimental data [30,34] provide substantial arguments for the existence of FICDW in α-(BEDT-TTF)₂KHg(SCN)₄ under pressure.

Fig. 3 shows the interlayer magnetoresistance of a high-quality sample of α-(BEDT-TTF)₂KHg(SCN)₄ in the field perpendicular to the layers recorded at T = 0.1 K at different pressures [34]. The strong rapid oscillations of the magnetoresistance originate from the Shubnikov–de Haas effect due to the Q2D carriers, which remain metallic in both the normal and CDW states [1–3]. We, however, focus here on slow oscillations observed in the field interval between ∼4 and 10 T under pressure. It is important that these new features emerge right at the critical value P_c ≈ 2.5 kbar necessary for the complete suppression of the CDW state in the absence of the field. This pressure range corresponds to the antinesting parameter t_y′ slightly exceeding the critical value t′^∗ that exactly matches the theoretical condition for the FICDW transitions [18]. As discussed in Refs. [34,35], the periodicity of the oscillations in the inverse field scale, F ≅ 20 T, as well as their evolution with changing the pressure and temperature are consistent with the FICDW scenario.

Fig. 3
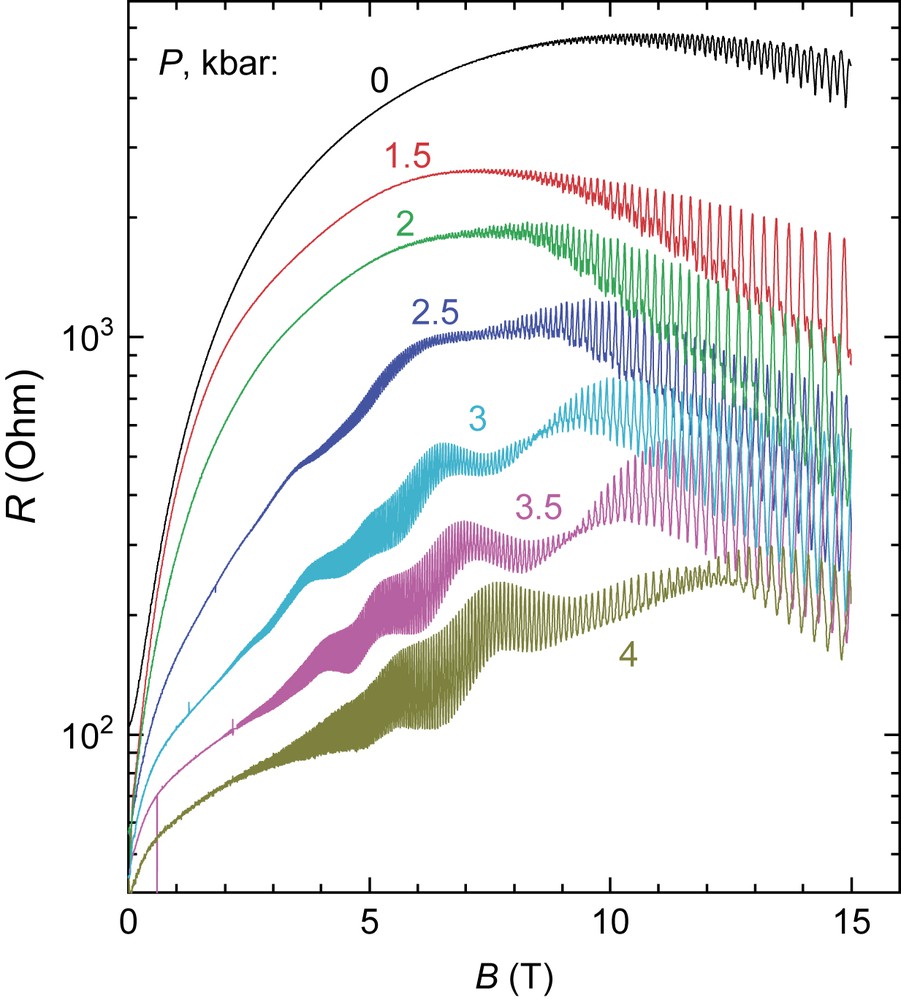
Interlayer magnetoresistance of α-(BEDT-TTF)₂KHg(SCN)₄ in fields perpendicular to the layers, at different pressures, T = 100 mK; data taken from Ref. [34]. The rapid oscillations are the Shubnikov–de Haas effect on the Q2D carriers. The slow oscillations emerging at the critical pressure, P_c = 2.5 kbar are associated with FICDW transitions.

As mentioned above, transitions between subsequent FICDW subphases are characterized by discontinuous changes of the wave vector Q_x; thus they are the first-order phase transitions. This is corroborated by the hysteretic structure of the field-dependent magnetoresistance: Fig. 4a shows the magnetoresistance measured under the pressure of 3 kbar, at increasing and decreasing magnetic fields; the difference between the up and down sweeps plotted in Fig. 4b exhibits a clear structure correlated with the slow oscillations. The peaks in the hysteresis are observed at the fields corresponding to the expected border between subsequent FICDW states.

Fig. 4
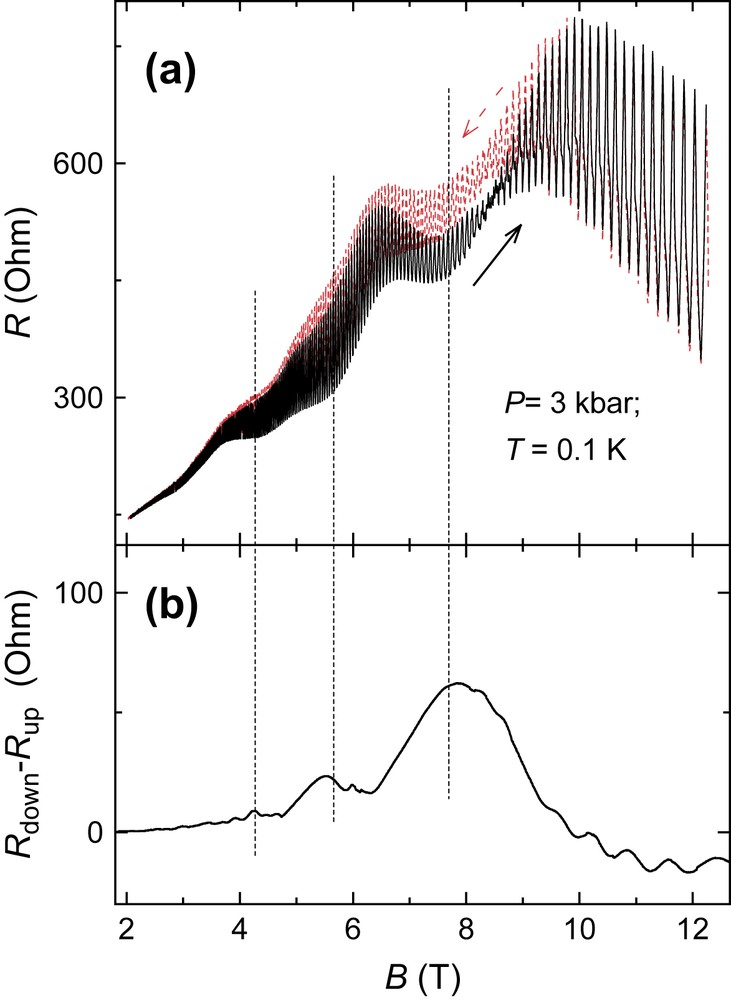
(a) Resistance at 3 kbar as a function of increasing (solid line) and decreasing (dashed line) magnetic field. (b) Difference between the down and upward sweeps. The structure of the hysteresis correlates with the slow oscillations in the upper panel as shown by the vertical dashed lines.

3.2 FICDW transitions in the CDW_x state

The FICDW transitions presented above are the consequence of the quantizing orbital effect of the magnetic field. In this respect they are very much alike FISDW phenomenon. The necessary condition for these effects is the complete suppression of the zero-field density-wave ground state. As we have shown, the latter can be achieved in α-(BEDT-TTF)₂KHg(SCN)₄ by applying sufficiently high pressure and thus increasing the antinesting parameter t_y′ above the critical value. Now we will consider another mechanism for the FICDW transitions which can be realized even at ambient pressure. This mechanism is associated with the superposition of the orbital quantization and the Pauli effect. The new transitions can be observed only in CDW systems since the SDW state is insensitive to the Pauli effect.

Fig. 5 shows the interlayer magnetoresistance (upper panel) and magnetic torque (lower panel) of α-(BEDT-TTF)₂KHg(SCN)₄ measured at zero pressure in a magnetic field strongly tilted with respect to the conducting layers [36]. The orientation is determined by the tilt angle θ as shown in the inset. The anomaly at B_k ≈ 12.5 T corresponds to the transition between the low-field CDW₀ state and the high-field CDW_x state. This transition is caused by the suppressing Pauli paramagnetic effect as discussed in Section 2. Additionally, both the magnetoresistance and torque display several anomalies above B_k. The hysteretic character of the anomalies suggests that they are associated with multiple first-order phase transitions. The transitions emerge at tilt angles above ≅65°, their positions in field being strongly dependent on θ. As shown in Fig. 6, they rapidly shift down, approaching B_k as θ increases towards 90°.

Fig. 5
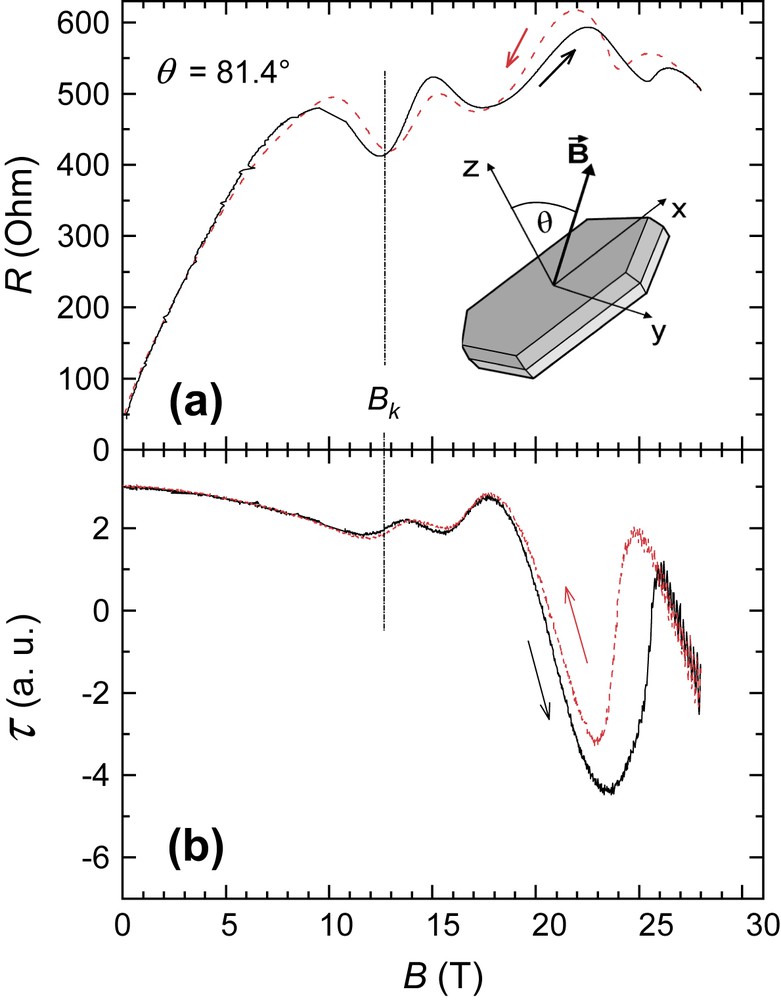
Resistance (a) and magnetic torque (b) versus magnetic field strongly tilted towards the layers [36]. The tilt angle θ is defined as shown in the inset; arrows show the directions of the field sweeps. B_k corresponds to the transition between the CDW₀ state with the fixed nesting vector and the CDW_x state with the field-dependent nesting vector.

Fig. 6
B–θ phase diagram of α-(BEDT-TTF)₂KHg(SCN)₄ [36]. The thick line indicates the transition between the CDW₀ state and the high-field CDW_x state; thin lines correspond to the multiple transitions within the high-field state.

The increasingly high sensitivity of the new transitions to changes in the tilt angle θ near 90° suggests that the orbital effect determined by the field component B_z = B cos θ plays a crucial role. On the other hand, it is important that they occur at B > B_k, i.e. in the fields producing a very strong Pauli effect. Therefore it is very likely that the new transitions originate from an interplay between the Pauli and orbital effects on the high-field CDW_x state.

To explain the origin of the observed transitions, we consider qualitatively the field dependence of the Q_x component of the nesting vector of a CDW system with a moderately imperfect nesting [36]. At zero-field, Q_x₀ = 2k_F corresponds to the optimal nesting; the CDW energy gap covers the whole Fermi surface. At a finite magnetic field, the optimal nesting conditions modify according to Eq. (1). This is illustrated by dashed lines in Fig. 7. Nevertheless, both spin subbands remain fully gapped and the system as a whole maintains the constant nesting vector Q_0x up to the critical field B_k ∼ Δ(B = 0)/2μ_B. Above B_k, Q_x₀ is no longer a good nesting vector as it leads to ungapped states in either subband. In this case the CDW energy can be minimized by introducing a field-dependent nesting vector $Q_{x}^{Pauli} (B)$ [18] which is schematically represented in Fig. 7 by the thin solid line asymptotically approaching the value Q_x₀ + 2μ_BB/ħv_F. This obviously improves the nesting conditions for one of the spin subbands (with spins parallel to the field) at the cost of an additional ‘unnesting’ of the other (spin-antiparallel). Now the situation for the second, unnested subband resembles that of the FICDW case considered above; the only difference is that now the nesting is destroyed by the Pauli effect rather than by pressure. Therefore, the orbital quantization condition in the form of Eq. (3) sets on the nesting vector. The corresponding quantized levels $Q_{x}^{N} (B)$ of the nesting vector for the subband with spins antiparallel to the external field are shown by dotted lines in Fig. 7. As a result, the most favorable values of the CDW wave vector above B_k are determined by the intersections of the continuous curve $Q_{x}^{Pauli} (B)$ with the straight lines $Q_{x}^{N} (B)$ . Thus, with changing the field we obtain a series of first-order transitions between CDW subphases characterized by different quantized values of the wave vector as schematically shown by thick lines in Fig. 7.

Fig. 7
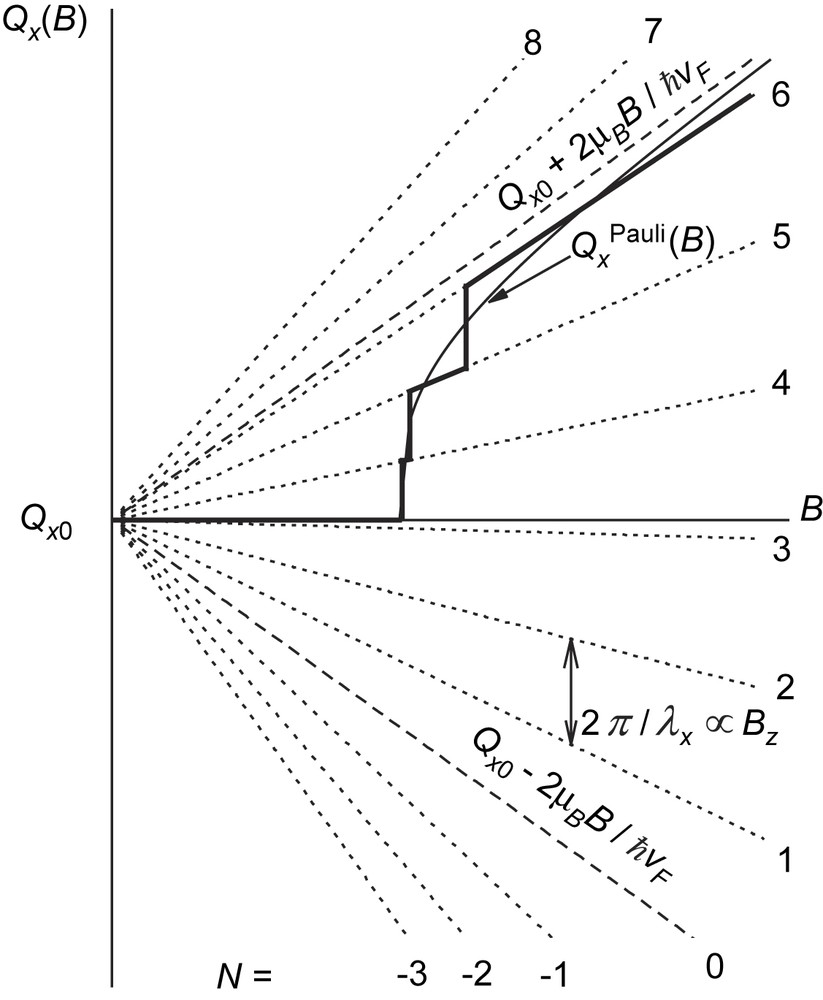
Schematic illustration of the field dependence of the CDW wave vector (thick line) originating from the superposition of the Pauli effect (Q_x^Pauli, thin solid line) [18] and orbital quantization (dotted lines).

The proposed model qualitatively explains the major features of the behaviour of α-(BEDT-TTF)₂KHg(SCN)₄ at high fields [36]. The multiple FICDW transitions can be observed when the distance 2π/λ_x between the quantized levels [see Eqs. (3) and (4)] is smaller than μ_BB/ħv_F. This condition is not fulfilled for the present compound at the field perpendicular to the layers. With tilting the field, the perpendicular field component B_z = B cos θ reduces, thus decreasing the value 2π/λ_x ∝ B_z, whereas the Pauli effect remains unchanged. Therefore, the transitions emerge starting from some threshold angle θ_c. From the experimentally determined angle θ_c ≈ 65° one can estimate the upper limit for the Fermi velocity of the Q1D carriers [36], v_F ≤ 2μ_B/3ea_y cos θ_c ≈ 9 × 10⁴ m/s; in good agreement with the independently obtained [37] value v_F = 6.5 × 10⁴ m/s.

4 Superconductivity and its coexistence with the CDW state

Under the quasi-hydrostatic pressure above the critical value, P ≥ P_c ≈ 2.5 kbar, the zero-field CDW state in α-(BEDT-TTF)₂KHg(SCN)₄ is completely suppressed and the normal metallic state undergoes the superconducting (SC) transition at low temperatures [38]. The maximum critical temperature T_c = (110 ± 5) mK at P = P_c and decreases at the rate dT_c/dP ≈ 30 mK/kbar with further increase in the pressure. It is interesting to note that both T_c and dT_c/dP are an order of magnitude lower than those found earlier in uniaxial strain experiments [39]. This dramatic difference is not understood at present and needs further investigation.

When the pressure is decreased below P_c, the CDW state emerges; however, the superconductivity does not disappear completely. As shown in Fig. 8, the resistive SC transition shifts down in temperature and broadens at lowering the pressure but even at P = 0 the resistance slightly decreases, indicating a partial transition to the SC state. The latter observation is in agreement with earlier reports by Ito et al. [40,41].

Fig. 8
SC transition in the interlayer resistance at pressures slightly above and below the critical pressure P_c = 2.5 kbar. Inset: ambient-pressure resistive transitions in different samples; data taken from Ref. [42].

The shape and magnitude of the SC transition below P_c are strongly sample dependent. To demonstrate this, examples of the zero-pressure transition on three different samples are presented in the inset in Fig. 8. The resistance of sample 3 is nearly zero at the lowest temperature. This, however, does not mean that the whole sample is in the SC state: d.c. magnetization measurements performed on the same sample have not shown any Meissner signal down to below 10 mK [42]. One can, therefore, conclude that below P_c the bulk superconductivity is suppressed and the SC phase exists in the form of minor inclusions into the CDW matrix.

The inhomogeneous nature of the superconductivity below P_c is also reflected in the critical field behaviour [35,42]. Fig. 9 shows the temperature dependence of the critical field, for three pressures: P = 2.0, 2.5, and 3.0 kbar. At zero-field, the critical temperature does not vary by more than 10% within this pressure interval. By contrast, the critical field shows a considerable enhancement at lowering the pressure, i.e. at entering the CDW region of the phase diagram. Moreover, the slope of the temperature dependence, linear above P_c, exhibits a clear positive curvature at the lowest pressure. This behaviour does not depend on the criterion chosen for the definition of the critical field [42]. Moreover, it seems to be a common feature of the compounds exhibiting a coexistence of the SC and density-wave states. Indeed, very similar effects have been reported for the CDW material NbSe₃ [43] and for the SDW organic conductor (TMTSF)₂PF₆ [44]. In all these compounds the SC and the density-wave phases are most likely separated in space, so that the superconductivity occurs only in a minor volume fraction.

Fig. 9
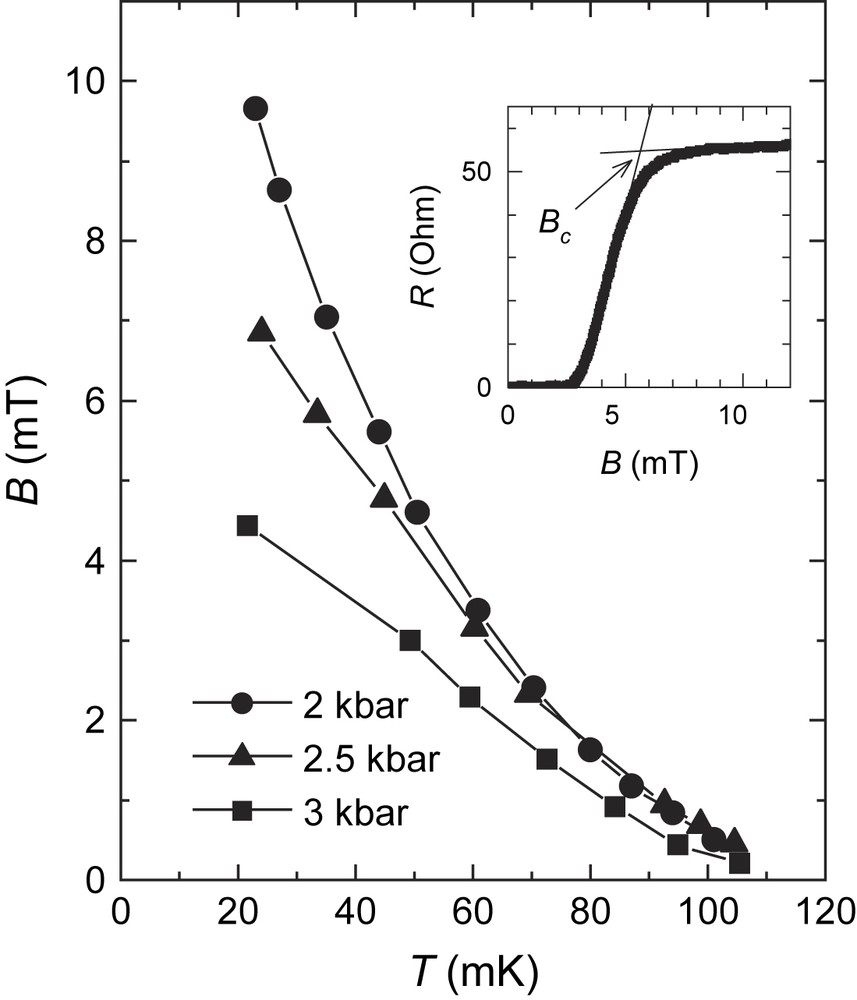
Temperature dependence of the critical field, determined as shown in the inset, at pressures around P_c [35].

The presented above results are fully consistent with the generally accepted concept of a competition between the CDW and SC instabilities in low-dimensional conductors [27,45]: the fraction of the SC phase rapidly decreases upon entering the CDW region and T_c shifts to lower temperatures. However, it was recently found [42] that the CDW surprisingly has a certain stimulating effect on the superconductivity in α-(BEDT-TTF)₂KHg(SCN)₄.

Fig. 10 shows, in an enlarged scale, the temperature dependence of the interlayer resistance at P = 2 kbar, at temperatures right above the main transition [42]. One can clearly see that the resistance starts deviating downwards from the normal metallic behaviour considerably above the temperature of the main resistive transition. This contrasts to the weak linear temperature dependence of the resistance above the critical pressure as demonstrated by the 3 kbar curve in Fig. 10. As can be seen from the figure, the accelerated decrease of the resistance at 2 kbar strongly depends on the level of the applied current; it also has been shown to be suppressed by a tiny magnetic field, ∼10 mT [42] that reveals its superconducting nature.

Fig. 10
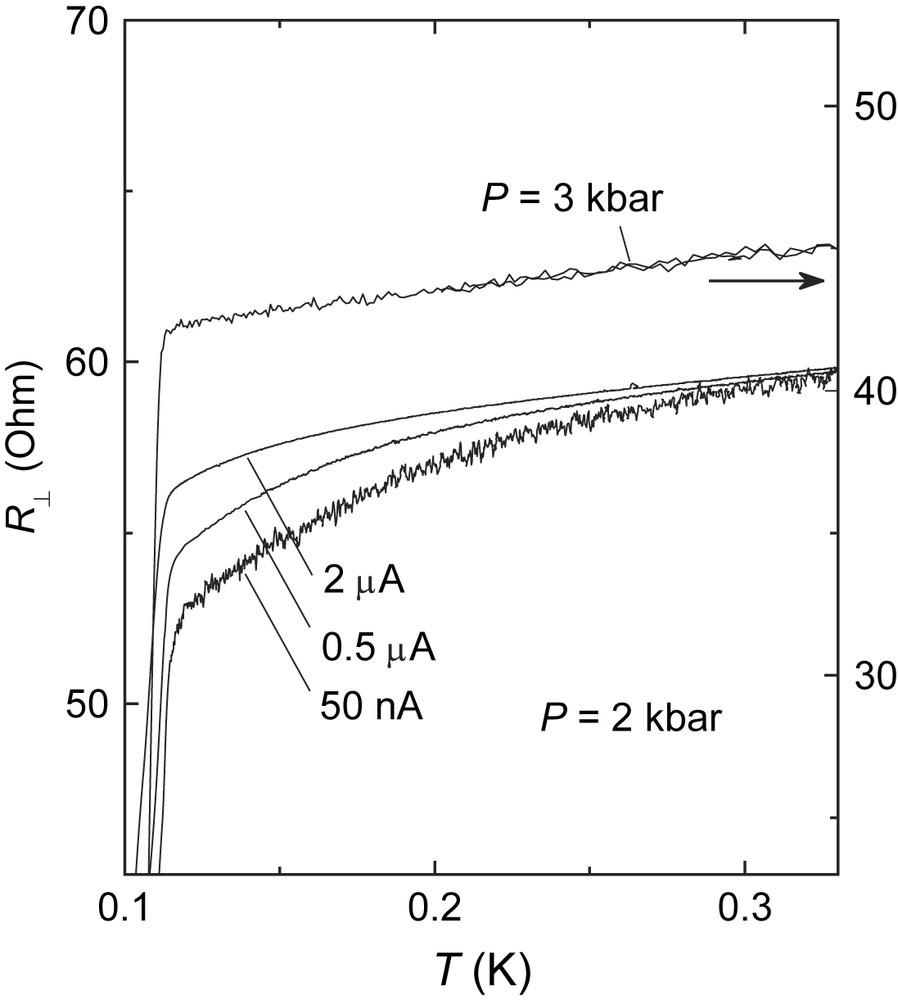
Onset of superconductivity at pressures above (3 kbar) and below (2 kbar) P_c. A clear SC precursor depending on current is seen in the lower pressure curves.

As a whole, the data on the SC transition can be summarized in the low-temperature P–T phase diagram as shown in Fig. 11. Above the critical pressure, the sharp transition indicates the bulk superconductivity in α-(BEDT-TTF)₂KHg(SCN)₄. At lower pressures the SC phase exists in the form of minor inclusions in the CDW matrix. The most surprising result is the dramatic increase of the SC onset temperature which is hardly consistent with the existing conventional theories of the competition between the SC and CDW states. One can speculate that in the neighborhood of the CDW phase the superconductivity is partially stimulated by charge fluctuations as proposed in several theoretical works [46–48]. Certainly, further studies are necessary to verify this hypothesis.

Fig. 11
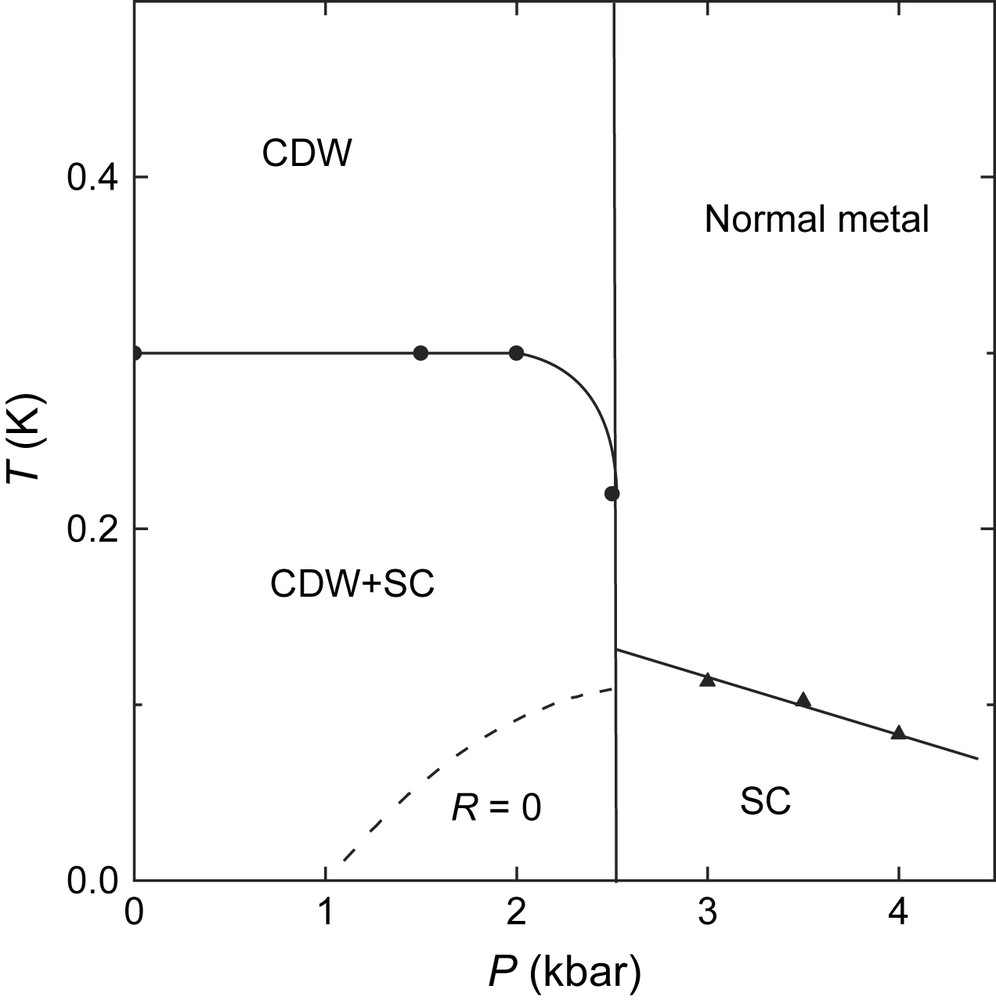
Low-temperature P–T phase diagram of α-(BEDT-TTF)₂KHg(SCN)₄ [42]. The SC and CDW phases coexist but are spatially separated below ≈ 2.5 kbar; the SC volume fraction decreases with decreasing pressure in this range.

5 Conclusion

The extremely low CDW transition temperature and, hence, the low energy gap in the organic conductor α-(BEDT-TTF)₂KHg(SCN)₄ provide a unique opportunity for comprehensive studies of the influence of a magnetic field on the CDW state. The experiment reveals strong, competing Pauli (paramagnetic) and orbital effects of the field:

• the Pauli effect gradually suppresses the CDW state and, at low temperatures, causes the transition into the new, field-dependent CDW_x state;
• the orbital effect enhances the CDW instability in an imperfectly nested Q1D system; in the case of a strongly imperfect nesting, t_y′ > t′^∗, it leads to a cascade of quantized FICDW subphases;
• the superposition of the Pauli effect and orbital quantization gives rise to a novel kind of FICDW transitions in tilted magnetic fields.

At very low temperatures, the SC state is found to exist in α-(BEDT-TTF)₂KHg(SCN)₄ in the broad pressure range, down to ambient pressure:

• at 0 ≤ P < P_c the SC and CDW phases coexist but are most probably spatially separated; the SC phase occupies only a minor volume fraction of the sample;
• the SC onset temperature drastically increases in the coexistence region; further studies are needed to clarify the mechanism of this unusual stimulating effect of the CDW on superconductivity.

Acknowledgements

The presented experimental data have been obtained on high-quality samples provided by H. Müller and N.D. Kushch. The authors are grateful to E. Balthes, A.G.M. Jansen, I. Sheikin, and P. van der Linden for their kind assistance during experiments in Grenoble High Magnetic Field Laboratory. The work was partially supported by the DFG-RFBR grant 436 RUS 113/592.

Bibliographie

[1] J. Wosnitza Fermi Surfaces of Low-Dimensional Organic Metals and Superconductors, Springer-Verlag, Berlin, Heidelberg, 1996

[2] M.V. Kartsovnik; V.N. Laukhin J. Phys. I, 6 (1996), p. 1753

[3] J. Singleton Rep. Prog. Phys., 63 (2000), p. 1111

[4] M.V. Kartsovnik; A.E. Kovalev; N.D. Kushch J. Phys. I, 3 (1993), p. 1187

[5] P. Foury-Leylekian; S. Ravy; J.-P. Pouget; H. Müller Synth. Met., 137 (2003), p. 1271

[6] M. Basletić; B. Korin-Hamzić; M.V. Kartsovnik; H. Müller Synth. Met., 120 (2001), p. 1021

[7] T. Fujita; T. Sasaki; N. Yoneyama; N. Kobayashi; T. Fukase Synth. Met., 120 (2001), p. 1077

[8] B. Dóra; A. Virosztek; K. Maki Phys. Rev. B, 64 (2001), p. 041101 (R)

[9] B. Dóra; K. Maki; A. Virosztek Phys. Rev. B, 66 (2002), p. 165116

[10] A.I. Schegolev; V.N. Laukhin; A.G. Khomenko; M.V. Kartsovnik; R.P. Shibaeva; L.P. Rozenberg; A.E. Kovalev J. Phys. I, 2 (1992), p. 2123

[11] J.S. Brooks; X. Chen; S.J. Klepper; S. Valfells; G.J. Athas; Y. Tanaka; T. Kinoshita; N. Kinoshita; M. Tokomoto; H. Anzai; C.C. Agosta Phys. Rev. B, 52 (1995), p. 14457

[12] C.E. Campos; J.S. Brooks; P.J.M. van Bentum; J.A.A.J. Perenboom; S.J. Klepper; P.S. Sandu; S. Valfells; Y. Tanaka; T. Kinoshita; N. Kinoshita; M. Tokumoto; H. Anzai Phys. Rev. B, 52 (1995), p. 7014

[13] S. Kagoshima; R. Kondo Chem. Rev., 104 (2004), p. 5593

[14] J. Sólyom Adv. Phys., 28 (1979), p. 201

[15] G. Grüner Density Waves in Solids, Addison-Wesley, Reading, 1994

[16] W. Dieterich; P. Fulde Z. Phys., 265 (1973)

[17] A.I. Buzdin; V.V. Tugushev Sov. Phys. JETP, 85 (1983), p. 428

[18] D. Zanchi; A. Bjelis; G. Montambaux Phys. Rev. B, 53 (1996), p. 1240

[19] P.D. Grigoriev; D.S. Lyubshin Phys. Rev. B, 72 (2005), p. 195106

[20] M.C. Cross Phys. Rev. B, 20 (1979), p. 4606

[21] V. Kiryukhin; B. Keimer; D.E. Moncton Phys. Rev. Lett., 74 (1995), p. 1669

[22] A.I. Larkin; Y.N. Ovchinikov Sov. Phys. JETP, 20 (1965), p. 762

[23] P. Fulde; R.A. Ferrell Phys. Rev., 135 (1964), p. A550

[24] R.H. McKenzie, cond-mat/9706235 (1997), unpublished.

[25] M.V. Kartsovnik; W. Biberacher; E. Steep; P. Christ; K. Andres; A.G.M. Jansen; H. Müller; N. Biskup; J.A.A.J. Perenboom; J.S. Brooks; J.S. Qualls; C. Proust; A. Audouard; A. Kovalev; D. Vignolles; M. Kartsovnik; L. Brossard; N. Kushch Phys. Rev. B, 86 (1997), p. 1933

[26] P. Christ; W. Biberacher; M.V. Kartsovnik; E. Steep; E. Balthes; H. Weiss; H. Müller JETP Lett., 71 (2000), p. 303

[27] T. Ishiguro; K. Yamaji; G. Saito Organic Superconductors, Springer-Verlag, Berlin, Heidelberg, 1998

[28] G. Montambaux Phys. Rev. B, 38 (1988), p. 4788

[29] M.V. Kartsovnik; D. Andres; W. Biberacher; P. Christ; E. Steep; E. Balthes; H. Weiss; H. Müller; N.D. Kushch Synth. Met., 120 (2001), p. 687

[30] D. Andres; M.V. Kartsovnik; W. Biberacher; H. Weiss; E. Balthes; H. Müller; N.D. Kushch Phys. Rev. B, 64 (2001), p. 161104 (R)

[31] L.P. Gorkov; A.G. Lebed J. Phys. (Paris) Lett., 45 (1984), p. L433

[32] A.G. Lebed JETP Lett., 78 (2003), p. 138

[33] P.M. Chaikin J. Phys. I, 6 (1996), p. 1875

[34] M. Kartsovnik; D. Andres; P. Grigoriev; W. Biberacher; H. Müller Physica B, 346–347 (2004), p. 368

[35] M.V. Kartsovnik; D. Andres; W. Biberacher; P.D. Grigoriev; E.A. Schuberth; H. Müller J. Phys. IV, 114 (2004), p. 191

[36] D. Andres; M.V. Kartsovnik; P.D. Grigoriev; W. Biberacher; H. Müller Phys. Rev. B, 68 (2003), p. 201101 (R)

[37] A.E. Kovalev; S. Hill; J.S. Qualls Phys. Rev. B, 66 (2002), p. 134513

[38] D. Andres; M.V. Kartsovnik; W. Biberacher; K. Neumaier; H. Müller J. Phys. IV, 12 (2002), p. PR9

[39] M. Maesato; Y. Kaga; R. Kondo; S. Kagoshima Rev. Sci. Instrum., 64 (2001), p. 155104

[40] H. Ito; H. Kaneko; T. Ishiguro; H. Ishimoto; K. Kono; S. Horiuchi; T. Komatsu; G. Saito Solid-State Commun., 85 (1993), p. 1005

[41] H. Ito; M.V. Kartsovnik; H. Ishimoto; K. Kono; H. Mori; N.D. Kushch; G. Saito; T. Ishiguro; S. Tanaka Synth. Met., 70 (1995), p. 899

[42] D. Andres; M.V. Kartsovnik; W. Biberacher; K. Neumaier; E. Schuberth; H. Müller Phys. Rev. B, 72 (2005), p. 174513

[43] A. Briggs; P. Monceau; M. Nunez-Regueiro; M. Ribault; J. Richard J. Phys. (Paris), 42 (1981), p. 1453

[44] I.J. Lee; P.M. Chaikin; M.J. Naughton Phys. Rev. Lett., 88 (2002), p. 207002

[45] A.M. Gabovich; A.I. Voitenko; M. Ausloos Phys. Rep., 367 (2002), p. 583

[46] K. Kuroki; R. Arita; H. Aoki Phys. Rev. B, 63 (2001), p. 094509

[47] S. Onari; R. Arita; K. Kuroki; H. Aoki Phys. Rev. B, 70 (2004), p. 094523

[48] J. Merino; R.H. McKenzie Phys. Rev. Lett., 87 (2001), p. 237002

Commentaires - Politique