1 Introduction
The κ-phase (BEDT-TTF)2Cu[N(CN)2]Z (with Z = Cl, Br) charge transfer salts (where BEDT-TTF denotes bis-ethylenedithiotetrathiafulvalene) have attracted considerable attention due to the wealth of electronic phases encountered as a function of temperature, hydrostatic pressure or anion substitution. According to the conceptual phase diagram proposed by Kanoda [1], the Z = Cl and the Z = Br salts lie on opposite sides of a bandwidth-controlled Mott transition. The ground state of the X = Cl salt has been identified as an antiferromagnetic insulator which can be transformed into a superconductor by either applying moderate pressure or substituting Cl by Br, see, e.g. [1] and references cited therein. The metal-to-insulator transition has been explored in detail by using resistivity measurements under hydrostatic pressure for the Z = Cl salt [2,3]. In its pressurized, metallic state, the Z = Cl system has been found to show the same unusual resistivity profile as known for the Z = Br metal at ambient pressure. Three distinct transport regimes have been identified [2]: (i) a semiconducting high-T range, (ii) a bad metal behaviour at intermediate temperatures characterized by a pronounced ρ(T) maximum followed by a steep drop upon cooling, and (iii) a ρ ∼ AT2 behaviour at low temperatures preceding the superconducting transition. A variety of different explanations have been proposed for the anomalous regimes (i) and (ii), see e.g. Ref. [4]. Among these are models considering a purely electronic origin: based on a dynamical mean field (DMFT) approach, Merino and McKenzie [5] attributed the drastic change in the charge transport around T∗ ≈ 40 K to a crossover from coherent Fermi liquid excitations at low temperatures to incoherent (bad metal) excitations above. Following this line of reasoning, Limelette et al. [2] applied the DMFT calculations to a Hubbard model on a hypercubic lattice. As a result, the authors proposed a semi-quantitative explanation for the anomalous resistivity behaviour over an extended temperature range covering also the anomalous resistivity maximum.
In contrast, it has been pointed out by some researchers that the resistivity for the Z = Br salt and related materials may show significant sample-to-sample variations, depending – in an as yet unknown way – on the preparation conditions, see e.g. [6].
Here we report on an extension of the work published in Ref. [7] which has disclosed striking sample-dependent resistivity profiles for the title compound. The focus of the present investigation is to study in more detail the pressure response of the inelastic scattering contributions and to look for interrelations between the resistivity profile and other characteristic properties of these materials. The latter involve the glass transition at Tg = 77 K associated with motional degrees of freedom of the terminal ethylene groups, the drastic change in the charge transport around T∗ ≈ 40 K, which has its correspondence in anomalies in the NMR relaxation rate [1,8], the sound velocity [9] and the coefficient of thermal expansion [10], as well as the superconducting transition temperature Tc.
2 Experimental
The crystals of the title compound were prepared along two different routes: while the high-resistance (HR) crystal was synthesized according to the standard procedure [11] using trichloroethane (TCE) as a solvent, all other crystals were grown from a mixture of tetrahydrofuran (THF) and ethyleneglycol (EG) (for details see Ref. [7]). According to standard electron-probe microanalysis measurements, there are no differences in the chemical compositions of the materials within the resolution of 1–2 at%. In addition, high-resolution X-ray measurements performed at 300 K and 100 K on crystals from both the preparation routes failed to reveal significant differences in the structure parameters [7]. The resistivity was measured using a standard four-terminal AC technique operating at a frequency of 17 Hz. Measurements have been performed only along the interlayer direction. The reason for using this measurement geometry is that, owing to the large in-plane vs. out-of plane anisotropy of this material together with the irregular shape of the crystals, the determination of the pure in-plane resistivity component is very difficult and can easily be affected by an admixture of the out-of-plane component. Thus, interlayer measurements provide the most reliable resistivity data. For the pressure experiments, a He-gas-pressure setup was used, ensuring hydrostatic pressure conditions. To determine the relative change of the resistivity between a zero-pressure and a finite-pressure experiment as a function of temperature, special care was taken to guarantee constant-pressure conditions. To this end the pressure cell, containing the sample, was directly connected via a thin capillary to a large He-gas reservoir kept at a pressure of p = 170 bar at room temperature. All measurements were performed at a very slow sweep rate of 6 K/h which minimizes disorder in the ethylene groups associated with the glass transition [4] at Tg = 77 K.
3 Results and discussion
Fig. 1 shows normalized interlayer-resistivity data for a selection of crystals together with their residual resistivity ratio RRR = ρ(300 K)/ρ(0 K), where the values for T = 0 K were extrapolated from the normal state ρ(T). Fig. 1 clearly demonstrates the strong sample-to-sample variations: while the HR crystal as well as the crystals #10, #7 and #2 exhibit a semiconducting increase in ρ(T) followed by a pronounced maximum around 90 K, crystal #3 and the LR crystal remain metallic below 300 K. Yet the shoulder around 100 K in their ρ(T) data is likely to be a remnant of this resistivity hump, see the discussion below.

Normalized interlayer resistivity of various κ-(BEDT-TTF)2Cu[N(CN)2]Br single crystals together with the residual resistivity ratios RRR as defined in the text.
It has been well known that the resistivity of this compound becomes strongly suppressed upon applying hydrostatic pressure, see e.g. [1,4]. However, as has been pointed out in Ref. [7], the pressure-induced reduction is strongly non-monotonous as a function of temperature. This becomes particularly clear by exploring the quantity ρ−1Δρ/Δp = ρ(0)−1(ρ(p > 0) − ρ(0))/p, i.e. the relative change of the resistivity upon increasing the pressure from 0 to a finite pressure p. Fig. 2 shows the temperature dependence of the so-derived relative pressure effect for p = 170 bar for the HR and LR crystals. Common to both data sets in Fig. 2 is the strong and highly non-monotonous pressure effect. The pressure response is particularly strong at intermediate temperatures where ρ−1Δρ/Δp shows a pronounced peak at 47.5 K and 45.5 K for the HR and LR crystals, respectively. Moreover, Fig. 2 demonstrates that the relative pressure effect on the resistivity is about the same for both crystals near room temperature, and below about 40 K, while it is markedly different at intermediate temperatures. The difference becomes largest around 50 K where ρ−1Δρ/Δp amounts to −(360 ± 20)%/kbar and −(250 ± 15)%/kbar for the HR and LR crystals, respectively. From the data shown in Fig. 2 we infer that the additional scattering contribution which gives rise to the resistivity maximum in the HR crystal (i) is characterized by an extraordinarily strong pressure dependence and (ii) is still active – though considerably reduced – in the LR crystal. The latter statement supports the view that the shoulder in ρ(T) for the LR crystal is a remnant of the resistivity maximum in the HR crystal.
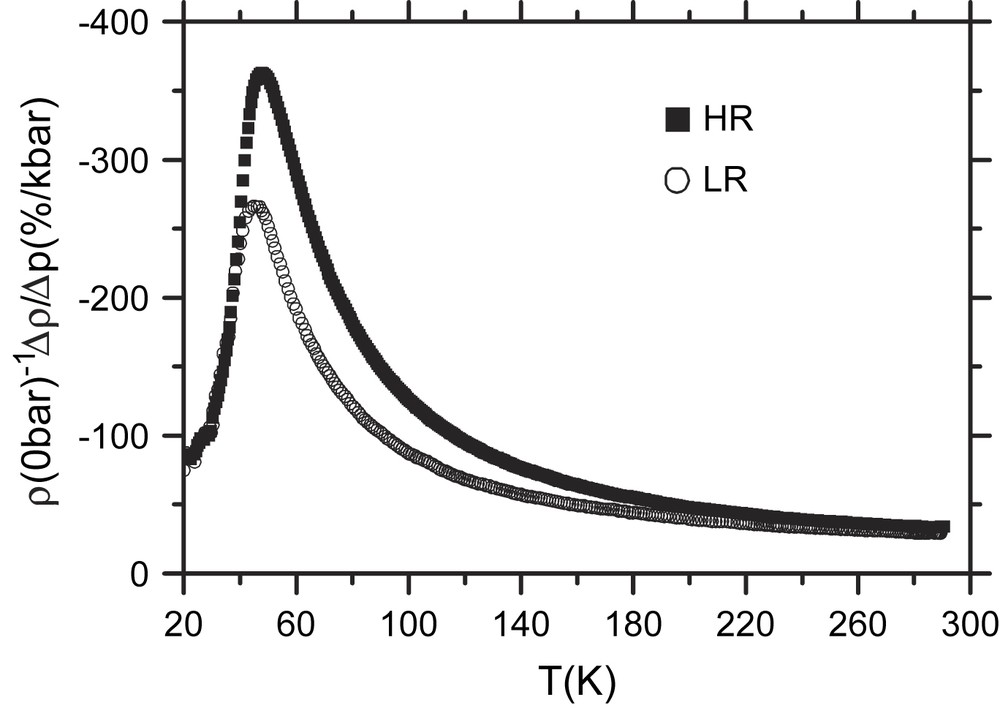
Normalized pressure response ρ−1Δρ/Δp = ρ(0 bar)−1(ρ(170 bar) − ρ(0 bar))/170 bar as a function of temperature for the HR and LR crystals.
As has been discussed in detail in Ref. [7], other characteristic temperatures of these materials, such as the glass transition at Tg and the temperature T∗ where pronounced anomalies show up in various magnetic and thermodynamic quantities, have their correspondence in clear signatures in the resistivity, i.e. somewhat broadened discontinuities in the derivative dρ/dT. More precisely, it has been found that the phase-transition-like anomaly in the coefficient of thermal expansion at T∗ [10] coincides with the midpoint of the low-T side of the dρ/dT maximum, which can be determined empirically by employing an ‘equal-areas’ construction.
In Fig. 3 we show the temperature derivative of the resistivity for a selection of crystals. The arrows in the data for the HR crystal mark the temperatures where phase-transition-like anomalies have been observed in the coefficient of thermal expansion [7]. Employing the same midpoint criterion enables us to determine the T∗ values from the dρ/dT data for the various crystals investigated, see Table 1.
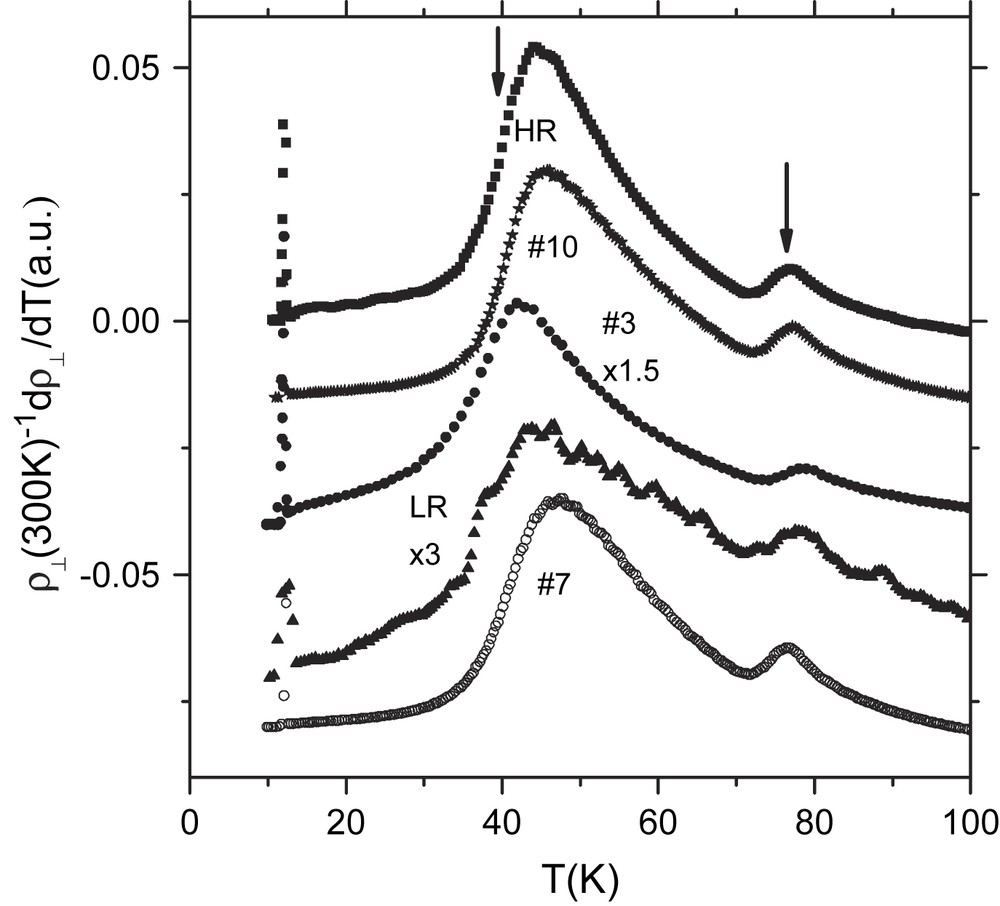
Temperature derivative of the interlayer resistivity, dρ⊥/dT, for some of the data shown in Fig. 1. For clarity, the data points at lowest temperature have been omitted and the curves have been shifted by a constant.
Compilation of various quantities defined in the text as derived from resistivity measurements on the various κ-(BEDT-TTF)2Cu[N(CN)2]Br single crystals studied here
| Sample | ρ(90 K)/ρ(300 K) | RRR | Tc (K) | 10–90% width (K) | Coefficient A (mΩ cm K−1) | T∗ (K) | T0 (K) | Tg (K) |
| LR | 0.8 | 158 | 12.20 | 0.2 | 1.6 | 39 ± 1 | 23 ± 0.5 | 77 |
| HR | 1.3 | 67 | 12 | 0.4 | 3 | 40 ± 0.7 | 28.6 ± 0.5 | 77 |
| #3 | 0.9 | 89 | 12.2 | 0.3 | 3.5 | 38 ± 0.7 | 24.5 ± 0.5 | 77 |
| #2 | 1 | 84 | 12 | 0.4 | 3.4 | 38.3 ± 0.7 | 22.4 ± 0.5 | 77 |
| #7 | 1.24 | 163 | 12.3 | 0.34 | ρ ∼ AT2.8 | 41 ± 0.7 | – | 77 |
| #10 | 1.2 | 163 | 12.1 | 0.35 | ρ ∼ AT2.8 | 41.1 ± 0.7 | – | 77 |
Concerning the low-temperature normal state, it has been found that the resistivity of the present material [12] and that of the pressurized Z = Cl salt [2] follows a ρ = ρ0 + AT2 dependence over an extraordinarily wide temperature range. This behaviour has been assigned to coherent Fermi liquid excitations [2,5] – an interpretation which has been challenged in Ref. [7] based on the ρ(T) results for the HR and LR crystals. As shown there, the low-T resistivity data follow indeed a ρ ∝ AT2 dependence over an extended range of temperature. However, the coefficients A and the temperatures T0, above which the data start to deviate from the T2 law were found to be strikingly different. In Table 1 we compile the coefficients A and the temperatures T0 derived from fitting the ρ(T) data for the various crystals studied here. Remarkably enough, for crystals #10 and #7 the resistivity data do not follow a T2 dependence at all. Here a Tx power law with x = 2.8 ± 0.1 is more appropriate to describe the low-T behaviour. Employing the same criterion (2% deviation from the fit), as used to determine the above T0 values, yields upper limits for the range of validity for this power-law dependence of (26.7 ± 0.5) K and (27.8 ± 0.5) K for crystals #7 and #10, respectively.
Concerning the superconducting transition temperature, as determined by resistivity measurements, the crystals studied here reveal small variations in their Tc values and their transition widths, cf. Table 1. The Tc values given in the table correspond to the temperature where the resistivity has reached 50% of its normal state. In addition, the 10–90% transition width is presented.
Table 1 indicates that despite considerable variations in the resistivity profiles, especially around 90 K, which manifest itself in a ρ(90 K)/ρ(300 K) ratio ranging from 0.8 to 1.3, and low-T ρ ∝ ATx dependencies with markedly different coefficients A and exponents x, all crystals have almost identical characteristic temperatures T∗ and Tc values with only moderate variations. This apparent decoupling of characteristic electronic energy scales from the resistivity behaviour is in clear contrast to the notion that the inelastic scattering in these materials is solely determined by electronic degrees of freedom [2,5]. Instead, the different resistivity profiles in Fig. 1 together with the unusual pressure response and its highly non-monotonous behaviour as a function of temperature in Fig. 2, strongly suggest that a significant fraction of the resistivity, especially at intermediate temperatures, is affected by sample-dependent, i.e. extrinsic scattering contributions. In the absence of significant differences in the crystals' structural parameters and chemical compositions, as proved by high-resolution X-ray and electron-probe-microanalysis [7], we attribute these extrinsic effects to real structure phenomena, i.e. disorder and/or defects which couple to the dynamics of the system. At the same time, our results rule out a magnetic scattering mechanism to account for the resistivity maximum. For the present singlet superconductor, magnetic scattering would be pair breaking and the strong sample-to-sample variations around the resistivity maximum should be accompanied by significant and systematic shifts in Tc which are not observed.
Table 1 demonstrates, however, that the presently available data do not make allowances for citing clear correlations between the sample quality (measured by the RRR value) and the superconducting properties (measured by Tc and the transition width) on the one hand to the presence of the additional inelastic scattering contribution on the other. Yet, the following trends can be recognized: (i) the relative size of the resistivity at 90 K, i.e. the ratio ρ(90 K)/ρ(300 K), is reduced with increasing RRR. This holds true for all crystals except crystals #10 and #7, where the resistivity shows a ρ(T) maximum at 100 K of intermediate strength although the RRR value is the largest among all crystals studied here. (ii) This reduction of the scattering contribution around 90 K with increasing RRR is accompanied by a slight increase in the superconducting transition temperature and a reduction of the transition width. Again, crystal #10 represents an exception to this trend showing a Tc and transition width of intermediate size. (iii) There is no obvious correlation between the coefficient A of the low-T ρ ∝ AT2 behaviour and the resistivity at 90 K. Remarkably, crystals #10 and #7 do not show a ρ ∼ AT2 behaviour at all, but instead reveal a ρ ∼ ATx with x = 2.8 ± 0.1 dependence over a similarly wide temperature range.
4 Conclusions
Comparative resistivity measurements on differently prepared single crystals of the title compound reveal strong sample-to-sample variations in the resistivity around 90 K. This indicates that the origin of the resistivity maximum, which has usually been observed in materials prepared along the standard procedure, is dominated by extrinsic effects. In the absence of any significant differences in the crystals' structural parameters and chemical compositions, this observation suggests that real structure phenomena, i.e. disorder and/or defects may significantly contribute to the inelastic scattering in this material. According to measurements under He-gas pressure on two crystals representing the two extreme cases of all samples studied here, these additional scattering contributions are characterized by (i) an extraordinarily strong pressure response and (ii) a highly non-monotonous temperature dependence with a particularly strong pressure effect around 50 K. Furthermore, no correlations have been found between the strength of these scattering contributions and other characteristic properties such as the glass transition at Tg = 77 K, the temperature T∗ ≈ 40 K, where the resistivity changes rather abruptly, or the superconducting transition temperature Tc.
On extending these measurements to other differently prepared crystals, it has to be shown whether or not the temperature, at which the anomalous pressure response shows a pronounced maximum, marks a characteristic feature of this additional scattering, or if it changes with the strength of this contribution. Additional measurements on a wider material basis will also enable us to address the issue of different power laws observed in the low-T normal-state resistivity and their correlations with other characteristic properties of these materials.
Acknowledgements
The authors thank M. Kartsovnik and N. Toyota for fruitful discussions and suggestions. The work was supported by the Deutsche Forschungsgemeinschaft under the auspices of the Forschergruppe 412. Work at Argonne National Laboratory is supported by the Office of Basic Energy Science, under contract no. W-31-109-ENG-38.


