1 Introduction
The electrical and magnetic properties of molecular crystals have been studied extensively in the past three decades, and various molecule-based conductors, superconductors and magnetic materials have been synthesized to date [1,2]. Heterocyclic thiazyl radicals possess unique chemical and physical properties [3]. They can be regarded as being on the borderline between organic and inorganic materials. They are chemically stable, in contrast to the instability of most organic radicals, so that they do not need protection groups on their molecular skeletons. This brings about a close packing in the solid state. Their molecular skeletons exhibit a large electronic polarization, leaving, respectively, a positive and a negative polarized charge on sulfur and nitrogen. These charges form short intermolecular and interatomic S⋯N contacts. Thiazyl radical solids always involve a multi-dimensional network consisting of face-to-face π–π overlaps and side-by-side S⋯N contacts. They have a strong spin–lattice interaction; a small lattice modification brings about a significant change in their magnetism, reflecting the fact that the SOMO (singly occupied molecular orbital) has a phase change between bonded sulfur and nitrogen. These interesting characteristics are believed to provide them with their unique solid-state physical properties.
2 Room-temperature magnetic bistability in TTTA
2.1 Magnetic properties
1,3,5-Trithia-2,4,6-triazapentalenyl (abbreviated as TTTA) was synthesized by Wolmershäuser and Johann in 1989 [4]. Recently, it was found that TTTA exhibits a first-order phase transition with a surprisingly wide thermal hysteresis loop at around room temperature [5,6]. Fig. 1(a) depicts the temperature dependence of the paramagnetic susceptibilities χp for a polycrystalline sample of TTTA. The bold arrow in this figure indicates the value of χp for the virgin sample just after sublimation crystallization. As the sample was cooled from room temperature, χp showed a slight decrease. At Tc↓ = 230 K, χp began to decrease rapidly, becoming zero at 170 K; TTTA is intrinsically diamagnetic at low temperatures. When the sample was heated from a low temperature, a diamagnetic-to-paramagnetic transition was found at Tc↑ = 305 K, indicating the large hysteresis loop. Since this loop goes through room temperature (290 K), TTTA is regarded as a magnetically-bistable material at room temperature. There was little change in the shape of the loop even after repeats of this thermal cycle.

(a) Temperature dependence of the paramagnetic susceptibility χp for a polycrystalline sample of TTTA. The bold arrow indicates the χp value for the virgin sample just after sublimation. (b) X-band EPR spectra of the HT and LT phases of TTTA at room temperature.
The temperature-variable X-band EPR experiments indicated the phase transition of TTTA at ca. 200 K and 310 K upon cooling and heating, respectively [6,7]. Fig. 1(b) compares the single-crystal EPR signals for the two phases at 300 K. The spectrum of the HT phase reveals an intense absorption, in contrast to the weak signal of the LT phase. The g-factor of the HT phase signal is , which is typical for thiazyl radicals. Since EPR is highly sensitive to the spin state of organic radicals, the two phases of TTTA can be very easily distinguished by EPR, rather than SQUID measurements.
2.2 Crystal structures
TTTA exhibited a significant difference between the crystal structures of the HT and LT phases [5–7]. The structure of the HT phase consisted of a polar 1D stacking column, in which the molecules were related by translational relations with a constant interval. This stacking column was surrounded by six neighboring columns with very short S⋯N and S⋯S contacts. By contrast, TTTA exhibited a strong dimerization along the stacking direction in the crystal structure of the LT phase. This radical dimerization must be responsible for the diamagnetic properties of the LT phase. Fig. 2 shows a schematic comparing the nearest-neighbor intermolecular arrangements in the two phases. It was notable that the molecules had an eclipsed overlap in the LT phase, in contrast to a shifted overlap in the HT phase. More specifically, the molecular planes in the LT-phase dimer were not parallel; the distance between the –S–N–S– moieties was shorter by ca. 0.09 Å than that between the –N–S–N– moieties, probably reflecting a bonding interaction between the unpaired electrons which were concentrated on the –S–N–S– moieties. This suggests that bond formation is the main driving force of this phase transition.
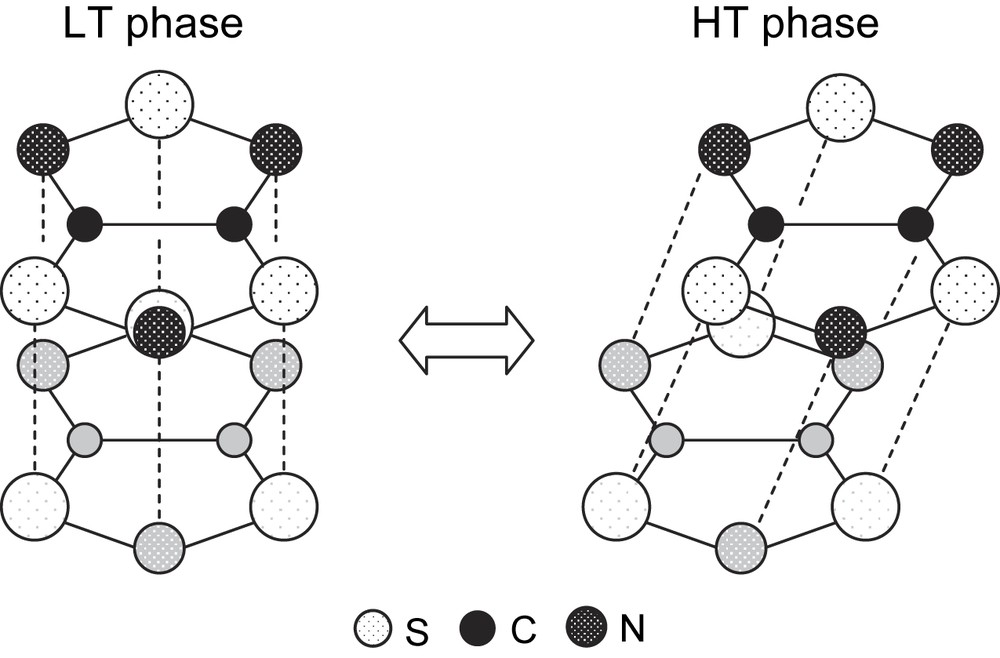
Nearest-neighbor intermolecular overlaps of TTTA in the HT and LT phases. The electrostatic interaction favors a shifted overlap, while the exchange interaction results in an eclipsed overlap.
We believe that there is a competition between the exchange and electrostatic interactions (see Fig. 2). The exchange interaction favors an eclipsed overlap, such as that found in the LT phase, because this structure maximizes the intermolecular overlap between the SOMOs. However, this is the most disadvantageous structure from the viewpoint of electrostatic energy because it includes intermolecular and interatomic contacts between polarized charges of the same sign, namely Sδ+⋯Sδ+ and Nδ−⋯Nδ−. It is presumably this competition that causes the drastic phase transitions in the thiazyl radical family.
2.3 Phase control by pressure and light irradiation
The effects of quasi-hydrostatic pressures on TTTA were studied to control the magnetic bistability; the temperature dependence of χp of TTTA was studied under 0.38, 0.75, and 1.5 GPa [8]. TTTA was found to undergo a sharp diamagnetic–paramagnetic transition even under pressure, with a significant shift in the transition temperature. The pressure dependences of Tc↑ and Tc↓ are shown in Fig. 3. Both Tc↑ and Tc↓ increased significantly with increasing pressure. Thus, the bistable range shifted toward higher temperatures. Although room temperature (290 K) is just below Tc↑ at ambient pressure, it falls in the center of the hysteresis loop at 0.75 GPa. That is, room-temperature bistability can be stabilized by pressure. The two solid curves in Fig. 3 are only eye guides, but the gradients at the ambient pressure are estimated to be roughly ⅆTc↓/ⅆp = 45 ± 20 K GPa−1 and ⅆTc↑/ⅆp = 20 ± 10 K GPa−1. The theoretical value of ⅆTc/ⅆp is given by the Clapeyron equation, ⅆp/ⅆTc = ΔS/ΔV = ΔH/(TcΔV), where ΔV is the volume change, though this equation is valid only under thermal equilibrium. The enthalpy changes for the transitions in TTTA were obtained by DSC measurements [6,7]. The difference between the unit cell volumes of the two phases is 3.4 Å3 at room temperature [5–7]. Since the unit cell contains four molecules, the volume difference is ΔVRT = 3.4NA/4 Å3 mol−1, where NA is Avogadro's constant. The theoretical value for ⅆTc/ⅆp at p = 0 GPa can be estimated as 60 K GPa−1 under the assumption that ΔV = ΔVRT. The agreement between the theoretical and experimental values is fairly good (the same order of magnitude), and the equation can explain the shift toward higher transition temperatures with increasing pressure.
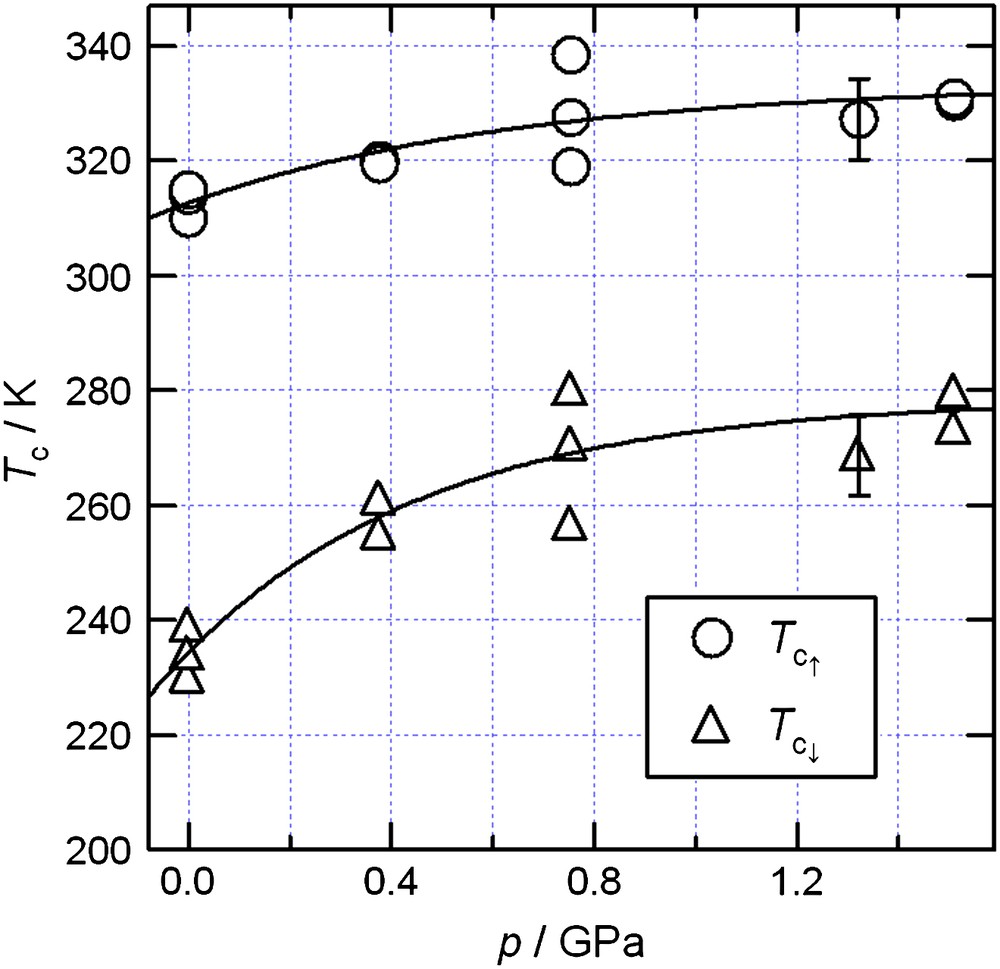
Pressure dependence of the transition temperatures, Tc↑ and Tc↓, for TTTA. The solid curves are eye guides.
The phase control of TTTA was also achieved using photoirradiation [9]. There is a very clear chromism between the crystal surfaces of the two phases under a polarized microscope, namely between red–purple in the HT phase and yellow–green in the LT phase. The photo-induced transition from the diamagnetic LT phase to the paramagnetic HT phase was observed after a single-shot (6 ns pulse) irradiation at 2.64 eV at 296 K. In addition, a clear threshold was identified in the dependence of the LT-to-HT conversion efficiency on the excitation photon density. This strongly indicated that the observed phenomenon was not a thermal effect, but a photo-induced phase transition [9].
2.4 Charge doping
The electrical properties of TTTA were examined. The conductivity for the HT phase was 10−8 Ω−1 cm−1, with an activation energy of 0.33 eV under a vacuum. The conductivity for the LT phase was two orders of magnitude lower. The HT phase was found to be an insulator despite its three-dimensional network structure free of radical dimerization, where each molecule has one unpaired electron. Thus, it is highly possible that the HT phase can be regarded as a Mott insulator, in which strong on-site electron–electron repulsion results in electron localization.
The carrier doping on the HT phase of TTTA was carried out with I2 vapor. The conductivity was quickly enhanced by four or five orders of magnitude, saturating after 10 h. The saturation was presumably due to a breakup of the crystal structure caused by penetration of the dopant. Since the doped material was very air-sensitive, we could not carry out further characterization. It was clearly demonstrated, however, that hole doping of the HT phase of TTTA brought about significant enhancement of the conductivity.
3 Complex phase transitions in BDTA: spin-gap, antiferromagnetic ordering and double melting
3.1 Diamagnetic–paramagnetic phase transition
1,3,2-Benzodithiazolyl (abbreviated as BDTA) was synthesized by Wolmershäuser et al. in 1984 [10]. Awere et al. reported its crystal structure: it consists of a centrosymmetric dimer, where the dimer units form a two-dimensional network with short S⋯S contacts [11]. This is very similar to the structure of the κ-modification of BEDT–TTF2·X compounds (BEDT–TTF = bis(ethylenedithio)tetrathia-fulvalene, X = Cu(NCS)2, etc.), which are known as organic superconductors whose critical temperatures exceed 10 K [12]. Awere et al. also reported that BDTA was diamagnetic at least below room temperature because of strong antiferromagnetic interactions in its structure [11]. In this section, we will describe the complex phase transitions in BDTA, which are characterized by interplay among the diamagnetic spin-gap phase, paramagnetic phase, antiferromagnetic ordered phase and liquid phase [13].
Fig. 4 depicts the temperature dependence of χp for BDTA above room temperature (open circles). BDTA was diamagnetic at room temperature due to its dimerized structure [11]. Upon heating, however, BDTA exhibited a first-order phase transition to a paramagnetic high-temperature phase at 346 K [13], though the structure of this phase has not yet been identified. In the cooling process, a paramagnetic-to-diamagnetic transition was observed at 320 K, which was associated with the hysteresis of 26 K. This value is much smaller than that of TTTA, but still larger than the others in typical molecular solids. It should be noted that this transition could be observed only for the aged BDTA samples, which were subjected to repeated thermal cycles over the 2–365 K range. These cycles facilitated the phase transition, probably due to an increase in the concentration of lattice defects. Thus, fresh samples always exhibited superheating and supercooling, as will be described in the next section.

Temperature dependence of χp for BDTA above room temperature. The gray plots indicate the effects of superheating and supercooling.
3.2 Superheating and supercooling
The most characteristic feature of BDTA is the occurrence of superheating and supercooling on the phase transition above room temperature. The magnetic behavior in these non-equilibrium processes is shown in Fig. 4 as gray circles. Fig. 5 depicts the Gibbs free energy for BDTA determined by magnetic measurements and visual observation. In this figure, L and MO denote the liquid and antiferromagnetic ordered phases, respectively. The intersection between the LT and HT curves indicates the diamagnetic–paramagnetic phase transition at 346 K. Upon further heating of the superheated LT phase, the material melted at 360 K once, but the liquid immediately solidified into the HT phase even upon heating. This is because the free energies decrease in the order LT > L > HT in the 360–364 K range. Upon heating, the LT phase relaxes into the HT phase through the L phase at 360 K. At 364 K, the solid BDTA in the HT phase exhibited a second melting. This process has been called double melting, and has been observed, for example, in molecular crystals and organic polymers [14].
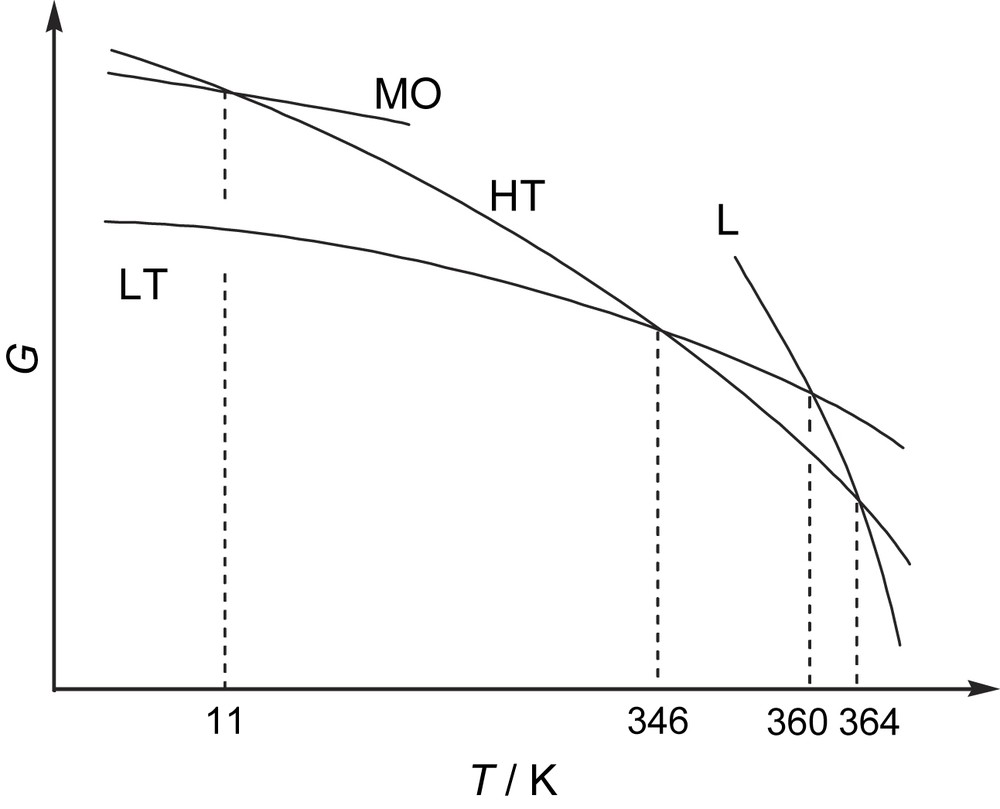
Gibbs energy phase diagram for BDTA. HT: high-temperature phase; LT: low-temperature phase; L: liquid; MO: antiferromagnetic ordered state.
Supercooling of the HT phase also occurred (see Fig. 4), and further cooling resulted in antiferromagnetic ordering at 11 K. The temperature dependence of χp for the supercooled HT phase followed the Curie–Weiss law. Below 15 K, χp showed a small anomaly with a rather abrupt change at around 11 K, suggesting antiferromagnetic ordering. The temperature dependence of the heat capacity cp exhibited a λ-shaped anomaly at 11 K, supporting the antiferromagnetic ordering at this temperature. The HT phase transforms into the MO phase below 11 K, as indicated in Fig. 5. The structures of the HT and MO phases must be nearly the same. Thus, it is thought that the crystal structures for the spin-gap state and the antiferromagnetic ordered state are switched at the phase transition at 346 K.
The complicated temperature dependence of the magnetic behavior of BDTA was clearly explained in terms of the cooperation between the double melting, solid-state phase transition and magnetic ordering, in which the HT, LT, L, and MO phases interplayed. Alternative relationships between the spin-gap state and the antiferromagnetic ordered state have been reported in low-dimensional magnetic materials, such as spin-Peierls compounds [15] and copper-oxide high-Tc superconductors [16]. While the competition between the two states occurs on the identical crystal structure in these materials, BDTA forms two states with different crystal structures that are linked at the structural phase transition.
4 Ferromagnetic interactions in molecular compounds of thiazyl radicals
4.1 Ferromagnetic coordination polymer in TTTA·[Cu(hfac)2]
Thiazyl radicals are useful as building blocks for supramolecular materials; they can operate as a ligand to various metal ions and as a donor to various acceptors. A 1:1 molecular compound, TTTA·[Cu(hfac)2] (Cu(hfac)2 = bis(hexafluoroacetylacetonato)-copper(II)), was obtained by the reaction of stoichiometric amounts of the components in a heptane solution under a nitrogen atmosphere [17]. The crystal structure is shown in Fig. 6, in which the CF3 groups of Cu(hfac)2 are omitted. TTTA molecules occupy the axial positions of the elongated octahedral around the Cu(II) ion, and bridge the distance between the Cu(II) ions, resulting in an infinite zigzag chain along the b axis. While Rawson et al. have reported the mono-, di-, and tri-metallic coordination compounds of 1,2,3,5-dithiadiazolyl radicals [18], TTTA·[Cu(hfac)2] is the first coordination polymer made of thiazyl radicals. While various nitronylnitroxides [19] and polynitroxyl radicals [20] are known to act as a bidentate bridging ligand and to form polymeric coordination compounds, the structure of TTTA·[Cu(hfac)2] clearly indicates that the polycyclic thiazyl radicals have a similar chemical capability. As shown in Fig. 6, the Cu(II) ion is sandwiched between two TTTA molecules, labeled A and B, at distances of 2.342 and 2.478 Å from the Cu(II) ion. The former distance is shorter by more than 0.1 Å. The molecular plane of TTTAA is nearly orthogonal to the plane defined by the four hfac oxygen atoms, while that of TTTAB is significantly tilted.
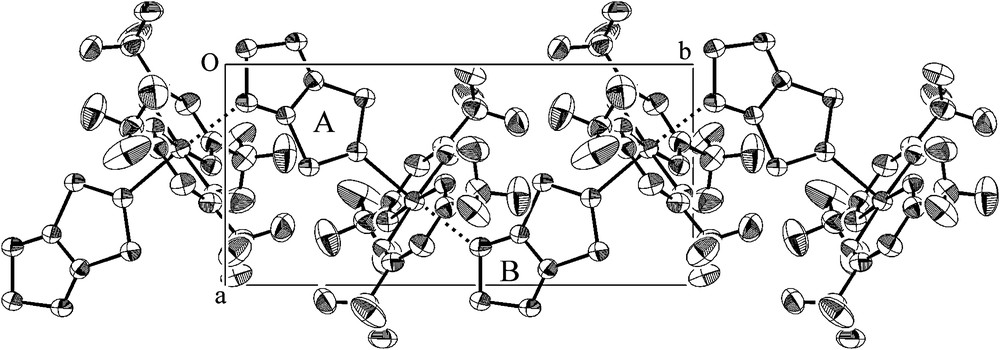
Crystal structure of TTTA·[Cu(hfac)2].
The χpT value for TTTA·[Cu(hfac)2] increases with decreasing temperature down to ca. 30 K, indicating a ferromagnetic coupling. After passing through a maximum at this temperature, χpT shows an abrupt decrease, suggesting a weak antiferromagnetic coupling between the ferromagnetic units. The ferromagnetic and antiferromagnetic interactions can be ascribed to the interactions on the sides A and B, respectively. The ferromagnetic coupling constant was calculated as J/kB = 5.1 K. This is stronger than those in the axial coordination compounds of Cu(hfac)2 and nitroxyl radicals [19], presumably because the energy level of the SOMO of TTTA is closer to those of the d orbitals of Cu(II).
4.2 Ferromagnetism in BBDTA salts driven by evaporation of crystal solvent
Benzo[1,2-d:4,5-d′]bis[1,3,2]dithiazole (abbreviated as BBDTA) was initially reported independently by Wolmershäuser et al. and by Wudl et al. [21,22]. Wolmershäuser reported the crystal structure and the 57Fe Mössbauer spectra of the radical cation salt BBDTA·Fe(III)Cl4·CH3CN [23]. In this crystal, BBDTA forms a ladder-type structure through which the FeCl4 anions are weakly linked. Mössbauer spectroscopy indicated antiferromagnetic ordering of the Fe3+ magnetic moments below 6.6 K. In the following section, we describe the bulk ferromagnetism in BBDTA salts driven by evaporation of the crystal solvent.
BBDTA·GaCl4·CH3CN was prepared by the reaction of BBDTA·Cl and GaCl3 [24]. The structure of BBDTA·GaCl4·CH3CN was found to consist of a face-to-face radical dimer, with half of the unit being crystallographically independent. The crystal solvent, CH3CN, occupied the space beside BBDTA, coordinating with the sulfur atom. These dimers were stacked via short S⋯N contacts, forming a ladder-type structure. Between the ladders, there was a rather short S⋯S contact, resulting in a 2D network parallel to the ab plane. The GaCl4 anions were located between the ladder layers.
As shown by the closed circles in Fig. 7, the χpT values for BBDTA·GaCl4·CH3CN are nearly zero in the whole temperature range [25]. This nonmagnetic property can be ascribed to a strong antiferromagnetic interaction in the dimer. However, we observed a dramatic change in the bulk magnetic properties after evaporation of the crystal solvent. The open circles in Fig. 7 show the magnetic data for a sample in which 75% of the CH3CN was removed by evacuation for 96 h. The material exhibited paramagnetism, in remarkable contrast to the nonmagnetic properties of the solvated form. As the temperature decreased, χpT increased gradually, which is indicative of ferromagnetism. The inset in Fig. 7 shows the temperature dependence of the ac susceptibilities (χ′: in-plane; χ″: out-of-plane) for the same sample. The plots of χ″ show an anomaly below 6.7 K with a rapid increase in χ, indicating ferromagnetic ordering. The isothermal magnetization curve at 2 K for this sample indicated that the material obtained was a soft magnet. BBDTA·FeCl4·CH3COCH3 exhibited similar solvation effects: it showed ferrimagnetic ordering at TN = 44 K upon evaporation of the volatile crystal solvent, acetone [25].
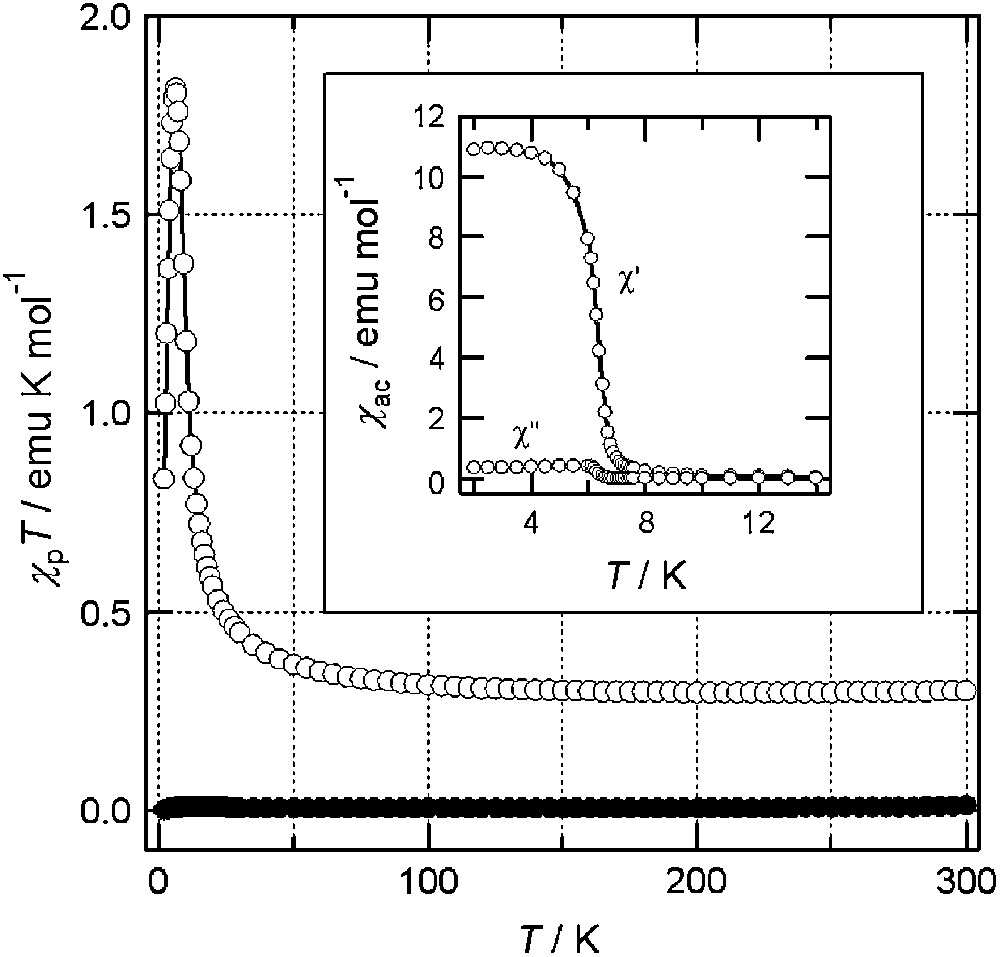
Temperature dependence of χpT for BBDTA·GaCl4 in the solvated (●) and non-solvated form (○). The inset shows the temperature dependence of χac for the non-solvated form.
The crystal growth of the solvent-free BBDTA·GaCl4 was also successful [26]. The crystals were prepared by recrystallization from a 1:1 mixed solvent of trimethylacetonitrile and dichloromethane at −23 °C. In the recrystallization, mixtures of at least three polymorphs of solvent-free BBDTA·GaCl4, labeled α (plates), β (needles), and γ (blocks), were obtained. The γ-phase, consisting of a 1D zigzag chain of BBDTA, exhibited a ferromagnetic transition at 7.0 K, suggesting that the desolvated material obtained from BBDTA·GaCl4·CH3CN would be in the γ-phase.
4.3 Possible supramolecular superexchange mechanism in BDTA·[Ni(mnt)2]
We prepared BDTA·[Ni(mnt)2] ([Ni(mnt)2] = bis(maleonitriledithiolate)-nickel(II)) by the reaction of BDTA·Cl and n-Bu4N·[Ni(mnt)2] in a 1:1 mixed solvent of dry MeCN and EtOH [27]. In this salt, BDTA is in a +1 state; BDTA is an S = 0 counter-cation for the S = 1/2 [Ni(mnt)2]− anion. The structure of BDTA·[Ni(mnt)2] consists of alternating stacking chains of BDTA and [Ni(mnt)2] along the crystallographic b axis (the side view is depicted in Fig. 8). Two neighboring stacking columns are connected by a short contact between BDTA and [Ni(mnt)2]; the dithiazole ring of BDTA is “tweezed” by the two nitrile groups of [Ni(mnt)2] in a lock-and-key structure. The intermolecular and interatomic S⋯N distances are 3.199 and 3.302 Å.
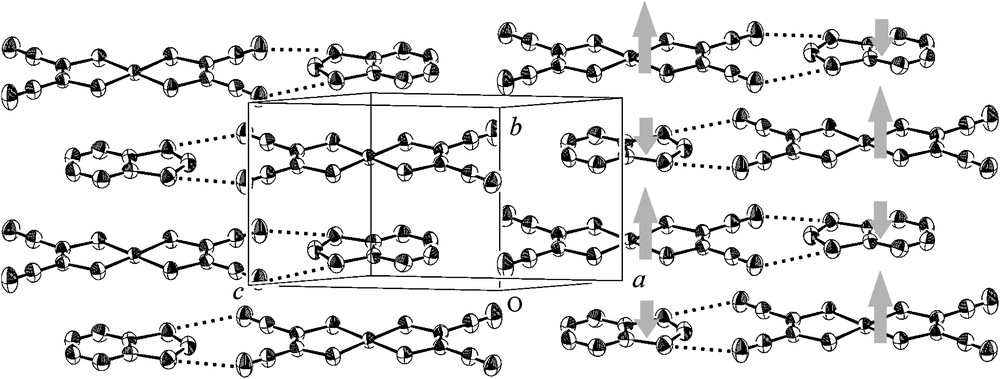
Side view of the alternating stacking structure in BDTA·[Ni(mnt)2]. Gray arrows indicate a possible alignment of the spin densities.
The magnetic measurements indicated coexistence of a ferromagnetic interaction and a weak antiferromagnetic interaction between the ferromagnetic units. A possible pathway of ferromagnetic coupling is D+A− stacking along the b axis. This implies superexchange ferromagnetic coupling between S = 1/2 [Ni(mnt)2] molecules through the nonmagnetic BDTA molecule. BDTA and [Ni(mnt)2] form a lock-and-key type contact, in which a nearly orthogonal overlap is expected. In this case, the SOMO of BDTA can be regarded as a node of the wave function for the magnetic orbital of the supramolecular species, BDTA·[Ni(mnt)2], such that the sum of the atomic spin densities on BDTA should be negative. The gray arrows in Fig. 8 indicate a possible spin alignment, which could explain the ferromagnetic coupling. This may be regarded as a supramolecular superexchange or an expanded McConnel's Type I mechanism [28].
5 Summary
We have described our recent work on thiazyl radicals and related materials. In Sections 2 and 3, we described the diamagnetic–paramagnetic phase transitions in TTTA and BDTA, and their novel solid-state properties, such as room-temperature magnetic bistability, photo-induced phase transition, supercooling and superheating. Research on bistability has become a new branch in molecular magnetism [5,6,29,30]. In Section 4, thiazyl radicals were shown to operate as building blocks for supramolecular materials, in which ferromagnetic interactions and magnetic ordering were achieved at rather high temperatures.
Acknowledgements
This article includes the results of the collaborations with Yasuhiro Nakazawa, Kazuya Saito, Michio Sorai, Masashi Takahashi, Masuo Takeda, Hiroyuki Matsuzaki, Hiroshi Okamoto, and Tamotsu Inabe. The authors are thankful for their kind support and fruitful discussions. This work was supported by Grants-in-Aid for Scientific Research from the Ministry of Education, Science, and Culture of Japan.


