Multifunctional interplay among the conductivity, magnetism and dielectricity in π–d interacting λ-(BETS)<sub>2</sub>FeCl<sub>4</sub>

Naoki Toyota; Takahiro Suzuki

doi:10.1016/j.crci.2006.09.010

Account / Revue

Multifunctional interplay among the conductivity, magnetism and dielectricity in π–d interacting λ-(BETS)₂FeCl₄

Naoki Toyota ¹ ; Takahiro Suzuki ¹

¹ Physics Department, Graduate School of Science, Tohoku University, Aoba-ku, Sendai 980-8578, Japan

Comptes Rendus. Chimie, Volume 10 (2007) no. 1-2, pp. 37-51.

Résumé

The title BETS salt is a quasi-two-dimensional paramagnetic metal with a high-spin localized at the Fe^III site in the tetrahedral anion FeCl₄. At T_MI = 8.3 K, however, it undergoes a metal-to-insulator transition spontaneously associated by antiferromagnetic (AFM) and ferroelectric-like orders, and also by the structural transition. An application of a high magnetic field makes this insulator unstable against reentering the metallic state, followed at higher fields by a transition to the superconducting state. These unique properties totally indicate noticeable spin- and charge-correlation of π electrons in the crystal lattice with localized d-spins. This article reviews these phenomena focusing on the AFM insulating states and high-temperature metallic states exhibiting a multifunctional interplay among the conductivity, magnetism and dielectricity. Discussions will be made on the anomalous metallic state, in comparison with the isostructural, superconductor GaCl₄ salt exhibiting contrasting anomalies in the metallic state.

Métadonnées

Reçu le : 2006-03-06
Accepté le : 2006-09-11
Publié le : 2006-12-14

DOI : 10.1016/j.crci.2006.09.010

Mots clés : Magnetic molecular conductors, Metal–insulator transition, Antiferromagnetic order, Colossal magnetodielectricity, Superconductivity, Charge order, Nonlinear transport

Affiliations des auteurs :

Naoki Toyota ¹ ; Takahiro Suzuki ¹

¹ Physics Department, Graduate School of Science, Tohoku University, Aoba-ku, Sendai 980-8578, Japan

@article{CRCHIM_2007__10_1-2_37_0,
     author = {Naoki Toyota and Takahiro Suzuki},
     title = {Multifunctional interplay among the conductivity, magnetism and dielectricity in \ensuremath{\pi}{\textendash}d interacting {\ensuremath{\lambda}-(BETS)\protect\textsubscript{2}FeCl\protect\textsubscript{4}}},
     journal = {Comptes Rendus. Chimie},
     pages = {37--51},
     publisher = {Elsevier},
     volume = {10},
     number = {1-2},
     year = {2007},
     doi = {10.1016/j.crci.2006.09.010},
     language = {en},
}

TY  - JOUR
AU  - Naoki Toyota
AU  - Takahiro Suzuki
TI  - Multifunctional interplay among the conductivity, magnetism and dielectricity in π–d interacting λ-(BETS)2FeCl4
JO  - Comptes Rendus. Chimie
PY  - 2007
SP  - 37
EP  - 51
VL  - 10
IS  - 1-2
PB  - Elsevier
DO  - 10.1016/j.crci.2006.09.010
LA  - en
ID  - CRCHIM_2007__10_1-2_37_0
ER  -

%0 Journal Article
%A Naoki Toyota
%A Takahiro Suzuki
%T Multifunctional interplay among the conductivity, magnetism and dielectricity in π–d interacting λ-(BETS)2FeCl4
%J Comptes Rendus. Chimie
%D 2007
%P 37-51
%V 10
%N 1-2
%I Elsevier
%R 10.1016/j.crci.2006.09.010
%G en
%F CRCHIM_2007__10_1-2_37_0

Naoki Toyota; Takahiro Suzuki. Multifunctional interplay among the conductivity, magnetism and dielectricity in π–d interacting λ-(BETS)₂FeCl₄. Comptes Rendus. Chimie, Volume 10 (2007) no. 1-2, pp. 37-51. doi : 10.1016/j.crci.2006.09.010. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2006.09.010/

Version originale du texte intégral

1 Introduction

There have been long-term studies about low-dimensional molecular metals, since the first discovery of a quasi-one-dimensional (Q1D) metal TTF-TCNQ [1]. During the last three decades or more a variety of salts in combination of donors such as TMTSF and BEDT-TTF (simply called ET) molecules and acceptors of linear, planar, polyhedral and polymeric molecules have been found to remain metallic down to low temperatures [2]. Moreover, not a few of these charge-transfer molecular crystals have been known to exhibit superconductivity. It has passed about two decades since some ET salts with polymeric anions such as Cu(NCS)₂ [3] and CuN(CN)₂Br [4] recorded the transition temperature T_C in a range of 10 K. To this day, however, a number of studies have been devoted to clarifing the superconducting and normal-conducting properties that are characteristic to these low dimensional, π electronic systems [5–9].

In parallel to these studies on molecular metals and superconductors, there have been explored highly conducting magnetic salts in which paramagnetic transition-metal ions are incorporated. In 1986, Hünig and his collaborators synthesized, (DCNQI)₂Cu, the first π–d interacting metal. The interplay of the conducting π electrons with the mixed-valent Cu states has been extensively studied, which are reviewed in Refs. [10–13]. Other attempts were made on TMTTF, TMTSF and ET donors with a tetrahedral anion FeCl₄ [14–16]. Although a weak antiferromagnetic (AFM) exchange interaction between the d-spins was observed, any evidences for π–d interaction-induced phenomena were not obtained, simply because the π electrons are localized in these insulators. On the one hand, a metallic conductivity stable down to low temperatures was observed in (ET)₃CuCl₄H₂O with a weak ferromagnetic (FM) interaction between Cu²⁺ ions with localized spins of S_d = 1/2 [17,18], while another paramagnetic salt β″-(ET)₄[(H₃O)Fe(C₂O₄)₃]C₆H₅CN synthesized by Kurmoo et al. was found to exhibit superconductivity at T_C = 7–6 K in coexistence with probably a short-range AFM order with S_d = 5/2 (Fe^III) [19,20]. In those days, Kobayashi and his collaborators synthesized BEDT-TSF (simply BETS) salts with FeX₄ (X = Cl, Br) having two different crystal morphologies of κ- and λ-type stacking of BETS donors [21,22]. This family of salts demonstrates that in the κ-type salt, a long-range AFM order below T_N = 2.5 K coexists with superconductivity below 1.1 K, and in the λ-type salt, it breaks up the metallic state to induce the metal–insulator (MI) transition. (The present review article concerns the latter λ-type salt.)

The last material to be introduced here is ET₃MnCr(C₂O₄)₃ synthesized by Coronado and his collaborators [23], which exhibits a coexistence of the metallic state with an FM long-range order. The bimetallic complexes [Cr^IIMn^III(C₂O₄)₃] form infinite layers of oxalate-bridged hexagonal networks sandwiching the β-type stacking layers of ET. This new type of π–d systems shows a long-range FM state with the Curie temperature T_C = 5.5 K and the saturation magnetization of 7.1μ_B. Moreover the metallic behavior with high conductivity remains stable down to low temperatures without exhibiting any prominent anomalies around T_C except a small negative magneto-resistance. These results indicate an existence of rather weak π–d interactions responsible for the inconspicuous interplay between magnetism and conductivity.

Comprehensive review articles [24–26] are available for details in chemical and physical properties of magnetic molecular conductors.

In this paper, we review the present state of studies on physical phenomena induced by π–d interactions in λ-(BETS)₂FeCl₄. We introduce the crystal structure and MI transition in Section 2 and then the theoretical understandings of magnetic exchange interactions and AFM order in Section 3. In Sections 4 and 5, we describe the anomalous metallic states and the AFM insulating states, respectively. In Section 6 we discuss the correlation between these two states in comparison with the isostructural, superconducting salt with nonmagnetic GaCl₄ anions, followed by concluding remarks in Section 7.

2 Crystal structure and metal–insulator transition

Fig. 1 illustrates the crystal structure of λ-(BETS)₂FeCl₄ which has a unique donor stacking as follows [27]. The crystal symmetry is triclinic with the space group $P \bar{1}$ having only an inversion center except the translation symmetry. The BETS donors stack along the a-axis, forming a tetradic column with two independent BETSs. Rather strong coupling between the columns along the c-axis makes the ac-plane most conductive as will be described below. The planes are bridged to each other by tetrahedral FeCl₄ anions through several coupling routes between Se and Cl shorter than the van der Waals distance. These characteristic couplings lead to π–d exchange interactions via the Cl 3p-orbitals as will be shown in Section 3.1.

Fig. 1
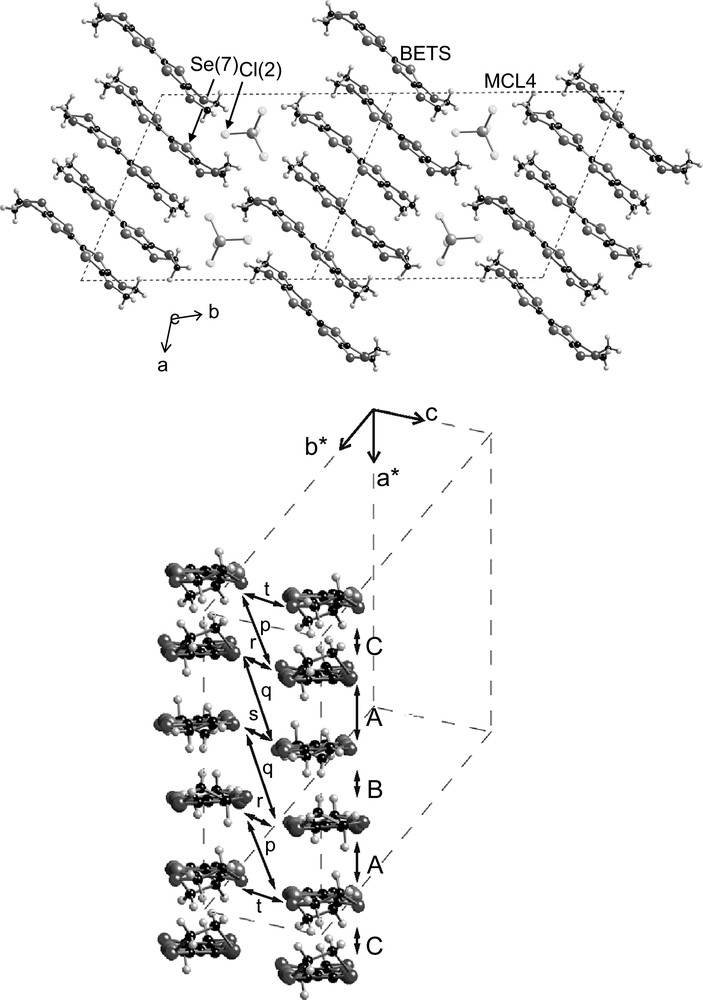
Crystal structure of λ-(BETS)₂MCl₄ (M = Fe, Ga); (upper part) projected along the c axis showing the double unit cells and (lower part) the perspective view featuring an inter-column coupling. The lattice parameters in M = Fe (Ga) are a = 16.164 (16.141) (Å), b = 18.538 (18.580) (Å), c = 6.593 (6.594) (Å), α = 98.40° (98.37°), β = 96.67° (96.77°), γ = 112.52° (112.55°), V = 1773.0 (1774.0) (Å³). The transfer integrals (in unit of 10⁻³) in M = Fe are t_A = 33.55, t_B = 18.27, t_C = 14.83, t_p = −2.80, t_q = −9.30, t_r = 13.00, t_s = 17.11 and t_t = 2.56 [28].

The transfer integral of π-orbitals [28] at A among the tetradic sequence (–A–B–A–C–) along the column is almost twice as large as those at B and C. The reason is found in the peculiar face-to-face configuration of a so-called ring-over-double bond realized solely at A. For the inter-column coupling due to the side-by-side configuration, the transfer integrals, in particular, along the routes of r and s in the figure are fairly large (comparable to those at B and C), making the ac- plane most conductive. Importantly to note, these coupling routes throw a bridge just across the dimers (A) on neighboring columns. (For comparison with other calculations for the transfer integrals [29], refer to the Appendix in Ref. [28].) These unique overlappings of π-orbitals suggest both the in-plane anisotropy in the electronic band structure and the characteristic exchange couplings with localized d-spins as will be described later.

Fig. 2 plots the in-plane resistivity ρ (normalized at 300 K) and magnetic susceptibility χ in the FeCl₄ salt as a function of logarithmic temperature, together with the resistivity in the GaCl₄ salt, a nonmagnetic superconductor with T_C = 4.8 K that is isostructural with almost the same lattice parameters (Fig. 1). There appears a broad maximum in the electrical resistance around 100 K as well as in κ-ET salts [3,30]. The inflection points in the sharply decreasing curve below 100 K are found at 60 K (FeCl₄) and 50 K (GaCl₄), which can be seen in the peaks of dρ/dT. (See the inset in Fig. 2.) These inflection points correspond to a so-called T^∗ anomaly in κ-ET salts [8,30]. With further decreasing temperature, the drastic MI transition appears at T_MI = 8.3 K inducing a sharp upturn in ρ by a factor of more than 10⁶, while the GaCl₄ salt undergoes a superconducting transition at T_C = 4.8 K.

Fig. 2
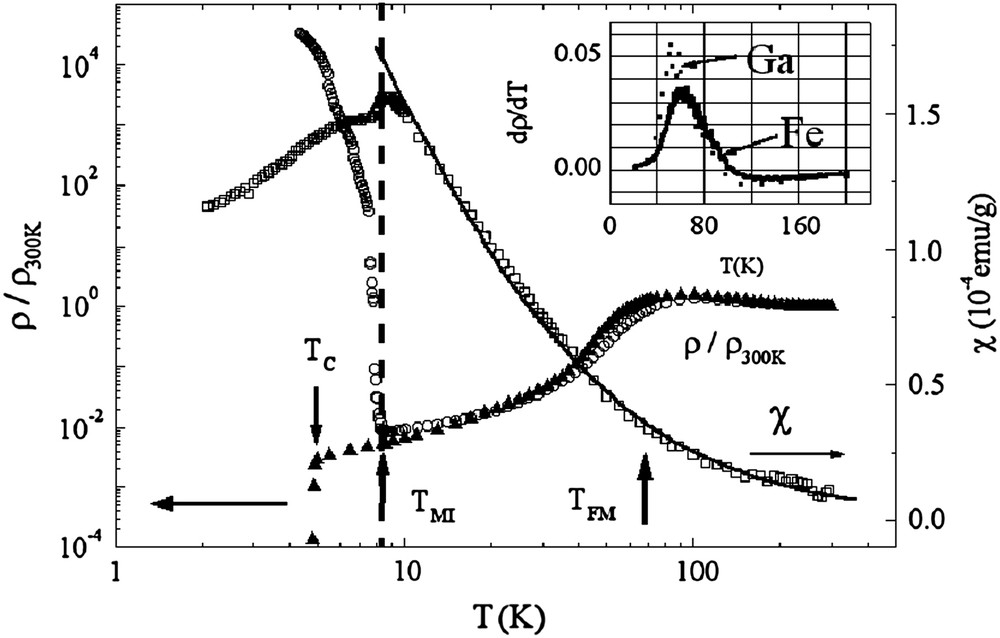
Temperature dependence of the in-plane electrical resistivity ρ normalized at the room temperature value and the magnetic susceptibility χ (H//ac-plane) of λ-(BETS)₂FeCl₄, shown by open symbols. The resistivity for the isostructural, superconducting GaCl₄ salt is also shown for comparison by the closed triangles. The solid line is a theoretical fit of the susceptibility data to a Curie–Weiss law. The inset shows the temperature derivative of the resistivity, dρ/dT, for both salts. For T_FM, see Section 4.1 [61].

The magnetic susceptibility above T_MI in the FeCl₄ salt follows a Curie–Weiss law with high- spins S_d = 5/2 localized at Fe³⁺ and the Weiss temperature Θ of about −10 K. These magnetic properties indicate that the crystal field effect in the tetrahedral anion is strong enough for the high-spin state to be realized and that the spins interact antiferromagnetically with each other in the paramagnetic metal (PM) states above T_MI. Just at this temperature T_N (=T_MI) = 8.3 K, the PM state turns into an AFM insulating (AFMI) state below which the localized π electrons take a quantum spin S_π = 1/2. It is verified in the magnetization drop as seen in the vicinity of T_N, and thus the MI transition accompanies an S_π–S_d coupled AFM order [31]. (Note that the ratio of magnetizations contributed by each spin system, S_π(S_π + 1)/S_d(S_d + 1), is about 0.08.) Really the two sub-lattice model [32] for these coupled spins can successfully explain the AFM resonance [32–34] that is attributed to the spin waves excited on the π spins. According to magnetic torque measurements [22,35], the spin easy axis tilts from the c-axis toward the b^∗-axis by about 30–40°, and the metamagnetic transition accompanying a spin-flop transition to the spin canted AFM state occurs at H_sf = 1.5 T [33].

To note, these conducting and magnetic properties in the λ salts are sensitively dependent on pressure and anion alloying [21,22]. For example, the isostructural mixed Fe_xGa_1−xCl₄ salts with 0.35 < x < 0.5 undergo successive transitions that the PM state turns into a superconductor at T_C ≈ 4 K, then being transformed to the AFMI state at lower temperatures [36]. These results clearly indicate that the AFMI state, which is definitely brought about via magnetic interactions with localized d-spins, should be energetically in a close proximity to superconductivity as observed in the nonmagnetic GaCl₄ salt.

3 Theories for magnetic exchange interactions and antiferromagnetic order

3.1 The Mori–Katsuhara theory

In order to understand the AFM order and its related phenomena, magnetic exchange interactions are calculated by Mori and Katsuhara (MK) [28] on the basis of intermolecular transfer integrals as described in preceding section. Here we summarize the results with reference to Fig. 3 illustrating the AFM spin arrangement based on a dimer model [28] in which π electrons are assumed to be localized at the dimers of A.

1. The direct d–d superexchange interaction J_dd acting through the Fe³⁺Cl₄⁻---Cl₄⁻Fe³⁺ channel is estimated to be −0.6 K. This weak coupling is due to the small transfer integrals.
2. The π–d superexchange interaction J_πd is caused by the couplings of singly occupied five d-orbitals with neighboring seven different π-orbitals of BETS mediated by 3p-orbitals of Cl⁻. Along the coupling channel Se(7)–Cl(2) (see Fig. 1 and also refer to Fig. 2(b) and Table 6 in Ref. [28]) the exclusively large J_πd(6) = −14 K and the effective ${\tilde{J}}_{πd} = - 14.5 K$ .
3. The third exchange interactions J_ππ's between π spins are treated with the dimer model. The effective ${\tilde{J}}_{ππ}$ is found to be −448 K.

Fig. 3
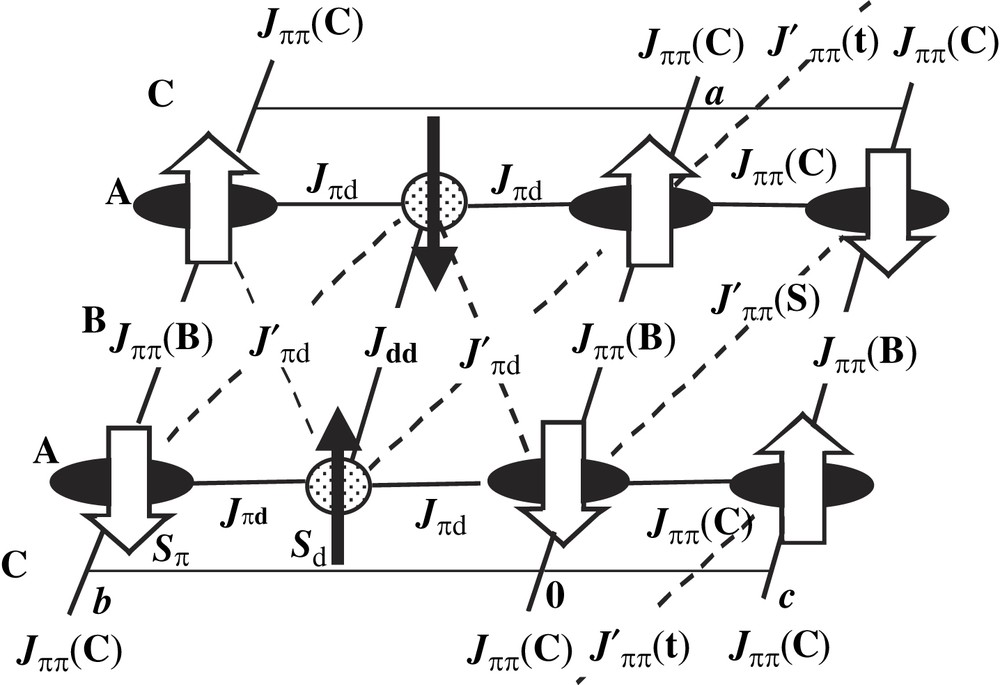
The dimer model [28] for antiferromagnetic spin arrangement in the ab and ac planes. Open and closed arrows represent, respectively, S_π = 1/2 assumed to be localized at the dimer A (Fig. 1) and S_d = 5/2 at Fe⁺³. The solid and dotted lines connecting these spins indicate the cooperative and frustrating (denoted with prime) exchange couplings for J_πd and J_ππ. The symbols B and C in the parenthesis of J_ππ correspond to the transfers as shown in Fig. 1. The exchange parameters are J_dd = −0.64 K, J_πd = −16 K, J′_πd = −1.55 K, J_ππ = −622 K and J′_ππ = −174 K.[28]. Notes: (a) J_dd(i,j) = −2t²_ij/U_dd, where U_dd is an on-site Coulomb interaction of the FeCl₄⁻ d-orbitals. (b) J_πd(i,j) = −2t²_ij/Δ_πd, where Δ_πd is an energy difference between the donor HOMO and the d-like molecular orbitals. The effective coupling constant ${\tilde{J}}_{πd} = J_{πd} - {J^{'}}_{πd} = 14.45 K$ . (c) J_ππ(i,j) = −2t²_ij/U_ππ, where U_ππ is an on-site Coulomb interaction of the donor HOMO. The effective coupling constant ${\tilde{J}}_{ππ} = J_{ππ} - {J^{'}}_{ππ} = 448 K$ . (d) All the numerators above, U_ππ, Δ_πd, U_dd are assumed to be 1 eV.

To evaluate T_N, MK [28] proposed a mean field theory based on an itinerant model instead of the dimer model above. With the Landau–Ginzburg free energy, T_N and Θ are discussed in terms of two independent contributions from the direct $J_{dd}$ and indirect ${\tilde{J}}_{πd}$ . (For the details, refer to Ref. [28].)

It is noted that the band-structure calculations [28] give a peak of the staggered electronic susceptibility around q_AF = (0, π/c) that corresponds to the 2k_F vector spanning two open Fermi surfaces. This is consistent with ⁷⁷Se- and ¹H NMR measurements on the superconducting GaCl₄ salt which reveal an existence of strong AFM spin fluctuations in its normal state [37,38], because the GaCl₄ salts can be iso-electronic to the FeCl₄ salt.

3.2 Mean-field theories based on Kondo–Hubbard model

The π–d interaction-induced phenomena are discussed with a so-called Kondo–Hubbard Hamiltonian [33,39–41] consisting of three terms; the 2D tight binding hopping term, the on-site Coulomb repulsion U_ππ, and the π–d exchange term. The indirect exchange interaction between d-spins can be derived as a well-known Ruderman–Kittel–Kasuya–Yoshida (RKKY) interaction, J_RKKY, mediated by a spin polarization of π electrons [42].

The mean field calculations are summarized as follows. Hotta and Fukuyama [39] proposed a phase diagram in which the ground states are quite sensitive to small changes in U_ππ, J_πd and the band width. In particular the AFMI transition is interpreted as a Mott transition caused by the critical on-site Coulomb energy U_ππ = 0.27–0.28 eV. On the other hand, in order to explain the phase diagram for λ-(BETS)₂Fe_xGa_1−xCl₄, Terao and Ohashi [41] discussed the inherent superconductivity by adding an effective BCS Hamiltonian [43]. There the exchange interaction with localized d-spins breaks up Cooper pairs and hence works as a strong pair breaker, reducing T_C so strongly as usual in a so-called Kondo superconductor [44–46]. An unusual insensitiveness of T_C to x, however, is ascribed to a correlation effect that would effectively reduce the magnetic impurity scatterings.

So far we have reviewed the experimental observations and theoretical discussions for the PM-to-AFMI transition and its related properties. These so-called π–d interaction-induced phenomena have readdressed a long-term problem of magnetism and (super)conductivity, which have been extensively studied on s–d or s–f interacting systems such as transition-metal and rare-earth (RE) compounds [46–48]. As will be described in following sections, some phenomena that are quite characteristic to the present low-dimensional, magnetic molecular metal have been found both in the high temperature PM and low temperature AFMI phases.

4 Anomalous metallic states

4.1 Microwave conductivity and ¹H NMR

High frequency conductivity (σ^∗ = σ₁ + iσ₂) measurements by a microwave- cavity perturbation technique reveal an anomalous metallic state of λ-(BETS)₂FeCl₄ [49,50]. Fig. 4 shows the real part σ₁ and the dielectric constant ɛ₁ (= 1 − (4π/ω)σ₂) along the c- axis as a function of temperature. The resonance width ΔΓ/2f₀ (f₀ = the resonant frequency) representing a microwave loss takes a broad maximum around 100 K, followed by a shallow minimum around 30 K. While the maximum is in accordance with the broad peak of the dc resistivity ρ_dc as shown in Fig. 2, the latter minimum indicates an existence of an anomalous microwave loss in the PM state that is not observed in ρ_dc depending on temperature monotonously. The magnitude of σ₁ becomes smaller than σ_dc^c (≡1/ρ_dc^c) around T_FM and, with further decreasing temperature, it becomes almost two orders of magnitude as small as σ_dc^c (see Section 6). On the other hand, the sign of ɛ₁ changes from being negative to positive around T_FM = 70 K. In particular the positive, large ɛ₁ along the c axis appears at T_MI < T < T_FM in the PM state and takes a sharp peak near T_MI, followed by a steep decrease in the AFMI state. The broad peak around 30 K in ɛ₁ is speculated [50] to be caused by an appearance of some relaxor- ferroelectrics domains [51,52] in the metallic background. It should be pointed out that the analysis of the complex conductivity using an electromagnetic formulation standing for a homogeneous state is inconsistent with the speculation for the heterogeneous state. However, the X-ray diffraction studies [53] provide an evidence for the domain structure as will be described later. If the domain size is large enough compared to the shielding length of π electrons, the positive ɛ₁ could be observed even in the heterogeneous metallic state.

Fig. 4
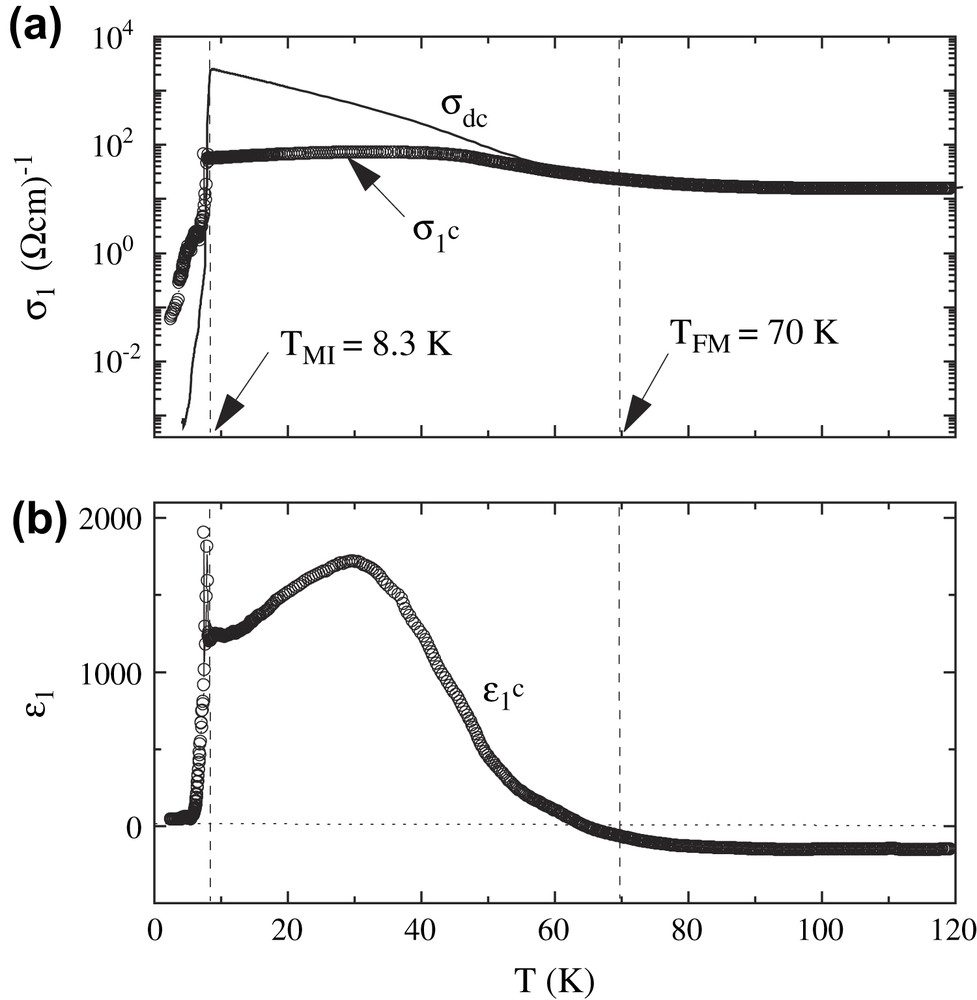
Temperature dependence of the microwave (44.5 GHz) conductivity, σ₁ (a) and ɛ₁ (b) along the c- axis of λ-(BETS)₂FeCl₄. For details, see the text [50].

On the other hand, ¹H NMR measurements [54] find out another aspect in this anomalous PM state. Fig. 5 shows the spin-echo intensity near the resonance field H₀, which gives a clear splitting of the resonance below 70 K (≈T_FM). The Gaussian deconvolution analysis with three independent components of P_c, P_s1 and P_s2 as shown in the figure can reproduce the observed resonance profiles. Asymmetric positions of two side peaks P_s1 and P_s2 mean that, below T_FM, three types of proton sites experiencing different local fields should exist. Since the paramagnetic susceptibility in this temperature range shows a simple Currie–Weiss behavior without any observable anomaly (Fig. 2), the anomalous splitting is not due to the local fields produced by the interaction between the proton nucleus and the d-spins, but due to the hyperfine field between the proton nucleus and π electrons. Here a possible change in the local charge density can be attributed to the distribution of local fields. As a consequence, a charge ordering [55] is discussed as a possible cause for the splitting of the proton resonance below T_FM. To note, this speculation is also supported by recent ¹³C NMR measurements [56] detecting the anomalous line broadening. Taking into account the heterogeneous state speculated from the anomalous microwave conductivity, it may be reasonable to suppose that a uniform metallic state could change into some phase-separated state in which a domain pattern consisting of metallic and dielectric regions might appear. There the metallic region seems to be responsible for the shift of the central peak, while the dielectric domains with modulated charge densities along the a- axis could provide two side peaks.

Fig. 5
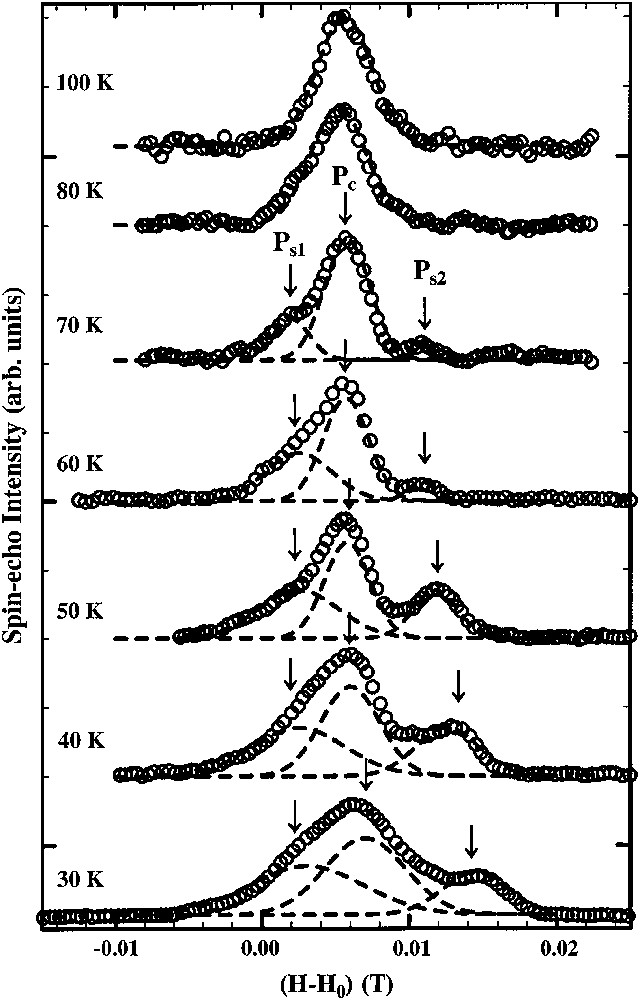
Profile of field-swept ¹H NMR spectra (94.95 MHz) at T = 100–30 K in λ-(BETS)₂FeCl₄. The dashed lines indicate the Gaussian deconvolution with three components P_c, P_s1, and P_s2, the peak positions of which are shown by arrows [54].

4.2 Structural anomalies

The temperature dependence of a peak profile of the (007) Bragg reflection reveals structural anomalies both in the vicinity of the PM-AFMI transition and in the anomalous metallic region T_MI < T < T_FM [53,57]. Around T_FM the reflection becomes broadened and deformed and, with decreasing temperature, the peak profile gets split. Fig. 6 shows the clear splitting seen in the intensity map which is obtained by the three-dimensional scan in the reciprocal space [53]. The magnitude of the splitting increases with decreasing temperature, and the splitting direction and magnitude are determined to be 0.017a^∗ − 0.010b^∗ + 0.002c^∗. This is explained by a change of 0.005 Å in the interplanar d-spacing along the c-axis. The split peaks giving different d^∗ values are ascribed to a phase-separated, heterogeneous structure, in which domains having the same structure with the low- temperature AFMI phase may appear in the high- temperature PM background. The domain size is evaluated to be of a mesoscopic scale of about 0.3–0.4 μm. These anomalies are totally consistent with the scenario of the highly dielectric domain and the charge ordering speculated from the microwave conductivity [49,50] and ¹H NMR [54] just described above. To note, the shielding length of π electrons in a unit cycle of the microwave is limited by the lifetime of the order of 10⁻¹³ s, and estimated to be in the order of 0.01 μm or less much smaller than the domain size. Therefore the dielectric domain can absorb the microwave energy, and hence the positive dielectric constant can be observable even in such a heterogeneous metallic state.

Fig. 6
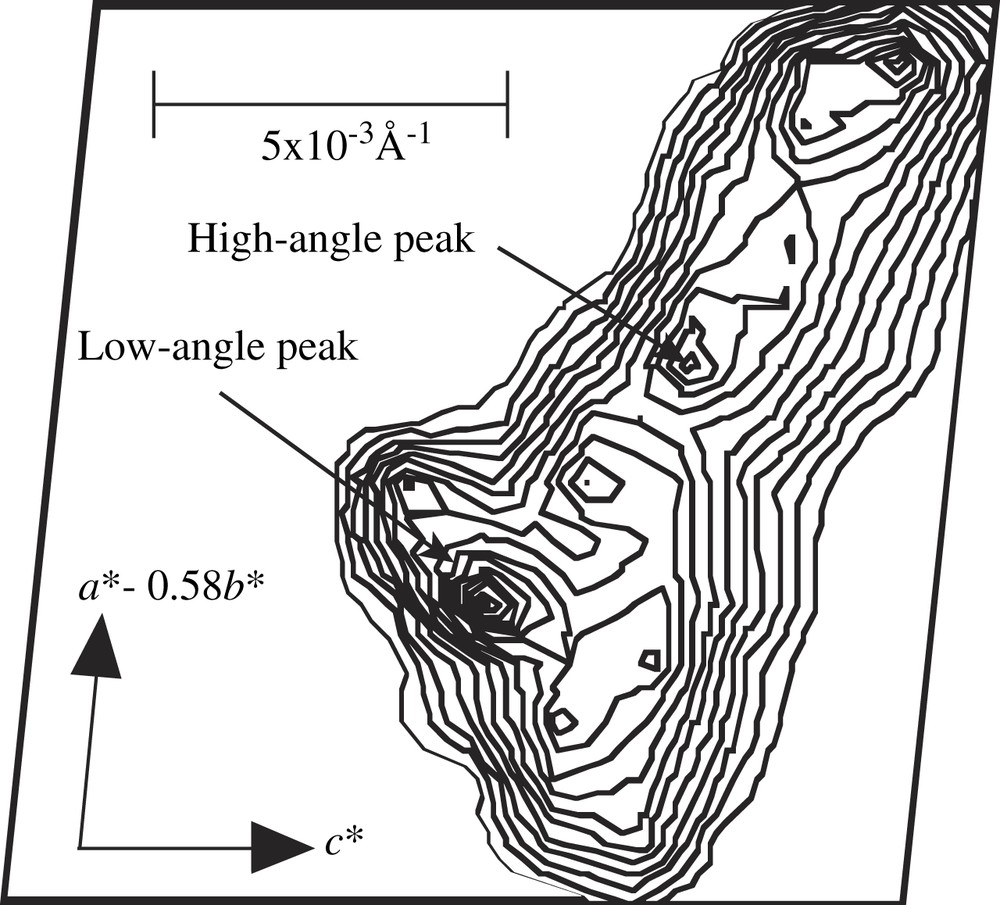
Sectional plane in the reciprocal space (the a^∗c^∗- plane) around the (007) Bragg reflection in λ-(BETS)₂FeCl₄ at 20 K. The data are obtained from a three-dimensional scan in the reciprocal space using the synchrotron facility of SPring-8 [53].

At T_MI a discontinuous structural change in the c^∗ axis appears, and moreover the splitting disappears so that the peak profile becomes single again but remains broad. The temperature dependence of the lattice constant 1/c^∗ calculated from each split peak is shown in Fig. 7. The solid circles are taken from earlier experiments [57] by the same group with a lower resolution in which the high temperature peak profiles are treated as a single broad peak. The high angle data indicate a discontinuous change of 1/c^∗ at T_MI more clearly, providing an evidence for the first-order structural phase transition associated with the PM-to-AFMI transition. Although the structural analysis is not conclusive, a uniform transformation from $P \bar{1}$ to the unique subgroup P1, the most primitive space group with loosing the inversion symmetry of $P \bar{1}$ , is most expected [53].

Fig. 7
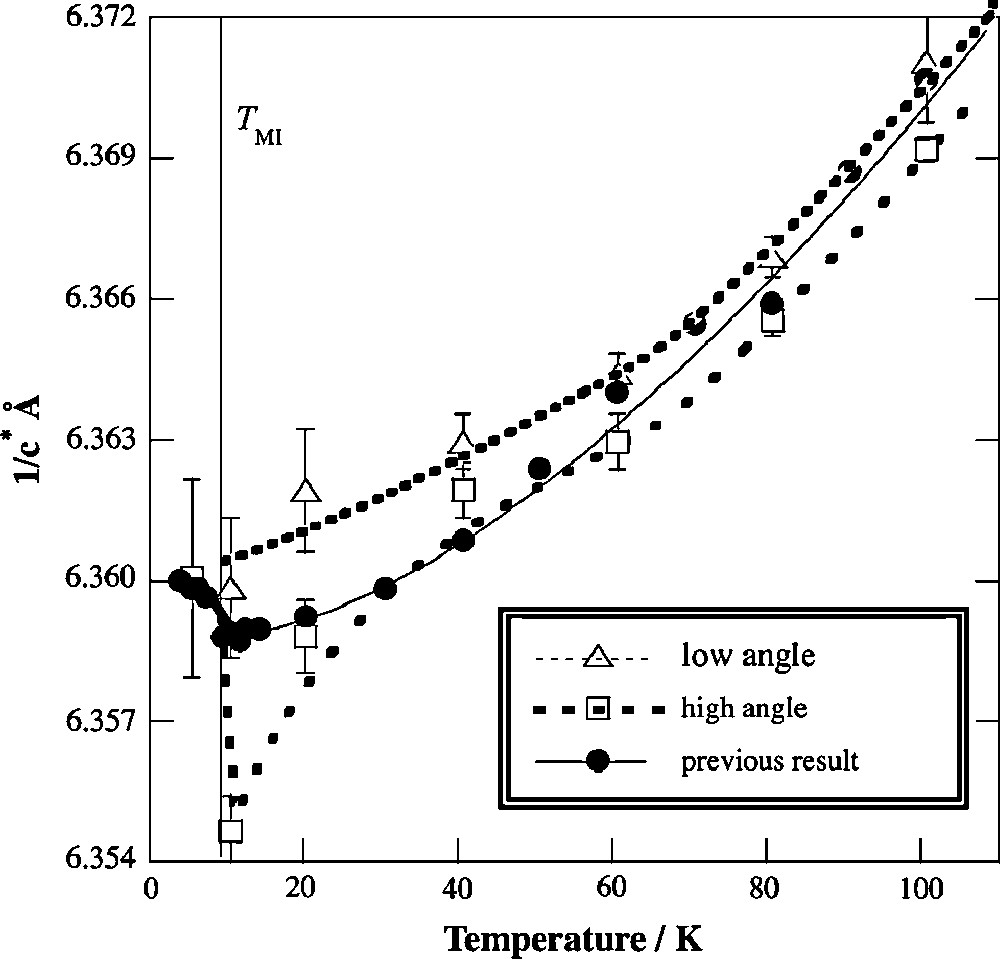
Temperature dependence of the lattice constant 1/c^∗ in λ-(BETS)₂FeCl₄, obtained from the high (open squares) and low (open triangles) angle points in the (007) peak profiles (Fig. 6). The previous data with a lower resolution obtained by the same group [57] are plotted by closed circles for comparison [53].

5 Antiferromagnetic insulating states

5.1 Magnetic field-induced phase transitions

Some of low-dimensional molecular conductors have been found to undergo electronic phase transitions in magnetic fields [5,6,9,58] such as to spin- or charge density-wave state. In the present λ-(BETS)₂FeCl₄, successive transitions from the AFMI to the reentrant PM [33,59] and then superconducting states [60] are observed.

Fig. 8 shows the magnetic field (//b^∗) dependence of the in-plane resistance R (//c) [61]. The critical field H_MI defined as an onset of the resistance upturn shifts to a higher field with decreasing temperature, approaching about 12 T at 1.8 K. These reentrant transitions are independent of the field orientation. As seen in the figure, the transition is associated with successive, step-like resistance jumps with hysteresis. These characteristic behaviors are noticeable in the transit region of H^∗ < H < H_MI (for example, H^∗ ≈ 8–9 T at 1.8 K), where the resistance decreases quite sharply.

Fig. 8
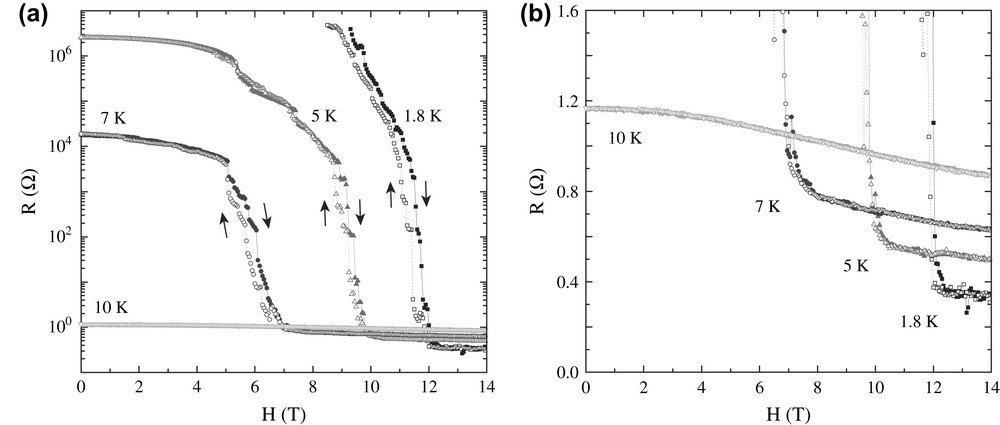
(a) Magnetic field (//b^∗) dependence of the in-plane resistance R of λ-(BETS)₂FeCl₄ and (b) the details of the onsets in the MI transition in a linear scale [61].

In the reentrant metallic state above H_MI, a negative magneto-resistance is observed as demonstrated in Fig. 8(b). This phenomenon can be attributed qualitatively to a reduction in π electron scatterings by d-spins continuously aligned by magnetic fields.

This reentrant transition appears also in the mixed salts with Fe_xGa_1−xCl₄, in which H_MI(0) can be scaled to T_MI with an empirical relation as μ_BH_MI(0) ≈ 1.5k_BT_MI [61–63]. Together with the fact that H_MI is isotropic with respect to the field orientation, this scaling suggests that the Pauli spin polarization of conducting π electrons, which would lower the electronic energy by μ_B²N(0)H² (N(0) is the density of states at the Fermi level), may play some important role in driving the transition. The mechanism for the transition, however, is not clearly explained yet, though the theoretical discussions are available in Refs. [33,40].

As shown in Fig. 9(a), an application of higher fields induces superconductivity that is called a field-induced superconductivity (FISC) [60,62–64]. (This phenomenon is also confirmed to appear in κ-(BETS)₂FeBr₄ [65,66].) It is noted that the FISC states are observed only when the magnetic field is applied parallel to the conducting planes as exactly as possible. In this field orientation, the upper critical field caused by the orbital effect would be quite high in these highly 2D superconductors because of the quite small interlayer coherence length [43]. The H–T phase diagram is shown in Fig. 9(b). At low temperatures, the FISC state is seen in a wide field range centered at H₀ ≈ 33 T with T_C0 ≈ 4 K.

Fig. 9
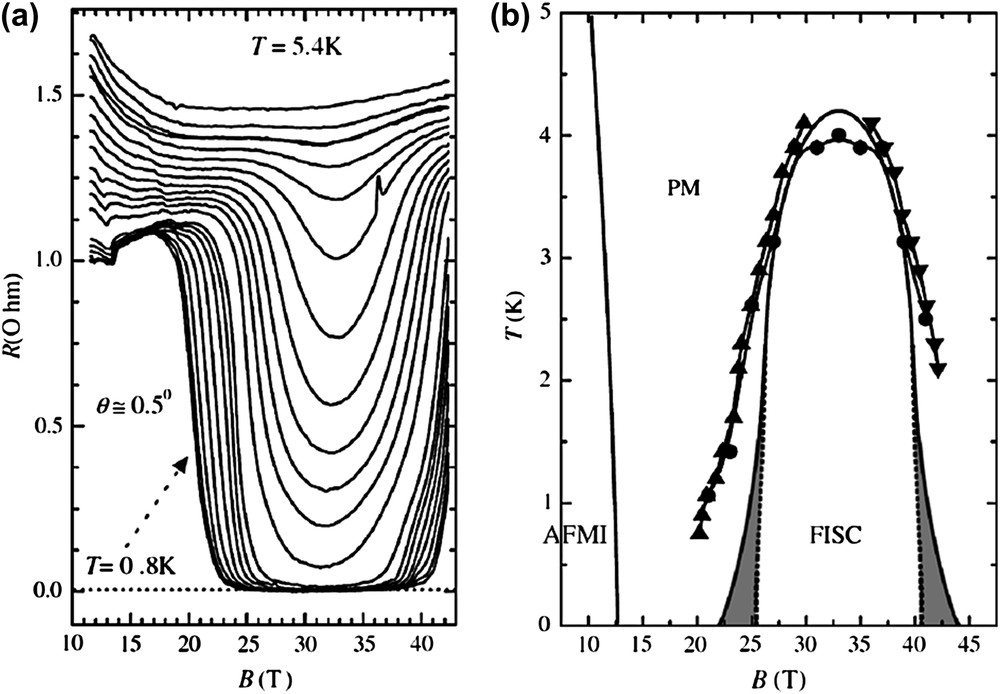
(a) In-plane resistance as a function of magnetic field applied parallel to the in-plane of λ-(BETS)₂FeCl₄ for temperature intervals of approximately 0.25 K between 5.4 and 0.8 K. (b) Magnetic field–temperature phase diagram showing the AFMI, PM and FISC. Solid triangles indicate the middle point of the resistive transition as a function of B from (a), while solid circles indicate the middle point of the resistive transition as a function of T [62].

These findings are clearly explained by a so-called Jaccarino–Peter (JP) effect [67]. This effect stating originally that superconductivity could be induced in a weak ferromagnet by applying a magnetic field had been predicted in 1962 almost two decades before it was firmly verified by resistance measurements on some of Chevrel phase compounds with localized 4f spins and the narrow d-band electrons [68,69]. The essential point in the JP effect is that, in case of the present π–d system, an external magnetic field H_ext aligning the localized spins S_d can compensate the π–d interaction-induced internal field H_int = 2(J_πd/gμ_B)S_d (antiparallel to H_ext since J_πd < 0) acting on π electrons' spins. With ${\tilde{J}}_{πd} = 14.5 K$ evaluated by the MK theory [28] mentioned in Section 3, H₀ = − H_int = 33 T which is in agreement with the experiment. This compensation effect is firmly verified [40] by the evaluation of H₀ from the observed splitting Shubnikov–de Haas oscillations [70,71] due to the exchange field-induced effect on the spin splitting factor [72].

By the way, a question may arise as for why FISC can be observed in the present salt with the AFMI ground state, in contrast to the superconducting ground states in κ-(BETS)₂FeBr₄ [65,66] and the rare-earth compounds above mentioned. The reason may be inferred to the fact that the T_C (= 4.8 K) in the superconducting GaCl₄ salt is rather close to T_C0 ≈ 4 K at H₀ (Fig. 9(b)). It is reasonable to suppose that the strength of an attractive electron–electron interaction mediated by phonons might be almost the same in both salts, since, except for the presence of localized spins, any differences in the electronic and phononic properties can be hardly expected.

5.2 Nonlinear transport and switching effect

Let us turn back to the AFMI ground state again, in which current–voltage (J–E) characteristics along the c axis are studied [73,74]. Fig. 10(a) shows the J–E curves at 4.2 K in magnetic fields up to 14 T applied to the interlayer b^∗ direction normal to the ac plane [64]. A so-called negative resistance (NR) effect is seen clearly at H < 6 T, followed by a monotonous nonlinear transport without NR at higher fields and eventually by a conventional ohmic transport in the reentrant metallic states at H = 12 and 14 T > H_MI ≈ 11 T (at 4.2 K). It is noted that the discontinuous drop of E in the low-J region is a switching effect to the low resistance state.

Fig. 10
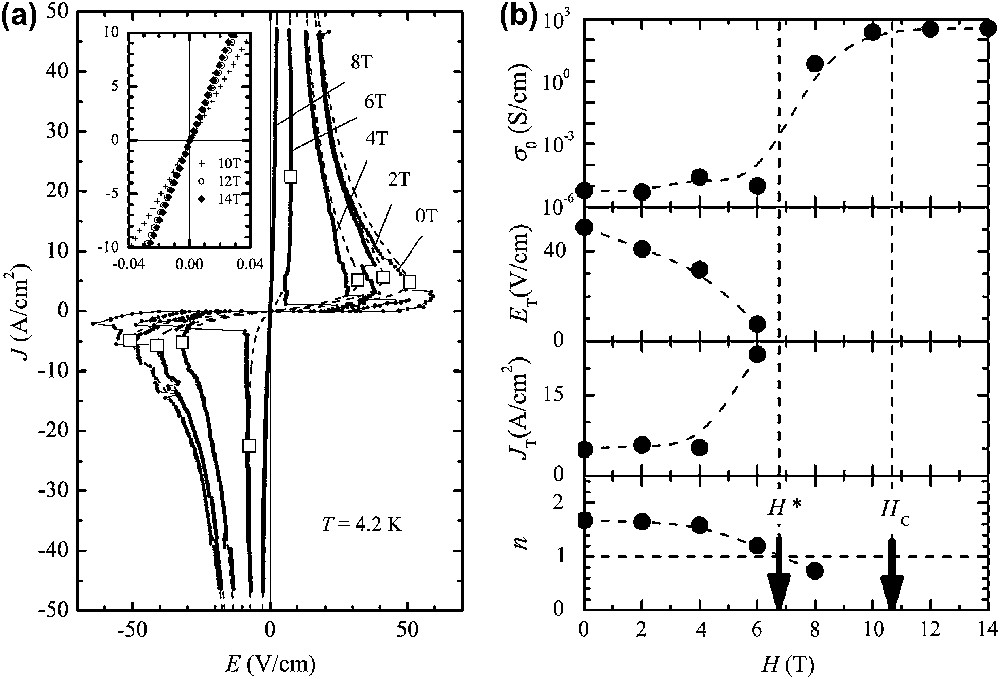
(a) J–E curves at 4.2 K under magnetic fields applied to the interlayer b^∗ direction of λ-(BETS)₂FeCl₄. Dashed lines represent Eq. (1). (b) Magnetic field dependence of parameters such as σ₀, E_T, J_T and n at 4.2 K. The dashed lines are for eye guide [74].

A following empirical relation for the temperature and current–density dependent conductivity σ(T, J) is used for the analysis.

σ (T, J) = σ_{1} \exp (- \frac{Δ}{k_{B} T}) + σ_{2} J^{n}

(1)

where σ₁ and σ₂ are constants. This equation has been applied to similar phenomena discovered in a variety of Q1D mixed-stack or segregated-stack insulators [75–77]. The total conductivity is expressed by an equivalent parallel circuit composed of two different conduction processes. The first term in Eq. (1) is a conventional J-independent ohmic conductivity caused by the thermal activation across an energy gap 2Δ characterizing an insulating state concerned. The second term represents a nonlinear conductivity with a power law dependence of J. If n > 1, Eq. (1) is rewritten as

σ (T, J) = σ_{0} (1 + \frac{1}{n - 1} {(\frac{J}{J_{T}})}^{n})

(2)

where σ₀(T) = σ₁ exp(−Δ/k_BT) and [J_T(T)]ⁿ = σ₀(T)/((n − 1)σ₂) (the threshold J_T is defined as (dE/dJ)_J_{=J_T} = 0, and E_T = J_T¹⁻ⁿ/nσ₂). This equation with n > 1 explains NR quite well, which can be appropriate in general for a positive feedback system [76]. The systematic change in the J–E curves with magnetic fields is clearly seen in the field dependence of parameters such as σ₀, E_T, J_T and n at 4.2 K as shown in Fig. 10(b). The thermally activated conductivity σ₀(T) starts to increase by seven orders of magnitude in the transit region H^∗(= 6 T) < H < H_MI, entering the metallic state above H_MI. Just above H^∗ a crossover from n > 1 to n < 1 occurs associated with both diminishing E_T and divergent J_T. As mentioned above, it is only in the case of n > 1 that the NR effect occurs and the threshold (E_T, J_T) can be defined. Since n = (1 − σ₀E_T/J_T)⁻¹, the systematic changes in n, E_T and J_T near H^∗ are totally consistent with each other. To summarize, the electronic transport phenomena differently appear in three regions; n > 1 with NR at H < H^∗, 0 < n < 1 without NR at H^∗ < H < H_MI and n = 0 with ohmic conductivity at H_MI < H.

As mentioned above, the NR effect is necessarily induced once the switching instability is triggered. Quite similar phenomena are observed in a Q1D, half-filled Mott insulator K-TCNQ which undergoes a spin-Peierls (SP) transition to a spin singlet ground state [77]. The optical microscopic observation for the NR state provides a photograph showing a periodic stripe pattern of the order of micrometers running perpendicular to the chain axis (//E). These stripes, which reversibly disappear at E < E_T, are identified to be a highly conducting pathway, where the localized π electrons are forced back to higher conducting states above the SP transition. In analogy to these explanations, it is supposed for the present salt that the switching and the subsequent NR effect may be, respectively, a local onset and its well development of π charge carriers' self-decondensation process. Thus magnetic and electric fields both make the AFMI ground state unstable more and more to facilitate the localized π electrons to be mobile [73,74]. These electronic instabilities sensitively controlled by both electric and magnetic fields are closely related to the dielectric properties.

5.3 Dielectric properties and charge ordering-induced polarization model

The temperature dependence of low frequency (10–10⁴ Hz) dielectric constants (ɛ^∗ = ɛ₁ + iɛ₂) along the c axis indicates a ferroelectric-like ordering in the AFI states [78]. These measurements with a three-terminal method are available only in the well ordered AFMI states with the low conductance G less than 10⁻⁴ S. The dielectric constant ɛ₁^c as large as 10³ at 2.5 K increases with increasing temperature, amounting to 10⁴ at 6.5 K, the highest measurable temperature, above which the conductivity recovers so sharply in the so-called transit region as already described in Sections 5.1 and 5.2. (For the measurable regime of T and H, see the inset of Fig. 12(a).) The electric-field bias E_bias dependence of ɛ₁^c and σ₁^c is quite nonlinear, where σ₁^c (= ωɛ₂/4π) is found to be exclusively determined by mobile π electrons responsible for the steady, nonlinear transport described in Section 5.2. This means that the dielectric loss of electric polarizations must be negligibly small.

Fig. 12
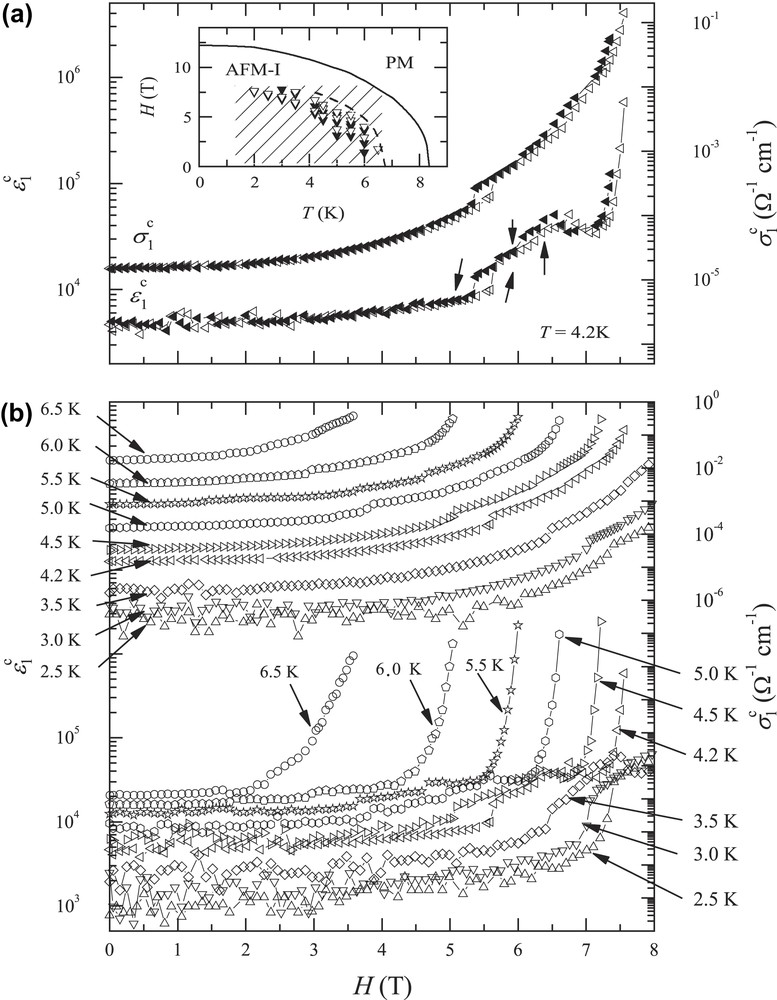
Magnetic field dependence of ɛ₁^c and σ₁^c in λ-(BETS)₂FeCl₄ at 4.2 K (a) and 2.5–6.5 K (b). The inset shows the H–T phase diagram. The solid and dotted lines plot, respectively, a phase boundary H_MI and upper limiting fields with G < 10² μS. The shaded region represents the measurable regime [78].

Fig. 11 shows the relative change of electric polarizations ΔP as a function of E_bias, which is evaluated by integrating ɛ₁^c with E_bias. At H ≤ 5 T, the saturated polarization ΔP_sat is almost independent of H, while E_bias, giving the saturation, decreases with H. At higher fields, however, there appears a sharp increase of ΔP at low E_bias, and ΔP_sat takes a sharp upturn as shown in the inset. To note, this crossovering behavior in the dielectric response occurs around H^∗ just as seen in the nonlinear transport (Fig. 10(b)). Furthermore it is clearly observed in Fig. 12 demonstrating a colossal magnetodielectricity (CMD) effect. There ɛ₁^c insensitive to low magnetic fields exhibits a huge increase by about two orders of magnitude up to the highest measurable field 7.5 T (> H^∗). The diverging increase shifts schematically to lower magnetic fields with increasing temperature. These results together with the nonlinear transport suggest that the origin of CMD can be attributed to π charge carriers' self-decondensation processes providing a drastic dielectric response as well as the NR effect, which are triggered by both magnetic and electric fields.

Fig. 11
Relative change of electric polarization ΔP in λ-(BETS)₂FeCl₄ as a function of E_bias at T = 4.2 K and H = 0–7 T. The inset shows the magnetic field dependence of the saturation value ΔP_sat [78].

On the basis of these dielectric dynamics together with the MK theory, a charge ordering-induced polarization (COP) model is proposed as illustrated in Fig. 13. Due to the exclusively large J_πd(6) through the coupling channel Se(7)–Cl(2) as described in Section 3.1, the charge and spin of π electrons are expected to be localized at the Se(7)-sites, forming the charge order of –1–0–0–1– sequence along the column. The AFM order between S_π and S_d, which is different from the dimer model (Fig. 3), is assumed to be realized by gaining the superexchange energy which may overcompensate the cost due to the inter-site repulsive Coulomb interaction between localized π electrons. In this model, therefore, the charge order can be considered as a primary origin not only magnetically but also electrically for the PM-to-AFMI transition. Consequently, as shown in the figure, the charge-ordered π electrons (holes) are able to form electric dipole moments (p_i with i = 1–4) with a negative charge distributed near the center of the tetrahedral anion. Note that ∑p_i = 0, provided that the inversion symmetry exists, because p₁ + p₃ = p₂ + p₄ = 0. It is noted, however, that some dielectric ordering with ∑p_i ≠ 0 is not excluded, because, as mentioned in Section 4.2, the low temperature phase plausibly loses the inversion symmetry in the high temperature $P \bar{1}$ phase [53]. Furthermore, as described in Section 4.1, the dielectric domains in the heterogeneous PM state, in which a charge order may be possibly induced [54], can be considered to appear as a precursor to the AFMI ground state.

Fig. 13
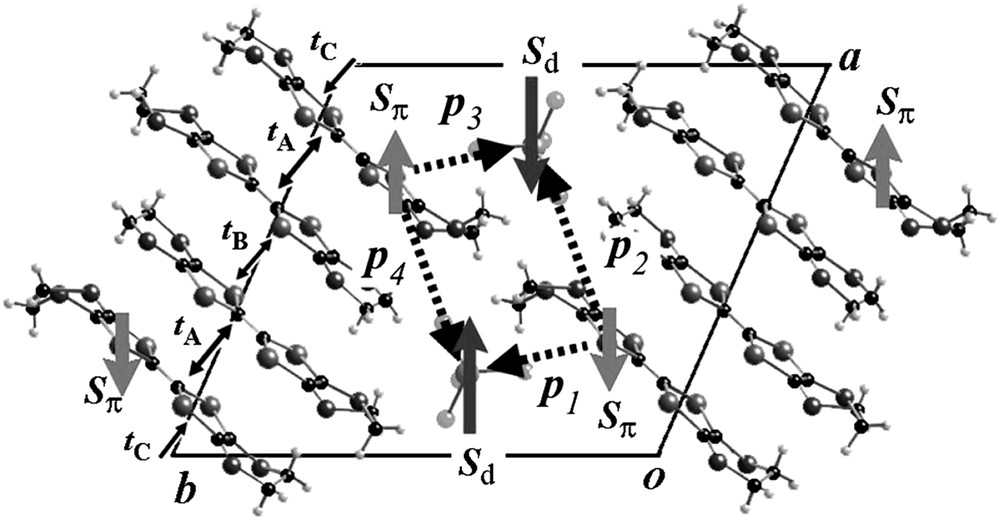
The AFM spin arrangement and possible electric dipoles proposed from the charge ordering-induced polarization (COP) model for the AFMI ground state in λ-(BETS)₂FeCl₄ [78].

From the nonlinear transport and dielectric properties in the AFMI state, we may arrive at a comprehensive picture that the localized π electrons tend to be unlocked or melted around H^∗ associated with the sharp upturn of the electric polarization and the CMD, and eventually turn into band electrons in the PM state at H > H_MI. Thus the present π–d system is considered to be a novel ferroelectromagnet [79–81] in which magnetic and dielectric orders coexist and interact with each other.

6 Comparison with the isostructural superconducting GaCl₄ salt

So far we have reviewed the current status of studies for (1) the anomalous metallic state which is interpreted as a heterogeneous metal with dielectric, charge-order domains and (2) the AFMI ground state and its dynamical instabilities under magnetic and electric fields. There the heterogeneous metallic state is considered as a precursor for the low temperature AFMI state in which a charge-ordered ferroelectric-like state is discussed. It may be interesting, therefore, to introduce another anomalous metallic state in the superconducting GaCl₄ salt [82].

The superconducting properties are summarized as follows. The specific heat jump at T_C, ΔC/γT_C = 1.37 ± 0.32, seems to be consistent with the BCS weak coupling limit [83]. The London penetration depth λ_L, which is obtained from the imaginary part σ₂ of the microwave conductivity, becomes saturated at T/T_C < 0.5, suggesting a fully gapped state of s-wave pairing symmetry [82]. On the contrary, a distorted fourfold anisotropy of the upper critical field H_c2 within the conducting plane is claimed as an evidence for d-wave superconducting state [84]. The H_c2–T phase diagram is obtained from measurements such as the radio-frequency [85], dc resistivity [61,84] and microwave conductivity [82]. Among these results, the microwave data [82] show the linear dependence on temperature near T_C as expected for a conventional type-II superconductor [43], while all the other data show a strong positive curvature in the temperature dependence. The latter behaviors are rather reminiscent of a so-called irreversibility line for a vortex melting transition. The Ginzburg–Landau coherence length ξ_GL = 8.7 × 10⁻⁷ cm is much shorter than the mean free path l = 1.1 × 10⁻⁵ cm evaluated from the Dingle temperature and Fermi velocity [85], indicating that the superconductivity is in the pure limit defined as ξ_GL ≪ l.

Fig. 14 shows the temperature dependence of the microwave conductivities σ₁ and σ₂ along the c axis. Above 60 K, σ₁^c coincides with σ_dc^c, but deviates downward from σ_dc^c down to T_C. To note, qualitatively similar behavior is also observed in the FeCl₄ salt as described in Section 4.1. From a classical Drude model, σ₁ can be hardly dispersive in a metal with an electron relaxation rate much higher than the microwave frequency. The difference between σ₁^c and σ_dc^c amounts to about one order of magnitude around T_C. On the other hand, σ₂^c, which should be zero in a conventional metal, shows a gradual upturn from 20–30 K down to T_C, followed by a saturation in the superconducting state. The continuous increase of σ₂^c around T_C may suggest that the anomalous metallic state continuously converges into the superconducting ground state. To note again, this anomaly with positive σ₂ is in strong contrast to the FeCl₄ salt with negative σ₂ (positive ɛ₁) as described in Section 4.1.

Fig. 14
The temperature dependence of σ₁^c and σ₂^c of the complex conductivity along the c-axis of λ-(BETS)₂GaCl₄ at 45 GHz. [82] The inset in the lower panel shows σ₂ in κ-ET₂Cu(NCS)₂ [86].

The finite positive σ₂ is also observed in κ-ET₂Cu(NCS)₂ with T_C = 10.4 K, which is plotted for comparison in the inset of the lower figure with the temperature scaled by each T_C [86]. Since these anomalies are too large to be explained by the tiny effect of thermodynamic superconducting fluctuations, they are discussed in terms of a pseudogap near a Fermi level [82]. From both the data that σ₂^c continuously increases through T_C and the fact that σ₂ is a measure of the number density of Cooper pairs in the bulk superconducting state, the reduction of σ₁^c from σ_dc^c is claimed to be a decrease in the number density of quasiparticles near the Fermi level, while the finite increase of σ₂^c with decreasing temperatures to T_C is discussed in terms of a preformation of incoherent, local electron pairs with finite lifetime above T_C. This scenario for the pre-formed pairs has been discussed in theoretical [87–89] and experimental [90,91] studies for high-T_C cuprates. It should be noted, however, that the pseudogap problem in general is still an issue of strong controversy. (Refer to the review articles [92–94].) In order to shed more light on the problem, it will be necessary to study low energy excitations in detail with an optical spectroscopy in particular using Tera-Hertz electromagnetic waves.

As already mentioned in Section 3.1, a significant enhancement of spin–lattice relaxation rate 1/(T₁T) is observed in the metallic state below 24 K by ¹H NMR studies [37]. This enhancement is interpreted as a development of AFM spin fluctuations that may be caused by a correlation effect of strong dimerization at A along the column (Section 2). It is noted that the splitting of the resonance observed in the FeCl₄ salt [54] does not appear in the GaCl₄ salt. This fact suggests that the charge ordering in the former salt is induced by the superexchange π–d interaction that is absent in the latter salt with the same correlation effect.

7 Concluding remarks

So far we have reviewed the physical phenomena in the Q2D, π–d interacting λ-(BETS)₂FeCl₄, which are induced by noticeable spin- and charge-correlation of π electrons in the crystal lattice with localized d-spins. In the high temperature PM phase, the metallic state seems to be phase-separated into highly conducting (normal metallic) and highly dielectric, charge-ordered domains. The latter domain of a mesoscopic scale in size appears as a precursor to the ferroelectric-like state in the low temperature AFMI phase where both dielectric and nonlinear transport properties are sensitively controlled by both electric and magnetic fields. It will be an important subject to clarify the similarity and dissimilarity of these anomalous metallic states with those studied so far extensively in κ-ET salts [8,30].

At high magnetic fields the AFMI state is broken up so that the reentrant PM state and then induced superconductivity appear. In short, the present material λ-(BETS)₂FeCl₄ exhibits, in the molecule-based crystalline space, a multifunctional interplay among conductivity, magnetism and dielectricity. Further extensive studies experimental and theoretical are encouraged in order to throw more light on the phenomena and their mechanisms.

Acknowledgements

The authors would like to acknowledge organizers of this symposium for inviting them to review the subject. They are grateful to M. Lang, F. Pratt, R. McKenzie, H. Kobayashi, A. Kobayashi, H. Naito, S. Kawamata, T. Sugimoto, K. Ueda, C. Hotta, H. Fukuyama, T. Mori, M. Terao, Y. Ohashi, J. Suzumura, Y. Tokura, and their colleagues from Tohoku University, M. Watanabe, Y. Noda, S. Komiyama, Y. Iwasa, T. Sasaki, T. Nojima, S. Nakamura, S. Ishihara, T. Tohyama, S. Takagi, H. Matsui, E. Negishi, H. Uozaki, S. Endo, Y. Abe, Y. Ishizaki, H. Tsuchiya, T. Kuwabara and S. Yabuta for discussions and/or collaborations.

Bibliographie

[1] L.B. Coleman; M.J. Cohen; D.J. Sandman; F.G. Yamagishi; A.F. Garito; A.J. Heeger Solid State Commun., 12 (1973), p. 1125

[2] U. Geiser; J.A. Schlueter Chem. Rev., 104 (2004), p. 5203

[3] H. Urayama; H. Yamochi; G. Saito; K. Nozawa; T. Sugano; M. Kinoshita; S. Sato; K. Oshima; A. Kawamoto; J. Tanaka Chem. Lett. (1988), p. 55

[4] A.M. Kini; U. Geiser; H.H. Wang; K.D. Carlson; J.M. Williams; W.K. Kwok; K.G. Vandervoort; J.E. Thompson; D.L. Stupka; D. Jung; M.-H. Whangbo Inorg. Chem., 29 (1990), p. 2555

[5] J. Wosnitza Fermi Surfaces of Low-dimensional Organic Metals and Superconductors, Springer, 1996

[6] T. Ishiguro; K. Yamaji; G. Saito Organic Superconductors, Springer, 1998

[7] J. Singleton Rep. Prog. Phys., 63 (2000), p. 1111

[8] M. Lang; J. Müller (K.H. Bennemann; J.B. Ketterson, eds.), The Physics of Superconductors, vol. II, Springer, Berlin, 2004, p. 453 (Chapter 7)

[9] N. Toyota; M. Lang; J. Müller Low-Dimensional Molecular Metals, Springer, 2007

[10] S. Hünig; P. Erk; S. Hünig J. Mater. Chem., 3 (1991), p. 225

[11] S. Hünig; M. Kemmer; H. Meixner; K. Sinzger; H. Wenner; T. Bauer; E. Tillmanns; F.R. Lux; M. Hollstein; H.-G. Gross; U. Langohr; H.-P. Werner; J.U. von Schütz; H.-C. Wolf Eur. J. Inorg. Chem. (1999), p. 899

[12] R. Kato Bull. Chem. Soc. Jpn, 73 (2000), p. 515

[13] S. Hünig; E. Herberth Chem. Rev., 104 (2004), p. 5535

[14] P. Batail; L. Ouahab; J.B. Torrance; M.L. Pylman; S.S.P. Parkin Solid State Commun., 55 (1985), p. 597

[15] T. Mallah; C. Hollis; S. Bott; M. Kurmoo; P. Day; M. Allan; R.H. Friend J. Chem. Soc., Dalton Trans., 859 (1990)

[16] H. Uozaki; K. Okamoto; S. Endo; H. Matsui; K. Ueda; T. Sugimoto; N. Toyota Synth. Met., 103 (1999), p. 1984

[17] L.I. Buravov; A.V. Gudenko; V.B. Ginodman; A.V. Zvarykina; V.E. Korotkov; N.D. Kushch; L.P. Rosenberg; A.G. Khomenko; R.P. Shibaeva; E.B. Yagubskii Izv. Akad. Nauka, Ser. Khim., N1 (1990), p. 206

[18] P. Day; M. Kurmoo; T. Mallah; I.R. Marsden; R.H. Friend; F.L. Pratt; W. Hayes; D. Chasseau; J. Gaultier; G. Bravic; L. Ducasse J. Am. Chem. Soc., 114 (1992), p. 10722

[19] M. Kurmoo; A.W. Graham; P. Day; S.J. Coles; M.B. Hursthouse; J.L. Caulfield; J. Singleton; F.L. Pratt; W. Hayes; L. Ducasse; P. Guionneau J. Am. Chem. Soc., 117 (1995), p. 12209

[20] A.W. Graham; M. Kurmoo; P. Day J. Chem. Soc., Chem. Commun. (1995), p. 2061

[21] H. Kobayashi; A. Kobayashi; P. Cassoux Chem. Soc. Rev., 29 (2000), p. 325 (For a review)

[22] H. Kobayashi; H. Cui; A. Kobayashi Chem. Rev., 104 (2004), p. 5265

[23] E. Coronado; J.R. Galan-Mascaros; C.J. Gomez-Garcia; V. Laukhin Nature, 408 (2000), p. 447

[24] S.J. Blundell; F.L. Pratt J. Phys.: Condens. Matter, 16 (2004) (For a review R771)

[25] E. Coronado; P. Day Chem. Rev., 104 (2004), p. 5419 (For a review and E. Coronado, this proceeding)

[26] T. Enoki; A. Miyazaki Chem. Rev., 104 (2004), p. 5449

[27] A. Kobayashi; T. Udagawa; H. Tomita; T. Naito; H. Kobayashi Chem. Lett., 1993 (1993), p. 2179

[28] T. Mori; M. Katsuhara J. Phys. Soc. Jpn, 71 (2002), p. 826

[29] H. Kobayashi; H. Tomita; T. Naito; A. Kobayashi; F. Sakai; T. Watanabe; P. Cassoux; H. Tanaka; A. Kobayashi; A. Sato; H. Akutsu; H. Kobayashi J. Am. Chem. Soc., 118 (1996), p. 368

[30] C. Strack; C. Akinci; V. Pashchenko; B. Wolf; E. Uhrig; W. Assmus; M. Lang; J. Schreuer; L. Wiehl; J.A. Schlueter; J. Wosnitza; D. Schweitzer; J. Müller; J. Wykhoff Phys. Rev. B, 72 (2005), p. 054511 (For this long-term puzzling phenomenon, recent studies below have evidenced that it be not intrinsic but extrinsic due to lattice defects, see: and references therein)

[31] H. Akutsu; E. Arai; H. Kobayashi; H. Tanaka; A. Kobayashi; P. Cassoux J. Am. Chem. Soc., 119 (1997), p. 12681

[32] T. Suzuki; H. Matsui; H. Tsuchiya; E. Negishi; K. Koyama; N. Toyota Phys. Rev. B, 67 (2003), p. R020408

[33] L. Brossard; R. Clerac; C. Coulon; M. Tokumoto; T. Ziman; D.K. Petrov; V.N. Laukhin; M.J. Naughton; A. Audouard; F. Goze; A. Kobayashi; H. Kobayashi; P. Cassoux Eur. Phys. J., B1 (1998), p. 439

[34] I. Rutel; S. Okubo; J.S. Brooks; E. Jobiliong; H. Kobayashi; A. Kobayashi; H. Tanaka Phys. Rev. B, 68 (2003), p. 144435

[35] T. Sasaki; H. Uozaki; S. Endo; N. Toyota Synth. Met., 120 (2001), p. 759

[36] A. Sato; E. Ojima; H. Akutsu; Y. Nakazawa; H. Kobayashi; H. Tanaka; A. Kobayashi; P. Cassoux Phys. Rev. B, 61 (2000), p. 111

[37] S. Takagi; D. Maruta; H. Uozaki; H. Tsuchiya; Y. Abe; Y. Ishizaki; E. Negishi; H. Matsui; S. Endo; N. Toyota J. Phys. Soc. Jpn, 72 (2003), p. 3259

[38] S. Takagi; D. Maruta; H. Sasaki; H. Uozaki; H. Tsuchiya; Y. Abe; Y. Ishizaki; E. Negishi; H. Matsui; S. Endo; N. Toyota J. Phys. Soc. Jpn, 72 (2003), p. 483

[39] C. Hotta; H. Fukuyama J. Phys. Soc. Jpn, 69 (2000), p. 2577

[40] O. Cepas; R.H. McKenzie; J. Merino Phys. Rev. B, 65 (2002), p. 100502

[41] M. Terao; Y. Ohashi Physica C, 412–414 (2004), p. 324

[42] K. Yosida, Springer, 1996 (For a textbook Theory of Magnetism)

[43] M. Tinkham Introduction to Superconductivity, McGraw Hill, New York, 1975

[44] A.A. Abrikosov; L.P. Gor'kov Sov. Phys. JETP, 12 (1961), p. 1243

[45] K. Maki (R.D. Parks, ed.), Superconductivity, vol. II, Marcel Dekker, 1969, p. 1035 For a review (Chapter 18)

[46] M.B. Maple; E.D. Bauer; V.S. Zapf; J. Wosnitza (K.H. Bennemann; J.B. Ketterson, eds.), The Physics of Superconductors, vol. II, Springer, 2003, p. 555 For a review (Chapter 8)

[47] M.B. Maple Physica B, 215 (1995), p. 110 (For a review)

[48] L.-P. Levy, Springer, 2000 (For a textbook Magnetism and Superconductivity)

[49] H. Matsui; H. Tsuchiya; E. Negishi; H. Uozaki; Y. Ishizaki; Y. Abe; S. Endo; N. Toyota J. Phys. Soc. Jpn, 70 (2001), p. 2501

[50] H. Matsui; H. Tsuchiya; T. Suzuki; E. Negishi; N. Toyota Phys. Rev. B, 68 (2003), p. 155105

[51] M.E. Lines; A.M. Glass Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, 2001

[52] B.A. Strukov; A.P. Levanyuk Ferroelectric Phenomena in Crystals, Springer-Verlag, 1998

[53] S. Komiyama; M. Watanabe; Y. Noda; E. Negishi; N. Toyota J. Phys. Soc. Jpn, 73 (2004), p. 2385

[54] S. Endo; T. Goto; T. Fukase; H. Matsui; H. Uozaki; H. Tsuchiya; E. Negishi; Y. Ishizaki; Y. Abe; N. Toyota J. Phys. Soc. Jpn, 71 (2002), p. 732

[55] H. Seo; C. Hotta; H. Fukuyama Chem. Rev., 104 (2004), p. 5005 (For a review)

[56] K. Hiraki; H. Mayaffre; M. Horvatic; C. Berthier; H. Tanaka; A. Kobayashi; H. Kobayashi; T. Takahashi J. Low Temp. Phys., 142 (2006), p. 185

[57] M. Watanabe; S. Komiyama; R. Kiyanagi; Y. Noda; E. Negishi; N. Toyota J. Phys. Soc. Jpn, 72 (2003), p. 452

[58] M.V. Kartsovnik Chem. Rev., 104 (2004), p. 5737

[59] F. Goze; V.N. Laukhin; L. Brossard; A. Audouard; J.-P. Ulmet; S. Askenazy; T. Naito; H. Kobayashi; A. Kobayashi; M. Tokumoto; P. Cassoux Europhys. Lett., 28 (1994), p. 427

[60] S. Uji; H. Shinagawa; T. Terashima; T. Yakabe; Y. Terai; M. Tokumoto; A. Kobayashi; H. Tanaka; H. Kobayashi Nature, 410 (2001), p. 908

[61] H. Uozaki, Doctor thesis, Tohoku Univ., 2001, unpublished.

[62] L. Balicas; J.S. Brooks; K. Storr; S. Uji; M. Tokumoto; H. Tanaka; H. Kobayashi; A. Kobayashi; V. Barzykin; L.P. Gor'kov Phys. Rev. Lett., 87 (2001), p. 067002

[63] S. Uji; T. Terashima; C. Terakura; T. Yakabe; Y. Terai; S. Yasuzuka; Y. Imanaka; M. Tokumoto; A. Kobayashi; F. Sakai; H. Tanaka; H. Kobayashi; L. Balicas; J.S. Brooks J. Phys. Soc. Jpn, 72 (2003), p. 369

[64] L. Balicas; V. Barzykin; K. Storr; J.S. Brooks; M. Tokumoto; S. Uji; H. Tanaka; H. Kobayashi; A. Kobayashi Phys. Rev. B, 70 (2004), p. 092508

[65] H. Fujiwara; H. Kobayashi; E. Fujiwara; A. Kobayashi J. Am. Chem. Soc., 124 (2002), p. 6816

[66] T. Konoike; S. Uji; T. Terashima; M. Nishimura; S. Yasuzuka; K. Enomoto; H. Fujiwara; B. Zhang; H. Kobayashi Phys. Rev. B, 70 (2004), p. 094514

[67] V. Jaccarino; M. Peter Phys. Rev. Lett., 9 (1962), p. 290

[68] M. Isino; N. Kobayashi; Y. Muto Ternary Superconductors (G.K. Shenoy; B.D. Dunlap; F.Y. Fradin, eds.), North-Holland, Amsterdam, 1981, p. 95

[69] H.W. Meul; C. Rossel; M. Decroux; Ø. Fischer; G. Remenyi; A. Briggs Phys. Rev. Lett., 53 (1984), p. 497

[70] S. Uji; C. Terakura; T. Terashima; T. Yakabe; Y. Terai; M. Tokumoto; A. Kobayashi; F. Sakai; H. Tanaka; H. Kobayashi Phys. Rev. B, 65 (2002), p. 113101

[71] S. Uji; C. Terakura; T. Terashima; T. Yakabe; Y. Imanaka; Y. Terai; S. Yasuzuka; M. Tokumoto; F. Sakai; A. Kobayashi; H. Tanaka; H. Kobayashi; L. Balicas; J.S. Brooks Synth. Met., 133–134 (2003), p. 481

[72] D. Shoenberg, Cambridge University Press, 1984 (For a textbook Magnetic Oscillations in Metals)

[73] N. Toyota; Y. Abe; H. Matsui; E. Negishi; Y. Ishizaki; H. Tsuchiya; H. Uozaki; S. Endo Phys. Rev. B, 66 (2002), p. 033201

[74] N. Toyota; Y. Abe; T. Kuwabara; E. Negishi; H. Matsui J. Phys. Soc. Jpn, 72 (2003), p. 2714

[75] Y. Tokura; H. Okamoto; T. Koda; T. Mitani; G. Saito Phys. Rev. B, 38 (1988), p. 2215

[76] Y. Iwasa; T. Koda; S. Koshihara; Y. Tokura; N. Iwasawa; G. Saito Phys. Rev. B, 39 (1989), p. 10441

[77] R. Kumai; Y. Okimoto; Y. Tokura Science, 284 (1999), p. 1645

[78] E. Negishi; T. Kuwabara; S. Komiyama; M. Watanabe; Y. Noda; T. Mori; H. Matsui; N. Toyota Phys. Rev., 71 (2005), p. 012416

[79] G.A. Smolenskii; I.E. Chupis Sov. Phys. Usp., 25 (1982), p. 475

[80] G. Srinivasan; E.T. Rasmussen; B.J. Levin; R. Hayes Phys. Rev. B, 65 (2002), p. 134402 (For rare-earth manganites, see:)

[81] N. Hur, S. Park, P.A. Sharma, J.S. Ahn, S. Guha, S.-W. Cheong, Nature 429 (2004) 392, and references therein.

[82] T. Suzuki, E. Negishi, H. Uozaki, H. Matsui, N. Toyota, Physica C 440 (2006) 17.

[83] Y. Ishizaki; H. Uozaki; H. Tsuchiya; Y. Abe; E. Negishi; H. Matsui; S. Endo; N. Toyota Synth. Met., 133–134 (2003), p. 219

[84] T. Kawasaki; M.A. Tanatar; T. Ishiguro; H. Tanaka; A. Kobayashi; H. Kobayashi Synth. Met., 120 (2001), p. 771

[85] C. Mielke; J. Singleton; M.S. Nam; N. Harrison; C.C. Agosta; B. Fravel; L.K. Montgomery J. Phys.: Condens. Matter, 13 (2001), p. 8325

[86] M. Dressel; O. Klein; G. Grüner; K.D. Carlson; H.H. Wang; J.M. Williams Phys. Rev. B, 50 (1994), p. 13603 (The authors do not comment the anomaly)

[87] V.J. Emery; S.A. Kivelson Phys. Rev. Lett., 74 (1995), p. 3253

[88] B. Jankó; J. Maly; K. Levin Phys. Rev. B, 56 (1997), p. R11407

[89] V.B. Geshkenbein; L.B. Ioffe; A.I. Larkin Phys. Rev. B, 55 (1997), p. 3173

[90] J. Corson; R. Mallozzi; J. Orenstein; J.N. Eckstein; I. Bozovic Nature (London), 398 (1999), p. 221

[91] H. Murakami; T. Kiwa; N. Kida; M. Tonouchi; T. Uchiyama; I. Iguchi; Z. Wang Europhys. Lett., 60 (2002), p. 288

[92] A.V. Puchkov; D.N. Basov; T. Timusk J. Phys.: Condens. Matter, 8 (1996), p. 10049

[93] T. Timusk; B. Statt Rep. Prog. Phys., 62 (1999), p. 61

[94] V.M. Loktev; R.M. Quick; S.G. Sharapov Phys. Rep., 349 (2001), p. 1

Commentaires - Politique