1 Introduction
The chemical thermodynamics of plutonium have been critically discussed in recent OECD/NEA-TDB reviews [1,2] which provide a well ascertained set of thermodynamic data and ion interaction coefficients for the system Pu/e−/H+/OH−/NaClO4 or NaCl/H2O. However, there is still a lack of knowledge and it is difficult to ascertain reliable predictions of the total concentration of dissolved plutonium under the geochemical conditions of nuclear waste repositories. The interpretation of experimental results is complicated by redox reactions of aqueous plutonium species, Pu(IV) colloids and solid plutonium phases. In particular the redox reactions of Pu(IV) colloids have not yet been understood. The present paper gives an overview on the solubility of plutonium at 20–25 °C in solutions without complexing ligands (carbonate, phosphate, silicate, etc.) where oxides, oxyhydroxides or hydroxides are the solubility controlling solids. The discussion covers solubility studies in the presence of reducing chemicals [3–7], in the absence of reducing or oxidising agents under Ar atmosphere [8–10] and in the presence of O2(g)/air [11–15].
Under reducing conditions Pu(III) is the dominant oxidation state in solution. However, there is only one study (Felmy et al. [3]) that provides experimental solubility data for Pu(III) hydroxide, Pu(OH)3(s), as equilibrium solid phase. Thermodynamic calculations show that Pu(OH)3(s) is a metastable solid phase, even under reducing conditions. The border line for the conversion into PuO2(am,hyd) is close to the line for the decomposition of water.
Crystalline PuO2(cr) is the stable Pu(IV) solid phase. However, recent papers on the solubility of tetravalent actinides [16–20] pointed out that the available solubility data for AnO2(cr) strongly indicate that the solubility is controlled by small amorphous particles included in the bulk crystalline solids or by amorphous hydrated surface layers. The measured An(IV) concentrations are similar to those determined with oxyhydroxide precipitates AnO2−n(OH)2n·xH2O(am) which may be designated as amorphous hydroxide, An(OH)4(am), or hydrous oxide, AnO2·xH2O(am) or AnO2(am,hyd). It has to be emphasized that amorphous or slightly crystalline hydrous oxides or oxyhydroxides like aged PuO2(s,hyd) that may show a weak XRD pattern [10,21] are not well defined compounds. They are inhomogeneous with regard to the degree of hydration and crystallite size. These properties can vary with time of ageing and with the solution conditions affecting the recrystallization kinetics [2]. The selected values for the solubility constant and standard molar Gibbs energy of formation must therefore be considered as average values for this kind of solids formed in aqueous solutions. On the other hand, these are the compounds relevant for aqueous systems and the storage of nuclear waste. Particularly in the case of highly active Pu wastes α-radiation damage leads to the amorphization of PuO2(cr) [21]. Despite these problems there is good agreement between the values derived for the solubility constant of Pu(IV) hydrous oxide by different authors and approaches [2]: (a) the solubility products calculated in Ref. [16,22] from the available Pu(IV) equilibrium concentrations with the hydrolysis constants for Pu(OH)n4−n reported in Ref. [23], (b) those derived from the solubility of PuO2(am,hyd) under reducing conditions in equilibrium with Pu3+ [4–6], and (c) the value obtained for colloidal PuO2(am,hyd) particles in equilibrium with Pu3+, PuO2+ and PuO22+ at pHc = 1.0 [24]. The equilibrium concentration of aqueous Pu(IV) species is usually low compared to those of Pu(III), Pu(V) and Pu(VI) which result from the known redox equilibria and depend on the redox potential and pH.
The solubility of amorphous Pu(V) hydroxide, PuO2OH(am), is relatively high and does not represent a retention barrier. Oxyhydroxides of Pu(VI) (thermodynamic data are only known for PuO2(OH)2·H2O(cr) [1,2]) might control the solubility under strongly oxidising conditions (e.g., in case of radiolysis in concentrated chloride brines where Pu(VI) is the dominant oxidation state in solution [8,15]), but these conditions are not further discussed here.
A few years ago Haschke et al. [25–28] reported the formation of PuO2+x(s) which has been discussed very controversially. Recent EXAFS and XPS studies [29,30] report that the formation of PuO2+x(s,hyd) is a partially oxidised mixed valent hydrated oxyhydroxide (PuV)2x(PuIV)1−2xO2+x−n(OH)2n(s,hyd). Our recent analysis of total Pu concentrations, oxidation state distributions and simultaneously measured redox potentials in solubility studies under air and under Ar (with only traces of O2(g) present) also indicates that oxygen is scavenged by solid PuO2(s,hyd) yielding mixed valent PuO2+x(s,hyd) that controls the solubility, i.e., the equilibrium concentrations of both Pu(IV) and Pu(V) [10]. However, the extreme stability of PuO2+x(s) and the thermodynamic data reported by Haschke et al. [27,28] cannot be correct [31,32]. These important findings are summarized in the present paper; thermodynamic data for PuO2+x(s,hyd) will be discussed as well.
1.1 Definition of redox conditions
The decisive solution parameters that govern the solubility and oxidation-state distributions of plutonium (in the absence of complexing ligands) are the H+ activity (pH = −log aH+) or concentration (pHc = −log [H+]) and the redox potential. The redox potential can be expressed as Eh versus the standard hydrogen electrode (SHE) or, analogous to pH, in terms of the apparent electron activity . Eh and pe are related by:
| (1) |
| 0.5H2O(l) ⇌ 0.25O2(g) + H+ + e− | (2) |
| H+ + e− ⇌ 0.5H2(g) | (3) |
| (4) |
For many other redox couples involving H+ ions the value of (pe + pH) is also constant, i.e., pe decreases with a slope of −1 with increasing pH. Typical examples relevant for nuclear waste repositories are reducing redox systems buffered at (pe + pH) = 2 ± 2 by mixtures of solid Fe(II) and/or Fe(III) and mixed valent Fe(II–III) oxides and oxyhydroxides which result from the corrosion of metallic iron (c.f., Ref. [3] and discussion in Section 2) or steal canisters. For example a redox buffer consisting of solid Fe(OH)2(s) or FeO(s,hyd) and Fe(OH)3(s) or FeO1.5(s,hyd) = 1/2 Fe2O3(s,hyd):
| FeO(s,hyd) + 0.5H2O(l) ⇌ FeO1.5(s,hyd) + e− + H+ | (5) |
| UO2(s,hyd) + 3H2O(l) ⇌ UO3·2H2O(cr) + 2(e− + H+) | (6) |
1.2 Equilibrium constants at zero ionic strength and ionic strength corrections
The standard-state equilibrium constants (I = 0, 25 °C) used to calculate redox, solubility and hydrolysis equilibria of plutonium in the oxidation states III, IV, V, VI are given in Table 1 (Appendix). Most of these equilibrium constants for solid compounds and aqueous complexes of plutonium and some oxidation state analogs are taken from the NEA-TDB reviews [1,2]. Some additional equilibrium constants will be discussed in the present paper. The specific ion interaction theory (SIT) recommended in the NEA-TDB reviews [1,2] is used for ionic strength corrections. The activity coefficients γi of aqueous species i are given by:
| (7) |
2 Solubility of plutonium under reducing conditions
If the solubility of plutonium under reducing conditions is controlled by Pu(OH)3(s) (analogous to other trivalent actinides or lanthanides in the absence of carbonate, phosphate, etc.), the concentration of Pu3+ and its hydroxide complexes Pu(OH)n3−n is given by the solubility product (Ksp = [Pu3+][OH−]3) and the formation constants (βn = [Pu(OH)n3−n]/[Pu3+][OH−]n) for the reactions:
| Pu(OH)3(s) ⇌ Pu3+ + 3OH− | (8) |
| Pu3+ + nOH− ⇌ Pu(OH)n3−n | (9) |
| Pu(OH)3(s) + 3H+ ⇌ Pu3+ + 3H2O | (10) |
| Pu3+ + nH2O ⇌ Pu(OH)n3−n + nH+ | (11) |
| (12) |
Depending on the given redox conditions, the equilibrium between dissolved Pu(III) and Pu(IV) can lead to Pu(IV) concentrations exceeding the solubility of Pu(IV) hydrous oxide; consequently this will lead to the precipitation of PuO2(am,hyd) and the complete dissolution of Pu(OH)3(s). Combining reactions (13)–(15) with the equilibrium constants log∗K°s,0 = 15.8 ± 0.8 for Pu(OH)3(s) and −2.33 ± 0.52 for PuO2(am,hyd) and log K°III–IV = −17.69 ± 0.04 for the redox couple Pu3+/Pu4+ [2]:
| Pu(OH)3(s) + 3H+ ⇌ Pu3+ + 3H2O | (13) |
| Pu3+ ⇌ Pu4+ + e− | (14) |
| Pu4+ + 2H2O ⇌ PuO2(am,hyd) + 4H+ | (15) |
| Pu(OH)3(s) ⇌ PuO2(am,hyd) + H2O + H+ + e− | (16) |
In the case of solubility control by PuO2(am,hyd), the equilibrium Pu(IV) concentration is given by the solubility product of PuO2(am,hyd) (Ksp = [Pu4+][OH−]4) and the formation constants of the Pu(IV) hydroxide complexes (βn = [Pu(OH)n4−n]/[Pu4+][OH− ]4). In addition PuO2(am,hyd) is in equilibrium with aqueous Pu(III) species. The dissolution equilibrium of PuO2(am,hyd) and the redox equilibrium between Pu4+ and Pu3+:
| PuO2(am,hyd) + 4H+ ⇌ Pu4+ + 2H2O | (17) |
| Pu4+ + e− ⇌ Pu3+ | (18) |
| PuO2(am,hyd) + e− + 4H+ ⇌ Pu3+ + 2H2O | (19) |
| (20) |
With this background the results of Felmy et al. [3], the only available study providing solubility data for Pu(OH)3(s), are discussed here. The experiments were performed at 23 °C under inert-gas atmosphere in the presence of iron powder. The solid was precipitated from a Pu(III) stock solution but not further characterised and suspended either in deoxygenated water or in concentrated chloride solutions (synthetic WIPP brines). The plutonium concentrations (after 1.8 nm filtration) were measured after relatively short equilibration times of 1–24 days. Fig. 1 shows the solubility data in the dilute solutions (I < 0.01 M) and the measured Eh values (those in the chloride brines are similar). The redox potentials are in the range (pe + pH) = 2 ± 1, typical for values in suspensions of corroding iron and clearly above the stability line of Pu(OH)3(s) at (pe + pH) = −0.4 ± 1.0 (fat dashed line in Fig. 1b). Under these conditions the initial Pu(OH)3(s) precipitate is metastable and should convert slowly into PuO2(am,hyd). Fig. 1a shows the equilibrium Pu(III) concentration calculated for Pu(OH)3(s) as solid phase (dashed line) and also the equilibrium Pu(IV) and Pu(III) concentrations calculated for (pe + pH) = 2 with PuO2(am,hyd) as solid phase (solid lines). The experimental Pu(III) concentrations of Felmy et al. [3] are between the dashed and solid line. The short equilibration times of 1–24 days are not sufficient for a complete solid phase transformation and the solubility constant derived from the data at pH 6–7, log∗K°s,0(Pu(OH)3(s)) = 15.8 ± 0.8 [3], is most probably correct. However, as indicated by the arrow in Fig. 1a, a number of data points show a tendency to the lower curve expected after transformation into PuO2(am,hyd).
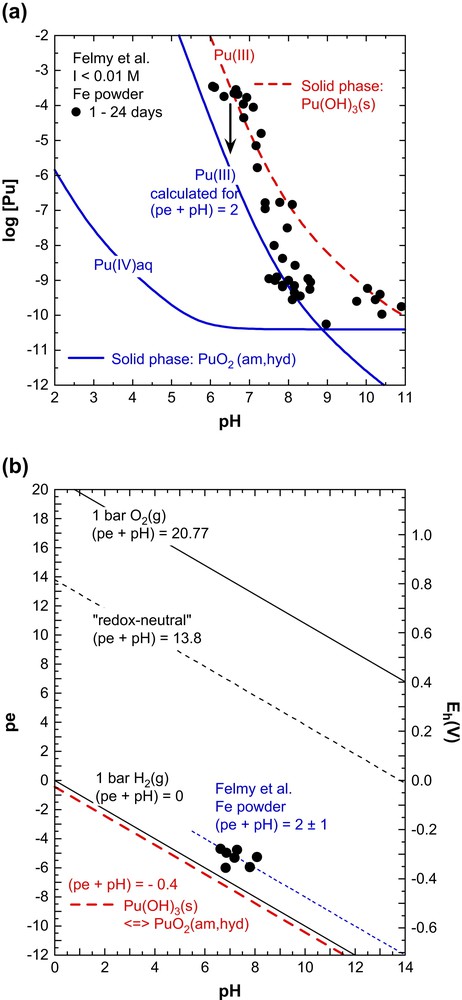
Solubility study of Felmy et al. [3] with Pu(OH)3(s) at 23 °C and I < 0.01 M. a) Experimental Pu concentration measured after 1.8-nm filtration and calculated solubility; the dashed line is calculated for solubility control by Pu(OH)3(s), the solid lines for solubility control by PuO2(am,hyd) at (pe + pH) = 2 ± 1. b) Redox potentials in the suspensions containing Fe powder [3]. The fat dashed line at (pe + pH) = −0.4 represents the stability line of Pu(OH)3(s) with regard to its transformation into PuO2(am,hyd). The solid lines at (pe + pH) = 0 and 20.77 define the stability field of water, the dashed line at (pe + pH) = 13.8 is calculated for redox-neutral aqueous solutions.
Contrary to the solubility constant of Pu(OH)3(s), the equilibrium constant for the reductive dissolution of PuO2(am,hyd) (Eqs. (19) and (20)) is well ascertained. A few years ago, Fujiwara et al. [4,5] and Rai et al. [6] investigated this reaction directly by measuring the Pu3+ concentration in solubility studies with PuO2(am,hyd) under various reducing conditions: (a) in 0.5, 1.0 and 2.0 M NaClO4 + 0.001 M Na2S2O4 (pH 3–9) with (pe + pH) = 10 ± 1 [4,5], (b) in 0.005 M CaCl2 or 0.01 M NaClO4 + 5.2×10−4 M hydroquinone (pH 3–9) with (pe + pH) = 4.0 ± 0.5 [6], and (c) in 0.01 M NaCl + 0.001 M FeCl2 with pe = 11 at pH 2 decreasing to pe = −7 at pH 11 [6]. All results can be consistently described with log∗K°IVs/III = 15.5 ± 0.6, close to the value of log∗K°IVs/III = 15.4 ± 0.5 based on the NEA-TDB selections [2]. The experimental solubilities and redox potentials in the Na2S2O4 and hydroquinone solutions and the corresponding calculations for (pe + pH) = 10 and 4, respectively, are compared in Fig. 2. As predicted according to Eq. (20), the increase of (pe + pH) from 4 and 10 leads to a decrease of the Pu(III) concentration by about six orders of magnitude.
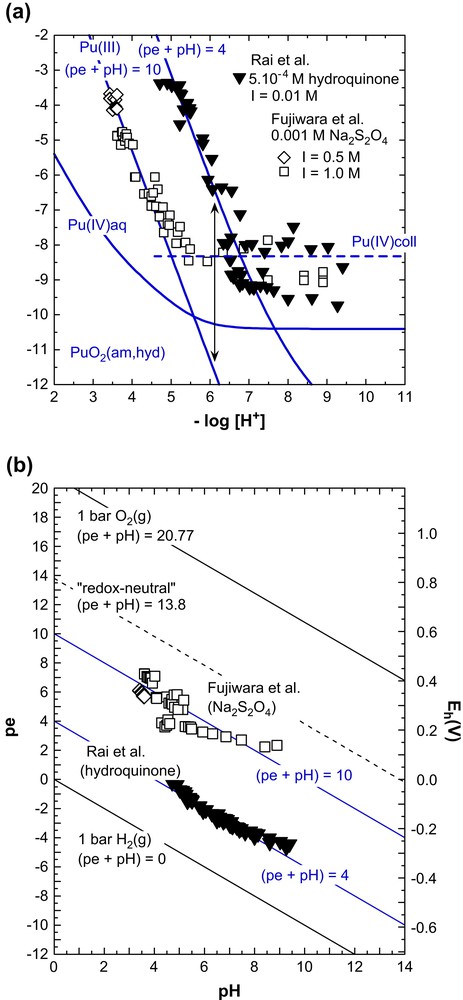
The effect of (pe + pH) on the solubility of Pu(IV) hydrous oxide under reducing conditions. (a) Solubility data of Fujiwara et al. [4,5] at (pe + pH) = 10 ± 1 (in 0.5 and 1.0 M NaClO4 + 0.001 M Na2S2O4) and Rai et al. [6] at (pe + pH) = 4.0 ± 0.5 (in 5.2 × 10−4 M hydroquinone solutions at I = 0.01 M) and corresponding calculations for these redox conditions, and (b) experimental redox potentials.
In a recent study, Nilsson [7] tried to determine the solubility of Pu(OH)3(s) at ambient temperature in 0.1 M NaCl under a pressure of 50 bar H2(g) in an autoclave containing a piece of Pt wire. Under these extremely reducing conditions, corresponding to (pe + pH) = −0.85, the X-ray amorphous Pu(OH)3(am) precipitated from a Pu(III) stock solution was expected to remain stable. However, the Pu concentrations measured after centrifugation (analyzed for [Pu]tot = [Pu(III)] + [Pu(IV)] after 150, 320 and 480 days and for [Pu(IV)] after 480 days) were much lower than expected for Pu(OH)3(s) (Fig. 3a) and the redox potentials measured after 480 days were much higher than expected for P(H2(g)) = 50 bar (Fig. 3b). Obviously, pe was not controlled by the reaction 0.5H2(g) ⇌ H+ + e−. From pH changes in their samples in the near neutral pH range and the changed colour of the solid Nilsson [7] concluded that the initially blue Pu(OH)3(am) transformed into green PuO2±x(am,hyd), but gave no quantitative data interpretation. Fig. 3 shows that the results can be well explained by Eq. (20) for the reductive dissolution of PuO2(am,hyd). The measured solubility data are reasonably consistent with the Pu(III) concentrations calculated for the experimental values of (pe + pH) = 8.5 ± 2 and an additional contribution from Pu(IV) colloids. It is difficult to find an explanation for the measured redox potentials, but accepting the measured pe values it is possible to calculate the solubility and aqueous speciation of plutonium.
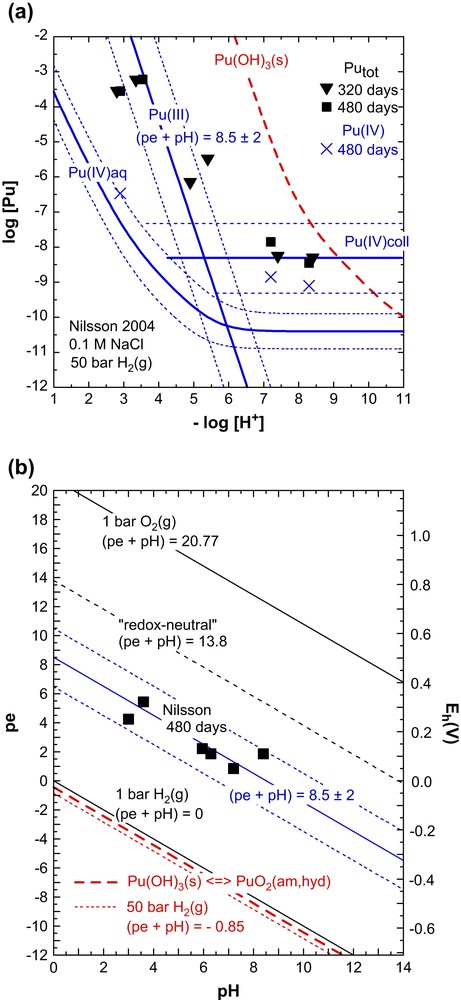
Solubility of Pu(IV) hydrous oxide (a) and redox potentials (b) determined by Nilsson [7] after 320 and 480 days in 0.1 M NaCl solutions under a pressure of 50 bar H2(g) after the transformation of the initial Pu(III) hydroxide precipitate. The calculated Pu(III) concentration refers to the experimental redox conditions of (pe + pH) = 8.5 ± 2. The dotted line at (pe + pH) = −0.85, calculated for P(H2(g)) = 50 bar is in the stability field of Pu(OH)3(s), slightly below the fat dashed stability line at (pe + pH) = −0.4. The expected solubility curve for the initial Pu(OH)3(s) precipitate is shown for comparison also as fat dashed line.
The concentration line for polymeric Pu(IV) oxyhydroxide species (1.5–2 nm colloids) included in Figs. 2a and 3a (log[Pu(IV)]coll = −8.3 ± 1.0) was determined in our recent solubility study with Pu(IV) hydrous oxide [10] from the difference of the Pu concentrations measured after 10 kDa ultrafiltration and in unfiltered aliquots taken carefully from the clear supernatant. Similar as in a previous study where we determined the pH-independent concentration of colloidal or polymeric Th(IV) at pH 6.5–13.5 (log[Th(IV)]coll = −6.3 ± 0.5) [38] the concentration [Pu(IV)]coll at pH 8–13 was reasonably reproducible and at a constant level. For both Th(IV) and Pu(IV) the level of [An(IV)]coll is about two orders of magnitude higher than the An(IV) concentration after 1.5 nm ultrafiltration or ultracentrifugation. This is consistent with a model on Pu(IV) polymer formation proposed by Fujiwara et al. [4] who supposed that the concentration of log[Pu(IV)] = −9 measured in 1 M NaClO4 (pH 7–9) after 2 nm filtration is primarily caused by small Pu(IV) polymers; [Pu(IV)]tot is expected to include further contributions from eigencolloids larger than 2 nm. The equilibrium concentration of mononuclear Pu(IV) species was calculated to be log[Pu(OH)4(aq)] = −10.3 ± 0.2 [4] which is close to the value of −10.4 ± 0.5 determined by Rai et al. [9] and used in the present calculations.
3 Solubility of plutonium in redox-inert solutions under argon atmosphere
In a recent study at our laboratory [10], Pu(IV) hydrous oxide was precipitated from an electrochemically prepared Pu(IV) stock solution containing a contamination of 0.5% Pu(VI) and the solubility was determined at I = 0.1 M (NaCl) and 22 ± 2 °C. The work was carried out in an Ar glove box (<10 ppm O2) using long-lived Pu-242 (t1/2 = 3.8×105 a) to minimize radiolysis effects. The batch samples at pH 2.5–13 (ca. 20 mg Pu-242 in 50 mL solution) were analyzed after equilibration periods between 6 and 104 days: Eh and pH were measured directly in the samples, the Pu concentrations (total Pu and the different Pu oxidation states) were measured after 10 kDa ultrafiltration (pore size ca. 1.5 nm). The constant values obtained after 34 days indicated that equilibrium was attained. The results are shown in Fig. 4.
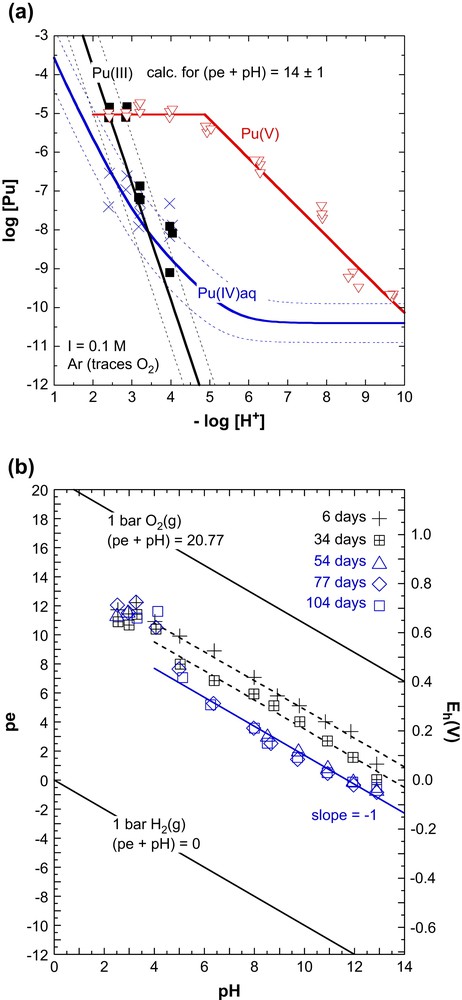
Experimental results from our solubility study with Pu(IV) hydrous oxide under Ar (<10 ppm O2) at 22 °C in 0.1 M NaCl [10]. (a) Equilibrium concentrations after 1.5 nm filtration: Pu(IV) (crosses), Pu(III) (filled squares) and Pu(V) (triangles), and (b) redox potentials measured after 6–104 days.
The samples at pH 2.5 and 3.0 contained about equimolar concentrations of Pu(III) and Pu(V), whereas the samples at pH > 3 showed only the absorption bands of the PuO2+ ion. Aqueous Pu(IV) species could not be detected by absorption spectroscopy and redox speciation by solvent extraction showed that the Pu(IV) concentrations are very low compared to the total dissolved Pu, almost exclusively non-extractable Pu(V). The Pu(IV) concentrations at pH < 4 are in the expected range (c.f., Fig. 4a). The total Pu concentrations at pH 8–13 were in the range of 10−9 to 10−10 M, close to values determined by Rai et al. [9] in dilute KOH solutions. The redox potentials measured in samples containing solid and colloidal Pu(IV) have a relatively large experimental uncertainty of ±50 mV [10], but the pe values at pH 4–13 clearly show a linear decrease with pH (slope −1, Fig. 4b). The values of (pe + pH) decreased from 14.9 ± 0.8 after 6 days to 13.5 ± 0.8 after 34 days and to constant values of 11.7 ± 0.8 after 54–104 days.
The Pu(III) concentrations at pH 2.5–3.3 and pe = 10–12 can be described by the reductive dissolution of PuO2(am,hyd). The experimental Pu3+ concentrations and the steep decrease of log[Pu3+] at pH > 3 are consistent with Eq. (20) and the calculations for (pe + pH) = 14 ± 1 (c.f., Fig. 4a). However, the experimental Pu(V) concentrations, up to pH 5 at a constant level of log[Pu(V)] = −5 and at pH 5–10 decreasing with a slope of −1, are not consistent with the oxidative dissolution of Pu(IV) hydrous oxide:
| PuO2(am,hyd) ⇌ PuO2+ + e− | (21) |
| (22) |
The values calculated for the equilibrium constant log K°IVs/V from the experimental PuO2+ concentrations and pe values deviate up to seven log-units from the value of log K°IVs/V = −19.8 ± 0.9 based on the data selected in the NEA-TDB [2] for PuO2(am,hyd) and PuO2+. Similar discrepancies observed in solubility studies under air [13–15] will be discussed below.
Another solubility study under Ar atmosphere was reported by Lierse and Kim [8] who titrated PuO2(s,hyd) suspensions in 1 M NaClO4 from pH 12 to pH 1. They obtained a similar solubility curve with log[Pu]tot decreasing with a slope of −1 from pH 3 to 10, but they did not report oxidation state analysis and redox potential measurements.
4 Solubility of plutonium in the presence of oxygen
4.1 The effect of oxygen on the total Pu concentration in solution
Fig. 5 shows the total Pu and Pu(IV) concentrations measured by Rai et al. [13–15] at pH 1–8 after up to 106 days and a few data from other authors at pH < 2 [11,12] in solubility studies with PuO2(s,hyd) at I = 0.01–1 M and 20–25 °C. In these studies the solutions were exposed to air and then kept in closed vials. The total Pu concentration at pH < 1.5 (log[Pu]tot, open points in Fig. 5) is slightly increased compared to log[Pu(IV)]aq (crosses). It passes through a plateau at pH 1–3 and decreases with a slope of −1 at pH > 3. Aqueous speciation by spectroscopy and solvent extraction showed that the dissolved Pu at pH 1–3 consists mainly of PuO22+ and PuO2+ while PuO2+ predominates at pH 3–9 [13–15]. The concentration of oxidised Pu ([PuO22+] + [PuO2+]) at pH < 3 corresponds to the available oxygen in these closed systems, given by the sum of [O2]aq = 2.5 × 10−4 M at P(O2(g)) = 0.2 bar and O2(g) in the gas phase above the solution [31].
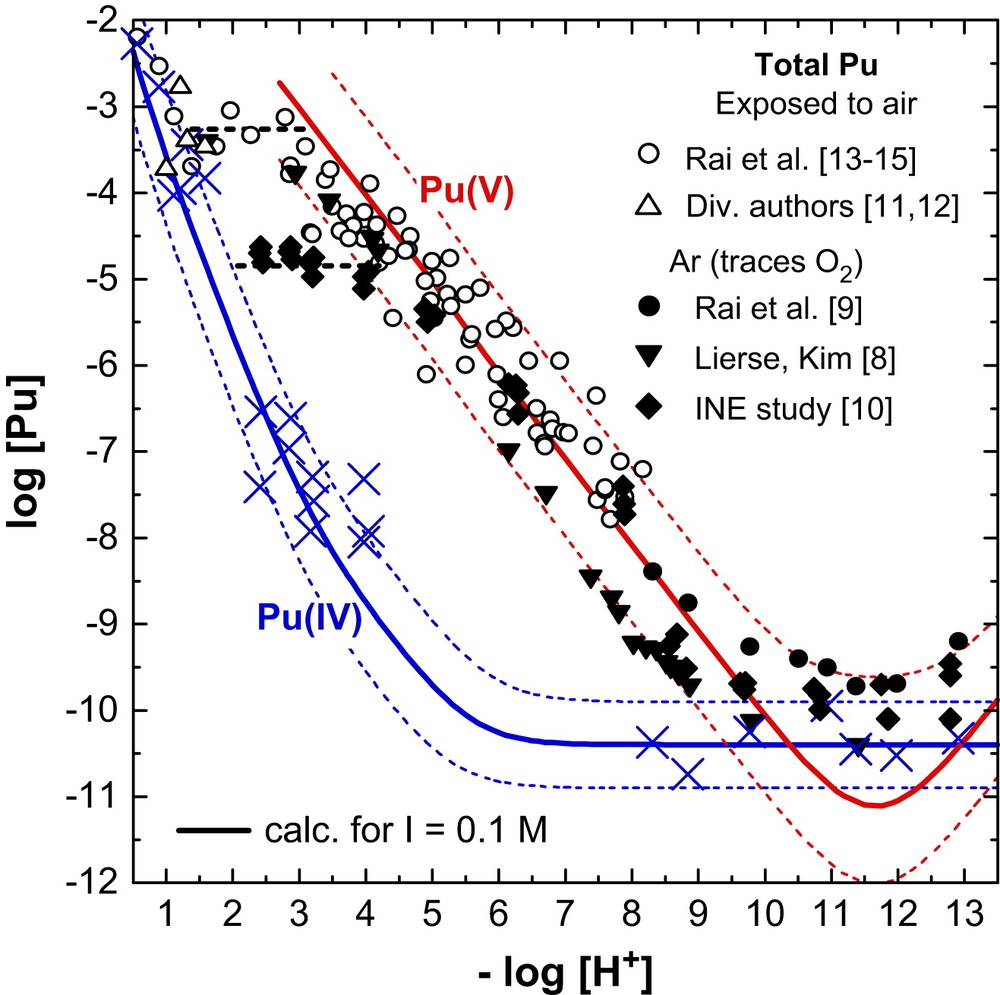
Solubility of Pu(IV) hydrous oxide at 20–25 °C and I = 0.01–1.0 M. Experimental data measured after ultrafiltration; open symbols: total Pu concentration in studies under air [11–15], filled symbols: total Pu concentration in studies under Ar atmosphere [8–10], and crosses: Pu(IV) concentrations [8–14].
The Pu concentrations measured by Lierse and Kim [8], Rai et al. [9] and in our previous study [10] under Ar atmosphere containing only traces of O2(g) are shown for comparison as filled points in Fig. 5. The Pu(V) concentrations at pH > 4 are, within the uncertainties, the same as those determined by Rai et al. [13–15] in samples kept under air. However, the constant level of [Pu(V)] = 10−5 M at pH < 5 in our study under Ar is considerably lower than the corresponding values under air. It corresponds to the 0.5% Pu(VI) in the initial Pu(IV) stock solution, if this fraction of oxidised Pu is co-precipitated with the Pu(IV) hydrous oxide and re-dissolved in the solubility experiments. The data of Lierse and Kim [8] who titrated PuO2(am,hyd) suspensions in 1 M NaClO4 under a continuous Ar stream from pH 12 to pH 1 may be explained if we assume that the Ar stream included a contamination of a few ppm O2 and that the total amount of oxidised Pu species accumulated during the titration experiment (2–3 months) [31].
4.2 Equilibrium Pu(V) concentrations and redox potentials: evidence for the formation of PuO2+x(s,hyd)
The Pu concentrations measured in the solubility studies under air or under Ar atmosphere cannot be explained without the knowledge of the redox potentials. It is helpful to divide the experimental data into different pH regions (Figs. 6a and b). Rai [14] has shown that the solubility of PuO2(am,hyd) under air at pH 1–3 (region A) is dominated by the oxidative dissolution reaction (23) and the redox equilibrium (24) between PuO2+ and PuO22+:
| PuO2(s,hyd) ⇌ PuO2+ + e− | (23) |
| PuO2+ ⇌ PuO22+ + e− | (24) |

(a) Solubility of PuO2+x(s,hyd) at 20–25 °C; Pu concentration measured after ultrafiltration and without removal of Pu(IV) colloids/polymers (crosses); comparison of data measured under air (open symbols) [13–15] and under Ar (filled symbols) [9,10]. (b) Simultaneously measured redox potentials (analogous symbols).
The redox potentials in region A, pe = 16.0 ± 0.3 [14], are consistent with the spectroscopically determined PuO2+ and PuO22+ concentrations and log K°V/VI = −15.82 ± 0.09 [1,2]. The equilibrium constant derived by Rai [14] for the oxidative dissolution of PuO2(am,hyd) from the experimental pe values and Pu(V) concentrations, log K°IVs/V = −19.45 ± 0.23 [14], is also in agreement with the value of log K°IVs/V = −19.8 ± 0.9 calculated with the standard molar Gibbs energies selected in the NEA-TDB [2] for PuO2(am,hyd), Pu4+ and PuO2+ from different, independent data. In our study under Ar [10] the redox potentials at pH 2.5–3.3 are much lower. Hence Pu(VI) is not observed, but only Pu(V) (and Pu(III) as expected according to Eq. (20)). However, the values of pe = 10–12 and log[PuO2+] = −5 are strongly inconsistent with log K°IVs/V = −19.8 ± 0.9.
At pH 3–4 the pe values in the studies under air [13–15] drop drastically to about 7 log-units lower values (Fig. 6b) while the solubility (log[Pu]tot ≈ log[PuO2+]) decreases continuously with a slope of −1 (Fig. 6a). Accordingly, the solubility constant log K°IVs/V derived from the experimental values of pe and [PuO2+] in region C would differ by seven orders of magnitude from the value derived in regions A and B [13,14]. As there was no evident explanation for this discrepancy, it was ascribed to possible experimental problems in the Eh measurements [14,15]. However, our results under Ar (P(O2(g)) < 10−5 bar) show that the redox potentials in region C are reproducible within a certain range. Moreover they coincide with those measured by Rai et al. [13–15] under air (P(O2(g)) = 0.2 bar). The redox potentials in region C and also the slopes of −1 in regions B and C (pe + pH = constant) can neither be explained by equilibria between aqueous Pu species nor by the oxygen partial pressures [10,15]. The experimental results in regions B and C are not consistent with the equilibria:
| PuO2(s,hyd) ⇌ PuO2+ + e− | (25) |
| PuO2(s,hyd) + 1/4 O2(g) + H+ ⇌ PuO2+ + 1/2 H2O | (26) |
The Pu(V) concentrations and pe values at pH > 3, which are more or less the same in the studies under air [13–15] and under Ar [10] can be explained with PuO2+x(s,hyd), mixed valent hydrous oxide (PuV)2x(PuIV)1−2xO2+x(s,hyd) or (PuO2.5)2x(PuO2)1−2x(s,hyd), as solubility controlling solid phase in equilibrium with both Pu(V) and Pu(IV) in solution. It can be formed by the oxidation of PuO2(s,hyd) with the oxygen present in the system:
| PuO2(s,hyd) + x/2 O2 → PuO2+x(s,hyd) | (27) |
The mixed valent hydrous oxide PuO2+x(s,hyd) = (PuV)2x(PuIV)1−2xO2+x(s,hyd) may be written formally as (PuO2.5)2x(PuO2)1−2x(s,hyd) in equilibrium with both Pu(V) and Pu(IV) in solution:
| PuO2+x(s,hyd) + (2−3x)H2O(l) ⇌ 2xPuO2+ + (1−2x)Pu4+ + (4 − 6x)OH− | (28) |
| (29) |
The solubility products for the formal fractions of PuO2.5(s,hyd) and PuO2(s,hyd) in PuO2+x(s,hyd) can be calculated separately, because the dissolved PuO2+ and Pu4+ ions and their hydroxide complexes do not undergo reversible redox reactions:
| Ksp(PuO2.5 in PuO2+x(s,hyd)) = [PuO2+][OH−] | (30) |
| Ksp(PuO2 in PuO2+x(s,hyd)) = [Pu4+][OH− ]4 | (31) |
The experimental Pu(IV) concentrations were previously used to calculate the solubility product of PuO2(am,hyd) [2,16,22] and the evaluation of the PuO2+ concentrations at pH 3–9 is given in detail in our recent paper [10]. The solubility product of PuO2.5(s,hyd) as a fraction of PuO2+x(s,hyd) was calculated from the different sets of data determined by Rai et al. [13–15] under air in dilute solutions of low ionic strength and in 0.4 and 4.0 M NaClO4 and NaCl and from the data determined under Ar atmosphere by Lierse and Kim [8] in 1.0 M NaClO4 and in our recent work in 0.1 M NaCl. All data sets yield consistent equilibrium constants at I = 0 with a mean value (±2σ) of log K°sp(PuO2.5 in PuO2+x(s,hyd)) = −14.0 ± 0.8 or log∗K°s,0(PuO2.5 in PuO2+x(s,hyd)) = 0.0 ± 0.8 [10] for the reactions:
| PuO2.5(s,hyd) + 1/2 H2O ⇌ PuO2+ + OH− | (32) |
| PuO2.5(s,hyd) + H+ ⇌ PuO2+ + 1/2 H2O | (33) |
The solubility product of PuO2.5(s,hyd) as a formal fraction of PuO2+x(s,hyd) is five orders of magnitude lower than that of Pu(V) hydroxide (log K°sp(PuO2OH(am,hyd)) = −9.0 ± 0.5 [1,2]). It compares well with the values for Np(V) pentoxide: log K°sp(NpO2.5(cr)) = −12.2 ± 0.8 (calculated from thermochemical data in Refs. [1,2]) and log K°sp(NpO2.5(s,hyd)) = −11.4 ± 0.4 (solubility study of Efurd et al. [40]) and appears to be in a reasonable order of magnitude, in particular as the solubility product of PuO2(am,hyd) is also about 2 log-units lower than that of NpO2(am,hyd) (log Ksp = log ([An4+][OH−]4); log K°sp = −58.3 ± 0.5 for Pu(IV) and −56.7 ± 0.5 for Np(IV) [2]).
Solubility control by PuO2+x(s,hyd) explains the redox potentials at pH > 3 under air, in particular the slope of −1 at pH 3–5 (region B in Fig. 6b) that could not be explained by Rai [14]. At low pH (region A) the Pu(V) fractions in the PuO2+x(s,hyd) solids are below the Pu(V) saturation concentration and completely soluble, but at pH > 3 they exceed the solubility of PuO2+x(s,hyd). Combining Eqs. (34) and (35) and the corresponding equilibrium constants (log K°IVs/V = −19.8 ± 0.9 [2], log∗K°s,0(PuO2.5 in PuO2+x(s,hyd)) = 0.0 ± 0.8 [10]):
| PuO2(s,hyd) ⇌ PuO2+ + e− | (34) |
| PuO2+ + 1/2 H2O ⇌ PuO2.5(s,hyd) + H+ | (35) |
| PuO2(s,hyd) + 1/2 H2O ⇌ PuO2.5(s,hyd) + e− + H+ | (36) |
At pH > 4, the pe values drop to drastically lower values and decrease up to pH 13 with a slope of −1 (c.f., region C in Fig. 6b where the line of (pe + pH) = 12.5 ± 1.2 covers the experimental data). These redox potentials can only be explained if the small colloidal or polymeric Pu(IV) oxyhydroxide species prevailing in neutral to alkaline solution (c.f., Fig. 6a and discussion in Section 2), are taken into consideration. On the one hand they have properties of small solid particles designated here as PuO2(coll,hyd), on the other hand they must be considered as large polynuclear aqueous species, in equilibrium with both small aqueous species and solid PuO2(s,hyd):
| PuO2(s,hyd) ⇌ PuO2(coll,hyd,aq) | (37) |
| PuO2(coll,hyd) + x/2 O2 + 2xH+ → (PuO2.5)2x(PuO2)1−2x(coll,hyd) + 2xH+ → 2xPuO2+ + xH2O + (1–2x)PuO2(coll,hyd) | (38) |
| PuO2(coll,hyd) ⇌ PuO2+ + e− | (39) |
| PuO2+ + 1/2 H2O ⇌ PuO2.5(s,hyd) + H+ | (40) |
The equilibrium constant for reaction (39), log K°IVcoll/V = −11.5 ± 1.3, can be calculated from ΔfG°m(PuO2(coll,hyd)) = −918.1 ± 7.0 kJ/mol and ΔfG°m(PuO2+) = −852.65 ± 2.87 kJ/mol [1]. Combining Eqs. (39) and (40) yields:
| PuO2(coll,hyd) + 1/2 H2O ⇌ PuO2.5(s,hyd) + e− + H+ | (41) |
5 The role of Pu(IV) colloids/polymers in the Pu(IV)–Pu(V) redox chemistry
Since tetravalent actinides have a high tendency towards polynucleation and colloid formation the solubility is usually measured after ultrafiltration or ultracentrifugation to remove these species, whereas redox potentials are usually measured directly in the samples [3–7,10,13–15]. As discussed above, the colloidal or polymeric Pu(IV) oxyhydroxide species present in neutral and alkaline solutions have a significant impact on the redox potentials in systems without oxidising or reducing chemicals. They are not “notorious troublemakers” in plutonium chemistry as recently stated by Nilsson [7] but part of the thermodynamic system as illustrated in Fig. 7.
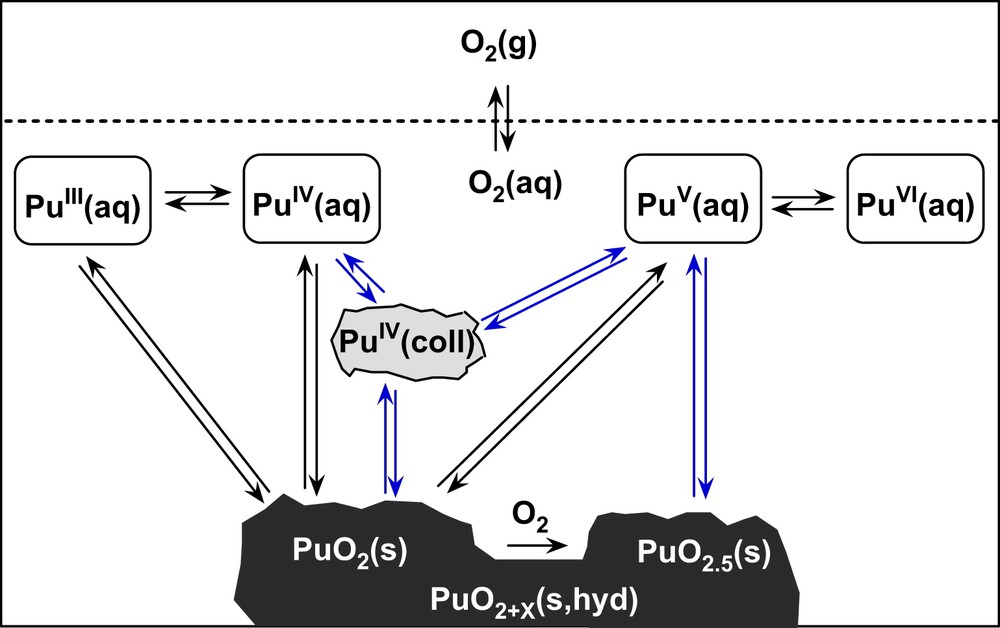
Solid–liquid and redox equilibria of plutonium under reducing conditions, in redox-neutral solutions and in the presence of oxygen.
Further experiments reported in Ref. [10] support the conclusion that the redox potentials in near neutral Pu(IV)–Pu(V) solutions correspond to a reversible equilibrium between PuO2(coll,hyd) particles and PuO2+ ions:
| PuO2(coll,hyd) ⇌ PuO2+ + e− | (42) |
Another recent study indicates that colloidal or polymeric Pu(IV) species play also an important role for the redox behaviour of Pu(IV) in acidic solutions [43]. Electrochemically prepared Pu(IV) solutions at pHc = 0.3–2.5 were investigated spectroscopically to study the formation of Pu(III), Pu(V) and/or Pu(VI), which is usually ascribed to the disproportionation of Pu(IV) into Pu(III) and Pu(V), followed by the reaction of Pu(V) with Pu(IV) into Pu(VI) and Pu(III) or by the disproportionation of Pu(V) into Pu(III) and Pu(VI). The steady state oxidation state distributions and pe values observed after 10–20 days were consistent with the known redox equilibria [1,2,24,44]. However, particularly the oxidation state distributions observed after short reaction times provide evidence that the underlying mechanism is not consistent with disproportionation reactions but with the formation of PuO2+ from colloidal or smaller polynuclear Pu(IV) species followed by the simultaneous equilibration of the reversible redox couples Pu(V)/Pu(VI) and Pu(III)/Pu(IV) which are related by pe (and pH because of Pu(IV) hydrolysis equilibria) [43]. Contrary to the reversible redox couples Pu3+/Pu4+ and PuO2+/PuO22+ the PuO2+ and Pu4+ ions and their mononuclear hydroxide complexes are not directly in equilibrium with each other but only indirectly via their reactions with solid, colloidal or polymeric Pu(IV).
6 Thermodynamic data for PuO2+x(cr) and PuO2+x(s,hyd)
In the following sections, thermodynamic data for hydrous PuO2+x(s,hyd) and for possible anhydrous crystalline compounds like PuO2.25(cr) = 1/4 Pu4O9(cr), PuO2.5(cr) = 1/2 Pu2O5(cr), and PuO3(cr) are discussed by comparing known standard molar Gibbs energies of formation ΔfG°m(298.15 K) of pure and mixed valent anhydrous oxides and hydrous oxyhydroxides of uranium, neptunium and plutonium in the oxidation states An(IV), An(V) and An(VI). The values for hydrous An(IV) and An(V) oxyhydroxides correspond to the formula AnO2+x(s,hyd), i.e., the contribution of H2O molecules is not included in the values for ΔfG°m(AnO2+x(s,hyd)). For better comparison, the ΔfG°m values for crystalline An(VI) oxyhydroxides with the formula AnO2O1−n/2(OH)n·yH2O(cr) are also normalized to values referring to the formula AnO3(cr,hyd) by subtracting (n/2 + y)ΔfG°m(H2O(l)), e.g., the value of ΔfG°m(PuO2(OH)2·H2O(cr)) = −1442.4 kJ/mol [1,2] ((n/2 + y) = 2) is transformed into ΔfG°m(PuO3(cr,hyd)) = −968.1 kJ/mol.
6.1 Standard molar Gibbs energies of formation of crystalline An(IV–V–VI) oxides and actinyl(VI) oxyhydroxides ΔfG°m(AnO2+x(cr), 298.15 K)
The standard molar Gibbs energies of formation ΔfG°m(AnO2+x(cr), 298.15 K) selected in the NEA-TDB [1,2] from experimental (thermochemical) data for anhydrous crystalline U(IV–V–VI) oxides, NpO2(cr), NpO2.5(cr) = 1/2 Np2O5(cr) and PuO2(cr) are shown in Fig. 8 (filled squares). The normalized values for the actinyl(VI) oxyhydroxides AnO3(s,hyd) of U(VI), Np(VI) and Pu(VI) (filled circles) were derived from the selected solubility constants [1,2]. Fig. 8 also includes estimated ΔfG°m values for NpO3(cr), PuO3(cr), and PuO2.5(cr) (open squares). These estimates for the unknown Np and Pu oxides are based on the two following assumptions.
- (1) The difference between the standard molar Gibbs energies of formation of the known neptunyl(VI) and plutonyl(VI) oxyhydroxides and the (unknown) anhydrous trioxides, NpO3(cr) and PuO3(cr), is assumed to be similar as for the analogous U(VI) compounds: ΔfG°m(UO3(cr,hyd), schoepite) − ΔfG°m(γ-UO3(cr)) = −16.5 ± 2.1 kJ/mol [2].
- (2) Mixed valent An(IV–V) and An(IV–VI) oxides are more stable than corresponding mixtures of the pure An(IV) and An(V) or An(VI) oxides (e.g., (1/3)ΔfG°m(U3O8(cr)) − {(2/3)ΔfG°m(UO3(cr)) + (1/3)ΔfG°m(UO2(cr))} = −15.4 kJ/mol). In Fig. 8, this stabilization effect is illustrated by the deviation of ΔfG°m for a mixed valent oxide from the dotted straight line between the ΔfG°m values of the pure An(IV) and An(VI) oxides. We may assume that the stabilization energy for mixed valent An(IV–VI) and An(IV–V) oxides is approximately the same for analogous compounds of U, Np and Pu as illustrated by analogous deviations between the solid and dotted lines in Fig. 8.

Normalized standard molar Gibbs energies of formation of crystalline An(IV, V, VI) oxides AnO2+x(cr) and actinyl(VI) oxyhydroxides AnO3(cr,hyd) as a function of x; known data (filled symbols) selected in the NEA-TDB [1,2] and estimated values for unknown Np and Pu oxides (open symbols).
The data in Fig. 8 clearly show that the standard molar Gibbs energy ΔrG°m for the oxidation of dry crystalline An(IV) dioxide AnO2(cr) with oxygen (ΔfG°m(O2(g)) = 0):
| AnO2(cr) + (x/2) O2(g) → AnO2+x(cr) | (43) |
| PuO2(s) + xH2O → PuO2+x(s) + xH2(g) | (44) |
The observed formation of H2(g) [25–28] cannot be explained by the thermodynamics of reaction (44) (ΔrG°m(44) > x200 kJ/mol), it must be caused by other mechanisms (e.g., induced by radiolysis effects). Another recent attempt to oxidise PuO2(cr) with water vapour (under strict exclusion of oxygen) at 315 °C failed [45]. However, it will be shown below that the formation of PuO2+x(s,hyd) in the presence of both water and oxygen is consistent with thermodynamic balances.
6.2 Standard molar Gibbs energies of formation of hydrous Np(IV–V) and Pu(IV–V) oxides ΔfG°m(AnO2+x(s,hyd), 298.15 K)
Mixed valent hydrous oxide PuO2+x(s,hyd) = (PuV)2x(PuIV)1−2xO2+x(s,hyd) is formally written as (PuO2.5)2x(PuO2)1−2x(s,hyd) which might suggest that it is considered as a solid solution. The chemical nature and structure of PuO2+x(s,hyd) is not yet clear. However, solubility studies with solids containing considerably different amounts of Pu(V) (x = 0.003 in a study under Ar [10] and x = 0.05–0.06 in studies under air [13–15]) led to very similar Pu(V) concentrations [10] (c.f., Section 4.2). This indicates that the Pu(V) concentration depends much less on the value of x than expected for a solid solution of PuO2.5(s,hyd) and PuO2(s,hyd). Accordingly PuO2+x(s,hyd) is treated as mixed valent compound and the following calculations refer to the definitions given by Eqs. (28)–(31). The standard molar Gibbs energy of formation of mixed valent PuO2+x(s,hyd) can be calculated from the formal solubility products of the Pu(V) and Pu(IV) fractions (log K°sp(PuO2.5 in PuO2+x(s,hyd)) = −14.0 ± 0.8, log K°sp(PuO2 in PuO2+x(s,hyd)) ≈ log K°sp(PuO2(s,hyd)) = −58.33 ± 0.52 [2]) and ΔfG°m(PuO2+) = −852.65 ± 2.87 kJ/mol, ΔfG°m(Pu4+) = −477.99 ± 2.70 kJ/mol, ΔfG°m(OH−) = −157.22 ± 0.07 kJ/mol, and ΔfG°m(H2O(l)) = −237.14 ± 0.04 kJ/mol [1,2]. With the ΔfG°m values for the two formal fractions:
- ΔfG°m(PuO2.5 in PuO2+x(s,hyd)) = −971.2 ± 5.4 kJ/mol
- ΔfG°m(PuO2 in PuO2+x(s,hyd)) = −965.5 ± 4.0 kJ/mol
| (45) |
As illustrated in Fig. 9 for Np and Pu the standard molar Gibbs energies of formation of An(IV) hydrous oxides are considerably less negative than those of the corresponding anhydrous crystalline An(IV) dioxides [2,16,17]. The difference of about 40 ± 10 kJ/mol, corresponding to seven log-units in the solubility constants, is due to effects from hydration and crystallinity (particle or crystallite size) as shown for ThO2(s) [17]. For the pentavalent actinides, e.g. Np(V), the difference between the standard molar Gibbs energies of hydrous oxides used in solubility studies and anhydrous crystalline oxides is much smaller. As a consequence and contrary to the slightly positive standard molar Gibbs energy for the oxidation of dry NpO2(cr), ΔrG°m for the oxidation hydrous NpO2(am,hyd) is negative, up to x = 0.5 (c.f., Fig. 9a). For hydrous plutonium oxide (Fig. 9b), ΔrG°m is slightly negative for x < 0.1 (and possibly up to x = 0.25), whereas ΔrG°m is expected to be equal to zero or slightly positive for x > 0.25, if we take into account that the value of ΔfG°m = −971.2 ± 5.4 kJ/mol calculated for PuO2.5(s,hyd) as a small fraction of PuO2+x(s,hyd), includes a stabilization energy of about 5–10 kJ/mol compared to pure PuO2.5(s,hyd). Therefore PuO2+x(s,hyd) is probably not stable beyond values of x > 0.25.
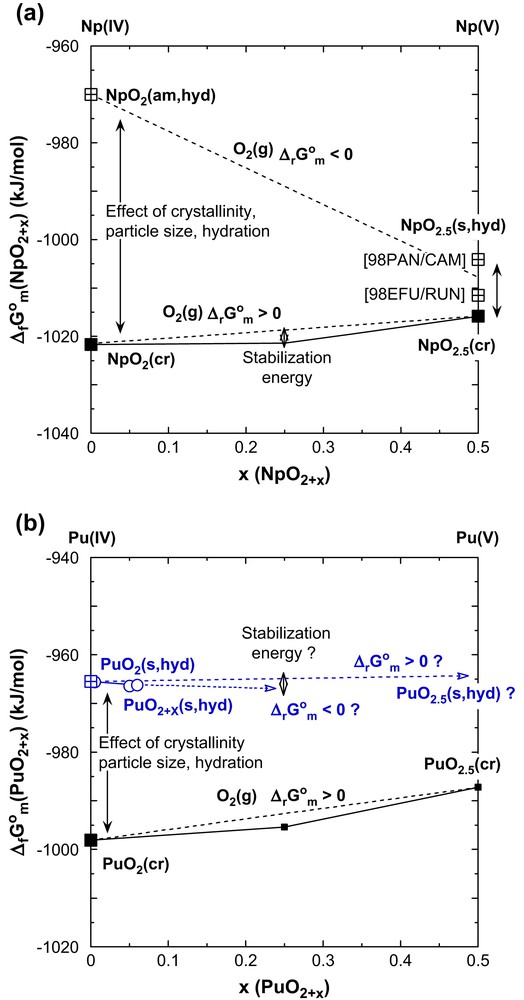
Normalized standard molar Gibbs energies of formation of hydrous Np(IV–V) and Pu(IV–V) oxides AnO2+x(s,hyd) as a function of x in comparison with the data for the anhydrous crystalline oxides AnO2+x(cr) from Fig. 8.
Anhydrous PuO2(cr) is considerably more stable than Pu(IV) hydrous oxide and cannot be oxidised by O2(g) unless the H2O(l) or H2O(g) creates a surface layer of hydrous oxide. The standard molar Gibbs energy for the hydration of the bulk PuO2(cr) is of course positive, but ΔrG°m for surface hydration is negative [46]. Hence in the presence of both water and oxygen, PuO2(s) is partially oxidised to PuO2+x(s) as reported by Haschke et al. [26,27]. However, contrary to the proposed water catalyzed mechanism [26,27], the role of water can be explained in terms of thermodynamics. The oxidation of PuO2(s) by water and the extremely high stability of PuO2+x(s) also claimed by Haschke et al. [25–28] can be ruled out.
7 Conclusions
- (1) The solubility and speciation of plutonium in the system Pu/e−/H+/OH−/H2O (25 °C) can be described in terms of equilibrium thermodynamics, provided pH and redox potentials (pe) are known. A summary of equilibrium constants for solids and aqueous species of plutonium is given in Table 1 (Appendix). They include the values selected in the OECD/NEA-TDB [1,2], oxidation state analogs for unknown data and additional data for mixed valent PuO2+x(s,hyd) and small Pu(IV) colloids/polymers in neutral to alkaline solutions. It has to be emphasized that irreversible redox reactions can lead to erroneous model predictions and must be excluded from the calculations (e.g., pe is usually not controlled by Eq. (2) and P(O2(g)). For the reasons discussed previously [16,17] data for anhydrous PuO2(cr) must be excluded as well.
- (2) Thermodynamic calculations show that the border line for the conversion of Pu(OH)3(s) into PuO2(am,hyd) is close to the lower stability line of water. Under most reducing conditions PuO2(am,hyd) is the solubility controlling solid phase, in equilibrium with aqueous Pu(IV) and Pu(III) species. In the absence of reducing agents, traces of O2(g) are sufficient to produce mixed valent PuO2+x(s,hyd). The equilibrium Pu(V) concentrations considerably exceed those of aqueous Pu(IV) species, but they are about 5 log-units lower than Pu(V) concentrations in equilibrium with PuO2OH(am). The latter is not the solubility limiting solid phase. The solubility of PuO2+x(s,hyd) can further be raised by Pu(VI) species, particularly at higher redox potentials caused by radiolysis in chloride brines [8,15] or in the presence of carbonate. Plutonyl(VI) oxyhydroxide is only stable under strongly oxidising conditions. The stability line of PuO2+x(s,hyd) with regard to the transformation into PuO2(OH)2·H2O(cr) is at (pe + pH) = 21.0 ± 1.3, in the range of the upper stability line of water at (pe + pH) = 20.77).
- (3) Aqueous Pu(IV) hydroxide complexes Pu(OH)n4−n are generally of minor importance. Their concentration is low compared to Pu(III) species at (pe + pH) < 14 (under reducing conditions), compared to Pu(V) species at (pe + pH) = 11–16 (in redox-inert solutions and in the presence of oxygen) or compared to Pu(VI) species at (pe + pH) > 16 (in the presence of oxidising agents). The low Pu concentrations in neutral and alkaline solutions are dominated by small Pu(IV) colloids/polymers. They are part of the thermodynamic system and play an important role for the redox reactions between Pu(IV) and Pu(V). As these neutral oxyhydroxide polymers/colloids have a high tendency towards sorption on oxidic and hydroxidic mineral surfaces they are also important species in sorption studies. Accepting that their formation from PuO2+ is a (slow) reversible equilibrium reaction, the sorption of PuO2(coll,hyd) from Pu(V) solutions has to be expected in any case, regardless whether the sorbing material is reducing or redox-inert, in particular if the Pu(V) concentration exceeds the solubility of PuO2+x(s,hyd) at given pH. The same holds for Pu(III) solutions exceeding the Pu(III) concentration in equilibrium with PuO2(am,hyd) at given pH and redox conditions (pe + pH). In this case the sorption of PuO2(coll,hyd) should dominate as well, regardless whether the sorbing material is oxidising or not. Corresponding observations were made in plutonium sorption studies supported by EXAFS measurements and reported by different authors at international conferences during the last years. The present paper may help to explain these observations.
Appendix
Equilibrium constants log K° for the system Pu/e−/H+/OH−/H2O at I = 0 and 25 °C
| Redox equilibria | ||
| Pu3+ ⇌ Pu4+ + e− | log K°III/IV = −17.69 ± 0.04 | [1,2] |
| PuO2+ ⇌ PuO22+ + e− | log K°V/VI = −15.82 ± 0.09 | [1,2] |
| PuO2(am,hyd) + e− + 4H+ ⇌ Pu3+ + 2H2O | log∗K°IVs/III = 15.36 ± 0.52 | [2] |
| PuO2(am,hyd) ⇌ PuO2+ + e− | log K°IVs/V =−19.78 ± 0.86 | [2] |
| PuO2(coll,hyd) ⇌ PuO2+ + e− | log K°IVcoll/V =−11.5 ± 1.3a | [10] |
| Solubility and hydrolysis equilibria of Pu(III) | ||
| Pu(OH)3(s) ⇌ Pu3+ + 3OH− | log K°sp = −26.2 ± 0.8b | [3] |
| Pu3+ + OH− ⇌ Pu(OH)2+ | log β°1,1 = 7.1 ± 0.3 | [1,2] |
| Pu3+ + 2OH− ⇌ Pu(OH)2+ | log β°1,2 = 12.9 ± 0.7 | Am analog [2] |
| Pu3+ + 3OH− ⇌ Pu(OH)3(aq) | log β°1,3 = 15.8 ± 0.5 | Am analog [2] |
| Solubility and hydrolysis equilibria of Pu(IV) | ||
| PuO2(am,hyd) ⇌ Pu4+ + 4OH− | log K°sp = −58.33 ± 0.52 | [2] |
| (log K°sp = −58.5 ± 0.7)c | [16] | |
| Pu4+ + OH− ⇌ Pu(OH)3+ | log β°1,1 = 14.6 ± 0.2 | [2,16] |
| Pu4+ + 2OH− ⇌ Pu(OH)22+ | log β°1,2 = 28.6 ± 0.3 | [2,16] |
| Pu4+ + 3OH− ⇌ Pu(OH)3+ | log β°1,3 = 39.7 ± 0.4 | [2,16] |
| Pu4+ + 4OH− ⇌ Pu(OH)4(aq) | log β°1,4 = 47.5 ± 0.5 | [2] |
| PuO2(am,hyd) + 2H2O ⇌ Pu(OH)4(aq) | (log K°s,4 = −10.4 ± 0.5)c | [16] |
| PuO2(am,hyd) ⇌ PuO2(coll,hyd,aq) | log K°IVcoll = − 8.3 ± 1.0a | [10] |
| Solubility and hydrolysis equilibria of Pu(V) | ||
| PuO2OH(am) ⇌ PuO2+ + OH− | log K°sp = − 9.0 ± 0.5 | [1,2] |
| PuO2.5(s,hyd) ⇌ PuO2+ + OH− | log K°sp = −14.0 ± 0.8d | [10] |
| PuO2+ + OH− ⇌ PuO2OH(aq) | log β°1,1 = 2.7 ± 0.7 | Np + Am analog [2] |
| PuO2+ + 2OH− ⇌ PuO2(OH)2− | log β°1,2 = 4.4 ± 0.5 | Np + Am analog [2] |
| Solubility and hydrolysis equilibria of Pu(VI) | ||
| PuO2(OH)2·H2O(s) ⇌ PuO22+ + 2OH− + H2O | log K°sp = −22.5 ± 1.0 | [1,2] |
| PuO22+ + OH− ⇌ PuO2(OH)+ | log β°1,1 = 8.5 ± 0.5 | [1,2] |
| PuO22+ + 2OH− ⇌ PuO2(OH)2(aq) | log β°1,2 = 14.8 ± 1.5 | [1,2] |
| PuO22+ + 3OH− ⇌ PuO2(OH)3− | log β°1,3 = 21.7 ± 0.4 | U analog [2] |
| PuO22+ + 4OH− ⇌ PuO2(OH)42− | log β°1,4 = 23.6 ± 0.7 | U analog [2] |
| 2PuO22+ + 2OH− ⇌ (PuO2)2(OH)22+ | log β°2,2 = 20.5 ± 1.0 | [1,2] |
a Equilibrium constant for Pu(IV) polymers/colloids (1.5–2 nm) formed in neutral and alkaline solution.
b Also selected in the NEA-TDB [1,2], but with increased uncertainty (±1.5).
c Used for the calculation of Pu(IV) concentrations; not selected in the NEA-TDB [2].
d For the fraction of PuO2.5(s,hyd) in PuO2+x(s,hyd) with x < 0.1.


