1 Introduction
The cleavage of the hydrogen molecule into protons and electrons,
| H2 ⇋ 2H+ + 2e− | (1) |
The present study relies on two recent X-ray crystallographic studies of oxidized NiFe-hydrogenases [2,3]. In these studies, structures have been obtained for the Ni-A and Ni-B states. After the Ni-A state has been formed as dioxygen has entered the active site, it takes several hours to restore the activity of the enzyme, which is why this state is termed unready. Ni-B returns faster to the active state, on the time-scale of seconds, which is the reason why it has been termed ready.
The two different structural analysis for the Ni-A and the Ni-B states are in basic agreement. The Ni-B state is concluded to have a bridging single oxygen-containing ligand between nickel and iron, which most likely is a hydroxide. The structure of the Ni-A state is interpreted to show a hydroperoxide in the bridging region. A rather surprising aspect of this structure is that the peroxide has a side-on, bidentate, binding mode to nickel, quite unusual in biology. In both studies there are also indications of cysteine ligand oxidation forming SO bonds, more so in the structure of D. vulgaris (Miyazaki) [3] than in Desulfovibrio gigas [2].
In the present study, hybrid DFT using the B3LYP functional is used to study the oxidized states of the NiFe-complex of hydrogenase. Of prime interest is the structure of Ni-A, but investigations have also been made for Ni-B and for the return of these states to the active state of the complex. Major difficulties have been encountered in modeling the Ni-A state, of structural and/or methodological nature. Future work in this area is therefore needed and suggestions of this type of work are made. There have been several earlier DFT studies of the Ni-B state of the NiFe-complex, mostly using quite small models [4–7]. Very recently, two studies have appeared where also the peroxide of the Ni-A state has been investigated, again using minimal models [8,9]. There is also a recent QM/MM study of the Ni-A and Ni-B states, which focuses on the structures [10].
2 Methods and models
In the present study, the starting coordinates of the active site of NiFe-containing hydrogenase were taken from the X-ray structure 1YQJ for the unready state of Desulfovibrio gigas [2]. Three different models were used, see Fig. 1. In the minimal model A, only the directly liganding groups were included, apart from nickel, iron and the substrate. In the model used in most studies here, model B, also Glu25, His79, Arg476 and Asp541 were included. Since Glu25 and Cys543 were considered likely to be directly involved in important proton transfers, the entire side chains of these amino acids were included in the model. For the other amino acids, only the functional groups were modeled, as shown in Fig. 1B. Following the experience of an earlier study of the same active site [11], some point(s) of each amino acid was (were) kept frozen at the corresponding position of the X-ray structure, marked with a∗ in Fig. 1. All other atoms in the complex were fully optimized. This is a procedure well tested for many enzyme active sites [12], but may turn out to have larger difficulties in this particular case, as described below, may be because of the unusually large number of charged amino acids. The charge states were chosen as those normal at pH = 7, i.e. carboxylates are negative and arginine positive. However, from the earlier modeling experience of the NiFe-active site [11], His79 and Glu25 were chosen to be protonated. In the largest model used here, see Fig. 1C, the entire side chains of all amino acids were included. In this case three points of the backbone of each group were kept frozen, no other atoms. This is a new type of modeling tried here for the first time, the idea being that this is a perfectly well-defined procedure. A possible problem is that this type of coordinate fixing could lead to a structure too rigidly following the X-ray structure, and this has been and will be investigated further in the future.

The three models used for the active site of NiFe-hydrogenase. Positions frozen from the X-ray structure are marked with ∗.
The calculations discussed here were made using the DFT hybrid functional B3LYP [13]. A small lacvp basis set was used for the geometry optimizations, a much larger cc-pvtz(-f) basis set for the energies, and in the dielectric cavity model calculations the lacvp∗ basis set was used with a dielectric constant equal to 4.0. In the large-basis single-point calculations, the metals were described by lacv3p in the two smaller models and by lacv3p+ in the largest model. No significant effect is expected due to these basis set differences. The spin state for the odd-electron systems is a doublet, while for the even-electron systems a triplet state was used. For the hydrogen molecule reaction, a closed shell singlet description has also been shown to be adequate [11]. Actually, in that case the results for the triplet and closed shell singlet are very similar. This cannot be expected when dioxygen is involved in the reactions studied, which was the reason why the triplet state was chosen. The spin state was checked in a number of cases and the triplet state was always found to be below the closed shell singlet state, sometimes quite significantly below. The accuracy aimed at for the present energies is 3–5 kcal/mol. However, as will be shown below, there is a particular case where this ambition failed remarkably. The geometry optimizations and single-point energies reported here were performed with the program Jaguar [14], while the Hessian calculations and transition state optimizations were performed with Gaussian03 [15].
3 Results
The B3LYP results for the structures of Ni-B and Ni-A and their activations will be described in the present sections. Three models have been used, as described above. The two models used for most of the results described here are shown in Fig. 1B and 1C. Which model has been used will be stated in each case with reference to this figure. The description will start with Ni-B since the results are less controversial in this case, with nearly full agreement with experimental interpretations. The results for Ni-A will then be discussed. As will be shown, there are striking discrepancies between the Ni-A results and those suggested by experiments. It is concluded that the most reasonable explanation for this discrepancy is a remaining problem in the chemical models used in the calculations. However, this problem is not easy to identify since the model is already quite large with nearly 120 atoms, and remains for future QM/MM investigations. A problem with the DFT method itself cannot be ruled out, but appears less likely.
3.1 Ni-B
The optimized structure for the Ni-B doublet state using the largest model is shown in Fig. 2. Although there are some minor discrepancies, the overall structure is in good agreement with structure 1YRQ of the X-ray analysis [2]. The discrepancies show the normal pattern for the present type of modeling: covalent and ionic bonds are too long and hydrogen bonds too short. The calculated Ni–Fe distance is thus 3.0 Å (exp. 2.8 Å), the Ni–OH distance 1.94 Å (1.89 Å) and the Fe–OH distance 2.04 Å (1.88 Å). The Ni–S distances are all too long by about 0.2 Å. The hydrogen bond between Cys546 and His79 leads to an S–N distance of 2.9 Å (3.3 Å), the one between Cys543 and Glu25 to an S–O distance of 3.2 Å (3.5 Å), and the one between Arg476 and OH to an N–O distance of 3.4 Å (3.5 Å). All these distances would most likely be improved if a larger basis set was used in the geometry optimization than the present small double-zeta quality lacvp basis set. However, numerous investigations have shown that the present accuracy of the geometry is sufficient for the mechanistic and energetic issues discussed here [16]. Some of the discrepancies to the Ni-B structure of D. vulgaris (Miyazaki) [3] are larger. For example, for that species the Ni–Fe distance is as short as 2.69 Å and, even more remarkably, the Ni–O distance is only 1.67 Å. This very short Ni–O distance indicates some double-bond character not seen in the present modeling. This result could perhaps suggest that the bridging oxygen-derived ligand is not protonated in this species.
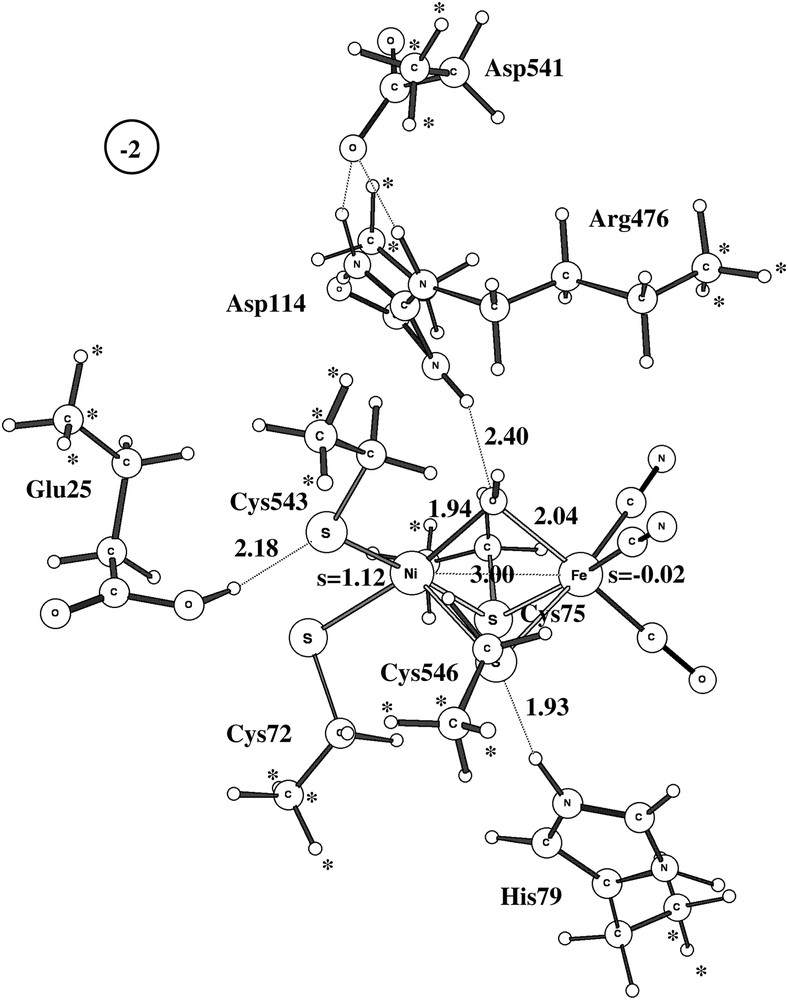
Optimized structure of Ni-B using the largest model. Important spins and distances are given. Positions frozen from the X-ray structure are marked with ∗.
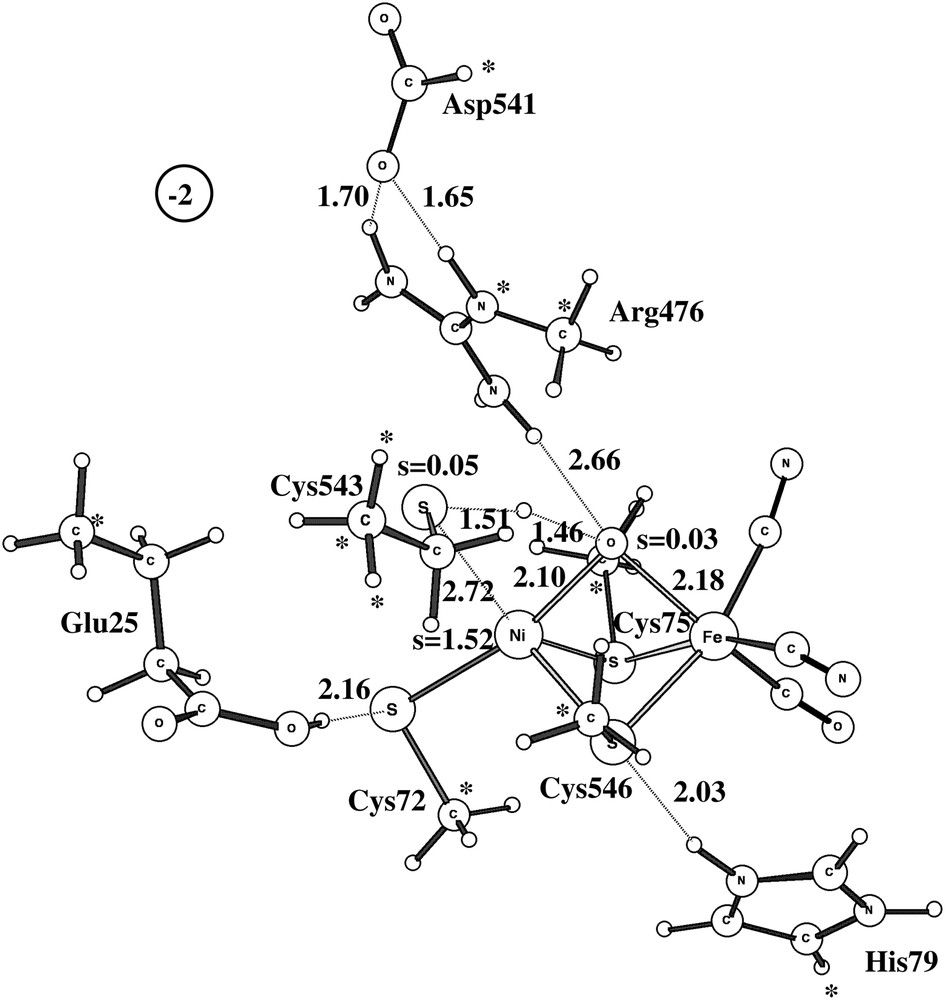
Two different pathways have been experimentally suggested for the activation of Ni-B [17–19,2]. One pathway activates Ni-B without additional electrons and is suggested to involve a hydrogen molecule. An approximate transition state for this type of activation using the medium-size model is shown in Fig. 3. The computed barrier is 19.4 kcal/mol, which is in line with an activation of Ni-B within seconds [2]. Attempts to locate a true transition state with one imaginary frequency failed because the potential surface is very flat and anharmonic in this region. However, the true TS should not have a significantly different barrier.
Approximate doublet transition state for the reaction between Ni-B and a hydrogen molecule.
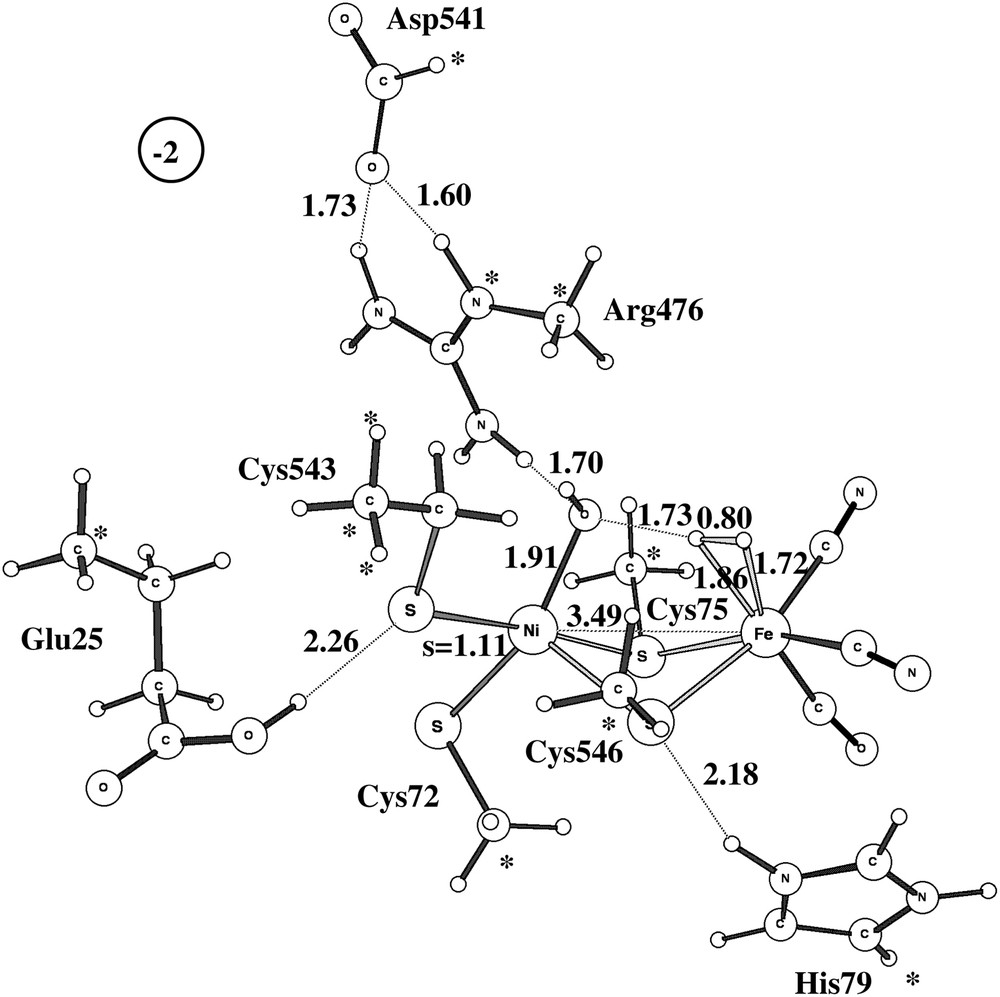
The second pathway suggested experimentally involves activation of Ni-B by adding an additional electron and proton. A fully optimized TS is shown in Fig. 4 for the medium-size model. The computed barrier is 19.2 kcal/mol, very close to the barrier for the other activation mechanism, and a rate in reasonable agreement with the experimentally observed activation in seconds.
Optimized triplet transition state for the activation of Ni-B with one electron and one proton.
The transition state obtained for activation of Ni-B by a hydrogen molecule is similar to the one found in a recent study by Jayapal et al. [8]. They obtained a barrier of 15.1 kcal/mol compared to the present 19.4 kcal/mol. This difference was expected, since they used the non-hybrid BP86 method, which is known to yield lower barriers than B3LYP. Another difference is that the hydroxide is pushed to the iron site in their TS rather than to the nickel site as in the present TS. Both TS were tested here, but the one in Fig. 3 was found to be significantly lower, probably due to the interaction between the hydroxide on iron with Arg476, not included in the model used by Jayapal et al. The second transition state, the one activated by adding an electron and a proton, was not determined by Jayapal et al. and any barrier was therefore not given.
3.2 Ni-A
As already indicated, the study of Ni-A led to serious modeling problems. After a large number of attempts, a structure very similar to the ones observed experimentally was finally found, see structure A in Fig. 5. As in the experimental structures, the protonated peroxide is bound side-on to nickel. There is a hydrogen bond to Arg476 holding it in place. Convergence to this structure was only obtained after first converging a quartet solution and then using this state as a starting point for the doublet. The critical peroxide-to-metal distances are all reasonably well reproduced by the calculations. The Ni–O distances are both 2.05 Å, while they are 1.90 Å and 2.11 Å experimentally [2]. Again, the discrepancy compared to the D. vulgaris (Miyazaki) [3] is larger. The short Ni–O distance reported for this structure is only 1.70 Å. It is not possible to explain the extremely short Ni–O distance by a possibly unprotonated peroxide for this species, since removing the proton (and an electron) makes the Ni–O distances still longer in the model calculations. The computed Ni–Fe distance of 3.0 Å is in reasonable agreement with the experimental values of 2.93 Å [2] and 2.80 Å [3], and so is the Fe–O distance of 2.09 Å compared to 1.90 Å [2] and 2.20 Å [3]. Overall, there is no question that structure A corresponds to the one observed experimentally. It should in this context be emphasized that no constraint was put on the Ni–O distances in the calculations.
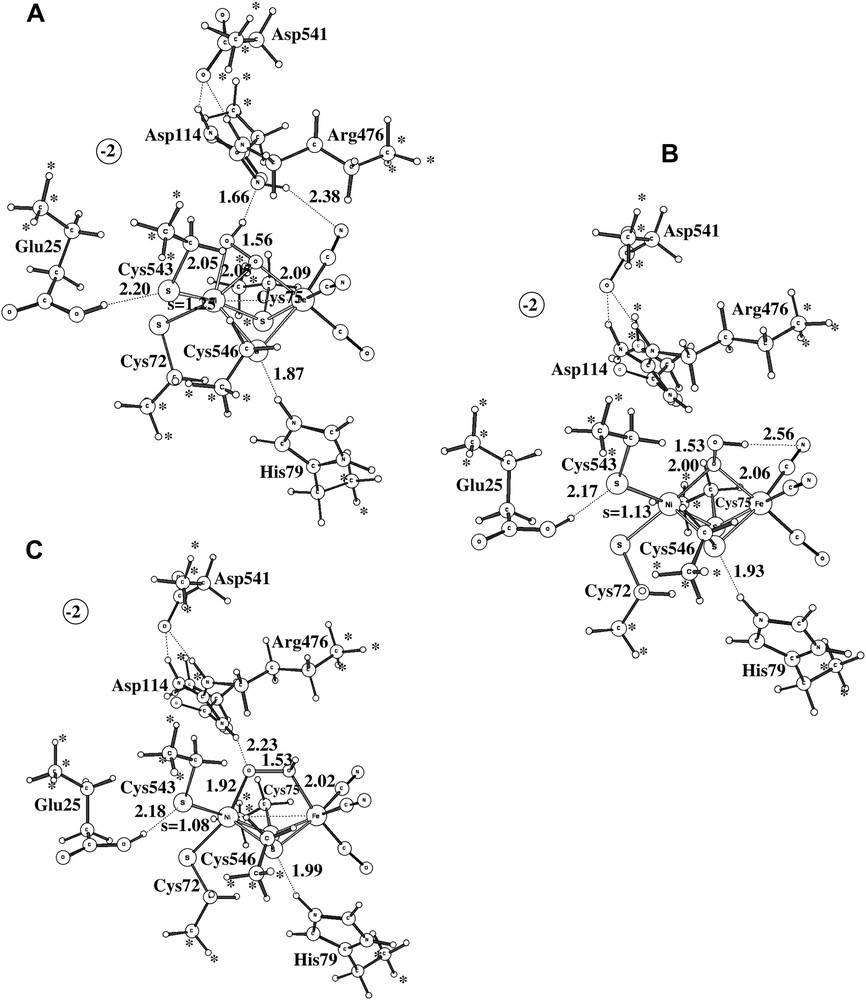
The three alternative structures obtained for Ni-A.
The problem of modeling Ni-A does not concern structure A in Fig. 5 but the tendency for the optimization to reach structure B in the same figure instead. This structure turns out to be as much as 13.7 kcal/mol more stable than structure A at the B3LYP level, which is clearly a severe discrepancy compared to experiments. The same problem has been noted in some earlier DFT studies [8,9]. The difference of 13.7 kcal/mol can be decomposed into different contributions. With the small lacvp basis set used for the geometry optimization, the difference is only 2.2 kcal/mol. The large cc-pvtz(-f) basis set increases the difference to 9.6 kcal/mol, and the differential dielectric effects of 4.1 kcal/mol leads to the final difference of 13.7 kcal/mol. The first suspicion of where the problem might be concerns the use of the B3LYP functional. The most critical parameter in B3LYP is the amount of exact exchange. Varying the amount of exact exchange is therefore a useful test to get an indication of the reliability of a B3LYP result. In all cases with significant discrepancies between B3LYP and experiments detected so far (an error of more than 5 kcal/mol), the results with non-hybrid methods (without exact exchange) have thus turned out to give results significantly different from those obtained with B3LYP. No counter-example of this rule of thumb has so far been found. In the present case, the results obtained using the non-hybrid methods BP86 and BLYP are quite similar to the ones obtained using B3LYP. The energy difference between the two structures is 13.0 kcal/mol at the BP86 level and 17.2 kcal/mol at the BLYP level. Following the normal rule of thumb, the conclusion would be that the B3LYP result should be quite reliable in this case.
Many alternative structures for the peroxide in Ni-A were tried. The best one of these is shown as structure C in Fig. 5. This structure is in fact very similar in energy, within 1 kcal/mol, to the best of the peroxide structures, structure B, and is thus nearly 14 kcal/mol more stable than the structure observed experimentally, structure A.
Assuming that the tests described above indicate that there is no problem in this case to describe Ni-A using the B3LYP functional, only one possibility remains to explain the error. This possibility is that the chemical model used is not adequate for some reason. Maybe, with a still larger model, some steric interaction will severely limit the stability of structure B (and C) in Fig. 5. The group most directly interacting with the peroxide is Arg476. In fact, if Arg476 is removed from the model, there is no longer a local minimum for structure A. Starting with structure A then leads directly to structure B without any barrier. The main interaction between the substrate and Arg476 should already be included in the model, but a remaining possibility is that in a larger model its position is even more rigid, even though three points in the backbone were kept frozen from the X-ray structure. A higher rigidity might be introduced by interactions with Arg476 from groups not included in the model. Another possibility is that some other atoms in the protein actually reach all the way to the substrate and cause a steric hindrance for structure B (and C). Investigations using QM/MM with much larger models are in progress to investigate these possibilities. It should in this context be noted that the only QM/MM investigation performed so far for Ni-A actually does obtain the correct structure A [10]. However, in that study X-ray scattering data were also directly used to define the structure. At the present stage, it will be assumed that some steric interaction is missing, even in the largest model used here, which, if included, would prevent the formation of structure B (and C). It will also be assumed that the present model is capable of adequately describing structure A.
For completeness, the activation of structure B of Ni-A was investigated following the pathways described above for Ni-B, even though structure B of Ni-A is not considered to be well represented by the model. The results indicate activation barriers using a hydrogen molecule, and using an electron and a proton, which are quite similar to the ones for Ni-B. If structure B was the optimal structure of Ni-A, the calculations therefore give no explanation for the experimental fact that Ni-A is so much harder to activate than Ni-B. Experimentally, Ni-B is activated in seconds, while it takes hours to activate Ni-A [17–19]. Furthermore, Ni-B is found experimentally to be activated without additional electrons, while this is not possible for Ni-A. The lack of differences in the activation of Ni-B and structure B of Ni-A could therefore be taken as another, independent, reason to disregard structure B as the one in Ni-A.
The activation of structure A of Ni-A is quite different from the one of structure B and the one of Ni-B. If a proton (and an electron) is transferred to the NiFe-complex, with the added proton going to the unprotonated oxygen of the peroxide, the O–O bond of the peroxide is automatically cleaved without any barrier. The product structure is shown in Fig. 6. This structure, which has one hydroxide in between nickel and iron, and one terminal hydroxide on nickel, is 46 kcal/mol more stable than H2O2 bound in between nickel and iron. The electronic structure of this state can be described as Ni(II)-triplet, coupled to Fe(III)-doublet, coupled to a sulfur radical delocalized on Cys72 and Cys543. To remove the two hydroxides to activate the enzyme would require two additional electrons and protons. Altogether, starting with the experimental structure A of Ni-A, three outside electrons and three protons would thus be required to activate the enzyme. This should be compared to the activation of Ni-B, which only requires one outside electron and one proton and which can even be activated without outside electrons if a hydrogen molecule is used. These scenarios could be the reason for Ni-A being so much harder to activate than Ni-B. However, additional calculations using QM/MM models would be required to substantiate these suggestions. Another indication that the presently suggested scenario could be correct is the fact that adding CO in fact helps activating Ni-A [17–19]. CO would then add at the empty terminal coordination site of nickel and could perhaps prevent the formation of structure A of Ni-A, which requires two empty coordination sites on nickel.
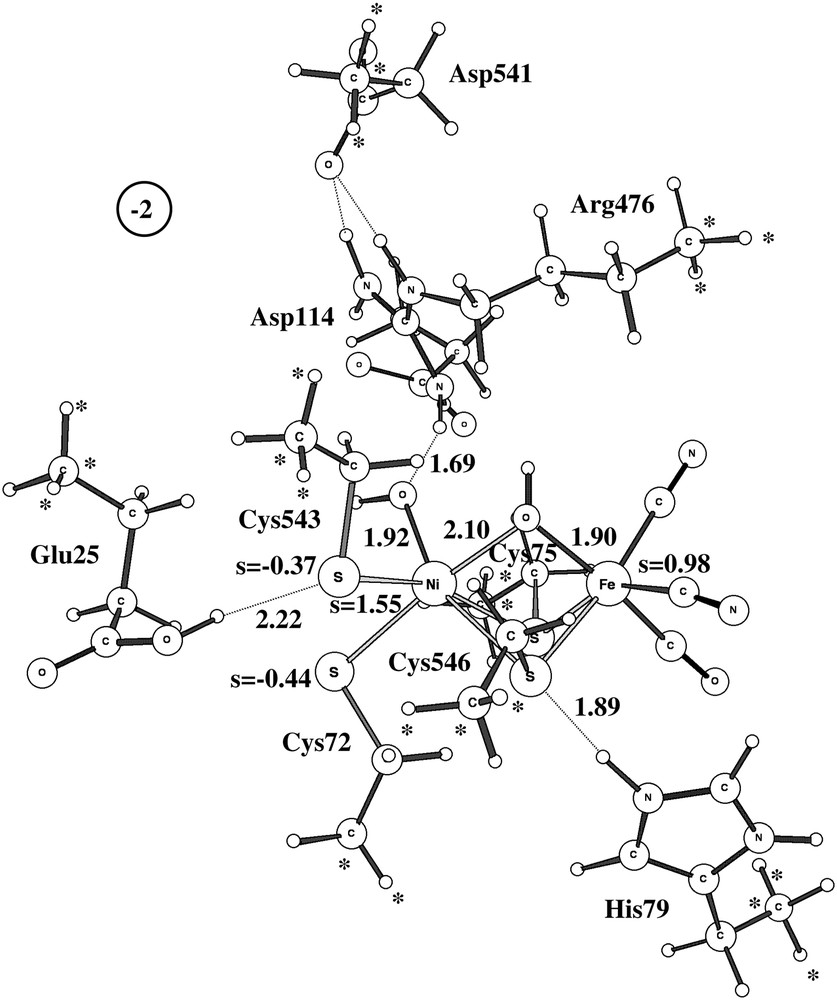
The triplet product structure after the dissociation of the O–O bond. One electron and one proton have been added to Ni-A.
As mentioned above, the experimental structures of Ni-A also show oxidation of some of the cysteines, forming SO bonds. A possible route to the formation of these bonds has finally been investigated. A transition state was first located for the reaction between O2, bound between nickel and iron, and the terminal cysteine Cys543, see Fig. 7. The calculated barrier, without entropy contributions, is 13.8 kcal/mol. Previous experience is that the van der Waals interaction with the protein, which is neglected here, and the underestimation of the bonding of O2 to transition metals by B3LYP tend to cancel essentially the effects of entropy. The estimate of 14 kcal/mol for the barrier is therefore probably not far away from the true result. This barrier will lead to a reaction in milliseconds and is thus an alternative to the formation of structure A of Ni-A. However, formation of Ni-A is likely to involve much smaller barriers and would therefore occur on a shorter time-scale, but not ruling out the formation of S–O bonds occasionally. The formation of the sulfur–peroxide bond is exergonic by 3.0 kcal/mol. It should be noted that the modeling of this reaction contains some uncertainties. First, the starting point is an end-on structure of the peroxide which may be hindered by the protein surrounding, see above. However, in this case the reactant energy for an end-on and a side-on peroxide is rather small and this should therefore not affect the barrier significantly. Second, in spite of the freezing of many coordinates from the X-ray structure, the transition state is surprisingly distorted. It is likely that a more realistic modeling would give a much smaller distortion. The energetic effect of the distortion is difficult to estimate at present and future QM/MM modelings will therefore be required for a better estimate of the barrier.
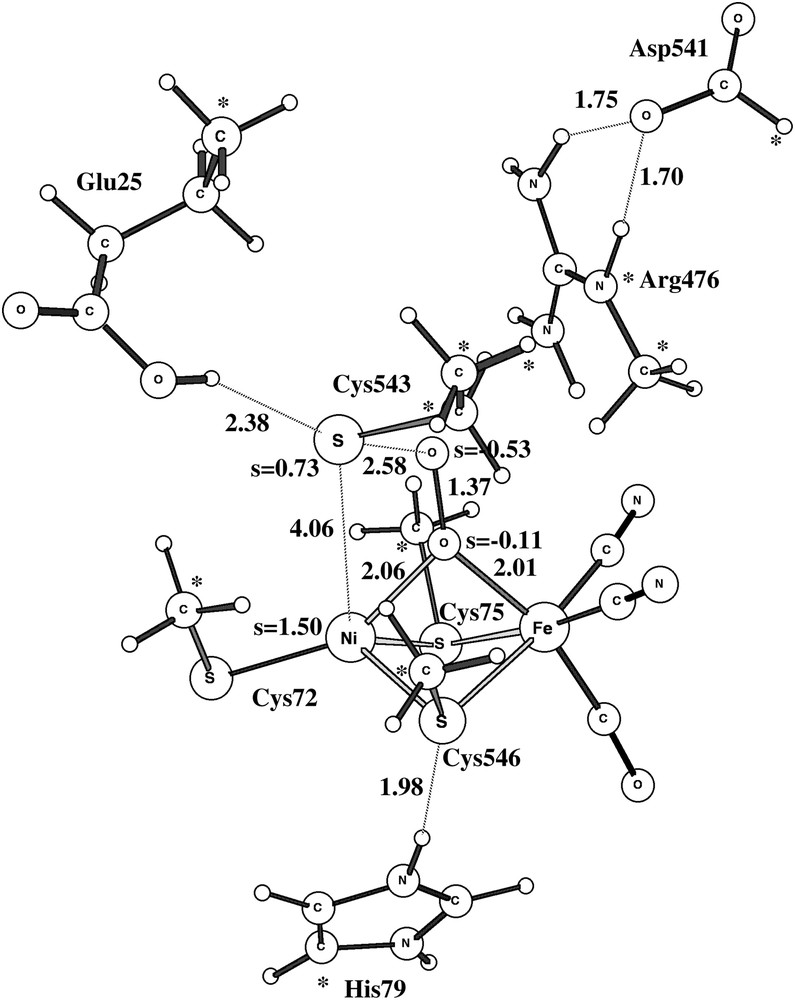
Optimized triplet transition state for the reaction between the bridging peroxide and Cys543.
The final step in the formation of an SO bond, after the sulfur–peroxide bond has been formed, is to cleave the O–O bond. The transition state for this process is shown in Fig. 8. The barrier is very low with 5.4 kcal/mol and the reaction is very exergonic after protonation of the bridging oxo, and is thus irreversible. A possible pathway for the removal of the SO bond was also followed. This pathway requires the addition of four electrons and four protons and involves a step where an S–OH bond is cleaved and where the hydroxide ends up in between nickel and iron, just as in Ni-B. The transition state is shown in Fig. 9. Overall, this pathway represents a plausible scenario where SO bonds will be formed occasionally and the reactivation will take a time on the order of seconds or longer.
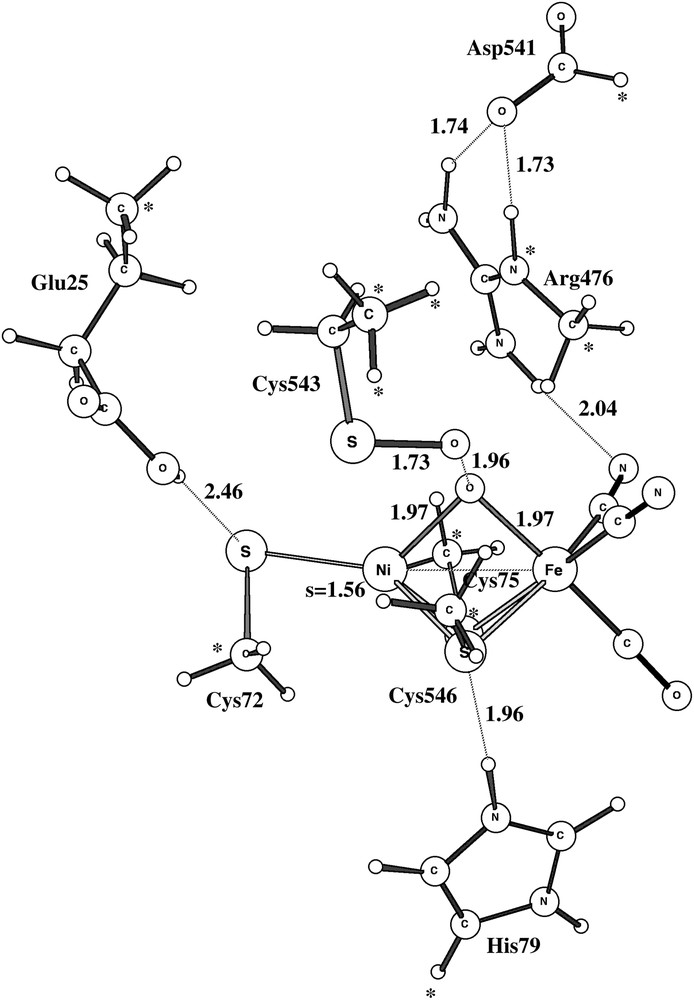
Optimized triplet transition state for the O–O bond cleavage of the sulfur–peroxide.

Optimized doublet transition state for the S–O bond cleavage of the sulfur–hydroxide.
4 Conclusions
Two of the oxidized states of the NiFe-complex of hydrogenase have been studied with hybrid DFT using the B3LYP functional. The results obtained for Ni-B are in good agreement with experimental structures and other information. Ni-B has a hydroxide bound between nickel and iron, which can be activated in two ways both on the time-scale of seconds. One pathway uses a hydrogen molecule and does not involve external electrons, while the second pathway leads to water formation after addition of one electron and one proton.
The modeling of Ni-A turned out to be much more problematic than for Ni-B. The structure observed experimentally, with a peroxide side-on bonded to nickel, was only obtained after a large number attempts. Without Arg476 this side-on structure is not a minimum but collapses to a structure where the peroxide is only bound with one of its oxygens to both nickel and iron. This end-on structure is strongly preferred by 14 kcal/mol also in the largest model used compared to the correct side-on structure. Varying the amount of Hartree–Fock exchange in DFT did not give any indication that the B3LYP result should be unreliable. Instead, a problem with the chemical model used appears most likely at the present stage. The model is probably still too small, even though it contains nearly 120 atoms. Calculations including a substantial part of the protein using QM/MM is in progress to shed further light on this problem.
The activation of Ni-A with the side-on bonded peroxide is likely to involve an initial addition of a proton to the peroxide and an outside electron. This will lead to an automatic cleavage of the O–O bond of the peroxide, forming two hydroxides. One of the hydroxides is bound inbetween nickel and iron, just as for Ni-B, while the other hydroxide is bound terminally to nickel. The cleavage of the O–O bond involves a very low barrier, if any, and is very exergonic and thus irreversible. The rest of the activation of Ni-A will then require two additional outside electrons and two protons, which could explain why the activation of Ni-A is so much slower than the one for Ni-B.
Acknowledgements
I am very grateful to Siem Albracht for numerous discussions and suggestions.


