Thermodynamics and the structure of binary and ternary complexation of Am3+ Cm3+ and Eu3+ with DTPA and DTPA + IDA

Gregory R. Choppin; Punam Thakur; Jagdish N. Mathur

doi:10.1016/j.crci.2007.03.018

Thermodynamics and the structure of binary and ternary complexation of Am³⁺ Cm³⁺ and Eu³⁺ with DTPA and DTPA + IDA

Gregory R. Choppin ¹ ; Punam Thakur ¹ ; Jagdish N. Mathur ¹

¹ Department of Chemistry and Biochemistry, Florida State University, Tallahassee, FL 32306-4390, USA

Comptes Rendus. Chimie, Volume 10 (2007) no. 10-11, pp. 916-928.

Résumé

The formation, their stability and the thermodynamic parameters of the binary complexation of Am³⁺, Cm³⁺ and Eu³⁺ with DTPA and of the ternary complexation of DTPA + IDA were studied in aqueous solutions of I = 6.60 m (NaClO₄) and temperatures of 0–60 °C by solvent extraction technique. The stability constants of these complexes increased with increasing temperature. Positive enthalpy and the large entropy values for the binary and the ternary complexation indicated significant effect of cation dehydration at such high ionic strengths. TRLFS and NMR (¹H and ¹³C) data provided insight into the structure of the ternary complexes in solution. In the binary [M(DTPA)]²⁻ complex, M³⁺ binds via five carboxylates and three nitrogens, while in the ternary complex [M(DTPA)(IDA)]⁴⁻, DTPA binds by the same eight coordination sites and IDA binds via one of its carboxylate anion groups.

Métadonnées

Reçu le : 2006-08-23
Accepté le : 2007-03-27
Publié le : 2007-08-27

DOI : 10.1016/j.crci.2007.03.018

Mots clés : Complexation thermodynamics, Binary, Ternary, DTPA, DTPA + IDA, TRLFS, ¹H and ¹³C NMR

Affiliations des auteurs :

Gregory R. Choppin ¹ ; Punam Thakur ¹ ; Jagdish N. Mathur ¹

¹ Department of Chemistry and Biochemistry, Florida State University, Tallahassee, FL 32306-4390, USA

@article{CRCHIM_2007__10_10-11_916_0,
     author = {Gregory R. Choppin and Punam Thakur and Jagdish N. Mathur},
     title = {Thermodynamics and the structure of binary and ternary complexation of {Am\protect\textsuperscript{3+}} {Cm\protect\textsuperscript{3+}} and {Eu\protect\textsuperscript{3+}} with {DTPA} and {DTPA\,+\,IDA}},
     journal = {Comptes Rendus. Chimie},
     pages = {916--928},
     publisher = {Elsevier},
     volume = {10},
     number = {10-11},
     year = {2007},
     doi = {10.1016/j.crci.2007.03.018},
     language = {en},
}

TY  - JOUR
AU  - Gregory R. Choppin
AU  - Punam Thakur
AU  - Jagdish N. Mathur
TI  - Thermodynamics and the structure of binary and ternary complexation of Am3+ Cm3+ and Eu3+ with DTPA and DTPA + IDA
JO  - Comptes Rendus. Chimie
PY  - 2007
SP  - 916
EP  - 928
VL  - 10
IS  - 10-11
PB  - Elsevier
DO  - 10.1016/j.crci.2007.03.018
LA  - en
ID  - CRCHIM_2007__10_10-11_916_0
ER  -

%0 Journal Article
%A Gregory R. Choppin
%A Punam Thakur
%A Jagdish N. Mathur
%T Thermodynamics and the structure of binary and ternary complexation of Am3+ Cm3+ and Eu3+ with DTPA and DTPA + IDA
%J Comptes Rendus. Chimie
%D 2007
%P 916-928
%V 10
%N 10-11
%I Elsevier
%R 10.1016/j.crci.2007.03.018
%G en
%F CRCHIM_2007__10_10-11_916_0

Gregory R. Choppin; Punam Thakur; Jagdish N. Mathur. Thermodynamics and the structure of binary and ternary complexation of Am³⁺ Cm³⁺ and Eu³⁺ with DTPA and DTPA + IDA. Comptes Rendus. Chimie, Volume 10 (2007) no. 10-11, pp. 916-928. doi : 10.1016/j.crci.2007.03.018. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2007.03.018/

Version originale du texte intégral

1 Introduction

The trivalent lanthanide and actinide cations can bind with as many as nine ligand donor sites in their coordination sphere. In the formation of the binary 1:1 complex [M(DTPA)]²⁻, DTPA (diethylenetriaminepentaacetate), the ligand occupies eight coordination sites of metal cations. The X-ray diffraction studies of the [Ln(DTPA)]²⁻ (Ln³⁺ = Nd, Gd, Dy, Ho and Yb) in solid [1,2] and the luminescence decay measurements in solution [3,4] indicate the presence of one water molecule in the inner coordination sphere of [Ln(DTPA)]²⁻ for a total coordination number of 9.0. In principle, the coordinated water molecule can be displaced by a small ligand resulting in the formation of a ternary complex. Such ternary complexes of Ln³⁺ with EDTA (ethylenediaminetetraacetate) and HEDTA (N-hydroxyethylethylenediaminetriacetate) as the primary ligands have been studied extensively [5–10]. Because of the presence of a single water of hydration, the [Ln/An(DTPA)]²⁻ complexes have a lesser tendency to form a ternary complex than the corresponding [Ln(EDTA)]⁻ and [Ln(HEDTA)]⁰ complexes. The ternary complexes investigated include ligands such as IDA²⁻ (iminodiacetate) [11], F⁻ (fluoride) [12], CO₃²⁻ (carbonate) and PO₄³⁻ (phosphate) [13]. Larger multidentate ligands such as cit³⁻ (citrate) do not form a ternary complex with [Ln(DTPA)]²⁻ [13].

Currently, large volumes of nuclear wastes from weapon processing and from reprocessing of spent fuel are stored in underground tanks. These tanks have solutions which contain highly radioactive Cs, Tc, Am, Cm, etc., nuclides and high concentrations of nonradioactive salts such as NaNO₃, Na₂CO₃, etc., as well as organic ligands (carboxylate and aminopolycarboxylates) [14,15]. Due to the radioactive decay, the temperatures of the tank solutions are significantly higher than the ambient temperature. The organic ligands present in the nuclear waste increase the solubility of the actinides by complexation. As a result, data on the complexation thermodynamics of lanthanides and actinides at the ionic strength and temperatures of the wastes are necessary to understand their behavior in the wastes media. Such studies have broadened the existing database for actinides and lanthanides, which are dominated by information on the binary systems. Studies on the ternary system are of fundamental interest as they offer the possibility to assess the steric interactions between ligands, the binding preference of various ligand donor groups and the coordination number of the cations.

The present investigation reports the complexation thermodynamics of the binary complexes of Am³⁺, Cm³⁺, and Eu³⁺ with DTPA and of their ternary complexes with DTPA + IDA at I = 6.60 m (NaClO₄) and temperatures of 0 to 60 °C. The NMR (¹H and ¹³C) spectra of the diamagnetic La³⁺/Y³⁺ complexes were studied to establish the coordination modes and structural aspects of the ligands in these binary and the ternary complexes. The luminescence lifetime measurements with Eu³⁺ were performed to provide knowledge on the hydration number of these cations in these complexes.

2 Experimental

All chemicals were of reagent grade or higher and distilled, deionized water (E-pure, Barnstead) was used in the preparation of solutions. Aqueous solutions of 6.60 m NaClO₄ (>98%, Sigma–Aldrich, ACS certified) were prepared and filtered through 0.45 μm membrane. Solutions of DTPA (Fisher Scientific) and IDA (Fluka) were prepared in 6.60 m (NaClO₄) and their concentrations were determined by pH-titration with standard NaOH. The Eu(ClO₄)₃, La(ClO₄)₃ and Y(ClO₄)₃ solutions were prepared from oxides (99.99%, Aldrich) in perchloric acid (60%, Fisher Scientific), followed by dilution to the desired concentrations. The concentrations of these solutions were determined by titration with solution of EDTA [16]. Di-(2-ethylhexyl) phosphoric acid, HDEHP (Sigma–Aldrich) and heptane (Fisher Scientific) were used as received.

The radioactive tracers ²⁴¹Am, ²⁴⁴Cm and ^{152, 154}Eu (Oak Ridge National Laboratory) were purified and their purity checked by α- and/or γ-spectrometry. The working stock of each tracer was prepared in HClO₄ solution of pH ∼3.0 such that a 10.0 μL of the solution has a count rate of ca. 50,000 cpm. The concentration of metal ions was ca. ∼1 × 10⁻⁶ M. The activities of ²⁴¹Am, ²⁴⁴Cm and ^{152, 154}Eu were measured in a Beckman Liquid Scintillation Counter (LSC) using Ecolite cocktail (ICN, Research Product Division).

An Accumet 950 (Fisher Scientific) pH meter was used with a glass electrode (Corning semi-micro combination) to measure the pH values. The KCl solution in the salt bridge was replaced with saturated NaCl solution as the low solubility of the KClO₄ at high ionic strengths resulted in erratic readings. The electrode was calibrated with 4.00 ± 0.01 and 7.00 ± 0.01 pH buffer. The meter readings (pHr) were converted to pH values using calibration curves obtained from a series of HClO₄ and NaOH solutions of known [H⁺] in I = 6.60 m (NaClO₄) and T = 0–60 °C as described in Ref. [17].

2.1 TRLFS

The ⁷F₀–⁵D₀ excitation spectra of Eu³⁺ were measured at room temperature in 1.00 cm quartz fluorimeter cells using an instrumental setup similar to that described in Ref. [17]. The [Eu³⁺] was fixed at ∼1 × 10⁻⁴ M in all solutions. Solutions of the complexes were prepared by mixing the Eu(ClO₄)₃ and the corresponding ligand solutions in 6.60 m (NaClO₄). For the binary systems the ratios of Eu:IDA varied from 1 to 10 and that of Eu:DTPA from 1:1 to 1:2, while for the ternary system the ratios of Eu:DTPA:IDA varied between 1:1:1 to 1:1:5 and 1:10:10. The pH of these solutions was varied from 3.60 to 13.0 with dilute HClO₄ or NaOH. To avoid precipitation of Eu³⁺, a constant ionic strength of I = 6.60 m (NaClO₄) was not maintained in the Eu–IDA studies. The coordination number, CN_C, of the complexes was calculated using the correlation CN_C = 0.237Δν + 0.628 [18], where Δν is the peak shift of Eu³⁺_(aq) upon complexation. The water of hydration $(N_{H_{2} O})$ associated with the complex was calculated by the equation $N_{H_{2} O} = 1.05 k_{obs} - 0.70$ (with an uncertainty of ± 0.5) [19,20], where k_obs is the luminescence decay constant. The peak deconvolutions of the spectra were done with Labspec software.

2.2 ¹H and ¹³C NMR

For NMR measurements, solutions of La(ClO₄)₃ and Y(ClO₄)₃ and the ligands were prepared in D₂O. The solutions of La(ClO₄)₃ and Y(ClO₄)₃ after dissolution in perchloric acid were evaporated several times in D₂O to eliminate water followed by dilution. Due to precipitation of La³⁺/Y³⁺, a constant ionic strength of I = 6.60 m (NaClO₄) was not maintained in these solutions. The concentrations of La³⁺ were ca. 0.05 M, while that of Y³⁺ were maintained at ca. 0.04 M. Samples for La/Y–IDA, La/Y–DTPA and La/Y–DTPA–IDA in D₂O were prepared by dropwise addition of La³⁺ to the IDA or DTPA and/or to the mixture of DTPA + IDA, followed by mixing to prevent precipitation of metal hydroxide. The pH of the solutions was adjusted with DCl or NaOD in D₂O. The ¹H and ¹³C spectra were obtained for solutions of (1) DTPA (0.50 M), pH = 9.60 (2) La:DTPA (1:1), pH = 9.60 and (3) La:DTPA:IDA (1:1:1–1:1:4, pH ∼10.00). The values reported are direct pH meter reading and no corrections for D₂O were made. All spectra were recorded at room temperature on a Bruker AC300 at 300.13 MHz for ¹H and at 75 MHz for ¹³C NMR and were referenced externally to spectra of sodium trimethylsilanolate, δ = 0.00 ppm (±0.1 ppm).

2.3 Metal ion distribution measurements

The distribution of the metal ions (Am³⁺, Cm³⁺ and Eu³⁺) between aqueous and organic phases was determined by the radiotracer distribution technique. Volumes of 3.0 mL of the aqueous phase (with or without ligands) and of the pre-equilibrated organic phase (HDEHP in heptane) were mixed in glass vials at pH = 3.60 ± 0.05 and I = 6.60 m (NaClO₄). Aliquots of 10.0 μL of ²⁴¹Am, ²⁴⁴Cm or ^{152, 154}Eu tracer, were added to the aqueous phase and the two phases were shaken for 60 min as described in Ref. [17]. For the measurements of binary constants, the concentration of DTPA was varied between 9.0 × 10⁻⁶ and 1.0 × 10⁻⁵ M and, for the ternary constants, the concentration of DTPA was fixed at 2.0 × 10⁻⁶ M for Am³⁺ and Cm³⁺ and at 1.0 × 10⁻⁷ M for Eu³⁺ while that of IDA was varied from 0.02 to 0.20 M. The details of the equilibrium experiments, counting procedures, equilibrium pHr measurements and conversion of pHr readings to pH at I = 6.60 m (NaClO₄) and at four temperatures were as described in Ref. [17].

2.4 Data analysis

2.4.1 M–DTPA system

The extraction of trivalent Am, Cm and Eu by HDEHP solution can be expressed as:

M³⁺_(a) + 3H₂A_2(o) ⇌ M(HA₂)_3(o) + 3H⁺_(a)

(1)

where H₂A₂ is the dimeric HDEHP, while (a) and (o) represent the aqueous and organic phases, respectively. In the presence of DTPA, the 1:1 metal–DTPA complexation reaction is:

M^{3 +} + {DTPA}^{5 -} \overset{β_{101}}{⇌} M {(DTPA)}^{2 -}

(2)

where β₁₀₁ is the stability constant of the complex formed. The distribution ratio of the trivalent metal ions between the HDEHP/heptane and the aqueous phase is expressed as:

D = {[M^{3 +}]}_{(o)} / {[M^{3 +}]}_{(a)}

(3)

where [M³⁺] represents the total metal ion concentration in the organic, and aqueous phases. The polynomial correlating D values with [DTPA⁵⁻] and log β₁₀₁ may be written as:

1 / D = 1 / D_{0} (1 + β_{101} [{DTPA}^{5 -}])

(4)

or D_{0} / D - 1 = β_{101} [{DTPA}^{5 -}]

(5)

where D₀ is the distribution ratio of metal ions with no DTPA.

2.4.2 M–DTPA–IDA system

The formation of the ternary complex with DTPA + IDA can be written as:

M^{3 +} + {DTPA}^{5 -} + {IDA}^{2 -} \overset{β_{111}}{⇌} M (DTPA) {(IDA)}^{4 -}

(6)

The stability constant, β₁₁₁ of the ternary complex is evaluated using the following equations:

D_{1} = {[M^{3 +}]}_{(o)} / {[M^{3 +}]}_{(a)} (1 + β_{101} [{DTPA}^{5 -}])

(7)

D = {[M^{3 +}]}_{(o)} / {[M^{3 +}]}_{(a)} (1 + β_{101} [{DTPA}^{5 -}] + β_{111} [{DTPA}^{5 -}] [{IDA}^{2 -}])

(8)

Eqs. (7) and (8) can be combined, and simplified to:

D_{1} / D - 1 = β_{111} [{DTPA}^{5 -}] [{IDA}^{2 -}] / (1 + β_{101} [{DTPA}^{5 -}])

(9)

where D₁ is the distribution ratio in the presence of [DTPA⁵⁻] with no [IDA²⁻]. From the slope of D₁/D − 1 vs [IDA²⁻], the stability constant β₁₁₁ can be calculated.

The stability constants of the complexes [M(DTPA)]²⁻, β₁₀₁, and [M(DTPA)(IDA)]⁴⁻, β₁₁₁, were evaluated by correlating D values with ligands concentrations. The associated thermodynamic parameters of the binary and the ternary complexes were determined from linear Van't Hoff plot of stability constants with temperature. The entropy values were calculated with the Gibbs–Helmoltz equation. The stability constant values in molarity were converted to values in molality using the equation [21]:

\log β_{m} = \log β_{M} + Σ_{r} ν_{r} \log θ

(10)

where (β_M) and (β_m) are the stability constants in molarity and molality, respectively, θ is the ratio of the values of molality to molarity for the specific ionic medium and Σ_rν_r is the stoichiometric coefficient of the reactions M³⁺ + DTPA⁵⁻ ⇌ [M(DTPA)]²⁻ and M³⁺ + DTPA⁵⁻ + IDA²⁻ ⇌ [M(DTPA)(IDA)]⁴⁻. ν_r is positive for the products and negative for the reactants, which gives a value of Σ_rν_r of −1 for the former and of −2 for the latter reactions. Density data of 6.60 m (NaClO₄) at four temperatures were taken from Ref. [17]. The protonation constant values of DTPA and IDA at I = 6.60 m (NaClO₄) over the temperature range of 0–60 °C were determined by the potentiometric titration method as described in Ref. [22]. The values obtained are listed in Table 1.

	Temp (°C)	pK₀₁₁	pK₀₂₁	pK₀₃₁	pK₀₄₁	pK₀₅₁
IDA (n = 1–2)	0	9.22 ± 0.05	2.72 ± 0.08	–	–	–
25	9.87 ± 0.03	2.82 ± 0.05	–	–	–
45	9.98 ± 0.05	2.86 ± 0.08	–	–	–
60	10.39 ± 0.05	2.94 ± 0.06	–	–	–

DTPA (n = 1–5)	0	9.12 ± 0.08	8.24 ± 0.09	4.21 ± 0.05	2.89 ± 0.08	2.21 ± 0.12
25	9.98 ± 0.07	8.62 ± 0.09	4.41 ± 0.07	2.94 ± 0.08	2.32 ± 0.09
45	10.25 ± 0.04	8.81 ± 0.03	4.49 ± 0.06	2.98 ± 0.08	2.35 ± 0.08
60	10.42 ± 0.02	9.03 ± 0.11	4.61 ± 0.08	302 ± 0.08	2.40 ± 0.12

3 Results and discussion

3.1 Complexation thermodynamics

Am³⁺, Cm³⁺ and Eu³⁺ in an aqueous solution of I = 6.60 m (NaClO₄), pH = 3.60 and at temperatures of 0–60 °C have linear curves of 1/D vs [DTPA]²⁻ which indicate the formation of the 1:1 complexes. The stability constants of their 1:1 complex was calculated using Eq. (5) and are listed in Table 2 with the constants reported for these metal cations at I ≤ 1.0 M. Our values for Am³⁺ Cm³⁺ and Eu³⁺ at I = 6.60 m (NaClO₄) are ca. 2.0 log units lower than the corresponding values at I = 0.1 m, reflecting the effect of the ionic media. With temperature, the stability constants of the 1:1 complex increase. DTPA is the main component in the trivalent Actinide–Lanthanide Separation by Phosphorous Extractants and Aqueous Komplexes (TALSPEAK) process, because of their larger separation factors for actinides–DTPA complexes relative to that of the lanthanides–DTPA [23]. The decreased values of Δlog β₁₀₁ (log β_{101, Am/Cm} − log β_{101, Eu}) with increasing ionic strength (Table 3) indicate that high concentrations of salt may hinder the separation of trivalent actinides from lanthanides by TALSPEAK process.

Temp (°C)	I (m)	log β₁₀₁	Ref.
Am	Cm	Eu
0	6.60 NaClO₄	18.19 ± 0.16	18.25 ± 0.15	18.29 ± 0.12	p.w.
10	6.60 NaClO₄	–	–	19.08 ± 0.13	p.w.
25	6.60 NaClO₄	19.89 ± 0.13	19.98 ± 0.12	19.82 ± 0.15	p.w.
25	0.1 NH₄ClO₄	22.92 ± 0.02	22.99 ± 0.01	22.40 ± 0.07	[42]
25	0.1 KNO₃	–	–	22.39 ± 0.08	[43]
25	0.5 NaClO₄	21.14	21.26	–	[44]
0.5 NaClO₄	–	–	20.87 ± 0.07	[45]
35	6.60 NaClO₄	–	–	20.09 ± 0.15	p.w.
45	6.60 NaClO₄	20.35 ± 0.16	20.38 ± 0.17	–	p.w.
60	6.60 NaClO₄	20.87 ± 0.14	20.95 ± 0.17	–	p.w.

I (m)	Δlog β₁₀₁
log β_{101, Am} − log β_{101, Eu}	log β_{101, Cm} − log β_{101, Eu}
0.10	0.52	0.59
0.50	0.27	0.39
6.60	0.07	0.16

In a mixture of DTPA + IDA, a linear plot of 1/D vs [IDA]²⁻ at a fixed concentration of [DTPA]⁵⁻ and temperatures of 0–60 °C (Fig. 1 is a representative graph for Am³⁺, Cm³⁺ and Eu³⁺ at 25 °C) indicates the formation of a ternary complex. The stability constants, log β₁₁₁ calculated using Eq. (9) are listed in Table 4 plus a ternary constant reported for Eu³⁺ at I = 0.2 M (NaClO₄). A difference of ca. 1.1 log units between our value of log β₁₁₁ for Eu³⁺ at 25 °C and those of the literature at I = 0.2 m reflects the effect of the ionic media and the different reactions viz. M³⁺ + DTPA⁵⁻ + IDA²⁻ = [M(DTPA)(IDA)]⁴⁻ in our case and the reaction [M(DTPA)]²⁻ + IDA²⁻ used in the literature to evaluate the constants. For Am³⁺ and Cm³⁺, no such constants are reported. The stability order of the 1:1:1 ternary complexes: DTPA + IDA > CDTA + IDA > EDTA + IDA (Table 4) at I = 6.60 m (NaClO₄) agrees with the stability order of these ternary complexes at lower ionic strengths and is consistent with the stability sequence of the 1:1 binary complexes of DTPA, CDTA and EDTA [24]. Fig. 2 illustrates the relationship between ΣpK_a and log β₁₁₁ of Eu³⁺ with EDTA, CDTA and DTPA as primary ligands and Ox, IDA and NTA as secondary ligands. Such linearity reflects the ionic nature of the bonding in these ternary complexes. The stability constant data for the ternary complexes of EDTA + NTA, IDA, Ox were taken from Refs. [25–27], for CDTA + IDA, NTA were from Ref. [28] and that of DTPA + IDA from the present study.

Fig. 1
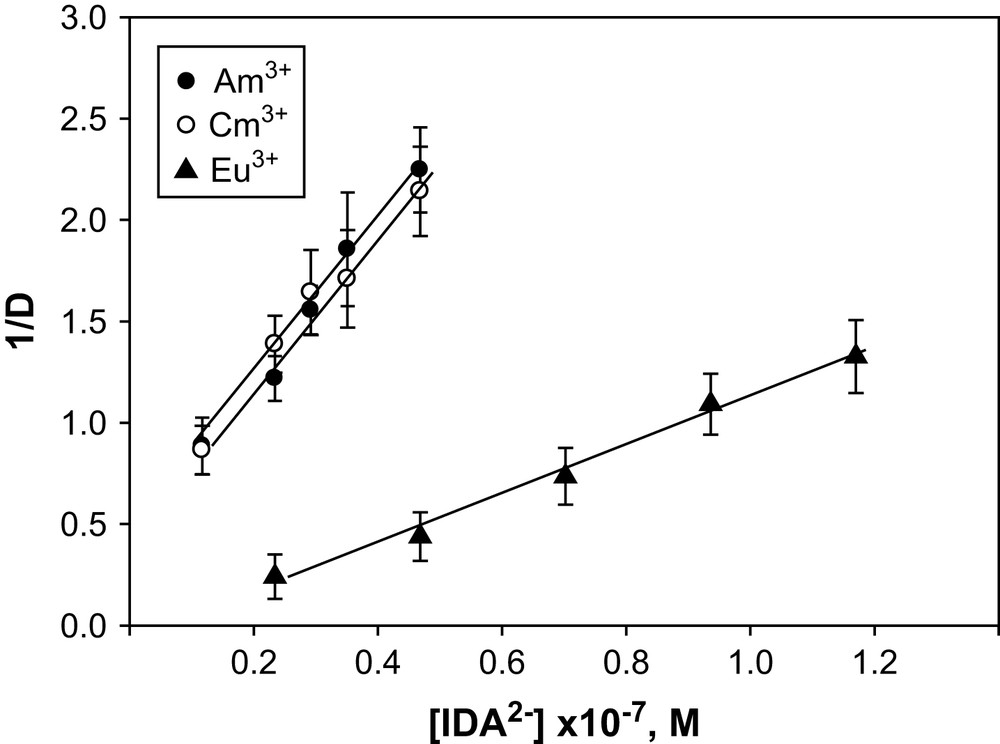
Plots of 1/D vs [IDA]²⁻ for Am³⁺, Cm³⁺ and Eu³⁺ at I = 6.60 m (NaClO₄); temp = 25 °C and pH = 3.60.

Temp (°C)	I (m)	Am	Cm	Eu	Ref.
25	6.60 NaClO₄	27.98 ± 0.22	28.07 ± 0.25	27.62 ± 0.23	p.w.
25^a	6.60 NaClO₄	23.95 ± 0.20	23.43 ± 0.19	22.95 ± 0.22	[27]
25^b	6.60 NaClO₄	24.12 ± 0.24	23.96 ± 0.24	23.62 ± 0.23	[28]
25	0.2 NaClO₄	–	–	26.50 ± 0.03	[11]
35	6.60 NaClO₄	28.37 ± 0.23	28.53 ± 0.27	28.17 ± 0.22	p.w.
45	6.60 NaClO₄	28.90 ± 0.25	29.01 ± 0.28	28.52 ± 0.24	p.w.
60	6.60 NaClO₄	30.03 ± 0.27	30.16 ± 0.29	29.89 ± 0.28	p.w.

^a log β₁₁₁ for EDTA + IDA.

^b log β₁₁₁ for CDTA + IDA.

Fig. 2
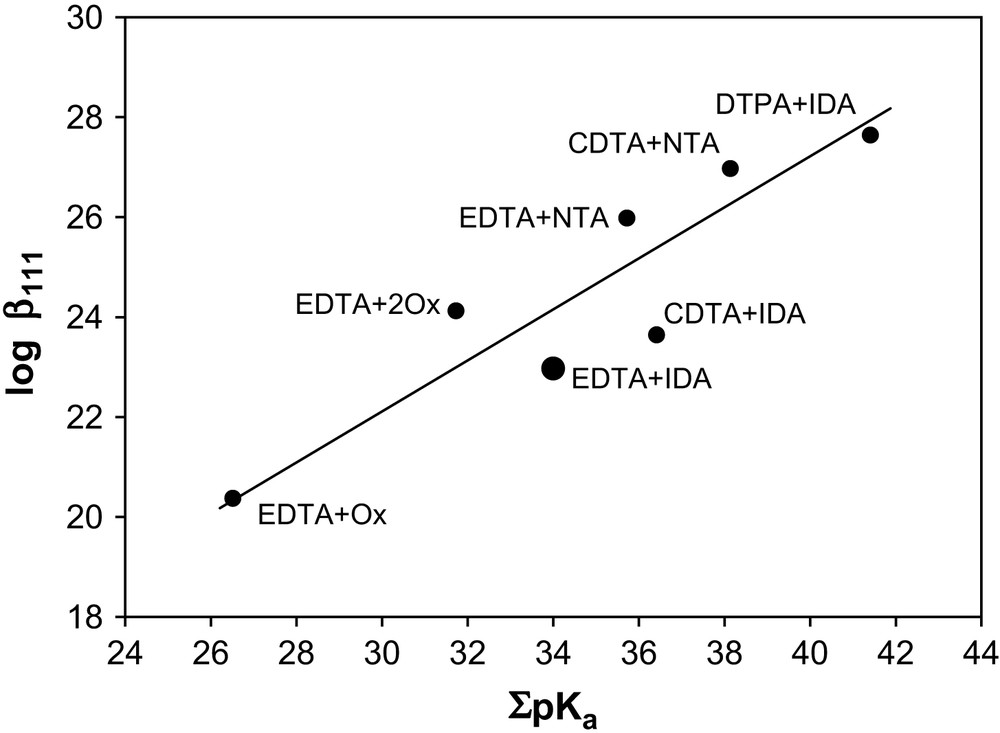
Relation of log β₁₁₁ for the formation of the 1:1:1 ternary complex of Eu³⁺ and the acid constants, ΣpK_a of the ligands.

The thermodynamic parameters for the formation of the 1:1 complexes in 6.60 m (NaClO₄) (after corrections for the heat for deprotonation of the last three protons of DTPA due to the ionic media, 68.83 kJ mol⁻¹ [17]) indicate that the complexation of M³⁺ with DTPA is accompanied by positive enthalpy and entropy contributions (Table 5). This is consistent with the greater dehydration of the metal cations at high ionic strength, as more energy is required to break the metal–water bonds than the energy released in the formation of the metal–ligand bonds. The net effect is endothermic enthalpies at high ionic strengths. By contrast, the exothermic enthalpy for these metal ions at lower ionic strength reflects that the metal–ligand interaction contribution is larger than that of the dehydration contribution. However, the dehydration dominates the entropy term at all ionic strengths.

	I (m)	ΔG₁₀₁ (kJ mol⁻¹)	ΔH₁₀₁ (kJ mol⁻¹)	ΔS₁₀₁ (J K⁻¹ mol⁻¹)	Ref.
Am	6.60 NaClO₄	−113.5 ± 0.7	6.8 ± 2.2	404 ± 15	p.w.
0.5 NaClO₄	−120.6 ± 0.3	−39.5 ± 1.0	272 ± 5	[29]
0.5 NaClO₄	−120.6 ± 0.3	−16.0 ± 2.0	350 ± 9	[29]

Cm	6.60 NaClO₄	−114.0 ± 0.7	7.2 ± 2.3	407 ± 16	p.w.
0.5 NaClO₄	−121.3 ± 0.6	−14.0 ± 2.0	360 ± 9	[29]

Eu	6.60 NaClO₄	−113.1 ± 0.9	15.4 ± 4.4	431 ± 21	p.w.
0.5 NaClO₄	−119.1 ± 0.4	−39.8 ± 1.5	266 ± 5	[29]
0.5 NaClO₄	−119.1 ± 0.4	−47.8 ± 0.4	239 ± 2	[29]

The complexation thermodynamics for the formation of the ternary complexes with DTPA + IDA (Table 6, values are corrected for the heat of deprotonation of the second proton of IDA (31.40 kJ mol⁻¹) [22] and of the last three protons of DTPA for the ionic media)) also reflects the predominant effect of the cation dehydration over the metal–ligand interaction effect, which is in agreement with the formation of corresponding ternary complexes with EDTA + IDA and EDTA + NTA at I = 6.60 m (NaClO₄) [25,27]. However, the cation dehydration and the rigid structure of CDTA contribute towards the endothermic values of enthalpy for the formation of the ternary complexes M(CDTA)(NTA)⁴⁻ and M(CDTA)(IDA)³⁻ [28].

	ΔG₁₁₁ (kJ mol⁻¹)	ΔH₁₁₁ (kJ mol⁻¹)	ΔS₁₁₁ (J K⁻¹ mol⁻¹)
Am–DTPA–IDA	−159.65 ± 1.25	10.06 ± 3.3	570 ± 48
Cm–DTPA–IDA	−160.16 ± 1.42	11.01 ± 4.2	574 ± 51
Eu–DTPA–IDA	−157.60 ± 1.35	18.48 ± 6.1	590 ± 56

In Fig. 3, the enthalpies of complexation of Am³⁺ with aminopolycarboxylates are plotted vs the total number of ligand coordination sites (carboxylate + nitrogen) at I = 0.5 and 6.60 m (NaClO₄) [29]. The straight line plot supports the participation of the carboxylate and nitrogen donors in the bond formation with Am³⁺. The deviation of CDTA from the straight line reflects extra dehydration of metal ions due to cyclohexane ring. However, the value for CDTA conforms to the straight line after correction for the excess ligand dehydration. The excess entropy for Am(CDTA)⁻ relative to that of Am(EDTA)⁻ due to the cyclohexane ring is calculated to be ca. 120 J K mol⁻¹ (ΔS_{101, CDTA} − ΔS_{101, EDTA} = 120 J K mol⁻¹) [28]. The calculated endothermic enthalpy has a value of ca. 35.76 kJ mol⁻¹ (using the relation ΔH = TΔS). The corrected enthalpy for Am(CDTA)⁻ is 47.74 − 35.76 = 11.98 kJ mol⁻¹, which is close to the enthalpy value of 14.7 kJ mol⁻¹ for the Am(EDTA)⁻ at I = 6.60 m (NaClO₄) [17]. The complexation enthalpy for the [Am(Ac)]²⁺ (Ac = acetate, with no metal–nitrogen bond) is endothermic; however, the values become more exothermic with increasing number of metal–nitrogen bonds from one in [Am(IDA)]⁺ to three in [Am(DTPA)]²⁻ formation. This confirms the exothermic enthalpic contribution of the metal–nitrogen interactions at I = 0.5 m [29]. However, at I = 6.60 m, the values of Am³⁺ are endothermic. The smaller endothermicity of [Am(DTPA)]²⁻ complexation (with three metal–nitrogen bonds) compared to that of the [Am(IDA)]⁺ complexation (with one metal–nitrogen bond) suggests that the positive dehydration contributions overcome the negative metal–nitrogen interactions at high ionic strength. The enthalpy value of the ternary complex of [Am(DTPA)(IDA)]⁴⁻ is close to that of the [Am(DTPA)]²⁻, each with three metal–nitrogen bonds, and the data point for [Am(DTPA)(IDA)]⁴⁻ falls on the straight line, indicating that the nitrogen of IDA is not involved in the bonding.

Fig. 3
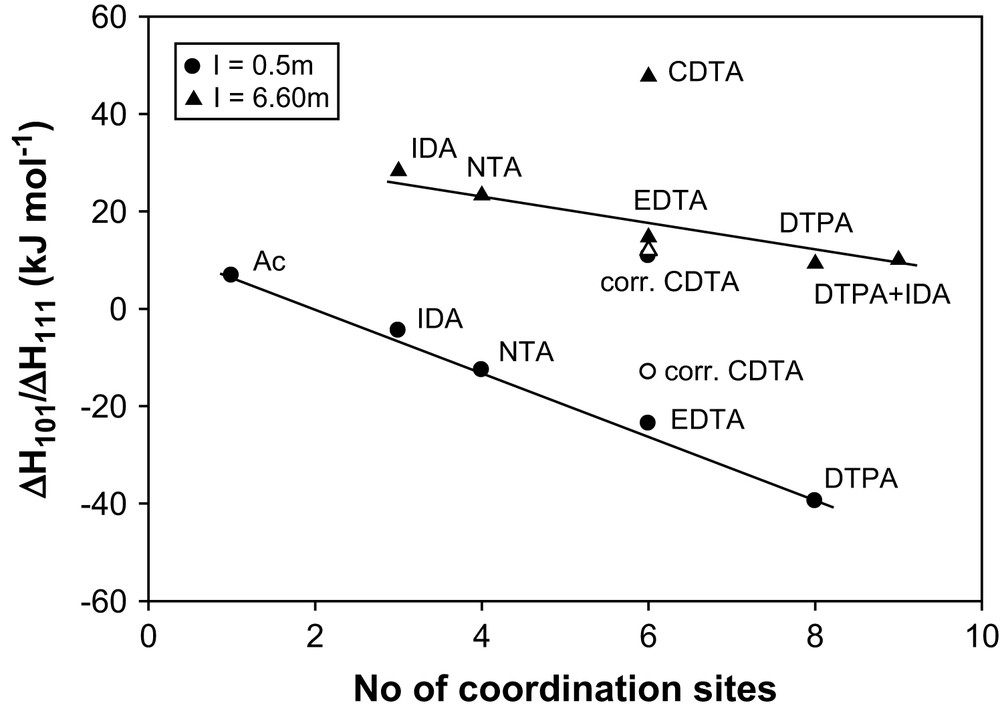
The relation between the entropy of complexation of Am³⁺ and the number of coordination sites (carboxylates + nitrogen) of aminocarboxylates.

3.2 TRLFS study

3.2.1 Eu_(aq), Eu–IDA and Eu–DTPA systems

The ⁷F₀–⁵D₀ excitation spectra of Eu³⁺ at various metal-to-ligand concentration ratios and pH are shown in Fig. 4 and the peak positions; luminescence lifetimes and the calculated values of $N_{H_{2} O}$ are listed in Table 7. For comparison purpose, the reported lifetimes and the $N_{H_{2} O}$ values for Eu³⁺, Eu–IDA and Eu–DTPA are also listed in Table 7. The excitation spectra of Eu³⁺ (0.01 M) in 6.60 m (NaClO₄) had a peak at 578.90 nm with a lifetime of 116 ± 3 μs and $N_{H_{2} O}$ value of 8.4, which is consistent the previous result [4]. The spectral peak and the luminescence lifetime of Eu³⁺ at I = 6.60 m (NaClO₄) had the same value as that at I = 0.1 m (NaClO₄), reflecting no effects of ionic media on the ⁷F₀–⁵D₀ excitation spectra of Eu³⁺. This is consistent with previous studies in which no significant effects were observed on the ⁷F₀–⁵D₀ excitation spectra of Eu³⁺ in solutions of ca. 10 M HClO₄ and NaClO₄; above that concentration, a variation in the patterns was observed [30].

Fig. 4
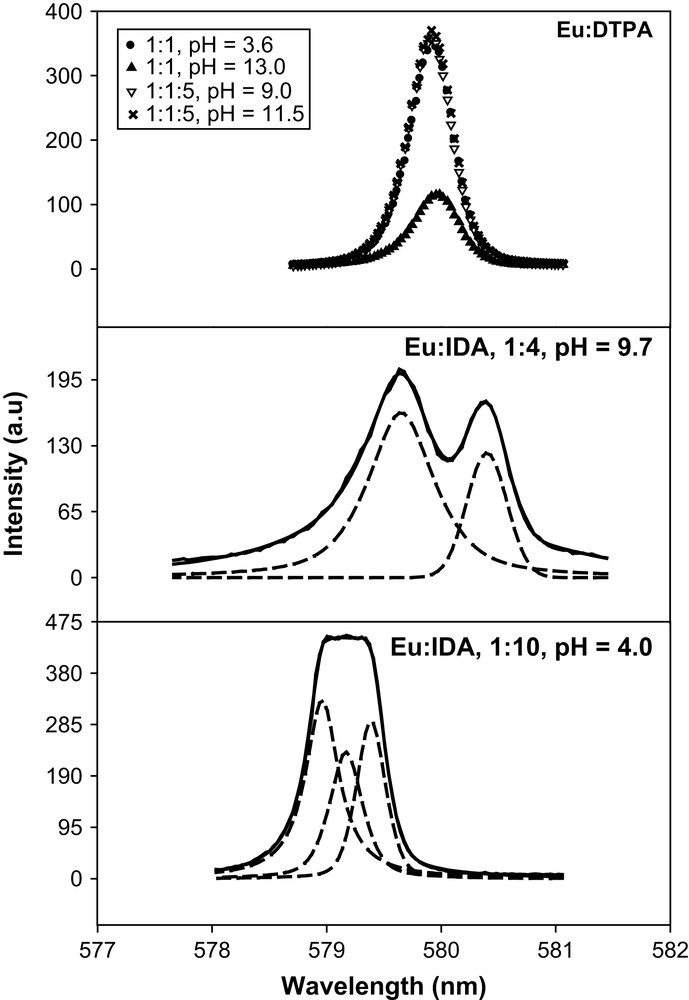
The ⁷F₀–⁵D₀ excitation spectra of Eu(III) in the binary, Eu–IDA, Eu–DTPA and the ternary Eu–DTPA–IDA systems; I = 6.60 m (NaClO₄); T = 25 °C (expt., —) and (fitted, - - -).

Species	pH	% Species (L = IDA)	Peak position (nm)	Lifetime (μs)	$N_{H_{2} O} (\pm 0.5)$	Ref.
Eu	EuL	EuL₂	EuHL	EuL₃
Eu³⁺(aq)	2.21			–			578.90	116 ± 3	8.4	p.w.
Eu³⁺(aq)	2.00			–			578.84	111 ± 2	9.0	[4]
Eu(IDA)⁺^a, 1:1	4.50	95.0	4.5	–	–	–	579.17	144 ± 1	6.6	p.w.
Eu(IDA)⁺, 1:1	6.00	36.0	63.2	–	–	–	579.14	161	5.8	[46]
Eu(IDA)⁺, 1:1	8.48	20.2	67.4	12.2	–	–	–	158 ± 1	6.3	[31]
Eu(IDA)₂⁻^a, 1:4	9.70	–	2.4	39.4	–	58.2	579.60	273 ± 3	3.1	p.w.
Eu(IDA)₃³⁻^a, 1.4	9.70	–	2.4	39.4	–	58.2	580.21	299 ± 2	2.8	p.w.
Eu(IDA)₂⁻	6.00	–	–	–	–	–	579.64	274	3.0	[46]
Eu(IDA)⁺^a, 1:10	4.00	95.1	1.5	–	3.2	–	579.14	143 ± 2	6.6	p.w.
Eu(IDA)₃³⁻^a, 1:10	11.00	–	–	9.4	–	90.5	580.28	303 ± 15	2.7	p.w.
Eu(IDA)₃³⁻	–	–	–	–	–	–	580.28	375	2.1	[33]

Eu(DTPA)²⁻, 1:1	3.60			–			579.91	657 ± 5	0.9	p.w.
Eu(DTPA)²⁻	11.50			–			579.91	657 ± 5	0.9	p.w.
Eu(DTPA)(OH)³⁻	13.00			–			579.98	549 ± 5	1.2	p.w.
Eu(DTPA)²⁻	5.50			–			580.05	680	1.1	[4]
Eu(DTPA)²⁻	4.00			–			580.05	627	1.2	[3]
Eu(DTPA)²⁻, 1:1:1	3.6–9.0			–			579.91	624 ± 8	1.0	p.w.
Eu(DTPA)²⁻, 1:1:5	3.60			–			579.91	606 ± 6	1.0	p.w.
Eu(DTPA)(IDA)⁴⁻	9.00			–			579.91	775 ± 5	0.6	p.w.
Eu(DTPA)(IDA)⁴⁻	11.50			–			579.91	757 ± 10	0.7	p.w.
Eu(DTPA)(IDA)⁴⁻, 1:10:10	3.60			–			579.91	763 ± 6	0.7	p.w.

^a No NaclO₄, p.w. = present work.

For Eu–IDA at a ratio of 1:1 and pH = 4.50 a broad peak at 579.17 nm was resolved into two peaks at 578.94 and 579.17 nm. The peak at 578.94 nm corresponds to the free Eu³⁺ and that at 579.17 nm, with a lifetime of 144 ± 1 μs and $N_{H_{2} O} = 6.6$ , is that of the complex [Eu(IDA)]⁺. Similarly for a ratio of 1:10 and pH = 4.00, a broad peak at 579.14 nm, can be deconvoluted into three peaks at 578.89, 579.17 and 579.40 nm. The peaks at 578.89 and 579.17 nm are due to the formation of Eu³⁺ and Eu(IDA)⁺, while that at 579.40 nm is that of the protonated complex EuH(IDA)₂⁻. The speciation calculations also indicated the presence of Eu³⁺, Eu(IDA)⁺ and Eu(HIDA)₂⁻ at these pH values (Table 7). With an increase in pH from 5.0 to 9.0, the peak narrowed significantly and shifted towards longer wavelength. On deconvolution this resolved into two peaks at 579.64 and 579.14 nm, consistent with the formation of complexes Eu(IDA)⁺ and Eu(IDA)₂⁻ (Table 7). The successive displacement of three water molecules by IDA in the formation of the complexes Eu(IDA)⁺ and Eu(IDA)₂⁻ are due to the binding via two carboxylates and one nitrogen [31].

At Eu:IDA of 1:4 and pH = 9.7, two peaks at 579.64 and 580.21 nm are due to the complexes Eu(IDA)₂⁻ and Eu(IDA)₃³⁻. At Eu:IDA of 1:10 and pH = 11.0, an asymmetric peak at 580.28 nm was resolved into two peaks at 580.28 and 579.98 nm, indicating the formation of the complexes Eu(IDA)₃³⁻ and Eu(IDA)₂⁻. These results indicate that at low pH values of 4–5, the complex most likely formed is [Eu(IDA)]⁺, while the complexes [Eu(IDA)₂]⁻ and [Eu(IDA)₃]³⁻ become dominant at pH > 8.0, which is consistent with the potentiometric and calorimetric studies of the formation of complexes [Ln(IDA)_n]³⁻²ⁿ (n = 1–3) [32]. In the present study although the peak shift of the ⁷F₀–⁵D₀ band is consistent with the formation of the [Eu(IDA)₃]³⁻ (CN_C = 9.6), the $N_{H_{2} O}$ value of 2.7 (Table 7) is higher than the calculated value of $N_{H_{2} O} = 0.5$ for the complex [Eu(IDA)₃]³⁻. This may be likely due to the quenching effect of a bonded N–H oscillator, which is about 1.5 times more effective than that of the O–H oscillator for Eu³⁺ [33] and/or due to an ambiguity in the luminescence lifetime measurements when there are several species present in solution as described in Ref. [33].

Eu–DTPA at a ratio of 1:1 and pH = 3.60 shows a peak at 579.91 nm with a lifetime of 657 ± 5 μs and $N_{H_{2} O} = 0.9$ consistent with the formation of complex [Eu(DTPA)]²⁻. The lack of change in $N_{H_{2} O}$ up to pH of ca. 11.50 indicates that the octadentate DTPA forms 1:1 complex over this pH range, which is consistent with the earlier study in which no further decrease in the $N_{H_{2} O}$ values was observed for the [Eu(DTPA)]²⁻ up to the pH of ca.11.00. The luminescence lifetime measurement study of Cm³⁺ also indicated the formation of 1:1 complex, [Cm(DTPA)]²⁻ over this pH range [4]. However, the $N_{H_{2} O}$ value of 1.7 for [Cm(DTPA)]²⁻ is larger than that of [Eu(DTPA)]²⁻. This can be assigned to the larger total average coordination number of Cm³⁺ as compared to that of the Eu³⁺ in aminopolycarboxylates (ca. 0.5 units larger) [4]. At pH ∼ 13.00, the peak had the same position but the intensity of the peak decreased by ca. 50%, consistent with the formation of the hydroxyl species as observed for the Eu–EDTA and Eu–DTPA-Dien (DTPA-Dien = 1,4,7-tris(carboxymethyl)-9,17-dioxo-1,4,7,10,13,16-hexaazocycloocta decane) complexes [34]. The formation of the protonated complex of DTPA was not observed in this study as such complexes usually form at pH < 3.00 [35].

3.2.2 Eu–DTPA–IDA system

The excitation spectra of Eu–DTPA–IDA at a ratio of 1:1:1 and pH = 3.60–9.00 and at a ratio of 1:1:5 and pcH = 3.60 have a peak at 579.91 nm. The lifetime and $N_{H_{2} O}$ values (Table 7) are the same as those for the [Eu(DTPA)(H₂O)]²⁻, it can be concluded that no formation of a ternary complex at these concentration ratios and the pH values. With an increase in pH value to 9.00, the position of the peak remains the same, but the lifetime of the species increased to 775 ± 5 μs and the $N_{H_{2} O}$ value decreases to 0.6, indicating the formation of a ternary complex [Eu(DTPA)(IDA)]⁴⁻. On further increasing the pH from 9.00 to 11.50, the peak had the same position with a lifetime of 757 ± 10 μs and $N_{H_{2} O} = 0.7,$ consistent with the presence of a ternary complex. For a solution ratio of 1:10:10 and pH = 3.60, the spectral patterns and the lifetime remained the same as in the solution ratio of 1:1:5 and pH = 9.00. The TRLFS results of ca. 0.7 ± 0.5 water of hydration in the formation of the ternary complex [Eu(DTPA)(IDA)]⁴⁻ is higher than the values usually observed for the nine coordinated europium complex (0.5 ± 0.5). Since both DTPA and IDA are hard base donors and show greater preferences for hard acid cation like Eu³⁺, it is reasonable to assume that the ternary complex [Eu(DTPA)(IDA)]⁴⁻ has no water of hydration attached to the inner coordination sphere of Eu³⁺.

3.3 ¹H and ¹³C NMR

The NMR spectra of diamagnetic La³⁺ and Y³⁺ with IDA, DTPA and DTPA + IDA were recorded to further substantiate the results of TRLFS and complexation thermodynamics. The ¹H NMR spectra of La–DTPA and the La–DTPA–IDA systems are shown in Fig. 5 and the assigned chemical shift values are given in Table 8. The spectrum of IDA shifts from HIDA⁻ (3.52 ppm, pH = 3.60) to IDA²⁻ (3.04 ppm, pH = 10.0), reflecting the effect of proton removal [36]. No N–H resonance is observed, presumably because of rapid N–H proton exchange with the solvent. At low pH of ∼ 4.10, the spectra of La–IDA at ratios of 1:1 and 1:3 consist of a broad peak at 3.52 ppm for methylene protons of IDA. With increase of pH to 9.50, the broad peak is shifted downfield and appears at 3.31 ppm indicating the formation of La–IDA. The broadness of the peak at lower pH value is due to the slow exchange between free IDA and bound IDA. At pH = 9.50 most of the IDA is bound to La³⁺, which gives rise to a sharp signal for methylene protons of IDA. The large downfield shifts of this peak relative to free IDA reflect the coordination of the nitrogen atom to La³⁺.

Fig. 5
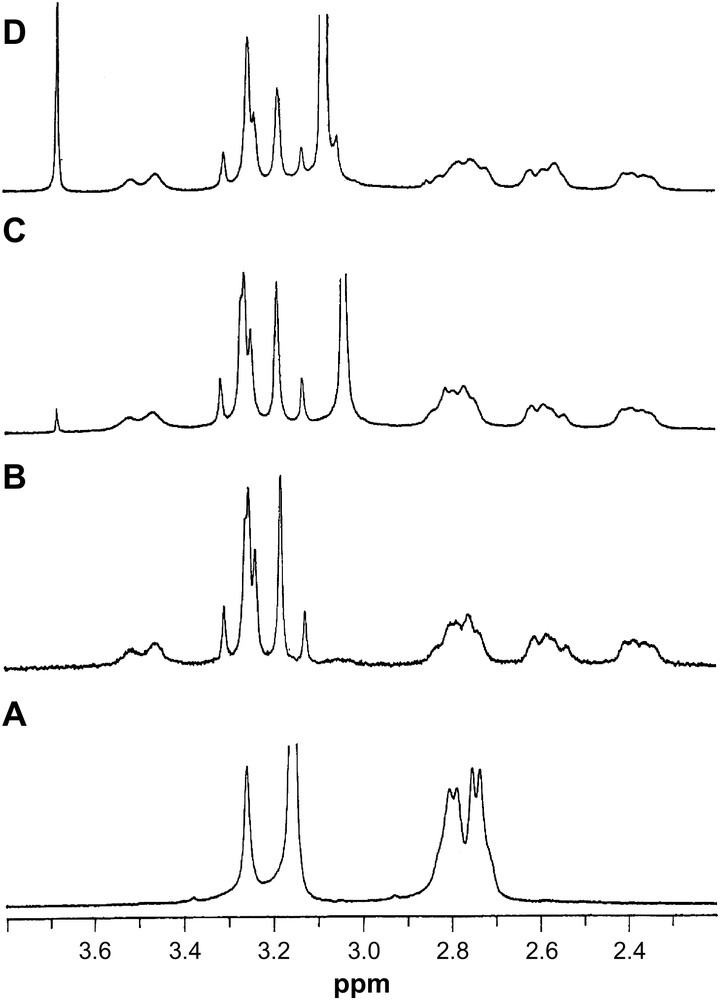
¹H NMR spectra of (A) DTPA, pH = 9.60; (B) La–DTPA, 1:1, pH = 9.60; (C) La–DTPA–IDA, 1:1:2, pH = 10.12; (D) La–DTPA–IDA, 1:1:4, pH = 10.20.

Species	pH	Chemical shifts δ (ppm)
¹H	¹³C
Acetate proton	Backbone protons	CO	CH₂COO	NCH₂CH₂
IDA	3.60	3.52	–	170.8	48.4	–
10.00	3.04	–	179.5	52.0	–
DTPA	9.60	3.25, 3.15(s)	2.80, 2.78(d)	178.5	58.6(4), 57.0(1)	51.7, 51.0
2.75, 2.73(d)

La:IDA (1:1)	4.10	3.51		173.0(w)	50.0(w)
1:9	9.50	3.31		178.8	51.1
Y:IDA (1:7)	4.09	3.49		171.7	49.5
1:7	9.50	3.11, 3.68 (N–H)		185.9	52.27

La:DTPA (1:1)	9.60	2 AB(q)(4)	2.78–2.75, 2.61–2.53	181.4, 180.7(4)	63.4(4)	57.7, 56.4
3.25(s)(1)	2.39–2.28	181.2(1)	65.4(1)
Y:DTPA (1:1)	9.60	2 AB(q)(4)	2.82–2.78, 2.58–2.54	181.49, 180.36(4)	66.1, 63.6	58.03, 56.07
3.26(s)(1)	2.40–2.35	180.52(1)	63.1
La:DTPA:IDA (1:1:2)	10.12	2 AB(q)(4)	2.81–2.77, 2.61–2.59	180.4, 180.7(4)	65.1, 63.4	57.7, 56.4
3.25(s)(1)	2.39–2.34	181.2(1), 179.5		51.8
La:DTPA:IDA (1:1:4)	10.20	2 AB(q)(4)	2.84–2.71, 2.61–2.55	181.3, 180.6(4), 181.2(1)	64.7, 63.4	58.8, 57.5, 56.4
3.25(s)(1)	2.40–2.36	179.5, 178.5		51.7, 51.5
Y:DTPA:IDA (1:1:2–1:1:4)	10.12	2AB(q)(4)	2.80–2.76, 2.59–2.57	181.7, 180.6	66.2, 63.8	58.2, 56.2
3.25(s)(1), 3.03(s)	2.39(b)	180.7, 179.4	63.3	51.8

The ¹H NMR spectra of unbound DTPA consist of two peaks at 3.15 ppm and 3.25 ppm for the four terminal acetate and the middle acetate, respectively, and the two groups of peak at 2.80–2.79 and 2.75–2.73 ppm for the ethylene protons. This is in contrast to that of singlet pattern observed for the ethylene protons in Ref. [37]. The difference in splitting pattern of the ethylene protons in these two studies is due to the differences in the resolution of spectra at 90 MHz in Ref. [37] and at 300 MHz in our study. In the complex [La(DTPA)]²⁻, two different AB patterns for the four terminal acetate protons and a singlet for the middle acetate protons were observed, which is consistent with the earlier report [37]. The two different AB patterns for the acetate protons are indicative of long-lived metal–nitrogen but with differing distances among the Ln–donor bonds. Nonequivalence of the Ln–donor bonds also have been observed for the Ln–HEDTA and MEDTA (N-methylethylenediaminetriacetate) complexes [38]. The singlet pattern for the middle acetate proton is due to the exchange averaging, while the multiplet for the ethylene protons is due to the existence of two different ethane conformations, which interconvert by wagging via an eclipsed transition state [39].

Similar chemical shifts were observed for the [Ln(DTPA)]²⁻ (Ln³⁺ = La, Lu and Y), but a heptadentate structure with unbound middle acetate group has been proposed [37]. ¹³⁹La NMR studies are also consistent with the heptadentate structure for the [Ln(DTPA)]²⁻ complex [40]. However, crystal structures of [Ln(DTPA)]²⁻ and the 2D-NMR techniques (¹H-COSY and 2D-exchange spectroscopy) of some paramagnetic lanthanides (Pr³⁺, Eu³⁺ and Yb³⁺) suggested octadentate coordination for the DTPA, binding via five carboxylate groups and three nitrogen [1,2,39]. Our ¹H NMR and the TRLFS studies are consistent with the octadentate coordination for the DTPA.

The ¹H NMR spectra of the La–DTPA–IDA at ratios of 1:1:1–1:1:2 and pH = 10.20 have peaks that are also in the 1:1 La–DTPA system plus an additional peak at 3.04 ppm, which is the chemical shift value of the free IDA protons at this pH, indicating no formation of the ternary complex at these concentration ratios. With an increase in concentration of IDA, as in a solution ratio of 1:1:4 (Fig. 5) although the La–DTPA part of the spectrum shows similar chemical shift, a new broad peak between 3.08 and 3.05 ppm indicating the formation of the ternary complex [La(DTPA)(IDA)]⁴⁻. It is difficult to detect the peak for the free IDA because the resonance for free IDA falls under the resonance for the complexed IDA. No significant shift of DTPA signals in the formation of the ternary complex [La(DTPA)(IDA)]⁴⁻ reflects that there is no additional steric crowding around the La³⁺ cation on formation of the ternary complex. The AB pattern of the acetate protons of DTPA implies that the metal–nitrogen bond remain long-lived in the ternary complex, which is consistent with the formation of corresponding ternary complexes [Ln(EDTA)(IDA)]³⁻ (Ln³⁺ = Pr, Eu and Yb) [6]. By contrast, the long-lived metal–nitrogen bond becomes short-lived with the formation of the ternary complex [Lu(EDTA)(IDA)]³⁻ [41], indicating two different modes of formation of the ternary complexes across the series. A small peak at ca. 3.68 ppm is due to the slow exchange of N–H proton with the solvent.

The ¹H NMR spectra of Y³⁺, which usually has a CN of 8.0, show expected shift of signals on complexation with the IDA and DTPA (Table 8). The spectra of Y–DTPA–IDA at ratios of 1:1:2 and 1:1:4 have in addition to the existence of the usual peaks for the Y–DTPA, a broad peak at 3.03 ppm due to the free IDA and a peak at 3.68 ppm, due to the slow exchange of the N–H proton with the solvent. No peak for the complexed IDA in the spectra of Y–DTPA–IDA indicates that the Y(DTPA)²⁻ does not form ternary complex with IDA.

The ¹³C spectra of unbound DTPA show a carboxylate peak at 178.5 ppm, two methylene carbon peaks at 51.0 (2C α-position to middle N) and 51.7 (2C α-position to terminal N) and the two peaks at 57.0 (1C CH₂COO) and 58.6 (4C CH₂COO) ppm (Fig. 6). On complexation with La³⁺ the five equivalent carboxylate groups are split into three peaks at 181.4 and 181.7 ppm for the terminal acetate and at 181.2 ppm for the middle acetate with an intensity ratio of ca. 2:1:2, consistent with the binding of all five carboxylate groups. The spectra of La–DTPA–IDA at ratios of 1:1:1–1:1:2 (Fig. 6) show no peaks for the complexed IDA, indicating no formation of the ternary complex at these concentration ratios. The spectrum of La–DTPA–IDA at a ratio of 1:1:4 has three peaks at 181.3, 181.2 and 180.6 ppm with an intensity ratio of ca. 2:1:2 for the binding of five carboxylate groups of DTPA and a new broad peak at 178.5 ppm, which is due to the formation of the ternary complex [La(DTPA)(IDA)]⁴⁻. The broadness of the peak indicates weakly coordination of the carboxylate groups of IDA to the metal cation, so that the one arm of the ligand coordinated to and detached from the metal rapidly. An additional peak at 179.5 ppm in the spectrum is due to the unbound carboxylate group of IDA.

Fig. 6
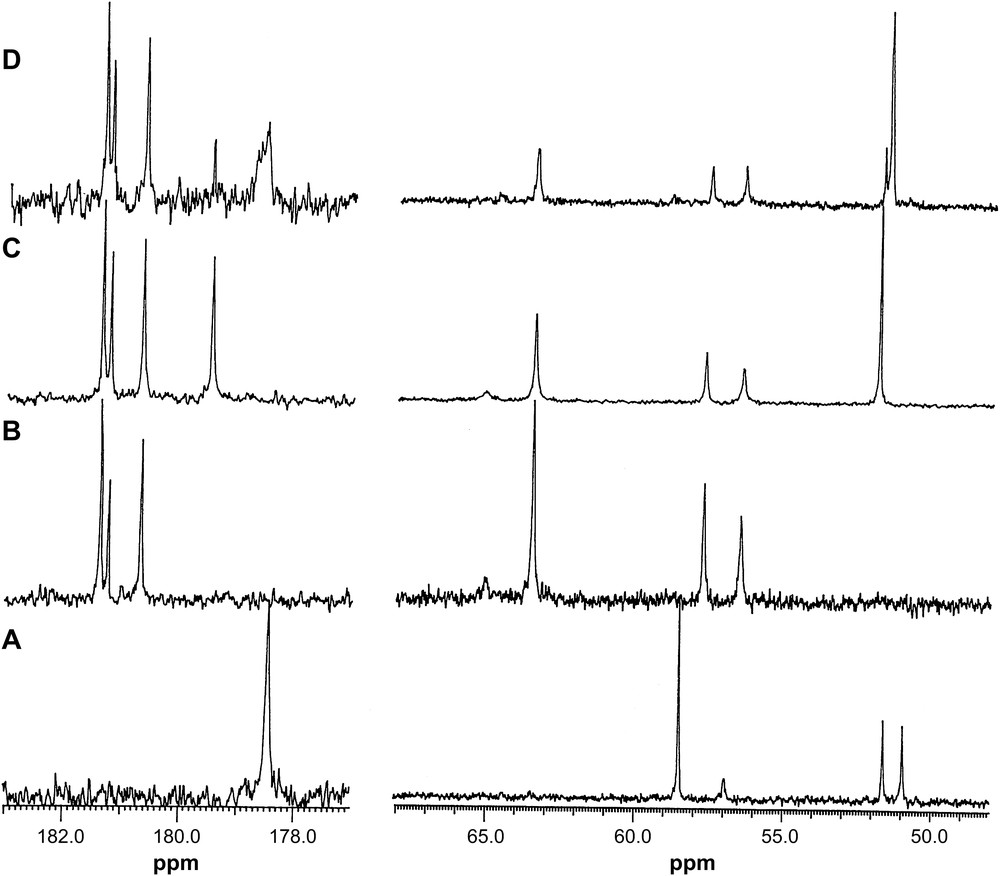
¹³C NMR spectra of (A) DTPA, pH = 9.60; (B) La–DTPA, 1:1, pH = 9.60; (C) La–DTPA–IDA, 1:1:2, pH = 10.12; (D) La–DTPA–IDA, 1:1:4, pH = 10.20.

The ¹³C NMR spectra of Y–IDA, Y–DTPA and the Y–DTPA–IDA complexes also support the finding of the TRLFS and ¹H NMR studies. The species formed and the assigned chemical shifts are given in Table 8. The ¹³C NMR spectra of IDA and DTPA show the expected shifts of signal downfield on complexation. The absence of complexed IDA peak in the spectra of Y–DTPA–IDA at ratios of 1:1:2–1:1:4 is consistent with no ternary complex formation for Y³⁺. The proposed structure of the ternary complex Eu(DTPA)(IDA)⁴⁻ showing the binding modes of the DTPA and IDA is given in Fig. 7.

Fig. 7
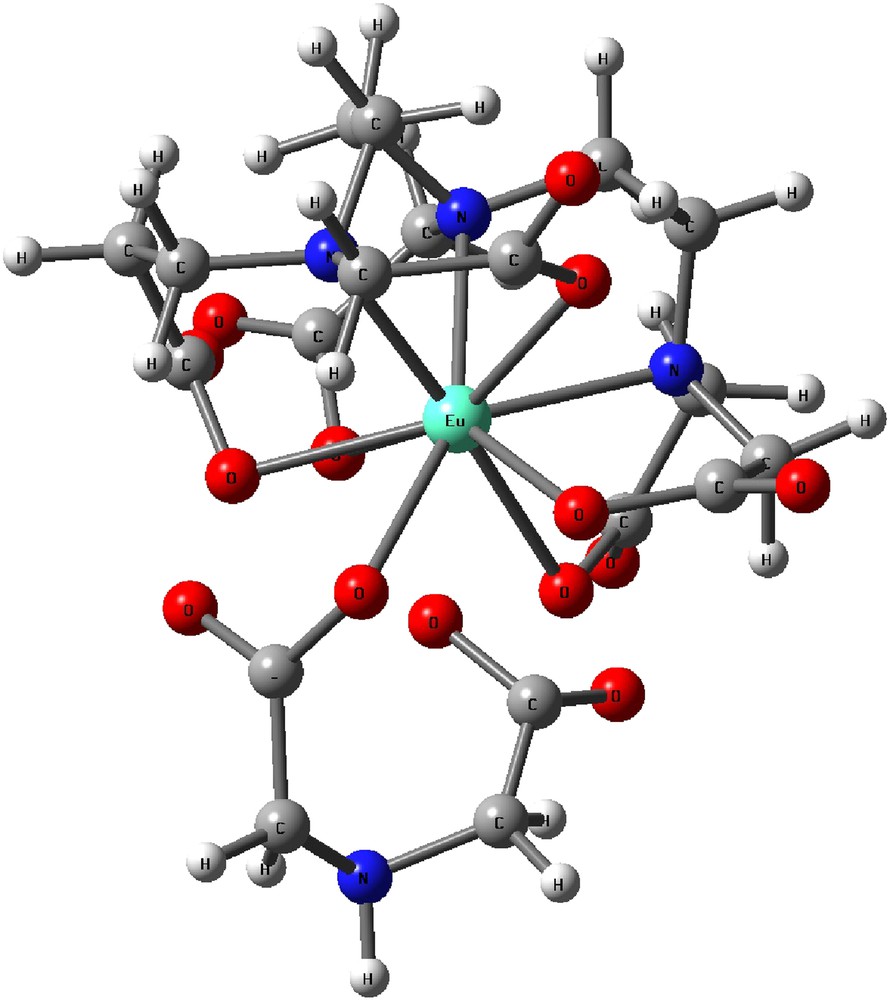
Proposed structure showing the binding of DTPA and IDA in the formation of the ternary complex Eu(DTPA)(IDA)⁴⁻; atoms: nitrogen – blue; oxygen – red; europium – green; carbon – grey. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4 Conclusion

The present studies establish the formation and the coordination modes of the binary and of the ternary complexes of trivalent lanthanides and the actinides with DTPA and DTPA + IDA. The size of the metal cations and the steric requirement of the ligands seem to play an important role in the formation of these ternary complexes. In the binary 1:1 complex, the DTPA binds via five carboxylates and three nitrogen atoms, while in the ternary 1:1:1 complex, DTPA does not undergo any structural change and binds by the same eight coordination sites with IDA binding weekly via one carboxylate group. The metal–nitrogen bond is found to be remained long-lived in the formation of these complexes. The smaller lanthanides do not form ternary complexes with DTPA + IDA. The residual water of hydration of ca. 1.0 ± 0.5 for the binary and ca. 0.7 ± 0.5 for the ternary complexes are consistent with the results of the NMR study (¹H and ¹³C).

The distribution measurement studies of Am³⁺, Cm³⁺ and Eu³⁺ (tracer concentrations) with DTPA and IDA in 6.60 m (NaClO₄) also support the formation of the ternary complex, [M(DTPA)(IDA)]⁴⁻ in the temperature range 0–60 °C. The complexation thermodynamics of these complexes reflected the significant contributions of a cation dehydration over that of the metal–ligand interaction contributions at such high ionic strengths. The high stability constant value of the ternary complex [M(DTPA)(IDA)]⁴⁻ indicates that the ternary species plus the mixed chelate hydroxyl species can increase the solubility of the trivalent lanthanides and actinides in the waste tanks.

Acknowledgements

This research was supported by a USDOE, Office of Basic Energy Sciences contract. We gratefully acknowledge Dr. Bert Van De Burgt and Dr. Thomas Gedris for their assistance in data accumulations.

Bibliographie

[1] A. Mondry; P. Starynowicz Polyhedron, 19 (2000), p. 771

[2] Y. Inomata; T. Sunakawa; F.S. Howell J. Mol. Struct., 648 (2003), p. 81

[3] C.C. Bryden; C.N. Reilley Anal. Chem., 54 (1982), p. 610

[4] T. Kimura; G.R. Choppin J. Alloys Compd., 213/214 (1994), p. 313

[5] R. Kiraly; I. Toth; L. Zekany; E. Brucher Acta Chim. Hung., 125 (1988), p. 519

[6] R.V. Southwood-Jones; A. Merbach Inorg. Chim. Acta, 30 (1978), p. 135

[7] E.S. Titova; D.F. Pyreu; E.V. Kozlovskii Russ. J. Inorg. Chem., 50 (2005), p. 958

[8] J.M. Gatez; E. Merciny; G. Duyckaerts Anal. Chim. Acta, 94 (1977), p. 91

[9] G. Geier; U. Karlen Helv. Chim. Acta, 54 (1971), p. 135

[10] J.N. Mathur; K. Cernochova; G.R. Choppin Inorg. Chim. Acta, 36 (2007), p. 1785

[11] S. Verma; M.C. Saxena J. Indian Chem. Soc., 27A (1988), p. 1068

[12] S.Y. Shetty; R.M. Sathe J. Inorg. Nucl. Chem., 39 (1977), p. 1838

[13] L. Burai; V. Hietapelto; R. Kiraly; E. Toth; E. Brucher Magn. Reson. Med., 38 (1997), p. 146

[14] J.A. Campbell; R.W. Stromatt; M.R. Smith; D.W. Koppenaal; R.M. Bean; T.E. Jones; D.M. Strachan; H. Babad Anal. Chem., 66 (1994), p. 1208A

[15] K.E. Grant; G.M. Mong; R.B. Lucke; J.A. Campbell J. Radioanal. Nucl. Chem., 211 (1996), p. 383

[16] A.I. Vogel A Text Book in Quantitative Inorganic Analysis, Longman, London, 1966

[17] K. Cernochova; J.N. Mathur; G.R. Choppin Radiochim. Acta, 93 (2005), p. 733

[18] G.R. Choppin; Z.M. Wang Inorg. Chem., 36 (1997), p. 249

[19] P.P. Barthelemy; G.R. Choppin Inorg. Chem., 28 (1989), p. 3354

[20] W.D. Horrocks; D.R. Sudnick J. Am. Chem. Soc., 101 (1979), p. 334

[21] R. Guillaumont; T. Fanghanel; J. Fuger; I. Grenthe; V. Neck; D.A. Palmer; H.M. Rand Update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium and Technitium (F.J. Mowpean; M. Illemassene; C. Domenech-Orti; K. Ben Said, eds.), Elsevier, B.V., Amsterdam, 2003

[22] P. Thakur, J.N. Mathur, R.C. Moore, G.R. Choppin, Inorg. Chim. Acta, in press, . | DOI

[23] B. Weaver, F.A. Kappelmann, Report ORNL-3559, Oak Ridge National Laboratory, 1964.

[24] R.M. Smith; A.E. Martell; R.J. Motekaitis NIST Critically Selected Stability Constants of Metal Complexes Database, Version 6.0. Users Guide, U.S. Department of Commerce, Technology and Administration, National Institute of Standards and Technology, Standard Reference Data Program, NIST, Gaithersburg, MD, 1999

[25] J.N. Mathur; P. Thakur; C.J. Dodge; A.J. Francis; G.R. Choppin Inorg. Chem., 45 (2006), p. 8026

[26] P. Thakur; J.N. Mathur; C.J. Dodge; A.J. Francis; G.R. Choppin J. Chem. Soc. Dalton Trans. (2006), p. 4829

[27] G.R. Choppin; P. Thakur; J.N. Mathur Inorg. Chim. Acta, 360 (2007), p. 1785

[28] P. Thakur, J.N. Mathur, G.R. Choppin, Inorg. Chim Acta, in press, . | DOI

[29] G.R. Choppin; P. Thakur; J.N. Mathur Coord. Chem. Rev., 250 (2006), p. 936

[30] S. Lis; G.R. Choppin Mater. Chem. Phys., 31 (1992), p. 159

[31] S. Lis; G.R. Choppin J. Alloys Compd., 225 (1995), p. 257

[32] I. Grenthe; G. Gardhammar Acta Chem. Scand., 25 (1971), p. 1401

[33] M. Latva; J. Kankare J. Coord. Chem., 43 (1998), p. 121

[34] S.L. Wu; W.D. Horrocks Anal. Chem., 68 (1996), p. 394

[35] N.A. Kostromina; N.N. Tananaeva J. Appl. Spectrosc., 4 (1969), p. 301

[36] J. Jiang; J.C. Renshaw; M.J. Sarsfield; F.R. Livens; D. Collison; J.M. Charnock; H. Eccles Inorg. Chem., 42 (2003), p. 1233

[37] G.R. Choppin; P.A. Baisden; S.A. Khan Inorg. Chem., 18 (1979), p. 1330

[38] P.A. Baisden; G.R. Choppin; B.B. Garrett Inorg. Chem., 16 (1977), p. 1367

[39] B.G. Jenkins; R.B. Lauffer Inorg. Chem., 27 (1988), p. 4730

[40] C.F.G.C. Geraldes; A.D. Sherry J. Magn. Reson., 66 (1986), p. 274

[41] T.V. Ternovaya; N.A. Kostromina Russ. J. Inorg. Chem., 18 (1973), p. 1266

[42] R.D. Baybarz J. Inorg. Nucl. Chem., 27 (1965), p. 1831

[43] T. Moeller; L.C. Thompson J. Inorg. Nucl. Chem., 24 (1962), p. 499

[44] D.D. Ensor, A.H. Shah, Progress Report, DOE/ER/10489-08, Oak Ridge National Laboratory, Oak Ridge, TN, December 1982.

[45] T.F. Gritmon; M.P. Goedken; G.R. Choppin J. Inorg. Nucl. Chem., 39 (1977), p. 2021

[46] B.H. Lee; K.H. Chung; H.S. Shin; Y.J. Park; H. Moon J. Colloid Interface Sci., 188 (1997), p. 439

Commentaires - Politique