1 Introduction
Magnetic systems have attracted much attention over the last decades considering their intrinsic fundamental behaviors and possible applications in nanoscale devices. Chemists have put much effort to design and fully characterize new families of systems which may exhibit unusual and fascinating properties arising from the strongly correlated character of their electronic structures. From a fundamental point of view, high-Tc superconducting copper oxides [1–3] and colossal magnetoresistant manganite oxides [4–9] are such families which cannot be ignored in the field of 2D and 3D materials. 1D chains [10–13] as well as molecular systems mimicking biological active centers [14–17] have more recently been considered as promising targets in the understanding of dominant electronic interactions. In such materials, a rather limited number of electrons is responsible for the observed intriguing properties. Theoretically, since these electrons (often referred to as magnetic electrons) are usually rather localized in space (e.g., d orbitals), the electronic wavefunction is intrinsically multireference which may dispose single reference strategies. Nevertheless, in numerous cases, a reasonably satisfactory energetics description of such systems can be obtained by the elegant broken symmetry (BS) method [18–21]. Let us mention that, in particular, BS Density Functional Theory (DFT) calculations have turned out to be very efficient in the determination of magnetic coupling constants (see Refs. [22–29] and references therein). Conversely, DFT has failed to predict the insulating behavior of nickel oxide NiO by using spin densities [30]. Nevertheless, a recent approach based on natural orbitals and their occupation numbers has shown to improve significantly the spin density description in highly correlated systems [31]. More recently, the inefficiency of DFT methods has been pointed out in the low-energy spectrum description of molecular systems [32–35].
In order to bridge the gap between experimental measurements and a detailed microscopic understanding, one traditionally searches for a rationalization based on effective valence bond (VB) Hamiltonians [36]. The latter aims at reducing the available electronic structure calculations into different effective integrals such as hopping, exchange and onsite repulsion energies. With this goal in mind, accurate ab initio quantum chemical calculations are extremely valuable, since information is available not only in energy differences but also in the wavefunctions. While the derivation of such parameters is straightforward from pure spin states, the correspondence between numerical results and the VB parametrized Hamiltonians is controversial as spin-unrestricted and non-orthogonal orbitals are used. This particular issue has been debated in the literature [37].
From the experimental point of view, open-shell systems have opened up new routes to large information storage. As prototype of such, spin transiting materials based mainly on Fe(II) ions architectures look very promising candidates for bistability behavior [38]. In the field of nanoscale objects' synthesis, single-molecule magnets (SMM) and single-chain magnets (SCM) have also been subject to intense development (see Refs. [12,13,39–41] and references therein) since the pioneering works on Mn12 compound [42–44]. As in biological porphyrins, some intriguing molecules associate radical ligands with metal d ions. This particular class of ligands, referred to as noninnocent, offers the possibility to tune magnetic interactions between rather different partners. Experimental setup (i.e. squid) performances have followed the need for size reduction.
In this paper, our goal is to exemplify the need for theoretical inspection in correlated materials. The paper will be organized as follows. We first recall the theoretical approaches which are currently available and introduce the important concepts of static and dynamical correlations. Wavefunction ab initio methods will be shortly presented using the complete active space self-consistent field (CASSCF) method as a featuring multireference technique. Then, using recent examples of molecular and extended systems, we will show that the ab initio machinery is likely to capture the crucial physical effects which lead to quantitative evaluations of observables and effective parameters.
2 Theoretical setup
For the systems under interest holding localized spin moments, the description goes through the inspection of the spatial distribution and energetics of the unpaired electrons. As the latter grows, the number of spin configurations becomes rapidly important (2N). Nevertheless, even multicentric architectures display a rather limited collection of so-called magnetic electrons (∼several tens at most) and one can provide at first a satisfactory, though qualitative, electronic picture. The different electronic configurations arising from the unpaired electrons in the field generated by the rest of the electrons (core electrons) and nuclei can be grasped along the CASSCF method [45] or its restricted RAS (i.e. restricted active subspace) analogue [46].
This configuration interaction (CI) method is based on the wavefunction expansion on all possible Slater determinants generated by distributing n electrons in m orbitals, so-called CAS(n,m). Along this framework generalizing the Hartree–Fock (HF) method to a multireference zeroth-order description, the failure of single determinantal SCF approaches is overcome. The CASSCF spin-adapted wavefunction provides a set of symmetry-adapted molecular orbitals (MOs) whose occupation numbers are either 2 or 0, defining the inactive and virtual MOs, respectively. The active space MOs have occupation numbers which range from 0 to 2 (see Fig. 1). Along this framework, one effectively introduces the so-called static correlation effects by evaluating the leading configurations on the same footing. In particular, quasi-degenerate configurations which play a dominant role in bond-breaking phenomenon are dealt with this zeroth-order wavefunction. Let us exemplify this treatment using the H2 molecule in a minimal atomic basis set {a,b}. The CASSCF wavefunction reads:
| (1) |
| (2) |
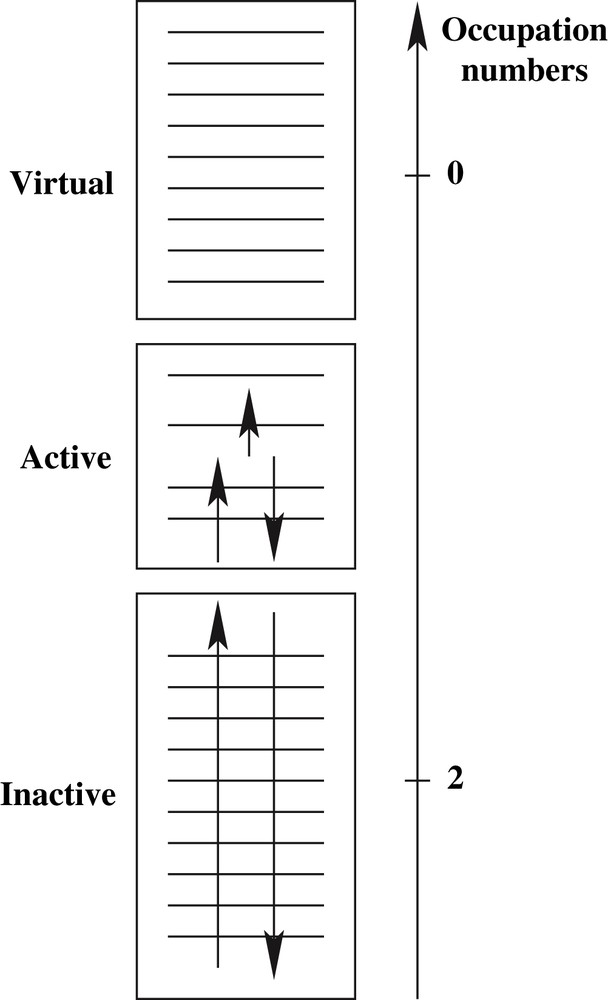
Electronic partitioning within the CASSCF framework.
In more elaborated architectures, the dynamical response of the core electrons to the fluctuation within the active space might be of crucial importance to account for subtle behaviors. The participation of the higher-lying electronic configurations can be performed along a variational CI expansion on top of the reference CASSCF function, or by using the second-order perturbation theory (so-called CASPT2) [47,48]. As an important method of the former strategy, the Difference Dedicated CI (DDCI) [49,50] approach has been extensively used for magnetic systems for which the relevant physical effects (spin polarization, dynamical correlation) are essential to explain and rationalize the experimental magnetic exchange coupling constants [51–53]. Being variational, the DDCI method allows the external correlation to modify the coefficients of the active space (see λ and μ in Eq. (1)). In particular, the weights of the ionic forms can be enhanced as instantaneous electronic relaxation responds to the electric field fluctuations. This impressively efficient method relies on the statement that the configuration interactions' expansion excludes all double excitations from inactive (i.e. doubly occupied) to virtual (i.e. vacant) molecular orbitals. As a matter of fact, it is shown that for vertical transitions which involve excitations depicted by the active space choice (i.e. at zeroth-order) such contributions cancel out at second-order of perturbation theory. Thus, one defines successively DDCI-1, 2 and 3 levels of calculation with respect to the number of degrees of freedom solicited in the configuration generation (see Fig. 2). A degree of freedom is defined as a hole or a particle created in doubly occupied or empty MOs in all reference configurations, respectively. This methodology was developed originally by Malrieu [51,54,55] and later implemented in the CASDI code [56]. More recently, this spectroscopy oriented methodology (so-called spectroscopy oriented configuration interaction, SORCI) [57] has been added to the ORCA package which offers a large amount of observable calculations, including relativistic effects [58]. This method has proven to be impressively accurate in the rationalization of low-energy spectroscopies, particularly for molecular [49,52,53,59–65] to extended magnetic systems [66–72]. Clearly, magnetic exchange coupling constant (J) calculations are challenges for theoreticians, since they usually range from a few cm−1 to a few hundred cm−1. In the meantime, let us mention that numerous studies have relied on DFT approaches using the BS approximation. In this framework, J is evaluated from the unrestricted highest multiplets and fictitious broken symmetry single reference wavefunction energies [22,73]. This method has turned out to be very useful for large systems and in magneto-structural characterization (for recent applications, see Refs. [23–29] and references therein). Nevertheless, it suffers from spin contamination problems inherent to spin polarized calculations. The main drawbacks of this method have been analyzed in the literature [35,37,74,75].
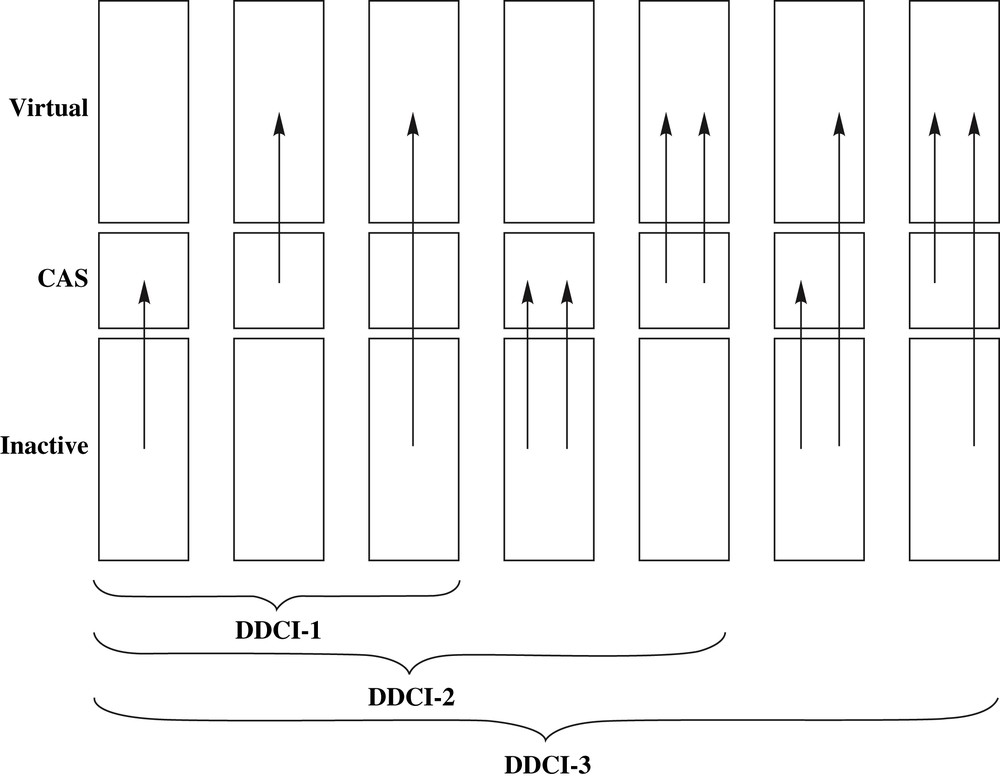
Schematic representation of the DDCI-1, DDCI-2, and DDCI-3 configurations.
Undoubtedly, there is a real demand for both experimental measurements' analysis and standard models' parametrization in the inspection of molecular and extended materials.
3 Machinery at work for experimental interpretation
Over the past decades, a huge amount of experimental data carried out on a wide panel of systems has received much attention from both CI and DFT-based frameworks. For the present purpose, we limit our inspection to a selection of architectures of various dimensionalities. Over the years, the possibilities to generate magnetic systems using versatile ligands coordinated to different metallic centers have been much considered in the light of porphyrin-like molecules' activity. Thus, the traditional scenario involving open-d shells in the environment of closed-shell magnetic couplers (see Sections 3.1 and 3.4) has been revisited based on both experimental and theoretical works (see Section 3.2). By varying the number (see Section 3.3) and nature (see Section 3.5) of metal ions, the possibility to tune, almost at will, magnetic properties has significantly increased as the number of spin states grows and occupations can be modulated by external stimuli.
3.1 Azido-based dinuclear complexes: a textbook example
Azido-bridged compounds including different metal ions in various dimensionalities have received much attention for several decades [76–78]. Interestingly, the azido group N3− turned out to be a remarkable magnetic coupler between metallic ions. The number of linkers may vary, and the symmetry of the coordination mode can finely tune the sign and amplitude of the magnetic constant parameter. Among this class of compounds, azido double-bridged copper(II) dinuclear systems are undoubtedly the most successful. Depending on the bridging mode, one traditionally distinguishes two families, the so-called End-On (EO) and End-to-End (EE) where the azido groups bridge the copper(II) ions through one terminal nitrogen atom or two terminal nitrogen atoms, respectively (see Fig. 3). Numerous examples of both classes are given in Refs. [79–92] (EO) and [93–98] (EE). Nevertheless, the determination of the structural parameters that may control the magnetic interaction nature is still much debated in the literature [87,89,93,96–100]. The general trend is that the EE mode affords antiferromagnetic interactions, whereas the EO mode favors ferromagnetic behavior. However, the alternation of short and long Cu–N distances, which corresponds to the asymmetric mode, may result in either ferro- or antiferromagnetic interactions whatever the coordination type [89]. Several magneto-structural explanations have been proposed to tentatively rationalize the experimental behavior. Theoretical investigations based on either state-of-the-art ab initio or DFT calculations have also played a major role in the discussions [62,89,100–104]. Both approaches proved to reach satisfactory agreement with experimental measurements in either the EO or the EE series. Nevertheless, correlated ab initio might be preferred as the information extracted from a multiconfigurational wavefunction is very insightful into the mechanism of magnetic interactions. Since Cu(II) ion is formally d1, a zeroth-order description lies in CAS(2,2)SCF calculations, allowing the occupations of the in-phase and out-of-phase linear combinations of atomic orbitals by two electrons.
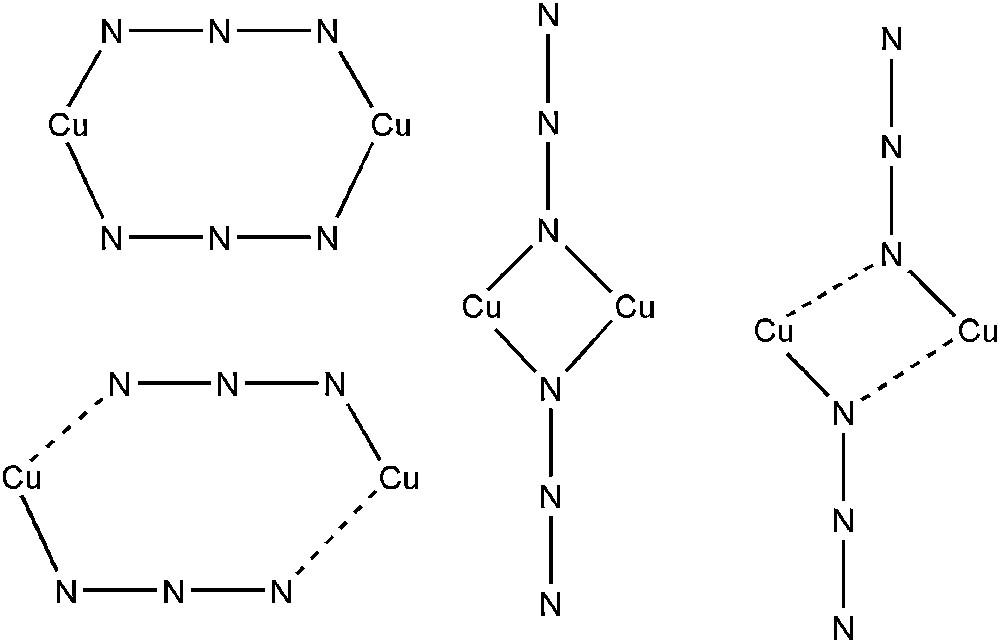
Symmetric and asymmetric End-to-End (μ1,3) and End-On (μ1,1) coordination modes.
As a recent illustration from our works, it has been demonstrated using CAS(2,2)SCF/DDCI calculations on fictitious analogues of the EE [Cu(N3L)]2 compound (L = 7-(dimethylamino)-1,1,1-trifluoro-4-methyl-5-aza-3-hepten-2-on-ato) (see Fig. 4) that EE diazido Cu(II) systems may exhibit either ferro- or antiferromagnetic behavior depending on one important structural parameter [105]. Practically, starting from the experimental geometry for which ferromagnetism had been theoretically elucidated [106], the Cu–N distances were modified to evaluate the sensitivity of the singlet–triplet gap with respect to this so-called “shearing-like” distortion (see Fig. 5). This geometrical parameter measures the amplitude d of the difference between the long and short Cu–N distances away from a perfectly symmetric bridging mode.
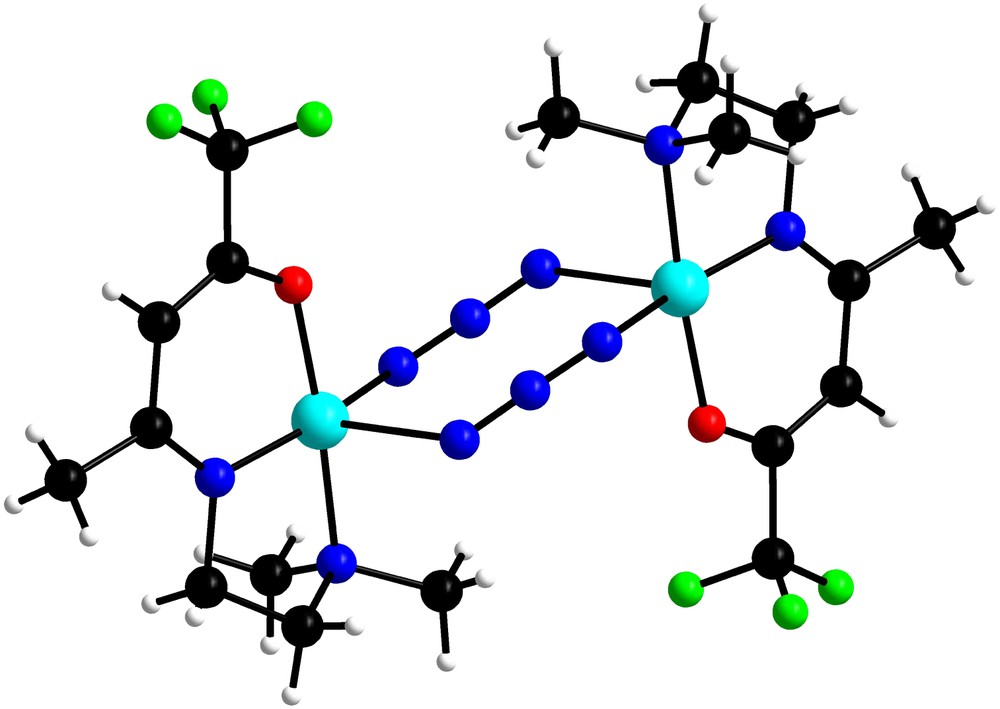
Structure of the EE [Cu(N3L)]2 compound with L = 7-(dimethylamino)-1,1,1-trifluoro-4-methyl-5-aza-3-hepten-2-on-ato.
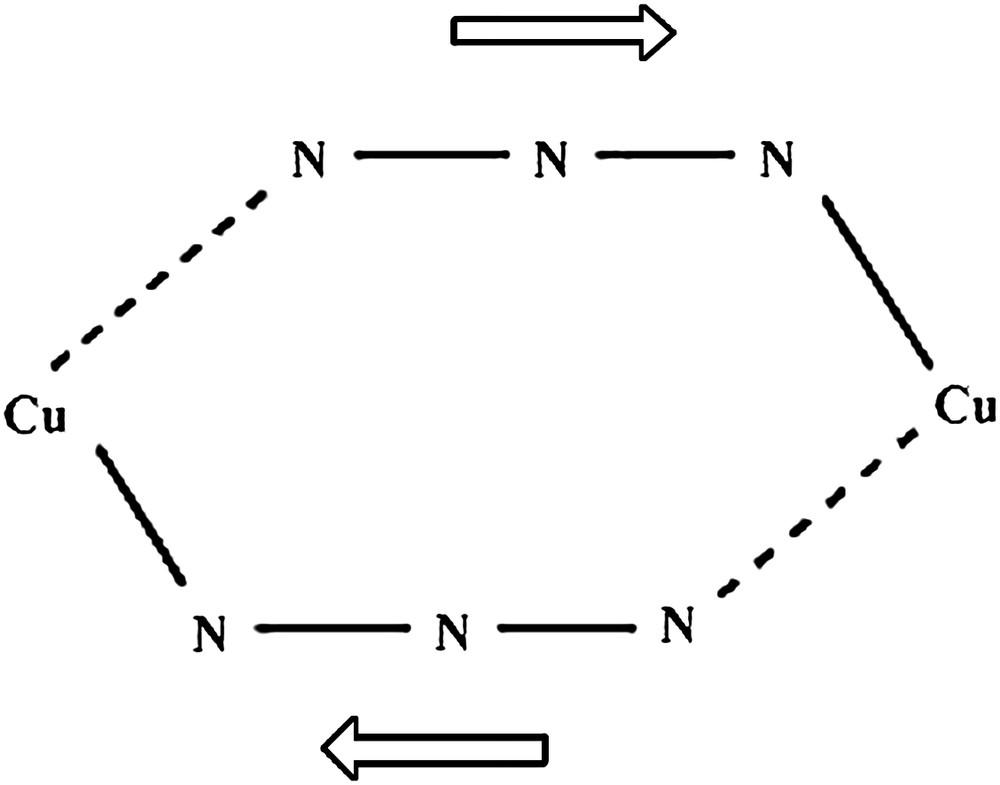
Asymmetric coordination mode of the EE azide bridge. The arrows indicate the sharing distortion.
A detailed analysis of the different leading contributions to the exchange magnetic coupling constant J (i.e. the spin polarization (SP) effects which are dominated by excitations involving the bridging-ligand orbitals and the dynamical correlation (DC) effects that arise from the instantaneous polarization of the copper ions environments [51–53]) has been carried out [105]. The variations of J, SP and DC contributions as a function of d are presented in Fig. 6. A detailed analysis of the wavefunction showed that the weights of the ionic forms (i.e. 2 electrons on one site) increase as d decreases. Therefore, the singlet is stabilized over the triplet. Similar analysis on previously published structures of pentacoordinate Cu compounds with only one exchange pathway turned out to be predictive. Even though other parameters cannot be ignored, this particular analysis has shed light on the leading contributions which may control the magnetic behavior.
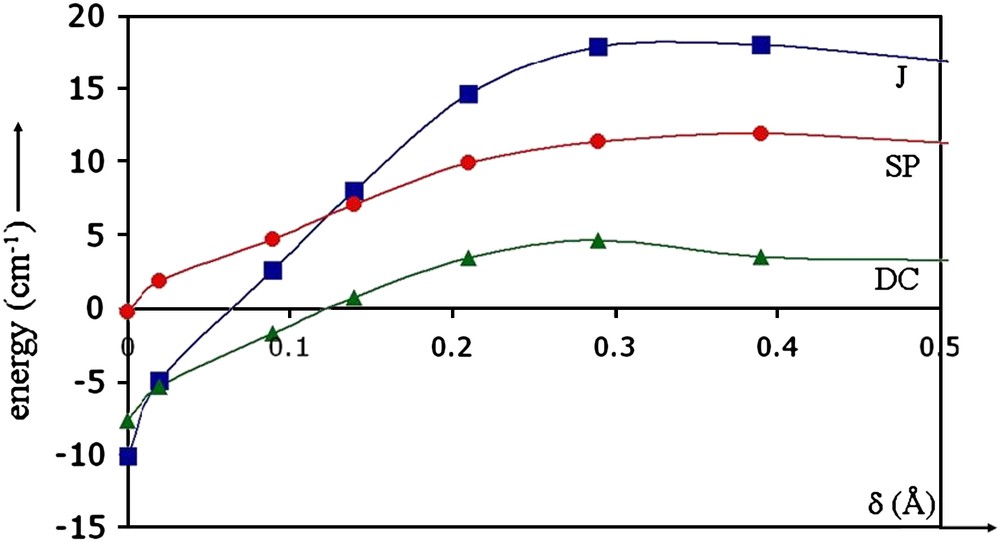
Calculated J, SP and DC energies (cm−1) in a series of hypothetical analogues of [Cu(N3L)]2 as a function of δ(A).
3.2 Open-shell ligands: noninnocence concept
Considering the possibility to generate high oxidation states ions (in iron chemistry, for instance, let us mention notable examples of Fe(IV) [107,108], Fe(V) [109–111] and Fe(VI) [112]), much synthetic effort has been devoted to the preparation of specific multidentate ligands. Upon electrochemical treatment, such partners are likely to undergo reversible redox reactions, leaving the metallic ion unchanged. Thus, the use of such ligands, known as noninnocent, has opened up the route to original synthetic materials, involving open shells on both metal and ligands partners (see some examples in Refs. [63,113–118]). The spectacular excited-state coordination chemistry concept in which a ligand coordinates in an excited electronic state to a metal center has emerged from this class of compounds [119]. The noninnocent term was suggested to emphasize the versatile character of this class of ligands which may not be considered as closed-shell entities. The generation of radical ligands in coordination compounds has emerged as a promising route to magnetic materials.
From the theoretical point of view, DFT as well as CI calculations have been undertaken to scrutinize the electronic structures of such noninnocent ligand-based systems [63,116,117,119,120]. In particular, the comparison between experimental and calculated exchange coupling constants and the analysis of the magnetic interactions has been the subject of intense work. While DFT has sometimes failed to fully account for the low-energy spectroscopy, the wavefunction based DDCI method has elucidated the unusual behavior of several complexes [63,119]. Among those, a striking example is given by the Fe(gma)CN complex containing the glyoxalbis(mercaptoanil) (gma) ligand (see Fig. 7) [32]. Even though the noninnocent character of the gma ligand was clearly demonstrated both experimentally and theoretically, DFT calculations were only partially successful in the description of the electronic structure of the full complex [119]. The magnetic susceptibility and zero-field Mössbauer measurements clearly favored a doublet ground state. Nevertheless, DFT calculations did not provide any clear evidence in that sense, the Ms = 1/2 solution exhibiting a low-spin Fe(III) (SFe = 1/2) coupled to a closed-shell gma ligand (Sgma = 0). Clearly, for a good description of the electronic structure of such a system, DFT and its monodeterminantal character is not appropriate and correlated ab initio calculations might be desirable.
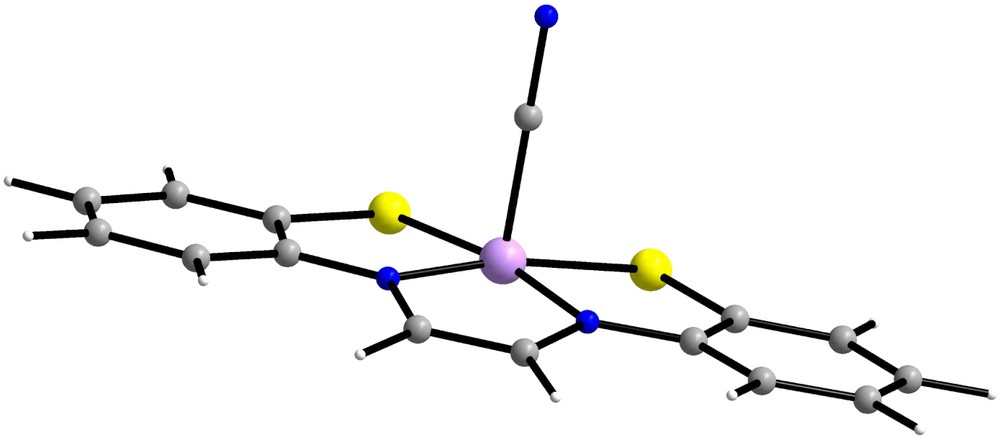
Structure of Fe(gma)CN.
Based on this statement, Messaoudi et al. performed correlated ab initio calculations on this particular system by means of DDCI-2 calculations on the top of the CAS(5,5)SCF wavefunction [32]. Interestingly, the active orbitals consist of three metal-centered and two ligand-centered MOs (see Fig. 8). This active space was strongly supported by experimental and calculated Mössbauer parameters [119]. The calculations showed that the low-energy spectrum exhibits a 200-cm−1 quartet-doublet gap, in agreement with different experiments and that the observed strong antiferromagnetic behavior is due to important ligand-to-metal charge transfer (LMCT). The resulting ground-state wavefunction which exhibits an intermediate magnetic/covalent character, is rather strongly correlated and is dominated by local (SFe = 3/2 and Sgma = 1) electronic configuration. Finally, whereas the gma ligand is clearly a closed-shell singlet when considered alone, it is likely to be a triplet when coordinated to the iron center. The multiconfigurational nature of the wavefunction has been identified in this example and makes this class of compounds still very challenging for theoreticians. For instance, it has been recently suggested that the energetics of low-lying states of coordination complexes based on porphyrins and related entities may not be accessible by means of DFT methodology (see Ref. [33] and references therein). More troublesome is the dependency of the spin density maps upon the functional choice.
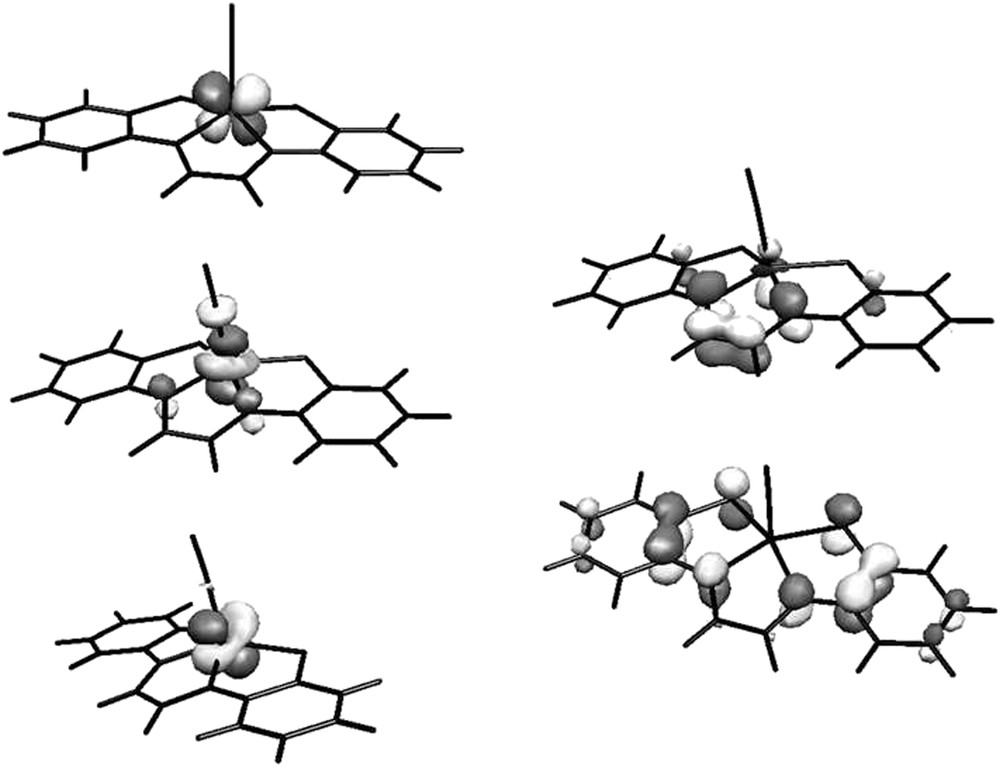
Optmized active average MOs for the lowest doublet and quartet states of Fe(gma)CN.
3.3 Trinuclear Cu(II) complexes: prototypes of oxidases
In this section, one deals with the important concept of spin frustration or more precisely with the possible deviation to the ideal spin frustrated character observed in trinuclear copper clusters. This concept was first introduced in 1977 in relation with the phenomenon of spin glass behavior [121]. Since this pioneering work, this concept has been widely applied in solid-state physics [122,123] and appeared more recently in the molecular magnetic community [10,17,124]. Exchange coupled trinuclear Cu(II) clusters have been the focus of tremendous attention for many years due to the richness of their implications in catalysis, magnetism and biology. These systems play a major role in the catalytic O2 reduction involving multicopper oxidases, the so-called “native-intermediates” [125–128]. Apart from the biological significance, this particular type of architectures has been reported in the literature as good prototypes for the evaluation of the relevance of magnetic exchange models [17]. The majority of the reported trinuclear Cu(II) complexes have either a linear arrangement of the metal centers [129–133] or a Cu3(μ3-X) unit (X = Cl, OR) (for numerous examples, see Refs. [134–148]). In its triangular arrangement, such metal complexes are of special interest in the understanding of geometrically frustrated antiferromagnetic compounds (Fig. 9).
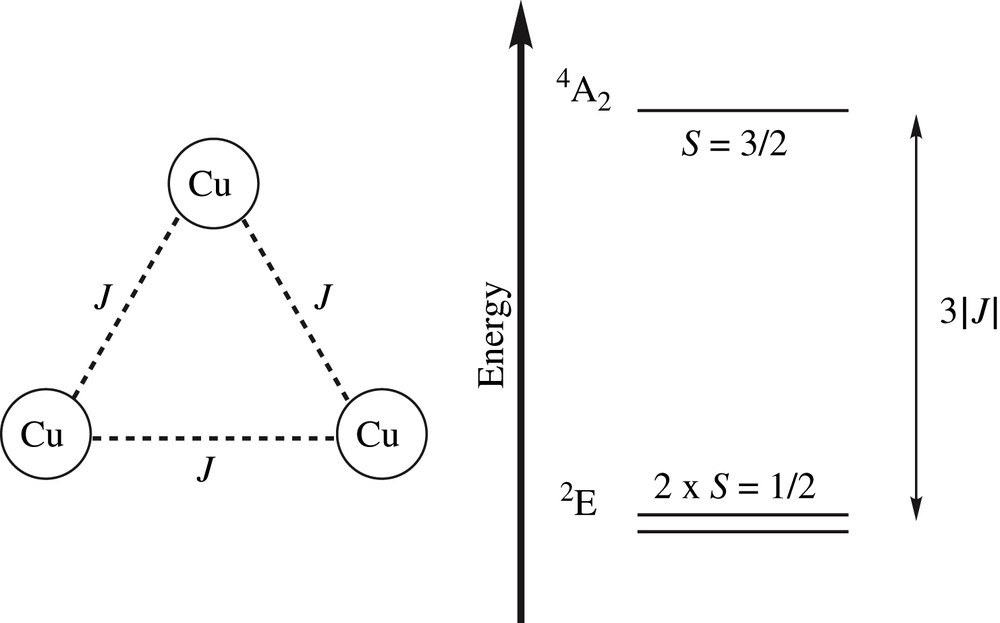
Energy diagram of an antiferromagnetically coupled Cu(II) trimer.
Each one of the three spins S = 1/2 can interact with the adjacent ones. Two Cu(II) atoms couple to form intermediate spins S′ = 1 and 0 which couple to the third one to give Stot = 1/2, 3/2 and 1/2. In perfect D3/C3 symmetric trimers, the non-interacting doublet states are energetically degenerate with the quartet state lying 3|J| (Heisenberg Hamiltonian ) higher in energy. The degeneracy in the ground state is known as spin frustration since, despite all pairwise spin interactions being antiferromagnetic, each spin configuration includes a pair of parallel spins. When the triangular architecture moves away from a threefold symmetry as a result of possible vibronic interactions, the energetic situation may vary drastically. Theoretical analyses based on either DFT or post-HF ab initio calculations have been tentatively used to propose a detailed description of their electronic structures and to rationalize the physical origins of their magnetic and spectroscopic features. A combined quantum and molecular mechanical (QM/MM) study has also been undertaken to analyze the O2 reductive cleavage in the catalytic cycle of multicopper oxidase [149]. Whereas DFT combined with the BS approach [19–21] has been successfully applied to the calculation of magnetic exchange interactions of binuclear systems (see for instance Refs. [89,101,150,151]), only few are devoted to trinuclear transition metal complexes [15,130,133,152–155]. The scarcity of theoretical studies based on monodeterminantal approaches might be explained by the known deficiencies of such methods in the treatment of spin states with a multireference character. To elude these limitations, correlated multireference approaches may be used. The first example of such calculations was proposed by Chalupsky and coworkers with a thorough analyses of spectroscopic parameters based on CASPT2 and multireference difference dedicated CI (MRDDCI2) [57] calculations for a series of (μ3-hydroxo)- and (μ3-oxo)-bridged trinuclear Cu(II) models [156].
In most of these studies, the structures are close to a perfect C3 symmetry. However, some coworkers have recently synthesized and characterized a Cu3 cluster exhibiting an arrangement of the Cu ions deviating from this point group (see Fig. 10) [157]. The most important distortion concerns the long Cu–O apical distances (Cu1–O1, Cu2–O2, Cu3–O3), one differing significantly from the other two (2.52 vs. 2.35 and 2.40 Å). To account for the deviation from a perfect C3 symmetry, the introduction of 2 or 3 constants in the fit of the experimental thermal behavior of the magnetic susceptibility led to several sets of parameters whose underlying physics had to be clarified. CASSCF/DDCI calculations were performed in order to investigate (i) the influence of the ML5 structural variations on the quartet–doublet spectrum, (ii) the role of the copper solvated hydroxy group linked to the three Cu(II) ions. This theoretical framework had already shown to provide accurate results for magnetic multicopper compounds [62]. A first approach, which was considered as “naive”, consisted in a dimer description of the Cu3 cluster involving three magnetic exchange coupling constants.1 Even though the antiferromagnetic character was conserved, such a set of parameters failed to accurately reproduce the experimental data (see the red curve in Fig. 11 (for interpretation of the references to color in this text, the reader is referred to the web version of this article)). This drawback was ascribed to the prime role played by the central oxygen atom O4.

Experimental and simulated cXMT vs. T curves.
Therefore, CAS(3,3)SCF/DDCI calculations were carried out on the whole Cu3 unit extracted from the experimental crystal structure. It is noteworthy that in this system the deviation from orthogonality between the magnetic orbitals (see Fig. 12) is rather small (∼10°). Therefore, ferromagnetic interactions might be anticipated. Indeed, this ferromagnetic behavior survived up to a DDCI-2 level of calculation. However, DDCI-3 calculations were likely to stabilize one of the doublet, splitting the speculated degeneracy of the doublet states by ∼8 cm−1. Such low-energy spectrum description allows one to recover the experimentally observed antiferromagnetic behavior.
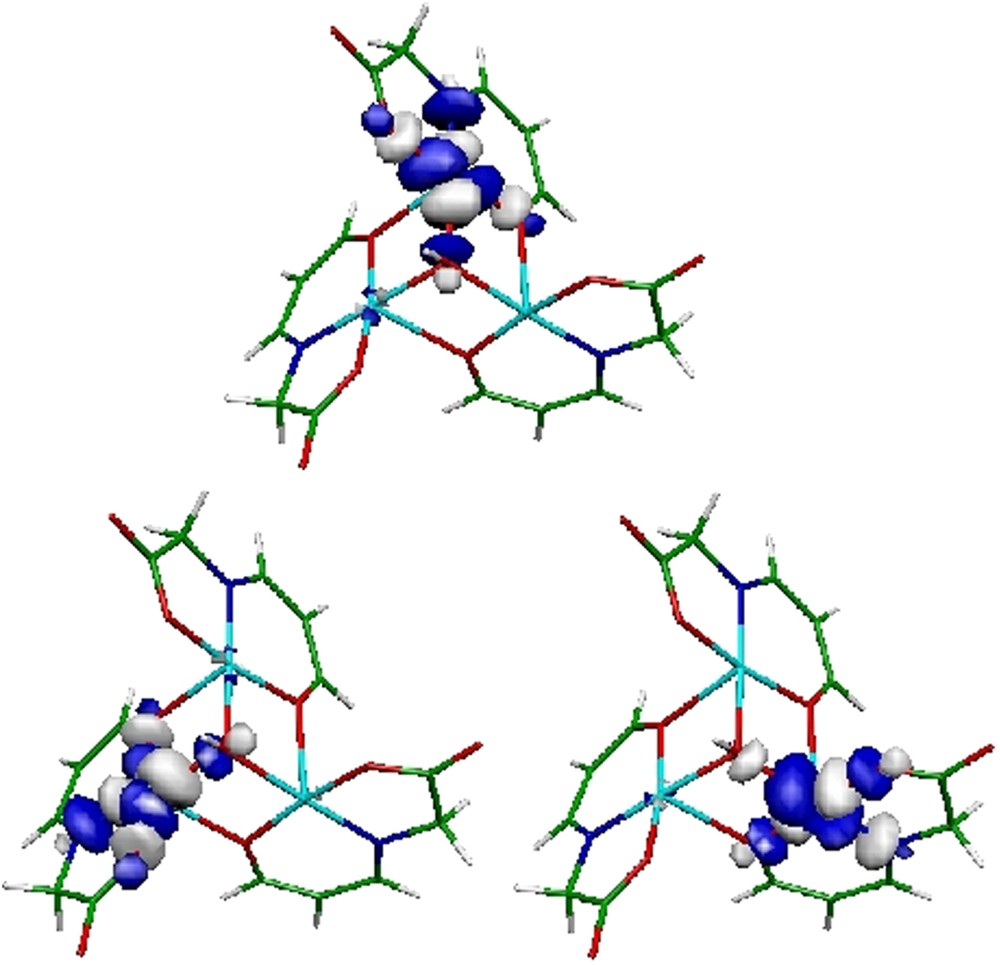
Magnetic orbitals of the [Cu3(L)3(μ3-OH)]− complex.
These calculations concluded on a picture favoring a doublet and quasi-degenerate quartet ground state with the second doublet lying slightly higher in energy (see Fig. 13). This example illustrates the necessity for a high enough level of calculations to reproduce quantitatively such tiny energy differences and to account for the experimentally observed magnetic behavior.
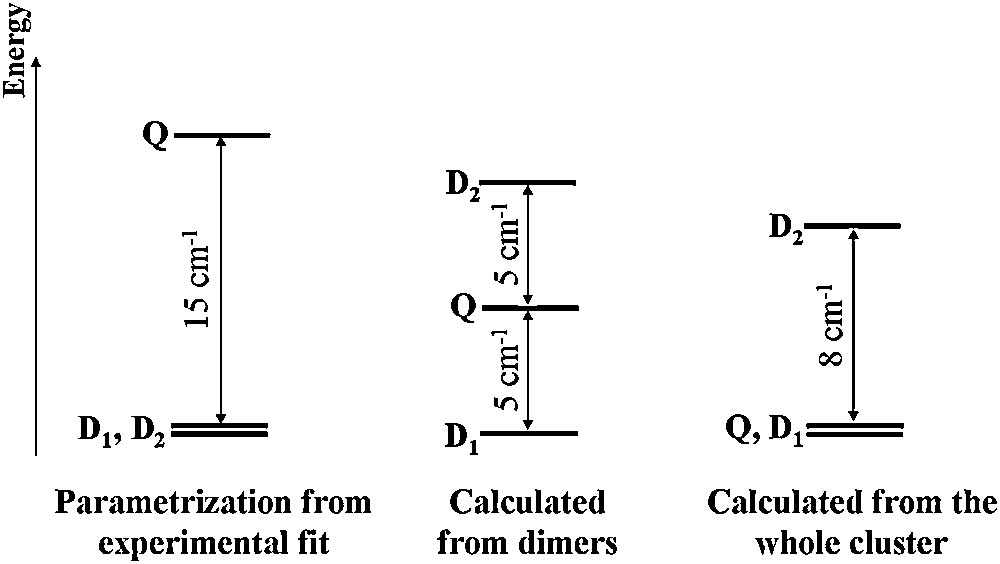
Q, D1, D2 energy spectrum with respect to the model approaches described in the text.
3.4 Growing 1D materials: Ni-azido chains
With the generation of magnetic properties goal in mind, experimentalists have prepared higher dimensionality materials. One of the main challenges in the synthesis of extended 1D systems is to prevent the local magnetic moments from canceling out. Obviously, this condition is fulfilled as soon as ferromagnetic interactions dominate. However, in the presence of most frequent antiferromagnetic interactions, pioneering approaches were devoted to regular heterospin ferrimagnetic chains [10] holding alternating spin carriers, coupled through a unique exchange constant. Another strategy consists in varying the magnetic exchange constants between homospin carriers [158,159]. Finally, the use of strong anisotropic metal ions to reduce the magnetization relaxation has generated the promising field of the SCM [11–13].
In this respect, the azido ligand turned out to be extremely appealing in linking metal ions and a remarkable magnetic coupler for propagating interactions between paramagnetic ions. The structural variety of the azido complexes ranges from molecular clusters to extended 1D to 3D materials [77,160–164]. An interesting prototype of such a system has been recently synthesized where a single azido unit bridges in an alternating End-On (EO) and End-to-End (EE) way the Ni(II) ions (see Fig. 14) [165]. The system can be considered from the chemical point of view as a quasi-1D chain. However, based on magnetic susceptibility measurements, it was suggested that the system should be described from the magnetic point of view as isolated dimers. Indeed, the introduction of a second magnetic interaction was shown to be irrelevant. Therefore, the question of the nature and amplitude of the magnetic interactions between the nearest Ni(II) ions deserved special attention. The alternation of EO and EE units strongly suggested the presence of two magnetic exchange pathways which can be accessible through Ni2 dimers' spectroscopy analysis. Thus, CAS(5,6)SCF/DDCI-2 calculations were performed on the molecular EE and EO fragments extracted from the available crystal structure. Let us mention that the geometries of these clusters were not relaxed. The active orbitals consist of the in-phase and out-of-phase linear combinations of the and metallic AOs (see Fig. 15) and the non-bonding MO of the N3− bridge.

Nickel(II) chain {Ni2 (μ1,1-N3)(μ1,3-N3)(L)2(MeOH)2]}n with alternating End-On/End-to-End single azido-bridges.
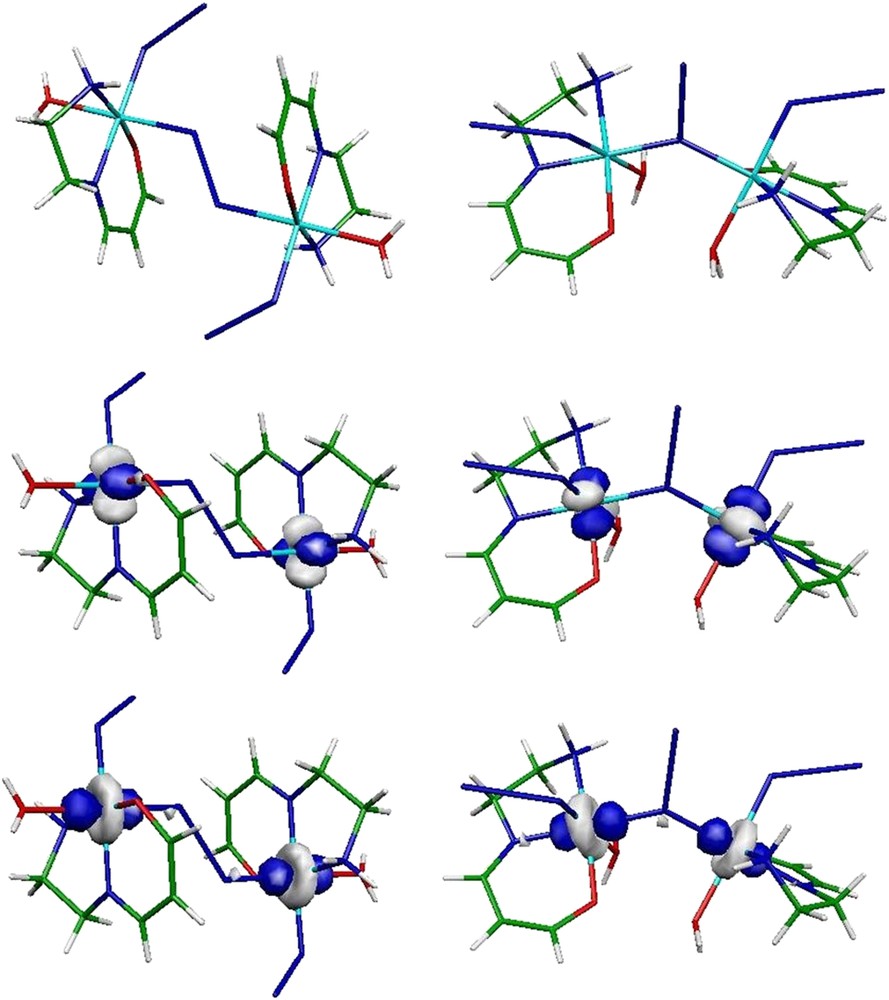
Molecular EE (left) and EO (right) fragments and in-phase active metallic MOs. For the sake of simplicity, the out-of-phase combinations are not shown.
Since the Ni(II) ion is formally d8, it is expected that exchange interactions between S = 1 ions should give rise to three spin states in the Ni2 units, namely singlet (S), triplet (T) and quintet (Q) states. In a Heisenberg picture (S1 = S2 = 1), the energy separations are 6|J| and 4|J| between the quintet and singlet, quintet and triplet states, respectively (see Fig. 16). Within the EE unit, a relatively large antiferromagnetic exchange constant (JEE ∼ −50 cm−1) was calculated in relatively good agreement with the unique value extracted from experiment (∼−40 cm−1). This is to be contrasted with the EO Ni2 unit, which exhibits a negligibly small magnetic interaction (a = JEO/|JEE| ratio ∼0.02) (see Fig. 17).
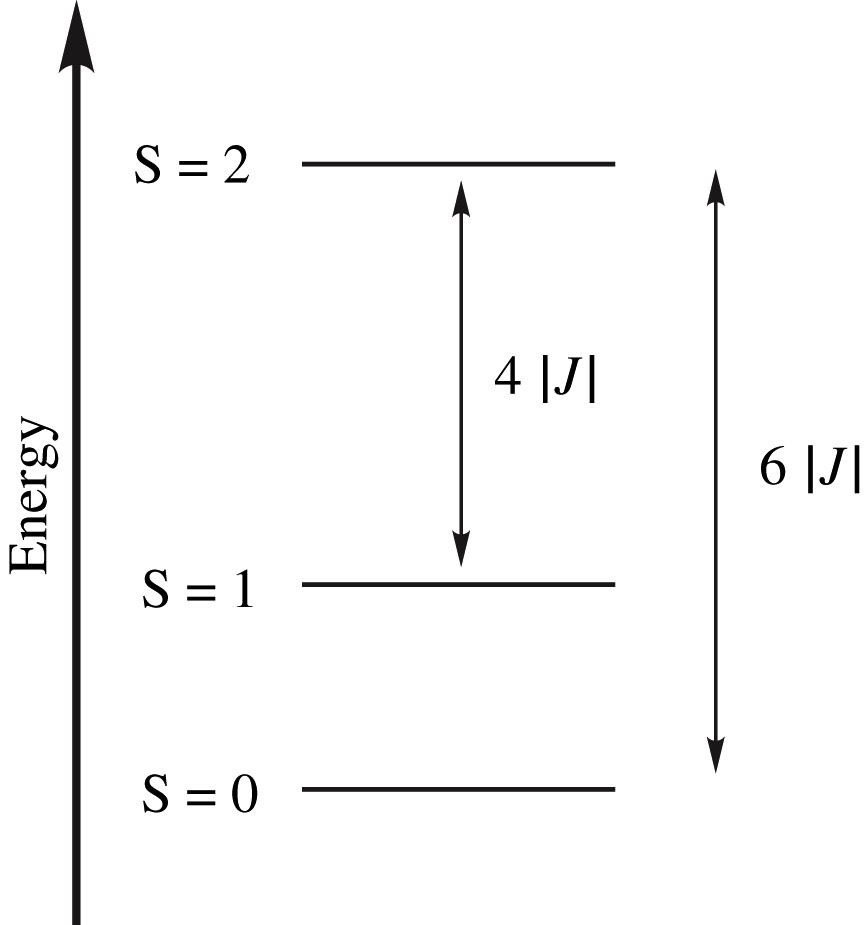
Energy spectrum of a two-center Heisenberg S = 1 Hamiltonian.

Schematic representation of the Ni-azido chain resulting from the isolated EE dimers' picture.
The calculations not only confirmed the isolated dimers picture, but also associated the leading antiferromagnetic exchange pathway with the EE bridging mode. In the light of the calculated (EQ − ES)/(EQ − ET) ratio, let us mention that the deviation from a pure Heisenberg picture is negligible (less than 2%), ruling out the speculated participation of quadratic terms. The attempt to generate high enough ferromagnetic interactions between S = 1 sites looked very promising, since the antiferromagnetic coupling between the resulting S = 2 units through EE bridges might have resulted in a Haldane chain with vanishingly small spin gap [166,167]. The versatility of the azido magnetic coupler should still be considered to generate synthetic models for theoretical physics analysis.
3.5 3D spincrossover materials: the CsFe[CrCN6] Prussian blue analogue
Whereas the previous sections were devoted to 0D and 1D systems, here we concentrate on 3D covalent materials. Prussian blue analogues (PBA) have been widely studied in the field of magnetic systems [168,169]. Currently, the interest for these compounds is motivated by two reasons. Firstly, the representatives of this family which contain vanadium and chromium cations behave as high-temperature magnets [170–172]. Secondly, some PBA display temperature- and photo-induced magnetic phase transitions [169,173,174]. These transitions usually result from temperature- or optically driven electron transfer between two metal ions in the lattice. The change of the oxidation states leads to changes of the metal ions' spin states, thus inducing or modifying the magnetic coupling between them. To date, only few theoretical studies have been devoted to the electronic structure and magnetic behavior of PBA. This can be ascribed to the lack of accurate crystal data, since these materials exhibit different defects types, namely metal ion vacancies, counterion crystallographic disorder, and presence of water molecules in the lattice.
The first theoretical studies, based on extended Hückel calculations on dinuclear models, have been proposed by Verdaguer et al, who attributed the exchange interactions between the metal ion centers to the overlap between the magnetic orbitals through the π system [168,175]. Periodic calculations, based on both HF and DFT methodologies, on idealized structures were performed to clarify the magnetic interactions between different divalent/trivalent ion pairs [176–179]. Multireference and DFT-based cluster calculations were also carried out to examine the exchange interactions [180–183], the metal-to-metal charge transfers [184] and the possibility to generate high Curie temperature materials [185].
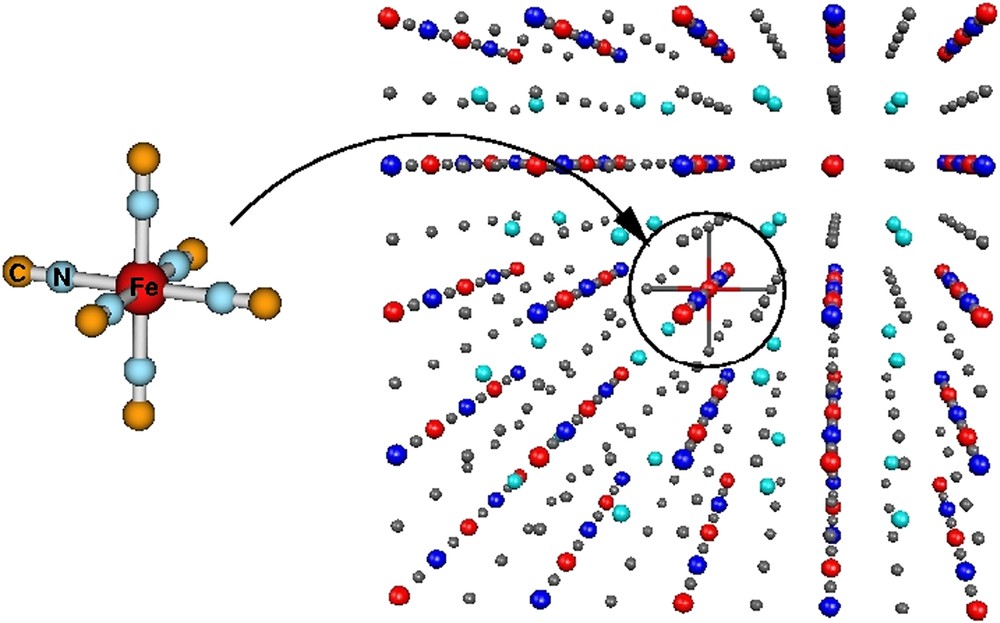
The interest for the recently synthesized and characterized CsFe[CrCN6] PBA has emerged from the spin transition which has been observed on the Fe(II) center (see Fig. 18) [186]. In this compound, the thermal spin transition results from the crossover of the high-spin (HS) and low-spin (LS) states of the Fe(II) ions without any intervalence electron transfer in the lattice. Surprisingly, from theoretical calculations, the [Fe(NC)6]4− unit is known to be HS as a result of the low ligand field generated by the octahedral arrangement of the NC− ions [187]. Thus, the stabilization of the HS state over the LS state apparently rules out the possibility of spincrossover phenomenon. One may wonder how much the environment produced by the rest of the crystal is likely to change this state of affairs. Consequently, using the smallest transiting core [Fe(NC)6]4−, the relative importance of the local ligand field and Madelung field generated by the rest of the crystal was estimated.

Spin transiting CsFe[Cr(CN)6] system. Fe, Cr, C and N atoms are shown in grey, green, blue and orange, respectively. Cs ions are omitted. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
With this goal in mind, CAS(6,5)SCF (Fe(II) ion being formally d6) and subsequently second-order perturbation-theory CASPT2 calculations were performed (i) in the absence of any environment (so-called gas-phase), and (ii) in the presence of various Madelung fields accounting for the PBA matrix effects (see Fig. 19) [188]. From the low-temperature (100 K) and high-temperature (265 K) crystal data available in the literature [189], a standard 0.15-Å lengthening of the Fe–N distances was observed. Using the corresponding Fe(II) geometries for the [Fe(NC)6]4− cluster, the non-Franck–Condon gas-phase spectroscopy based on CASPT2 calculations showed that the HS state is lower than the LS state by ∼16,700 cm−1 (see Fig. 20). Interestingly, unrestricted HF periodic calculations performed on the 100 and 265 K crystal structures revealed a significant charge reorganization on the Fe center (1.65 → 2.15), whereas the Cr ion Mulliken charges remain almost unchanged (1.85 → 1.90). This is to be contrasted with the picture based on formal charges (+2, +3 on Fe and Cr, respectively) which holds for both spin states. Including the Madelung field effect, it was shown from these CASPT2 calculations that the Franck–Condon spectroscopy of a d6 ion immersed in a frozen charge matrix is consistent with the Tanabe–Sugano diagram for an isolated complex, leaving the HS state lower than the LS state by ∼17,000 cm−1 (see Fig. 20). Nevertheless, as the environment charges are varied following the periodic calculation results, the situation is greatly modified. As a matter of fact, the LS state immersed in a LS environment is stabilized by ∼12,500 cm−1 over the HS state in a HS field (see Fig. 20).
Gas-phase (left) and immersed in a Madelung field (right) [Fe(NC)6]4− model for the LS and HS energies' determination.
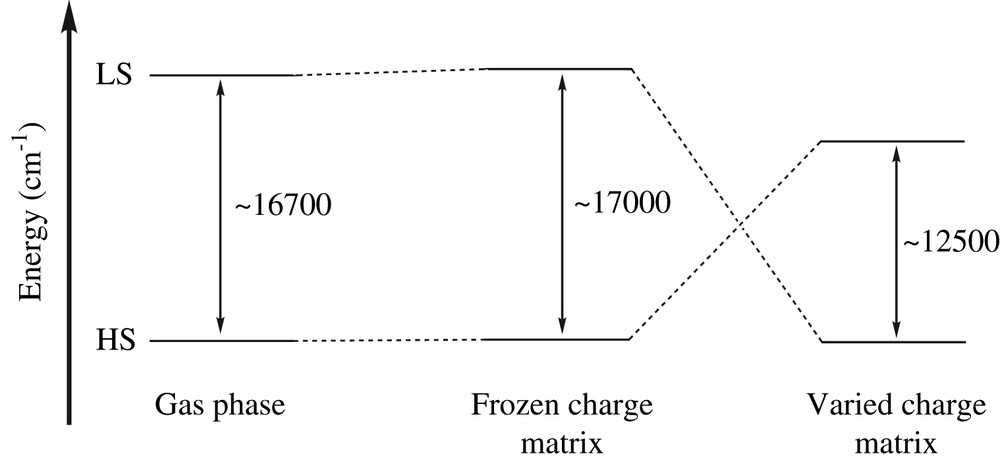
Non-Franck–Condon spectroscopy in the gas-phase (left), in the presence of a frozen charge environment (middle) and in a matrix accounting for the charge reorganization (right).
CASPT2 quantum chemical calculations have thus demonstrated that the crystal matrix of the CsFe[Cr(CN)6] compound creates conditions for spin transition of the Fe(II) ion, a phenomenon which does not exist for an isolated [Fe(NC)6]4− complex. The apparent competition between the ligand field and the fluctuating Madelung environment in the FeII(NC)6 complex seems to govern the spin crossover phenomenon. While the former effects are short range, the latter are representative of long-range contributions which are crucial for cooperativity manifestation.
4 Concluding remarks
In conclusion, quantum chemical calculations have become valuable means of investigation which cannot be ignored. As spectroscopy accuracy can be reached down to several tens of wavenumbers, ab initio techniques have the ability to rationalize interactions in magnetic systems. Interestingly, the different contributions to energy splitting are accessible and the underlying physical phenomena can be interpreted in terms of kinetic exchange, instantaneous charge fluctuations, spin polarization and dynamical correlation effects. The information which is conveyed by the wavefunction is crucial in the characterization of model Hamiltonians. Undoubtedly, significant efforts must be devoted to extract the relevant parameters in a “boil down” procedure of the ab initio information. Even though certain CI methodologies might be very demanding when dealing with large systems, they allow one to manipulate symmetry and spin-adapted eigenstates of the exact Hamiltonian. With this pursued goal in mind, unrestricted DFT-based calculations are also very valuable, since the size limitation is significantly displaced. Such methodology has opened up new routes to important issues involving biological systems. Nevertheless, some specific systems including open-shell compounds are the concern of explicitly correlated calculations which allow an efficient treatment of both non-dynamical and dynamical correlations.
Acknowledgments
VR is sincerely thankful to J.-P. Malrieu and N. Guihéry for extraordinary discussions on the many-body problem.



