1 Introduction
Cyclodextrins (CDs) (Fig. 1) are cyclic oligosaccharides obtained by the enzymatic degradation of starch. They are formed by the association of six, seven or eight units of glycopyranose linked by α (1, 4) connections and named respectively α, β and γ CD. They bear hydrophobic cavities capable of forming inclusion complexes with a variety of organic molecules. In particular, β-CD has an internal cavity shaped like a truncated cone about 8 Å deep and 6.0–6.4 Å in diameter and this cavity possesses a relatively low polarity [1–3].

Top view of (a) Glycopyranose unit. (b). β Cyclodextrin. (c) N-(2-choloroethyl) N-nitroso N’-sulfamide piperidine.
These inclusion complexes do not contain any covalent bond between host and guest molecules and their stability depends on molecular size and shape complementation but also on the external medium and environmental conditions. The most important driving forces in the inclusion complexes are electrostatic, van der Waals, hydrophobic interactions, hydrogen bonding, release of conformational strain, exclusion of cavity-bound energy water and charge transfer interaction [4,5].
This property of CDs to form inclusion complexes became the subject of intense theoretical studies using molecular mechanics, molecular dynamics and quantum mechanical methods because the combination of experiment and theory leads to successful results in solving structural, energetic and dynamic problems [6–44].
N-nitroso-N’-(2-chloroethyl)-N’-sulfamide piperidine (CENS) (Fig. 1) constitutes a new compound exhibiting an antitumoral activity and which is capable to replace chloroethylnitrosourea (CENU) [45–52]. Recently, it was shown that CENS have some instability and low solubility in water. These properties are clearly enhanced by the formation of inclusion complexes with β-CD [53,54].
It has been shown [53,54] that in the mass spectrum of CENS, the molecular peak (M) does not appear and that the base peak at 192 corresponds to [(MNO)]+. However, the mass spectrum of the corresponding complex β-CD – CENS revealed unexpectedly that this peak does not appear, which means probably that the NO group is protected inside the β-CD cavity.
Such inclusion complexes implying CDs have been studied in the case of other molecules than CENS such diclofenac [29], acetphenone [33], miconazol [23], 4, 4, benzidine [16], 4, 4, toludine [16], N-phenylphtalamide [39], N-adamantyl phtalamide [39], 1, 2, 4, oxadiazole derivative [19], methylated benzoic acids [42], diphenyl (4-phenyl) phosphine [43], alkylated phenols [21], bromobenzensulfonamide [9], halogenobenzoic acid [37], catechin [26], epicatechin [26], quercetin [25,30], tagitinin C, spironolactone [7], miconazole [28], 4-fluorophenol [38]. To our knowledge, the complexation of β-CD with CENS has not yet been studied theoretically. In this paper, we present a theoretical study on the inclusion complex between CENS and β-CD using current DFT techniques with an aim to determine its geometry and the conformational changes of CENS inside the β-CD cavity. More particularly, we shall focus our attention on the position of the NO group in the complex and the role of H-bonding in the stability of this system.
2 Computational details
All calculations were carried out using the Gaussian 03 quantum mechanical package [54].
The initial structures of β-CD and CENS molecules were built with the help of Chemoffice 3D ultra (version 6, Cambridge software) [56]. The structures of β-CD and CENS are shown on Fig. 1.
The coordinate system used to define the process of complexation is shown on Fig. 2.

The relative position between CENS and β-CD. Head orientation. (b) Tail orientation.
We followed the method described by Liu and al. to locate the lowest energy minimum of the CENS-β-CD inclusion complex [32]. Thus, the glycosidic oxygen atoms of β-CD were placed onto the YZ plane, the centre of β-CD being defined as the centre of the coordinate system. Bond 1-2 of CENS is coincident with the X-axis and the relative position between β-CD and CENS is measured by the X coordinate of sulphur atom of CENS. For the complexation process, the host β-CD was kept in this position while the guest approaches along the X-axis toward the wide rim of the β-CD torus. The following nomenclature will be used. For simplicity, when the piperidine cycle is inserted first into β-CD, we call this the ‘head orientation’ and when the sulfamide group is introducing first this orientation is called ‘tail orientation’.
CENS was initially located at a X-coordinate equal to 7 Å and was moved into the β-CD cavity along the X-axis to – 6 Å with a 1 Å step. The generated structures at each step were optimized, allowing them to change from the initial conformations keeping the displacement of the sulphur atom and the cyclodextrin structure totally restricted. In order to find an even more stable structure of the complex, each CENS molecule was rotated around bond 1-2 of CENS coinciding with the X-axis, by 20° from 0° to 360°. Once the preliminary energy minima were determined for each X-coordinate, the system was re-optimized removing restraint on β CD and sulphur atom. PM3 semi-empirical method [57] was firstly used to study the complexation process as describe above. Then, DFT calculations have been carried out at the B3LYP/6-31G(d) and MPW1PW91/6-31G(d) levels [58–61]. We used this latter functional which is a modified Perdew–Wang one [61] because it is well suited for non bonded interactions and transition state studies and leads to results which are as reliable as B3LYP's regarding the ground state properties.
In order to investigate the driving forces leading to the actual complex between CENS and β-CD, we made use of complexation and deformation energies, defined as follows (Eqs. (1)– (3):
| (1) |
The more negative complexation energy gives the more thermodynamically favorable inclusion complex. The deformation energy of the guest or the host molecule can be obtained by Eqs. (2) and (3):
| (2) |
| (3) |
Finally, charge transfers between host and guest molecules have been studied using both Mulliken and natural bond orbital (NBO) population analyses. Moreover, in the NBO approach [22], a stabilization energy E(2) related to the delocalization trend of electrons from donor to acceptor orbitals is calculated via perturbation theory. A large stabilization energy E(2) between a lone pair LP(Y) of an atom Y, and an antibonding σ* (XH) orbital, is generally indicative of a XH … Y hydrogen bond.
3 Results and discussion
3.1 The search of the energy minimum
As given by the semi-empirical PM3 method, the inclusion processes produce two different complexation energy curves (Fig. 3). The energy minimum for the tail orientation is located quite precisely around X = 2 Å whereas for the head orientation we obtain almost a flat energy minimum between −2 Å to + 2 Å.
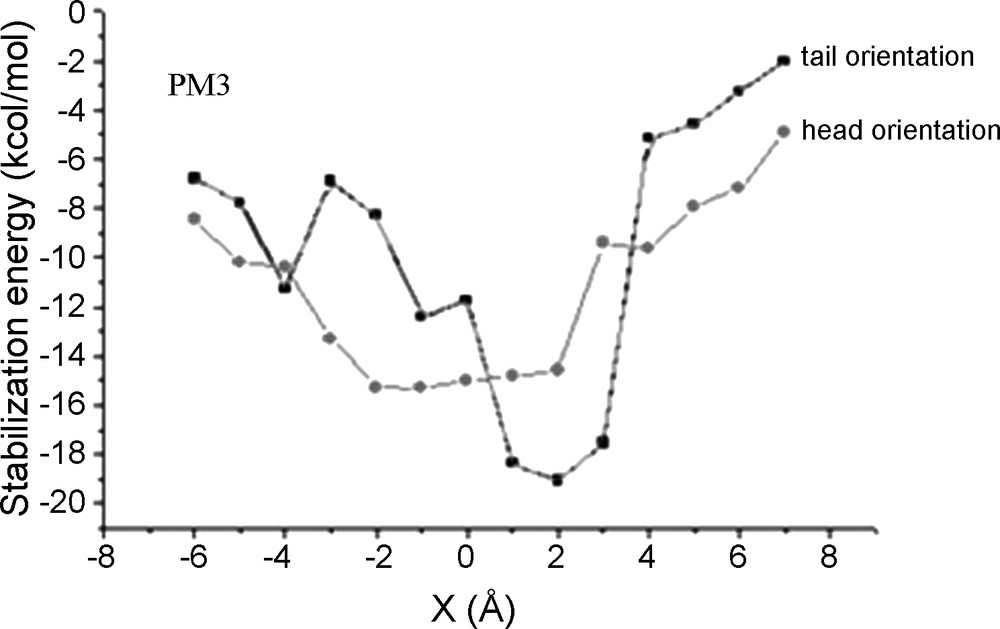
PM3 stabilization (complexation) energy of the inclusion complex (CENS-β-CD).
Starting from the structures obtained with PM3 at minimum energy, we carried out B3LYP and MPW1PW91 full geometry optimizations using first the 6-31G(d) basis set then the more extended 6-31 + G(d,p) one which includes diffuse orbitals on heavy atoms. We remind that the latter functional is supposed to give a better description of long distance interactions than B3LYP [61]. We found that B3LYP and MPW1PW91 gave almost identical optimized geometries (given in the supplementary material). The following table (Table 1) shows the complexation and the deformation energies of the inclusion complexes obtained for the head or tail orientations.
Energies (kcal/mol) and dipole moments μ (Debye).
| B3LYP/6-31G(d) | MPW1PW91/6-31G(d) | |||||
| Orientation | Head | Tail | Difference | Head | Tail | Difference |
| Ecomplexation | −2.2 | −8.1 | 5.9 | −1.4 | −7.3 | 5.9 |
| Edeformation [CENS] | 1.0 | 1.7 | −0.7 | 0.9 | 1.7 | −0.8 |
| Edeformation [β-CD] | 9.7 | 2.7 | 7.0 | 7.4 | 2.3 | 5.1 |
| μ-complex | 5.3 | 3.3 | 2.0 | 5.3 | 3.1 | 2.2 |
| μ-CENS | 4.9 | 4.8 | ||||
| μ-β−cd | 4.7 | 4.9 |
The complexation energies reported in Table 1 show that the tail orientation leads to the more stable inclusion complex, the energy difference between the two inclusion complexes being equal to 5.9 kcal/ mol (B3LYP) and 5.8 kcal/mol (MPW1PW91).
The computed deformation energies given in Table 1 indicate that CENS needs only 1.7 kcal/mol to conformational adaptation inside the β-CD cavity for the tail orientation, and ca. 1 kcal/mol for the head orientation. On the contrary, the β-CD deformation energy is important in the case of the head orientation; this deformation of β-CD seems to be one of the driving factors leading to the favored tail inclusion complex. Indeed, the head mode of inclusion of CENS into β-CD is more energy demanding relatively to the tail orientation by an amount of 7.0 kcal/mol (B3LYP) and 5.2 kcal/mol (MPW1PW91).
3.2 Structure of the inclusion complexes
Fig. 4 shows the structures of CENS in the complex (in the tail and the head orientations) obtained with B3LYP (MPW1PW91 leads to similar results). In Fig. 5 are displayed the geometries of the two inclusion complexes. The conformation of CENS is significantly altered during complexation. Anti and syn conformations (between NO and SO2 groups) appear in the head and tail orientations respectively. We note that the anti-conformation of CENS in the tail orientation ensures a simultaneous penetration of the SO2 and NO groups and makes possible to form H-bonds with H6O groups.
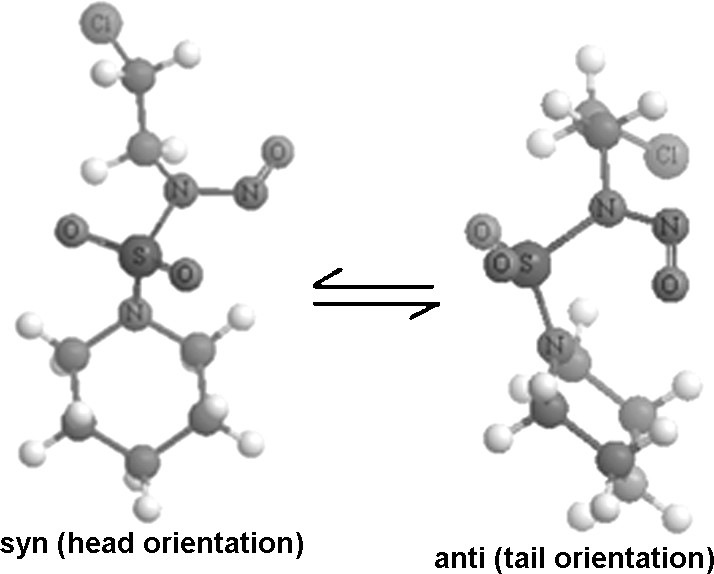
Anti and syn conformation of CENS.
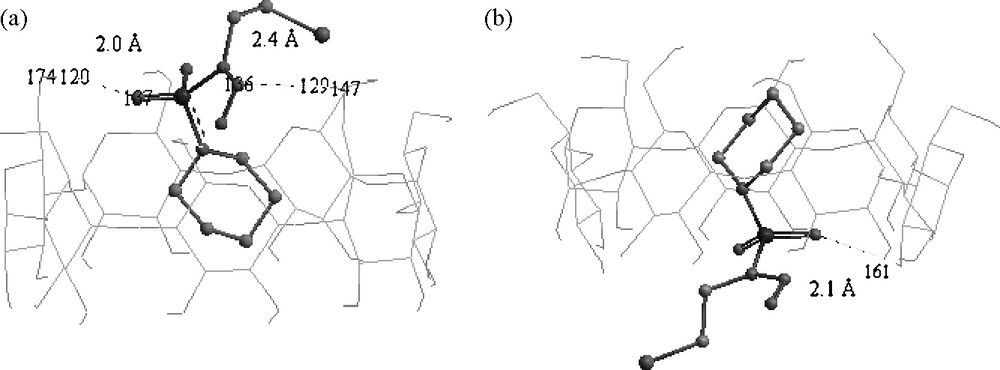
Structures of the B3LYP/6-31G(D) energy minima obtained for CENS-β-CD. (a) Tail orientation (b) Head orientation.
Fig. 5 shows clearly that the piperidine cycle is totally embedded inside the cyclodextrin cavity for the tail and head orientations, while the SO2 group remains on the rim of the β-CD and could form a H-bond with H6O (H120) positioned at 2.0 Å with an angle of 162.7° for the head orientation and with H2O (H161) located at 2.1 Å with an angle of 170.8° for the tail orientation. However, the CH2CH2Cl group remains completely outside the cyclodextrin cavity for the tail and head orientations.
An inspection of the geometry of the two orientations (Fig. 5) shows that the NO bond of CENS has two directions according to the conformation of CENS in the inclusion complex. Thus, in the head orientation, it is directed towards the outside of the cavity putting the nitrogen and oxygen atoms at distances higher than 4 Å from H2O/H3O; in such a case no hydrogen bond could be considered. On the other hand, for the tail orientation it is directed towards the inside of the cyclodextrin cavity. This allows the lone pair of the nitrogen atom to work as an auxiliary H-bond acceptor thus stabilizing the complex with H6O (H129) positioned at ca. 2.4 Å and an angle equal to 173.0°. This H-bond is assisted by a second weak H-bond namely a CH⋯O one, which can play a significant role in the stability of inclusion complexes [26,55]. In our case, this bond is expected between the oxygen atom (O169) and H5C (H91) separated by 2.5 Å with a CH⋯O angle equal to 148.7°.
Comparing in β-CD and in the inclusion complex, the bond lengths of the involved OH bonds in hydrogen bonding, i.e. O147H129 and O174H120 we observe a small lengthening of the OH distance indicative of such an interaction (Fig. 6, Table 2).
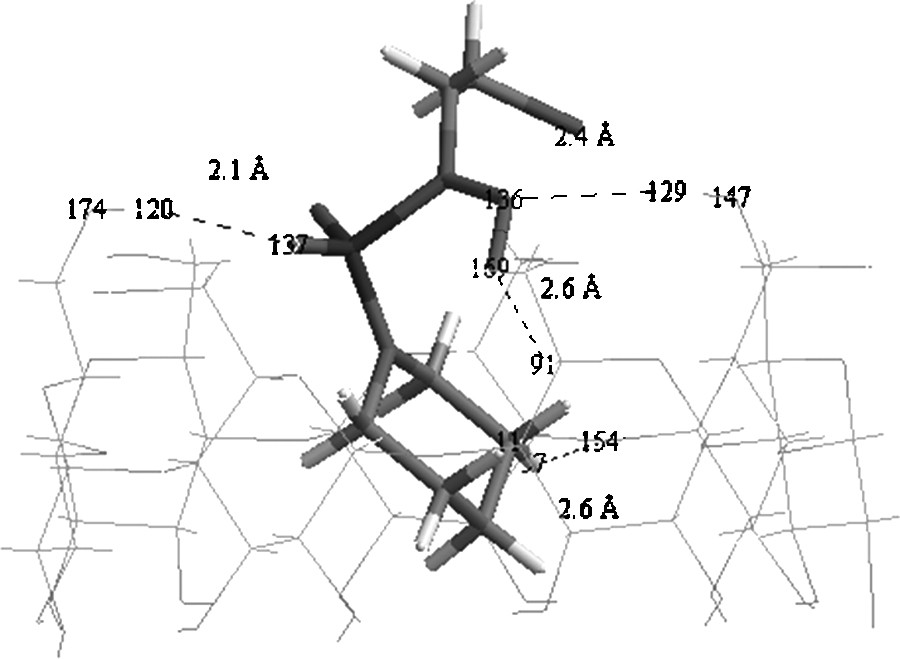
Conventional and weak hydrogen bonds in the inclusion complex (tail orientation).
Computed OH bond lengths (Å) in β-CD and in the inclusion complex (tail orientation).
| B3LYP | MPW1PW91 | |||||
| CD | Complex | Difference | CD | Complex | Difference | |
| O147H129 | 0.968 | 0.971 | 0.003 | 0.965 | 0.967 | 0.002 |
| O174H120 | 0.968 | 0.973 | 0.005 | 0.965 | 0.969 | 0.004 |
The small distances between the proton acceptor of CENS and β-CD hydrogen atoms H129 and H120 i.e. H120… O137 equal to 2.031 Å and H129… N136 equal to 2.365 Å give further evidence of such hydrogen bonds. We note also the rather short distance equal to 2.578 Å between O154 and H57 of the H57C11 bond and equal to 2.550 Å between O169 and H of H91C25 bond. The following population and NBO analyses will confirm the occurrence of these hydrogen bonds.
In order to investigate more accurately complexation energies and hydrogen bonding within the complexes under consideration, we made use of the more extended 6-31 + G(d,p) one. The MW1PW91/6-31 + G(d,p) geometry optimizations of β-CD, CENS and the two complexes that we carried out led us to almost the same optimized structures as those obtained at the MW1PW91/6-31G(d) level of calculation. MPW1PW91/6-31 + G(d,p) results are given in Tables 3 and 4. The MPW1PW91/6-31 + G(d,p) study entirely confirms that the head orientation is unfavourable relative to the tail one, the difference in complexation energy being equal to 6.1 kcal/mol (versus 5.9 kcal/mol when using MW1PW91/6-31G(d).
MPW1PW91/6-31 + G(d,p) energies (kcal/mol) and dipole moments μ (Debye).
| Orientation | Head | Tail | Difference |
| Ecomplexation | 1.2 | −4.9 | 6.1 |
| Edeformation [CENS] | 0.59 | 1.38 | −0.79 |
| Edeformation [β-CD] | 8.7 | 3.7 | 5.0 |
| μ-complex | 5.9 | 2.6 | 3.3 |
MPW1PW91 main E(2) hydrogen bonds interactions energies.
| CENS | β-Cyclodextrin | E(2) (kcal/mol) | |
| 6-31G(d) | 6-31 + G(d, p) | ||
| CENS proton acceptor and CD donor | |||
| LP (O 137) | σ*(H120O174) | 3.6 | 3.2 |
| LP (N 136) | σ*(H129O147) | 2.8 | 2.7 |
| LP (O 169) | σ* (C25H91) | 0.8 | 0.9 |
| CD proton acceptor and CENS donor | |||
| LP (1) O154 | σ* (C11H57) | 1.2 | 1.2 |
3.3 Hydrogen bonding and population analysis
In the NBO analysis of XH…Y hydrogen bonded systems, the interaction between the LP(Y) lone pair of the proton acceptor and σ* (XH) anti-bond of proton donor is characterized by a significant E(2) stabilization energy. The latter values are given in Table 4 in the case of the tail inclusion complex.
Indeed, as it can be seen significant interaction energies are obtained for the expected hydrogen bonds, especially the O174H120… O137 one. These hydrogen bonds are also highlighted by the NBO populations of the proton acceptors; the O137 lone pair bears an electronic charge equal to 1.787 (instead of 2) and LP(N136) a charge of 1.944, indicating the expected electron transfers.
As it was expected the interaction energies of the C25H91… O169 and C11H57… O154 hydrogen bonds are small, respectively 0.8 and 1.2 kcal/mol; these values are typical of weak hydrogen bonds for which energies vary between 0.5 and 2 kcal/mol [9].
Despite its well-known limitations, Mulliken Population Analysis (MPA) may indicate roughly the major charge transfers occurring in a molecule. In our case, charge transfers due to hydrogen bonding could be evidenced by MPA, since the gross atomic populations of the proton acceptors of CENS should decrease when passing from isolated CENS to the complex. Indeed we find, for instance in the case of B3LYP/6-31G(d) calculations, that the negative MPA charge of O136 atom decreased from −0.343 (in CENS) to −0.328 in the inclusion complex whereas the value of the positive charge of N136 atom increased from 0.177 (in CENS) to 0.198 in the inclusion complex (tail orientation).
Finally, it seemed interesting to compare the value and the direction of the dipole moments of the complexes to those of isolated β-CD and CENS. Computed μ-complex values using the 6-31G(d) basis set (Table 1) are 3.3 D (B3LYP) and 3.2 D (MPW1PW91) in the tail orientation and 5.3 D (B3LYP or MPW1PW91) in the head orientation. The dipole moment of β-CD is directed from the narrow rim towards the wider rim and is equal to 4.7 D (B3LYP) and 4.9 D (MPW1PW91) whereas the dipole moment of CENS is directed towards the sulfamide group and has a value of 4.9 D (B3LYP) and 4.8 D (MPW1PW91). We note that the dipole moments of CENS and β-CD are almost of the same magnitude. Contrarily to the head orientation, the tail inclusion of CENS leads to an anti-parallel orientation of the dipole moments of the guest and host molecules. As a consequence, the dipole moment of the inclusion complex decreases for the tail orientation by 1.4 D (B3LYP) and 1.7 D (MPW1PW91) whereas it increases for the head orientation by 0.6 D (B3LYP) and 0.4 D (MPW1PW91). Thus, the polarity of the cyclodextrin cavity decreases during the complexation processes in the tail orientation. The MPW1PW91/6-31 + G(d,p) computations (Table 3) entirely confirm these conclusions. This is in agreement with a point of view which stipulates that an anti-parallel arrangement of the dipole moments of the host and guest molecules is preferable when forming the inclusion complex because it ensures a better interaction and a reduction of the polarity of cyclodextrin [33,16].
4 Conclusions
The inclusion process of CENS in β-CD was investigated using Density Functional Theory. The DFT results show clearly that the tail orientation of CENS inside β-CD is more favourable than the head one, in agreement with mass and 15N NMR spectroscopy observations. The head introduction of CENS should lead to higher deformation energy of β-CD than for the tail orientation; this effect is one of the main driving effects leading to the actual inclusion complex. The dipole moments of the host and the guest molecules are anti-parallel leading to a less polar inclusion complex. In the inclusion complex the NO bond of CENS is directed inside the cavity leading CENS to form four H-bonds with β-CD, three as proton acceptor and one as donor. This ensures a better protection of the NO bond and a greater stability to the complex.
Acknowledgements
The investigation was supported by the Algerian Ministry of Higher Education and Scientific Research through Project CNEPRU E2401 /52/ 06. C.I.N.E.S. (Centre informatique national de l’enseignement supérieur of Montpellier) where the more time consuming computations have been carried out is acknowledged.


