All-electron CASPT2 study of Ce(η8–C8H6)2

Andrew Kerridge; Nikolas Kaltsoyannis

doi:10.1016/j.crci.2010.02.006

All-electron CASPT2 study of Ce(η⁸–C₈H₆)₂

Andrew Kerridge ¹ ; Nikolas Kaltsoyannis ¹

¹ Department of Chemistry, University College London, 20, Gordon Street, London WC1H 0AJ, UK

Comptes Rendus. Chimie, Volume 13 (2010) no. 6-7, pp. 853-859.

Résumé

CASSCF wave functions and CASPT2 energies are presented for the ground and 15 and 31 excited states of the D_2d and D_2h conformers respectively of the f-element sandwich molecule CePn₂ (Pn = η⁸–C₈H₆). The ground states of both conformers are found to be strongly multiconfigurational, analogous to cerocene, CeCOT₂ (COT = η⁸–C₈H₈), as reported in Journal of Physical Chemistry A 113 (2009) 2896. Investigation of the nature of the multiconfigurational character shows that the analogy with cerocene is indeed strong. It is shown that the occupations of the natural orbitals produce a more reliable description of the CePn₂ ground state than does the configurational admixture, and that these occupations can be used to deduce a value for the total f-density in the system. This density is found to be slightly lower than that of cerocene, and is in good agreement with that found experimentally. A density functional theory calculation of the same system is able to broadly capture the important features of the electronic structure, but is unable to replicate the experimental value of the total f-density. CASPT2 calculations reproduce the energy of the first band in the UV/Vis spectrum of CePn*₂ (Pn* = η⁸–C₈Me₆) to within 0.01 eV. Although this extremely good agreement is probably somewhat fortuitous, it highlights the fact that multiconfigurational methods are required in order to model systems such as CePn₂ to a high level of accuracy.

Métadonnées

Reçu le : 2009-11-10
Accepté le : 2010-02-09
Publié le : 2010-03-24

DOI : 10.1016/j.crci.2010.02.006

Mots clés : Electronic structure, Cerium, Computer chemistry, Ab initio calculations, Density functional calculations, Metallocenes, Lanthanides

Affiliations des auteurs :

Andrew Kerridge ¹ ; Nikolas Kaltsoyannis ¹

¹ Department of Chemistry, University College London, 20, Gordon Street, London WC1H 0AJ, UK

@article{CRCHIM_2010__13_6-7_853_0,
     author = {Andrew Kerridge and Nikolas Kaltsoyannis},
     title = {All-electron {CASPT2} study of {Ce(\ensuremath{\eta}\protect\textsuperscript{8}{\textendash}C\protect\textsubscript{8}H\protect\textsubscript{6})\protect\textsubscript{2}}},
     journal = {Comptes Rendus. Chimie},
     pages = {853--859},
     publisher = {Elsevier},
     volume = {13},
     number = {6-7},
     year = {2010},
     doi = {10.1016/j.crci.2010.02.006},
     language = {en},
}

TY  - JOUR
AU  - Andrew Kerridge
AU  - Nikolas Kaltsoyannis
TI  - All-electron CASPT2 study of Ce(η8–C8H6)2
JO  - Comptes Rendus. Chimie
PY  - 2010
SP  - 853
EP  - 859
VL  - 13
IS  - 6-7
PB  - Elsevier
DO  - 10.1016/j.crci.2010.02.006
LA  - en
ID  - CRCHIM_2010__13_6-7_853_0
ER  -

%0 Journal Article
%A Andrew Kerridge
%A Nikolas Kaltsoyannis
%T All-electron CASPT2 study of Ce(η8–C8H6)2
%J Comptes Rendus. Chimie
%D 2010
%P 853-859
%V 13
%N 6-7
%I Elsevier
%R 10.1016/j.crci.2010.02.006
%G en
%F CRCHIM_2010__13_6-7_853_0

Andrew Kerridge; Nikolas Kaltsoyannis. All-electron CASPT2 study of Ce(η⁸–C₈H₆)₂. Comptes Rendus. Chimie, Volume 13 (2010) no. 6-7, pp. 853-859. doi : 10.1016/j.crci.2010.02.006. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2010.02.006/

Version originale du texte intégral

1 Introduction

The f-element metallocenes M(η⁸–C₈H₈)₂ (M = Ln, An) have received considerable attention, both experimental and theoretical, since the original synthesis of uranocene, UCOT₂ (COT = C₈H₈), in 1968 by Streitwieser and Müller-Westerhof [1]. Subsequently, Th, (substituted) Pa, Np and Pu analogues of uranocene have been synthesized [2–4], along with the lanthanide analogue, cerocene, CeCOT₂ [5,6]. Compounds incorporating the other example of an aromatic eight-membered ring system, pentalene (Pn = C₈H₆), have, however, received comparatively little attention, “in part due to synthetic difficulties” [7]. Compounds with substituted pentalene ligands have been reported for Th and U [7,8] and Ce [9,10], but computational investigations have not been performed to the same theoretical level as for the COT-containing systems. This is of particular importance for the cerium compounds, for whilst there is little doubt that the actinocenes synthesized to date contain a tetravalent actinide ion, opinion with regard to cerocene is divided. We have discussed this is in detail in recent publications [11,12], and so only briefly summarise here.

Streitwieser et al. [6] and Raymond et al. [13,14] have argued strongly for a +4 oxidation state in cerocene. This interpretation, however, implies the presence of two highly reducing COT²⁻ rings in close proximity to the strongly oxidizing Ce⁴⁺ cation. An alternative to this (somewhat unlikely) formulation was proposed by Neumann and Fulde [15] and supported by sophisticated ab initio calculations on cerocene and the actinide analogue [16–19] by Dolg et al. They concluded that the ground states of both systems is ¹A_1g, and that thorocene is clearly a Th(IV) compound. Cerocene, however, exhibits strong multiconfigurational character, with the dominant (c. 80%) configuration involving the occupation of a single metal-localised valence 4f_δ level, with a corresponding hole in the highest occupied ring-based π orbitals of e_2u symmetry. Thus CeCOT₂ is best described as a Ce(III) compound containing two COT rings each carrying a formal 1.5– charge. This view has received (strong) experimental support via XANES measurements [20,21], and optical spectroscopic properties of substituted cerocenes have been shown to be more consistent with a bonding model based on Ce(III) than Ce(IV) [22].

Recent attention has turned to the pentalene (Pn, η⁸–C₈H₆) analogue of CeCOT₂. Balazs et al., after detailed spectroscopic, magnetic and density functional theory (DFT) [23,24] studies, conclude that for CePn₂, “a classification of a formal oxidation state IV is recommended” [9]. Interestingly, some of the same authors have also studied the permethylated analogue, CePn*₂ (Pn* = η⁸–C₈Me₆) using similar methodology, and concluded that “the [XANES spectroscopy] gives strong evidence for a formal valency close to Ce(III) in this molecule” [10]. The continuing division in opinion regarding the formal oxidation state of these cerium compounds has led us to perform a CASPT2 study of CePn₂. We have recently carried out similar studies of cerocene, thorocene and protactinocene [11], and find that in the case of cerocene strong hybridization between the metal f_δ and ligand π(e_2u) levels can lead to an ambiguous interpretation of the degree of ‘f¹’ character in the ground state wavefunction in terms of configurational admixture. We instead use the natural orbital occupations [25] (NOOs) along with the corresponding natural orbitals (NOs) in order to interpret the multiconfigurational nature of the cerocene ground state and obtain a value for the total f occupation, n_f. We find active space NOOs of 1.751 and 0.216 for the ‘ligand’ and ‘metal’ NOs of e_2u symmetry, respectively. Such deviation from integer occupation is an indicator of strong multiconfigurational character [26], yet under the assumption of localized orbitals, in which there is no hybridization between the ligand and metal e_2u levels, yields an n_f value of only = 0.43. The natural orbitals, however, show approximately 20% metal character in the ‘ligand’ level and vice versa. Taking this hybridization into account allows us to calculate a revised value of n_f = 0.90 ± 0.04, in excellent agreement with that found experimentally [21], yet without near-integer occupation of a localised f_δ level.

In this contribution, we apply the same high-level methodology we have successfully employed on cerocene to establish if a similar description of the ground state is appropriate for CePn₂.

2 Computational details

The Gaussian 03 code [27] was used to investigate CePn₂ at the DFT level, using the TPSS exchange-correlation functional [28]. All results from DFT calculations were obtained using the small core SDD pseudopotential [29] and associated basis set for cerium, and the cc-pVDZ set [30] for carbon and hydrogen.

Complete active space self-consistent field (CASSCF) [31] calculations were performed using the MOLCAS 6.4 code [32], and dynamic correlation was accounted for using complete active space second order perturbation theory (CASPT2) [33]. Details of the active spaces employed for both the D_2h and D_2d isomers are given in the main text (and Tables 2 and 4). For the D_2h isomer, the number of orbitals kept frozen in each irrep during the CASPT2 procedure were: a_g: 11, b_1g: three, b_2g: four, b_3g: four, a_u: one, b_1u: six, b_2u: five, b_3u: five. For the D_2d isomer which, as discussed in the main text, was calculated in the C_2v point group, the number of orbitals kept frozen in each irrep during the CASPT2 procedure were: a₁: 17, a₂: four, b₁: nine, b₂: nine.

	A₁	A₂	B₁	B₂
Inactive (occupied)	31	10	18	18
Active (occupied)	2	2	1	1
Active (virtual)	2	2	3	3

	A_g	B_1g	B_2g	B_3g	A_u	B_1u	B_2u	B_3u
Inactive (occupied)	18	6	7	9	4	13	11	9
Active (occupied)	1	1	1	0	1	1	0	1
Active (virtual)	1	1	1	1	1	1	2	2

Scalar relativistic effects were included using the second order Douglas-Kroll Hamiltonian [34], whereas spin-orbit coupling, which we have previously shown to be very weak in CeCOT₂ [11], was neglected. All electron ANO basis sets were used for these calculations. For cerium, the ANO set was constructed by Roos [35], contracted as (25s22p15d11f)/[9s8p5d4f], and is of approximate cc-VQZ quality. The basis sets were of cc-pVDZ quality for C and H. This basis set combination has been shown [11] to produce results of comparable accuracy to those obtained using sets of cc-pVQZ quality for Ce and of cc-pVTZ quality for C and H. To aid comparison with CASPT2 results, MOLCAS 6.4 was also used to perform DFT calculations using the B3LYP exchange-correlation functional [36] and the same ANO basis in order to consider the differences in f-orbital occupation when using the CASPT2 and DFT methods.

3 Results and discussion

3.1 DFT study

Crystalline $CeP {n^{'}}_{2}$ (Pn′ = C₈H₄(SiⁱPr₃-1,4)) is found to contain two distinct conformers [9], which can be characterized in terms of the twist angle, i.e. the angle between the bridgehead C-C bonds in the two Pn′ ligands. One of the conformers is approximately staggered, with a twist angle of 85.0°, whilst the other is semieclipsed, with a twist angle of 33°. The situation is similar in $CeP n_{2}^{*}$ (Pn^* = C₈Me₆), where three conformers are reported [10]: an approximately staggered conformer with twist angle of 79.8°, and two semieclipsed conformers with twist angles of 20.1 and 40.1° respectively. Bearing this in mind, the CePn₂ structure was optimized using the Gaussian 03 code within the constraints of the D₂, D_2d and D_2h point groups. The D₂-constrained optimization resulted in a structure of D_2d symmetry, and this structure was found to be a minimum. The D_2h structure was found to have one imaginary frequency at i35.9 cm⁻¹, and to lie 0.13 eV (12.5 kJ/mol) higher in energy. These results are in good agreement with previous DFT work [9] using the B3LYP and BP86 [36,37] exchange-correlation functionals. Table 1 summarises relevant parameters of the optimized D_2d structure. There is good general agreement between the optimized structure obtained here and those found previously [9,10], with TPSS giving a slightly reduced Ce-C(β) separation and corresponding increased ligand fold angle.

Parameter	Calculated	Experimental
	Ref [9]	Ref [10]	Present Work	$CeP {n^{'}}_{2}$ [9]	$CeP n_{2}^{*}$ [10]
Ce-C (br)	2.51	-	2.50	2.49–2.52	-
Ce-C (α)	2.74	-	2.72	2.73–2.76	-
Ce-C (β)	2.88	-	2.86	2.89–2.93	-
$\bar{Ce - C}$	2.72	2.67	2.70	2.73	2.68
Ligand fold ∠	24.4	24.0	25.6	23.0	24.7
Twist ∠	87.72	90^a	90^a (90.04^b)	85.0	79.8

^a Optimization performed under constraints of D_2d symmetry.

^b Optimised twist angle, differing from 90° due to convergence criteria.

We find the DFT calculated electronic structure of the D_2d conformer to be as reported previously [9,10]. The ground state is ¹A₁, with the a₂ symmetry HOMO and b₁ HOMO-1 displaying significant f_δ and d_δ character respectively. The LUMO is of e-symmetry and is an almost completely localized f-level. The ground state of the higher energy D_2h conformer is analogous: the state symmetry is ¹A_g, with the a_u symmetry HOMO and b_3g HOMO-1 displaying significant f_δ and d_δ character respectively. The lowest lying unoccupied levels are localized f-levels. We defer consideration of the degree of f-character in the ground state until Section 3.2.3, where comparison is made between DFT and CASPT2 calculations using identical basis sets.

3.2 CASPT2 study

CASPT2 calculations were performed on both the D_2h and D_2d conformers at the TPSS-optimised geometries. In the case of the D_2d conformer, computational restrictions enforced in MOLCAS required calculations to be performed in the C_2v point group (an Abelian subgroup of D_2d). Such a reduction in symmetry can, in principle, allow mixing of orbitals that would be forbidden in the full point group, and such mixing was monitored and eliminated during the calculations. Throughout the remainder of this study we will refer to orbitals and states in terms of their C_2v symmetry labels and, where appropriate, will give the corresponding D_2d labels in parentheses. In the case of the D_2h conformer, the full point-group could be employed in the calculations, and so no complication arises.

Although CePn₂ can be considered to be analogous to CeCOT₂, we have used a larger active space in the present calculations than was used in our CeCOT₂ study. In the previous study, an active space explicitly correlating eight electrons in 14 orbitals, denoted CASPT2(8,14), was used. This active space included the eight electrons occupying the highest energy π₂ ligand orbitals spanning the doubly degenerate e_2u and e_2g irreps of the D_8h point group, and was sufficient since the energy gap between these orbitals and those below them (π₁ orbitals of e_1g and e_1u symmetry) was large. The lower point groups employed here strongly affect the relative energies of these orbitals, resulting in a significant reduction in the π₂-π₁ energy gap when the CePn₂ complexes are considered. This effect is shown graphically for the tetra-anionic ligand systems in Fig. 1, where the π₂-π₁ energy gap reduces from 2.97 eV (CeCOT₂) to 1.06 eV (CePn₂, D_2h) and 1.17 eV(CePn₂, D_2d), and led us to expand the active space in the present calculations to include the higher lying of the π₁ levels. We therefore present CASPT2(12,16) calculations, using our adopted notation. It should be noted that this active space allows for occupation of any of the twelve 4f and 5d levels.

Fig. 1
Energy levels and molecular orbitals of COT₂⁴⁻ and the D_2h and D_2d conformers of Pn₂⁴⁻. The blue and red levels indicate the lowest lying π₂ and highest lying π₁ level respectively.

3.2.1 The D_2d conformer

The two energetically lowest singlet and triplet states of each irrep of C_2v (the working point-group) were obtained at the CASPT2 level, using the active space defined in Table 2. Input orbitals were generated from a restricted Hartree-Fock (RHF) [38,39] calculation, with the improved virtual orbital (IVO) method [40] used to produce more compact virtual orbitals.

Our CASPT2 calculations find a ¹A₁ ground state, in agreement with our DFT results. This state lies 0.87 eV below the doubly degenerate first excited state, of B₁/B₂ (E) symmetry and singlet multiplicity. We quantify the multiconfigurational character in terms of the natural occupation numbers; NOOs which deviate from integer values by more than 0.1 are indicative of a strongly multiconfigurational system [26]. Table 3 shows the energies and the largest deviation from integer orbital occupancy within the active space for each of the sixteen states we consider here. The ground state is strongly multiconfigurational, with significant (0.383) occupation of the anti-bonding a₂ level of dominant f_δ character. This occupation is a direct result of the deoccupation of the corresponding bonding a₂ level (with a deoccupation of 0.391). This state bears a strong resemblance to that which we have previously reported as the cerocene ground state (as can be seen from the natural orbital diagrams of Fig. 2), with the difference here that the lower symmetry splits the degeneracy of the two f_δ orbitals, resulting in the multiconfigurational character being almost exclusively attributable to charge transfer between the bonding and antibonding a₂ orbitals with f_δ character, as opposed to contributions from both components of the doubly degenerate e_2u cerocene orbitals. The largest deviation from integer occupancy in the other active space orbitals is just 0.052, confirming the origin of the multiconfigurational character. By contrast to the CASPT2 ground state, the fifteen other states under consideration here have much lower multiconfigurational character. Again, this is strongly reminiscent of our cerocene results.

	Singlet	Triplet
	Energy (eV)	Δ_NOO	Energy (eV)	Δ_NOO
A₁	0.00	0.391	1.16	0.054
2.34	0.086	2.24	0.106
A₂	2.72	0.068	2.72	0.068
3.19	0.072	3.21	0.073
B₁	0.87	0.054	0.88	0.054
2.01	0.086	1.94	0.086
B₂	0.87	0.054	0.88	0.054
2.01	0.086	1.94	0.086

Fig. 2
CePn₂ ground state natural orbitals obtained from CASSCF(12,16) calculations, and CeCOT₂ ground state natural orbitals obtained from a CASSCF(8,14) calculation [11]. Only NOs with signifcantly non-integer occupation are shown.

Experimentally, an “intense and broad absorption” is observed at 2.34 eV in the UV/Vis spectrum [10]. Time-dependent DFT calculations find a transition with oscillator strength f = 0.071 at an energy of 2.85 eV, due to excitation from a largely ligand based orbital with some Ce d_δ character into an Ce f_δ orbital, with the intensity of the transition arising from the d to f character of the transition [10]. Our CASPT2 calculations also identify this transition, but give better agreement with experiment. We find an oscillator strength of f = 0.345 for the transition, which we calculate to occur at 2.35 eV. Whilst this extremely good agreement is no doubt somewhat fortuitous, it again highlights the fact that multiconfigurational methods are required in order to model systems such as CePn₂ to a high level of accuracy.

3.2.2 The D_2h conformer

The two energetically lowest singlet and triplet states of each irrep of D_2h were obtained at the CASPT2 level, using the active space defined in Table 4. Input orbitals were generated from a restricted Hartree-Fock (RHF) [38,39] calculation, with the improved virtual orbital (IVO) method [40] used to produce more compact virtual orbitals.

As with the G03 DFT calculations we find an ¹A_g ground state for the D_2h conformer. At the CASPT2 level this state lies 0.24 eV (23.2 kJ/mol) above the D_2d ground state. The D_2h ground state bears strong similarities to both that of the D_2d conformer and cerocene, i.e. a strongly multiconfigurational wavefunction resulting from the strong (0.378) occupation of the antibonding a_u orbital of dominant f_δ character. Again, this occupation results almost exclusively from deoccupation of the corresponding bonding a_u level (deoccupation of 0.388). The ground state is stable by 0.93 eV relative to the first excited state of ¹B_2g symmetry. The low lying excited states typically have only small deviations from integer occupancy, as is the case for the D_2d conformer (compare Tables 3 and 5). There are, however, several excited states (of B_1g, A_u and B_1u symmetry and both spin multiplicities) which are strongly multiconfigurational. These multiconfigurational excited states exhibit the strong occupation of the antibonding a_u orbital of dominant f_δ character, in common with the ground state, but also correspond to ligand to metal charge transfer excitations. This is in contrast to cerocene, where all excited states were found to be well described by a single-configuration wavefunction.

	Singlet	Triplet
	Energy (eV)	Δ_NOO	Energy (eV)	Δ_NOO
A_g	0	0.388	1.21	0.060
2.36	0.194	3.96	0.710
B_1g	2.21	0.054	2.22	0.055
2.78	0.578	2.55	0.561
B_2g	0.93	0.052	0.97	0.050
2.08	0.066	2.11	0.061
B_3g	0.96	0.054	0.98	0.052
2.09	0.066	2.10	0.054
A_u	1.60	0.241	1.60	0.231
3.38	0.060	3.41	0.083
B_1u	2.45	0.087	2.30	0.109
2.63	0.434	2.63	0.424
B_2u	2.18	0.076	2.06	0.085
4.59	0.148	3.26	0.097
B_3u	2.13	0.092	2.01	0.093
3.70	0.017	3.66	0.125

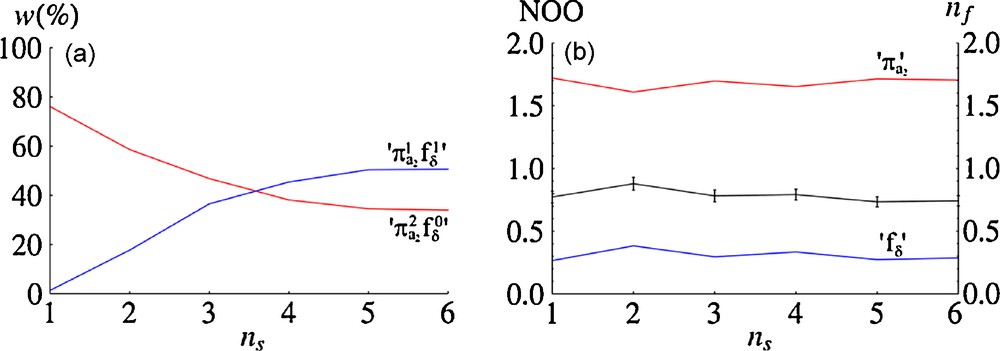
3.2.3 Evaluation of the f-density

Fig. 3a shows the variation in the configurational weights of the $` π_{a_{2}}^{2} f_{δ}^{0}'$ and $` π_{a_{2}}^{1} f_{δ}^{1}'$ ¹configurations in the D_2d conformer of CePn₂ when the size of the state average in the calculation is varied. This variation is marked, and shows that such weights are not a reliable measure of multiconfigurational character, as we found in our previous study of cerocene. Fig. 3b shows the corresponding natural orbital occupations, which are more robust with respect to the size of the state average, and which we use to calculate a value for the total f-density (n_f). We have described our approach for obtaining n_f in detail elsewhere [11], and so will only briefly describe it here. We calculate the total f-contribution to each of the natural orbitals comprising the active space and multiply by the corresponding natural orbital occupation to obtain a value for the f-density. This procedure assumes the metal and ligand basis functions are orthogonal, which is not the case, but the error associated with this assumption can be estimated by consideration of the normalization constants of each orbital, and results in the error bars present in Fig. 3b. Our calculations suggest that an appropriate value of n_f for this system is 0.78 ± 0.04. This is a little smaller than the value we have previously calculated for cerocene (0.90 ± 0.04), and is in good agreement with that found experimentally by Ashley et al.; 0.87 ± 0.05 [10]. Our calculations show that the ground state of CePn₂ can be considered analogous to that of cerocene.

In order to compare this result with that obtained from a single-configuration DFT calculation, MOLCAS was used to generate a set of Kohn-Sham orbitals for CePn₂ using the B3LYP functional and the same basis set and molecular geometries as was used for the CASPT2 calculations. The D_2d conformer was again found to be the lowest energy structure, and was stable by 0.21 eV (20 kJ/mol) with respect to the D_2h conformer. Inspection of the Kohn-Sham orbitals for the D_2d conformer reveals the a₂ HOMO and LUMO to be almost indistinguishable from the partially-occupied natural orbitals shown in Fig. 2, and n_f is calculated to be 0.62 ± 0.01. This value, whilst significant, is substantially lower than that obtained from the natural orbitals, and is a result of the inability of the single-configurational method to represent the partial occupation of the a₂ LUMO of dominant f_δ character.

4 Summary and conclusions

CePn₂ has been shown experimentally [9,10] to bear a striking resemblance to cerocene, for which the debate as to the oxidation state of the cerium ion continues. We have shown computationally that the electronic structure of CePn₂ is extremely similar to that of cerocene, and that whilst multiconfigurational methods are required to accurately describe the ground state wavefunction, it is not dominated by a ‘π³f_δ¹’ configuration. Instead, our analysis via natural orbital occupancies suggests that CePn₂, like CeCOT₂ [11], is best described as a Ce(IV) system in which the transfer of electron density from ligand to metal through partial occupation of a metal dominated orbital results in a significant metal 4f density. This conclusion is not in conflict with the XANES data of [9,10]: in fact, our calculated value for the Ce ion f-density is in good agreement with that found experimentally. However, our analysis suggests that experimental measures of the effective (as opposed to formal) oxidation state cannot necessarily be used to unambiguously define the detailed electronic structure of complexes such as CePn₂.

Acknowledgements

We are grateful to the EPSRC for financial support (via grants EP/C533054 and GR/S06233) and for the use of its National Service for Computational Chemistry Software (http://www.nsccs.ac.uk). We also thank UCL for computing resources via the Research Computing “Legion” cluster and associated services.

¹ The used of inverted commas is to remind the reader that these orbitals are not localized, and the labels refer to dominant character.

Fig. 3(a) configurational weights and (b) natural orbital occupancies as a function of state average size (n_s) for the D_2d conformer of CePn₂. Also shown in (b) are the calculated f-densities (n_f).

Bibliographie

[1] A.J. Streitwieser; U. Müller-Westerhof J. Am. Chem. Soc, 90 (1968), p. 7364

[2] A. Streitweiser; N. Yoshida J. Am. Chem. Soc, 91 (1969), p. 7528

[3] J.P. Solar; H.P.G. Burghard; R.H. Banks; A.J. Streitwieser; D. Brown Inorg. Chem, 19 (1980), p. 2186

[4] D.G. Karraker; J.A. Stone; E.R. Jones; N. Edelstein J. Am. Chem. Soc, 92 (1970), p. 4841

[5] A. Greco; S. Cesca; G. Bertolini J. Organomet. Chem, 113 (1976), p. 321

[6] A. Streitwieser; S.A. Kinsley; J.T. Rigsbee; I.L. Fragala; E. Ciliberto; N. Rosch J. Am. Chem. Soc, 107 (1985), p. 7786

[7] F.G.N. Cloke; P.B. Hitchcock J. Am. Chem. Soc, 119 (1997), p. 7899

[8] F.G.N. Cloke; J.C. Green; C.N. Jardine Organometallics, 18 (1999), p. 1080

[9] G. Balazs; F.G.N. Cloke; J.C. Green; R.M. Harker; A. Harrison; P.B. Hitchcock; C.N. Jardine; R. Walton Organometallics, 26 (2007), p. 3111

[10] A. Ashley; G. Balazs; A. Cowley; J. Green; C.H. Booth; D. O’Hare Chem. Commun (2007), p. 1515

[11] A. Kerridge; R. Coates; N. Kaltsoyannis J. Phys. Chem. A, 113 (2009), p. 2896

[12] R. Coates; M. Coreno; M. DeSimone; J.C. Green; N. Kaltsoyannis; A. Kerridge; N. Narband; A. Sella Dalton Trans (2009), p. 5943

[13] K.O. Hodgson; K.N. Raymond Inorg. Chem, 11 (1972), p. 171

[14] K.N. Raymond; C.W. Eigenbrot Acc. Chem. Res, 13 (1980), p. 276

[15] C.S. Neumann; P. Fulde Z. Phys. B-Cond. Matt, 74 (1989), p. 277

[16] M. Dolg; P. Fulde; W. Kuechle; C.S. Neumann; H. Stoll J. Chem. Phys, 94 (1991), p. 3011

[17] M. Dolg; P. Fulde; H. Stoll; H. Preuss; A. Chang; R.M. Pitzer Chem. Phys, 195 (1995), p. 71

[18] W.J. Liu; M. Dolg; P. Fulde J. Chem. Phys, 107 (1997), p. 3584

[19] W.J. Liu; M. Dolg; P. Fulde Inorg. Chem, 37 (1998), p. 1067

[20] N.M. Edelstein; P.G. Allen; J.J. Bucher; D.K. Shuh; C.D. Sofield; N. Kaltsoyannis; G.H. Maunder; M.R. Russo; A. Sella J. Am. Chem. Soc, 118 (1996), p. 13115

[21] C.H. Booth; M.D. Walter; M. Daniel; W.W. Lukens; R.A. Andersen Phys. Rev. Lett, 95 (2005), p. 267202

[22] H.D. Amberger; H. Reddmann; F.T. Edelmann J. Organomet. Chem, 690 (2005), p. 2238

[23] P. Hohenberg; W. Kohn Phys. Rev. B, 136 (1964), p. B864

[24] W. Kohn; L.J. Sham Phys. Rev, 140 (1965), p. 1133

[25] P.O. Löwdin Phys. Rev, 97 (1955), p. 1474

[26] M.W. Schmidt; M.S. Gordon Ann. Rev. Phys. Chem, 49 (1998), p. 233

[27] M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, J. Montgomery, J. A., T. Vreven, K.N. Kudin, J.C. Burant, J.M. Millam, S.S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G.A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J.E. Knox, H.P. Hratchian, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, P.Y. Ayala, K. Morokuma, G.A. Voth, P. Salvador, J.J. Dannenberg, V.G. Zakrzewski, S. Dapprich, A.D. Daniels, M.C. Strain, O. Farkas, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J.V. Ortiz, Q. Cui, A.G. Baboul, S. Clifford, J. Cioslowski, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, M. Challacombe, P.M.W. Gill, B. Johnson, W. Chen, M.W. Wong, C. Gonzalez, J.A. Pople, Gaussian 03 revision D.01, Gaussian, Inc., Wallingford CT, 2004.

[28] J.M. Tao; J.P. Perdew; V.N. Staroverov; G.E. Scuseria Phys. Rev. Lett, 91 (2003), p. 146401

[29] M. Dolg; H. Stoll; H. Preuss J. Chem. Phys, 90 (1989), p. 1730

[30] T.H. Dunning J. Chem. Phys, 90 (1989), p. 1007

[31] B.O. Roos; P.R. Taylor Chem. Phys, 48 (1980), p. 157

[32] G. Karlstrom; R. Lindh; P.A. Malmqvist; B.O. Roos; U. Ryde; V. Veryazov; P.O. Widmark; M. Cossi; B. Schimmelpfennig; P. Neogrady; L. Seijo Comp. Mat. Sci, 28 (2003), p. 222

[33] K. Andersson; P.A. Malmqvist; B.O. Roos; A.J. Sadlej; K. Wolinski J. Phys. Chem, 94 (1990), p. 5483

[34] M. Douglas; N.M. Kroll Ann. Phys, 82 (1974), p. 89

[35] B.O. Roos, Unpublished.

[36] A.D. Becke Phys. Rev. A, 38 (1988), p. 3098

[37] J.P. Perdew Phys. Rev. B, 33 (1986), p. 8822

[38] D.R. Hartree Proc. Cam. Phil. Soc, 24 (1928), p. 89

[39] V.A. Fock Ann. Phys. (Leipzig), 61 (1930), p. 126

[40] W.J. Hunt; W.A. Goddard Chem. Phys. Lett, 3 (1969), p. 414

Commentaires - Politique

Ces articles pourraient vous intéresser

From magnetic molecules to magnetic solids: An ab initio expertise

Boris Le Guennic; Vincent Robert

C. R. Chim (2008)

Exchange coupling in Cu^IIGd^III dinuclear complexes: A theoretical perspective

Jordi Cirera; Eliseo Ruiz

C. R. Chim (2008)

Sub-picosecond C $=$ C bond photo-isomerization: evidence for the role of excited state mixing

Damianos Agathangelou; Partha Pratim Roy; María del Carmen Marín; ...

C. R. Phys (2021)