1 Introduction
Boron and boronic acid containing organic compounds have become an object of recent increasing interest due to their extensive application potentials in the field of material science, supramolecular chemistry, analytical chemistry, medicine, biology, catalysis, organic synthesis and crystal engineering. A wide range of biologically important boronic acid derivatives have been synthesized as anti-metabolites [1–8]. Boron-based compounds show preferential localization in tumor containing tissues making the boron-10 neutron capture therapy possible [9]. The boronic acid moiety has been also employed in the synthesis of anti-tumor and anti-viral agents [10].
Density functional theory (DFT) calculations provide excellent agreement with experimental vibrational frequencies of organic compounds, if the calculated frequencies are scaled to compensate for the approximate treatment of electron correlation, basis set deficiencies and anharmonicity [11–17]. Moreover, the Gauge Including Atomic Orbitals/Density Functional Theory (GIAO/DFT) approach is extensively used for the calculations of chemical shifts of different types of compounds [18–23].
Solid and solution state NMR methods are very useful tools for structural identification of isolated or synthesized molecules and they allow to get faster and easier structural information. The standard 1D and 2D hetero- and homonuclear NMR experiments are greatly helpful for assignment of organic compounds and effective to afford molecular structure information [24–26]. Biological activity is closely related to the molecular preferences [18]; therefore, especially solid state NMR and theoretical data of 2,4-dmpba seem to be valuable. Since shielding is very sensitive to the geometric structure and chemical environment, DFT calculations can be used to investigate solid state structure and inter–intramolecular interactions [27,28]. In this work, the most stable conformers of 2,4-dmpba have been studied within the framework of DFT. A detailed interpretation of the vibrational spectra of 2,6-dmpba has been conducted on the basis of the calculated total energy distribution (TED) [29]. 1H, 13C (CP/MAS) NMR chemical shifts and HETCOR spectra of 2,4-dmpba have been reported. The vibrational wavenumbers, 1H, 13C chemical shifts and some important structural parameters have been also calculated at B3LYP level of theory using 6-31++G(d,p) basis set. The results of the theoretical and spectroscopic studies are reported here.
2 Experimental
A commercial sample of 2,4-dmpba was purchased and used without further purification. FT-IR spectrum of 2,4-dmpba was recorded using Perkin Elmer Spectrum 2000 spectrometer with the resolution of 2 cm−1 in the spectral region of 4000–400 cm−1. The Raman spectrum was obtained using a Bruker Senterra Dispersive Raman microscope spectrometer with 532 nm excitation from a 3B diode laser having 3 cm−1 resolution in the spectral region of 3700–400 cm−1. All NMR spectra of the compounds were recorded on a Bruker Avance II 500 NMR spectrometer at ambient probe temperature. The operating frequencies were 500.13 and 125.76 MHz 1H and 13C, respectively. 1H and 13C NMR spectra were measured in CDCl3, with tetramethylsilane (TMS) as internal reference in 5 mm NMR tubes. The pulse conditions used in the solution state NMR experiments were as following: for 2,4-dmpba, 1H NMR spectra: spectrometer frequency (SF) 500.13 MHz, spectral width (SW) 5498.53, acquisition time (AQ) 5.96 s, number of scan (NS) 32, P1 14.15 μs, receiver gain (RG) 50.8, digital resolution (DR) 23 Hz, dwell time (DW) 90.93 μs, prescan delay (DE) 6.00 μs; 13C NMR spectra: SF 125.76 MHz, SW 29761.90, AQ 1.10 s, NS 64, P1 8.30 μs, RG 724, DR 21 Hz, DW 16.80 μs, DE 6.00 μs. The (CP/MAS) NMR experiments were carried out on a Bruker Avance-300 WB equipped with a 4 mm (CP/MAS) probe. The operating frequencies were 75.47 and 30.41 MHz for 13C. External referencing was performed relative to glycine molecule. All solid experiments were performed using high power hydrogen decoupling. A zirconium oxide rotor with a 4 mm diameter was used to acquire the NMR spectra of 13C and sample was spun at 7 kHz. For 13C (CP/MAS) NMR spectroscopy of 2,4-dmpba, contact time of 2.0 ms, repetition time of 5.0 s and spectral width of 24038.46 Hz and 6.0 μs delay time before acquisition were used for accumulation of 512 scans.
3 Calculations
Many possible conformers could be proposed for 2,4-dmpba but here the discussion is limited to tt(C1), ct(C1), cc(C1), tt(Cs), ct(Cs) and cc(Cs) isomers (Fig. 1), where t and c stand for trans and cis, respectively. For the calculations, six forms of 2,4-dmpba were first optimized by B3LYP with 6-31++G(d,p) basis set in the gas phase. The optimized geometric structures relative to the minimum on the potential energy surface were provided by solving the self-consistent field (SCF) equation iteratively. For the vibrational calculations, the vibrational wavenumbers of 2,4-dmpba were calculated using the same method and the basis set under the keyword freq = Raman. The assignments of the vibrational modes of the title molecule were provided by animation option of the GaussView package program for the B3LYP/6-31++G(d,p) level of calculation. TED calculations, which show the relative contributions of the redundant internal coordinates to each normal vibrational mode of the molecule and thus make it possible to describe the character of each mode numerically, were carried out by the scaled quantum mechanical (SQM) program [17,29] using the output files created at the end of the wavenumber calculations. For the NMR calculations, all suggested forms of the title molecule were first fully optimized at 6-31++G(d,p) level in chloroform using the PCM method [30]. After optimization, 1H and 13C NMR chemical shifts (δH and δC) of 2,4-dmpba were calculated using the GIAO method [31] in chloroform at the B3LYP/6-311++G(d,p) level. Relative chemical shifts were then estimated using the corresponding TMS shieldings calculated in advance at the same theoretical levels as the references. All calculations were performed using Gaussian 03 program on a personal computer [32].
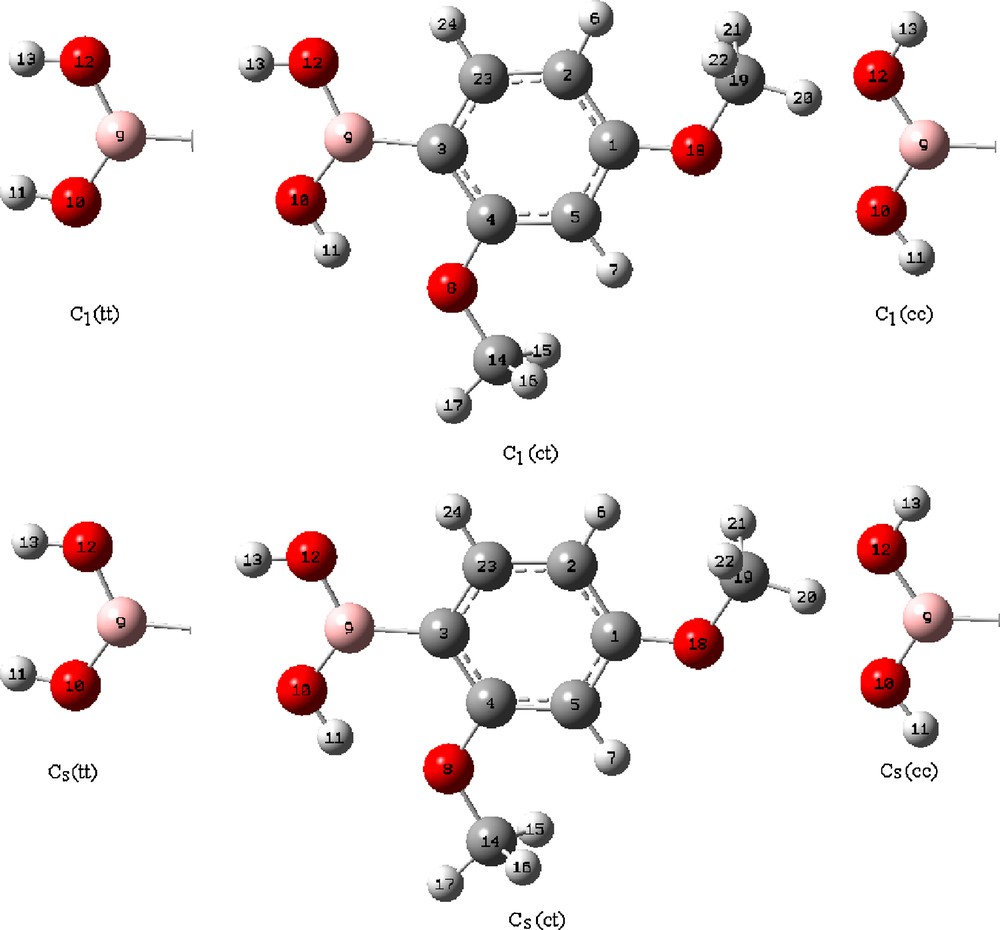
The theoretical optimized possible six geometric structures with atom numbering of 2,4-dmpba.
4 Results and discussion
4.1 Geometrical structures
The optimized geometric parameters (bond lengths, bond and dihedral angles) calculated with B3LYP/6-31++G(d,p) are listed in Table 1. Considering the calculated geometric parameters, it is possible to construct the structures of six possible isomers given in Fig. 1. The phenylboronic acid molecule was studied by X-ray diffraction [33]. Since the crystal structure of 2,4-dmpba is not available in the literature up to now, the structural parameters were compared with phenylboronic acid. The magnitude of D(3;9;10;11) and D(3;9;12;13) angles are about 0.00° and 180.00° for ct(Cs) and ct(C1) conformers, which indicates that both hydrogens are almost in the OBO plane. In general, B–O distances are 1.359 Å [34] in compliance with strong p-interactions. Chen et al. [10] found nearly the same value for this bond length using HF/6-31G(d) levels of theory for the few boronic acids including phenylboronic acid. For the 2,4-dmpba molecule B–O distances including ct(Cs) and ct(C1) forms were found from 1.371 to 1.375 Å. Bhat et al. [35] calculated BC bond length 1.566 Å and 1.567 Å for form of phenylboronic acid using B3LYP and MP2 methods, respectively. The BC bond length for the title molecule is calculated as 1.567 Å for ct(Cs) and ct(C1) forms. The calculated BO and BC bond lengths for 2,4-dmpba are in good agreement with previously reported data found in the X-ray structure [36]. Regarding the relative energy differences given in Table 2, the relative mole fractions of tt(C1), cc(C1), tt(Cs) and cc(Cs) could be ignored since their relative energy differences compared to ct(Cs) and ct(C1) isomers are more than 2.0 kcal/mol. As for the ct(Cs) and ct(C1), the following equations can be written for the mole fractions of individual conformers:
Optimized geometric parameters of 2,4-dmpba for ten conformers calculated by B3LYP with 6-31++G(d,p) basis set.
| Parameters | B3LYP/6-311G(d,p) | ||||||
| tt(C1) | ct(C1) | cc(C1) | tt(Cs) | ct(Cs) | cc(Cs) | Exp. [34] | |
| R(10;11) | 0.964 | 0.969 | 0.968 | 0.964 | 0.969 | 0.968 | |
| R(12;13) | 0.963 | 0.966 | 0.961 | 0.963 | 0.966 | 0.961 | |
| R(9;10) | 1.375 | 1.371 | 1.363 | 1.375 | 1.371 | 1.363 | 1.362 |
| R(9;12) | 1.386 | 1.375 | 1.375 | 1.386 | 1.375 | 1.375 | 1.378 |
| R(3;9) | 1.561 | 1.567 | 1.584 | 1.561 | 1.567 | 1.584 | 1.568 |
| R(3;4) | 1.422 | 1.417 | 1.421 | 1.422 | 1.417 | 1.421 | 1.404 |
| R(4;5) | 1.397 | 1.392 | 1.393 | 1.397 | 1.392 | 1.393 | 1.378 |
| R(5;1) | 1.402 | 1.404 | 1.403 | 1.402 | 1.404 | 1.403 | |
| R(1;2) | 1.398 | 1.398 | 1.397 | 1.398 | 1.398 | 1.398 | |
| R(2;23) | 1.397 | 1.398 | 1.398 | 1.397 | 1.398 | 1.398 | 1.378 |
| R(3;23) | 1.404 | 1.402 | 1.402 | 1.404 | 1.402 | 1.401 | 1.404 |
| R(4;8) | 1.361 | 1.379 | 1.376 | 1.361 | 1.379 | 1.376 | |
| R(8;14) | 1.420 | 1.425 | 1.426 | 1.420 | 1.425 | 1.426 | |
| R(1;18) | 1.366 | 1.365 | 1.363 | 1.366 | 1.365 | 1.363 | |
| R(18;19) | 1.423 | 1.424 | 1.424 | 1.423 | 1.424 | 1.424 | |
| R(14;17) | 1.091 | 1.091 | 1.090 | 1.091 | 1.091 | 1.090 | |
| R(19;20) | 1.091 | 1.091 | 1.090 | 1.091 | 1.091 | 1.090 | |
| R(5;7) | 1.082 | 1.082 | 1.082 | 1.082 | 1.082 | 1.082 | 1.000 |
| R(2;6) | 1.083 | 1.083 | 1.083 | 1.083 | 1.083 | 1.083 | 1.000 |
| R(23;24) | 1.085 | 1.086 | 1.088 | 1.085 | 1.086 | 1.088 | |
| A(9;10;11) | 115.16 | 110.71 | 110.78 | 115.17 | 110.61 | 110.69 | 111.0 |
| A(9;12;13) | 115.97 | 111.54 | 115.10 | 115.99 | 111.54 | 115.08 | 111.0 |
| A(10;9;12) | 121.85 | 117.92 | 114.73 | 121.84 | 117.94 | 114.76 | |
| A(4;3;9) | 125.47 | 124.02 | 123.52 | 125.49 | 124.00 | 123.52 | 122.0 |
| A(4;8;14) | 119.31 | 119.41 | 119.70 | 119.33 | 119.42 | 119.73 | |
| A(4;3;23) | 116.31 | 116.24 | 115.29 | 116.32 | 116.25 | 115.31 | 120.0 |
| A(8;14;17) | 105.60 | 105.85 | 105.74 | 105.60 | 105.84 | 105.73 | |
| A(4;5;1) | 120.15 | 119.53 | 119.83 | 120.13 | 119.50 | 119.80 | |
| A(5;1;2) | 120.37 | 120.39 | 120.11 | 120.38 | 120.40 | 120.12 | |
| A(1;5;7) | 117.64 | 117.77 | 117.69 | 117.66 | 117.81 | 117.72 | |
| A(1;18;19) | 118.55 | 118.57 | 118.59 | 118.51 | 118.53 | 118.56 | |
| A(18;19;20) | 105.77 | 105.73 | 105.72 | 105.77 | 105.74 | 105.73 | |
| A(1;2;6) | 121.79 | 121.59 | 121.74 | 121.80 | 121.59 | 121.75 | |
| A(2;23;24) | 118.43 | 118.80 | 116.51 | 118.43 | 118.80 | 116.53 | |
| A(15;14;16) | 109.36 | 109.74 | 109.84 | 109.36 | 109.75 | 109.84 | |
| A(21;19;22) | 109.46 | 109.53 | 109.60 | 109.46 | 109.52 | 109.59 | |
| D(11;10;9;3) | 179.98 | −0.01 | −0.01 | 180.00 | 0.00 | 0.00 | |
| D(10;9;3;4) | −0.14 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | |
| D(3;4;8;14) | −179.95 | −179.99 | 179.99 | 180.00 | 180.00 | 180.00 | |
| D(4;8;14;17) | 179.94 | 179.99 | −179.99 | 180.00 | 180.00 | 180.00 | |
| D(8;4;5;7) | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| D(4;5;1;18) | −180.00 | 180.00 | 179.99 | 180.00 | 180.00 | 180.00 | |
| D(5;1;18;19) | 179.99 | 180.00 | 179.99 | 180.00 | 180.00 | 180.00 | |
| D(1;18;19;22) | 61.25 | 61.25 | 61.29 | 61.23 | 61.23 | 61.26 | |
| D(4;8;14;16) | 61.23 | 61.22 | 61.28 | 61.30 | 61.25 | 61.29 | |
| D(11;10;9;12) | −0.04 | −180.00 | 179.99 | 0.00 | 180.00 | 180.00 |
Geometry, point groups, mode distribution, optimized energy and energy differences of 2,4-dmpba calculated by B3LYP with 6-31++G(d,p) basis set.
| Geometry | Point group | Mode distribution | Optimized energy (Hartree) | Energy differencesa (kcal/mol) |
| Trans–trans | C1 | 66A | −637.209369 | 7.750 |
| Cis−trans | C1 | −637.221650 | 0.004 | |
| Cis–cis | C1 | −637.215722 | 3.763 | |
| Trans–trans | Cs | 43A′+23A′′ | −637.210064 | 7.314 |
| Cis–trans | Cs | −637.221719 | 0.000 | |
| Cis–cis | Cs | −637.215950 | 3.620 |
a Relative energy differences were calculated compared to ct(Cs) conformer.
According to equilibrium given above, we can write
Kc = Na/Nb and Na + Nb = 1
where Kc is conformational equilibrium constant between a and b forms, Na and Nb are mole fractions of conformers a and b.
Here Na = 1/(1 + Kc), Nb = Kc/(1 + Kc), Kc = e−δΔG/RT, R = 1.987 × 10−3 kcal/mol K, T = 298 K and δΔG = ΔGb − ΔGa [37].
Regarding the calculated free energies for the gas phase, mole fractions of ct(Cs) and ct(C1) are almost the same. Relative percentage of ct(Cs) conformer is only slightly bigger than ct(C1) conformer.
4.2 Vibrational studies of 2,4-dmpba
2,4-dmpba consists of 24 atoms, so it has 66 normal vibrational modes and it belongs to the point group Cs in its lowest energy case calculated at 6-31++G(d,p) level of theory. According to the calculations, 13 normal vibrational modes of the title molecule are below 400 cm−1. Cs and C1 point groups are possible for 2,4-dmpba as given in Table 2. Since the cis–trans conformation with Cs point group is the most stable one, all the experimental infrared and Raman results were compared to the theoretical results of ct(Cs) form of 2,4-dmpba. The calculated infrared and Raman wavenumbers together with experimental data of the title molecule are presented in Table 3. Theoretical and experimental (IR and Raman) spectra of 2,4-dmpba are given in Figs. 2 and 3.
Comparison of the experimental and the calculated vibrational wavenumbers (cm−1) of 2,4-dmpba.
| M. | TED (≥ 10%)a | Expb | S. wavenumber | B3LYP/6-311+G(d,p) | ||||
| Cis–trans–Cs | ||||||||
| IR | R | να | νβ | νθ | IIR | IR | ||
| ν66 | νOH(100) | 3480 | – | 3676 | 3445 | 3849 | 15.12 | – |
| ν65 | νOH(100) | 3339 | – | 3600 | 3374 | 3770 | 35.82 | – |
| ν63 | ν6-2(92) | 3063 | 3088 | 3084 | 3076 | 3229 | 1.80 | 44.29 |
| ν61 | ν17-14(84) | 3007 | 3010 | 3012 | 2998 | 3154 | 2.91 | 48.93 |
| ν60 | ν20-19(86) | 2996 | 2999 | 3012 | 2998 | 3154 | 5.01 | 51.33 |
| ν59 | ν15-14(50) + ν16-14(50) | 2972 | 2973 | 2959 | 2946 | 3098 | 6.10 | 23.94 |
| ν58 | ν21-19(50) + ν22-19(50) | 2946 | 2950 | 2949 | 2936 | 3088 | 7.14 | 27.57 |
| ν57 | ν15-14(44) + ν16-14(44) | – | 2882 | 2893 | 2880 | 3029 | – | 72.23 |
| ν56 | ν21-19(45) + ν22-19(45) | 2837 | 2841 | 2887 | 2873 | 3023 | 12.36 | 76.08 |
| ν55 | ν5-4(22) + ν23-22(18) + ν23-3(11) + ν5-1(10) | 1603 | 1605 | 1615 | 1614 | 1653 | 74.57 | 100.00 |
| ν54 | ν2-1(29) + ν4-3 (15) + ν5-1(12) + ν23-3(11) | 1574 | 1574 | 1574 | 1575 | 1611 | 23.16 | 12.87 |
| ν53 | ν4-3(11) + ν5-1(11) | 1508 | 1505 | 1503 | 1501 | 1538 | 5.45 | 13.35 |
| ν51 | δ21-19-22(28) | 1463 | – | 1473 | 1466 | 1508 | 13.33 | – |
| ν50 | δ15-14-16(11) | – | 1450 | 1463 | 1454 | 1497 | – | 19.78 |
| ν47 | δ20-19-18(16) + δ20-19-21(14) δ20-19-22(14) + δ21-19-22(14) δ21-19-18(13) + δ22-19-18(13) | – | 1435 | 1443 | 1436 | 1477 | – | 8.38 |
| ν46c | ν23-2(8) + δ15-14-17(8) δ16-14-17(8) + ν5-4(8) | 1417 | 1412 | 1421 | 1420 | 1455 | 28.42 | 1.28 |
| ν45 | ν12-9(39) + ν10-9(10) + δ11-10-9(10) | 1400 | 1391 | 1370 | 1375 | 1402 | 39.20 | 6.09 |
| ν44 | ν10-9(31) + ν9-3(19) + δ13-12-9(10) | 1342 | 1325 | 1345 | 1350 | 1377 | 100.00 | 42.04 |
| ν43 | ν23-3(19) + ν2-1(15) + ν4-3(14) | 1298 | 1299 | 1308 | 1306 | 1339 | 32.70 | 25.59 |
| ν42 | ν18-1(20) + ν23-2(10) | 1280 | – | 1280 | 1277 | 1310 | 27.44 | – |
| ν41 | δ24-23-3(21) + ν23-3(14) δ24-23-2(11) + ν8-4(10) | 1256 | 1262 | 1255 | 1253 | 1285 | 21.51 | 23.85 |
| ν40 | δ17-14-8(18) + ν8-4(14) | 1207 | 1207 | 1208 | 1202 | 1236 | 33.64 | 5.39 |
| ν39 | δ20-19-18(29) + δ17-14-8(17) | 1185 | 1186 | 1180 | 1175 | 1208 | 0.45 | 9.70 |
| ν38 | δ17-14-8(13) + δ20-19-18(12) + ν8-4(11) δ7-5-4(10) | 1153 | 1152 | 1158 | 1153 | 1185 | 32.55 | 3.19 |
| ν37 | ν23-2(25) + δ6-2-23(18) + δ6-2-1(12) | 1120 | – | 1145 | 1142 | 1172 | 18.32 | – |
| ν34 | δ11-10-9(26) | 1094 | 1110 | 1101 | 1101 | 1127 | 0.32 | 28.05 |
| ν33 | δ11-10-9(26) + ν14-8(21) + ν12-9(10) | 1051 | 1048 | 1059 | 1055 | 1084 | 20.01 | 8.82 |
| ν31 | ν14-8(19) + δ11-10-9(16) + δ13-12-9(15) | 1033 | 1016 | 1024 | 1027 | 1048 | 13.31 | 12.56 |
| ν30 | δ13-12-9(50) + ν10-9(25) + ν12-9(16) | 1013 | 992 | 985 | 982 | 1008 | 30.62 | 5.35 |
| ν28 | ν19-18(19) + ν8-4(16) + ν18-1(11) | 911 | 916 | 913 | 914 | 935 | 2.49 | 26.38 |
| ν27 | τ7-5-4-8(27) + τ7-5-1-18(26) τ7-5-4-3(13) + τ7-5-1-2(10) | 819 | ||||||
| 820 | 823 | 816 | 842 | 8.26 | 0.04 | |||
| ν26 | τ6-2-1-18(25) + τ3-23-2-6(22) τ6-2-1-5(15) | 773 | - | 797 | 791 | 816 | 2.00 | – |
| ν25 | ν2-1(12) + ν4-3(11) + δ2-23-3(11) | 739 | – | 730 | 732 | 747 | 5.16 | – |
| ν24 | τ7-5-4-3(10) + τ10-9-3-4(10) | – | 734 | 726 | 726 | 743 | – | 60.62 |
| ν23 | τ11-10-9-12(53) + τ11-10-9-3(42) | 681 | 674 | 671 | 666 | 687 | 10.35 | 1.43 |
| ν22 | ν9-3(22) + ν18-1(10) | 658 | 659 | 660 | 665 | 676 | 1.12 | 7.41 |
| ν21 | τ13-12-9-10(15) | 640 | – | 646 | 643 | 661 | 10.42 | – |
| ν20 | τ13-12-9-10(11) | 614 | – | 620 | 617 | 635 | 6.65 | – |
| ν19 | δ19-18-1(14) + δ5-4-8(13) + δ2-1-18(11) | 603 | 607 | 595 | 606 | 609 | 0.81 | 12.28 |
| ν18 | ν8-4(14) + δ5-4-3(11) | 545 | – | 528 | 534 | 540 | 16.66 | – |
| ν17 | τ13-12-9-3(50) + τ13-12-9-10(28) | 533 | 535 | 527 | 524 | 539 | 0.57 | 29.44 |
| ν15 | τ3-23-2-1(15) + τ2-23-3-4(13) τ23-2-1-18(10) | 455 | 457 | 452 | 449 | 463 | 3.46 | 2.97 |
a Our vibrational wavenumbers assignments on the basis of total energy distribution (TED) calculations.
b Our experimental IR and Raman wavenumbers, ν, δ, τ: stretching, bending and torsion, respectively.
c TED ≥ 8.
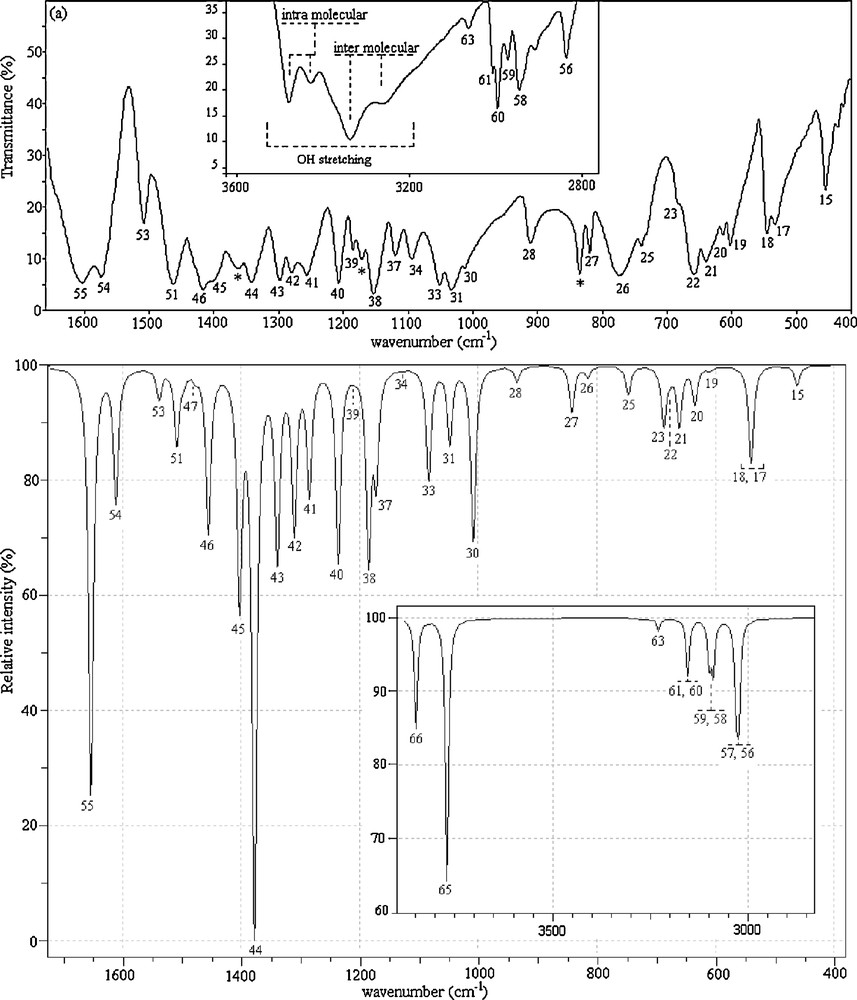
Experimental (a) and unscaled calculated (b) infrared spectra of 2,4-dmpba (mode numbers are given above the respective peaks).
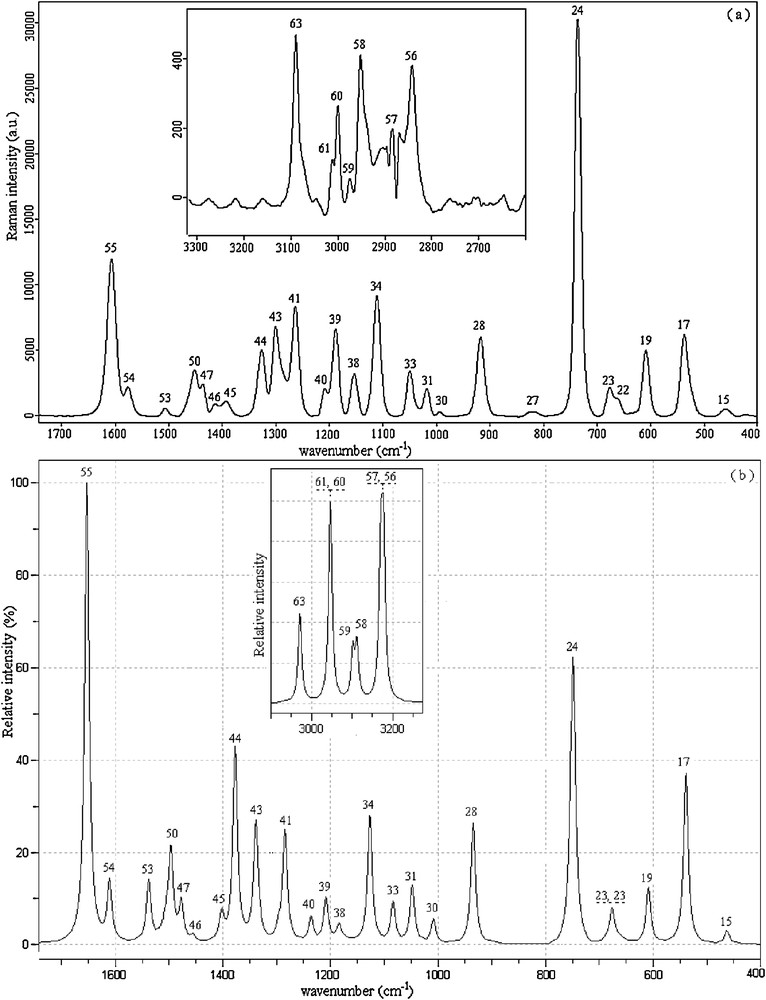
Experimental (a) and unscaled calculated (b) Raman spectra of 2,4-dmpba (mode numbers are given above the respective peaks).
Calculated infrared intensities were modified by assigning the highest intensity peak to 100%. Calculated Raman activities were converted to relative Raman intensities (IR) using the following relationship derived from the intensity theory of Raman scattering [38,39]:
The carbon–carbon stretching modes of the phenyl group occur in the range of 1620 to 1320 cm−1 [40]. In this study, the carbon–carbon stretching vibrations of 2,4-dmpba have been observed at 1605 (R), 1603 (IR), 1574 (IR, R), 1508 (IR) and 1505 cm−1 (R). The corresponding theoretical values of these vibrations are 1615, 1574 and 1503 cm−1. CH3 antisymmetric and symmetric vibrations arise between the region of 1508–1417 cm−1. OBO antisymmetric stretching vibrations were observed at 1391 (R) and 1362 cm−1 (IR). CH stretching vibrations for heteroaromatic structures are commonly appeared in the region of 3000–3200 cm−1. In the high wavenumber region, CH stretching modes of phenyl ring were observed at 3088 (R) and 3063 cm−1 (IR). In the OH region, very strong and broad-band in the spectra of some boronic acid molecules occur at ∼3300 cm−1. In the spectra of phenylboronic acid, [41] and 4-pyridineboronic acids, [42], absorption bands were observed at 3280 and 3467 cm−1, respectively. Special attention is required for OH vibrations of the title molecule. Four OH stretching modes are observed at 3480–3262 cm−1 in the FT-IR spectrum for 2,4-dmpba. Two of them are broad while the remaining two have comparatively lower line width. These results suggest that some of O(11)H possibly include in the formation of intramolecular hydrogen bonding, which lead to two OH bands at 3480 and 3431 cm−1. Likewise, O(12)H tends to be involved in intermolecular hydrogen bonding, resulting in two broad OH bands at 3339 and 3262 cm−1. In short, as seen in Fig. 3a, multiple OH bands could be attributed to potential inter–intra molecular interactions. We also made measurements in the frequency region of 1300–200 cm−1. These vibrations have revealed to be mixed type of vibrations as given in Table 3. In general, B3LYP/6-31++G(d,p) level of calculation with dual scaling factors used in this study [43] provided reasonable agreement with the experimental findings. The results obtained in this study also indicate that B3LYP/6-31++G(d,p) method is reliable and it makes easier the understanding of vibrational spectrum and structural parameters of 2,4-dmpba. In general, B3LYP/6-31++G(d,p) level of calculation with the dual scaling factors [43] and SQM [17,29] methodology used in this study provided reasonable agreement with the experimental findings. The results obtained in this study also indicate that B3LYP/6-31++G(d,p) method is reliable and it makes easier the understanding of vibrational spectrum and structural parameters of 2,6-dmpba. However, during the approximate mode explanations, intra–intermolecular interactions should be taken notice as calculations were performed for a single molecule, which disregards intermolecular interactions. For instance, as in the case observed for OH vibrations, OH groups, which possess intramolecular hydrogen bonding, have lower line width and they appear in the high frequency region compared to broad OH vibrational bands indicating intermolecular hydrogen bonding. In the theoretical calculations, the latter was appeared in the high frequency region. The peaks marked with asterisks in Fig. 2 were possibly due to the hydrogen bonding interactions or they are not available with ct(Cs) conformer.
4.3 NMR studies of 2,4-dmpba
All the experimental and theoretical chemical shift values for 13C (CP/MAS) NMR and 1H measurements are given in Table 4. Considering the chemical environment, 2,4-dmpba shows seven different carbon atoms in its solution state 13C NMR spectrum (Fig. 4a), which is surprisingly not in agreement with the structure regarding molecular symmetry. C2 and C3 seem to have equal chemical shieldings, therefore, they give a singlet. Contrary to averaged solution 13C NMR values, in 13CP/MAS NMR spectrum of 2,4-dmpba (Fig. 4b), C3 gives another broad singlet, which indicates that the chemical environment of C3 in the powder form is different than C3 in the solution form or intramolecular rotation is inhibited. Broadening of C3 is probably due to boron-11, which is a quadrupolar nucleus of spin 1 and so its anisotropy is strongly dependent on x, y and z coordinates relative to boron-11 located at the origin or (0,0). Solution to solid chemical shifts (Δ = δsolution − Δ = δsolid) reflect intermolecular and intramolecular interactions [18]. The biggest chemical shift differences for carbon between the solid and solution sates are 2.79 ppm (C3), which confirm the presence of inter–intramolecular hydrogen bondings, where H11 and H13 are possibly involved. According to the obtained 1H NMR spectrum of the title compound (Fig. 5), protons of OH appear as a singlet at 6.18 ppm, which indicates that both OH protons have the similar chemical environment in solution state, which also requires hydrogen bonding. H6 appears as doublet at 6.59 ppm due to only one neighboring proton. H7 group gives a singlet at 6.49 ppm. Methoxy protons appear at 3.92 and 3.87 ppm. The correlations between C14H15–17, C19H20–22, C5H7, C2–H6 and C23H24 are clearly observed in HETCOR spectrum (Fig. 6).
Experimental and calculated 13C and 1H NMR chemical shifts (ppm) of 2,4-dmpba.
| Nucleus | Experimental (ppm) | Calculated (ppm) | |
| Liquid/solid phase | ct (C1) | ct (Cs) | |
| C4 | 166.45/165.23 | 163.37 | 164.58 |
| C1 | 164.05/163.81 | 160.47 | 161.04 |
| C23 | 138.37/137.71 | 137.01 | 136.87 |
| C3 | 105.49/112.96–108.69a | 109.04 | 107.69 |
| C2, C3 | 105.49/102.70 | 103.62 | 103.03 |
| C5 | 98.29/98.79 | 95.56 | 96.04 |
| C19 | 56.62/56.30 | 55.01 | 55.33 |
| C14 | 55.51/54.12 | 54.69 | 54.67 |
| H24 | 7.81 | 8.26 | 8.18 |
| H6 | 6.59 | 6.68 | 6.75 |
| H7 | 6.49 | 6.52 | 6.57 |
| H11 | 6.18 | 7.06 | 7.20 |
| H13 | 6.18 | 5.05 | 5.06 |
| C(14)H3 | 3.92 | 3.94 | 3.95 |
| C(19)H3 | 3.87 | 3.89 | 3.95 |
a Cannot be cited with high accuracy.
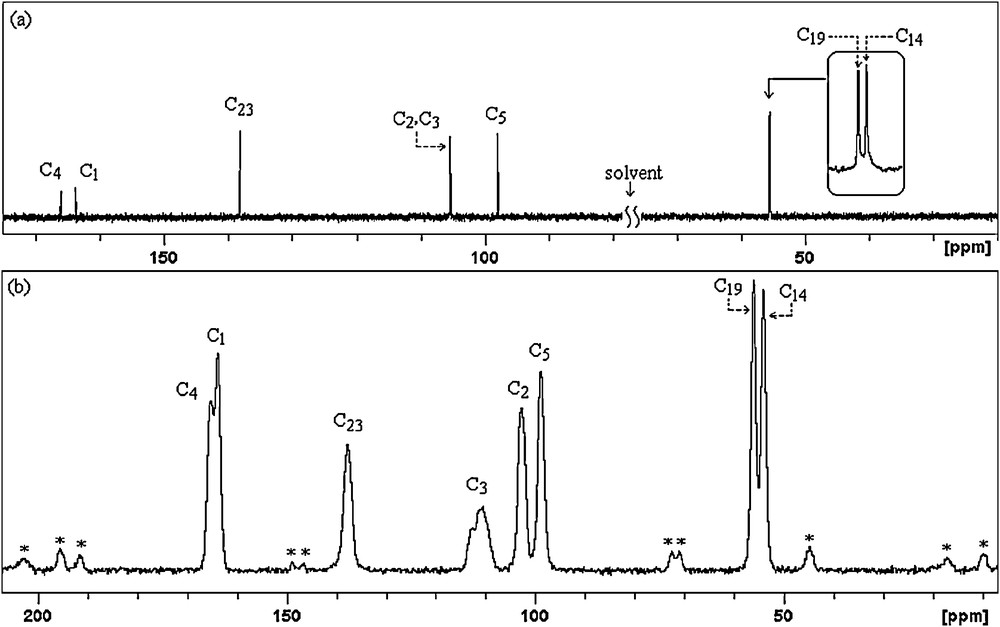
13C NMR (a) and 13C (CP/MAS) NMR (b) spectra of 2,4-dmpba (* indicates spinning sidebands).
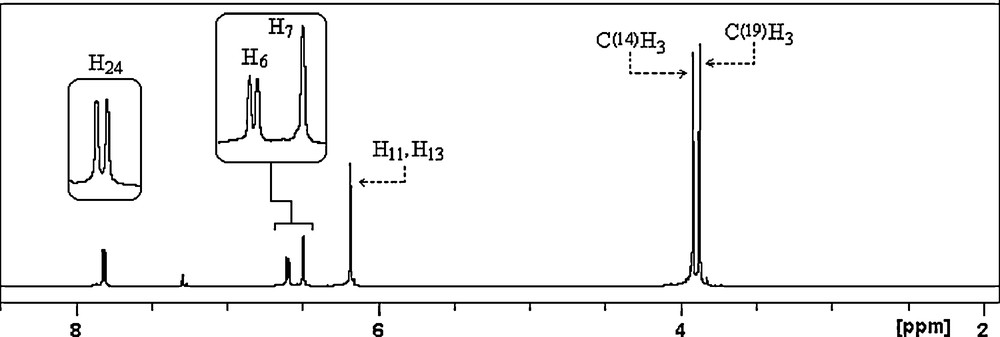
1H NMR spectrum of 2,4-dmpba.
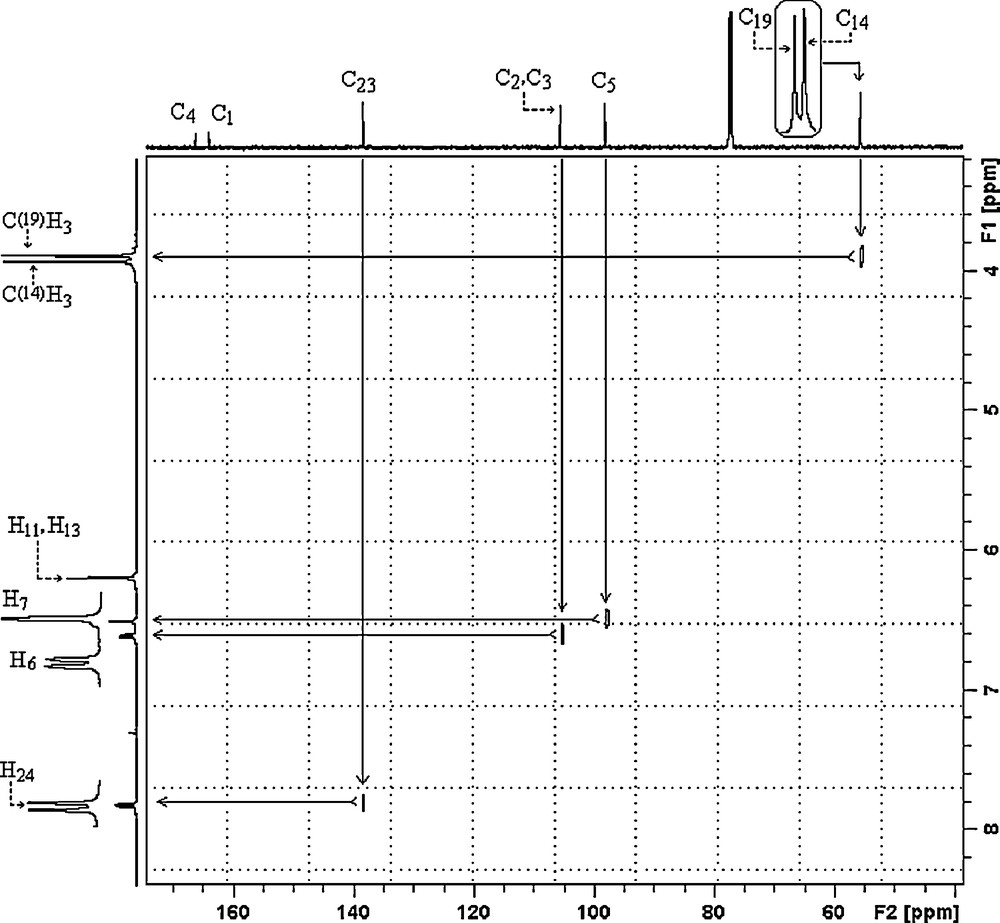
HETCOR NMR spectrum of 2,4-dmpba.
5 Conclusion
This article presents the experimental and theoretical vibrational IR, Raman and (CP/MAS) NMR spectra of 2,4-dmpba molecules. The FT-IR and FT-Raman spectra have been recorded in the range 4000–400 cm−1. Due to the lack of experimental information on the structural parameters available in the literature, theoretical calculations were compared with those for a similar molecule. Some important vibrational bands have been discussed and assigned based on the calculated infrared and Raman intensities. The molecular geometry and all of the vibrational wavenumbers and nuclear magnetic shieldings of 2,4-dmpba in the ground state have been calculated using the density functional method B3LYP/6-31++G(d,p) level. Based on the theoretical calculations following six different molecular structures were proposed: tt(C1), ct(C1), cc(C1), tt(Cs), ct(Cs) and cc(Cs). Optimized energies of the proposed structures indicate that ct(Cs) and ct(C1) are the most stable conformers. Any differences observed between the experimental and the calculated wavenumbers and chemical shifts could be due to the fact that the calculations have been performed for single molecule in the gaseous state contrary to the experimental values recorded in the presence of intermolecular interactions, which is the case in present study and revealed by 13C CP/MAS NMR measurements. Henceforth, the assignments made at B3LYP/6-31++G(d,p) level of theory with only reasonable deviations from the experimental values seem feasible.


