Numerous studies have been carried out these last two decades on strongly correlated electron systems due to their great ability to exhibit magnetic and transport properties susceptible of various applications as functional materials. In this respect, transition metal oxides present a great potential, due to the mixed valence, and to the various coordinations of the transition elements. These characteristics are at the origin either of the delocalisation of charge carriers or of charge ordering, and of the great flexibility of the structures, of numerous transition metal oxides. Among these materials, the high TC superconductivity cuprates, the colossal magnetoresistance (CMR) manganites, the high thermoelectric power cobaltites and the very recently explored multiferroic oxides, have been extensively studied for these promising applications.
The high TC superconducting cuprates have been the object of thousands of publications since the discovery of their properties in 1986. At the present time, three of these oxides, YBa2Cu3O7, called “YBCO”, Bi2Sr2CaCu2O7 and Bi2−xPbxSr2Ca2Cu3O10, called Bi2212 and Bi2223 respectively, are considered for applications, due to their zero resistance and magnetic levitation properties above 77 K, allowing liquid nitrogen to be used as refrigerant for electrotechnical applications such as distribution and connecting cables, transformers, magnets, generators, magnetic bearings and ship propulsion systems, but also in electronic devices, such as mobile phone filters, SQUID detectors in medical imaging, fault current limiters. In fact, these oxides belong to various systems: Y-Ba-Cu-O, La-Ba-Ca-Cu-O, Bi-Sr-Ca-Cu-O, Tl-Ba-Ca-Cu-O and Hg-Ba-Ca-Cu-O. One important condition for the appearance of superconductivity in these oxides deals with the fact that they exhibit the mixed valence Cu2+/Cu3+. This characteristic makes that the positive carriers (holes) provided by Cu3+ species, can be delocalized over the “copper-oxygen” framework leading to a semi-metallic or metallic type conductivity. However, this property is not sufficient to induce superconductivity, a second condition must be fulfilled, which deals with the bidimensionality of the structure. In fact, the structure of superconductive cuprates should consist of layers of “CuO4” square planar units sharing corners as schematized in Fig. 1. Such [CuO2]∝ layers are superconductive, i.e. contain the delocalized holes and are separated from each other by hole reservoir layers (of Bi, Pb, Sr, La, Y oxides). It is this anisotropy which hinders strong magnetic interactions between the copper-oxygen layers and is necessary for the appearance of superconductivity at high temperature in oxides. This bidimensionality of the structure is strongly favoured in cuprates, owing to the Jahn Teller effect of copper which allows an elongation of the Cu–O bonds corresponding to the dz2 orbitals of copper. As a result, copper can accommodate various coordinations, as illustrated for the bismuth cuprates superconductors (Fig. 2), which consist of quadruple hole reservoir layers “Bi2Sr2O4” stacked with superconductive copper oxygen layers, built up either of elongated CuO6 octahedra like in Bi2Sr2CuO6, or CuO5 pyramids like in Bi2Sr2CaCu2O8, or of CuO5 pyramids and CuO4 square planar groups like in Bi2Sr2Cu3O10. In this way, the critical temperature TC increases with the number of coupled copper layers from 22 K for Bi2Sr2Cu2O6 (n = 1) to 110 K for Bi2Sr2Ca2Cu3O10 (n = 3). Thus, the key factors which govern the superconducting properties of the cuprates are mainly the mixed valence Cu2+/Cu3+ and the associated hole carrier density which needs to be optimized, the Jahn-Teller effect of copper and the bidimensionality of the structure. Importantly, these superconductors exhibit a short coherence length, which makes that their utilisation as polycrystalline materials is limited by grain boundary effect, so that numerous investigations have been carried out for the texturation of these materials in order to enhance their performances in the form of ribbons or films or wires with a preferred orientation.

Schematic representation of the [CuO2]α layers in superconductive cuprates built up of corner-shared CuO4 square planar groups. Between these layers, rock salt layers (SrO, BaO, TlO, BiO…) play the role of hole reservoirs.
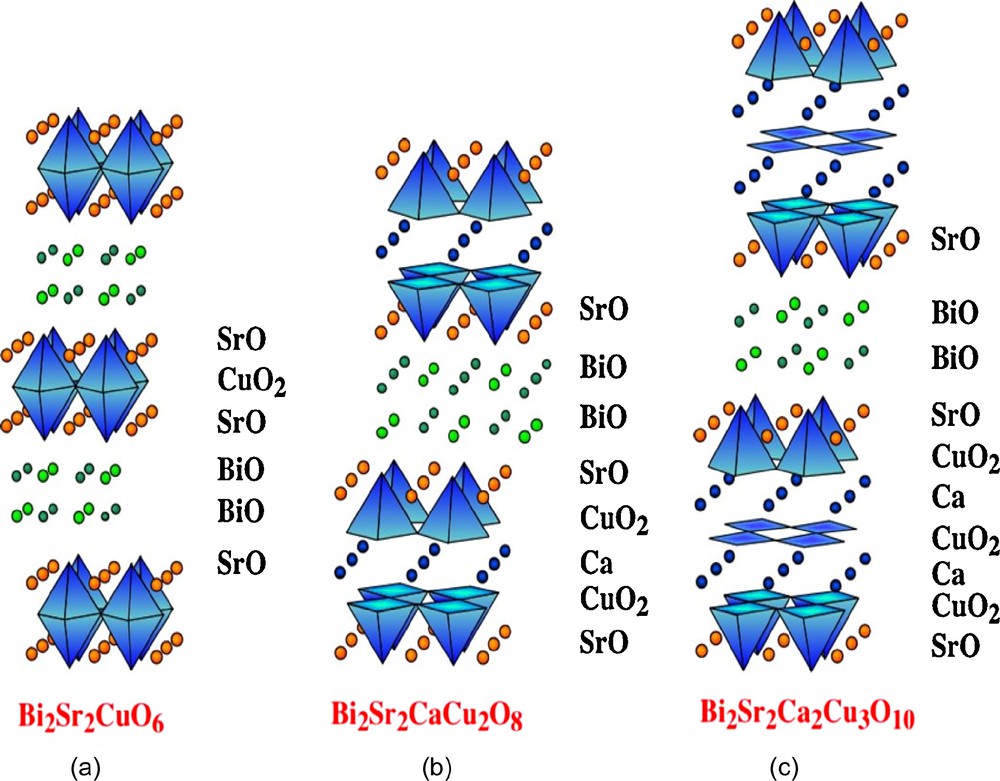
Structures of the high TC superconductive cuprates, where the Jahn-Teller effect of copper allows single octahedral copper layers (a) or double pyramidal copper layers (b) or triple pyramidal/square planar layers (c) to be formed.
The CMR manganites have also been the subject of numerous investigations since 1995, due to their ability to exhibit a decrease of their resistivity by several orders of magnitude by applying a magnetic field. In fact, these manganese oxides belong to the perovskite family with the generic formulation Ln1−xAxMnO3, where Ln is a lanthanide element and A is a divalent cations (Ca, Sr, Ba). The introduction of a bivalent cation, A = Ca, Sr, Ba, into the cages of the perovskite structure of LaMnO3 (Fig. 3) induces the mixed valence Mn3+/Mn4+, according to the formula Ln1−xAIIxMnIII1−xMnIVxO3. Like for the cuprates, the existence of this mixed valence of manganese is absolutely crucial for the appearance of CMR properties. Indeed, the appearance of magnetoresistance in such oxides corresponds to the transition from an insulating or semi-conducting state to a semi-metallic or metallic state by applying a magnetic field. This is illustrated, as an example for the oxide Pr0.7Ca0.25Sr0.05MnO3 (Fig. 3), whose resistivity is decreased by 15 orders of magnitude at 30 K under a magnetic field of 5 T. Thus, the possibility of existence of a semi-metallic state requires, here again a delocalisation of the holes provided by the Mn4+ species over the [MnO3]∝ framework of the perovskite. The mechanism of the CMR effect can easily be understood by considering the orthorhombic perovskite Pr0.5Ca0.5 MnO3 (Fig. 4), which in the absence of magnetic field exhibits charge and orbital ordering, i.e. rows of Mn3+ species alternating with rows of Mn4+ species. The former exhibits a distorted perovskite structure with an elongation of the Mn3+ octahedra along the direction of the dz2 orbitals, whereas the Mn4+ octahedra remain practically regular. As a consequence, the lack of orbital overlapping along the Mn3+–O–Mn4+ bonds makes that this oxide is an antiferromagnetic insulator. By applying a high magnetic field (> 25 T), the distortion of the structure tends to disappear leading to a practically cubic perovskite (Fig. 4). It results in a complete overlapping of the Mn-O-Mn orbitals which are oriented at 180°, so that charge ordering disappears, through double exchange phenomena. It is this double exchange which is responsible for the appearance of metallic conductivity and ferromagnetism. In other words, the CMR effect corresponds to the transition from an antiferromagnetic insulating (AFMI) to a ferromagnetic metallic (FM) state. Starting from this point, it can be seen that the magnetic field value of 25 T is much too high to be used for CMR application. In order to decrease the value of the applied magnetic field, we have to decrease the value of the applied magnetic field, i.e. to decrease dramatically the Jahn-Teller effect of Mn3+, so that the AFMI phase becomes metastable, and concomitantly the charge-orbital ordering on the manganese sites would be destroyed. For this purpose, the doping of the Mn3+ sites with a non Jahn-Teller cation is of great interest since it destroys locally the elongation of the octahedra and favours a 180° overlapping of the d orbitals (Fig. 5a). Such a doping of the Mn3+ sites by trivalent cations (1 to 5%) such as Ga3+, Al3+ has indeed allowed to decrease the H value to less than 4 T. Importantly, the doping with a magnetic cation such as Cr3+ is still more efficient, since additionally it expands the ferromagnetic state through an antiferromagnetic coupling of Cr3+ with surrounding Mn species (Fig. 6). Thus, in such systems a new physics appears, which deals with magnetic and electronic phase separation, as illustrated schematically on Fig. 7. Around each doping cation (Ga3+, Cr3+) FM clusters are formed within the AFMI matrix (Fig. 7a). The crystal symmetry of these FM islands is higher than that of the AFMI matrix, developing strains at the interfaces. Then the FM regions grow, by increasing the magnetic field (Fig. 7b), leading to percolation so that the material becomes FM. This transformation which has been shown to be martensitic, requires a doping with only some percents of M3+ cations. Note that a similar effect can be obtained by doping the A sites of the perovskite structure with large divalent cations, such as Ba3+ or Sr2+. This is illustrated on Fig. 5b which shows that for small cation like Ca2+, the perovskite cage is distorted favouring the Jahn-Teller effect of Mn3+, whereas introducing a larger cation like Ba2+ tends to make the cage more symmetric and favours the formation of more symmetric domains around Ba2+, and consequently tends to destroy locally the Jahn-Teller effect of Mn3+. Thus the mixed valence Mn3+/Mn4+ and the Jahn-Teller of manganese are, similarly to cuprates, key factors which play a capital role in the CMR effect of manganese. However differently, there are several other parameters, namely charge-orbital ordering and nanoscale phase separation which must be taken into consideration to tune the CMR properties of these oxides. Though they appear as very promising materials for magnetic recording and storage, and as actuators and sensors, the performances of the CMR manganites remain still far from the application, requiring a magnetic field of 500 mT to reach a magnetoresistance of ∼8% at room temperature, i.e. far from the giant magneto resistance thin films discovered by A. Fert, and already commercially available.
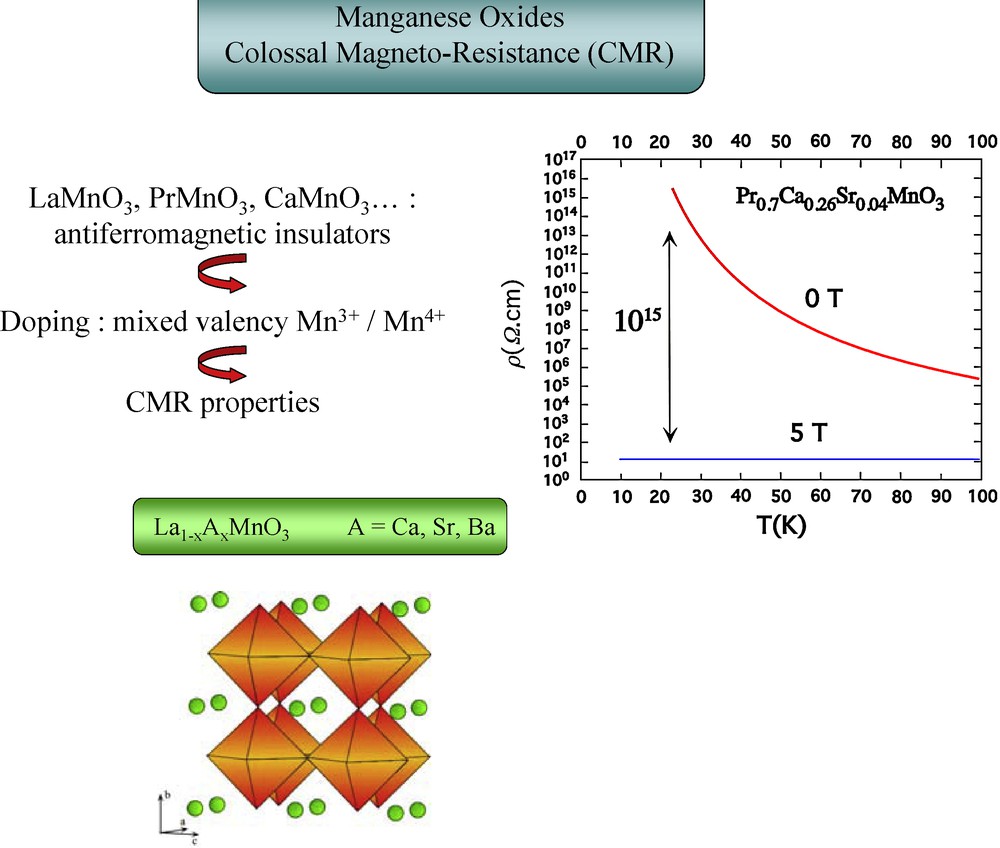
Example of ρ(T) curves in zero magnetic field (0 T) and under 5 T for a perovskite Pr0.7Ca0.26Sr0.04, showing a large magneto resistance effect at low temperature.
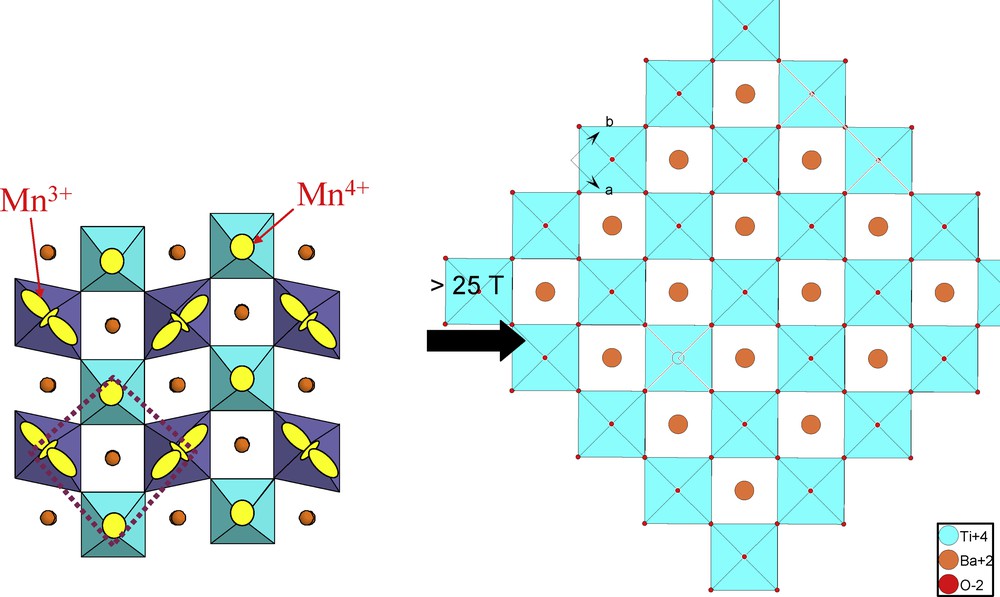
Pr0.5Ca0.5MnO3 perovskite: transition from the distorted orthorhombic structure, involving charge orbital ordering in the form of Mn3+ and Mn4+ rows to a cubic or pseudo cubic perovskite characterized by a delocalisation of the manganese charges, by applying a magnetic field larger than 25 T.
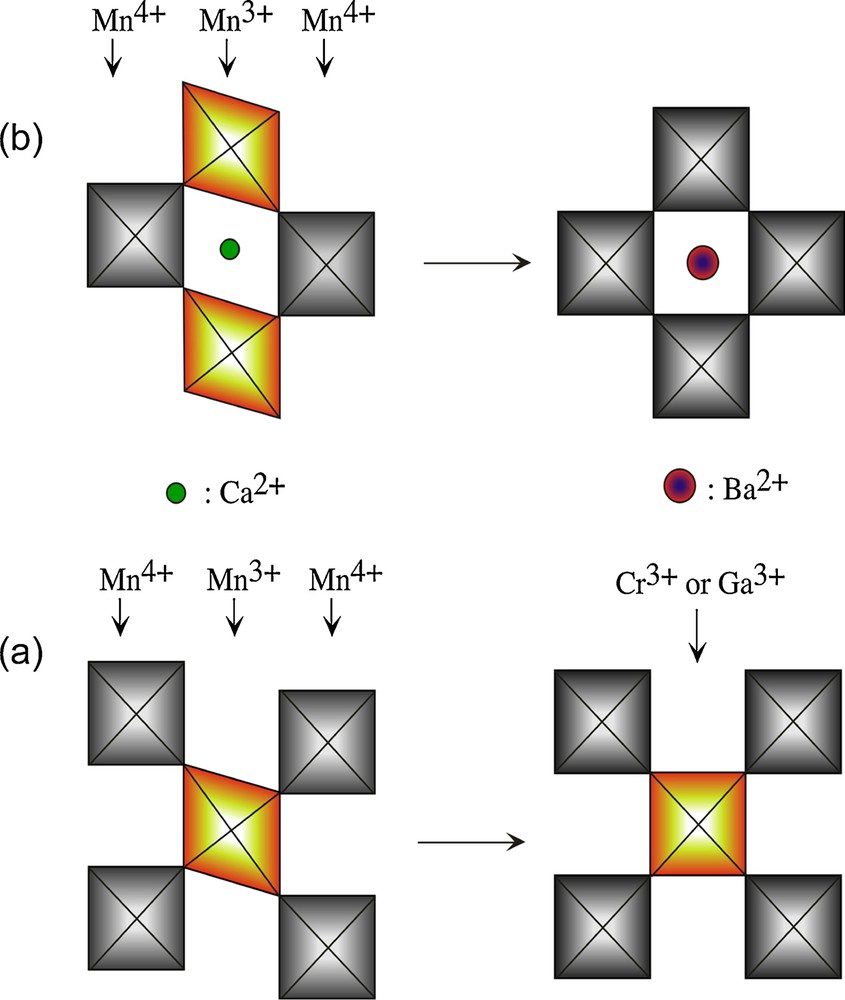
Local destruction of the Jahn-Teller effect of Mn3+ by local doping: (a) of the Mn3+ sites by non Jahn-Teller cations (Ga3+, Cr3+), (b) of the Ca2+ sites by larger Ba2+ cations.
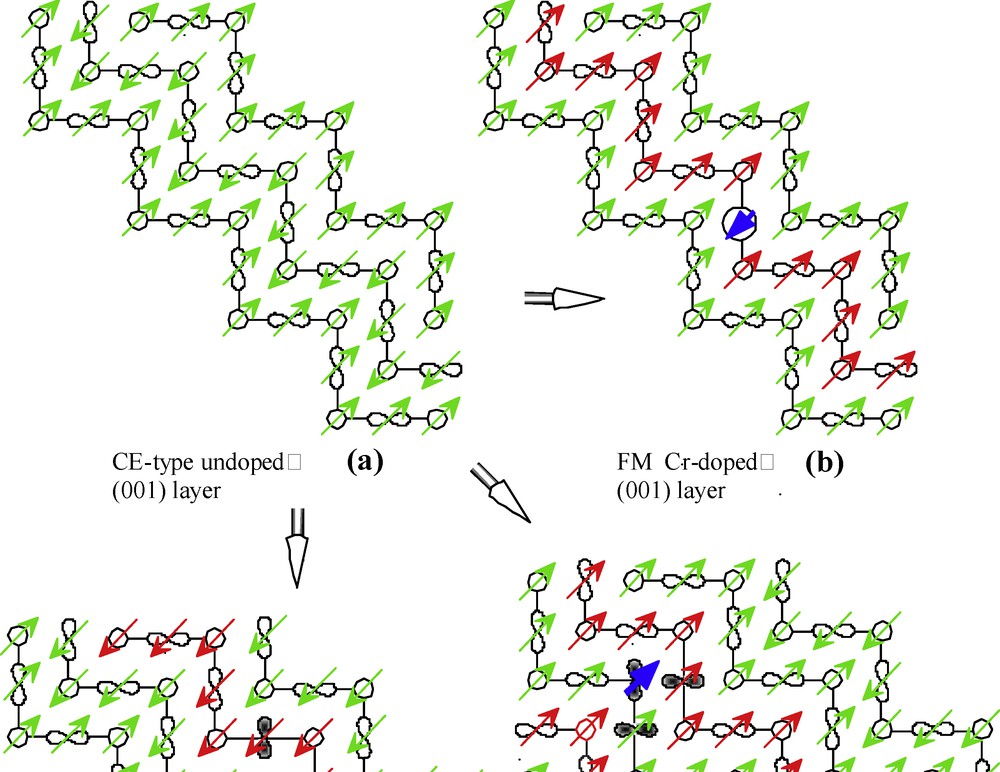
Effect of doping Mn3+ sites with a magnetic cation such as Cr3+ (blue arrow). The latter induces a local antiferromagnetic coupling with its Mn neighbours, which induces spin reversal and creates locally ferromagnetic domains, even in the absence of applied magnetic field.
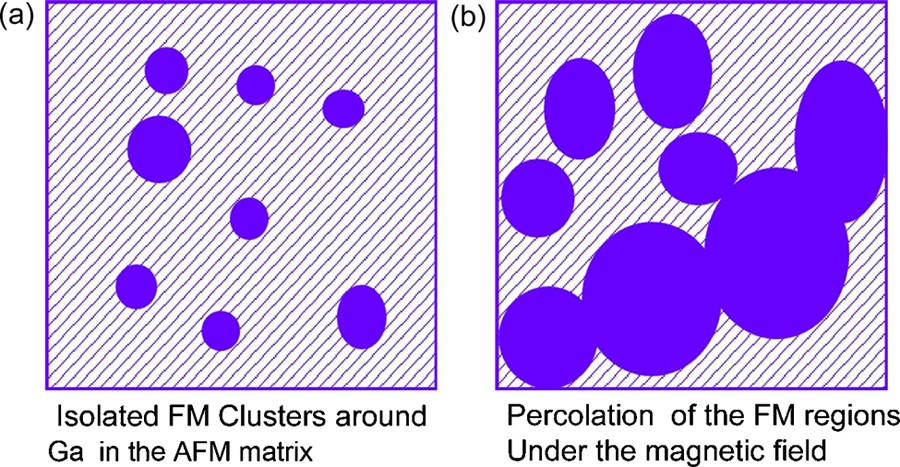
Magnetic phase separation scenario showing: (a) ferromagnetic clusters (FM) formed around each non Jahn-Teller cation such as Ga within the antiferromagnetic (AFM) matrix (hatched) and, (b) expansion of these clusters under a magnetic field leading to percolation of the FM regions.
The growing needs in energy have incited to consider the wasted heat as a possible source for producing electricity, since a great part of energy is wasted in incinerators, factories, but also in cars and trucks. For instance, in a car only ∼25% of the gasoline is used for the mobility, whereas ∼40% is lost as heat at the exhaust pipe and ∼30% for cooling (Fig. 8). For this reason, thermoelectric oxides were recently revisited in view of discovering new materials susceptible to be used for the conversion of heat into electrical energy. Indeed, by coupling p-type and n-type semi-conductors, a thermogenerator can be set up based on the Seebeck effect and involving a temperature gradient between a hot and cold surface (Fig. 9). In order to be efficient, such thermoelectric oxides should exhibit a high thermoelectric power (S), a low resistivity (ρ) and a low thermal conductivity (k) according to the figure of merit ZT = (S2/ρk) T, where T is the temperature. Moreover, these thermoelectric materials should work at high temperature, i.e. in the range 900–1200 K in oxidizing atmosphere. Very few compounds, except transition metal oxides, can be used in such conditions without encapsulation. In this respect, the cobaltite NaxCoO2 and the recently discovered misfit cobaltites of the systems Ca-Co-O, Tl-Sr-Co-O, Bi-Sr-Co-O and Pb-Sr-Co-O are quite remarkable and are promising p-type thermoelectric materials. Again, the existence of rather high conductivity of these oxides, requires the mixed valence Co3+/Co4+ to be fulfilled, the positive carriers being provided by Co4+ species. The structure of these cobaltites consists of [CoO2]α layers built up of edge-sharing CoO6 octahedra similar to the CdI2-type structure, as exemplified for Na0.5CoO2 (Fig. 10) and for the misfit oxide (Bi0.87SrO2)2 (CoO2)1.82 (Fig. 11). The triangular geometry of such layers favours magnetic frustration and allows in this way better electronic conductivity. The Na+ layers in Na0.5CoO2 (Fig. 10), as well as the quadruple oxygen deficient rock salt layers [(Bi0.87SrO2)2]α (Fig. 11) weaken the magnetic interactions between the layers, and may also contribute to the decrease of thermal conductivity due to a partial disordering of their cations and anions. For these reasons Na0.5CoO2, exhibits a rather high thermoelectric power, S ≅ 100 μV/K, much larger than for a normal metal, in spite of its rather low resistivity, ρ ∼ 2.10−4 Ωcm. The value of the thermoelectric power is even substantially increased for the bismuth based misfit cobaltites up to ∼ 140 μV/K (Fig. 12), for rather low resistivity values, which are so far not completely optimized. Thus, these cobalt oxides appear as promising thermoelectric materials, showing that the mixed valence Co3+/Co4+ and the bidimensionality of the structure are key factors for the realisation of p-type thermoelectrics working at high temperature. Nevertheless, the ZT figure of merit remains still rather low, i.e. close to 0.4–0.5 and will require further investigations of mixed valent oxides for applications.

Typical energy path in gasoline fueled internal combustion engine vehicle.

Principle of Seebeck effect of a thermogenerator.

Lamellar structure of Na0.5CoO2 built up [CoO2]∝ triangular layers of edge-shared CoO6 octahedra interleaved with Na+ cations.

Lamellar structure of the misfit cobaltite (Bi0.87SrO2)2 (CoO2)1.82 built up of triangular [CoO2]α layers intergrown with [Bi0.87SrO2]2 rock salt layers.
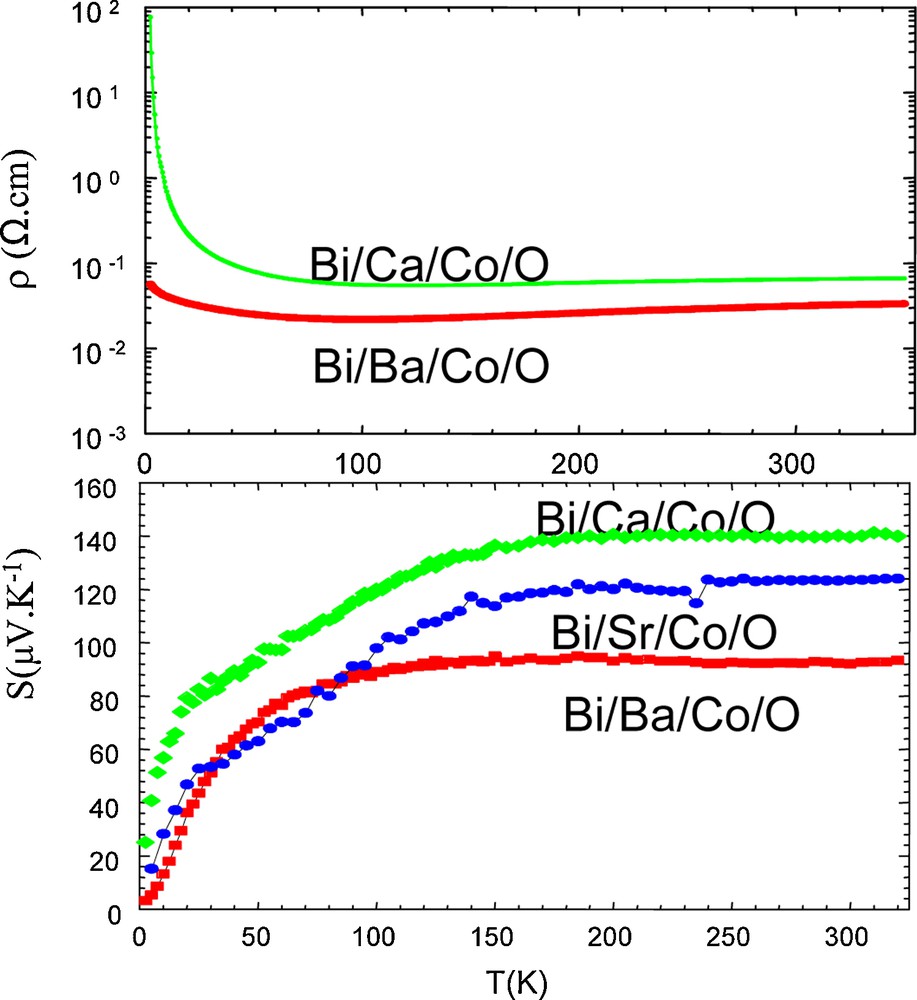
Some S(T) and ρ(T) curves obtained for the misfit cobaltites of the Bi-A-Co-O systems with A = Ca, Sr, Ba.
Transition metal oxides are also involved in the investigations performed these last years for the research of new multiferroic materials. In such systems, ferroelectricity and magnetism (antiferromagnetism or ferromagnetism) coexist within the same matrix of a single phase. Importantly, this coexistence is not sufficient to create multiferroism, i.e. a coupling between ferroelectricity and ferromagnetism or antiferromagnetism, called magnetoelectric coupling is necessary. Thus, in a multiferroic material, the spontaneous magnetization can be switched by an electrical field, and reciprocally an electrical polarization can be switched by a magnetic field. It results that multiferroics have potential applications for memory storage, since they can exhibit additional degree of freedom in device design compared to pure magnetic materials involved in spintronics. Therefore, it should be possible to design multiple-state memory elements, by storing the data in both magnetic and electrical polarizations, and novel memory media should be considered by writing of ferroelectric data and reading of the magnetic field generated by association. Attention must be drawn on the fact that, for applications, it is absolutely necessary to control the magnetoelectric coupling by a magnetic field. Consequently, among all the multiferroics that can be discovered, only those which are ferromagnetic are of interest for such applications. The magnetoelectric properties of oxides, mainly perovskites, are known since more than 30 years, but most of the compounds are antiferromagnetic (Table 1) if one excepts BiMnO3, which can only be obtained under high pressure of several kbars. Several strategies have been used to discover new multiferroic oxides, considering to date mainly perovskites. The first strategy which consists in doping a ferroelectric matrix, such as BaTiO3 at Ti sites by magnetic cations (such as Fe, Mn, Co) is, as expected inappropriate since it involves both magnetic dilution and ferroelectricity destruction. In the same way, the doping of a ferromagnetic matrix, such as (Ln, Sr)MnO3 at Mn site with ad d0 “ferroelectric” element (such as Ti, or Nb) is inefficient since it leads to a destruction of ferromagnetism. A second strategy was proposed which can be described as the macroscopic association of a ferrimagnetic spinel such as Fe3O4 (for instance in the form of rods) within a ferroelectric matrix such as BaTiO3. An interesting effect described as multiferroism was observed, but these results were not confirmed subsequently. The third strategy which is realized in the case of thin films, is so far the most fruitful. It consists of the stacking of ultrathin layers of a ferroelectric material (e.g. BaTiO3) with a ferromagnetic material (e.g. (La, Ca) MnO3) as schematized in Fig. 13. In this way, numerous superlattices can be constructed, whose multiferroic properties can be tuned by varying the thickness of the layers, the thickness of the film and the distribution of the cations. These compounds offer a vast field of investigation, where the role of the interfaces between the layers, of the strains and of the charge distribution are still not completely understood. Finally, a fourth direction of research has been started recently, which is based on the association of one ferroelectric sublattice, with one ferromagnetic sublattice within the same crystals structure. This strategy can be applied to the perovskite structure ABO3, where the B sublattice which forms the BO6 octahedra can be occupied by magnetic cations (e.g. Fe, Co, Mn) forming the ferromagnetic sublattice, whereas the A sublattice can be occupied by lone pair cations such as Bi3+ or Pb2+, which may induce ferroelectricity. This is the case of the perovskite La0.5Bi0.5Mn0.5Fe0.5O3, which exhibits both a hysteresis loop characteristic of ferromagnetism (Fig. 14) and a reversal of its electric polarization in an applied electric field of 3.5 kV/cm (Fig. 15). These results suggest strongly the magnetoelectric character of this oxide, through the interaction between magnetism and ferroelectricity has to date not been proved. Finally, it is worth to emphasize that there remains a vast field for the investigation of this phenomenon, but that to date no result has been obtained at sufficiently high temperature for applications.
Some multiferroic oxides.
| Ferroelectric order | Magnetic order | Tc (K) | TN (K) or Tc (K) | |
| Pb(Fe2/3W1/3)O3 | FE | AFM | 178 | 363 |
| Pb(Fe1/2Ta1/2)O3 | FE | AFM | 233 | 180 |
| Pb(Fe1/2Nb1/2)O3 | FE | AFM | 387 | 143 |
| BiFeO3 | FE | AFM | 1123 | 650 |
| BiMnO3 | FE | FM | 773 | 103 |
| YMnO3 | FE | AFM | 913 | 80 |
| HoMnO3 | FE | AFM/WFM | 873 | 76 |

Stacking of BaTiO3 (BTO) and (La, Ca)1MnO3 (LCMO) ultrathin layers for the realisation of multiferroic superlattices in thin films.
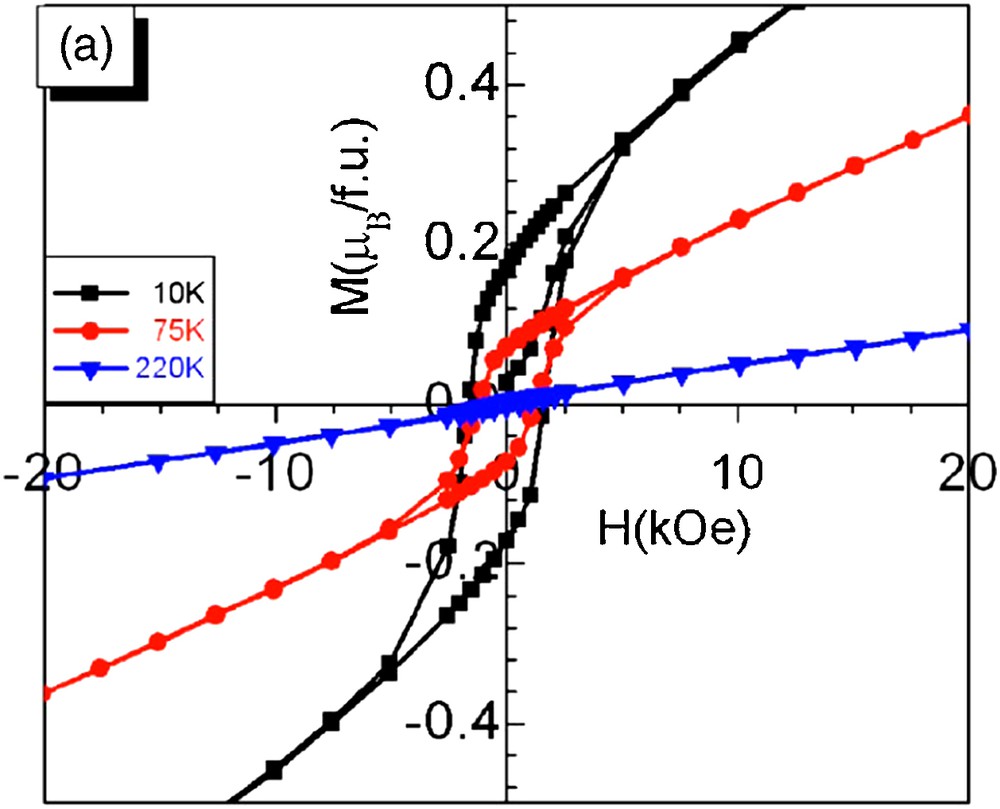
Isothermal magnetization M(H) of La0.5Bi0.5Mn0.5Fe0.5O3 perovskite registered at various temperatures.
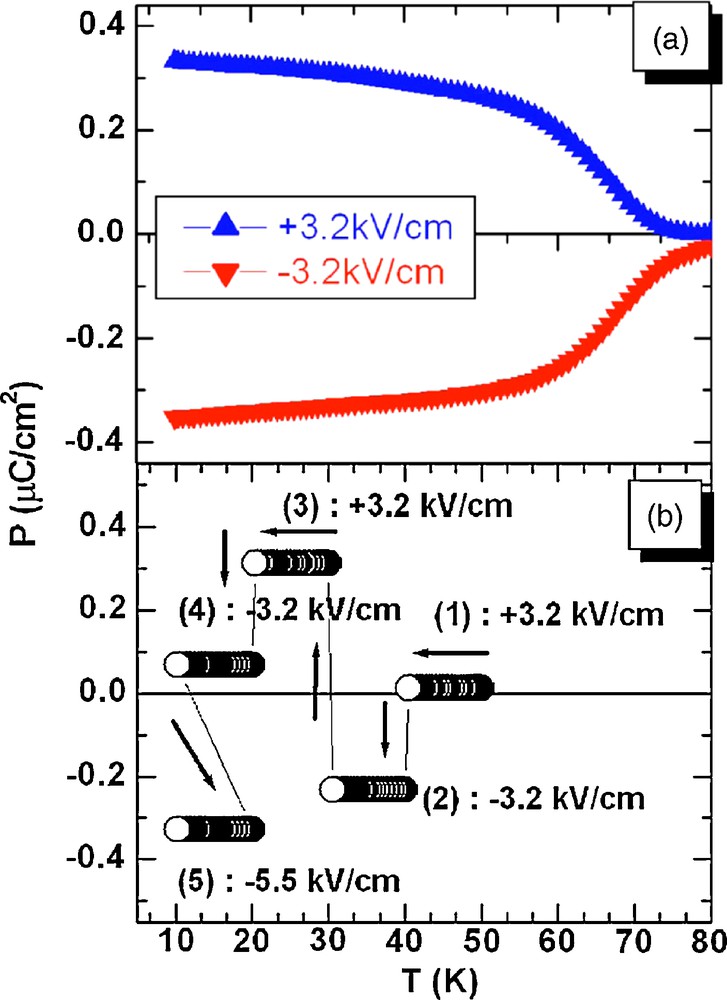
La0.5Bi0.5Mn0.5Fe0.5O3: (a) temperature dependence of electric polarization in an applied field of 3.2 kV/cm. (b) Electric field-dependant reversal at low temperature on different applied field directions. The arrows and numbers indicate the way the measurement is made.
In conclusion, transition metal oxides represent an extraordinary rich domain for the exploration of strongly correlated electron systems. The study of their physics, especially magnetism and transport properties requires a simultaneous investigation of their crystal chemistry, bearing in mind that complex phenomena such as electronic or magnetic phase separation, or charge-orbital ordering may appear, and can be influenced by oxygen non stoichiometry, Jahn-Teller effect, order-disorder phenomena. Importantly such materials can be regarded as a source for various applications.


