1 Introduction
Polyoxometallates “POM” anions belong to a fascinating class of big polynuclear metal-oxygen highly charged clusters of versatile structure and composition, whose properties (e.g. redox and acido-basic behavior, reactivity, magnetism, formation of supramolecular assemblies) result from the interplay between their intrinsic structural and electronic features and interactions with the solvent, counterions and other solute species [1,2]. Because many POMs applications (e.g. chemical analysis, catalysis, multifunctional materials, medicine) involve reactions occurring in solution or at liquid interfaces [3] it is important to not only characterize their precise composition, geometrical and electronic structure, but also to understand how they interact with the heterogeneous surrounding medium and with each other. The main theoretical approaches to address these issues are quantum mechanics QM and molecular dynamics MD, respectively [4]. Car-Parrinello dynamics simulations based on DFT representation of the potential energy can combine both approaches, but are still restricted to relatively small systems (see e.g. the CPMD study of the possible intermediates forming the W6O192− Lindqvist anion in water [5]). For the prototypical Keggin anion [XМ12O40]n− (M is W6+ or Mo6+, and X is a main group element or transition metal ion) and analogues, there are indeed QM studies on electronic and structural features, sometimes modelling the solvent by a continuum polarizable medium (for recent accounts see refs. [6–8]) whereas MD simulations on solutions focused on its solvation and dynamics. More specifically, Lopez et al. studied the hydration and dynamic properties of α-PW12O403− (hereafter noted PW3−; Fig. 1) with Na+ counterions, [9] whereas Leroy et al. focused on the effect of charge of [XW12O40]n− anions (X = P/Si/W) and of counterions (Li+/Na+/K+) on ion pairing and dynamics in water [10]. Dendrimer encapsulated PW3− anions have been simulated by MD in trichloromethane solution to model dendrizyme, a hybrid material where the POM ion is surrounded by a shell of cationic dendrimers [11]. The structure and dynamics of water encapsulated in porous POM - based nanocapsules has also been simulated by MD [12]. Our own MD interest in the POM domain started 20 years ago by the simulation of the V12O324− “concave anion” in water and acetonitrile solutions, stimulated by the QM studies of Marc Bénard and Marie-Madeleine Rohmer [6]. More recently, we studied aqueous solutions of PW3− Mn+ salts at two concentrations, comparing cations of different charges and hydrophilic character: NBu4+, Cs+, H3O+, H5O2+, UO22+ and Eu3+ [13]. We found that, in spite of their mutual repulsions, PW3− anions can make short contact in water (at P…P distances of ca. 11 Å), and that the amount and lifetime of (PW3−)n dimers and oligomers are modulated by the nature of the Mn+ counterions. The specific role of water was highlighted by comparing water to methanol solutions: in methanol, no anion pairing was observed, but the salts formed aggregates involving cation mediated interactions PW3−Mn+(MeOH)pPW3−.

The simulated PW3− anion (PW12O403−; W atoms in blue; O atoms in red).
In this article, we more quantitatively investigate the effectiveness of like-ion interactions in solution, by calculating the free energy profiles as a function of the PW3−…PW3− distance d. By coupling perturbation statistical thermodynamics with MD simulations that sample representative states of the solvent, the solute and counterions at each d distance, it is indeed possible to calculate the change in free energy ΔG when d is smoothly varied (potential of mean force PMF calculations [14,15]). The PMFs studied here involve a single PW3−…PW3− pair in a water box with either H3O+, UO22+ or Eu3+ counterions, corresponding to concentration of ca. 0.02 mol/l. For the PW2(Eu)2 salt, further investigations are pursued: (i) First, the effect of aqueous concentration, by simulating a more concentrated solution (ca. 0.2 mol/l) with 20 PW(Eu) species per box. (ii) On the methodological side, we want to assess to which extent the PMF results are model dependent (For the related case of alkali halide ions in water, the PMF dependence on water models (SPC, TIP3P, SPC/E, TIP4P-Ew, TIP5P-E) and ion models (e.g. OPLS, Dang, JJ) has been discussed by [16]), by comparing three water models (TIP3P, SPC/E and the polarizable POL3 model), as well as three representations of the PW3− atomic charges. (iii) The sampling issue is also addressed by comparing different simulation times for each PMF. Furthermore, to assess the specific role of the PW3− shape and granularity on ion pairing in water, we compare the PW3−…PW3− pair (Eu3+ counterions) to: (iv) the fictitious PW3+…PW3+ analogue (with all inversed charges on PW and “Eu3−” as counterion); and (v) the S3−…S3− pair with spherical model analogues of PW3−. Finally, the specific role of water is investigated by comparing the PW3−…PW3− PMF in water versus methanol solutions.
2 Methods
2.1 Molecular dynamics
The systems were simulated by classical molecular dynamics “MD” using the modified AMBER.10 software [17] in which the potential energy U is empirically described by a sum of bond, angle and dihedral deformation energies and pair wise additive 1-6-12 (electrostatic + van der Waals) interactions between non bonded atoms.
| (1) |
Cross terms in van der Waals interactions were constructed using the Lorentz-Berthelot rules. The PW12O403−anion's parameters have been taken from the work of Lopez et al., [9] using their CHELPG atomic charges. Tests with their Mulliken and “hand made” charges were also performed. The Eu3+ and UO22+ ions parameters were from refs [18] and [19], respectively, and the H3O+ charges have been fitted on electrostatic potentials (DFT-B3LYP/6-31G** calculations).
For the solvents, we used the TIP3P model [20] for water and the OPLS model for methanol [21]. We also tested the SPC/E model of water for the PW2(Eu)2 solution [22] and the polarizable POL3 model of Kollman and Caldwell [23] for the PW2(H3O)6 solution, in conjunction with the H3O+ model of ref. [24]. The 1-4 van der Waals and 1-4 coulombic interactions were scaled down by 2.0. The solutions were simulated with 3D-periodic boundary conditions, using an atom based cutoff of 12 Å for non-bonded interactions, and correcting for the long-range electrostatics by using the PME (particle -particle mesh Ewald) summation method [25]. The characteristics of the different simulated systems are given in Table 1.
Characteristics of the simulated systems.
| Solute | PW3− Charges | Solvent | Box Size (Å3) | Temp (K) |
| 2 PW3−, 2 Eu3+ | CHELP | 6989 H2O (TIP3P) | 59.8 × 59.8 × 59.8 | 300 |
| 2 PW3−, 2 Eu3+ | Mulliken | 6989 H2O (TIP3P) | 59.8 × 59.8 × 59.8 | 300 |
| 2 PW3−, 2 Eu3+ | Hand Made | 6989 H2O (TIP3P) | 59.7 × 59.7 × 59.7 | 300 |
| 2 PW3−, 2 Eu3+ | CHELP | 6989 H2O (SPCE) | 59.5 × 59.5 × 59.5 | 300 |
| 2 PW3−, 2 Eu3+ | CHELP | 3201 MeOH | 62.9 × 62.9 × 62.9 | 300 |
| 20 PW3−, 20 Eu3+ | CHELP | 6550 H2O (TIP3P) | 59.6 × 59.6 × 59.6 | 300 |
| 2 PW3−, 3 UO22+ | CHELP | 7002 H2O (TIP3P) | 59.9 × 59.9 × 59.9 | 300 |
| 2 PW3−, 6 H3O+ | CHELP | 7036 H2O (TIP3P) | 60.0 × 60.0 × 60.0 | 300 |
| 2 PW3−, 6 H3O+ | CHELP | 7041 H2O (POL3) | 60.8 × 60.8 × 60.8 | 300 |
| 2 PW3+, 2 Eu3− | CHELP | 6989 H2O (TIP3P) | 59.8 × 59.8 × 59.8 | 300 |
| 2 S3−, 2 Eu3+ | CHELP | 6989 H2O (TIP3P) | 59.8 × 59.8 × 59.8 | 300 |
The MD simulations were performed at 300 K starting with random velocities. The temperature was monitored by coupling the system to a thermal bath using the Berendsen algorithm [26] with a relaxation time of 0.2 ps. In the (NPT) simulations, the pressure was similarly coupled to a barostat [26] with a relaxation time of 0.2 ps. A time step of 2 fs was used to integrate the equations of motion via the Verlet leapfrog algorithm.
2.2 Potential of mean force “PMF” calculations
We calculated the free energy profiles ΔG(d) for PW3−…PW3− and analogues with different counterions in aqueous and methanol solutions as a function of the P…P distance d. The PMF simulations started (λ = 1) after 5 ns of MD equilibration with separated anions (P…P distance d = 22.5 Å). The d distance was linearly reduced by steps Δd = 0.01 Å, until the energy became repulsive (d = 8–10 Å, depending on the system; λ = 0).
| (2) |
The change in free energy at each step λ was calculated using the thermodynamic integration method (TI) based on Eq. (2) [27]. For each system, we performed two PMF simulations, (noted PMF5+10 and PMF10+40, respectively) that differed by the times of equilibration + data collection and averaging at each λ step: 5 + 10 ps and 10 + 40 ps, respectively. The total simulated times amount to ca. 20 ns and 65 ns, respectively per PMF. For the PW3−…PW3− pair (with either H3O+, UO22+ or Eu3+ as counterions), we further calculated PMFs using larger steps (Δd = 0.1 Å) and increased sampling at each step (50 + 200 ps). They are noted PMF50+200.
3 Results
Unless otherwise specified, we discuss the results obtained with the TIP3P water model, ChelpG charges on PW3−, and the PMF10+40 procedure that yields similar energy curves as the PMF5+10 procedure (red curves and green curves, respectively in Figs. 2–4). Methodological tests on selected systems will be also reported.
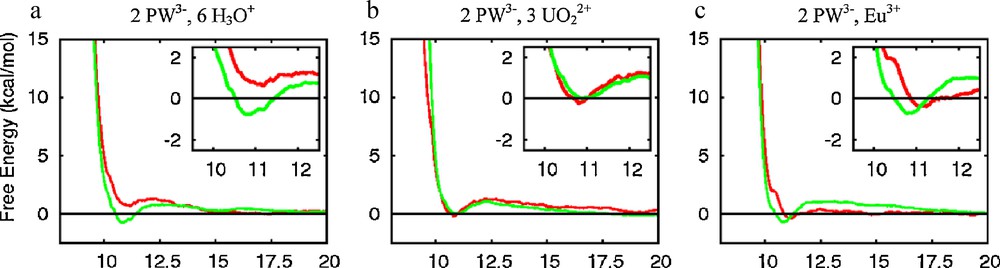
2 PW3− Mn+ ions in TIP3P water: Free energy profile (in kcal/mol) as a function of the P…P distance d in (Å), calculated with two sampling + averaging time procedures: 5 + 10 ps (red curve PMF5+10), 10 + 40 ps (green curve PMF10+40) and Δd = 0.01 Å.
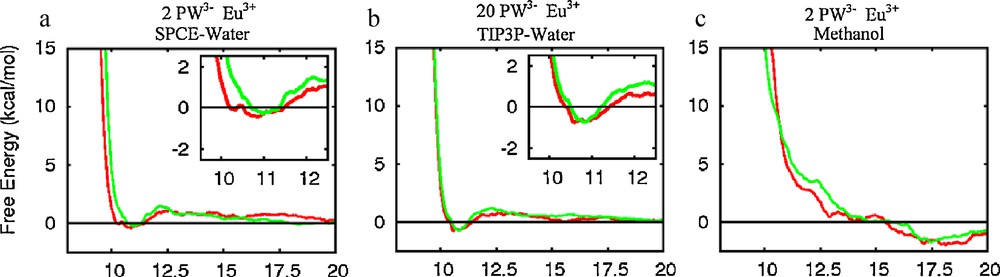
PW3− Eu3+ in water or methanol: Free energy profile (in kcal/mol) as a function of the P…P distance d in (Å). Red curve: PMF5+10; green curve: PMF10+40, Δd = 0.01 Å.
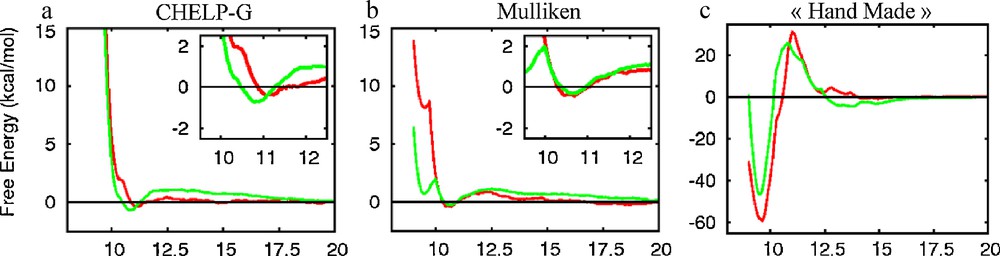
2 PW3− Eu3+ in TIP3P water: Free energy profile (in kcal/mol) as a function of the P…P distance d in (Å) with three PW3− charge models: Chelp-G, Mulliken and “Hand Made”. Red curve: PMF5+10; green curve: PMF10+40 with Δd = 0.01 Å.
3.1 PW3−…PW3− interactions with H3O+, UO22+, or Eu3+ counterions in water
The free energy profiles obtained with mono-, di- and tri-valent cations (Fig. 2) are strikingly similar: as the P…P distance d decreases from 20 to ca. 12.5 Å, the energy slightly increases (by ca. 1 kcal/mol), and then decreases to nearly zero at ca. 10.9 Å. Below ca. 10 Å, the energy becomes strongly repulsive due to steric repulsion between the anions. Thus, according to these results, there is neither repulsion, nor clear attraction between the two PW3− anions in the studied range of distances with either H3O+, UO22+ or Eu3+ counterions in water. Repeating the same PMF calculation for the PW(Eu) salt, but at a higher concentration (10 times higher) yields a similar “flat”energy profile, with a tiny minimum at ca. 10.9 Å (Fig. 3b).
To investigate the possible model dependence of the PMF results, [16] we decided to first compare two water models and several charge representations of the anions of the PW(Eu) “diluted solution”. The TIP3P water model was thus compared to the SPC/E one that yields, among others, smaller diffusion coefficients [28] and different interfacial properties of neat water and ionic solutions [29]. The PMFs obtained with both models (Figs. 2c and 3a) are quasi superimposable, however, indicating that their features are not critically dependent on the water model.
Polarization effects also modulate the solvent properties and, possibly, the PMF results. Note, however, that in cases (e.g. Na+…Cl− [30], or Guanidinium+…Guanidinium+ pairs [31]) where PMFs with simple 1-6-12 additive models have been compared to those with added polarization, the effect of polarizability has been found to be small. For the present study, quantitative assessment of polarization effects would require full reparametrization of, among others, PW charges. As exploratory investigation, we decided to calculate the PMF curve for PW3− dimerization (H3O+ counterions) in polarizable POL3 water [23], using larger steps (Δd = 0.1 Å) and a reduced sampling at each λ step (5 + 10 ps) to avoid prohibitive computer costs. The results (Fig. 5) are in fact similar to those obtained without polarization (see PMF5+10 red curve of Fig. 2a). Interestingly, with polarization, the contact ion pair gets more stabilized (by ca. -1.5 kcal/mol) than in TIP3P water.

2 PW3− + 6 H3O+. PMF5+10 with polarisable POL3 water: free energy profiles as a function of the P…P distance d (5ps + 10 ps, Δd = 0.1 Å).
For PW3−, different sets of charges (ChelpG, Mulliken and “hand made”) have been reported by Lopez et al. [9]. See also ref. [32]. Because the Ot and Ob oxygens are less charged with the Mulliken model (−0.72 and −0.94 e, respectively) than with the ChelpG model (−0.85 and −1.55 e), they yield lower polarity of the W–Ot and W–Ob bonds and hence weaker and more labile H–bonds with water [9]. However, PMF results obtained with Mulliken and ChelpG charges are similar (Fig. 4), confirming that the calculated lack of effective Anion…Anion repulsion in water is little sensitive to the electrostatic representation of PW3−: with both sets of charges, the PW3−…PW3− dimer has comparable free energies at ca. 10.9 Å and 20 Å. Not surprisingly, the PMF obtained with the “hand made” model (−2 charged oxygens) that exaggerates H-bonding interactions differs from the other two PMFs, thereby exaggerating the repulsion at ca. 12 Å (+25 kcal/mol) and the attraction (−42 kcal/mol) at contact distances.
The sampling issue was also further investigated by recalculating the PW3−…PW3− PMF's with increased sampling at each step (50 + 200 ps), while the step size was increased to Δd = 0.1 Å. The PMF50+200 results obtained with either Eu3+, UO22+ or H3O+ counterions (Fig. 6) display similar trends as the corresponding PMF10+40 curves, but reveal interesting features at short distances: a small minimum appears now at ca. 10.8 Å for Eu3+ and UO22+ salts, corresponding to an energy stabilization of ca. 0.7 kcal/mol. With H3O+ as counterions there is no such minimum, which would be consistent with increased effective attractions between PW's when their counterions get more charged.
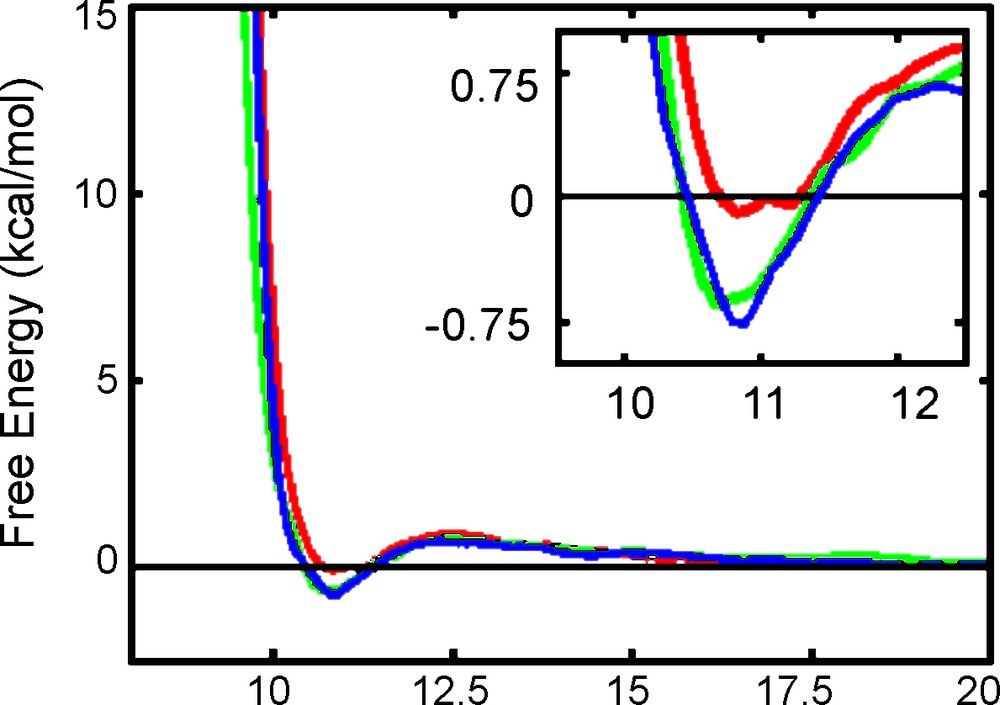
2 PW3− + m Mn+ (m Mn+ = 2 Eu3+ (blue), 3 UO22+ (green) and 6 H3O+ (red)): Free energy profiles as a function of the P…P distance d (TI method, 50ps + 200 ps, Δd = 0.1 Å).
Examination of the solvation patterns at contact distances (P…P = 10.8 Å) confirms the presence of bridging H-bonding interactions with water (Figs. 7 and 8a). As observed in unconstrained MD simulations [13], one finds ca. 6 H2O molecules forming Ot…H–O–H…Ob relays between terminal and bridging oxygens of adjacent PW's. It thus seems that the latter partly compensate for the coulombic repulsion between the PW's.
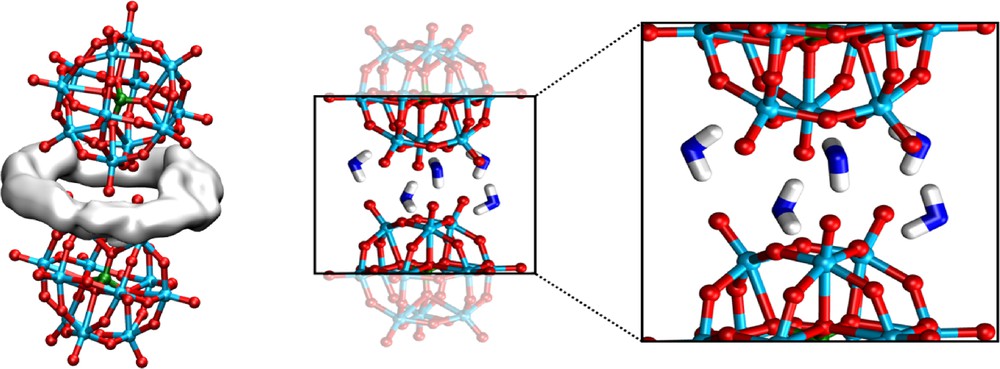
PW3−…PW3− dimer in water: HH2O density between two PW's (averaged over 500 ps; left) and snapshot of bridging water molecules (middle and right).

Snapshot of water molecules between two PW3−, 2 S3− or 2 PW3+ ions.
3.2 How important are bridging water interactions? Comparisons with other systems
3.2.1 PMF simulations on fictitious analogues of PW3− in water and comparison with a methanol solution
From the observation of water-mediated formation of PW3− “dimers”, it can be surmised that replacing PW3− by S3− spherical analogues (modelled with AMBER parameters R* = 6.0 Å, ɛ = 0.1 kcal/mol) will yield somewhat different free energy profiles. In fact (Fig. 9a), the two S3− anions approach each other from 20 to 15 Å without free energy penalty, as for the PW3− anions. At shorter distances, however, ΔG increases first smoothly (by ca. 2 kcal/mol at 10 Å), and then sharply, due to steric + coulombic repulsions. Comparison with the PW3−…PW3− PMF indicates a small energy gain (ca. 2 kcal/mol) with the latter at short contacts, due to the granularity of the anion. In fact, one also finds bridging H2O molecules between the two S3− anions at contact distances (Fig. 8b), but the resulting H-bonds are non-specific and thus weaker than those connecting the two PW3− anions.

PMFs of S3− and PW3+ analogues of PW3− in TIP3P water: Free energy profiles (in kcal/mol) as a function of the distance d in (Å). Red curve: PMF5+10; green curve: PMF10+40.
According to continuum solvation models like the Born model [33], the solvation energy of a given ion of Q charge depends on Q2, yielding in principle the same energies for a cation and anion of “identical” sizes like the AsPh4+ and BPh4− ions (TATB hypothesis) [34]. Specific interactions with the solvent due to the sign of the ion's charge can be important, however [35]. This is shown here by the calculated PW3+…PW3+ PMF between the fictitious cation analogues of PW3− (with all atomic ChelpG charges inversed and with fictitious Eu3− counterions). The ΔG(d) profile (Fig. 9b) is somewhat more repulsive at short distances (ca. +2 kcal/mol between 12.5 and 10.9 Å) for the PW3+…PW3+ pair than for the PW3−…PW3− pair. Indeed, water cannot afford bridging H-bonds with the cationic dimer but solvates the contact region of this dimer via its OH2O oxygens (Fig. 8c). Thus, as found for charged nanosized solutes, interactions between anions are more attractive than between cations [36].
The specific role of water on PW dimerization is shown by the PMF results for PW3−…PW3− (Eu3+ salts) in water versus methanol solutions (Fig. 3c). In methanol solution, a free energy minimum is observed at a P…P separation of ca. 17.5 Å, while ΔG becomes repulsive at shorter distances (ΔG = +3 kcal/mol at 12 Å). The free energy minimum corresponds to a cation separated pair, of PW3−…Eu(MeOH)93+…PW3− type, where the MeOH protons are H-bonded to PW3− oxygens (Fig. 10). Clearly, uncomplexed methanol molecules cannot afford bridging relays between PW3− anions, preventing stabilization of PW3− dimers in solution.
Snapshot of the PW3−… Eu(MeOH)93+ …. PW3− pair at a P…P distance of 17.5 Å, corresponding to the free energy minimum along the PMF in methanol.
3.2.2 Effect of the charge's sign on aggregation in water: comparison on concentrated solutions of PW3− Eu3+ versus PW3+ Eu3−
According to the above PMF results, inverting the sign of the PW ion changes the short range effective interaction between PWs from slightly attractive (ca. −1 kcal/mol or less with PW3−) to slightly repulsive (ca. +2 kcal/mol with PW3+). To further appreciate this sign effect on aggregation, we compared concentrated aqueous solutions (20 ion pairs per box) of PW3− Eu3+ versus fictitious PW3+ Eu3− salts, and analyzed as in ref. [13] the amount of like-ions pairs between PW's. The criteria for ion pairing was to select P…P distances d below 12 Å along the dynamics. For the PW3+ Eu3− salt one finds almost no oligomerization: only 3% of dimers and 97% of monomers. This contrasts with the PW3− Eu3+ salt that forms 35% of oligomers (24% of dimers, 9% of trimers and 2% of tetramers; Fig. 7 in ref. [13]) and 65% of monomers during the dynamics in water. These results are consistent with the small differences in free energy profiles between the two types of ion pairs.
4 Discussion and conclusions
Free energy calculations are the keystone of modelling “effective interactions” in solution [15]. PMF results are reported for the PW3−…PW3− like-ion pair and analogues in water as a function of the ionic separation, comparing different water and PW models. They show that the free energy profiles are quite flat, with the different hydrophilic counterions investigated (H3O+, UO22+, or Eu3+). Thus, in spite of their high coulombic repulsion (ca. +250 kcal/mol at a P…P distance of 11 Å), the −3 charged ions can approach each other from ca. 20 Å up to 10.9 Å, without free energy penalty, to form “contact” ion pairs. In the “best” simulations (highest sampling for PMF50+200 with UO22+ and Eu3+ counterions, polarized POL3 water for PMF5+10 with H3O+ counterions), the “contact” ion pair even corresponds to a small energy minimum at P…P distances comparable to those found in hydrated crystals (10.4 Å for PW12O40(Na2H), [37] 9.75 Å for PW12O40(K3) [37], 10.8 Å for PW12O40(H5O2)3) [38]. Effective interactions in solution result from the interplay between ion/ion interactions, solute/solvent and solvent/solvent interactions, involving enthalpic and entropic components [39]. In principle, the PMF simulations account for changes of these components, providing neither individual thermodynamic contributions, nor contributions of cations/anions/solvent interactions, though. Our comparisons with methanol and with S3− and PW3+ analogues of PW3− clearly point to the importance of water environment and related mediated contacts between the anions. In the following, we compare PW's with other ions that tend also to approach each other in aqueous solution, and discuss some implications in POM's chemistry.
4.1 Analogy with other like-ion dimers: from halides to macro-ions and neutralization by counterions
4.1.1 Bridging water molecules
The PW3−…PW3− “dimers” found at contact distances display interesting analogies with those evidenced by PMF simulations on X−…X− halides. Indeed, the PMF curves of F−…F− and Cl−…Cl− like-ions display a free energy minimum at short distances in water [40]. The dimers are stabilized by bridging water molecules, as revealed by analysis of the MD trajectories, by QM results on X−(HOH)mX− aggregates and by crystal structure analysis, showing a correlation between the OH2O…Cl distances with bridging H2O molecules and Cl…Cl distances [41]. Furthermore, in the gas phase, the F−(HOH)mF− aggregates are more stable than their Cl−(HOH)mCl− analogues of same composition, due to stronger H-bonds with water in the former [41]. In non-aqueous solution (e.g. methanol [42] or DMSO [43]), no such dimers can form. Di-cation analogues (Na+…Na+) that cannot be solvated by bridging water molecules are unstable in water [44] as well as in non-aqueous solvents [42]. In the case of PW3− anions, one also finds specific microsolvation patterns, namely a relay of bridging water molecules between the two ions at contact, but the resulting energy gain is modest (a few kcal/mol), as indicated by the comparison between PW3− and the S3− spherical analogues or the fictitious PW3+ cations. On the computational side, note that the stabilization of the (PW3−)2 dimer, compared to the (S3−)2 analogue highlights the importance of atomistic representation of the anion and of the solvent.
4.1.2 Hydrophobic effects
Hydrophobic forces also contribute to the apparent “attraction” between like-ions, a well-known feature of charged amphiphiles [45]. Even “big spherical” ions seem to attract each other in water. For instance, dicarbollide anions [(B9C2H8Cl3)2Co]− have been found by MD simulations and light scattering experiments to condense in water in the form of large aggregates whose size, shape and dynamics depend on the Mn+ counterion [46]. Likewise, mono- or di-charged cryptates can display short contacts in water, with marked counterions effects [47,48]. These species can be viewed as hydrophobic (relatively small) macro-ions with reduced charges that tend to self-assemble in water. PMF simulations on bigger like-charged nanosized spherical solutes (of 11 Å radius, i.e. twice the radius of S3−) show that hydrophobic attractions in water are strong enough to overcome coulombic repulsions [36]. Other cases of like-ion association by hydrophobic forces involve flat ions like Pic− (picrate = 2,4,6-trinitrophenoxide). According to PMF simulations, a free energy minimum is observed for the π-stacked (Pic−)2 dimer in water, but not in methanol [49]. Stacking releases water from the hydrophobic faces of Pic− (this is entropically favorable) while retaining hydrophilic hydration (H-bonds) at the periphery. Likewise, the flat guanidinium N(CH2)3+ cations are found to form dimers and stacks in water [31,50]. Thus, solvation forces (plus some dispersion attractions) can be strong enough to overcompensate the coulombic repulsions in these stacked dimers (ca. +60 kcal/mol). PW3− anions are quite voluminous (ca. 600 Å3) and thus display hydrophobic features, as do their S3− and PW3+ isosteric analogues that can also, according to our PMF results, approach each other in water with modest energy penalty. On the experimental side, hydrophobic forces likely contribute to the extraction of H3PW12O40 and related heteropolyacids (e.g. H3PMo12O40, H4SiW12O40, H4SiMo12O40) from acidic water to organic solvents, presumably in the form of solvated cation(s) - anion pairs [51,52]. Even the more charged P2W17O6110−, P2W18O626−, SiW11O398− polyanions can be extracted (with some protons) from acidic water to TBP/dodecane mixtures [53]. Thus, in spite of their strong interactions with water, POMs can be expelled out of water to the heterogeneous oxygenated organic phase.
4.1.3 Counterion effects
As mentioned above, counterions also contribute to the stability of dimers. Experimentally, counterions are known to determine critical aspects of the POM's synthesis and structure, catalytic and aggregation behavior and nanoscale architecture [54,55]. POM's and the studied PW3− ions can be viewed as small macro-ions or nanoparticles that tend to “attract each other” in water [56]. According to Monte Carlo simulations [57], the clustering mechanism of highly charged (e.g. −12 or −24 charges) macro-ions likely involves partial neutralization by Mn+ counterions (trivalent are more efficient than di- or mono-valent ones), as suggested for colloïdal systems [58].
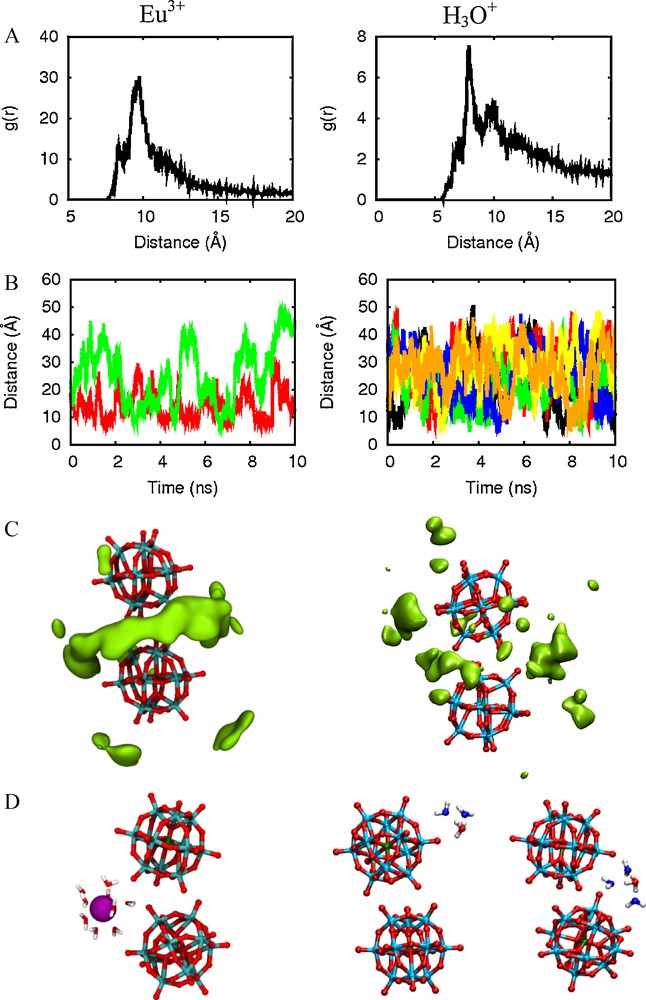
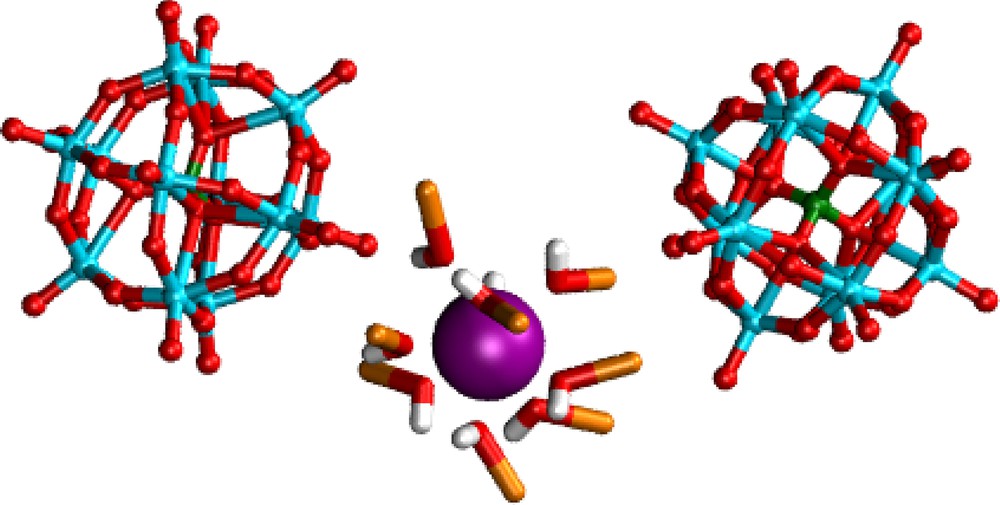
To analyze the distribution of counterions around the PW3−…PW3− dimer, we decided to simulate the latter for 10 ns of dynamics, comparing Eu3+ to H3O+ counterions1. The results (Fig. 11) evidence partial (ca. 45%) charge neutralization of the −6 charge by Eu3+: the COM…Eu RDF (COM = Center of Mass of the dimer) peaks at ca. 10 Å and integrates to 0.9 Eu3+ cations within 15 Å (Fig. 11A). The COM…Eu distances fluctuate with time between ca. 10 and 40 Å (Fig. 11B), showing that the Eu3+ ions are highly mobile, though, with lifetimes of ca. 2 ns near contact distances with the dimer (10 – 12 Å). The highest density regions of Eu3+ correspond to a tore (Fig. 11 C), thus acting as a “cationic glue” connecting the two PWs. Note that Eu3+ never displays direct contacts with PW3− since it is fully hydrated, forming to the Eu(H2O)93+ species (Fig. 11D)2. With H3O+ counterions, interactions with the anionic dimer are much weaker: the COM…OH3O+ RDF peaks at ca. 8 Å but integrates to only 1.0 H3O+ within 15 Å (This can be compared to the simulation results of Leroy et al. [59] who find that ca. 0.24 Na+ cations are in contact with PW3− in water. Within 9 Å, we find 0.22 H3O+ cations around the dimer), and the hydrated protons diffuse rapidly. The highest density regions are more delocalized for H3O+ than for Eu3+: some correspond to bridging positions, while others correspond to hydrogen bonding interactions with more remote Ot oxygens of PW3− or to more remote water-mediated contacts. See typical snapshots in Fig. 11D. Surprisingly, however, the differences between Eu3+ and H3O+ distributions around the dimer are not reflected by the PMF curves that are quite similar, possibly due to still insufficient sampling of counterion states at every P…P distance along the PMF calculations, and to the neglect of polarization effects in these calculations2.
4.1.4 Implications in POMs chemistry: dimerization, assembling, third phase formation and surface activity
The PMF results are relevant in several domains of POMs chemistry, such as condensation and assembling. Condensation depends on the nature of the POMs constituents and basicity, and on the medium [8,60]. At the early stages of dimerization or assembling, the ions must approach each other at short contacts, which should be prevented by coulombic repulsions alone. Our PMF results however indicate that this can be a facile process in aqueous solution. Likewise cluster growing should be facilitated by the lack of effective repulsions between big negatively charged anionic components [61]. Another fascinating feature of POMs is self-assembling into hollow spherical superstructures in solution, reminiscent of micelles formed by charged amphiphiles, with pronounced medium and counterion effects [61,62]. Interestingly, it has been observed that the radius of the shell grows linearly with the inverse of the dielectric constant of the medium in which POMs are dispersed, i.e. with the water content and related hydrophobic forces [63].
Effective attraction between like-ions is also apparent in the formation of “third phase” in liquid–liquid extraction processes. Upon extraction of PWs from a nitric acid solution to a TBP/Octane phase, a third phase appears at very low PW concentration, much lower than the so far most effective third-phase forming inorganic acid (HClO4) [52]. According to SANS studies, each PW is surrounded by ca. 3 TBPs in the third phase, and the interparticle interactions are estimated to be ca. −1.4 kT at the limiting concentration in the organic phase. Thus, weak interparticle interactions are sufficient to induce phase separation of PW-containing particles [64].
4.1.5 Surface activity
Like-ions aggregation in water is a well known feature of amphiphiles that can assemble into aggregates, micelles or membranes and thus adsorb at aqueous interfaces [45]. Generally speaking, there is a deep relationship between ion aggregation in water and surface activity, even for big “spherical” ions [65]. For instance, according to MD simulations, spherical Sn+ and Sn− ions [66], tetrahedral AsPh4+ and BPh4− ions [67], 222-cryptates[47], +4 charged tetrahedral macrocyclic receptors [68], or a −6 charged metallic complex [69] display surface activity, and also aggregate somewhat in water. Likewise, dicarbollide anions that aggregate in water also adsorb at aqueous interfaces, with marked counterion effects [46,70]. Soft anions can also be “attracted” by non-polar surfaces of proteins, [71] possibly contributing to the attraction between positively charged proteins prior to crystallization [72] and to the Hofmeister classification of salts [73]. PWs can adsorb at aqueous interfaces with classical fluids, hydrophobic ionic liquids or solids (graphite) [74]. Adsorption at surfaces promotes processes like formation of films via self assembly [2,75], or catalytic activity at aqueous interfaces [55]. The bigger the POM anion, the higher is the corresponding cavitation energy in water [76], and its tendency to aggregate in water and to be surface active. The interplay between pH-dependent POM/cation and POM/POM interactions, ions hydration and solvent induced attraction between like charged POM's is stressed to strongly determine self assembly processes, a challenge for future simulation and experimental studies.
Acknowledgements
The authors are grateful to IDRIS, CINES, Université de Strasbourg and GNR PARIS for computer resources, and to Etienne Engler for assistance.
1 The P-P distance was constrained at 10.8 Å via an harmonic potential and a force constant of 20 kcal.mol−1Å−2.
2 Note that in the present simulations, interactions are represented by 1-6-12 pairwise addititive potentials without accounting for electronic reorganization effects (mainly charge transfer and polarization) at short distances. These effects should be of increasing importance when the charge of the counterion increases, i.e. from H3O+ to UO22+ and Eu3+. Cooperative polarization effects should strengthen the stability of dimers by increasing, among others, the polarity of bridging water molecules and of water ligands in UO2(H2O)52+ or Eu(H2O)93+ hydrates.