Electronic fine structure calculation of [Gd(DOTA)(H<sub>2</sub>O)]<sup>–</sup> using LF-DFT: The zero field splitting

Florian Senn; Lothar Helm; Alain Borel; Claude A. Daul

doi:10.1016/j.crci.2011.10.008

Résumé

Zerfo field splitting plays an important role in determining the electron spin relaxation of Gd(III) in solution. We understand the ZFS as an effect depending on the f electron structure and treat it in the framework of ligand field-density functional theory (LF-DFT). We apply this theory to calculate the ZFS of [Gd(DOTA)(H₂O)]⁻ from first principles, having an insight concerning the contributions determining the ZFS.

1 Introduction

Paramagnetic Gd(III) induces a strong NMR-relaxation enhancement of neighboring water protons and therefore a wide application of Gd(III) exists as contrast agent in medical magnetic resonance imaging (MRI) [1]. The free Gd(III) ions are very toxic, so binding them to stable complexes is a prerequisite for their in vivo use [2]. The macrocyclic ligand DOTA (1,4,7,10-tetraaza-1,4,7,10-tetrakis (carboxymethyl) cyclododecane) [3] has been developed for such a complexation and nowadays [Gd(DOTA)(H₂O)]⁻ is one of the most successful MRI contrast agents [3]

The efficiency of the induced NMR relaxation is, among others, influenced by the spin relaxation of the Gd(III) unpaired electrons. Since zero field splitting plays a dominant role in the electron spin relaxation of Gd(III), one “[...] can say, that for Gd(III) ions, the structure and dynamics of the electronic density of the chelate framework surrounding the metal determine the ZFS and therefore the electron spin relaxation rates in solution.” [4]. Electron spin relaxation in gadolinium complexes is described by a static ZFS modulated by rotational motion of the compound and by a transient ZFS modulated by inharmonic distortions of the coordination environment of Gd(III) [5]. Broadly speaking, the efficiency of the induced NMR relaxation is influenced by the exchange rate of water molecules bound to the metal with the bulk solution (linked to electrostatic and steric effects), the rotational correlation time (linked to the size of the molecule) and the spin relaxation of the Gd(III) electrons [1].

It is generally accepted that the main cause of the electron spin relaxation of the Gd(III) electrons is ZFS, namely splitting of the ⁸S_7/2 ground state multiplet in the absence of an external magnetic field, due to small admixtures of states with other L and S vlaues into the L = 0 ground state through the ligand field and spin-orbit coupling. To minimize the static ZFS and therefore electron spin relaxation it is important to know how non-spherical coordination influences ZFS. A quantitative understanding of the structural causes of the ZFS can therefore provide useful clues for the design of contrast agents with improved electronic properties.

“The magnetic and spectroscopic properties of the lanthanide ions depend on the f electron structure, which is generally understood in the framework of a model where the f orbitals are considered shielded from the chemical environment.” [6]. The ZFS is therefore very small in Gd(III) complexes and difficult to assess with quantum chemical calculations [7]. We can obtain a description of the multiplet structure and energies of states in this given basis of f spinors using the ligand field density functional theory (LF-DFT) [8]. LF-DFT is a DFT-based LF model, mapping the energies of the microstates of the whole LF-manifold from DFT single-determinant calculations to the corresponding LF microstates, thus allowing us to estimate all Racah and LF-parameters in a least square sense. With these parameters, and including spin-orbit coupling, a LF calculation is then performed. This theory has already been adapted to a smaller Gd(III) system, [Gd(H₂O)₈]³⁺ [6].

We calculate in this work the static ZFS of [Gd(DOTA)(H₂O)]⁻ from first principles and give an insight concerning contributions that determine its amplitude. The Gd³⁺ ion in the DOTA complex is nine coordinated with four nitrogen atoms and four carboxylate oxygens forming an anti-prismatic cage (Fig. 1). On top of the square formed by the four oxygens is a water molecule coordinated. In aqueous solution the complex exists in two diastereoisomeric forms called square-antiprismatic (SA) ans twisted square antiprismatic (TSA) [9]. In the SA form, which is the major isomer found for [Gd(DOTA)H2O)]⁻ in aqueous solution, the complex is in the Δ(λλλλ) (Fig. 1) or Λ(δδδδ) enantiomeric form.

Fig. 1
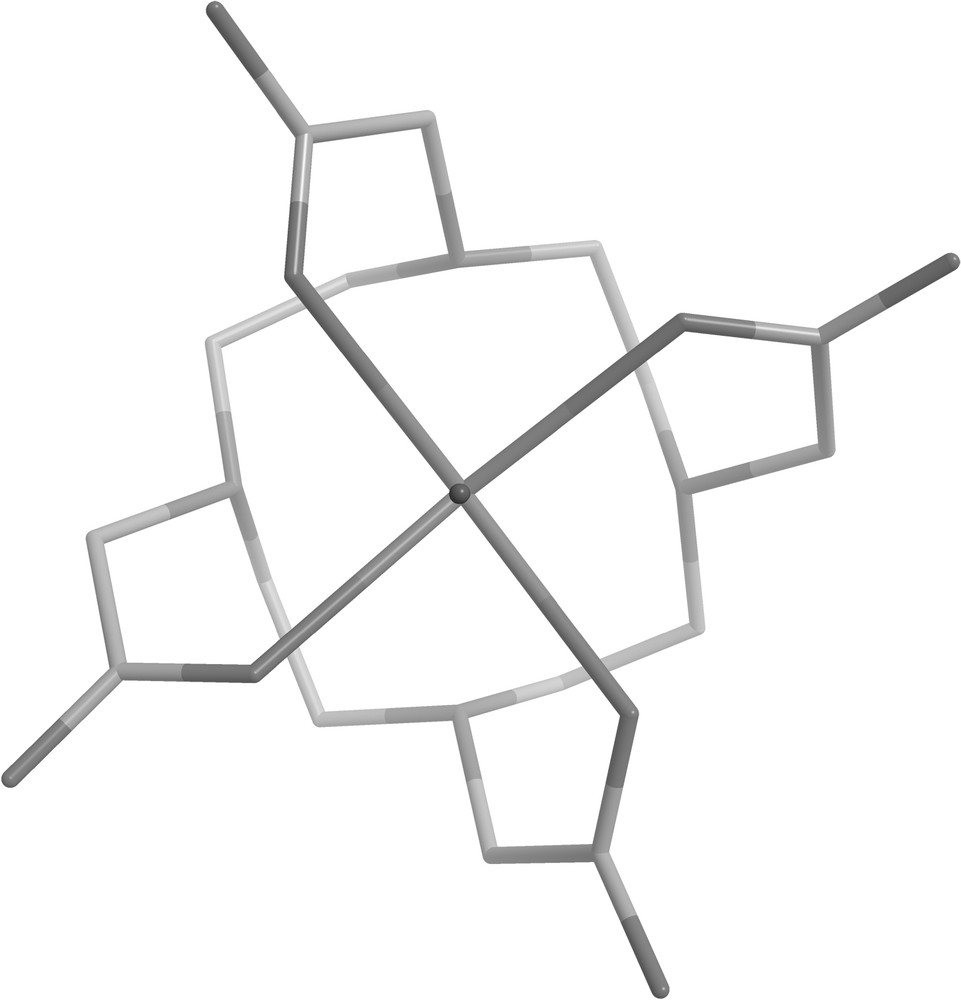
Schematic representation of [Gd(DOTA)(H₂O)]⁻ in the SA geometry used for the calculations; the coordinated water molecule (with the Gd-O(H₂) axis pointing out of plane) has been omitted for clarity.

2 Theoretical part

As in reference [6], we use a model where the f orbitals are considered shielded from the chemical environment and so we work in a ligand field approach considering the complex as an ‘ionic molecule’. Thus, we interpret the magnetic and spectroscopic properties of the lanthanide ions as depending on the f electron fine structure. We perform all calculations starting in the basis of the 14 gadolinium 4f spinors. Our Ansatz is for the Ligand Field part the same as in reference [6] and so we give here just a short survey of the most important parts and underline the essential differences. We write the general Hamiltonian acting upon the atomic metal f orbitals, which besides the central potential of the nucleus looks like in reference [6] as

H = H_{ER} + H_{SO} + H_{LF}

(1)

where the three terms correspond to the inter-electron repulsion (

H_{ER}

), the spin-orbit coupling (

H_{SO}

) and the ligand field (

H_{LF}

), respectively.

The matrix elements for each of these operators can be expressed in a basis of single Slater determinants, $Ψ_{μ} = ϕ_{1} \times \dots \times ϕ_{n}$ , where $ϕ_{i}$ is a single-occupied spinors and n ist the number of f electrons. So our 14 gadolinium 4f spinors span a set of $(\begin{array}{c} 14 \\ 7 \end{array})$ single Slater determinants, which we use as our new working basis, that is μ = 1, 2,..., 34332. We can write the matrix elements of $H_{ER}$ as linear combinations of a limited number of reduced two-electron electrostatic matrix elements. Working with f electrons, we use the four Slater-Condon parameters F_k (k = 0,2,4,6). With this convention, the matrix elements of the inter-electron repulsion are given by

\begin{array}{c} 〈Ψ_{μ} | H_{ER} | Ψ_{ν}〉 & = \sum_{g, h, i, j = 1}^{n} A_{ER}^{g h i j} 〈ϕ_{g} ϕ_{h} | H_{ER} | ϕ_{i} ϕ_{j}〉 & (a) \\ = \sum_{g, h, i, j = 1}^{n} \sum_{k = 0,2,4,6} A_{ER}^{g h i j} C (k, g, h, i, j) F & (b) \end{array}

(2)

“The real coefficients A_ER combine the Coulomb and exchange matrix elements in an orbital basis set according to Slater's rules. The C (k, g, h, i, j) are products of the vector coupling coefficients for real spherical harmonics.” [6]. Using Slater's rules, the spin-orbit coupling elements are simply given by

〈Ψ_{μ} | H_{SO} | Φ_{ν}〉 = ζ \sum_{i \in μ, j \in ν}^{n} A_{SO}^{i j} 〈ϕ_{i} | l \cdot s | ϕ_{j}〉

(3)

where

ζ = 〈\frac{1}{r} \frac{d V}{d r}〉

is the spin-orbit coupling constant. The ligand field terms are described by linear combinations of the matrix elements of the effective ligand field potential V_LF acting upon the f orbitals. The 7 × 7 matrix is reduced to a set of 28 independent matrix elements by the Hermicity of the ligand field Hamiltonian

〈Ψ_{μ} | H_{LF} | Ψ_{ν}〉 = \sum_{i \in μ}^{7} \sum_{j \in ν}^{i} A_{LF}^{i j} 〈f_{i} | V_{LF} | f_{j}〉 .

(4)

In order to get all the required parameters for equation (1), we use LF-DFT [8]. LF-DFT is a DFT-based LF model, mapping the energies of the microstates in the LF-manifold from DFT single-determinant calculations to the corresponding LF microstates, thus allowing us to estimate all Racah and LF-parameters in a least squares sense. We stress out that thereby the matrix elements $〈f_{μ} | V_{L F} | f_{ν}〉$ and two electron integrals F_k are all obtained from the same mapping over the whole manifold of the $(\begin{array}{c} 14 \\ 7 \end{array})$ single Slater determinants.

This is different from the approach used in reference [6], where the seven molecular orbitals with dominant 4f character were projected onto the reduced basis set of the atomic f orbitals and therefore the matrix elements of V_LF were calculated from the Kohn-Sham molecular orbitals energies ɛ^KS and from the projected coefficients $c_{μ} = 〈f_{μ} | ϕ^{KS}〉$ , so that

〈f_{μ} | V_{LF} | f_{ν}〉 ≃ \sum_{i = 1}^{7} c_{μ i} c_{ν i} \in_{i}^{KS} .

(5)

3 Results and discussion

From the calculated ZFS energies in Table 1, one can see that the ⁸S_7/2 ground state, corresponding to the molecular ⁸A₁ ground state, splits into four Kramers doublets when including both LF and spin orbit interaction.

[A]	[B]	[C]	[D]	[E]	[F]	[G]	[H]	[I]	[Exp]
0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
0.6	0.8	0.7	0.5	0.7	0.4	0.5	0.4	0.6	0.11
1.8	2.5	2.0	1.5	2.0	1.3	1.5	1.2	1.9	0.19
3.6	4.8	3.9	3.0	3.9	2.6	3.0	2.5	3.7	0.23

Experimentally, an axial static ZFS was observed with a parameter D = −0.019 cm⁻¹ [4] and therefore a maximal multiplet splitting of 0.23 cm⁻¹, which is an order of magnitude smaller than our results, see Table 1. Furthermore, we note that the sign of the D-tensor leads to relative splittings of 2D, 4D and 6D between the four Kramers doublets ( ${(\frac{3}{2})}^{2} - {(\frac{1}{2})}^{2}$ , ${(\frac{5}{2})}^{2} - {(\frac{3}{2})}^{2}$ and ${(\frac{7}{2})}^{2} - {(\frac{5}{2})}^{2}$ ), predicted out of the formula, e.g. [10]:

\begin{array}{c} H' & = S . D . S & (a) \\ = D (S_{z}^{2} - \frac{1}{3} S (S + 1)) + E (S_{x}^{2} - S_{y}^{2}) . & (b) \end{array}

(6)

with the D tensor,

D = \frac{3}{2} D_{z}

E = \frac{1}{2} (D_{x} - D_{y})

, (6b) refers to prinipal axes. Our results are obtained, as explained in the theoretical part, from a mapping, where DFT calculations are involved. Thus it is not surprising that they are tributary to the chosen approximate functional (Table 1). For our common LF-DFT calculations, GGA/PW91 [11] (Computational details) proved to give satisfactory results and therefore we keep it here for our discussion of parameters influencing the ligand field theory, even if in our calculations the obtained results are not in best agreement with the experimental findings.

As one can see from Eq. (1), there are three different contributions to the ZFS in our model, which we analyze now separately.

The influence of the spin-orbit coupling ζ is shown in Table 2. We observe that spin-orbit coupling has a strongly positive effect on the zero field splitting energy. Like in reference [6], we used a value calculated with XATOM [12], with the difference of taking into account relativistic effects (mass-velocity and Darwin corrections) and obtain ζ = 1183 cm⁻¹, which is small than ζ = 1283 cm⁻¹ in reference [6]. This is significant, considering that a 10% inrease in the spin-orbit coupling already leads to a 20% larger value for the total splitting of the ⁸S_7/2 ground state with respect to the reference value.

1ζ	0.5ζ	0.9ζ	1.1ζ	1.5ζ
0.0	0.00	0.00	0.00	0.00
0.6	0.08	0.45	0.81	1.93
1.8	0.23	1.33	2.43	6.23
3.6	0.46	2.64	4.81	12.25

As one can see from the results shown in Table 3, a linear variation of the electron repulsion acts in the opposite direction. This behaviour is of course expected if we consider that zero field splitting is due to the mixing of higher excited states into the ground state through the ligand field. A stronger electron repulsion will increase the relative energies of these excited states, and thus decrease the amount of mixing that takes place. Nevertheless, we note that the interplay of 2nd, 4th and 6th order electron repulsion parameters makes the situation more complex than this simple picture. If one compares our presently obtained values F₂ = 417.8, F₄ = 39.1, F₆ = 0.2, to the experimental values obtained for the Gd(III) ion in aqueous solution, F₂ = 384, F₄ = 91.8, F₆ = 5.8 [13], it is obvious that we overestimate F₂ and especially F₄, while our value of F₆ is significantly smaller.

1ER	0.5ER	0.9ER	1.1ER	1.5ER
0.0	0.00	0.00	0.00	0.00
0.6	4.33	0.83	0.46	0.18
1.8	15.81	2.52	1.37	0.54
3.6	30.09	4.97	2.71	1.06

Both the spin-orbit coupling and the electron repulsion show the same behaviour as in reference [6]. We observe the same trends and the magnitude of the effect relative to the changes is similar.

This cannot be confirmed for the ligand field contribution, where we obtain a nearly linear behaviour for a modest change (Table 4). In order to probe the influence of the LF parameters on the ZFS pattern, we inverted their sign. We observed that the splitting pattern of the ⁸S_7/2 ground state is reversed in this case. The cordination of the ligands has the effect of breaking the spherical symmetry and therewith splitting the 2J + 1 degeneracy of the free ion state [14]. Thus this mentioned change in the splitting pattern is not suprising from a LF point of view, where the ligands and their influence on the potential give the LF parameters.

1LF	0.2LF	0.5LF	0.9LF	1.1LF	1.5LF	5LF	−1LF
0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
0.6	0.1	0.3	0.5	0.7	0.9	4.1	1.7
1.8	0.4	0.9	1.6	2.0	2.8	11.2	2.9
3.6	0.7	1.8	3.2	4.0	5.5	21.2	3.4

Together with the assumption in Eq. (5), this shows the importance of the qualitative order of Kohn-Sham orbitals in the DFT calculation. It has been showed by Zbiri et al. [15] that the qualitative behaviour of the Kohn-Sham Molecular-Orbitals with dominant Gd f-character and therefore corresponding to f-orbitals can be corrected using a so-called embedding potential. But as one can see out of Table 1 this does not influence our result significantly. We have to note that due to technical reasons we had to use Eq. (5).

Both, the method used in reference [6] to estimate the LF splitting (5) as well as the present approach going over full ligand field manifold yield similar results concerning the splitting energies.

While the method and functional of our DFT calculations have a clear influence on the amplitude of the overall zero field splitting of the ground state, we obtain with all of them the same qualitative splitting, corresponding to a D > 0: As well for the splitting, as for the single determinant coefficients. The first one obeys nicely to the relations ${(\frac{3}{2})}^{2} - {(\frac{1}{2})}^{2}$ , ${(\frac{5}{2})}^{2} - {(\frac{3}{2})}^{2}$ and ${(\frac{7}{2})}^{2} - {(\frac{5}{2})}^{2}$ (and thus 2D, 4D and 6D), predicted in Eq. (6b). Furthermore, the coefficients of the single determinants with all parallel spin (and therefore S_z = ± 7/2) contribute to each state of the highest Kramers doublet for the ground state splitting, i.e. $c_{S_{z} = - 72}^{2} + c_{S_{z} = + \frac{7}{2}}^{2} ≃ 0.9$ (slightly depending on the calculation).

This is in contrast to the experimental result D < 0 of Benmelouka et al. [4].

4 Computational details

All DFT calculations were performed using the Amsterdam Density Functional (ADF) program package (release 2009.01 or, if COSMO model is used, release 2004.01) [16]. For all calculations using the generalized gradient approximation (GGA), this has been done using it in form of Perdew-Wang 91 (PW91) [11] for exchange-correlation functionals. Local density approximation (LDA) calculations have been done using the Vosko-Wilk Nusair (VWN) [17] for exchange-correlation functionals. As a non-representative example for hybrid functionals B3LYP has been used as implemented in ADF with VWN5 in B3LYP functional (20% HF exchange) [18]

For all calculations an all-electron ZORA triple-ζ Slater type orbital (STO) plus one polarization function (TZP) basis set has been used. Relativistic effects have been taken into account through ZORA, implemented in ADF.

LF-DFT calculations were used to obtain the energies and wave functions of the ⁶⁴Gd 4f spinors using Matlab [19] scripts ([8], [20]), XATOM program [12] for the spin-orbit calculation, respectively. The value for the effective nuclear charge by a 4f electron, Z_eff = 24.014, has been taken from reference [21]. Of course for the spin-orbit coupling constant ζ, the approximation $ζ_{n l m} ≃ ζ_{n l} ≃ orf ζ_{n l}^{atom}$ (orf: orbital reduction factor) has been used.

The geometry of [Gd(DOTA)(H₂O)]⁻ has been taken from the published crystal structure [22] and therefore the SA isomer in its Δ(λλλλ) form (=A1, M1 in [23]). The DFT calculations correspond to a single molecule in vacuum. To mimic solvent effects and to deal with the negative charge, COSMO model (with water as solvent, Van der Waal radii from reference [24] in adf2004.01, standard values in adf2009.01, respectively) has been used for all calculations.

Calculations for the pure Gd³⁺ atom have been made using GGA/PW91.

GGA/PW 91 is known to overestimate bond lengths in geometry optimizations, hence geometry for corresponding calculation has been optimized with LDA/VWN [17] starting from the mentioned crystal structure.

For point-charge calculation we replaced all ligand-atoms by their point charges. The values of the point charges are Mulliken point charges of the corresponding atom of a [Gd(DOTA)(H₂O)]⁻ calculation in vacuum, also using GGA/PW91.

For the embedding potential, the PW91k [25] approximant has been used. The density of the embedding potential has been calculated replacing the gadolinium atom in [Gd(DOTA)(H₂O)]⁻ by a point charge of +3, wherefore we skiped the ‘freeze-and-thaw’ cycle [15].

5 Conclusion

In this work, we calculated the ZFS of [Gd(DOTA)(H₂O)]⁻ from first principles. While the absolute error is in the order of cm⁻¹, the relative one is still a full order of magnitude. In reference [6] “[...] the full ab initio parameters (SO, ER and LF) lead to a significant overestimation of the ground state splitting.”, where “[...] the final splitting is one order of magnitude larger than with Carnall's SO and ER parameters.” [6]. In our work we obtained the same order of error, an overestimation of the ZFS by an order of magnitude and confirm the approach using eq. (5) for getting the ZFS.

As all used methods result in the same splitting pattern and a D > 0, therefore neither the obtained wavefunctions nor the eigenvalues are really suitable. We look at this findings with regret, as they would have led us to use these values to obtain further properties for calculations involving 4f elements like done for 3d transition metals as for example in references [26] and [27].

In a first calculation, the use of an embedding potential does not show any improvement. But for further investigations this reduction to an atomic problem promisses an improvement, not least as it has already been mentioned in reference [15], that the splitting energies “[...] obtained from embedding calculations are clearly superior to that derived from supermolecular Kohn-Sham results for the whole system”. Newman and Ng give in reference [28] an explanation using Angular Overlap Theory. This theory should be consistent with our approach using an embedding potential, but it's validity for our case of [Gd(DOTA)(H₂O)]⁻ has first to be proved in a future study.

Acknowledgements

We acknowledge the help of Mr Tomasz A. Wesolowski and his group concerning our calculations using the embedding potential.