1 Introduction
A previous report announced the discovery of some heretofore never described hydronium cations [1]. Two of these hydronium cations shared the same composition (H11O5+) but they have totally different geometrical structures, one acyclic and the other cyclic. In the Cambridge Structural Database [2–5]1 they are indexed as BEXFEQ [6] (acyclic) and IYEPEH [7] (cyclic). In as much as the X-ray diffraction data which gave rise to these structures was considered to be reliable, an obvious question to ask is “which of the two as described by the crystallographic coordinates is more stable”. Also, if the molecular geometry is optimized by quantum mechanics, what would happen? In a related investigation, we discovered an acyclic, a new hydronium ion, never before described. Its REFCODE in CSD is NEBDII [8] and its composition is H15O7+. A unique feature of BEXFEQ and NEBDII is that they are both acyclic and highly asymmetric in that, in both cases, the H3O+ species is flanked by a water molecule on one side, and by a long chain on another side. These features are displayed in Figs. 1–3. Once more, the question is “what is the relative stability of these species and what happens when their structures are optimized?” The answers to those questions are supplied below. The structures of BEXFEQ, IYEPEH and NEBDII, as they are found in the crystalline state are pictured in Figs. 1–3.
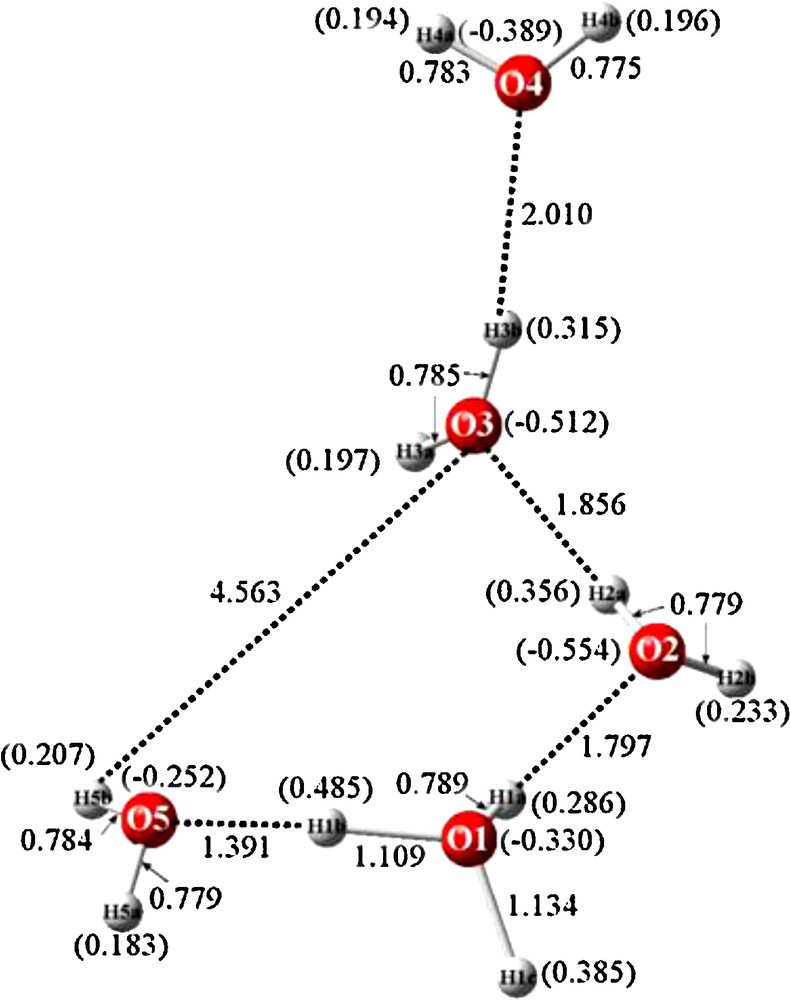
Bond distances of crystal structure and calculated Mulliken charges (in parentheses) for BEXFEQ H11O5+.
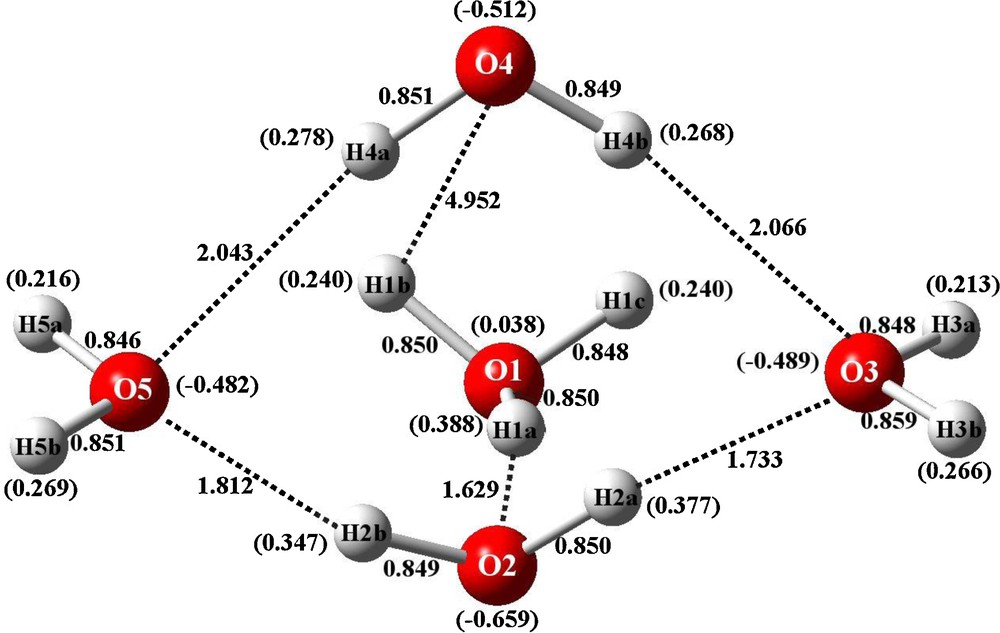
Bond distances of crystal structure and calculated Mulliken charges (in parentheses) for IYEPEH H11O5+.
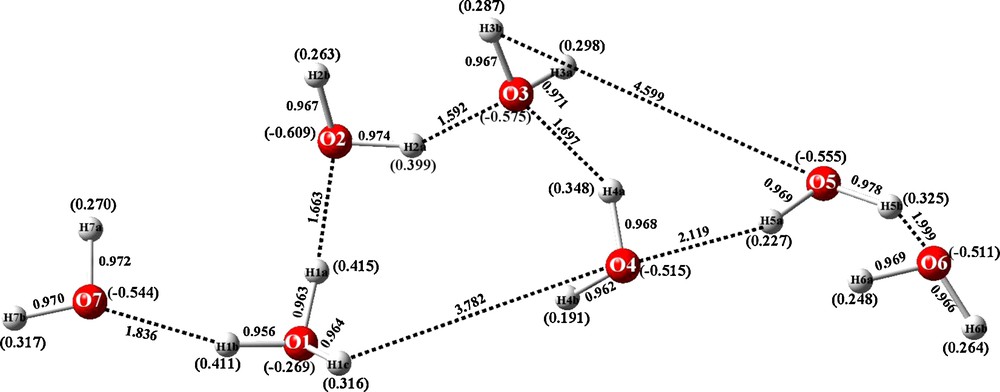
Bond distances of crystal structure and calculated Mulliken charges (in parentheses) for NEBDII H15O7+.
A result of energy optimizing the NEBDII molecule starting from its crystal structure was that it folded into a structure resembling a cube which is missing one corner. This suggested to us the procedure of simply adding one water molecule to the missing corner and then seeking the optimized geometry from that starting point. This starting geometry was therefore obtained from the theoretical geometry of NEBDII, and thus differs from all other optimizations of this paper which begin from experimental crystallographic geometries (Figs. 1–3). The results of optimizing from an assumed cubic-like guess were unexpected and are displayed in the results below, and discussed in the conclusions of our paper.
2 Method of theoretical calculations
The Hartree–Fock method is perhaps the best-known and most thoroughly understood type of ab initio quantum calculation. It is simple in that the Hartree–Fock wave function is a Slater determinant of orthonormal molecular orbitals whose molecular energy is a minimum. An inherent independent particle model, such as the Hartree–Fock model, chemistry does not account for the correlation energy, which in absolute terms is quite small, although it is nonetheless chemically important. We have used instead density functional theory (DFT) [9,10], which in its modern form dates from the Hohenberg–Kohn theorem [11] and its numerical implementation in the Kohn–Sham equations [12]. Here too the wave function is a single Slater determinant of orbitals, but these Kohn–Sham orbitals have the defining characteristic of delivering, in principle, the exact electron density. The Kohn–Sham equations are similar to the Hartree–Fock equations, but they are simpler because they contain only local potentials. The Kohn–Sham potential contains a representation of both the exchange and the correlation effects, of which the latter are inherently absent from the Hartree–Fock equations. Although the exact Kohn–Sham exchange correlation potential is unknown, in practice it is fitted to empirical data and theoretical constraints and is approximated rather successfully. Because of their simplicity and inclusion of correlation, DFT Kohn–Sham equations are the equations for the calculation adopted here.
These calculations were completed using Gaussian 09 [13] on a parallel computing grid running the GNU/LINUX operating system. The calculation methods used included AM1, LSDA, and B3LYP, all of which are implemented in Gaussian 09. AM1 is a semi-empirical method for the quantum calculation of molecular electronic structure. It is an empirically parameterized neglect of differential diatomic overlap integral approximation. AM1 results may be used as the starting points for energy optimizations by more accurate approximations. The local spin density approximation (LSDA) is a DFT method, which incorporates a combination of a Slater exchange functional and a uniform electron gas correlation functional [14], used in this paper together with DGDZVP basis set. The DGDZVP is a fairly large basis set, used in DGauss [15], including double-zeta valence plus polarization functions. It can deliver fairly accurate energies when used together with DFT calculations [15]. The LSDA method is faulted for delivering more stability to chemical bonds than is warranted, but it may be used as a good starting method to discover optimized structures. All of the final optimizations of this paper have been obtained using the chemical model DFT/B3LYP/6-311+G(2d,2p), the same level at which the electron densities were obtained. The DFT/B3LYP approximation is the most widely used density functional method for calculating molecular structures. The density functional upon which it is based is a sum of two parts, an empirical Becke 3 parameter exchange contribution [16], and a Lee-Yang-Parr correlation contribution, which is patterned upon the correlations of Colle and Salvetti [17]. The Gaussian basis set 6311+G(2d,2p) combined with B3LYP is expected to be especially suitable for representations of the hydrated molecular systems of this paper [18].
The relative accuracy of theoretical results mentioned above is presumed to increase in the direction from AM1 to LSDA to B3LYP. Most of the energy optimizations of this paper have proceeded in that same direction starting from either an experimental (Figs. 1–3) or theoretical (Fig. 6) geometry. The vibrational frequencies of all the structures so optimized have been calculated to check whether they are energy minima.
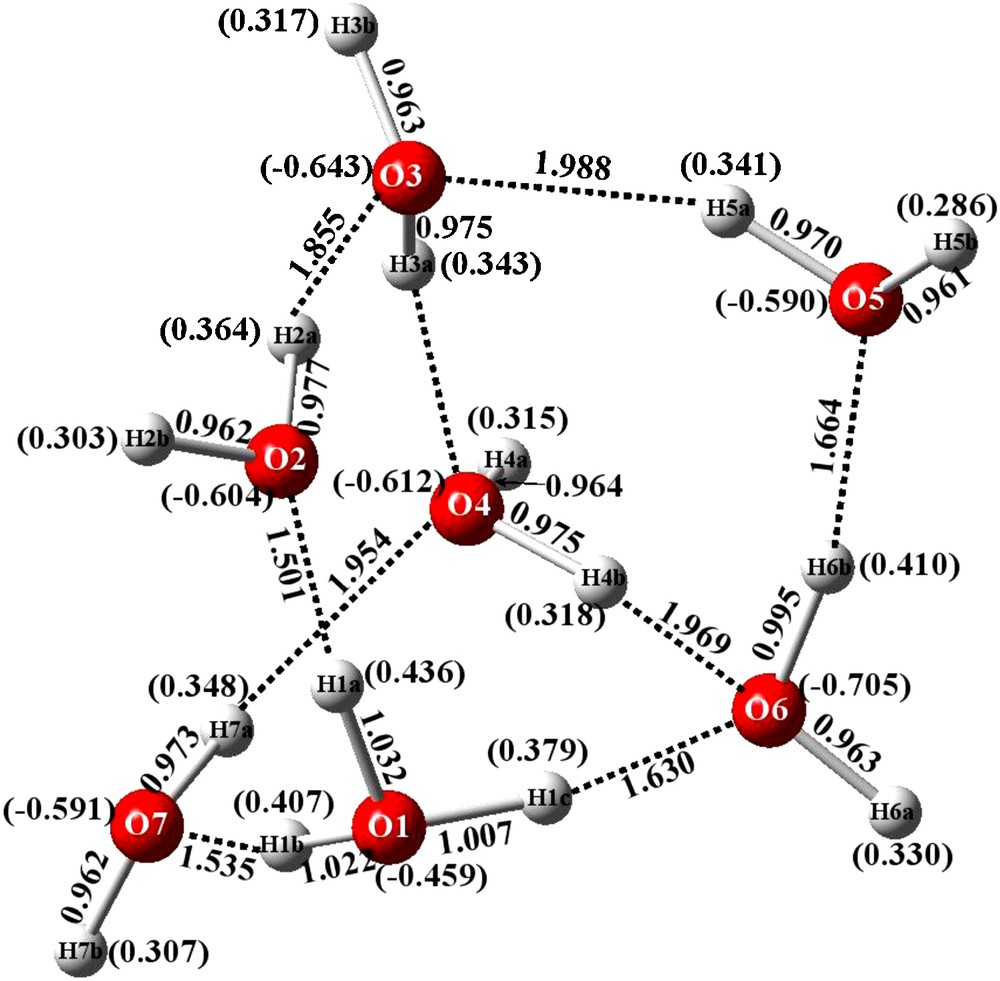
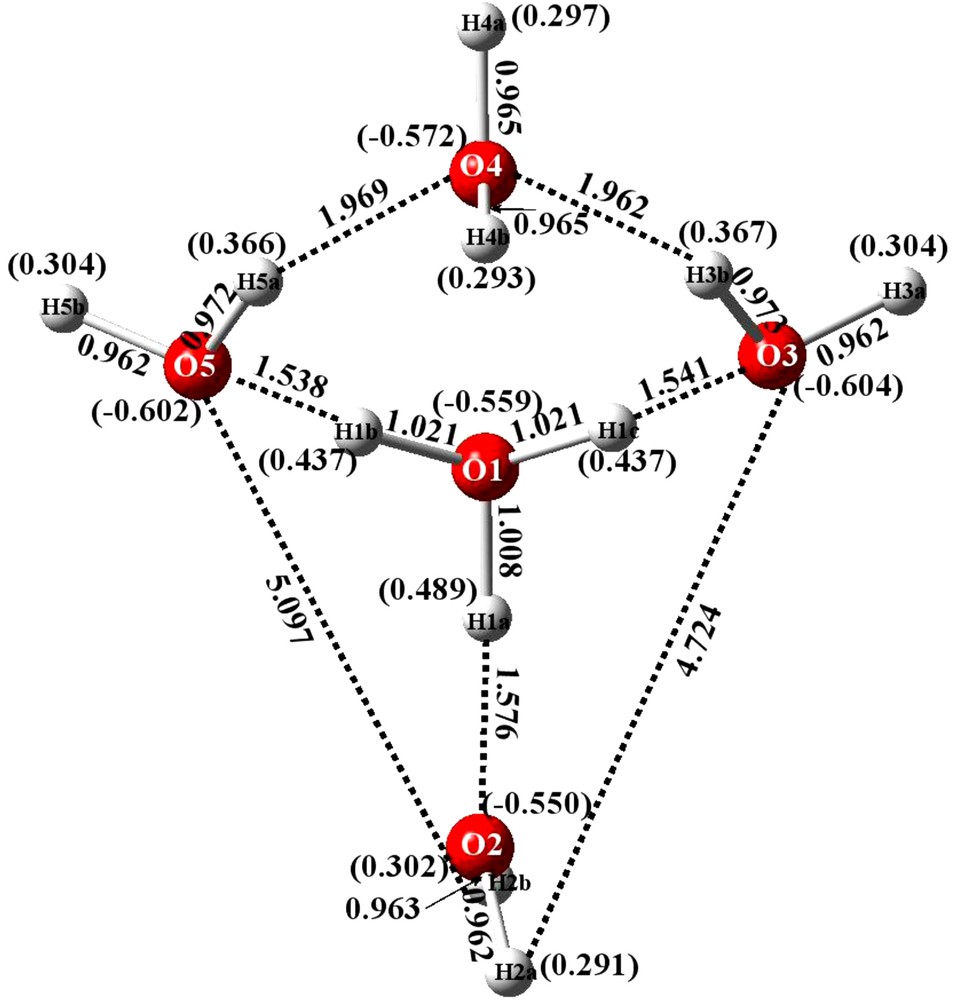
Bond distances of energy optimized structure and Mulliken charges (in parentheses) for NEBDII H15O7+.
3 Results
All of the Figs. 4–7, Tables 1–3 of this article contain results calculated within the chemical model B3LYP/6-311+G(2d,2p) using the computer program Gaussian [13]. We have calculated the molecular energies of the three clusters discussed above, viz., IYEPEH, BEXFEQ, and NEBDII. Their energies at the coordinates of their crystal structures were calculated first. Secondly, the geometry of each cluster was optimized without constraints and its final total energy obtained at the optimized geometry. These energy values, crystal and optimized, along with the respective total binding energies are listed in Table 1. Binding energies are defined as the difference between the sum of the energy, at the optimized geometries, of the isolated water molecules H2O and isolated hydronium ions H3O+ and the energies of the clusters (these results are listed at the bottom of Table 1, together with the formula used to calculate the binding energies). The optimized hydronium ions are seen to be structurally stable with binding energy (in atomic units, au), –0.1462, –0.1400, and –0.1860 for IYEPEH, BEXFEQ, and NEBDII, respectively.
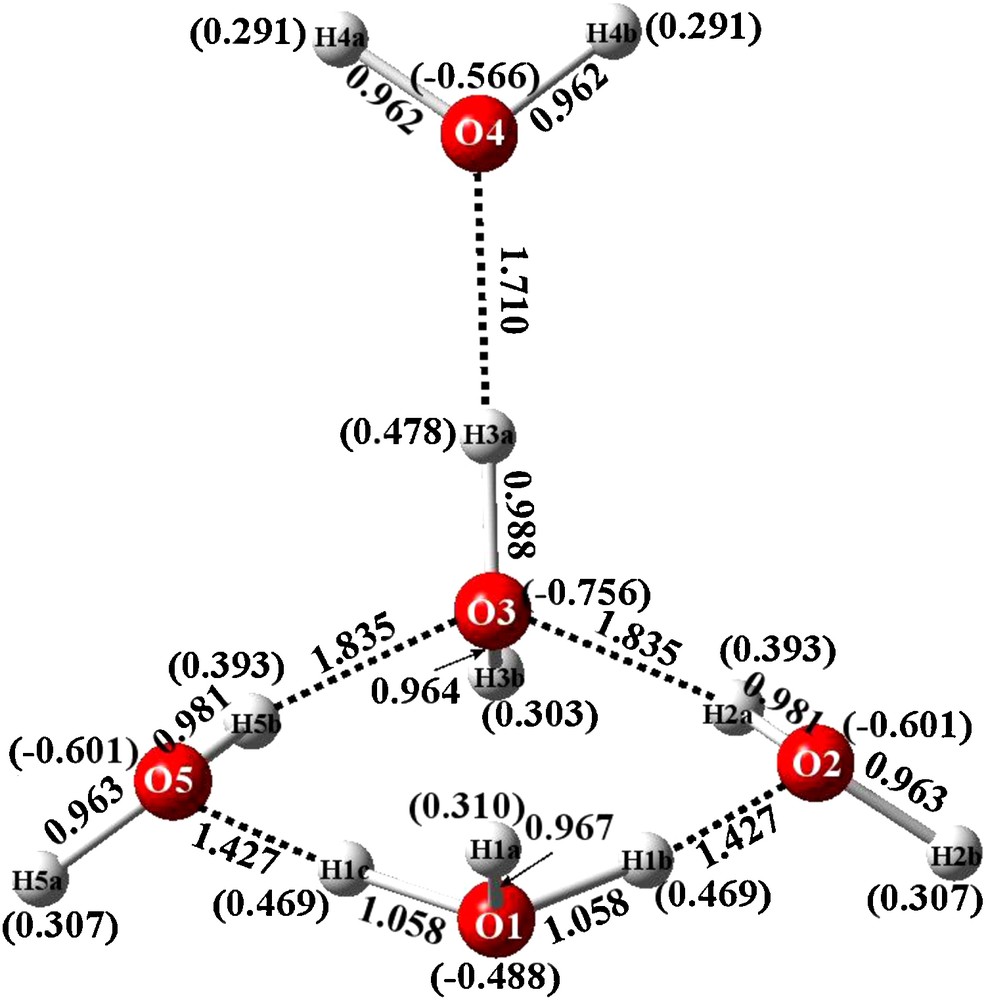
Bond distances of energy optimized structure and Mulliken charges (in parentheses) for BEXFEQ H11O5+.
Bond distances of energy optimized structure and Mulliken charges (in parentheses) for IYEPEH H11O5+.

Two views of the cubane-like structure of H17O8+ energy optimized at the B3LYP level. (a): geometrical distances before (in parenthesis) and after optimization; (b): Mulliken atomic charges before (in parentheses) and after optimization.
Calculated [B3LYP/6-311+G(2d,2p)] energies at crystal and optimized geometries, and binding energies of two isomeric H11O5+ molecules and an H15O7+ complex.
| H11O5+ | H11O5+ | H15O7+ | ||||
| IYEPEH Crystal | Optimized | BEXFEQ Crystal | Optimized | NEBDII Crystal | Optimized | |
| Energies (au) | –382.4535 | –382.7280 | –382.2127 | –382.7218 | –535.5680 | –535.6918 |
| Binding energya (au) | –0.1462 | –0.1400 | –0.1860 |
a
3.1 Optimized geometry and charge distributions of BEXFEQ
The optimized structure of BEXFEQ is cyclic, as can be seen in Fig. 4. The hydronium cation includes atom O1 and partakes in a four-membered ring with an exocyclic water residing above one of the ring water molecules. The question arises as to whether or not this is an unexpected result. But, in retrospect, this result accords with previous related experience. In a recent paper [19], the energies of two isomeric hydronium cations, one containing a four-membered ring while the other consisted of a six-membered ring, were compared. In both cases, for the crystalline structure and also for the optimized structure, the four-member ring system was preferred.
3.2 Optimized geometry and atomic charges of IYEPEH
The results obtained with IYEPEH are consistent with the above remarks. That is, energy optimization of the structure results in retaining the cyclic observed crystallographic structure, as shown in Fig. 5. This time, though, H3O+ is found in the 4-membered ring with an exocyclic water above H3O+ fragment ion.
3.3 Optimized geometry and atomic charges of NEBDII
Finally, optimization of NEBDII is also consistent with previous observations. Crystallographically, the cation is acyclic (Fig. 3) but, the optimized structure is cyclic and consists of a group of four fused rings. One is a five-membered ring, and three are four-membered arrays as seen in Fig. 6. The hydronium ion is shown including atom O1. The current results form a consistent group, within themselves, and also with those of reference [19].
Table 2 (supplementary information) includes a listing of the coordinates for each of the clusters discussed above. The coordinates for each cluster are given for their crystal and optimized geometries starting from the crystal structures as initial guesses. The reader can find in Figs. 1–6 the Mulliken atomic charges of the three clusters. The charges are given for both the crystal and optimized geometries. The vibrational frequencies of the optimized structures have been calculated and are all real, consistent with the mathematical characteristic which proves a given optimized geometry actually corresponds to an energy minimum, a necessary condition for molecular stability.
3.4 Energy optimized geometry and atomic charges of H17O8+
The energy optimized structure of H17O8+ [20–22] is depicted in Fig. 7. We obtained this structure differently than in the cases of the previous hydronium ion clusters. In each of those cases, we began with a known crystal structure and proceeded by energy optimizing the structures. But in this last case, we proceeded without a beginning crystal structure. Instead, we noticed that the optimized structure of H15O7+ (Fig. 6) took on the appearance of a cube with one corner of the cube missing. Therefore, we speculated that the symmetry of the cube could be completed by placing the oxygen of a water molecule at the empty vertex of the H15O7+ molecule. We inserted a water molecule at the empty corner and then let the hydronium ion cluster energy optimize following the same procedure as occurred for the molecules we have discussed above. The cubic figure shown in Fig. 7 together with the coordinates shown in Table 3 (supplementary information) is the energy optimized result.
The cubic cluster of Fig. 7 has a B3LYP total energy of –612.1288 au and a binding energy of –0.1610 au. This elevated binding energy and its high symmetry makes this cluster most interesting. For this reason, this particular cluster is examined more closely in terms of its electron density distribution and the associated topological properties and bond paths.
The quantum theory of atoms in molecules (QTAIM) [23–25] provides an unambiguous indicator of chemical bonding termed the “bond path”. A bond path is a line of maximal electron density joining the nuclei of atoms generally recognized as chemically bonded [26–28]. The bond path and its topological properties provide a rigorous quantitative characterization of bonding interactions, as has been reviewed elsewhere [26–28]. The bond path concept is thus of importance in characterizing the new bonded structure of this interesting hydronium ion cluster.
Fig. 8 displays views of the energy optimized molecular geometries along with molecular graphs calculated at the B3LYP/6-311+G(2d,2p) level of theory (the level used to obtain most other results in this paper). Vibrational frequency calculations at the B3LYP level revealed the presence of two small magnitude nearly degenerate imaginary frequencies [Im(ν)/cm−1 = –253, and –239] which may hint at the possible breakup of the cube in two different reaction channels, and that the structure lies on a second order saddle point on the potential energy hypersurface (see an example in reference [29]). However, the corresponding LSDA frequency calculation resulted in all real vibrational frequencies, suggesting that the small imaginary frequencies at the B3LYP level are possibly a numerical artifact.
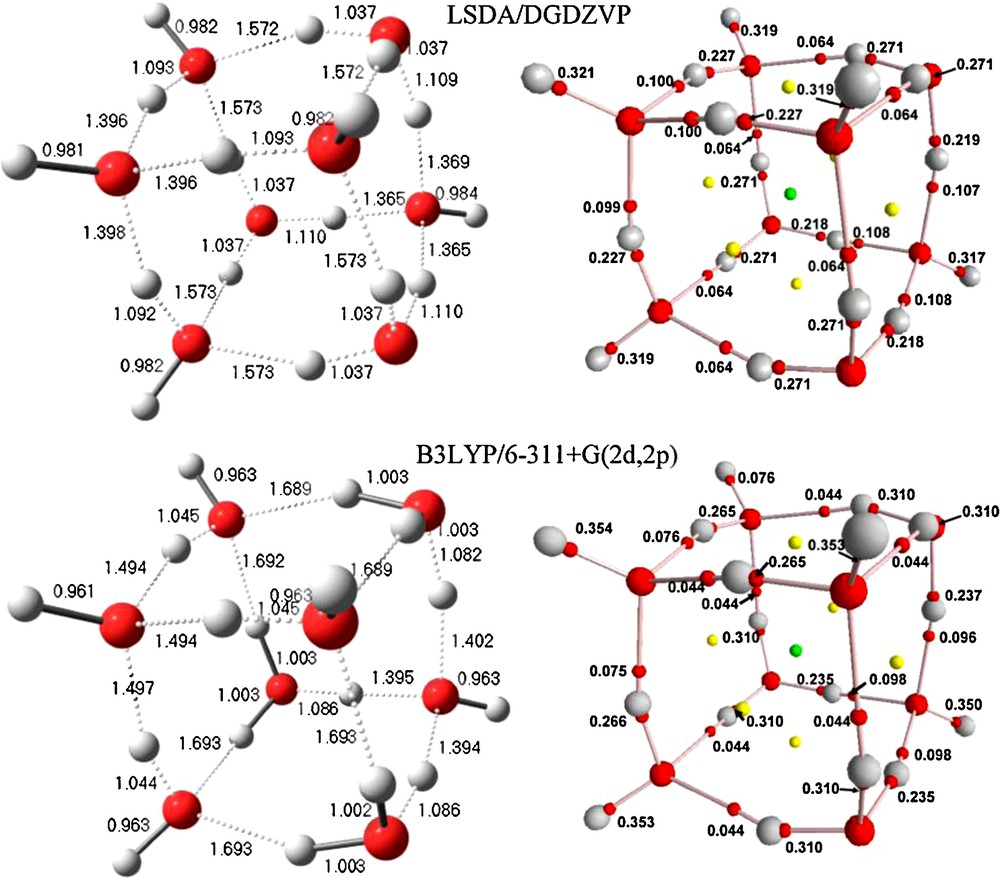
(Left) a ball-and-stick representation of the energy optimized geometry (bond lengths in Å) of the hydronium cation and (right) the corresponding molecular graphs at the two DFT levels indicated on the drawing, respectively. The positions of oxygen nuclei are denoted by large red spheres, those of the protons by large grey spheres. In the molecular graphs (right), the lines connecting the nuclei are the calculated bond paths the small red spheres placed on each of which denote the positions of the bond critical points (BCP). The yellow dots appearing near the centroid of each 8-membered ring is the ring critical point (RCP), the point of minimum density in the plane of the ring but maximal along a line perpendicular to the ring at this point. Finally, the green dot in the centroid of the cubical structure is a cage critical point (CCC) and it denotes the location where the electron density is a minimum in a volume completely enclosed by ring structure, as in this case. The numerical values are those of the electron density at the labeled bond critical point (ρBCP) in atomic units (1 au = 1 electron/bohr3). Masquer
(Left) a ball-and-stick representation of the energy optimized geometry (bond lengths in Å) of the hydronium cation and (right) the corresponding molecular graphs at the two DFT levels indicated on the drawing, respectively. The positions of oxygen nuclei are denoted ... Lire la suite
Fig. 8 also displays views of the molecular graphs at approximately the same orientation as the corresponding ball-and-stick representation of the molecular geometry. These graphs have been obtained at the fully relaxed geometry at the given level of theory followed by a QTAIM topological analysis of the resulting electron density using AIM2000 [30]. The graph displays the position of the nuclei and the lines of maximal electron density linking them, namely, the bond paths which collectively constitute the molecular graph. The positions of the bond critical points (BCPs) are depicted on the plots as small red dots lying on the bond paths. The positions of the ring and cage critical points, respectively abbreviated as RCP and CCP, are also indicated on the molecular graphs. A count of the number of each of the three types of critical points (BCP, RCP, CCP) and of nuclear critical points (NCC) must satisfy the Poincaré-Hopf relationship. For isolated finite (non periodic) systems, if n indicates the number of the subscripted type of critical point, then this relationship is [23]:
| (1) |
In the case of H17O8+, and as can be counted from Fig. 8, this equation is clearly satisfied:
| (2) |
Fig. 9 displays another view of the H17O8+ cluster that emphasizes its cubic geometry, along with bond lengths calculated at both the LSDA and the B3LYP levels of theory in Å. The bond length of the OH bond in an isolated H2O is 0.975 (0.961) Å LSDA (B3LYP), with corresponding electron densities at the bond critical point of 0.334 (0.373) au, respectively. As can be seen from Figs. 8 and 9, in the cubic cluster H17O8+, and with the exception of the four peripheral hydrogen atoms that stick out of the cubic arrangement, all of the other 13 hydrogen atoms are bonded to two oxygen atoms: On one side with a strong/short bond and on the other with a weaker (but significant) hydrogen bond. All covalent OH bonds linking each of the 13 “internal” hydrogen atoms, each to its bound oxygen atom, is typically 1.1 Å in length (significantly longer than in the case of the isolated water molecule) and also exhibits a reduced electron density at the BCP to the extent of 0.25 au (instead of the value in isolated H2O of 0.33 au). The hydrogen bond is short (bond lengths ≈ 1.4–1.6 Å) and a density at the bond critical point ρBCP falling ≈ 0.05–0.1 au, typical of strong hydrogen bonds. The strong covalent OH bonding to the four “external” hydrogen atoms presents nothing unusual.

A view of the energy optimized geometry of the cubic H17O8+ cluster. Based on bond lengths, this cluster can be considered to consist of the following stoichiometry [H3O+]3[H2O]3[OH−]2. (Bond length, in Å, are obtained from two DFT levels of theory, namely: (a) LSDA/DGDZVP, and (b) B3LYP/6-311+G(2d,2p). The reader can see that the qualitative picture that emerges is similar and hence the two levels of theory reinforce our confidence in the presented results (see text).
There is, thus, a clear-cut demarcation between the two modes of bonding within the cubic structure, and one can, thus, identify strongly-bonded species within the cluster whether on purely geometrical grounds or on the basis of BCP values. This grouping of moieties results in the following stoichiometry of the H17O8+ cluster:
| (3) |
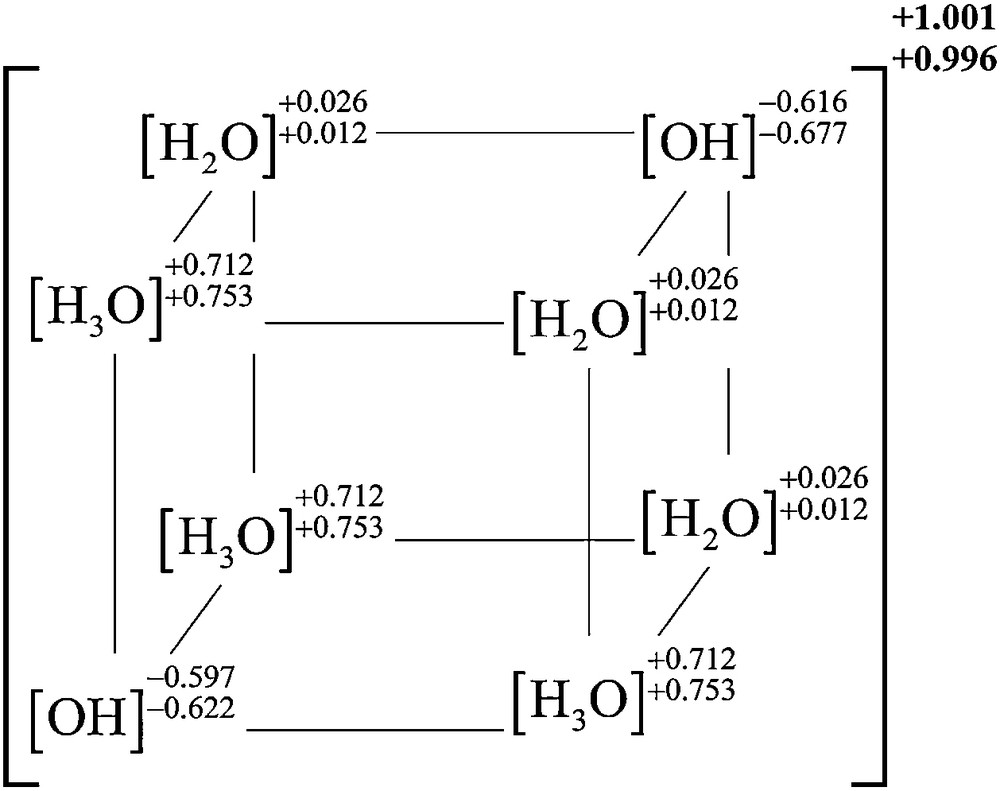
The structure of the cubic H17O8+ ([H3O+0.7]3[H2O]3+0.1[OH–0.6]2) cluster along with the integrated QTAIM charges (in atomic units) of the indicated species calculated at the LSDA/DGDZVP level (top) and B3LYP/6-311+G(2d,2p) level (bottom). The cluster consists of three hydronium cations, two hydroxyl radicals, and three (electrically neutral) water molecules. The overall charge of the cluster is indicated outside of the parentheses – where the slight departure from the ideal value of +1 is the result of small cumulative numerical integration errors.
It is thus, very interesting to note that the presence of a hydronium cation in this cluster induces the seven (originally neutral) water molecules to undergo significant exchanges of protons. The hydronium cation loses 30% of its charge and induces a significant polarization in the remaining water molecules, which results in the creation of two other similar H3O+ cations, but with only 70% of the charge on an isolated hydronium cation. The formation of two hydronium cations from the original group of seven water molecules is accompanied with the creation of two hydroxyl radicals, but these as well do not carry the charge they would have in vacuum, since each only has negative charge magnitude of approximately 0.6 au. The other “intact” water molecules receive a small partial charge which collectively accounts for the remaining difference between the charge carried by the three hydronium cations and the two hydroxyl anions. The overall arrangement of the three constitutive species of the cube can be depicted diagrammatically as in Fig. 10.
4 Discussion and conclusions
The existence of new hydronium ion structures is a matter of some interest. These include the hydronium cations (H11O5+) of two totally different geometrical structures, one BEXFEQ [6] (acyclic) and one IYEPEH [7] (cyclic). By calculating their molecular energies, the issue of which of the two structures is most stable has been settled. As indicated in Table 1, IYEPEH is more stable than BEXFEQ in the crystal structure, and also by 0.0062 [au] (3.9 [kcal/mol]) calculated with the optimized structures. Another hydronium ion cluster of interest is that of NEBDII [8] (H15O7+). This cluster has also been examined in this work at the crystal and optimized geometries, as listed in Table 1. All three optimized structures are seen to be quite stable as judged by their binding energies. It seems that crystal forces are capable of stabilizing hydronium ions in geometries which differ considerably from their gas phase energy optimized geometries. The stability of these latter geometrical arrangements indicates, however, that they may be found in solution with possibly some likelihood.
This article reports new stable structures of hydronium ion clusters. Those proceeding from known crystal structures are pictured in Figs. 4–6 together with their calculated bond distances and (Mulliken) atomic charges. All of these optimized clusters of the hydronium ions adopt ring structures.
Finally, the empty corner of the optimized H15O7+ structure induced us to place a water molecule into that corner. Upon energy optimization, Fig. 7, a cubic structure is found, which is one of the most interesting hydronium ion clusters studied, in this paper. Except for the cubic structure, in the other cases studied, the smallest hydronium ion unit H3O+ is discernable as a single fragment within the total molecule, designated as in the chemical formula H3O+(H2O)n, where the subscript n indicates a count of a discrete number of water molecules. But in the cubic structure, the positive charge is distributed rather evenly over all the protons’ basins, and instead of a single discernable H3O+ fragment, there are three such equivalent species. The unexpected occurrence of two more hydronium species is counterbalanced by the (also) unexpected occurrence of two hydroxides. The fully optimized hydronium ion H17O8+ adopts a structure analogous to that of cubane. The formation of this cubane-like structure involves 13 internal hydrogen atoms, each of which is shared between two oxygen atoms – on one side involving a strong H…O hydrogen bond and on the other a weakened covalent OH bond (as determined from an examination of bond lengths and the electron density concentrated at the respective bond critical points). Thus, the interaction of a hydronium ion with seven neutral water molecules induces proton transfers resulting in the species
Acknowledgements
The research reported in this article was supported by funding from the PSC-CUNY, & the Naval Research Lab. (L.M.), the Office of Naval Research (L.H.), and (C.F.M.) acknowledges financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC), Canada Foundation for Innovation (CFI), and Mount Saint Vincent University. (S.W.) thanks RCMI and MBRS-NIH grants to Hunter College, for their support.
1 The Cambridge Structural Database (CSD), The Cambridge Crystallographic Data Centre (CCDC) (http://www.ccdc.cam.ac.uk/) (2012).


